Hippocampal Place Fields Maintain a Coherent and Flexible Map Across Long Time Scales

Summary

To provide a substrate for remembering where in space events have occurred, place cells must reliably encode the same positions across long time scales. However, in many cases place cells exhibit instability by randomly reorganizing their place fields between experiences, challenging this premise. Recent evidence suggests that, in some cases, instability could also arise from coherent rotations of place fields, as well as from random reorganization. To investigate this possibility, we performed in vivo calcium imaging in dorsal hippocampal region CA1 of freely moving mice while they explored two arenas with different geometry and visual cues across eight days. The two arenas were rotated randomly between sessions, and then connected, allowing us to probe how cue rotations, the integration of new information about the environment, and the passage of time concurrently influenced the spatial coherence of place fields. We found that spatially coherent rotations of place field maps in the same arena predominated, persisting up to six days later, and that they frequently rotated in a manner that did not match that of the arena rotation. Furthermore, place field maps were flexible, as mice frequently employed a similar, coherent configuration of place fields to represent each arena despite their differing geometry and eventual connection. These results highlight the ability of the hippocampus to retain consistent relationships between cells across long time scales and suggest that, in many cases, apparent instability might result from a coherent rotation of place fields.

eTOC Blurb

Kinsky et al. demonstrate that hippocampal place fields in mice maintain a stable configuration across long time scales under low attentional demand. Coherent rotations of place fields frequently occurred between sessions, indicating that in some cases instability commonly attributed to global remapping might actually be a map rotation.

Introduction

The well-established place coding properties of hippocampal neurons [1,2] are generally thought to provide a neural mechanism for remembering where events occurred in an environment [3]. A key assumption underlying this mechanism, supported by early studies in single neurons in the rat, is that the spatial map composed of place cells remains stable over long periods [4,5]. While these and other studies have demonstrated that place cells in mice and rats can remain remarkably stable across long time-scales [4,6,7], other recent studies have demonstrated that place cells in mice are unstable across days in the absence of strong attention trained to specific landmarks. This manifests as global remapping: a complete reorganization of place fields when the animal is re-exposed to the familiar environment [8–10]. Still, other recent findings suggest that this instability might instead reflect the use of different cues across days, in the form of a reorientation (or rotation) of the same overall map during the re-exposure. These studies have shown that, when disoriented, rodents utilize the geometry of an environment rather than single visual cues to reorient [11–13]. Recent studies extended this result by demonstrating that spatially tuned cells in the hippocampus and medial entorhinal cortex concurrently reorient their firing locations in accordance with the animal’s behavior during reorientation to environmental geometry [14,15] (see [16] for review). Thus, while in many cases global remapping underlies place field instability observed upon repeated exposures to an environment, in other cases this instability might result from the coherent re-alignment of the spatial map to a cue undetected by the experimenter. To address how this re-alignment behaves longitudinally, we employed in vivo calcium imaging in dorsal CA1 while mice explored two distinct environments that were rotated daily for eight consecutive days. This allowed us to investigate the stability of spatial maps in each environment, the differences in maps between environments, responses of maps to cue rotations, and their evolution over time. Additionally, we connected the environments on two days to investigate whether this would disrupt the configuration of established maps.

By leveraging the strength of calcium imaging to identify large numbers of the same neurons across multiple recording sessions, we were able to compare ensemble spatial firing patterns during exposures to the same and different environments across days. We predicted that comparisons between sessions in the same environment would yield largely the same map, and that comparisons between sessions in different environments would reveal global remapping. We hypothesized that place field maps within the same arena would either rotate with the arena in accordance with the mouse’s use of arena cues for orientation, or globally remap consistent with the observation of long-term instability during open-field recordings [8]. While some comparisons produced results consistent with these predictions, in most cases we found that mice utilized a coherent map: a configuration of place fields that maintain the same angle and distance from one another. Consistent with recent studies [14,15], however, we found that coherent maps frequently rotated in a manner that does not utilize specific arena cues or larger room cues for orientation. Maps were flexible as mice frequently employed a coherent map between the two different arenas while simultaneously modulating activity in a subset of cells to discriminate between them. Arena connection caused the neuronal population to temporarily sharpen discrimination between the arenas without permanently disrupting coherent maps in each arena afterward. Finally, coherent maps persisted in a significant proportion of the neuronal population across all eight days of the experiment despite constant turnover of cells actively participating in the ensemble each day. These findings highlight that in many cases place fields can maintain structure across days, and suggest that while instability frequently indicates global remapping it may sometimes also reflect the re-orientation of a coherent map to different cues.

Results

Experimental Outline

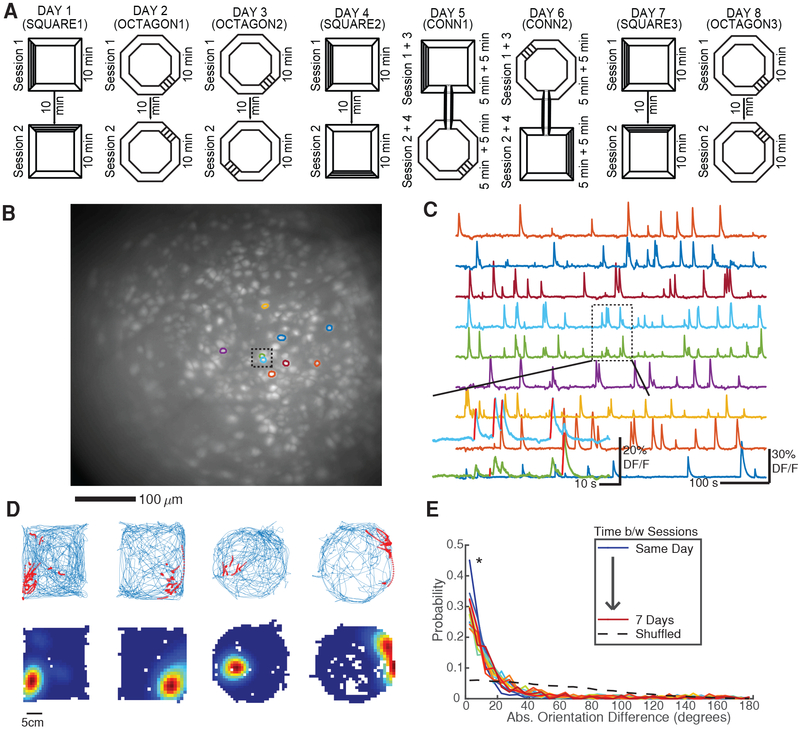
Mice (n = 4) explored two arenas – a square and an octagon of equal area, painted the same color and with distinct visual cues (horizontal/vertical black stripes) – over the course of eight days (Figure 1A). The arenas were surrounded by curtains designed to obscure any extra-maze (room) cues and heighten the salience of arena cues that the mice might use for orientation. Initially, each mouse underwent two 10 minute sessions per day in the same arena with the arena pseudorandomly rotated 90 degrees clockwise or counterclockwise between sessions. This repeated until the mouse experienced two days in each arena (SQUARE1–2 and OCTAGON1–2). On days 5/6 (CONN1/CONN2) the arenas were connected via a previously hidden hallway and the mouse explored the combined arena in one continuous session broken up into alternate 5 minute blocks in each arena. On the last two days (SQUARE3 and OCTAGON3) the arenas were again separated.

Figure 1: Experimental setup.

A) Mice explored two different arenas across 8 days. SQUARE1–3 and OCTAGON1–3: Two 10 minute sessions with arena pseudorandomly rotated between sessions. CONN1 and CONN2: Arenas were connected with a hallway and mice were given two 5 min blocks in each in alternating fashion.

B) Maximum projection from a recording session with nine neuron ROIs overlaid. Dashed box indicates two closely spaced ROIs. See also Figure S1.

C) Example calcium traces for ROIs highlighted in A. Dashed box demonstrates the ability of the cell/transient detection method to disambiguate crosstalk between neighboring neurons by assigning putative spiking epochs (red lines) to the appropriate neuron.

D) Example place fields. Top: Blue = mouse’s trajectory, red = calcium event activity. Bottom: Occupancy normalized calcium event rate maps. Red = peak calcium event rate, Blue = no calcium activity.

E) Distribution of ROI orientation (major axis angle) differences between sessions for one mouse. Since the majority of ROIs are elliptical, the small changes in ROI orientation shown here indicate that neurons are properly registered between sessions. *p < 1e-28 all session-pairs, one-sided Kolmogorov-Smirnov test vs shuffled.

We employed in-vivo calcium imaging with a microendoscope to track neural activity in the dorsal CA1 region of the hippocampus via virally expressed GCaMP6f [6,17]. Using this technique we recorded large numbers of neurons (n = 194 to 548 per 10 minute session, Figure 1B, Figure S1) from which we extracted calcium traces, identified putative spiking epochs (Figure 1C), and created calcium event rate maps exhibiting the well-established spatial tuning of hippocampal neurons [1,2] (Figure 1D). The number of neurons remained steady throughout the experiment (p = 0.73, Kruskal-Wallis ANOVA for SQUARE1–3 and OCTAGON1–3). Additionally, we were able to reliably identify the same neurons across all 8 days of the experiment (Figure 1E, Methods). These results establish the feasibility of tracking calcium events in large numbers of spatially tuned neurons across all eight days of the experiment.

Coherent Maps Predominate in the Hippocampus

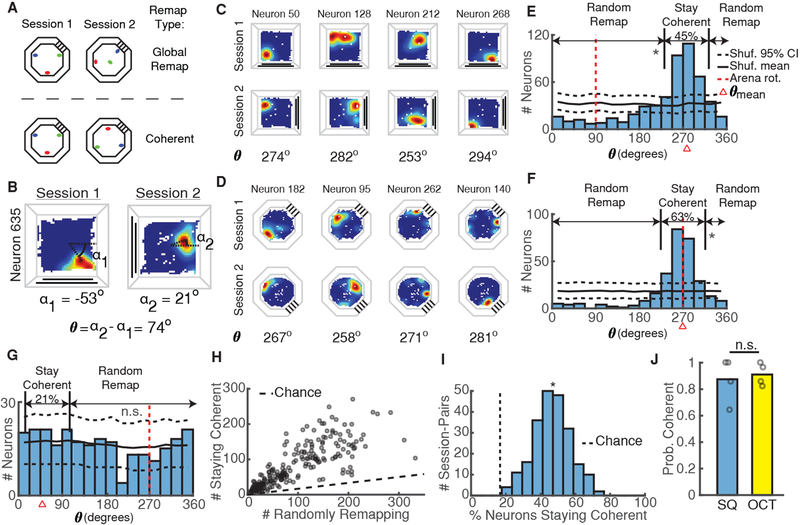
Does instability of hippocampal spatial representations in mice always result from a random reorganization of place fields, or might place fields retain structure between sessions? As noted in the introduction, instability observed in previous studies during random foraging [18,19] could result from global remapping of place fields (Figure 2A, top). Alternatively, we hypothesized that the trial-by-trial rotations of place fields observed in a recent study [14] might persist over longer time scales (Figure 2A, bottom). In agreement with this study, we likewise found that place fields frequently rotated together coherently between sessions by maintaining the same distance and angle from each other (Figure 2C–D). To quantify the level of coherent rotation we identified the angle θ that each neuron’s place field rotated between sessions (Figure 2B) and plotted the distribution of θ for each session-pair (Figure 2E–G). In line with a previous study [20], we reasoned that if a significant proportion of place-fields maintained a coherent structure and rotated the same amount, then the distribution of θ should exhibit clustering around the mean angle of the distribution, θ_mean (Figure 2E–F). On the other hand, if all the place fields independently reorganized between sessions (global remapping), we would observe a uniform distribution of θ (Figure 2G). We applied this approach to every pair of sessions in the same arena, regardless of arena rotation and day lag between sessions, and found that mice predominantly utilized a coherent spatial map to represent each arena (Figure 2J); nonetheless, some mice still exhibited global remapping between sessions in a minority of cases (percentages for each mouse: 36%, 14%, 0%, and 0% in square, 21%, 7%, 14%, and 0% in the octagon). We obtained similar results using an alternative analysis method to identify place field rotations (Figure S2).

Figure 2: Coherent Maps Predominate in the Hippocampus.

A) Schematic of null hypothesis of global remapping between sessions (top) and alternate hypothesis of coherent mapping between sessions (bottom) using three example place fields (red, green, blue). In global remapping, all place fields randomly reorganize. In coherent mapping, place fields retain the same configuration but may or may not rotate.

B) The place field rotation between sessions (θ) was calculated as the difference between α₁ and α₂, the angle from the arena center to the occupancy bin with the peak calcium event rate in session 1 and session 2, respectively. See also Figure S2.

C) Calcium event rate maps from 4 simultaneously recorded neurons between two square arena sessions demonstrating coherent mapping. The rotation of each neuron’s place field is indicated at the bottom. Note that all rotations are close to 270 degrees.

D) Same as C, but for two octagon sessions from a different mouse.

E) Distribution of place field rotations for the coherent session-pair shown in C demonstrates clear clustering of rotations. Percentages of neurons staying coherent (|θ − θ_mean| < 30) or randomly remapping (|θ − θ_mean| >= 30) are indicated above the distribution. Black solid/dashed lines = shuffled mean and 95% CI. Red dashed line = arena rotation. Red triangle = θmean. *p < 0.001, shuffle test.

F) Same as E, but for the coherent session-pair shown in D. *p < 0.001.

G) Same as E-F but for an infrequent session-pair exhibiting global remapping. p = 0.15.

H) Number of neurons staying coherent versus randomly remapping for all session-pairs. Dashed line indicates numbers expected by chance.

I) Percentage of neurons whose place fields stay coherent for all mice/session pairs. *p = 1.8e-108 (t-test vs chance).

J) Probability of using a coherent map in each arena. Open circles indicate proportions for each mouse. p = 1, Wilcoxon rank-sum test.

Are coherent rotations an all-or-nothing phenomenon, or does some of the population deviate and randomly remap between sessions? To address this, we defined a place cell as coherent if its field’s rotation matched that of population mean within a 30 degree range (|θ – θ_mean| < 30); we designated the remaining cells as randomly remapping. Using these classifications, we found that approximately half the population typically stayed coherent between sessions (Figure 2H–I). These results combined confirm previous studies finding a mixture of stability and dynamics in hippocampal neurons [6,7] and extend their work to a two-dimensional, non-goal directed task.

Coherent Maps Do Not Consistently Utilize Arena Cues For Orientation

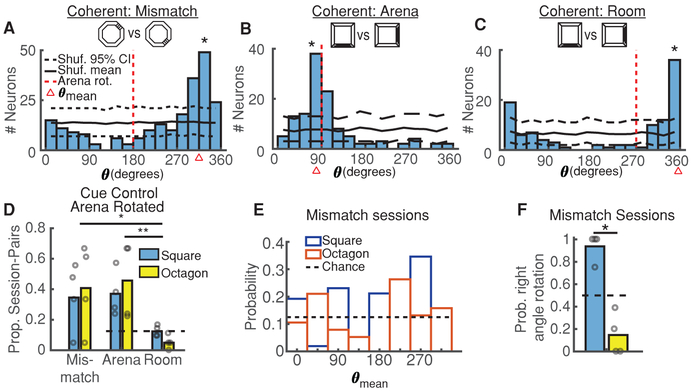
Previous studies have found that CA1 place fields will move together to follow the rotation of visual cues within an arena [21], indicative of the mice using these cues to orient themselves. Alternatively, a recent study [14] demonstrated that disoriented mice frequently ignore purely visual cues and instead utilize geometry to concurrently reorient themselves and their place field maps. In support of this work, in many cases where two sessions shared a coherent spatial map, place fields rotated incongruously with arena cues (Figure 3A). We thus examined the relationship between arena and place field rotations, reasoning that if mice utilized arena cues to orient their spatial map, the rotation of the map (θ_mean) would match the arena rotation (θ_arena) between sessions. Applying this criteria, we found that coherent maps did frequently rotate with the arena (Arena designation: θ_mean ≈ θ_arena, Figure 3B), but just as often rotated in a different direction (Mismatch designation: θ_mean ≠ θ_arena ≠ 0, Figure 3A). One possible explanation of this effect could be that despite our best efforts to minimize extra-maze cues, mice oriented themselves in the larger room (Room designation: θ_mean≈ 0, Figure 3C). However, these session-pairs only occurred at chance levels (Figure 3D), suggesting mice were unable to reliably extract extra-maze cues for orientation. The high prevalence of mismatch session-pairs was consistent within arenas (Figure 3D), and coherent rotations occurred even when the arena was not rotated between sessions (32% ± 24% of session-pairs). Thus, while spatial maps typically remained coherent between sessions, they frequently did not use arena cues for map alignment.

Figure 3: Coherent Maps Do Not Consistently Utilize Arena Cues For Orientation.

A) Session-pair in the octagon arena demonstrating a mismatch between arena and place field rotations (|θ_mean − θ_arena| > 30). Black solid/dashed lines = shuffled distribution mean and 95% CI. Red dashed line = arena rotation. Red triangle = θ_mean. *p < 1/1000, shuffle test. See also Figure 2C,E.

B) Session-pair in the square arena demonstrating control of place field rotations by arena rotations (θ_mean ≈ θ_arena). Same conventions as A. *p < 1/1000. See also Figure 2D,F.

C) Session-pair in the square arena demonstrating a lack of place field rotations (θ_mean ≈ 0), consistent with orientation in the larger room. Same conventions as A. *p < 1/1000.

D) Probability mice orient their place field maps per A-C indicates a high prevalence of mismatch session-pairs. Open circles indicate individual mouse probabilities. Dashed line indicates chance. p = 0.0042, Kruskal-Wallis ANOVA, *p = 0.028, **p = 0.0057 post-hoc Tukey test. All comparisons between square and octagon are not-significant (p > 0.05, Wilcoxon rank-sum test).

E) Distribution of mean place field rotation angles for all square (blue) and octagon (orange) mismatch session-pairs. See also Figure S3.

F) Proportion of mismatch session-pairs with place field rotations at right angles. Same conventions as D. Dashed line indicates chance. *p = 0.014, Wilcoxon rank-sum.

If mice utilize the geometry of the room to orient their spatial maps [14,15], is the stability of these maps worse in more rotationally uniform arenas? To investigate this, we divided the arena into 45 degree bins and examined the distribution of mean place field rotations between sessions (Figure 3E). We found that almost all mismatch sessions rotated in 90 degree increments in the square whereas few did so in the octagon (Figure 3F). Thus, place field instability resulting from coherent rotations might be exaggerated in more rotationally uniform arenas like the octagon. We found no relationship between the mouse’s initial location/orientation upon entering the maze and the rotation of maps in mismatch sessions (Figure S3). Taken together, our findings extend the work of Keinath et al. [14] by demonstrating that coherent rotations controlled by arena geometry occur even when mice are not intentionally disoriented and are more common in circular arenas. Thus, instability in place fields could result from a rotation as well as from global remapping.

Coherent Maps Generalize Across Different Environments

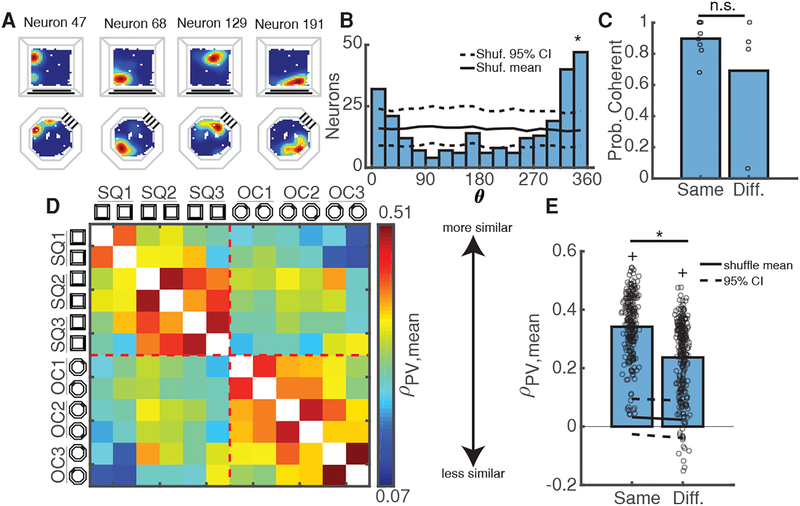
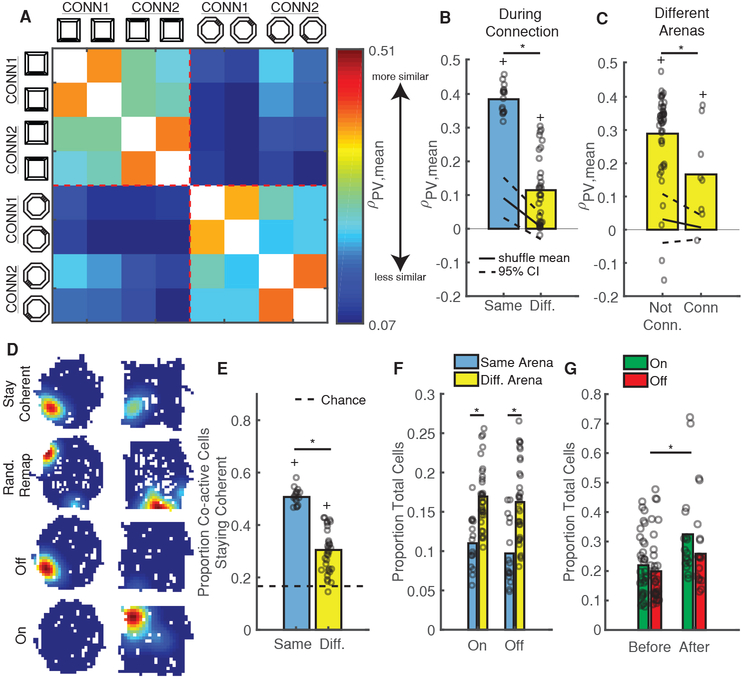
Mice could employ a unique place field map in each arena to reflect differences between them [22,23]. Alternatively, they could utilize a similar map to link common experiences in both arenas [24]. We thus tested if, and to what extent, mice utilized the same map between arenas. Applying the method described above for within-arena comparisons, we found that mice often employed a coherent map to represent both arenas despite their distinct visual and geometric cues (Figure 4A–C). Of course, the use of coherent maps between arenas might also indicate that mice failed to perceive the arenas as different. To address this question, we utilized a population vector (PV) analysis, which is sensitive to changes in both neuron firing location and calcium event rate. The PV analysis allowed us to compare the relative similarity of the neuronal population between visits to different arenas, after taking into account the mean place field rotation of the population. We found that PV similarity between sessions in the same arena was significantly higher than between sessions in different arenas (Figure 4D–E, Figure S4A), indicating that the mice were capable of discriminating arenas at the neuronal level. We obtained similar results using PVs constructed without taking into account place field rotations and using only the maximum event rate for each neuron (p=1.4e-8, Wilcoxon rank-sum test of PV correlations in same vs. different arena), indicating that event rate changes alone were sufficient for the population to distinguish between arenas. Thus, the use of a similar map of place fields between arenas might support the role of the hippocampus in providing a contextual memory that links memories occurring in each arena [24] across space and time [25].

Figure 4: Coherent Maps Generalize Across Different Environments.

A) Calcium event maps from 4 simultaneously recorded neurons indicate place fields stay in the same location between arenas.

B) Distribution of place field rotations for coherent session-pair shown in A. Black solid/dashed lines = shuffled mean and 95% CI. *p < 0.001, shuffle test.

C) Probability of using a coherent map remains high within and between arenas. Open circles = mean for each mouse/comparison-type. *p = 0.48, Wilcoxon rank-sum test.

D) Mean population vector (PV) similarity between all non-connected sessions in each arena, grouped by arena and averaged across mice. Warmer/cooler colors indicate higher/lower PV similarity between sessions. See also Figure S4A.

E) PVs are more similar within arenas than between arenas. Open circles indicate mean PV correlations for all mice/session-pairs. Black solid/dashed lines = shuffled distribution mean and 95% CI. *p = 1.3e-28 Wilcoxon rank-sum test. +p < 1e-37, sign-rank test vs upper 95% CI.

Connecting Arenas Temporarily Sharpens Discrimination

A notable previous study demonstrated that rats initially exposed to two connected arenas discriminated between them to a much greater extent than counterparts who only experienced each arena separately [26], suggesting that rodent’s prior experience in an arena has a strong effect on its subsequent representations therein. We thus wondered if we could also induce arena discrimination via connection, but after mice had already established representations of each arena. In support of this, we observed relatively low PV similarity for repeated trips to different arenas versus trips to the same arena during connection (Figure 5A–B, Figure S4B). Furthermore, PVs on CONN1 and CONN2 exhibited lower similarity than PVs on un-connected days while still staying above chance (Figure 5C, Figure S4A–B). Despite this sharpened discrimination, we found that the probability of utilizing a coherent map was no different than before/after connection (p = 0.34, balanced Kruskal-Wallis ANOVA). In fact, the presence of the hallway seemed to align place fields between arenas (Figure 5D, Coherent neuron), potentially by providing a unique geometric feature that could be used for orientation [14]. In support of this, the mean place field rotation angle between arenas was near zero (0.93 ± 1.38 degrees) during CONN1 and CONN2. Thus, introducing the hallway increased discrimination between the octagon and square arenas by the population without inducing a wholesale shift to global remapping.

Figure 5: Connecting Arenas Temporarily Sharpens Discrimination.

A) Mean PV similarity on connected days, grouped by arena and averaged across mice. Same color scale as Figure 4D. See also Figure S4B.

B) PVs are more similar within arenas (blue) than between arenas (yellow) during connection. Open circles are for all mice/session-pairs. Black solid/dashed lines = shuffled distribution mean and 95% CI. *p = 2.3e-8, Wilcoxon rank-sum test. +p < 0.001, sign-rank test vs upper 95% CI.

C) PV similarity between arenas on un-connected days are higher than on connected days. Same conventions as B. All session-pairs considered were 1 day apart. *p = 0.041, Wilcoxon rank-sum test. +p < 0.04, sign-rank test vs upper 95% CI.

D) Example event rate maps for neurons that either stay coherent, randomly remap, turn “off” (active in 1^st arena, inactive in 2^nd), or turn “on” (inactive in 1^st arena, active in 2^nd) between arenas.

E) The size of the population staying coherent decreases between arenas. Open circles indicate proportions for all mice/session-pairs during connection. Black Dashed black line = chance. *p=2.3e-8, Wilcoxon rank-sum test. +p = 2.3e-8 sign-rank test vs chance.

F) More neurons turn on/off between different arenas than within the same arena. Same conventions as E. *p < 2e-4, Wilcoxon rank-sum test.

G) Arena connection induces a lasting increase in the number of on/off neurons. Same as F but for session-pairs before and after connection. *p = 0.026, Wilcoxon rank-sum test.

Several mechanisms could support simultaneous discrimination and coherent mapping of the two environments. First, the subpopulation of neurons staying coherent (Figure 5D, Coherent neuron) could decrease in size. In support of this, we observed a reduction in the proportion of neurons staying coherent between different arenas versus in the same arena (Figure 5E); as a result, after accounting for rotation, the neuronal population also tended to shift its place fields more between arenas than within arenas (Figure S4F). Second, in line with previous electrophysiological studies [27–29], neurons could modulate their calcium event rate both up and down between arenas (Figure S4C,G) with some neurons highly active in one arena or the other (On/Off Cells in Figure 5D and selective cells in Figure S4G). Indeed, we observed a substantial increase in the proportion of on/off cells occurring between different arenas (Figure 5F). These two mechanisms (reducing the coherent population size and modulating event rate between arenas) were sufficient to support arena discrimination, since PVs formed with only non-selective, coherent neurons failed to distinguish between arenas (Figure S4H). Despite inducing substantial changes on CONN1 and CONN2, however, we found little lasting effect of connection as PV similarity and the proportion of neurons staying coherent remained unchanged in the sessions following arena connection (Figure S4D–E). However, we did observe a small but significant increase in the number of on/off cells from before to after arena connection (Figure 5G), indicating that rate modulation effects [27–29] might provide a mechanism for persistent arena discrimination. These results indicate that arena connection temporarily sharpened discrimination between arenas without inducing substantial long-term changes in the hippocampal representation of each.

Properties of Activity Across Long Time Scales

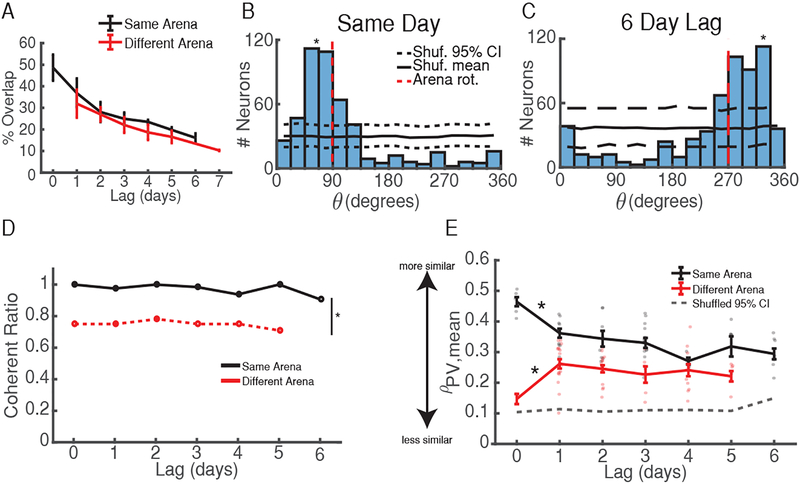
How stable are coherent maps across long time-scales? Based on previous work establishing that population spatial representations evolve over hours to days [6,7,30] we hypothesized that the probability of two sessions utilizing a coherent map would decrease with time. In support of this, and in agreement with previous studies [6,7,31], we found that the percentage of cells reactivated in a later session decreased with time between sessions (Figure 6A). These findings indicate that time influenced which neurons made up the active ensemble. However, θ histograms exhibited significant clustering around one angle for sessions at short and long time lags (Figure 6B–C), indicating that maps stayed coherent even at long time scales. Furthermore, the probability of maintaining a coherent subpopulation of neurons did not change with increasing time lag, remaining high for sessions up to six days apart (Figure 6D). This finding is further supported by PV analyses demonstrating that ensemble similarity remains high up to six days later (Figure 6E), even when putative silent neurons are included in the population (Figure S5A). These results combined indicate that, while neurons continuously dropped in/out of the active population, those that remained active between sessions tended to retain the same, coherent map of place fields at long time scales.

Figure 6: Properties of Activity Across Long Time Scales.

A) % Cell overlap vs. time lag between sessions demonstrates that fewer neurons are reactivated with time. Data are shown as mean ± s.e.m. Black = same arena, red = different arena.

B) θ distribution for session-pair occurring the same day. Black solid/dashed lines = shuffled mean and 95% CI. Red dashed line = arena rotation. *p < 0.001, shuffle test.

C) θ distribution for session-pair occurring 6 days apart. Same conventions as B. *p < 0.001.

D) Time does not influence the probability of maintaining a coherent map between sessions. p > 0.5 Kruskal-Wallis ANOVA for same (black) and different (red) arena session-pairs across time. *p = 6.5e-5 Wilcoxon rank-sum test.

E) High PV correlations at ~θ_mean supports the use of coherent maps at all time lags between sessions. Grey dashed = upper 95% CI from shuffled distribution. Colored dots indicate mean for each session-pair across mice. Error bars = s.e.m. *p < 0.001, Wilcoxon rank-sum test vs upper 95% CI at all time lags. See also Figure S5.

Discussion

While place cells can remain remarkably stable [4,6], the finding of long-term instability in mice place fields by others [8,9] challenges the proposed role of the hippocampus in supporting memory of where events occur in space [18,19], raising the question: how can a randomly changing spatial representation reliably retrieve the appropriate memory of previously encountered arena? We argue that, in some cases, the hippocampus can maintain an intact configuration of place fields, and that the aforementioned instability might sometimes result from a change in orienting this coherent map between arena exposures [14]. Here, we performed in vivo calcium imaging in the mouse hippocampus to record from large numbers of cells across eight days and comprehensively address this hypothesis. We found that within the same arena, place fields largely stayed coherent between sessions (Figure 2), even at long time scales (Figure 6). However, we also occasionally observed global remapping between sessions (Figure 2J). Consistent with previous studies [14,15], coherent maps frequently ignored visual cues for alignment between sessions (Figure 3). Analyses done assuming adherence of spatial maps to arena cues revealed relatively low correlations (Figure S5B). Thus, our data support the view that instability in place fields could stem from either global remapping or from a map orientation change relative to arena cues. These results also build upon previous findings [14] by extending this phenomenon to longer time scales (Figure 6), by demonstrating that coherent rotations exist even when mice are not intentionally disoriented, and by indicating that coherent rotations are not an all-or-nothing phenomenon (Figure 2H–I). Additionally, our results suggest that more rotationally uniform arenas contribute to rotational instability of place fields (Figure 3E–F). Taken together, our work suggests that future studies could perform rotation analyses (e.g. see [20,32,33]) to determine whether global remapping or coherent place field rotations underlie instability, especially in arenas with high degrees of symmetry.

Our results appear to conflict with recent studies [6,7] that found stable place field maps across long time-scales without random, coherent rotations. However, this discrepancy is likely due to task differences: the linear track paradigm employed in the previous studies results in stereotypic, goal-directed behavior that causes highly directional firing of hippocampal neurons [34]. This could also sharpen attention to external cues, thus enhancing place field stability relative to visual cues between sessions [8,10]. Notably, after taking into account coherent rotations of place fields between arenas, our results appear entirely consistent with these studies [6,7], which demonstrate a stable yet dynamic hippocampal spatial representation across long time-scales. Our results thus extend previous work [6,7] to a non-goal directed task in a two-dimensional arena.

Hippocampal place field maps might support contextual learning and memory by providing a neural substrate for triggering the appropriate behavioral response in a given context [35]. However, task demands can also play an important role in dictating hippocampal representations of context [35,36]. Supporting this idea, non-spatial cues can modulate activity of spatially tuned hippocampal neurons when task demands differ in the same physical location [37–39]. Here, we find that the complement also holds: while performing a similar task, mice use the same map to represent different arenas (Figure 4). Of course, this could occur due to poor processing of spatial information by mice (see below). Alternatively, coherent place field rotations might go hand-in-hand with map generalization, since mapping the relationships between spatial locations without regard to specific visual cues could provide flexibility to utilize the same hippocampal map across multiple arenas [40] and group them into similar learning contexts [25]. This idea is supported by recent work demonstrating the ability to artificially reactivate memories by optogenetic stimulation [41–44]. In these studies, the simultaneous stimulation of hippocampal neurons tagged during contextual fear conditioning was sufficient to trigger expression of the fear memory even in a different, neutral arena. Thus, one possibility is that the natural reactivation of the same set of neurons, as would occur when mice utilized the same place field configuration in different arenas, could also elicit a similar behavioral response in each arena. This idea warrants future studies testing whether the degree to which fear conditioned mice utilize a coherent map between shock and neutral arenas predicts how much they generalize freezing to the neutral arena.

Our work appears to directly contradict previous studies demonstrating remapping between arenas [27,28,33] and even within arenas [8,9]. Much of these discrepancies likely result from differences in methodology. The arenas in our study differed only in shape/visual cues, whereas rats in the other studies demonstrating remapping between environments explored arenas that also varied in combinations of color, texture, odor, etc. Consistent with our results, in the one study [28] using arenas with the same color/texture but different shape, rats initially utilized similar place field configurations between arenas. The gradual divergence of place fields between arenas observed in this study over time could result from interference between jointly acquired memories [33] since rats experienced arenas in alternating fashion each day [28], whereas mice in our study explored only one arena per day. The level of attention rodents pay to an environment, as well as what cues rodents attend to, has been shown to influence the stability of place fields [8,10]. Thus, the differences in methodology employed by these studies, as well as ours, could strongly influence how stable place fields remain between sessions by adjusting the level/locus of the rodent’s attention. The heterogeneity in results highlights that future studies are warranted to uncover what dictates when mice utilize a coherent but rotationally unstable spatial map and when their place fields exhibit global remapping. Yet another seminal study demonstrated that rats can in fact maintain the same place field configuration between arenas while modulating neuron firing rates to distinguish between arenas in the phenomenon of “rate remapping” [29]. Furthermore, they showed that rate remapping varies depending on the magnitude of differences between arenas. Our results are entirely consistent with this study, as we observe similar drops in PV correlations between arenas while still remaining above chance (Figure 4D-E, 5B), and demonstrate that changes in neuron event rate contribute to PV discrimination between arenas (Figure S4H). Furthermore, our results demonstrate that calcium imaging can identify coarser aspects of rate remapping in the form of neurons turning on/off between arenas (Figure 5F).

Another explanation for the discrepancies between previously mentioned studies [27,28] and ours could be the use of different species. Perhaps mice simply have a greater tendency to perceive two different arenas as similar? In support of this, a previous study [45] demonstrated that mouse place cells orient to local cues to a greater extent than rats, indicating that mice attend less to distant cues. This could result in a greater tendency of mice to view the arenas as similar and to exhibit coherent place field rotations, since more immediate features like arena material are less useful than other visual cues for disambiguating similar arenas or re-orienting in the same arena. Thus, increased attention to local cues by mice could increase the likelihood that they utilize the same map between arenas. While this effect might predominate in mice, it still likely exists in rats. First, as mentioned above, rats do frequently use the same map of place fields between two arenas ([29] and early sessions in [28]), even when they are permanently connected [46,47]. Second, disoriented rats frequently utilize geometry to reorient [11–13] and sometimes exhibit coherent rotations in the firing fields of upstream grid and head-direction cells in medial entorhinal cortex [15] and place cells in the hippocampus [48]. Thus, rats can also form spatial maps not tied to specific arena features. However, since studies that explicitly test for coherent rotations of maps between arenas are the exception [20,32,33] rather than the rule, future studies will be needed to comprehensively address this.

Perhaps the best explanation for discrepancies between our results and others is that an animal’s prior experiences can have a strong effect on its subsequent hippocampal representation of an arena. This is demonstrated by an elegant study [26] which found that hippocampal neurons in rats that first experienced arenas as connected discriminated between them to a much greater extent than in rats that only experienced them as separate. Consistent with this study, we found that connecting arenas mid-way through the experiment sharpened discrimination between them (Figure 5C). Despite this, however, the connection induced no substantial effect on later representations of each arena (Figure S4D–E). Thus, our results support the importance of prior knowledge in accommodating future learning [49–51] since the initial formation of coherent maps allowed for temporary modification but rendered them resistant to permanent disruption.

Overall, our results highlight the capability of the hippocampus to retain stable relationships between place fields across long time scales while simultaneously encoding the differences between experiences. These findings warrant future studies that investigate if non-spatially tuned hippocampal neurons [10,52–54] also maintain a consistent structure over days to weeks.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Inquiries for reagent and resource sharing should be directed to the Lead Contact, Nat Kinsky (kinsky@bu.edu) and they will be fulfilled, assuming reasonable requests.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animal Subjects

Subjects were 5 male C57/BL6 mice (Jackson Laboratories) weighing 25–30g, age 3–8 months. One mouse was excluded from the study after performing the experiment due to the inability to correct motion artifacts in his imaging videos. Mice were socially housed with 1–3 cage mates in a vivarium on a 12hr light/12hr dark cycle with lights on at 7am and given ad libitum access to food and water. Mice were singly housed after surgery. All procedures were performed in compliance with the guidelines of the Boston University Animal Care and Use Committee.

Viral Constructs

We obtained an AAV9-syn-GCaMP6f.WPRE.SV40 virus from the University of Pennsylvania Vector Core at a titer of ~4×10¹³GC/mL and diluted it to ~ 5–6×10¹²GC/mL with 0.05M phosphate buffered saline prior to infusion into CA1.

METHOD DETAILS

Stereotactic Surgeries

Naïve mice, age 3–8 months, underwent two stereotaxic surgeries and one base plate implant for calcium imaging [6]. All surgeries were performed under 1% isoflurane mixed with oxygen, and were given 0.05mL/kg analgesic buprenorphine, 5.0mL/kg anti-inflammatory Rimadyl (Pfizer), and 400mL/kg antibiotic Cefazolin (Pfizer) subcutaneously immediately after induction. Mice received the same dosage of buprenorphine, Rimadyl, and Cefazolin twice daily for three days following surgery. In the first surgery, a small craniotomy was performed at AP −2.0, ML = +1.5 and 250nL of GCaMP6f virus was injected at 1.5mm below the brain surface at 40 nL/min. 10 minutes after the infusion was finished, the needle was slowly removed, the mouse’s scalp was sutured, and then the mouse was removed from anesthesia and allowed to recover.

3–4 weeks after viral infusion, mice received a second surgery to attach a gradient index (GRIN) lens (GRINtech, 1mm × 4mm). After inducing anesthesia and providing pre-operative analgesia/antibiotics, a 2mm craniotomy centered at AP = 2.25, ML = 1.5 was performed and the cortex overlying region CA1 of the dorsal hippocampus was aspirated under constant irrigation with cold sterile saline. Aspiration stopped after removing the medial-lateral striations of the corpus callosum, which revealed anterior-posterior striations. Successive rounds of Gelfoam and cold saline were applied for 5–10 minutes to control bleeding, after which any saline left on the brain was suctioned out. The GRIN lens was then stereotactically lowered to the brain surface and depressed an additional 50 μm to compensate for brain swelling during the surgery. Kwik-Sil (World Precision Instruments) was applied to seal any gaps between the skull edge and the GRIN lens, and the lens was cemented in place using Metabond (Parkell). After building up a well of Metabond, the GRIN lens was subsequently covered with Kwik-Cast (World Precision Instruments) for protection. For two of the mice used in this study, the GRIN lens was not implanted directly. Rather, a 2mm cannula with a glass cover plate was implanted, filled in Kwik-Sil for protection, and the GRIN lens was later cemented in the cannula with Metabond during the camera attachment. For these mice, the cannula was not depressed 50 μm but allowed to rest upon the surface of the brain while Kwik-Sil and Metabond were applied. Mice received the same post-operative care and injections as occurred after they first surgery.

After one week of convalescence, mice underwent a final procedure to attach a miniature epifluorescence microscope (Inscopix). No tissue was cut during this procedure – the mouse was put under anesthesia solely to make him immobile and facilitate camera attachment. After induction, a baseplate was attached to the microscope, which was set at the middle of its focal range, and the camera was lowered toward the GRIN lens until a clear picture of the brain was achieved (~50–100μm below any visible vasculature, and/or when any calcium events from putative neurons were observed). When the ideal distance between GRIN lens and microscope objective was achieved, the camera was then raised up 50μm to compensate for the subsequent downward pull of Metabond during curing. The bottom of the base plate was first attached to the well of dried Metabond below using Flow-IT ALC Flowable Composite (Pentron), followed by a layer of opaque Metabond, which adhered to the sides of the base plate for reinforcement and blocked out ambient light.

After recovery from the second surgery, mice were food deprived and maintained at no less than 85% of their pre-surgery weight. 2–3 weeks prior to the experiment, they were allowed to forage randomly for chocolate sprinkles in a variety of arenas in order to identify the focal depth that maximized the number of in focus neurons. This also allowed us to habituate each mouse to the general experimental procedure, and to establish a baseline level of background fluorescence and calcium activity.

Experimental Outline

The experimental set-up consisted of a square and octagon of approximately equal area constructed from 3/8” plywood. All direction references (e.g. north, southwest, etc.) are given in reference to the standard configuration (see below). The square arena was 25cm × 25cm × 15cm. The octagon area had 8 – 11cm × 15cm sides (approximate diameter of 28cm). One wall of each arena was marked with a polarizing visual cue for orientation: vertical black stripes for the square and horizontal black stripes for the octagon. The arenas were oriented in the same manner (hereafter referred to as the standard configuration) for the first session of each day (with the exception of day 6). The standard configuration occurred when the arenas were rotated such that the visual cues were located on the south wall of the square and the northeast wall of the octagon. In this configuration the east wall of the square and the west wall of the octagon each had a 5cm gap that was hidden by a removable wall. Each arena was wiped down thoroughly with 70% ethanol prior to each recording session to eliminate any olfactory cues. Room cues were minimized as follows: by placing opaque plastic sheeting around the arenas, by playing white noise, by carrying the mouse from his homecage to the recording arena in a random, circuitous manner for each session, and by having the experimenter move every 15–30 seconds.

Prior to the first recording session of each day, the imaging camera was attached and the focal depth was verified by eye. Two mice were lightly anesthetized (30–60s) in order to attach the microscope and given 30 minutes to recover prior to recording; the other two were gently handled and kept awake during camera attachment 5–10 minutes prior to recording. Mice began each session in their homecage, which was placed just outside the plastic sheeting. On days 1, 4, and 7 (SQUARE1, SQUARE2, and SQUARE3, respectively), mice underwent two 10 minute sessions in the square arena; on days 2, 3, and 8 (OCTAGON1, OCTAGON2, and OCTAGON3, respectively) the mice underwent two 10 minute sessions in the octagon arena. The 1^st session on each of these days occurred in the standard configuration, after which the mouse was removed to his homecage while the arena was cleaned and then rotated pseudorandomly 90 degrees clockwise (CW) or counterclockwise (CCW) for the 2^nd recording session. The arena was also randomly moved between one of three different, adjacent positions between sessions SQUARE1–3 and OCTAGON1–3. For one mouse, the arena was not rotated between sessions on day 1 and day 8.

On day 5 (CONN1) the mice received one continuous 20 minute (minimum) recording session. The session began the same as day 4 with the mouse placed in the square arena in the standard configuration. After 5 minutes of exploration, the hidden east wall was lifted to reveal a hallway connected to the west wall of the octagon for the first time. After the mouse entered the octagon arena, the west wall was lowered to contain the mouse in the octagon, and he was allowed to explore this arena for 5 minutes. The same procedure was repeated twice more until the mouse had explored each arena twice. Day 6 (CONN2) was similar to day 5 except the mouse started in the octagon arena, which was rotated 180 degrees from the standard configuration, and ended in the square. See Figure 1a for a pictorial outline summarizing the above procedure.

Image Acquisition and Processing

All brain imaging data was acquired using nVista HD (Inscopix) v2 and v3. All movies were obtained at 1440 × 1280 pixels and 20 frames/second. Raw imaging data was first pre-processed in Mosaic software (Inscopix) by spatially downsampling by a factor of 2 (final pixel size = 1.18 microns/pixel) performing motion correction, and cropping to eliminate any dead pixels due to motion correction or areas with no clear calcium activity. A minimum projection (Figure S1b) of the final motion corrected, cropped movie was produced for later neuron registration across sessions/days (in the instances where 2 sessions were recorded on the same day they were both motion corrected to the same reference frame to ensure trivial session registration (see Neuron Registration section below). Isolated dropped frames (maximum 2 consecutive frames) were replaced with the previous good frame. In the rare case where extended chunks of dropped frames occurred, these frames were excluded from all analyses.

Behavioral Tracking

Position tracking of mice was performed using Cineplex v2/v3 (Plexon) software at 30 frames/sec. Brain imaging data and behavioral data were synchronized by sending a TTL pulse sent from the Cineplex computer, which signaled the beginning of behavioral tracking to the nVistaHD data-acquisition and triggered image acquisition. Each behavioral video was visually inspected, and any errors in tracking were corrected using custom-written software in MATLAB (available at https://github.com/SharpWave/PlacefieldAnalysis) which also interpolated behavioral imaging data to match imaging data.

Histology

Mice were perfused transcardially with 10% phosphate buffered saline (KPBS) followed by formalin. Brains were then extracted and post-fixed in formalin for 2–4 additional days, and were transferred to a 30% sucrose solution in KPBS for 1–2 additional days. Brains were then frozen and sliced in 40 μm sections on a cryostat (Leica CM 3050S), mounted, and cover slipped with Vectashield Hardset mounting medium with DAPI (Vector Laboratories). Slides were then imaged using a Nikon Eclipse Ni-E epifluorescence microscope at 4x, 10x, and 20x to verify viral expression levels, location, and GRIN lens placement above the CA1 cell layer.

QUANTIFICATION AND STATISTICAL ANALYSIS

All significance values are reported in figure legends or directly in the text. Unless otherwise noted, all statistics are done using either a Kruskal-Wallis ANOVA, a Wilcoxon rank-sum test, or using a bootstrap shuffling procedure (details provided in the appropriate section below). If the Kruskal-Wallis ANOVA is significant (p < 0.05), post-hoc Tukey test p-values are reported in the text/figure legend. All data points shown in figures are for all mice/session-pairs unless otherwise noted. We utilized custom MATLAB by Berens [55] to perform all circular statistics.

Neuron and Calcium Event Identification

Neuron regions-of-interest (ROIs) and calcium events were identified using a custom written, open source algorithm employed in MATLAB 2016b called A Technique for Extracting Neuronal Activity from Single Photon Neuronal Image Sequences (Tenaspsis) [56]. Tenaspis is open-source and available at: https://github.com/SharpWave/TENASPIS. First, Tenaspis filters each calcium imaging movie with a band-pass filter per [57] to accentuate the separation between overlapping calcium events. Specifically, Tenaspis smooths the movie with a 4.5 μm disk filter and divides it by another movie smoothed with a 23.6 μm disk filter. Second, it adaptively thresholds each imaging frame to identify separable pockets of calcium activity, designated as blobs, on each frame. Blobs of activity are accepted at this stage of processing only if they approximate the size and shape of a mouse hippocampal neuron, as measured by their radius (min = ~6 μm, max = ~11 μm), the ratio of long to short axes (max = 2), and solidity (min = 0.95), a metric used by the regionprops function of MATLAB we employ to exclude jagged/strange shaped blobs. Third, Tenaspis strings together blobs on successive frames to identify potential calcium transients and their spatial activity patterns. Fourth, Tenaspis searches for any transients that could results from staggered activity of two neighboring neurons. It rejects any transients whose centroid travels more than 2.5μm between frames and whose duration is less than 0.20 seconds. Fifth, Tenaspis identifies the probable spatial origin of each transient by constructing putative regions-of-interest (ROIs), defined as all connected pixels that are active on at least 50% of the frames in the transient. Sixth, Tenaspis creates initial neuron ROIs by merging putative transient ROIs that are discontinuous in time but occur in the same location. Specifically, it first attempts to merge all ROIs whose centroids are less than a distance threshold of ~0.6μm from each other. In order to merge two transient ROIs, the two-dimensional Spearman correlation between the ROIs must yield r² > 0.2 and p < 0.01. Tenaspis then successively increases the distance threshold and again attempts to merge ROIs until no more valid merges occur (at a distance threshold of ~3μm, typically). Seventh, Tenaspis integrates the fluorescence value of each neuron ROI identified in the previous step across all frames to get that neuron’s calcium trace, and then identifies putative spiking epochs for each neuron. Specifically, it first identifies the rising epochs of any transients identified in earlier steps. Then, it attempts to identify any missed transients as regions of the calcium trace that have a) a minimum peak amplitude > 1/3 of the transients identified in step 3, b) a high correlations (p < 0.00001) between active pixels and the pixels of the average neuron ROI identified in step 6, and b) a positive slope lasting at least 0.2 seconds. Last, Tenaspis searches for any neuron ROIs that overlap more than 50% and whose calcium traces are similar and merges their traces and ROIs.

Place cells

Calcium transients were spatially binned (4cm × 4cm) and normalized by occupancy. Spatial mutual information (SI) was computed from the following equations, adapted from [58]:

$$I_{pos}\left(x_i\right)=\sum _{k=0}^1{P}_{k|x_i}\text{\hspace{0.17em}log}\left(\frac{P_{k|x_i}}{P_k}\right)$$

$$SI\text{ =\hspace{0.17em}}\sum _{i=1}{P}_{x_i}{I}_{pos}\left(x_i\right)$$

where:

• P_xi is the probability the mouse is in pixel x_i

• P_k is the probability of observing k calcium events (0 or 1)

• P_k|xi is the conditional probability of observing k calcium events in pixel x_i.

The SI was then calculated 1000 times using shuffled calcium event timestamps, and a neuron was classified as a place cell if it 1) had at least 5 calcium transients during the session, and 2) the neuron’s SI exceeded 95% of the shuffled SIs. We obtained similar results using smoothed occupancy rate maps, which were constructed using 1cm × 1cm bins and applying a Gaussian filter (σ = 2.5cm). We defined the extent of a place field as all connected occupancy bins whose smoothed event rate exceeded 50% of the peak event rate occupancy bin.

Neuron Registration

Neuron registration occurred in two steps: session registration and neuron registration.

Session registration

Prior to mapping neurons between sessions, we determined how much the imaging window shifted between sessions. In order to isolate consistent features of the imaging plane for each mouse (such as vasculature or coagulated blood), we created a minimum projection of all of the frames of the motion-corrected and cropped brain imaging movie for each recording session. One session (“registered session”) was then registered to a base session using the “imregtform” function from the MATLAB Image Processing Toolbox, assuming a rigid geometric transform between images, and the calculated transformation object was saved for future use.

Neuron Registration

Next, each ROI in the registered session was transformed to its corresponding location in the base session. Each neuron in the base session was then mapped to the neuron with the closest center-of-mass in the registered session, unless the closest neuron exceeded our maximum distance threshold of 3 pixels (3.3μm). In this case the base session neuron was designated to map to no other neurons in the registered session. If, due to high density of neurons in a given area, we found that multiple neurons from the base session mapped to the same neuron in the registered session, we then calculated the spatial correlation (Spearman) between each pair of ROIs and designated the base session ROI with the highest correlation as mapping to the registered session ROI.

For multiple session registrations, the same procedure as above was performed for each session in two different ways. First, we registered each session directly to the first session in the experiment and updated ROI locations/added new ROIs to the set of existing ROIs with each registration. This helped account for slight day-to-day drift in neurons ROIs due to shifts in vasculature, build-up of fluid underneath the viewing window, creep/shrinkage of dental cement, etc. Second, to ensure that neuron ROIs did not drift excessively across sessions we also performed all the above steps but did NOT update ROI locations allowing us to register each set of ROIs to those furthest away chronologically. The resulting mappings were then compared across all sessions, and any neuron mappings that differed between the two methods (e.g. ROIs that moved excessively across the duration of the experiment) were excluded from analysis. Those that remained in the same location, and were included.

Place Field Rotation Analysis

We employed two methods to identify how much the spatial calcium activity of each neuron rotated between sessions.

Center-out Method

First, occupancy normalized calcium event maps were generated for each session by summing up calcium activity (defined as any frames with a rising calcium trace) for each neuron when the mouse was moving faster than 1cm/s in 1 cm bins and smoothing with a Gaussian kernel (σ = 2.5 cm). Next, we identified the location of each neuron’s place field(s) (see Place Fields section above), and calculated the angle from the center of the arena to the place field. We designate this angle as α. For neurons with multiple place fields, we defined this angle as the circular mean of the angles for all its place fields. We then calculated the place field rotation, θ, as the difference between α values in each session. We also calculated a metric of how well the population rotated together between sessions as follows:

$$rotationalaccuracy=\sum _{i=1}^n\left|{\theta }_i-{\theta }_{mean}\right|/n$$

Where θ_i is the rotation of the ith neuron and θ_mean is the circular mean rotation of all neurons.

Correlation Method

First, occupancy normalized calcium event maps were generated for each session by summing up calcium activity (defined as any frames with a rising calcium trace) for each neuron when the mouse was moving faster than 1cm/s in 1 cm bins and smoothing with a Gaussian kernel (σ = 2.5 cm). Second, the Spearman correlation between smoothed calcium event maps was then calculated for each neuron active in both sessions (the Spearman correlation is undefined for neurons that have no calcium events when the mouse is running above the speed threshold). Third, the mouse’s trajectory in the second session was rotated by the angle ɸ (in 90 degree increments for the square and 15 degree increments for the octagon, following the right hand rule) and the above process was repeated for each rotation between 0 and 360 degrees. Finally, the optimal rotation (ɸ_opt) of each neuron was taken as the rotation of the mouse’s trajectory in the second session that produced the maximum correlation. Chance-level ɸ_opt values were obtained by randomly shuffling each neuron’s identity in the second session and performing the above procedure 1000 times. For octagon-to-square comparisons, we first transformed rotated octagon arena trajectories to square trajectories using the method utilized by Lever, et al. [28]. We obtained similar results utilizing calcium event maps created using 4cm occupancy bins and without smoothing. To quantify the use of coherent maps between the two arenas, we first transformed the mouse’s trajectory in the octagon arena to square coordinates [28]. This method is not as sensitive as the center-out method, since the resolution of ɸ_opt values is equal to the increments in which the data is rotated. However, unlike the center-out method, it does not require making any assumptions about the location of each place field.

Coherent and Remapping Designations

Center-out Method

A significantly large number of place-fields had to rotate together in order for a session-pair to be designated as sharing a coherent map. To quantify this, we first identified circular mean of all place field rotations, designated as θ_mean. We then calculated n_close, the number of neurons that were < 30 degrees from θ_mean. We then compared this number to chance n_chance, calculated in the same manner but after randomly shuffling neuron identity between sessions. We the repeated this step 1000 times, and calculated a p-value for each session-pair, defined as 1 – (# times nclose > nchance)/1000. In order to be designated as coherent, a session-pair had to have a p-value < 0.05 after Bonferroni correction (p < 0.05/m, where m = the number of session-pairs, i.e. 28 for square-to-square and octagon-to-octagon comparisons, and 64 for octagon-to-square comparisons).

Correlation Method

In order for session-pairs to be identified as coherent, they had to satisfy a stringent, two-pronged criteria. First, the distribution of ɸ_opt had to significantly differ from a uniform distribution (p < 0.05 for χ² test). Second, a permutation test was performed in order to rule out the possibility that the population breaks into multiple coherent subpopulations [59]. The permutation test was performed as follows. Tuning curves for the population were constructed by calculating the mean correlation between the calcium event maps of all neurons at each rotation. Then, the p-value was calculated as the number of times that the peak value of the shuffled tuning curve exceeded that of the actual data, divided by the number of shuffles. In order to be designated as coherent, a session-pair had to have a p-value < 0.05 after Bonferroni correction (p < 0.05/m, where m = the number of session-pairs, i.e. 28 for square-to-square and octagon-to-octagon comparisons, and 64 for octagon-to-square comparisons). Sessions that did not meet both criteria were designated as global remapping sessions. The χ² test p-value is reported throughout the text unless it is smaller than the permutation test p-value, in which case both are reported. Note that neurons with poor spatial firing properties will have lower correlations than neurons with punctate firing fields and/or high spatial information. Thus, to bias our results against the hypothesis of predominantly coherent spatial representations, we included all neurons in the coherency analysis, regardless of their spatial information content.

Coherent Rotation Designations

Coherent session-pairs within arenas (square-to-square and octagon-to-octagon) were further sub-divided into groups based on which cues the mice appeared to use to orient their place field maps. Coherent session-pairs where the arena was rotated between sessions were designated as “Coherent: Arena” if |θ_mean − θ_arena| < 30 degrees, “Coherent: Room” if θ_mean < 30, and “Coherent: Mismatch” otherwise. When there was no arena rotation between sessions (and thus there was no mismatch between arena and room cues), coherent session-pairs were designated as “Coherent: Arena/Room” if θ_mean < 30 and “Coherent: Mismatch” otherwise. θ_mean was calculated using the center-out method above.

Entry Angle vs. Rotation Analysis

We manually identified the wall over which the mouse was carried into the arena (θ_entrywall), the angle he was facing when he crossed over this wall (θ_entrydir), and the angle he was facing when he first touched down (θ_touchdown) in the arena. Since place fields tended to rotate in 90 degree increments in the wall, we likewise defined the angle of entry for the mouse in 90 degree increments (e.g. the east wall = 0 degrees, the north wall = 90 degrees, etc.). We then calculated the change in entry angle between sessions, subtracted it from the change in θ_mean between sessions, designated it as Δθ_{mean,entrywall}. We reasoned that, if the mouse utilized the wall over which he entered to anchor this place field map, then his entry angle rotation should match the place field rotation between sessions for all mismatch sessions and Δθ_{mean,entrywall} should equal zero. We thus counted up all the Δθ_{mean,entrywall} values <= 15 degrees from zero and compared this number (n_data) to chance (n_shuffle), determined by randomly shuffling entry angle between session and repeating the procedure above 1000 times. We then calculated a p-value as 1 – the number of times n_data exceeded n_shuffle. We then repeated the above procedure for the angle the mouse was facing when he first entered the maze (Δθ_{mean,entrydir}) and the angle he was facing upon touchdown in the arena (Δθ_{mean,touchdown}).

Population Vector Calculations

Population vectors (PV) were constructed for each occupancy bin (4cm × 4cm) by taking the calcium event rate of each neuron from the corresponding occupancy bin in its unsmoothed calcium event map. In order to account for coherent rotations of the map between sessions, the mouse’s trajectory in the second session was rotated by ~θ_mean (in 90 degree increments for the square and 15 degree increments for the octagon) before calculating the PV in the second session. Spearman correlations were calculated for each occupancy bin, and the mean correlation across all bins was taken as the mean spatial PV correlation between sessions. Chance level for all PV analyses was calculated by shuffling occupancy bins and calculating mean correlations 1000 times for each session-pair. We also performed rate-only PV similarity analyses by forming PVs without rotating the data between sessions and using each neuron’s maximum event rate to form the PV.

For the connected day analyses and time lag analysis without silent cells, PVs included neurons only if they met the following criteria instituted to exclude any low event rate neurons whose changes could artificially skew our results: 1) the neuron was active (at least one calcium transient) each day, and 2) the neuron produced more than 5 calcium transients and had a p-value for spatial MI (see Placefields section) of < 0.05 on at least one day. For connected day analyses, inactive cells were those that produced no calcium transients when the mouse was above the 1cm/s speed threshold, but had at least one calcium transient during the session. For all comparisons within CONN1 and CONN2, we considered each continuous 5 minute visit to an arena as its own session. However, we combined visits in each arena into one 10 minute session in each arena for any PV analyses between CONN1/CONN2 and un-connected days in order to ensure similar length sessions for between day comparisons.

For the time lag analysis, included neurons had to pass the transient number and p value thresholds on at least one session but only needed to be active in one session. A silent neuron (one that became active in the second session or were active in only the first session) was only considered if its ROI in one session did not overlap with any other neighboring ROIs in the other session. This precluded neurons that might be misidentified as silent due to overly conservative neuron registration between sessions (e.g. those that overlapped with another ROI but were just outside the stringent distance threshold required to be mapped as the same cell). Additionally, we have not shown comparison exactly 7 days apart due to a scarcity of data at that time lag between sessions; the removal of this data does not alter the results shown in Figure 6e.

Single Neuron Classifications

On/off cells were identified by first registering all neurons, without filtering for spatial selectivity or transient number, across sessions and then identifying any neurons that were active in the second/first session but not the first/second session. Additionally, since neuron registration does not take into account the speed threshold of 1cm/sec we applied for all analyses above, we identified additional on/off neurons as those that were detected by Tenaspis in each session, but did not produce any calcium events while the mouse was above the speed threshold in the first/second session. Additionally, we calculated a Discrimination Index for each neuron to determine its preference for being active in one arena versus the other, defined as (ER_square − ER_octagon)/ (ER_square + ER_octagon), where ER = calcium event rate. We defined neurons as “selective” if |DI| > 0.66, which indicated that they had 66% or more calcium events in the square than the octagon, or vice versa. Neurons with |θ − θ_mean| < 30 were designated as staying coherent. Neurons were designated as random remapping otherwise. We obtained similar results to Figure 2i for cutoffs of 15 degrees, 30 degrees, and 45 degrees.

DATA AND SOFTWARE AVAILABILITY

All custom-written MATLAB code is freely available at https://github.com/nkinsky/ImageCamp and https://github.com/SharpWave/TENASPIS.

Data presented in this publication can be accessed online. Raw data: https://drive.google.com/open?id=1sXafOu7-gAWpW8gM8RgQL-o49BldKGyb. Processed data: http://doi:10.17632/73xj2dx44k.1

Highlights.

• Mice use a stable place field configuration, or coherent map, over long time scales

• Mice employed coherent maps within the same arena and between different arenas

• Random reorganization – global remapping – also occurred, but was infrequent

• Coherent map rotations between sessions could underlie instability