Challenges in Diffusion MRI Tractography - Lessons Learned from International Benchmark Competitions

Abstract

Diffusion MRI (dMRI) fiber tractography has become a pillar of the neuroimaging community due to its ability to noninvasively map the structural connectivity of the brain. Despite widespread use in clinical and research domains, these methods suffer from several potential drawbacks or limitations. Thus, validating the accuracy and reproducibility of techniques is critical for sound scientific conclusions and effective clinical outcomes. Towards this end, a number of international benchmark competitions, or “challenges”, has been organized by the diffusion MRI community in order to investigate the reliability of the tractography process by providing a platform to compare algorithms and results in a fair manner, and evaluate common and emerging algorithms in an effort to advance the state of the field. In this paper, we summarize the lessons from a decade of challenges in tractography, and give perspective on the past, present, and future “challenges” that the field of diffusion tractography faces.

INTRODUCTION

Diffusion magnetic resonance imaging (dMRI) fiber tractography [1, 2] has become a pillar of the neuroimaging community, revealing fundamental insights into how connectivity underlies brain function, development, and cognition, and leading to a better understanding of brain dysfunction in aging, mental health disorders, and neurological disease [3]. Additionally, in the neurosurgical setting, tractography has provided clinically relevant information during pre-operative planning as well as intra-operative mapping of brain tumor resections [4]. Despite its widespread use in both clinical and research domains, the process from data acquisition to generation of 3D connectivity maps is a multi-step procedure with numerous assumptions and uncertainties that can ultimately affect the ability of tractography to faithfully represent the true axonal connections of the brain. Because of this, validating the accuracy and reproducibility of these techniques is critical for sound scientific conclusions and effective surgical outcomes. It is necessary to measure the ability of these techniques to track white matter fibers from region to region, and to also quantify the ability of dMRI to assesses the underlying fiber orientation distribution (FOD) within each voxel. Towards this end, there have been a large number of dMRI community-wide efforts, or “challenges”, which aim to investigate the reliability of the tractography process.

Publicly organized challenges are widespread in biomedical image analysis. In this domain, an algorithm or solution may be developed to address a particular challenge in the field - a challenge that is likely being, or has already been, tackled by multiple laboratories, researchers, and algorithms. However, for many problems, there is no public database and reference standard available, and results are typically reported on proprietary datasets which may vary widely due to differences in acquisition and hardware, making fair comparisons between algorithms not practical. For this reason, public challenges are organized to provide a platform to compare algorithms and results in a fair manner, and evaluate common and emerging algorithms in an effort to advance the state of the field. In biomedical image analysis, challenges have included a number of imaging modalities, anatomies, and evaluation goals. Examples include segmenting tumors and lesions from MR, CT, and PET scans [5–7], detecting pulmonary nodules in chest CT [8], particle tracking [9], evaluating neuronal reconstructions [10, 11], estimating knee cartilage [12], motion correction on cardiac data [13], segmenting histological images [14], and segmenting a number of organs [15–18]. A comprehensive list of past and ongoing challenges can be found at https://grand-challenge.org/all_challenges/.

In the tractography community, these challenges provide a unique opportunity for neuroscientists, computer scientists, biomedical engineers, and MRI physicists to fairly compare tractography algorithms in an unbiased format. Traditionally, most have focused on either local modeling of the fiber geometry, or on the evaluation of tractography as a whole. These challenges have provided us with valuable lessons regarding the tractography process - resulting in quantitative measures of the reliability and limitations of existing approaches - and left us with unique opportunities for advancements in brain mapping using ideas and algorithms from different disciplines, research labs, and scientific communities. In this manuscript, we aim to summarize the lessons learned from a decade of challenges in tractography, and to give perspective on the past, present, and future “challenges” that the field of diffusion tractography faces.

We begin with a brief review of “The Challenges” that have provided insight into fiber orientation reconstruction, tractography, and brain connectivity. Next, we summarize the insights and “Lessons Learned” from these studies, and conclude with a discussion on the “Opportunities and Perspectives” on open issues in the field and the future of tractography.

1. . THE CHALLENGES

The basic anatomy of a challenge includes (1) defining the challenge itself, i.e. the task and desired output, (2) providing a set of images for participants to apply their algorithm on, (3) creating the reference standard, or ground truth, against which all submissions are compared, (4) defining an evaluation procedure, or metrics to quantify performance, and (5) final evaluation of all submissions. In this section, we present a brief history of past tractography challenges in chronological order. We note that several past challenges have focused on the microstructural modelling problem (ISBI 2015: White Matter modelling Challenge [19]; MICCAI 2014: Sparse Reconstruction Challenge [20]), or diffusion harmonization (CDMRI MICCAI 2017 and 2018: Multi-shell Diffusion MRI Harmonisation Challenge), but this review focuses only on the challenges investigating fiber tractography and FOD reconstruction.

The basic anatomy of each challenge is presented, with highlights summarized in Table 1. In all cases, the data and ground truth remain publicly available at the websites listed in the last column of the table, and detailed formulations of evaluation criteria are given in Appendix A.

Table 1.

Challenges in fiber tractography.

YEAR	CONFEREN CE	NAME	VALIDATIO N	STRATEGY	THE CHALLENG E	INFORMATION
2009	MICCAI	FiberCup	Tractography	Physical Phantom	Find 16 existing connections	http://www.tractometer.org/original fibercu p/
2011- 2015	MICCAI	DTI Challenge	Tractography	In Vivo Data reviewed by neurosurgeo ns	Reconstruct Pyramidal Tract in 4 Neurosurgic al Cases	http://dti-challenge.org
2012	ISBI	HARDI Reconstructi on Challenge	Fiber orientation	Simulated orientation fields	Estimate local single and crossing fiber configuratio ns	http://hardi.epfl.ch/static/events/2012_ISBI/
2013	ISBI	Tractometer: HARDI Reconstructi on Challenge	Local modeling evaluated with tractography	Physical Phantom + Online evaluation tool	Recover valid connections and fiber bundles	http://hardi.epfl.ch/static/events/2013_ISBI/index.html
2015	ISMRM	Tractography Challenge	Tractography	Simulated diffusion data based on in vivo human acqusition	Find 25 ground truth bundles	http://www.tractometer.org/ismrm_2015_challenge/
2017	ISMRM	TraCED Reproducibili ty Challenge	Tractography Reproducibili ty	Scan-rescan data of single subject on two scanners	Submit most reproducible tractogram for 10 fiber structures	https://my.vanderbilt.edu/ismrmtraced2017/
2018	ISBI	3D VoTEM	Tractography	Physical Phantom + Histological Validation	Find ground truth bundles and connections in all datasets	https://my.vanderbilt.edu/votem/

FiberCup: MICCAI 2009

The FiberCup [21] was the first community effort at a quantitative evaluation of tractography algorithms on a common dataset. The challenge was to find 16 existing connections on a physical fiber phantom [22] (Figure 1A). The phantom was composed of hydrophobic acrylic fibers positioned within a 2D frame in order to simulate a coronal section of the human brain, containing a number of distinct bundles with geometries known to hinder tractography, including fiber crossings, kissing, and splitting, and configurations with varying curvatures. Because the phantom was physically manufactured, the true pathways trajectory and orientation are well-defined. Contestants were asked to submit a representative fiber of the bundle traversing each of 16 known pathways - in this case, these 16 ground truth pathways were actually single streamlines as opposed to the delineation of a full bundle (as done in the ISBI 2013 Tractometer challenge run on the same FiberCup phantom). Participants were given 16 seed voxels and were asked to reconstruct the path associated with each. Each submission was evaluated based on spatial proximity to the ground truth and orientation accuracy of the streamline trajectory. In all, 10 reconstruction methods were evaluated.

Figure 1.

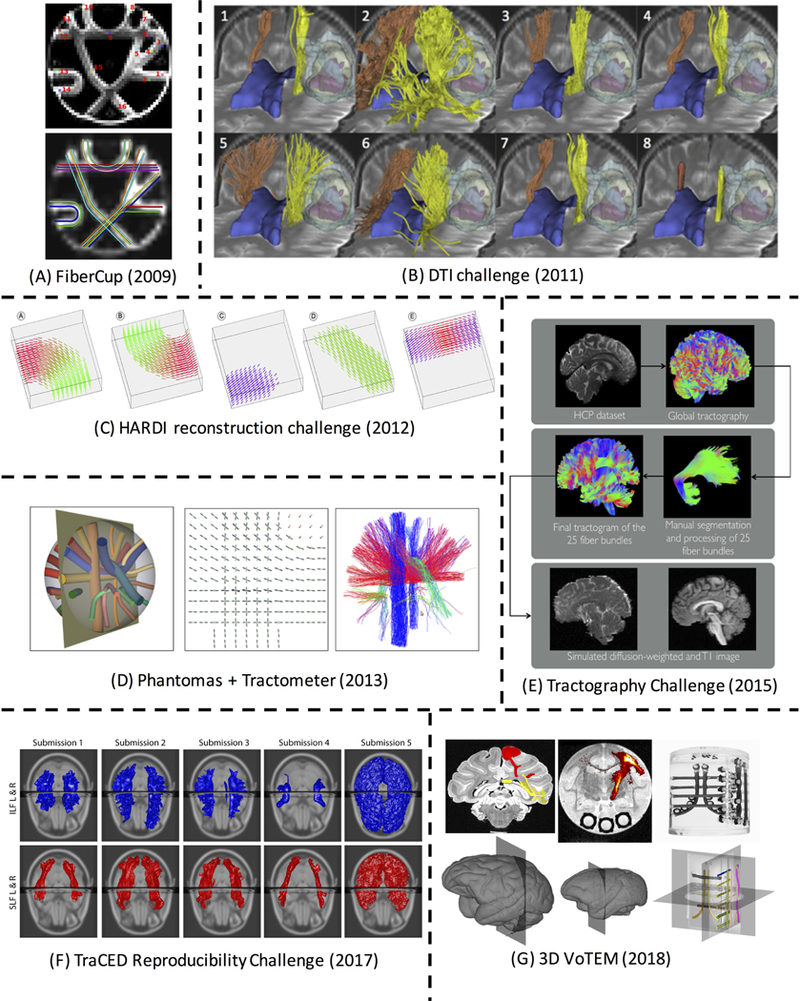
Past challenges in fiber tractography. Detailed description of data, ground truth, and evaluation are described in the text. (A) FiberCup Phantom pathways with 16 ground truth bundles [21]. (B) Eight example CST reconstructions from the DTI Challenge [23]. (C) Synthetic fiber fields from the HARDI Reconstruction Challenge [26]. (D) Phantomas [27] dataset for Tractometer evaluation [28]. (E) Creation of simulated in vivo human dataset for the ISMRM Tractography Challenge [29]. (F) Example submissions from the TraCED Reproducibility Challenge for two white matter pathways. (G) 3D-VoTEM ground truths defined on the macaque, squirrel monkey, and phantom (from left to right). Reproduced and modified from Fillard et al. (2011), and Schilling et al. (2018) with permission from Elsevier; from Pujol et al. (2105) with permission from Wiley; from Daducci et al. (2014) with permission from IEEE, and from Maier-Hein et al. (2017) under a Create Commons license from Nature Publishing Group.

DTI Challenge: MICCAI2011–2015

This multi-year challenge focused on the validity of tractography findings for making neurosurgical decisions [23]. The challenge was to reconstruct the “best” cortico-spinal tract (CST) as judged by a panel of experts (Figure 1B). The pyramidal tract was chosen due to its well defined anatomical origin and terminations, contributions to motor function, and clinical relevance [24, 25]. In each edition of the DTI Challenge, MRI data were acquired on four patients presenting with a glioma near the motor cortex area, thus the patient data was of quality expected from clinical scanners (30 diffusion directions, b=1,000 s/mm2). Two datasets were release for training and testing algorithms, while the remaining two were processed on site live at the challenge forum. Thus, the notion of “speed” of processing (and reliability of systems) was important, the method needed to run in less than 1 hour on the day of the challenge. Qualitative evaluation was performed by a panel of two neurosurgeons and three DTI experts by assessing the presence of false-positive and false-negative tracts, with a quantitative comparison performed to calculate the distances between reconstructed pathways estimates. Twenty five international teams submitted reconstructions on both the affected and contra-lateral hemispheres.

HARDI Reconstruction Challenge: ISBI 2012

This challenge focused on validating the local fiber orientation distribution from diffusion MRI data, with the aim to recover the best local estimation of single and crossing configurations [26]. The diffusion signal was numerically simulated from two generated fields of crossing, kissing, and bending fiber bundles (Figure 1C). This numerical data synthesis offered a versatile way to assess performance of algorithms across a broad range of experimental conditions, including varying sampling schemes, noise levels, fiber configurations, and signal generation models. Participants, in effect, requested their own acquisition scheme (including b- values and gradient schemes), and applied their algorithm of choice to the received data. Performance was assessed based on the correct estimation of the number of fiber compartments in each voxel, and the angular accuracy in their orientation. In total, 20 algorithms for recovering fiber structure were compared, ranging from standard DTI schemes and sparse reconstructions with minimal data, to DSI-like schemes containing hundreds of diffusion volumes.

HARDI Reconstruction Challenge (Tractometer): ISBI 2013

In a continuation of the previous year’s challenge, the 2013 ISBI conference featured a local reconstruction challenge that was evaluated by assessing the resulting tractography [27]. Here, algorithms were run on a dataset numerically created using the Phantomas library [27]. Importantly, running this challenge led to the refinement and widespread adoption of the Tractometer [28], an online evaluation and validation system for tractography processing pipelines (Figure 1D). This system accepts as input any acquisition scheme, pre-processing of data, orientation estimation technique, or tracking strategy, and explores the rest of the variables and parameter space. For example, if a new reconstruction technique is developed, this can be added to the software, and tractography can be run using all other existing pipelines (i.e. all other pre-processing and tracking strategies) in combination with the proposed reconstruction. Tractography was assessed by evaluating how well streamlines covered the true physical pathway, the percent of valid (true positive) and invalid (false positive) streamline connections, and the number of valid and invalid bundles. This evaluation strategy resulted in more than 57,000 fiber tractograms created on the FiberCup dataset.

Tractography Challenge: ISMRM 2015

This challenge was to provide the best possible reconstruction of fiber pathways in a realistically simulated replication of a whole brain diffusion-weighted dataset with properties typical of a clinical acquisition [29]. Twenty-five manually segmented white matter bundles served as the ground truth, from which challenge data was synthesized using Fiberfox signal simulation tool (Figure 1E) [30]. Evaluation metrics were the same as those implemented in Tractometer, including valid connections and bundles, invalid connections and bundles, as well as the volume-based measures of bundle overlap and bundle overreach. A total of 96 tractography submissions from 20 international research groups were evaluated and analyzed.

TraCED Reproducibility Challenge: ISMRM 2017

The Tractography-reproducibility Challenge with Empirical Data (TraCED) [31] featured a scan-rescan of a single subject, on two different scanners, with 5 acquisition repetitions per session, resulting in 20 diffusion datasets (2 sessions x 2 scanners x 5 repetitions). Participants were asked to reconstruct 10 white matter pathways on each dataset (Figure 1F). Rather than validating the accuracy of tractography, the goal of TraCED was to assess the reproducibility of emerging pipelines using clinically feasible imaging sequences by evaluating Dice overlap and Intra-class correlation coefficients (ICC) of tractography within sessions, across sessions, and across scanners. Nine research groups submitted 46 tractography algorithms for evaluation.

3D VoTEM Challenge: ISBI2018

The 3-D Validation of Tractography with Experimental MRI (3D-VoTEM) [32]presented three different validation strategies, composed of three separate ground truth datasets with which diffusion tractography can be compared and evaluated against (Figure 1G). This included a physical phantom with 16 fiber bundles (Synaptive Medical, Toronto, Canada), a high-resolution ex vivo macaque dataset [33] with an atlas of known connections [34], and an ex vivo squirrel monkey dataset with histological tracer injections [35–37]. The challenge, then, is to estimate the ground truth bundles and connections in all datasets. Anatomical accuracy was evaluated based on connectivity, using sensitivity and specificity, as well as based on spatial overlap, using bundle overlap and overreach. Across all three datasets, a total of 176 distinct tractography reconstructions across 9 research groups was submitted.

2. LESSONS LEARNED

These challenges have resulted in a number of insights into the tractography process, its interpretations, strengths, and limitations. We summarize here the main lessons learned from these challenges.

Following local orientations can reconstruct valid connections

A common, and encouraging, theme of these challenges is that diffusion tractography is able to reconstruct valid fiber bundles, and these connections are typically very close spatially to the ground truth. For example, on the FiberCup phantom [21], given a single seed voxel, multiple algorithms are able to successfully delineate the starting and ending regions of the bundle, even across regions that cross, split, and curve sharply (Figure 2). In the Tractometer evaluation of 57,000+ algorithms, over 6,000 recovered 100% of the valid bundles [28]. While this represents only 10% of the pipelines tested, this is reassuring because it means that there is a large number of different parameters, combinations, and strategies that produce good streamline outputs. In addition to phantoms, valid reconstructions can be reconstructed in datasets on the human and monkeys. In human-like geometries, algorithms reconstructed a median 23/25 valid bundles [29] (ISMRM 2015 Tractography Challenge), and adequately reconstruct the CST even in the presence of a tumor [23] (DTI Challenge). In monkeys, a number of algorithms result in true positive rates (sensitivity) of 80% or above (3D-VoTEM). In all cases, a majority of these correctly reconstructed streamlines are spatially close to the ground truth, consistently within 1–2 voxels from the true pathway along the entire length of the streamline, for all physical bundles [21]. These algorithms that are successful at reconstructing valid connections, intuitively have streamlines that tend to align well with the underlying structure, highlighting the importance of accurately predicting fiber orientation [21].

Figure 2.

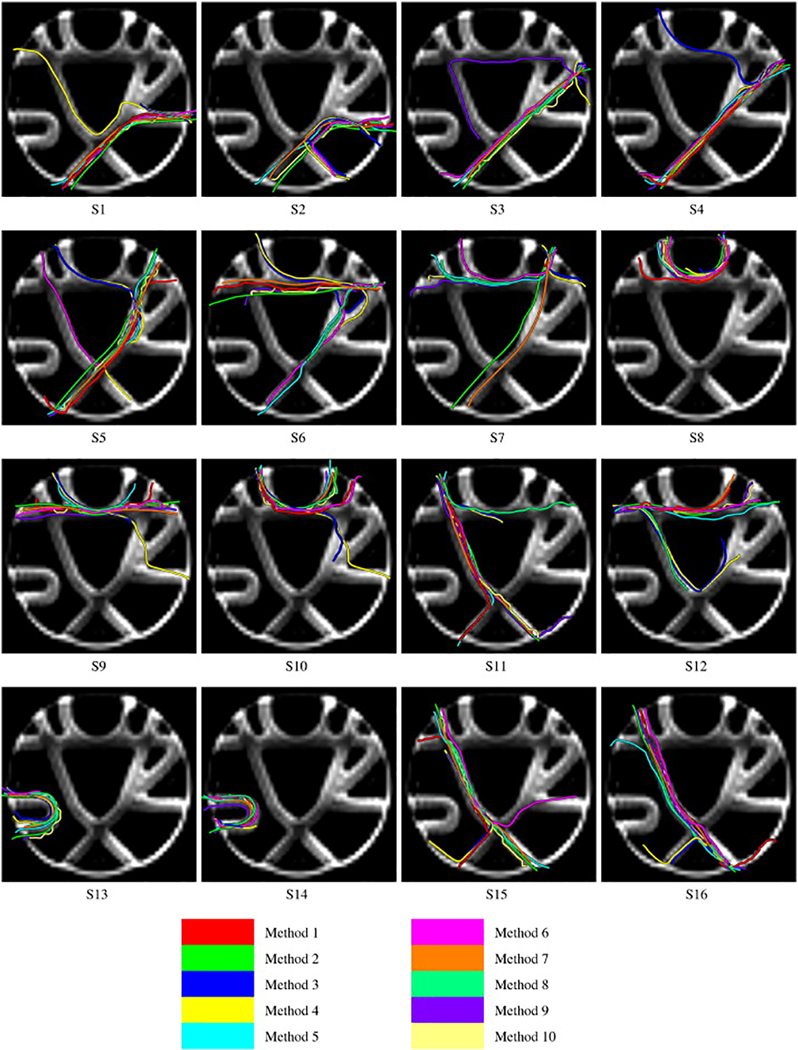
Following local orientations, many algorithms are able to reconstruct valid connections. Images show the reconstructed fiber of all submissions (Methods #1–10) for each seed of the phantom (S1-S16). Variability across methods is apparent, and some pathways are more successful than others. Compare to Figure 1A for ground truth connections of each seed. Reproduced from Fillard et al. (2011) with permission from Elsevier.

Despite successes in reconstructing valid bundles that are spatially and orientationally correct, a number of limitations are immediately apparent. This includes complications in crossing fiber regions (a well-known hindrance to DTI), incorrect splitting and branching decisions, low overall bundle coverage, and a low percent of valid connections relative to invalid connections or no determined connections. Together, these results have emphasized several important messages that should be kept in mind when implementing these techniques [21, 28]: (1) signal averaging, or more recently, denoising, (in order to increase image SNR) improves tractography quality, (2) sharp estimates of fiber distributions improve results, (3) priors on spatial smoothness make reconstruction and tractography more robust to noise, (4) seeding strategies have a large impact on tractography results, (5) probabilistic tractography results in larger bundle coverage, and (6) deterministic tractography tends to have the best valid/invalid connection trade-offs, but at the expense of spatial bundle coverage.

There are limitations to the use of Tractography for clinical decision-making

Using the neurosurgical glioma datasets, the DTI Challenge [23] provides interesting insight into the use of tractography for neurosurgical planning. In this context, identifying the pyramidal tract, and its location relative to the tumor, is necessary for tractography to be a useful pre- or post-operative tool. Notably, experts noted the consistent presence of false- negative and false-positive pathways in the submitted tractograms. Qualitatively, tractography algorithms were able to delineate some pathway from the cerebral peduncles, through the internal capsule, and continuing to some portion in or near the motor cortex [23]. However, most were limited to the medial portion of the motor strip, and only a few could trace the lateral projections associated with the hand, face, and tongue movements (Figure 3, from DTI Challenge). In addition to the absence of pathways in the lateral regions of the motor cortex, other false-negatives were consistently found in the edematous regions, and false-positives in the frontal and parieto-occipital portions of the corona radiata and even in the surgical cavities (known to contain no pathways). Of the 8 submissions judged by experts, one was graded as excellent in reconstructing the CST, six as good, and one as fair [23], with results generally consistent across patients.

Figure 3.

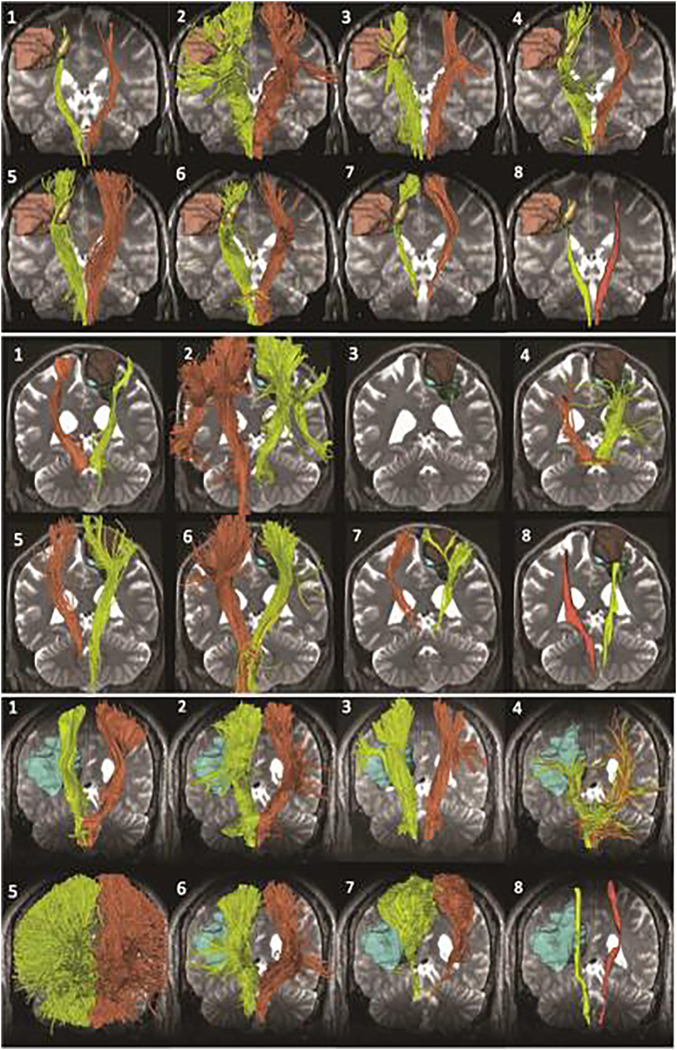
There are limitations to the use of tractography in clinical decision making - reconstruction of the CST results in a number of false positive and false negative connections. The figure shows eight tractography reconstructions of the pyramidal tract for patient 2 (top), patient 3 (center), and patient 4 (bottom). Each view presents the tracts (yellow: tumor side; orange: contralateral side) overlaid on axial and coronal T2-weighted image. Reproduced from Pujol et al. (2105) with permission from Wiley.

Interestingly, tractography did quite well in determining the presence or absence of white matter infiltration in tumorous regions [23]. For example, in lesions which were cystic, or not expected to contain tracts (anaplastic oligoastrocytoma grade III, anaplastic oligoastrocytoma grade III, and glioblastoma grade IV), all algorithms consistently resulted in little or no streamlines visiting the lesion volume (less than 1.5% volume of tumors visited). Conversely, in a tumor of infiltrative nature (anaplastic oligodendroglioma grade III), the volume fraction of tumor visited by tractography was much higher (up to 22% of the tumor volume). Despite successes in tumor infiltration measures, a large difference in reconstructions was noted (see “Tractography is reproducible” below), as indicated by large Hausdorff and mean distances between the 8 tractography submissions. However, the presence of tumor did not affect inter-algorithm variability, as disagreement between methods was similar on healthy side as on pathological side with distortions and pathological tissue.

In summary, the large inter-algorithm variabilities, presence of false negative pathways, and disagreement among methods suggests that there are still limitations to the clinical use of tractography for neurosurgical decision making. It is important to point out that the model pathway used in this system is one of the most commonly studied, with relatively clear anatomical definition. Difficulties encountered in the pyramidal tract are likely to be more challenging for less well-defined pathways with surgical relevance, e.g., optic radiation and arcuate fasciculus. In short, these shortcomings suggest that differences in algorithms and results can potentially affect clinical decisions, and advocate caution in interpreting tractography results in the clinical settings. Further, this motivates the need for benchmarks and datasets on which test-retest reproducibility can be evaluated.

We are good at estimating local orientations

Since the recognition that DTI fails in regions of crossing and complex fibers - which may occur in as many as 90% of all voxels - a large number of algorithms have been proposed which aim to resolve crossing fibers [38–45]. Typically, these are referred to as high angular resolution diffusion imaging (HARDI) methods to distinguish them from DTI, and indicate the need for a typically larger number of diffusion images. When a new algorithm is proposed, large consideration is given to the number of resolvable fiber populations and the crossing angle of the populations. For example, a more acute crossing angle is generally harder to “resolve” than orthogonal crossings [46], thus, a proposed algorithm able to resolve smaller angles might be considered “better” at reconstruction than others.

The 2012 HARDI Reconstruction challenge is currently the largest quantitative validation of voxel-wise fiber reconstruction methods on a common dataset with known ground truth [26]. The main takeaway from this study is that the relationship between the diffusion signal and underlying fiber distribution is generally well understood, and, despite the large number of modeling strategies in literature, in general they all adequately reflect the underlying fiber geometry and orientations in each voxel (Figure 4). Methods do show differences in minimum resolvable angle, angular accuracy, and success rates, but there was no “optimal” method for a given acquisition, and none outperformed others in every experimental condition [26]. In fact, good crossing estimation is possible with a low number of sampling directions, thanks to sparse-estimation approaches, with results on par with HARDI-like approaches, and even approaches with 200+ directions (i.e., DSI-like approaches). The authors point out that noise removal procedures, in the form of image denoising or spatial regularization, tend to improve reconstruction performance in all metrics, and the main sources of inaccuracy is caused by overestimation of fiber populations for low SNR data and underestimation for high SNR data [26].

Figure 4.

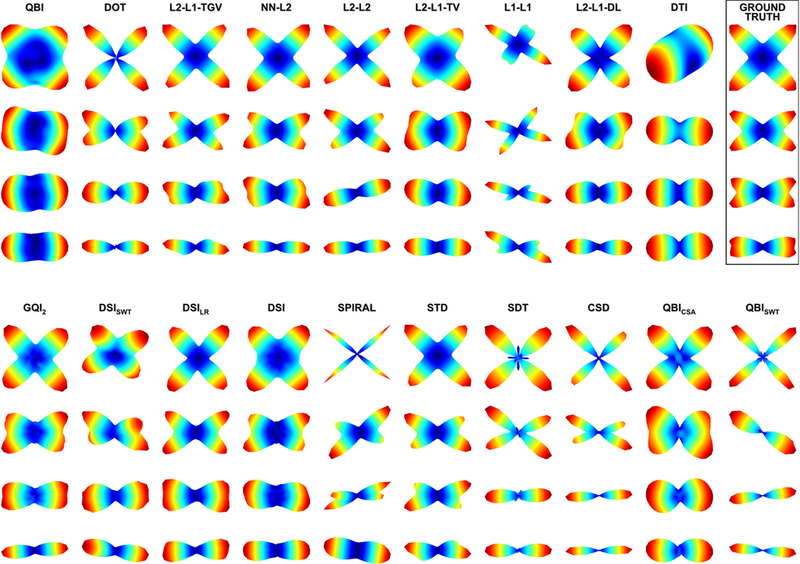
Most reconstruction methods adequately resolve the fiber orientation distribution, even with limited data. A representative diffusion profile (e.g., ODF or FOD) as reconstructed by varying algorithms is shown for four different crossing configurations (90°, 60°, 45°, and 30°), with an SNR = 30. Reproduced from Daducci et al. (2014) with permission from IEEE.

While it is certainly quite an overstatement to say that the “reconstruction problem is solved”, it is clear there are a number of techniques that perform quite well at estimating fiber numbers and orientations across a range of acquisition and experimental conditions.

Good local performance does not guarantee good tractography performance

It is intuitive to think that better local reconstructions lead to better tractography performance. And it is not a stretch to think that perfect representation of local fiber orientations could, or should, lead to perfect tractography. Several challenges have had the opportunity and data available to investigate this, including the 2013 ISBI HARDI Reconstruction Challenge and the 2015 ISMRM Tractography Challenge. On the physical phantom, and in agreement with simulations from the previous year, most techniques performed well in local orientation estimation, yet connectivity metrics varied greatly [28]. Reconstructions resulted in coherent geometries reconstructed in single fiber regions, and crossing geometries resolved in crossing fiber regions, but a good local performance on average did not guarantee a good average performance for tractography. Many algorithms still suffered from a high percent of invalid or no-connections, low percent of valid connections, and low bundle coverage. Tracking parameters, rather than reconstruction quality, greatly influenced results. For example, seeding and masking strategies greatly impacted the fiber count and density of bundles, and subsequent measures of valid/non-valid connections. In addition, the choice of deterministic versus probabilistic methodologies influenced results, with probabilistic methods generally producing large numbers of no-connections and invalid connections, but also resulting in the largest bundle coverage for valid bundles. This study highlighted that some errors are more costly than others, and that connectivity metrics are largely driven by tractography parameters rather than orientation estimation [28].

The simulated human brain dataset from the 2015 ISMRM Tractography challenge [29] confirmed many of the findings of previous phantom challenges. Submissions were able to reconstruct most of the ground truth bundles, with over 70% of submissions reconstructing 23 or more of the 25 valid pathways. However, tractography pipelines again had poor recovery of the spatial extent of bundles, with mean overlap values of only 36% of the true volumes. Most notably, even though many correct pathways were identified, an average of more than 4x as many invalid bundles were reconstructed. The false positive bundles were consistently identified across submissions as dense, thick, structured pathways, despite not being a part of the ground truth (Figure 5). Further investigation revealed that many of these invalid bundles could be attributed to the ill-posed nature of tractography in “bottle-neck” regions [29]. These bottlenecks typically consist of groups of voxels where the number of valid bundles outnumber the number of “peak” directions in the diffusion signal (Figure 5), due to many bundles temporarily aligning and re-emerging. Current tractography algorithms cannot differentiate the large number of possible end-point combination possibilities, making it very easy to track non-existent tracts.

Figure 5.

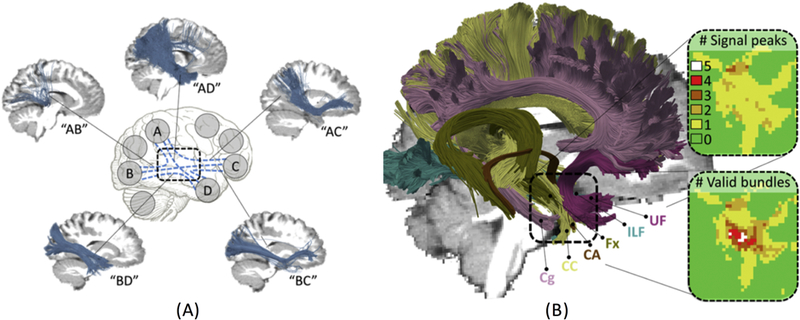
Challenges in tractography include bottle-necks and ambiguities cause by the ill-posed nature of tractography. (A) Example invalid bundles consistently identified in a majority of submissions, where tractography cannot differentiate the valid pathways due to the high amount of possible connections through a bottle-neck region. (B) For example, in the temporal lobe, six ground truth bundles converge in a parallel manner, resulting in more valid bundles per voxel than the number of unique peak directions, contributing to the tracking ambiguity. Reproduced and modified from Maier-Hein et al. (2017) under a Create Commons license from Nature Publishing Group.

These challenges facing tractography, including low bundle overlaps and low percent of valid connections, were improved with high image resolution, although the number of invalid bundles remained high [29]. Going one step further, these ambiguities were not resolved even when running tractography on the ground truth field of orientations, which still resulted in 4x as many invalid as valid bundles [29]. Thus, even with perfect local orientation reconstruction, accurate tractography is not guaranteed. However, several strategies improved tracking, including good pre-processing (distortion, motion, artifacts corrections), anatomical priors, post-filtering of streamlines, and manual intervention or tract cleaning.

Tractography is reproducible, but algorithms can give very different results

For tractography to be a useful biomedical tool, it must not only be anatomically faithful, but also reproducible. Despite the wide range of validation challenges (and even more individual validation studies in the literature), only the TraCED challenge has focused solely on the reproducibility of tractography. The main takeaway is that the process of tractography is largely reproducible, but different tractography processes result in fundamentally different reconstructions [31].

Encouragingly, a majority of tractography algorithms are relatively stable within sessions, across sessions or time, and even across scanners, and for varying acquisition conditions [31]. For several algorithms, ICC reached values of 0.90 or higher indicating high reproducibility, with a majority of algorithms resulting in ICCs of 0.6 or more (moderate reproducibility). Importantly, reproducibility was maintained across imaging sessions and scanners. However, differences in reproducibility were observed based on the specific white matter pathway of interest. Highly reproducible pathways included the forceps minor, corticospinal tract, inferior longitudinal fasciculus, superior longitudinal fasciculus, and inferior fronto-occipital fasciculus, while those at the lower end of the spectrum included the uncinate fasciculus and fornix.

Alarmingly, a large variability was observed across algorithms [31]. Because of this variability, essentially any voxel in the brain could be attributed to any given pathway using at least one of the algorithms. For example, when all submissions are viewed together, a selected white matter pathway would appear to cover the full spatial extent of the brain hemisphere, however all individual submissions resulted in plausible pathway reconstructions (Figure 6). The authors chose to further investigate how well the submissions are contained, or nested, within the others. If reconstructions are able to be nicely nested within each other when re-ordered from smallest to largest, much like a stack of Russian dolls, then this would suggest that all algorithms are identifying the same connection “patterns” with only differences in sensitivity/specificity. This can be likened to varying the visitation threshold of probabilistic tractograms. For larger pathways (which are also the more reproducible), this nesting explains a large percentage of the variance in results. However, for smaller pathways, less than 50% of the variance is explained by these sensitivity/specificity tradeoffs, which means that the different algorithms are resulting in reconstructions of fundamentally different structures. In summary, although most individual tractography algorithms are reproducible, different algorithms result in highly variable reconstructions.

Figure 6.

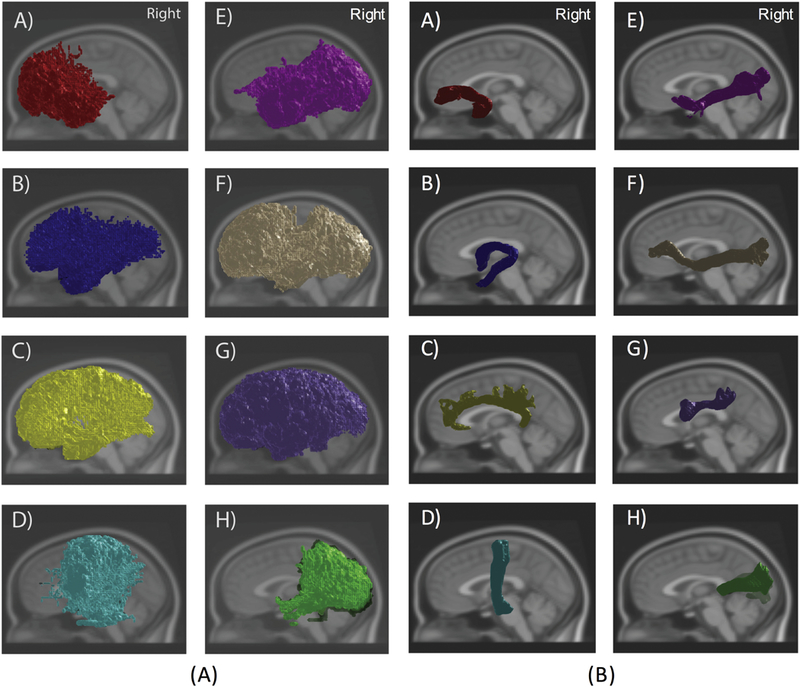
Tractography is reproducible within an algorithm, but highly variable across algorithms. (A) Overlay of all 46 Traced Challenge submissions from all sessions for several white matter tracts shows widespread spatial extent of various pathways. (B) Visualization of a single submission shows reasonable results for all pathways. White matter pathways include: A) Uncinate B) Fornix C) Cingulum D) Corticospinal tract E) Inferior Longitudinal Fasciculus F) Inferior Fronto-Occipital Fasciculus G) Superior Longitudinal Fasciculus H) Forceps major.

Despite known pitfalls, the accuracy of tractography is still limited

These challenges, and the large collection of validation studies in literature, have revealed a number of pitfalls, uncertainties, and sources of error in the tractography processes. As described above, the sources of error occur and accumulate throughout the tracking process, from image acquisition, to local reconstruction, and finally to tracing streamlines from voxel to voxel. In image acquisition, artifacts associated with susceptibility distortions, head motion, and eddy currents can all result in failure in the tracking process. At the reconstruction stage, although algorithms are largely successful, any angular orientation error or unresolved fibers, as well as ambiguous orientational information, could results in inaccurate streamline propagation. Finally, the tracking process itself has been shown to be subject to biases, parameter selection, and ambiguities in pathways selection. Together, this has led to several authors, in both challenges and classic literature, to suggest that inferring connectivity from diffusion information alone is complex inverse problem, that may also lead to inherently limited anatomical accuracy. The most recent tractography challenge, 3D VoTEM [32], combines three separate, classic, validation studies - all of which have previously been used in individual validation studies - and asks “given known pitfalls, and advances in image acquisition, modeling, computation, and tracking algorithms that aim to address these pitfalls, has the anatomical accuracy improved in recent years?”.

The results of this study show that the anatomical accuracy of the most modern algorithms, implemented and optimized by the algorithm developers themselves, is still quite limited, both in assessing the spatial extent of pathways, and in determining connectivity between regions of interest [32] . Not only are false positive (invalid) bundles a source of error, in agreement with the 2015 ISMRM Tractography challenge, but many algorithms are also dominated by false negative connections, and low spatial overlap with true fiber pathways. A tradeoff in tracking sensitivity and specificity is apparent (Figure 7), with most algorithms lying at one of the two extremes of the ROC curve. Importantly, these results hold across all three sub-challenges, or validation strategies, which vary significantly in image quality, image acquisition (b-value, number of diffusion directions), and geometric complexity of the ground truth pathways (e.g. a complex motor pathway of a monkey versus a simple coherent fiber bundle in a phantom). This challenge confirms what individual research groups have shown for a long time in validating and testing their methods and algorithms, that the overall anatomical accuracy of tractography remains limited, and highlights that the ROC curves have not shifted significantly in recent years.

Figure 7.

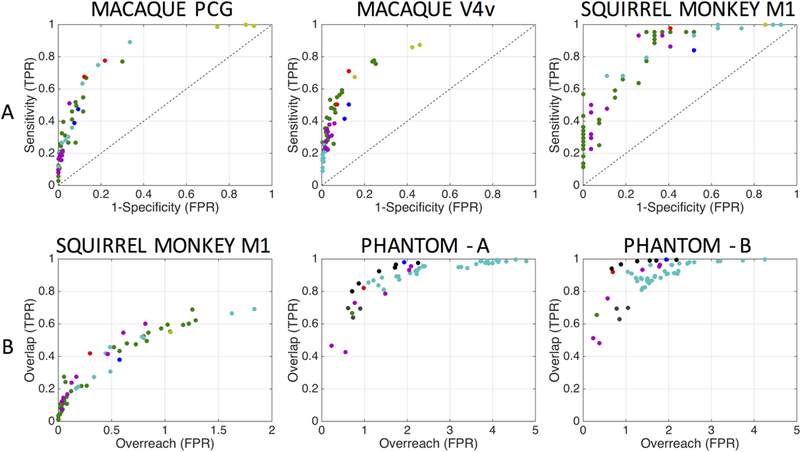
Anatomical accuracy of tractography is limited. (A) Region-to-region connectivity validation is shown as ROC curves for the macaque (PCG seed and V4v seed) sub-challenge and squirrel monkey (M1 seed) sub-challenge. (B) Voxel-wise spatial overlap validation is shown with plots of overlap versus overreach for the squirrel monkey sub-challenge and phantom sub-challenge (scanner A and scanner B). One marker is shown for each submission, with marker colors indicating unique research groups. A common theme in this, and other challenges, is that a specificity/sensitivity (or overlap/overreach) tradeoff is inherent in all tractography algorithms and pipelines. Reproduced and modified from Schilling et al. (2018) with permission from Elsevier.

3. OPPORTUNITIES AND PERSPECTIVES

We end with a discussion on perspectives on the challenges and the future of tractography, opportunities for advancements, and open issues in the field.

Building phantoms is hard

The most “challenging” aspect of a community challenge (from the organizers perspective) is defining the ground truth against which submissions are evaluated against. Building phantoms with realistic geometries and realistic signal is hard. In addition, very few institutions have the resources (both MR and optical imaging), algorithms (image processing and registration), and know-how (MR, histology, and animal surgery) required to validate tractography with ex vivo and histological ground truths.

While simulated data offers a versatile way to assess reconstruction and tractography performance across a range of experimental conditions, they may be an over-simplification of the geometry when compared to the enormous complexity of in vivo tissue. In addition, assumptions must be made about the relationship between the diffusion signal and the synthesized tissue, which may favor algorithms that make similar assumptions. Physical phantoms introduce realism with respect to data acquisition conditions and signal generation, but are still an over-simplification of geometry. However, even simple physical and synthetic phantoms allow the ability to quantitatively compare algorithms, evaluate accuracy, and find limitations, as demonstrated in many challenges of both local reconstruction [26] and connectivity analyses [21, 28, 29]. These phantoms show the same sensitivity/specificity and overlap/overreach tradeoffs as the more complex histological validations (3D-VoTEM challenge), although algorithms were generally better at recovering the full phantom pathways than ex vivo datasets.

There are opportunities for the design of newer, more complex, phantoms to be used as benchmarks to compare algorithms. A number of phantoms have been designed by the microstructural community for validating tissue models, with realistic microstructural features of compartment sizes, axon densities, axon diameters, and fiber dispersions [47–50] (See [51] for a review). Despite an improved realism obtained using electrospining, hardware phantoms are still far from being able to mimick real brain tissues because they only reproduce axonal fibers, but miss the glial cells also populating white matter including astrocytes and oligodendrocytes, and the microvasculature. To our knowledge, there does not exist any process to create such complex cell geometries. However, their presence has an impact on the diffusion NMR signal and should be taken into account.

An alternative to hardware phantoms are in silico phantoms elaborated using numerical simulation tools. Their realism relies on three factors: the ability of the software tool to create realistic microstructural tissue environment, the ability of the software tool to simulate the underlying biophysical processes occurring in the brain (diffusion, relaxation, perfusion, etc.) and the ability of the software tool to create large field-of-view phantoms. Developing an algorithm to generate ultra-realistic virtual brain tissues requires a computationally efficient approach to prevent overlaps of generated cells, and requires defining generative parameters for each type of cell population in an optimal way in order to reduce the global number of parameters to a few tens of them. For instance, the generation of a single fiber population requires definition of: its main direction, its volume fraction, the distribution tuning the axon diameters, the distribution tuning the distance between Ranvier nodes, the distribution tuning the thickness of the myelin sheath, the global fiber dispersion, the local tortuosity, the distribution of permeability of fibers - already amounting to more than a dozen of parameters. The second aspect concerns the simulation of the diffusion-weighted NMR signal. Contrary to existing simulators relying of mixtures of analytical response functions, Monte-Carlo simulators are probably the most general approaches to simulate the diffusion process occurring in tissues, since they do not put any a priori on the response of cells to the diffusion process, and must be preferred to analytical generative models.

A key advantage of in silico phantoms is obviously that it theoretically allows to simulate the diffusion process for any ultra-realistic tissue environment and for any diffusion-weighted pulse sequence [52, 53], contrary to hardware phantoms that generally mimic a reduced set of fiber configurations. However, Monte-Carlo-based numerical simulations are computationally expansive and requires access to high-performance computing (HPC) centers. This is the price to pay to have access to a dense sampling of the plethora of possible microstructural configurations and their associated diffusion-NMR signatures, but then, it offers the possibility to efficiently create any numerical phantom with a field of view able to reach the size of a human brain. There is potential to use these constructions over extended distances for tractography validation, potentially varying microstructural parameters along or between pathways, or including orientation complexity at multiple scales, including bending and curving over many voxels as well as curving (or fiber undulations) within voxels. This would enable evaluating the efficacy of microstructural informed techniques [54, 55], or post-processing of streamlines based on tissue components [54, 56].

While tracers in animals are considered the “gold standard” to determine white matter connectivity, they are not without their own limitations. Tracer uptake, staining sensitivity, and distortions in image processing all contribute to potential error in creating the ground truth connections. In addition, the number of tracers in an animal is limited (with all tracers in diffusion validation containing only a single injection per brain), and validation in one tract does not necessarily validate other pathways.

Polarized-light imaging (PLI) is an alternative to the use of tracers to reveal axonal connections at the microscopic scale, since it does not have such limitations [57]. The birefringence of myelin is exploited using a polarized source of light applied along various angles in the plane of histological sections and several tilting angles that, in combination with a microscope, provides a series of PLI scans allowing computation of a map of 3D orientation distribution functions that can be used to perform tractography at a microscopic resolution, much smaller than current ex vivo diffusion datasets. This ultra-high spatial resolution allows drastically reducing the number of voxels corresponding with complex configurations such as crossings, kissings or splittings. One limitation of PLI is that there does not exist any analytical method to reconstruct ODF in the case of two crossing fibers, where the birefringence model is not valid anymore due to the higher complexity of the underlying optical paths.

These difficulties, in addition to difficulties associated with generating or manufacturing physical or numerical phantoms, stresses the need for sharing and distribution of MRI datasets with reference standards, with community challenges being the perfect platform to do so. The 3D-VoTEM challenge was the first attempt to tackle the validation problem using a variety of approaches, but there is opportunity for more. Much like the white matter microstructure database (https://osf.io/yp4qg/) provides freely-accessible and curated microscopy data that can be used for validating microstructural models (or any quantitative MRI method), it is necessary to collate a collection of gold standards for tractography, and implement a Tractometer-like system to evaluate future algorithms based on a number of quantitative accuracy metrics.

We do not know our anatomy

Not only do most challenges highlight the extreme variation in reconstructed pathways, but the DTI Tractography challenge actually underscores a large variation in how we define and interpret pathways. Specifically, in the CST, arguably the most studied pathway in not only diffusion but also anatomical literature, discrepancies were described in the way experts judged the quality of reconstructions [23]. In addition, the pathway was defined differently by nearly every team in the challenge. For example, defined as the pathway that courses through the cerebral peduncles to the pre- and post-central gyrus, or as the pathway that passes through the pons to the temporal lobes and somatosensory cortex. Although, strictly, these are the regions of interest used to extract streamlines, they still represent how the pathway is defined by the diffusion streamlines. Stated another way, even if a pathway is relatively well-defined anatomically, there is a wide variation in how image analysts chose to interpret that definition. This highlights that no single strategy, even with prior anatomical knowledge, was particularly successful in all neurosurgical cases. Thus, there is an opportunity, or rather a need, for computational diffusion MRI experts to work closer with expert neuroanatomists - neurosurgeons, MDs, and dissectionists.

Collaboration is necessary not only to better understand definitions and “what” we should strive to represent, but also to better understand “how” these techniques are being used, particularly in the operating room. This could prompt relevant questions that could shape future validation studies and algorithms. For example, how important is it to be exactly accurate in delineating pathways, or connectivity? The answer to this certainly varies between surgeons and anatomists, by procedure, or by hypotheses. In some practice, it could be that the spatial pathway is more important than connection strengths, or the presence/absence of infiltration into tumor, or tumor zones themselves. Anatomists may be interested simply in the presence or absence of connections, or may need some measure of connection strength, which could include some measure(s) of axon density, axon number, axon sizes, or conduction abilities. Further, this could clarify the metrics that have traditionally been used to quantify algorithms, lending insight into what metric we should be validating accuracy with.

It is also important to mention that not all the white matter anatomy is known, even from neuroanatomists. This is particularly the case for the sub-cortical white matter that the Klinger’s dissection technique is technically unable to reach, but that diffusion MRI can reveal [58]. The sub-cortical connectivity is intrinsically related to the advanced brain functions supported by the neocortex and the beauty here is that a tight collaboration between neuroanatomists and diffusion MRI experts is prone to offer new insights about the fine anatomy of the human brain connectivity.

Finally, it is crucial to emphasize to those utilizing these algorithms that tracking truly is an art, and not a singular process that always results in exact reconstruction of neuronal pathways. Thus, be careful about the impact of tractography “beauty” on emotions, interpretation, and use of data.

A revolution in tractography?

A consistent result across the challenges, and existing validation literature, is that the anatomical accuracy of the current state of tractography is limited, and tract reconstruction based on orientation information alone is not enough to overcome current challenges in tractography. Even with more data, and better data, simply stepping through a 3D vector field will likely not solve these problems [29]. Tractography needs something more from this data, or from modalities, contrasts, or knowledge outside of diffusion itself [29, 32].

An obvious first step is to use the decades of neuroanatomy research, functional imaging, animal tracer studies, and human dissections to improve the definition of white matter pathways, and better define where streamlines should start and where they should end. This may reduce variability across the methodologies, but may not improve overall measures of both sensitivity and specificity. In addition to better priors, maybe more priors would advantageous, both logical ANDs and NOTs, defining exactly where a pathway goes and where it does not go [59, 60]. Although if this were known at such a fine scale, tractography would not be providing that much additional knowledge.

Methodological innovations are needed, with several strategies to overcome these limitations currently under investigation. Microstructural measures along the fiber orientations could improve specificity by helping to trace orientations belonging to the same pathway [55], which should have the same properties. A number of these techniques are actively being developed, with these algorithms broadly referred to as “Microstructure-Informed Tractography”[61]. Currently, this has been implemented utilizing microstructural models of axon diameters and densities [54, 55], but could in the future include (1) other tissue properties derived from conventional diffusion data, including axon dispersion, volume fractions, and compartment diffusivities [55, 62–67], (2) those derived from non-conventional diffusion acquisitions including double diffusion encoding [68, 69], multiple diffusion encoding [70, 71], oscillating gradients [72, 73], (3) those derived from alternate contrasts such as myelin water imaging [74, 75], T1/T2 relaxometry [76], tract-steering with functional imaging [77–79], or even EEG and EMG [80, 81], and (4) utilizing microstructural or anatomical priors [82]. However, when informing tractography with microstructural or novel features, it is critical to ensure biological plausibility, model validation, and the ability of the model to adequately separate multiple fiber populations [61].

Global tractography approaches can provide a convenient framework to take into account any anatomical priors since it only requires adding a regularization term to the objective function to be optimized. For instance, the trajectory of fibers entering the cortical mantel can be efficiently monitored using anatomical prior like the pial surface to infer the direction perpendicular to that surface as well as microstructural prior knowledge like the orientation dispersion to release the constraint on fiber curvature when the dispersion is high, allowing sharp turns to be created [83]. Some efforts still need to be made to further regularize the inference of connections by using all the available anatomical priors able to constrain their creation during the generative process.

Alternatively, with the terabytes of data generated by submissions in these challenges, as well as initiatives such as the Human Connectome Project [84], Alzheimer’s Disease Neuroimaging Initiative [85], and the Baltimore Longitudinal study of Aging [86], among others, there are opportunities to learn both reconstructions and tracking. We could learn from the ground truth itself in combination with submissions to better determine successes and failures, or optimal tracking parameters. Algorithms could also learn artifacts and errors in diffusion data, could learn structures on individuals given large numbers of existing tractograms, or could learn individualized ROI placement for optimal tracking [87, 88].

Overall, there is a need to possibly rethink tractography. It is necessary to think about the algorithm logic we use to create these streamlines, and compare this to the logic or anatomy that real tissue uses to determine its pathways, locations, and connectivity [89]. Axons elongate following guidance cues, both attractive and repulsive cues, that differ over time and space. While tractography traditionally uses orientation as a guide, and ROIs as logical cues, these are typically unchanging. There has been some exploration into, in effect, changing orientation based on streamline obstacles allowing exploration of new spaces, but tractography could still benefit from anatomical knowledge of axon growth, connectivity targets, and how axons and development influence brain geometry and vice-versa.

Solving tractography in phantom does not solve tractography in humans

Perfect reconstructions in simulations and physical phantoms does not necessarily guarantee perfect reconstruction in the human brain. However, even using simple geometries allows a better understanding of the mistakes and pitfalls of tractography, as well as the behavior of algorithms in different acquisition or geometric scenarios. Similarly, solving this in a more geometrically complex animal model also does not mean the same in the in vivo human. Verifying the accuracy of one pathway does not validate the others, and this is especially true when comparing white matter across species. Rather, the aim of validating tractography is not necessarily to reconstruct the “perfect” animal pathway (for that, we have tracers), but to better understand its reliability in the human. Towards this end, there is, again, need for better phantoms that both combine well-defined ground truths with the geometric complexity of the human brain system.

While the lessons learned from these challenges largely highlight limitations, and may seem to take a pessimistic view of tractography, there are several positive takeaways. First, the crossing fiber problem is relatively solved locally. Extracting orientations can be done quite well, for a number of acquisition settings, fiber geometries, and reconstruction methods. Second, despite differences between algorithms, there are a number of algorithms which are able to capture the full spatial extent of pathways. Alternatively, others have high specificities, where the presence of connecting streamlines may more confidently indicate the presence of true connections. Third, reassuringly, with neurosurgical cases in particular, there will almost always be human involvement in the tracking process. Depending on goals and/or hypothesis, manual editing, varying of parameters, or changing of ROIs is possible in order to generate desired pathways, and with current software this is now both easy and in real-time (although ideally we would advocate for a fully automated, reproducible processing and tractography pipeline). Finally, even though most lessons learned are made through mistakes and errors in tractography, it is reassuring that all challenges reach consistent conclusions regarding reliability: (1) we can reconstruct true connections, (2) but should be cautious in interpreting reconstructions in a clinical environment; (3) local orientations are largely consistent with ground truth, (4) but this does not guarantee accurate tractography; (5) tractography is reproducible, (6) but the anatomical accuracy is still limited.

Validation is important

Mapping the structural connectivity of the human brain has been a fundamental goal of neuroscience for decades. A 3D network of the brains fiber pathways has the potential to help in better understanding brain injury and disease, as well as providing insights into basic neuroscience. New techniques are constantly introduced, not only in tractography but also in the microstructural community. Application of tractography continually results in findings and advances in understanding conditions such as stroke, multiple sclerosis, Parkinson’s disease, and schizophrenia, as well as normal brain development, leading to excitement in the use and application of these techniques. However, the application of these methods is racing ahead of our ability to understand the data and their limitations. For these techniques to be used in safe and effective manners, we must be sure of their effectiveness. For these reasons, it is important to take a step back and ask what it is we are really measuring, how accurate and precise these results are, and how reliably are these results interpreted. There are several hard inverse problems that we must solve: reconstructing fiber geometries from the diffusion signal, and reconstructing continuous white matter pathways from discrete estimates of orientation. Thus, these techniques can, and should be validated on both levels. Community challenges provide the ideal platform for investigations and comparisons of all aspects of the tracking process, for both algorithms of the past, and emerging algorithms. There is still room for improvements and innovations in the challenge process itself [90]. For example, combining the knowledge and skillsets of the tractography community with the microstructural community could lead to improvements in phantoms, ground truth evaluations, and potentially unique features that could increase tracking accuracy. On the other end, there is potential to collate all validation datasets from the literature to not only assess tracking accuracy, but to compare individual algorithms across datasets to uncover successes and failures under different acquisition or geometrical conditions.

APPENDIX A. CHALLENGE EVALUATION METRICS

FiberCup: MICCAI 2009

Evaluation was performed for all 16 pairs of submitted/ground-truth fibers to evaluate both the spatial matching of curves as well as trajectories and smoothness [21]. All metrics are based on a symmetric Root Mean Square Error (sRMSE) between the candidate fiber and the corresponding ground truth:

$$sRMSE(f_1,f_2)=\frac{1}{2}\left(\sqrt{{\displaystyle {\int }_0^{1}dis{t}^2(f_1(s),f_2(c_1(s)))d_s+}}\sqrt{{\displaystyle {\int }_0^{1}dis{t}^2(f_2(s),f_1(c_2(s)))d_s}}\right)$$

where f₁ and f2 are the two fibers being compared, s the arc length in the range [0, 1], c a function giving for each arc length s of f₁ the corresponding arc length of f₂, and dist a metric measuring how similar the points f1(s) and f2(c(s)) are. The choice of c is made to associate fiber points which are closest spatially, and the RMSE is symmetrized (sRMSE) because the mapping c is not guaranteed to be symmetric.

Importantly, the sRMSE depends on the chosen metric dist. In this work, the spatial metric is calculated when dist is formulated as an L2 norm (high values when fibers are distant from each other, and vice-versa), the tangent metric when dist is formulated as the angular difference between tangents (sRMSE is low when fibers are parallel, and vice-versa), and the curve metric when dist is formulated as the difference of curvature between two fiber points.

Spatial metric

The spatial metric expresses the distance metric as the L₂ norm between two fiber positions. With pi and P2 as two spatial positions, the metric is:

$$dist(p_1,p_2)=\sqrt{\parallel P1-P2{\parallel }^2}=\sqrt{{\left(P2-P1\right)}^T\left(P2-P1\right)}$$

Tangent metric

The tangent metric measures agreement of orientation. With v₁ and V₂ as normalized tangent vectors along streamlines, the tangent metric is:

$$dist\left(v_1,v_2\right)=|\text{a}\cos (|v_1^T{v}_2|)\frac{180}{\text{π}}|$$

Curve metric

The curvature at any position of a curve is given by $K\left(f\right)=\frac{\Vert f^{\text{'}}\times f^{"}\Vert }{{\Vert f^{\text{'}}\Vert }^3}$. The curvature metric is then expressed as the absolute difference of curvature between two fibers points as the dist measure in the sRMSE:

$$dist\left(K_1,K_2\right)=\left|\left(k_2-k_1\right)\right|$$

DTI Challenge: MICCAI 2011–2015

Qualitative Evaluation

Tractography results were evaluated qualitatively based on the 3D viewing of tracts by a panel of five judges (two neurosurgeons and three DTI experts) [23]. Tractography results were evaluated based on the presence of false-positive and false-negative tracts and anatomical accuracy of the reconstructed bundles. Submissions were graded ranging from A (excellent) to D (poor).

Quantitative Evaluation

Quantitative evaluation measures the distance between two fiber bundles, fx and fy (from submission x and y) using the Average Mean Distance (AMD) and the Hausdorff distance. The AMD is defined as the average of the closest distance between fiber fx and fiber fy, and the Hausdorff distance is the maximum of the closest distances between fiber fx and fiber fy. These measures were computed for all pairs of fiber bundles for each time, separately calculated on the tumor side and contralateral side, for all patient datasets.

HARDI Reconstruction Challenge: ISBI 2012

Quality of local reconstructions were assessed by focusing on 1) correct assessment of the number of fiber populations in each voxel, and 2) angular accuracy in their orientation [26]. These metrics were computed by comparing the fiber populations (or simulated fiber compartments) of the ground truth dataset with those estimated by each submission.

In order to assess the correct estimation of number of fiber components, the success rate (SR) was employed. The SR is simply the proportion of voxels in which a reconstruction algorithm successfully estimates the correct number of fiber populations. Additionally, the number of overestimated fiber populations and underestimated fiber populations in each voxel were computed in order to better understand incorrect assessment of the number of fiber populations. These measures were calculated by simply counting the number of fiber populations in each voxel and comparing to the number simulated. All three measures were also recomputed using a tolerance cone, where estimated directions are successfully resolved only if they fall within a tolerance cone around a real, simulated, fiber population (set to 20° in the challenge).

The angular accuracy in orientation of the estimated fiber compartments was then computed by calculating the average error (in degrees) between the estimated fiber directions and the true ones present in a voxel:

$$\stackrel{-}{\theta }=\frac{180}{\pi }\text{arccos(}\left|d_{true}\cdot d_{estimated}\right|)$$

where unit vectors d_true and d_estimated are the true fiber population orientation and the closest estimated direction.

All submissions were assessed as a function of SNR, as well as the crossing angle of the simulated fiber populations.

HARDI Reconstruction Challenge (Tractometer): ISBI 2013

The Tractometer proposed six new tractography validation metrics [28]:

Average Bundle Coverage (ABC): the proportion of the true fiber bundle covered by submitted streamlines, reported as a percentage. Calculated as the average number of voxels crossed by streamlines divided by the total number of voxels in the bundle.

Valid Connections (VC): the percent of streamlines connecting expected ROIs and not exiting the expected fiber bundle mask.

Invalid Connections (IC): the percent of streamlines connecting unexpected ROIs or streamlines connecting expected ROIs but exiting the expected fiber bundle mask.

No Connections (NC): the percent of streamlines that do not connect two ROIs, primarily composed of streamlines that stopped prematurely due to angular constraints or exiting the tracking masks.

Valid Bundles (VB): the number of bundles connecting expected ROIs. In this challenge, the maximum number of VB was 7.

Invalid Bundles (IB): the number of bundles connecting unexpected ROIs. Similar to IC, but at the scale of bundles (rather than streamlines). In theory, there could be a total of 39 possible IB in this challenge.

Tractography Challenge: ISMRM 2015

This challenge [29] utilized and adapted many of the Tractometer metrics for submission evaluation [28]. Streamlines (and bundles) are classified and the following metrics were calculated:

Valid Connection (VC) Ratio: The number of VC divided by the total number of streamlines, expressed as a percentage.

Valid Bundles (VB): the number of bundles connecting expected ROIs. The maximum number of VB in this challenge was 25.

Invalid Bundles (IB): the number of bundles connecting unexpected ROIs. There are 1250 potential IB connections in this challenge.

Bundle Overlap (OL): the proportion of voxels that contain the ground truth volume that are traversed by at least one streamline. The OL describes how well tractography is able to describe the volume occupied by the ground truth.

Bundle Overreach (OR): the number of voxels containing streamlines that are outside of the ground truth volume divided by the total number of voxels within the ground truth bundle. The OR describes how much the streamlines extend beyond the ground truth bundle volume.

TraCED Reproducibility Challenge: ISMRM 2017

Tractograms within a submission were evaluated based on reproducibility of tracts using the intra-class correlation coefficient (ICC) and the Dice Overlap coefficient, calculated for intrasession, inter-session, same scanner, and inter-scanner analysis, for each reconstructed fiber bundle and all submissions (20 tractograms per submission) [31].

ICC: The ICC is a measure of conformity among observations, and, in this case, measures consistency between k tractographic segmentations of a given reconstructed white matter bundle:

$$ICC=\frac{M{S}_b-M{S}_w}{M{S}_b+(k-1)M{S}_w}$$

where MS_b is the mean squares between segmentations (between group mean squares) and MSw denotes the mean squares within segmentations (within group mean squares).

Dice Overlap Coefficient (D): measures the overall similarity between repeated segmentations, X and Y, by taking twice the shared information (intersection) over the sum of the cardinalities:

$$D=\frac{2|X\cap Y|}{\left|X\right|+\left|Y\right|}$$

Containment index (CI): this metric examines how well the different submitted tract volumes can be nested within one another, defining the containment index for two tract volumes X and Y as:

$$CI(X,Y)=\{\begin{array}{c}\left|X\right|=0:1\\ \left|X\right|\ne 0\text{and}\left|Y\right|=0:0\\ \text{otherwise}:|X\cap Y|/\left|Y\right|\end{array}$$

For example, if tract Y is fully contained within X, the resulting containment CI(X,Y) = 1. From this, an optimal ordering (or nesting) of tractograms can be computed by maximizing the containment energy (CE), which is the sum of CI for all tracts versus the tracts earlier than the one under consideration:

$$argma{x}_{o\in perm(1\dots |Entry|)}CE=argma{x}_{o\in perm(\mathrm{1...}|Entry|)}{\displaystyle \sum _i{\displaystyle \sum _{j\le i}C}}I\left(Entry\left\{o_i\right\},Entry\left\{i_j\right\}\right)$$

where perm denote the permutation operator, and Entry is a list of all entered tractograms. The main idea behind the CE is to find the ideal order to stack the tractograms inside each other, where the first tract is the “most inside” subsequent tracts and the last is “most outside” all others. This analysis allows investigation of whether differences in results (in this case, differences in reproducibility) are caused by fundamentally different reconstructed pathways, or simply driven by differences in volumes around the same “core” structures of the tracts.

3D VoTEM Challenge: ISBI 2018

This challenge featured “ROI-based” and “voxel-wise” anatomical accuracy measures [32]. The ROI-based measures characterized the validity of tract region-to-region connectivity, while the voxel-wise measures assessed the spatial extent of reconstructed pathways on the scale of individual voxels.

ROI-based measures

For the sub-challenges featuring the macaque and squirrel monkey, ROI-based connectivity to the seed regions was assessed using white matter and gray matter ROIs.

Sensitivity: True positive rate; measures the proportion of positives (regions that are occupied by ground truth) that are correctly identified as such (using tractography). Sensitivity measures the ability to correctly detect all connections of the seed region.

Specificity: True negative rate; measures the proportion of negatives (regions that do not contain ground truth) that are correctly identified as such (do not contain streamlines). Specificity measures the ability to correctly identify voxels that do not have connections with the seed region.

Youden’s J statistic: Sensitivity+Specificity-1; a statistic that captures the performance of a diagnostic test, and estimates the probability of an informed decision, ranging from −1 to 1. A value of 1 indicates a perfect test with no false positives or false negatives.

Voxel-wise measures

Phantom and squirrel monkey sub-challenges featured ground truth volumes that were defined voxel-wise. Spatial accuracy of pathways was assessed using Tractometer metrics [28].

Bundle Overlap (OL): The proportion of voxels that contain the ground truth volume that are traversed by at least one streamline.

Bundle Overreach (OR): the number of voxels containing streamlines that are outside of the ground truth volume divided by the total number of voxels within the ground truth bundle:

Dice Overlap Coefficient (D): measures the overall similarity between ground truth and tractography volume by taking twice the shared information (intersection) over the sum of the cardinalities.