Comparison of NODDI and spherical mean signal for measuring intra-neurite volume fraction

Abstract

Purpose:

Neurite orientation dispersion and density imaging (NODDI) is a clinically feasible approach to measure intra-neurite volume fraction (f_in). However, the sophisticated fitting procedure takes several hours. And the NODDI model relied on several questionable assumptions. Recent analytical work demonstrated that f_in could be simply calculated from the spherical mean signal (MEANS) averaged over all gradient directions with a more solid theoretical foundation. The current study aims to compare NODDI and MEANS for measuring f_in in human brain and investigate the potential of MEANS as a fast approach in clinics.

Methods:

NODDI f_in and MEANS f_in were measured and compared on the same dataset. NODDI f_in was obtained using the NODDI MATLAB Toolbox. MEANS f_in is the product of the spherical mean signal and $2\sqrt{bD/\pi },$ where D is the intra-neurite intrinsic diffusivity.

Results:

NODDI f_in and MEANS f_in maps are similar. The voxel-by-voxel correlation suggests that NODDI f_in and MEANS f_in are approximately equivalent to each other.

Conclusion:

MEANS may have potential to serve a fast and simple approach to estimate f_in in clinics.

Introduction

Diffusion MRI has been widely used to measure tissue microstructure non-invasively. The conventional diffusion tensor imaging (DTI) technique models restricted water diffusion as a simple ellipsoid with three eigenvectors and corresponding eigenvalues [1]. The principal eigenvector is assumed to be the fiber orientation and the calculated fractional anisotropy (FA) is assumed to be an indicator of fiber density. However, it is well known that DTI is not an appropriate model in situations with crossing fibers, which commonly exist in brain white matter [2–4]. Based on the concept of high angular resolution diffusion imaging (HARDI), a large number of methods have been developed to estimate fiber orientation distribution [5–8] and fiber density [9–13]. Among them, neurite orientation dispersion and density imaging (NODDI) has been widely used to detect axonal injury in various neurological diseases [14–19] and assess neurite density changes in brain development [20–22].

NODDI is based on a three-compartment tissue model with distinct diffusion properties for each compartment [11]. The intra-neurite compartment is highly restricted for water diffusion perpendicular to neurites, and thus the intra-neurite perpendicular diffusivity is reasonably assumed to be 0. The extra-neurite compartment is also anisotropic but less restricted than the intra-neurite compartment. The third compartment is isotropic to mimic the diffusion behavior of free water. The diffusion weighted signals are measured along different gradient directions at multiple b-values and then fit to the analytical model. From the fitting, several parameters can be derived including the intra-neurite volume fraction. Note that the number of fitted parameters depends on the complexity of the model [23].

Instead of fitting the measured signals individually, recent works have proposed to focus on the spherical mean signal averaged over all gradient directions at the same b-value [24,25]. The reason is that the spherical mean signal is independent of the fiber orientation distribution [8]. In other word, the spherical mean signal based analysis can factor out the confounding fiber orientation distribution information and reduce the number of unknown parameters in the fitting, which in turn makes the fitting procedure more robust. Because of its substantial advantage in estimating tissue microstructure, the spherical mean signal based analysis has been applied in several recent mathematical modeling studies [26–32]. The spherical mean signal based NODDI fitting was implemented efficiently and resulted in similar results with the standard NODDI fitting [27,31]. Moreover, if the diffusion weighting b-value is sufficiently large, the intra-neurite volume fraction is simply the product of the spherical mean signal and, $2\sqrt{bD/\pi },$ where D is the intra-neurite intrinsic diffusivity [33].

If the intrinsic diffusivity D is constant, as assumed in the NODDI model, the intra-neurite volume fraction can be calculated directly from the spherical mean signal without any fitting procedures. Besides, NODDI is based on several other assumptions. The fiber orientation distribution is assumed to be a single Watson distribution which could not account for fiber crossings. The extra-neurite perpendicular diffusivity is simplified with a simple tortuosity model and the extra-neurite water is modeled in fast exchange over all fiber orientations. The spherical mean signal is not affected by these assumptions. The current study aims to compare NODDI and spherical mean signal for measuring intra-neurite volume fraction and investigate the potential of spherical mean signal as a fast approach in clinics.

Materials and methods

Human Connectome Project (HCP) data

High-quality HCP data from 6 healthy adults, as part of the MGH-USC Adult Diffusion Dataset, were downloaded from ConnectomeDB (http://db.humanconnectome.org). Diffusion data were acquired with 4 different b-values ranging from 1 ms/μm² to 10 ms/μm², but only b = 1 ms/μm² and b = 3 ms/μm² were used in the current study. The number of gradient directions was 64 at each shell and the number of b = 0 images was 10. Other imaging parameters were: repetition time (TR) = 8800 ms, echo time (TE) = 57 ms, gradient duration (δ) = 12.9 ms, gradient separation (Δ) = 21.8 ms, image resolution = 1.5 × 1.5 × 1.5 mm³, parallel imaging acceleration factor = 3, and multiband factor = 1. The data were preprocessed with corrections for gradient nonlinearity distortions, head motion, and eddy current artifacts [34]. All the 10 b = 0 images were averaged and then segmented to gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) using FSL fast command [35,36].

Data analysis

As modeled in NODDI, the diffusion weighted signal (S) measured along gradient direction g can be written as

$$S(b,g)=S_0\cdot \left[f_{in}\cdot S_{in}(b,g)+\left(1-f_{in}-f_{iso}\right)\cdot S_{ex}(b,g)+f_{iso}\cdot S_{iso}(b)\right]$$ (1)

where S₀ is the signal for b = 0; S_in and f_in are the normalized signal and volume fraction of the intra-neurite compartment; S_ex is the normalized signal of the extra-neurite compartment; and S_iso and f_iso are the normalized signal and volume fraction of the CSF compartment. The intra-neurite intrinsic diffusivity D is fixed as 1.7 μm²/ms. Details of other assumptions can be found in the original work [11], which have also been discussed in several recent studies [26,27,37,38]. NODDI f_in was obtained using the NODDI MATLAB Toolbox.

When the diffusion weighting b-value is sufficiently large (b ≥ 3 ms/μm²) [33], the extra-neurite water contribution is negligible and the spherical mean diffusion weighted signal $\left(\overline{\text{S}}\right)$ can be expressed as

$$\overline{S}(b)=S_0\cdot f_{\text{ in }}\cdot \frac{\sqrt{\pi }}{2\sqrt{bD}}$$ (2)

Here the $\overline{\text{S}}$ -based f_in is termed MEANS f_in. Only b = 3 ms/μm² was used in Eq. (2) to calculate MEANS f_in. The Rician bias was reduced by using the adjusted signal $\sqrt{S^2(b,g)-{\sigma }^2}$ [25,39], where σ is the median of the standard deviation calculated voxel-by-voxel from all the b = 0 images.

Clinical data

As a supplementary analysis, NODDI f_in and MEANS f_in were further compared on clinical data. Three children (12–36 months, 2 boys) with focal cortical dysplasia at Nemours/Alfred I. duPont Hospital for Children were retrospectively selected for the analysis. Two children were scanned on a 3T GE MR750 scanner, and the other one was scanned on a GE SIGNA PET/MR scanner using the same diffusion protocol. The b-values were 1, 2 and 3 ms/μm² with 15, 20 and 25 gradient directions, respectively. The number of b = 0 images was 6. Other diffusion imaging parameters were: TR = 9700 ms, TE = 99 ms, number of slices = 56, slice thickness = 2.5 mm, field of view = 240 × 240 mm², in-plane image resolution = 2.5 × 2.5 mm², and parallel imaging acceleration factor = 2. Diffusion images were preprocessed with corrections for head motion, and eddy current artifacts using FSL eddy command [40]. NODDI f_in and MEANS f_in were obtained subsequently following the above data analysis. T1 weighted, T2 weighted and T2 FLAIR structural images were co-registered to the mean b = 0 image using FSL flirt command [41]. The study was approved by local Institutional Review Board.

Results

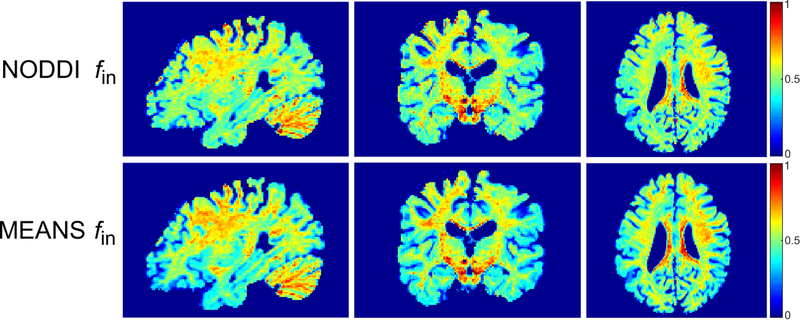
Fig. 1 shows the NODDI f_in and MEANS f_in maps acquired from a representative HCP subject at three anatomical planes. The two methods result in similar contrast. Consistent with previous NODDI studies [11,27,31], the value of f_in is higher in white matter than in gray matter.

Figure 1.

The top row shows the fitted NODDI f_in maps from a representative HCP subject at sagittal, coronal and axial planes. The bottom row shows the corresponding MEANS f_in maps.

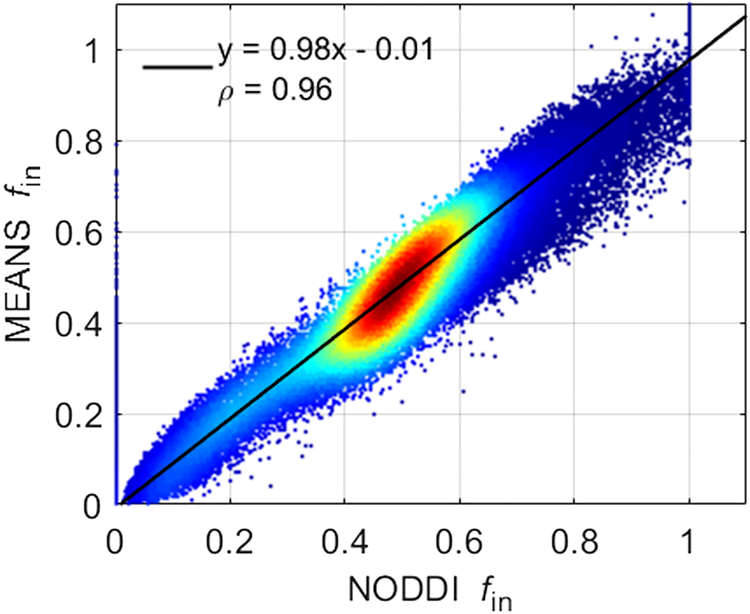
Fig. 2 shows the correlation between NODDI f_in and MEANS f_in. The density plot is from all gray matter and white matter voxels of the same subject shown in Fig. 1. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting. The fitting slope is close to 1 and the intercept is close to 0. Pearson’s linear correlation coefficient (ρ) is also provided. The correlation coefficient ρ = 0.96 ± 0.01 over six HCP subjects. Fig. 2 suggests that NODDI f_in and MEANS f_in are approximately equivalent to each other.

Figure 2.

Density scatter plot and Pearson correlation between NODDI fin and MEANS fin using all gray matter and white matter voxels of the same subject shown in Figure 1. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting.

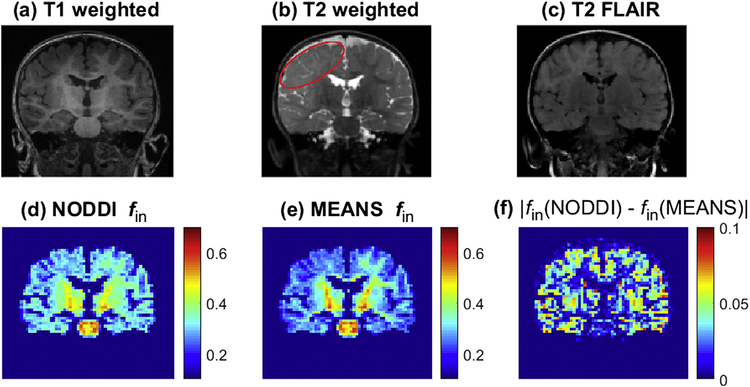
Fig. 3 shows representative structural images, NODDI f_in, MEANS f_in, and the absolute difference between NODDI f_in and MEAN f_in (|f_in(NODDI) − f_in(MEANS)|) acquired from a patient with focal cortical dysplasia. Structural images demonstrate subtle cortical dysplasia in the right cerebral hemisphere as evidenced by poor gray-white matter differentiation and T2 hyper-intense signal. The cortical dysplasia lesion region is outlined with red curve in Fig. 3 (b). Consistent with previous NODDI work [18], the lesion shows reduced NODDI f_in compared with the contralateral side. Fig. 3 (e) suggests that MEANS f_in has slightly better contrast than NODDI f_in in this patient. The whole brain mean |f_in(NODDI) − f_in(MEANS)| is 0.026 ± 0.002 over three patients and the difference is more significant in gray matter than in white matter.

Figure 3.

Images of T1 weighted (a), T2 weighted (b), T2 FLAIR (c), NODDI f_in (d), MEANS f_in (e) and the absolute difference between NODDI f_in and MEANS f_in (f) acquired from a representative patient with focal cortical dysplasia. The red curve in (b) outlines the cortical dysplasia lesion.

Discussion

The current study compared NODDI and MEANS for measuring intra-neurite volume fraction on the same human brain data. Both methods are based on multi-compartment tissue modeling. NODDI fits the measured diffusion weighted signals to the analytical model individually. Instead, MEANS focuses on the spherical mean signal and derives intra-neurite volume fraction from spherical mean signal directly. The comparison results suggest that NODDI f_in and MEANS f_in are approximately equivalent. It should be noted that the current study is not aimed to assess which method is more accurate. Without the information of ground truth, it is unable to assess their accuracy. However, the comparison of different methods may help investigate their similarities and differences.

Compared with NODDI, MEANS is based on a more solid theoretical foundation. NODDI assumes a simple fiber orientation distribution and models the extra-neurite water diffusion in specific form. MEANS is not affected by these assumptions. NODDI and MEANS share two common assumptions: 1) the intra-neurite perpendicular diffusivity is 0 and 2) the intra-neurite intrinsic diffusivity D is constant over the whole brain. Due to the small restricting size [42] and long diffusion time on human scanner [9,43], the first assumption is usually agreed to be reasonable. Recent power law scaling studies demonstrated that the spherical mean signal decay behavior is consistent with Eq. (2) in white matter [37,44]. However, the spherical mean signal decay in gray matter is substantially faster, which makes the first assumption inappropriate for microstructural modeling in gray matter [37,44]. Water permeability [37] and fiber curvedness [45] have been proposed to explain the gray/white matter difference. Thus, the accuracy of f_in quantification in gray matter is compromised by the first assumption. Though the measured NODDI f_in or MEANS f_in is not accurate in gray matter, it may still be able to provide some useful information about structural changes [46,47]. As for the second assumption, it is evident from Eq. (2) that the calculated MEANS f_in will be biased when the assumption is violated. A recent study [48] found that the intra-neurite intrinsic diffusivity D is about 2.25 μm²/ms rather than 1.7 μm²/ms as assumed by NODDI. MEANS f_in would increase by 15% when the intrinsic diffusivity D changes from 1.7 μm²/ms to 2.25 μm²/ms. And NODDI f_in is expected to be affected similarly. Several studies have proposed to estimate f_in and D simultaneously using multi-shell diffusion data [26,28–30,32] or novel diffusion sequences [27,49], but the results have not been validated yet. An accurate measurement of D would assist in better understanding the strengths and limitations of NODDI and MEANS.

The main difference between NODDI and MEANS is that NODDI requires at least two b shells. Besides f_in, NODDI provides two more valuable indices: fiber orientation dispersion index ODI and isotropic water volume fraction f_iso [11]. As mentioned in the original NODDI work [11], ODI can be estimated with just a single shell. Hence, the single shell data used in MEANS can also be used to estimate ODI through the standard NODDI fitting. Alternatively, the single shell data can be used to obtain the full fiber orientation distribution [50], which in turn can be used to calculate the orientation dispersion entropy [26]. The simultaneous fitting of f_in and f_iso indeed requires at least two shells. But previous studies observed an overestimated NODDI f_iso in white matter [11,27]. A simple biexponential-T2 approach may estimate f_iso more accurately [51].

NODDI protocol has been optimized and investigated through simulations extensively [11,21,22,52]. It was shown that the maximal b-value could be reduced to 2 ms/μm² without significant effect on the estimated parameters [11]. As for MEANS, a high b-value (~3 ms/μm²) [9] or even higher [37,44] is required to fully suppress the extra-neurite water contribution. The effect of b-value and number of gradient directions on the accuracy of MEANS f_in has been investigated recently [30,37,53,54]. The measured signal at b = 3 ms/μm² is highly correlated with that at b = 5 ms/μm² for human brain white matter, which suggests that b = 3 ms/μm² is sufficient for spherical mean signal based studies in human brain white matter [53]. And it was recommended to use 10 × b / b₁ (b₁ = 1 ms/μm²) uniformly distributed gradient directions for typical human diffusion studies with signal-to-noise ratio ~ 20 [54].

Compared with NODDI, MEANS f_in shows greater potential for clinical applications. First, $\overline{\text{S}}$ -based data analysis is independent of fiber orientation distribution [8,25], MEANS f_in is likely to be more accurate than NODDI f_in. Second, MEANS estimates only one parameter. Diffusion-based microstructural modeling is generally associated with low signal-to-noise ratio and low image resolution [46,55]. Multi-shell diffusion data are needed to estimate extra parameters [11,26,29]. High resolution MEANS f_in map is achievable by increasing the number of gradient directions at a single b-value. And the consequential signal-to-noise ratio is expected to be proportional to the square root of the number of gradient directions [49,54]. Third, the contrast is the same with the arithmetic mean signal, which may be generated on the scanner and read by radiologists soon after the scan is complete.

Conclusion

NODDI and MEANS were compared for measuring intra-neurite volume fraction in human brain. The voxel-by-voxel correlation suggests that NODDI f_in and MEANS f_in are approximately equivalent to each other. Without the need of sophisticated fitting, MEANS may have potential to serve a fast and simple approach to estimate f_in in clinics.