Skip to main content
PMC home page
Molecules logoLink to Molecules
. 2015 Jun 29;20(7):11875–11890. doi: 10.3390/molecules200711875

Investigations on Synperiplanar and Antiperiplanar Isomers of Losartan: Theoretical and Experimental NMR Studies

Jacek Kujawski 1,†,*, Kornelia Czaja 1,†, Tomasz Ratajczak 2,*, Elżbieta Jodłowska 1, Marcin K Chmielewski 2
Editor: Derek J McPhee
PMCID: PMC6332005  PMID: 26132909

Abstract

Losartan inhibits the renin-angiotensin-aldosterone system by blocking the angiotensin II receptor. It is commonly used in cardiovascular diseases, such as hypertension. Several publications applied the ab initio and density functional theory methods to investigate the molecule of losartan. Only in one of them were the nuclear magnetic resonance spectra calculations carried out, and their results were correlated with the experimental values. The authors focused their attention on calculations of the anion form of losartan, taking into consideration both its synperiplanar and antiperiplanar configurations. Coefficients of determination and mean absolute deviation parameters were calculated for the experimental and calculated chemical shifts for every used basis set. They showed a noticeably stronger correlation for the anti-isomers than for the syn-isomers. Moreover, the solvation model increased the value of this parameter. The results of calculations confirmed that an anti-conformation of the analyte seems to be the preferred one, and such an orientation might be most potent within the receptor cavity, which is in agreement with the results of previous studies.

Keywords: losartan, NMR calculations, DFT, MP2

1. Introduction

Losartan is a drug that inhibits the renin-angiotensin-aldosterone (RAA) system by blocking the angiotensin II receptor. Thus, it is commonly used in cardiovascular diseases, such as hypertension. Angiotensin II receptor-1 antagonists (ARBs) reveal fewer side effects than angiotensin-converting enzyme inhibitors (ACEI), as they do not block the metabolism of bradykinins. In turn, they rarely cause angioedema or dry cough. Losartan was the first ARB-type drug available on the market and was accepted for clinical use in 1995 [1]. The increasing prevalence of cardiovascular diseases results in a greater popularity of drugs that block the RAA system. Therefore, it is important to thoroughly investigate the properties of the currently used ARBs and to draw conclusions concerning their affinity to the receptor and the efficiency of blocking it. The in vivo losartan hydroxyl group is oxidized to a carboxylic moiety through an aldehyde intermediate by cytochrome P-450 [2]. This metabolite has a relatively long time of action and a considerably greater affinity to the receptor, which lengthens the activity of losartan despite the short half-life of losartan itself [3,4]. Nevertheless, both losartan and its derivative bind with the enzyme, and both were investigated in docking studies in their antiperiplanar form [5].

The experimental analyses carried out previously showed that losartan prefers an anti conformation of the tetrazole and imidazole moieties with relation to the phenyl ring [6]. The results of the NOESY approach indicated the proximity of n-butyl to both the methylene moiety and the phenyl ring [6]. In 2014, there were two publications addressed the ab initio and density functional theory (DFT) methods to investigate the molecule of losartan for the first time [7,8]. Only one of them included the 1H- and 13C-NMR calculations (the Gaussian 03W program at the B3LYP/6-31G(d,p) level of theory) and their correlation with the experimental values [7]. However, the calculations were not carried out using the polarizable continuum model (PCM), so the solvent was not taken into consideration, and no other basis sets were used. The authors focused primarily on carbon atoms and did not discuss the values acquired for particular hydrogen atoms in detail. The authors described the discrepancies between the calculated and experimental results; however, calculations were carried out for an isolated losartan molecule in the gaseous phase. Continuing our computational chemistry investigations on biologically-active azoles [9,10,11], we focused our attention on calculation of the chemical shifts of losartan (1H-NMR spectrum) applying different basis sets and methods in the gaseous phase and using the conductor-like polarizable continuum model (CPCM) solvation model, so that the influence of the solvent environment is also accounted for. Apart from the DFT formalism, losartan was also investigated using molecular dynamics (MD) techniques [5,12]. The main goal of our investigations was to prove what basis sets or methods yield results in the best agreement with the experimental data. Moreover, we hoped to explain which conformation of the analyte is preferred from the standpoint of quantum chemistry.

2. Results and Discussion

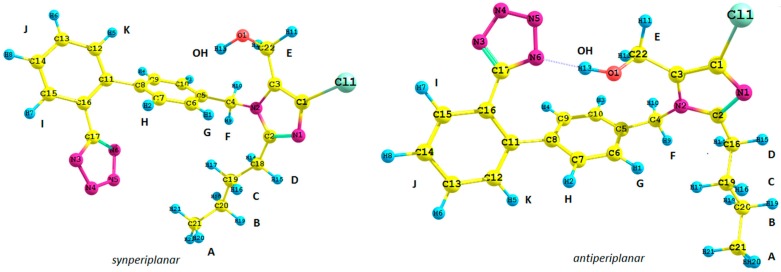
Continuing our investigations on the interactions of biologically-important azahetarenes with the environment, we focused our attention on losartan potassium salt. The present study deals, inter alia, with simulation of the 1H-NMR spectrum of losartan in its anion form (1 given in Figure 1).

Figure 1.

Figure 1

Open in a new tab

Structure of possible isomers of the losartan anion (1): antiperiplanar conformation (anti) and synperiplanar conformation (syn).

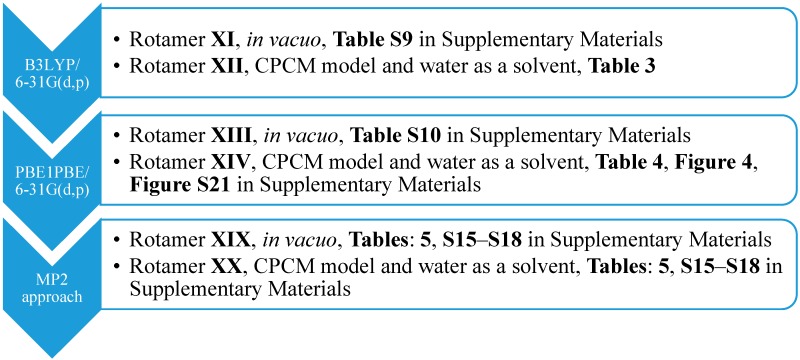
Basing on the already published reports [7,8,12], we decided to carry out a simulation of the 1H-NMR spectrum of anion 1. We took into consideration the position of the tetrazole ring and the butyl chain connected with the imidazole ring with respect to the biphenyl moiety of 1, i.e., its synperiplanar (syn) and antiperiplanar (anti) isomers. Previously reported studies concerning the spectroscopic analysis of losartan require a brief commentary. Generally, the results are difficult to emulate due to the lack of supplementary materials [7,8]; they were just a repetition of previous findings [8]; or only one functional was used for calculations [7,12]. In our paper, we generated the theoretical 1H-NMR spectrum for all of the most stable syn rotamers of 1 using the gauge-including atomic orbital (GIAO) method [13] implemented in Gaussian G09 D.01 (Gaussian, Inc.: Wallingford, CT, USA, 2009). Therefore, we carried out the optimization of particular rotamers and NMR spectrum generation at the same level of theory. To show the results more clearly, only one most stable rotamer was considered with the lowest energy, optimized at the (1) B3LYP/6-31G(d,p), (2) B3LYP/6-311+G(d,p), (3) CAM-B3LYP/6-31G(d,p), (4) PBE1PBE/6-31G(d,p) and (5) MP2/6-31G(d,p) level of theory, both in the gaseous phase, using the conductor-like polarizable continuum model (CPCM) solvation model and water as a solvent (Scheme 1).

Scheme 1.

Scheme 1

Open in a new tab

The approaches used for the optimization together with the numbers of syn-rotamers. CPCM, the conductor-like polarizable continuum model.

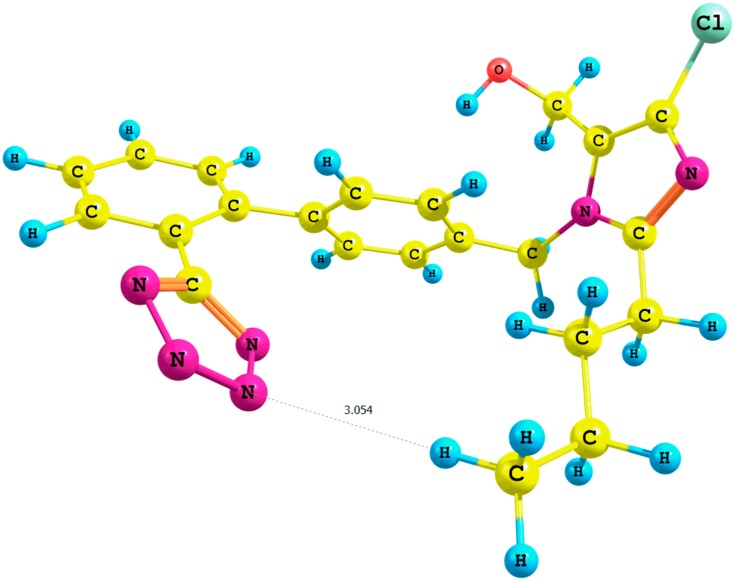
The calculated values showed a strong correlation with the NMR experimental data for Compound 1. The highest relative percentage error was observed for the protons of the hydroxyl and methyl functionality (A) as a part of the n-butyl chain. This is due to the lability of the hydroxyl proton, the shielding of the methyl protons and the proximity of the tetrazole ring. The distance between the methyl protons of the butyl chain and the N2 nitrogen of the tetrazole ring for Rotamers II, IV, VI, VIII (Figure 2) equaled after optimization approximately 3 Å (CPCM model, Figure 2).

Figure 2.

Figure 2

Open in a new tab

Optimized structure of the syn-losartan anion 1 (PBE1PBE/6-31G(d,p) level of theory, Rotamer VIII, CPCM solvation model).

Moreover, the application of the CPCM solvation model for syn isomers 1 (Rotamers II, IV, VI, VIII; Table 1 and Table 2) resulted in a considerable improvement of the relative percentage errors of the chemical shifts of the methyl protons A (93%, 16%, 21% and 14%; Table 1, Table 2, Tables S3 and S5, respectively) when compared to the rotamers optimized in the gaseous phase (Rotamers I, III, V, VII, respectively). The relative percentage error of the chemical shift of these protons equaled: 93%, 86%, 100% and 94% (gaseous phase; Tables S1, S2, S4 and S6, respectively). Such improvement was particularly noticeable for rotamers calculated using the hybrid functional PBE1PBE (PBE0 functional).

Table 1.

Calculated and experimental data recorded at 293 K for losartan anion (1) Rotamer II (isomer syn); the following parameters were determined for their proton groups: experimental (Exp.) and calculated values of the chemical shifts (II), absolute errors (δ2) and values of the relative percentage errors (E); calculated NMR shielding for proton Href = 31.740 ppm for TMS (tetramethylsilane) (B3LYP/6-31G(d,p)/gauge-including atomic orbital (GIAO)/CPCM; R2 = 0.73, mean absolute deviation (MAD) = 0.58.

Proton Signals Exp. Water
II δ2 E
A 0.826 1.592 0.766 93
B 1.270 1.278 0.008 1
C 1.497 1.718 0.221 15
D 2.515 2.407 0.108 4
E 4.328 4.386 0.058 1
OH 5.304 0.263 5.041 95
F 5.228 5.010 0.217 4
G 6.917 6.881 0.035 1
H 7.108 7.473 0.364 5
I 7.553 8.966 1.413 19
J 7.370 6.883 0.487 7
K 7.293 6.836 0.458 6
Open in a new tab

Table 2.

Calculated and experimental data recorded at 293 K for losartan anion (1) Rotamer VIII (isomer syn); the following parameters were determined for their proton groups: experimental (Exp.) and calculated values of the chemical shifts (VIII), absolute errors (δ8) and values of the relative percentage errors (E); calculated NMR shielding for proton Href = 31.642 ppm for TMS (PBE1PBE/6-31G(d,p)/GIAO/CPCM; R2 = 0.75, MAD = 0.77.

Proton Signals Exp. Water
VIII δ8 E
A 0.826 0.940 0.114 14
B 1.270 1.367 0.097 8
C 1.497 1.311 0.186 12
D 2.515 2.599 0.083 3
E 4.328 4.418 0.089 2
OH 5.304 0.214 5.090 96
F 5.228 5.239 0.011 0
G 6.917 7.269 0.352 5
H 7.108 7.439 0.331 5
I 7.553 8.154 0.601 8
J 7.370 7.712 0.342 5
K 7.293 7.617 0.323 4
Open in a new tab

Herein, we focused our attention only on the electrostatic interactions between the solute and water as the solvent (in order to simulate the cellular environment). These are in fact the interactions that generally dominate solvent effects, especially in polar solvents (i.e., water). As a matter of fact, continuum models were originally developed to describe this type of interaction [14].

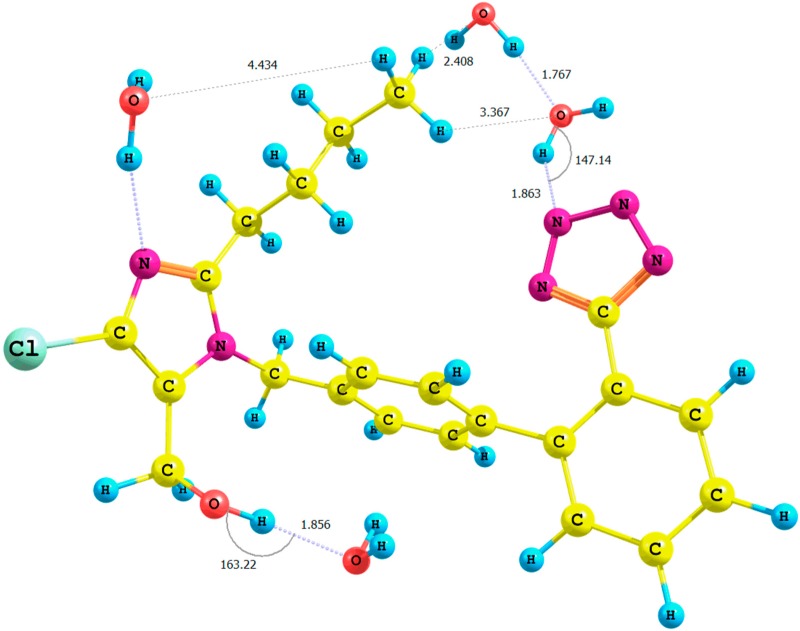
The optimization of clusters of the syn isomers 1 with water molecules resulted in a considerable decrease of the relative percentage error of the chemical shifts of A protons and the hydroxyl moiety in the in silico 1H-NMR spectrum. During the optimization of the IX cluster (B3LYP/6-31G(d,p)/gas level of theory; Table S7, Supplementary Materials), we observed a migration of three water molecules surrounding the methyl group A to the tetrazole ring. Concurrently, the distance n-butyl–N5terazole within the X cluster (Figure 3, PBE1PBE/6-31G(d,p)/gas level of theory) decreased from 2.9 to 2.5 Å in comparison with the corresponding VII rotamer (PBE1PBE/6-31G(d,p)/gas level of theory; the numeration of nitrogen atoms is taken from the output files, and the visualization of all rotamers is given in the Supplementary Materials).

Figure 3.

Figure 3

Open in a new tab

Optimized structure of the syn-losartan anion cluster 1 with water molecules (Rotamer X); interaction of 1 with three water molecules (PBE1PBE/6-31G(d,p) level of theory, gas).

This caused a decrease in relative percentage errors of the methyl group from 93% (Rotamer I) to 43% (Cluster IX) calculated using the B3LYP functional in the gaseous phase and from 94% (Rotamer VII) to 50% (Rotamer X) estimated applying the PBE0 functional in the gaseous phase. A similar trend was observed for the hydroxyl proton in terms of the values of its chemical shift. We noticed a decline in the relative percentage errors within the results of calculations using the PBE0 functional in the gaseous phase: from 95% (Rotamer I, B3LYP functional) to 27% (Cluster IX, B3LYP functional) in the gaseous phase and from 94% (Rotamer VII, PBE0 functional) to 30% (Cluster X, PBE0 functional).

Subsequently, we used an analogous methodology for the antiperiplanar (anti) rotamers of 1 (Figure 1). The anti-rotamers were obtained by rotating the bonds C17–C16, C11–C8, C5–C4, C4–N2, C3–C22 and C2–C18 (1 in Figure 1) in torsion angle increments of 20°. Then, they were optimized at the DFT or MP2 level of theory using the Gaussian 09 D.01 program (Scheme 2), namely: (1) B3LYP/6-31G(d,p) and (2) PBE1PBE/6-31G(d,p) basis set and the MP2 approach in the gaseous phase and applying the CPCM solvation model (water as a solvent).

Scheme 2.

Scheme 2

Open in a new tab

The approaches used for the optimization together with the numbers of anti-rotamers.

Analogously, we calculated NMR shielding for TMS proton (Href) at the (1) B3LYP/6-31G(d,p), (2) PBE1PBE/6-31G(d,p) or (3) MP2/6-31G(d,p) level of theory (both gaseous phase and the CPCM solvation model with water as a solvent). The application of B3LYP/6-311+G(d,p) and CAM-B3LYP functionals for the syn isomers 1 did not result in a significant improvement of the agreement between the calculated and the experimental values of chemical shifts in the 1H-NMR spectrum. Therefore, the calculations of the anti-isomers 1 were limited to the two abovementioned functionals. In this case, the application of CPCM solvation model resulted in a decline in the relative percentage error of the hydroxyl proton from 27% (anti-isomer, B3LYP/6-31G(d,p)/gas level of theory, Rotamer XI; Table S9) to 7% (anti-isomer, B3LYP/6-31G(d,p)/CPCM level of theory, Rotamer XII; Table 3) or from 31% (anti-isomer, PBE1PBE/6-31G(d,p)/gas level of theory, Rotamer XIII; Table S10) to 12% (anti-isomer, PBE1PBE/6-31G(d,p)/CPCM level of theory, Rotamer XIV; Table 4; Figure 4; Figure S21 in the Supplementary Materials).

Table 3.

Calculated and experimental data recorded at 293 K for losartan anion (1) Rotamer XII (isomer anti); the following parameters were determined for their proton groups: experimental (Exp.) and calculated values of the chemical shifts (XII), absolute errors (δ12) and values of the relative percentage errors (E); calculated NMR shielding for proton Href = 31.740 ppm for TMS (B3LYP/6-31G(d,p)/GIAO/CPCM; R2 = 0.99, MAD = 0.28.

Proton Signals Exp. Water
XII δ12 E
A 0.826 1.038 0.212 26
B 1.270 1.549 0.279 22
C 1.497 1.794 0.298 20
D 2.515 2.658 0.143 6
E 4.328 4.270 0.058 1
OH 5.304 5.699 0.395 7
F 5.228 4.986 0.242 5
G 6.917 7.482 0.566 8
H 7.108 7.261 0.153 2
I 7.553 8.145 0.592 8
J 7.370 7.566 0.197 3
K 7.293 7.519 0.226 3
Open in a new tab

Table 4.

Calculated and experimental data recorded at 293 K for losartan anion (1) Rotamer XIV (isomer anti); the following parameters were determined for their proton groups: experimental (Exp.) and calculated values of the chemical shifts (XIV), absolute errors (δ14) and values of the relative percentage errors (E); calculated NMR shielding for proton Href = 31.642 ppm for TMS (PBE1PBE/6-31G(d,p)/GIAO/CPCM; R2 = 0.99, MAD = 0.37.

Proton Signals Exp. Water
XIV δ14 E
A 0.826 1.030 0.204 25
B 1.270 1.509 0.239 19
C 1.497 1.805 0.309 21
D 2.515 2.676 0.161 6
E 4.328 4.270 0.058 1
OH 5.304 5.955 0.651 12
F 5.228 5.053 0.175 3
G 6.917 7.640 0.723 10
H 7.108 7.421 0.313 4
I 7.553 8.356 0.803 11
J 7.370 7.741 0.371 5
K 7.293 7.698 0.405 6
Open in a new tab

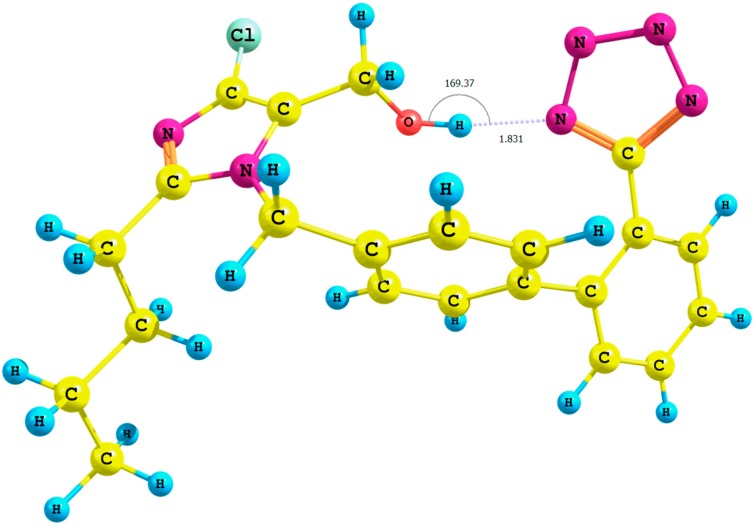
Figure 4.

Figure 4

Open in a new tab

Optimized structure of the anti-losartan anion 1 (PBE1PBE/6-31G(d,p) level of theory, Rotamer XIV, CPCM solvation model).

It is important to emphasize the influence of tetrazole nitrogen atoms and their distance to the hydroxyl group. The difference of the N6tetrazole–HO distance after optimization of the XI and XII or XIII and XIV rotamers was equal to 0.04 Å (numeration of nitrogen atoms is taken from the output files, and the visualization of all rotamers is given in the Supplementary Materials). A greater proximity of the tetrazole to the hydroxyl in the optimized XI or XIII rotamers (gaseous phase) intensified the polarization of the O-H bond and caused the deshielding of the proton. These changes were reflected by the higher relative percentage error of its chemical shift in the theoretical NMR spectrum. However, an analogous influence of the solvation model using B3LYP and PBE0 functionals for the anti-isomers 1 was not observed for the methyl protons (A) (Table 5). Instead, we noted an insignificant increase of the relative percentage error: from 20% (anti-isomer, B3LYP/6-31G(d,p)/gas level of theory, Rotamer XI; Table S9) to 26% (anti-isomer, B3LYP/6-31G(d,p)/CPCM level of theory, Rotamer XII; Table 3) or from 18% (anti-isomer, PBE1PBE/6-31G(d,p)/gas level of theory, Rotamer XIII; Table S10) to 25% (anti-isomer, PBE1PBE/6-31G(d,p)/CPCM Rotamer XIV; Table 4; Figure 4). The changes of the relative percentage error of hydroxyl and methyl (A) protons are gathered in Table 5.

Table 5.

Calculated relative percentage errors (E) of protons A and OH of losartan anion (1) rotamers recorded at 293 K and values of coefficient of determination (R2) and mean absolute deviation (MAD) parameters as a factor describing the correlation of 1H-NMR with experimental data; the following approaches were considered: (a) B3LYP/6-31G(d,p); (b) PBE1PBE/6-31G(d,p); (c) MP2/6-31G(d,p).

Protons Relative Percentage Error (E) (%)
a b c
Vacuum Water Vacuum Water Vacuum Water
I XI II XII VII XIII VIII XIV XVII XIX XVIII XX
syn anti syn anti syn anti syn anti syn anti syn anti
A 93 20 93 26 94 18 14 25 94 18 28 28
OH 95 27 95 7 94 31 96 12 97 30 95 12
Parameters
R2 0.71 0.96 0.73 0.99 0.72 0.95 0.75 0.99 0.72 0.97 0.75 0.99
MAD 0.76 0.40 0.58 0.28 0.77 0.43 0.63 0.37 0.67 0.34 0.65 0.36
Open in a new tab

Moreover, the interaction of N6tetrazole and the hydroxyl moiety seems to be confirmed by the experimentally recorded NMR spectra of 1 at different temperatures (Figure S23, Supplementary Materials) and concentrations (Figure S25, Supplementary Materials). Based on the literature data, it is known that the shifts are mightily affected by hydrogen bonding, with large downfield shifts of H-bonded functionalities compared to the hydroxyl substituent [15]. Moreover, intra- and inter-molecular types of hydrogen bonds can be easily discriminated by means of NMR spectroscopy, where only in the second case, the resonance frequencies of the OH group are concentration dependent [16]. Our experiments clearly have shown that the triplet relating to the OH group moves upfield together with increasing temperature, while the changes in concentration of 1 do not affect the chemical shift of the hydroxyl moiety. Basing on these facts, we confirmed the results of in silico calculations, where the OH group was engaged in the formation of the strong intramolecular hydrogen bond with the nitrogen atom in a tetrazole ring.

The correlation analysis of the 1H-NMR spectra of the anti-isomers with the experimental data showed a stronger correlation for the anti-isomers optimized using the CPCM solvation model (proven by the higher values of the coefficient of determination R2 and lower values of the mean absolute deviation MAD) in comparison with the syn isomers (Table 5).

The results of the QTAIM (quantum theory of atoms-in-molecules) analysis [17,18] carried out using the AIMAll 14.11.23 software [19] (Figure S21 and Table S19 in the Supplementary Materials) suggested the interactions between the tetrazole ring and the hydroxyl proton within the XIV rotamer (isomer anti, PBE1PBE/6-31G(d,p)/CPCM level of theory; Figure 4), as well. The proposed model showed the existence of a bond critical point localized on the bond path between the interacting moieties N6tetrazole···HO–CH2–imidazole.

Therefore, it can be concluded that a lower value of the relative percentage error for hydroxyl and methyl (A) protons 1 were obtained for the anti-isomers. The only exception was the relative percentage error of methyl protons of syn/anti isomers, i.e., VIII and XV rotamers, respectively, optimized using the PBE0 functional and the CPCM model. The reasons for this finding can be explained due to the considerable relaxation of the C-C bonds within the anti-isomer 1 and a possible rotation of the methyl group of the butyl chain. Such a phenomenon in this case was not limited by the heterocyclic moiety and, thus, lack of the shielding effect of the analyzed protons, which was observed in the syn isomers 1. Moreover, contrary to the anti-isomers 1 (where the hydroxyl was stabilized by the nitrogen atom of the tetrazole ring by means of electrostatic interactions), for the syn isomers 1, the hydroxyl moiety undergoes shielding due to the steric hindrance (phenyl moiety connected with the methylene bridge). We can conclude that from the stereochemical point of view, losartan preferentially adopts the anti form. The results of the calculated energy indicated that the anti-isomers of 1 were always characterized with lower energy (more negative) (Table S17, Supplementary Materials). Furthermore, the correlation analysis of the theoretical and experimental 1H-NMR spectra of the rotamers 1 indicates unambiguously the tendency for a stronger correlation being obtained for the anti-isomers (higher values of the coefficients of determination R2 and lower values of the mean absolute deviation MAD parameters; Table 1, Table 2, Table 3, Table 4, Table 5, and Tables S1–S15, Supplementary Materials) in comparison with the syn isomers.

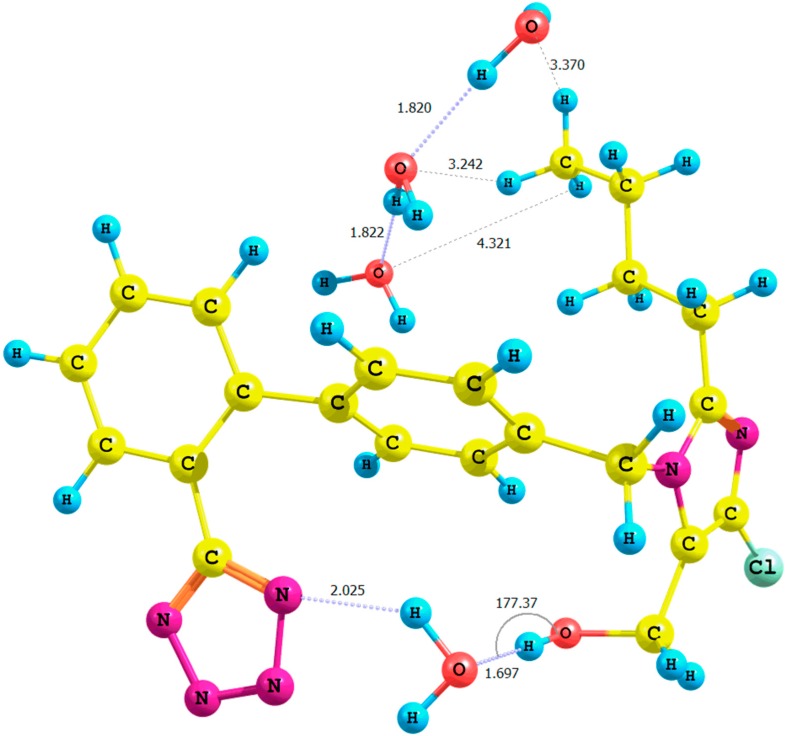
The application of the B3LYP or PBE0 functional for the anti-clusters of losartan surrounded by water molecules, optimized in the gaseous phase (Cluster XV and Cluster XVI; Figure 5, respectively), when compared to the single anti-isomers 1 (Rotamer XI, B3LYP/6-31G(d,p)/gas level of theory; Rotamer XIII, PBE1PBE/6-31G(d,p)/gas level of theory, respectively), did not result in an improvement of the relative percentage error of the chemical shift of the methyl (A) and hydroxyl protons.

Figure 5.

Figure 5

Open in a new tab

Optimized structure of the anti-losartan anion cluster 1 with water molecules (Cluster XVI); interaction of 1 with three water molecules (PBE1PBE/6-31G(d,p) level of theory, gas).

Only when comparing the XI and XV clusters optimized in the gaseous phase at the B3LYP/6-31G(d,p) level of theory did we observe a small decline in the relative percentage error of the hydroxyl proton chemical shift: from 27% (Rotamer XI) to 25% (Rotamer XV).

In our study, we also compared the experimental values of chemical shifts with the calculated results obtained for the syn- and anti-romaters optimized using the MP2 method (MP2/6-31G(d,p) level of theory). For this purpose, we considered the gaseous phase (syn- and anti-isomers, Rotamers XVII and XIX, respectively) or the CPCM solvation model (water as a solvent, syn- and anti-isomers, Rotamers XVIII and XX, respectively). Calculated NMR chemical shifts for protons of these rotamers (MP2/6-31G(d,p)/GIAO approach) are gathered in Table 5 and Tables S15–S18 (Supplementary Materials). The obtained data showed a smaller value of the relative percentage error for the methyl (A) and hydroxyl protons of the anti-isomer of losartan in comparison with syn-isomers. Only for the methyl proton in the CPCM model did the relative percentage error for syn- and anti-isomers equal 28%. In contrast to our cost-effective DFT approach, the perturbation methods seem to be a too time consuming of an approach when used for calculating the 1H-NMR spectra of 1. Nevertheless, the lower energy of the anti-isomers 1 (MP2 approach) also suggested their greater stability (Table S17, Supplementary Materials). Moreover, the MP2 method gave a better correlation between the calculated and experimental NMR chemical shifts for the anti-isomers (a higher value of the R2 and a lower value of the MAD parameters; Table 1, Table 2, Table 3, Table 4, Table 5, and Tables S1–S16, Supplementary Materials).

Our hypothesis that losartan Anion 1 adopts preferentially the anti form is in agreement with the literature data [6,12,20,21]. Molecular dynamics (MD) simulations in implicit solvation models supported the theoretical existence of the anti and syn conformations. On the other hand, an MD simulation run in the lipid bilayers revealed that losartan forms the hydrogen bonds with the lipid glycerol backbone and the phosphate groups [12]. The authors concluded that the anti conformation of losartan seems to be favored in the cellular environment, pointing to this isomer as the active one in a membrane environment. The results presented in our paper were also in accordance with the proposed two-step mechanism (involving lipid bilayers) or direct action of losartan in the AT1 receptor [21]. The results of energy, NMR, as well as QTAIM calculations presented herein proved that the anti conformation of 1 is most stable from the structural standpoint and allow us to assume that this orientation might be the most effective within the receptor cavity.

3. Experimental Section

The salt of losartan potassium 1 (1.2 mg, 0.26 µmol; Biofarm Sp. z o.o., Poznań, Poland) was added to 530 µL DMSO-d6 (99.8 atom%D, ARMAR Chemicals, Döttingen, Switzerland) and mixed for one hour at 293 K until the content was completely dissolved. The solution was moved to a 5-nm thin-wall tube with a final sample volume of 530 μL, and the 1D 1H-NMR spectra, as well as 2D homonuclear spectra were directly recorded starting from 293 K on a 400-MHz spectrometer (Bruker Daltonics, Billerica, MA, USA) operating at the frequency of 400 MHz (1H). Spectra were acquired within 4424.8-Hz spectral width and processed and prepared with TopSpin 3.0 Bruker software (Bruker BioSpin, Billerica, MA, USA). Density functional calculations were executed, and the geometries of losartan anion (1) were optimized at the DFT [22] level of theory (Becke three-term correlation functional; the Lee, Yang and Parr exchange functional B3LYP, or long range corrected version of the B3LYP functional, or the Perdew, Burke and Ernzerhof functional PBE1PBE) or applying the Mőller–Plesset second order perturbation theory MP2 using the Gaussian 09 D.01 program [23], namely the (1) B3LYP/6-31G(d,p) [24], (2) CAM-B3LYP/6-31G(d,p) [25], (3) B3LYP/6-311+G(d,p) [26,27], (4) PBE1PBE/6-31G(d,p) [28,29] and (5) MP2/6-31G(d,p) [30] approach in the gaseous phase and applying the conductor-like polarizable continuum model (CPCM, water as a solvent) [27,31,32]. The vibrational frequencies and thermodynamic properties were calculated by applying the ideal gas, rigid rotor and harmonic oscillator approximations, and the energy minimum was confirmed by the frequency calculation for all rotamers; no negative frequencies were detected in the generated vibrational spectrum of the analyzed rotamers. All of the syn-/anti-rotamers were obtained by rotating the bonds C17–C16, C11–C8, C5–C4, C4–N2, C3–C22 and C2–C18 (Figure 1) in torsion angle increments of 20° (changes in torsion angles are gathered in Table S18 given in the Supplementary Materials), and a total of 1080 rotamers were obtained. NMR shielding for proton (Href) was calculated for TMS (tetramethylsilane) at the (1) B3LYP/6-31G(d,p), (2) CAM-B3LYP/6-31G(d,p), (3) B3LYP/6-311+G(d,p), (4) PBE1PBE/6-31G(d,p) and (5) MP2/6-31G(d,p) level of theory (gaseous phase and CPCM solvation model and water as solvent) at 293 K. It is noteworthy that the difference between dielectric constant values of water and DMSO are not significant (ε = 78.3 and 46.8, respectively [23]). Moreover, the results of the NMR calculations carried out using DMSO as a solvent in comparison with the corresponding data (water as a solvent) were very similar (Tables S1b and S6b for syn-isomers or Tables S9b and S10b for anti-isomers given in the Supplementary Materials). Particular clusters with water molecules were constructed by adding water molecules to protons of hydroxyl and methyl groups and then optimized. In order to discriminate the protons in 1, they were marked according to Figure 1 positions (experimental values of chemical shifts are given in ppm and are in good agreement with reference data [10]; Figures S22–S24, Supplementary Materials): 1H-NMR (DMSO-d6, 400 MHz, 293 K) ppm: I 7.553 (H7; 1H; d; 3JHH = 9.2 Hz), J 7.370 (H6, H8; 2H; m; overlapping signals), K 7.293 (H5; 1H; d; 3JHH = 9.2 Hz), H 7.108 (H2, H4; 2H; d; 3JHH = 8.0 Hz), G 6.917 (H1, H3; 2H; d; 3JHH = 8.0 Hz), F 5.228 (H9, H10; 2H; s), OH 5.304 (H13, 1H, t, 3JHH = 5.2 Hz), E 4.328 (H11, H12; 2H; d; 3JHH = 4.8 Hz), D 2.51 (H14, H15; 2H, s), C 1.497 (H16, H17; 2H; m), B 1.270 (H19, H18; 2H; m), A 0.826 (H22–H20; 3H; t; 3JHH = 7.6 Hz). The 1H-NMR spectra were recorded in DMSO-d6. For Losartan, the 1H-NMR spectrum was acquired within the 4424.8 Hz spectral width. A total of 128 scans was collected.

The compound of interest (1) and reference compound (TMS) were calculated using the same method, and the reference compound was used to obtain the chemical shifts of 1 according to the following equation: δi = σref − σi, where δi was the chemical shift of i-nuclei of 1 and σref and σi were the calculated isotropic magnetic shielding tensor for the TMS and 1, respectively [9,10,33]. The calculated chemical shifts for the homotopic protons were averaged. The Chemcraft 1.7 software was utilized for visualization of all optimized rotamers [34]. The calculations were carried out using resources provided by Poznan Supercomputing and Networking Center (Reef cluster), as well as the Wrocław Center for Networking and Supercomputing (Supernova and Bem clusters).

4. Conclusions

This study involves a calculated theoretical 1H-NMR spectrum of losartan potassium 1, taking into consideration its synperiplanar and antiperiplanar configuration and its correlation with the corresponding experimental data. For the calculations, the DFT formalism and the Mőller–Plesset second order perturbation MP2 level of theory were used. Each rotamer was optimized in the gaseous phase and using the CPCM solvation model, and their clusters with water environment were optimized in the gaseous phase. The highest relative percentage error in the generated NMR spectrum (GIAO method) was observed for the hydroxyl and methyl (A) protons. For the syn isomers 1, it was primarily caused by the steric hindrance from the tetrazole ring, the limited rotation of the butyl chain and the proximity of the phenyl ring to the hydroxyl group. For the anti-isomers, not only the influence of the tetrazole ring on the polarization of the hydroxyl functionality was essential (the Ntetrazole···HO contact was confirmed basing on the results of QTAIM investigations, as well as NMR experiments), but also a smaller steric hindrance from the butyl moiety. In general, lower values of the relative percentage error of the calculated chemical shifts of methyl (A) protons were obtained for anti-isomers of 1 when compared to the corresponding syn isomers. Values of the coefficients of determination (R2) calculated for the theoretical chemical shifts of each rotamer related to the experimental value of chemical shifts have shown that they are noticeably lower for the syn ones. Moreover, the CPCM solvation model used for the NMR calculations increased the value of this parameter. A stronger correlation between the calculated and experimental NMR chemical shifts for the anti-isomers was also proven by their lower values of the MAD parameters. Thus, the computational methods showed a considerably superior correlation with the experimental results for the anti- than the syn-rotamers. The results of NMR experiments, supported by energy and QTAIM investigations, proved the intramolecular type of bond formation between the hydroxyl group and a tetrazole ring and confirmed that an anti conformation of 1 seems to be the preferred one. Thus, such an orientation might be most potent within the receptor cavity, which is in agreement with the results of previous studies [6,12,20,21].

Acknowledgments

The calculations were carried out using resources provided by Poznan Supercomputing and Networking Center (Grant No. 199/2014), as well as Wrocław Center for Networking and Supercomputing (Grant No. 327/2014). This research was also supported by the European Regional Development Fund within the Innovative Economy Program (Grant No. POIG.01.03.01-30-045). This publication was also supported by the Polish Ministry of Science and Higher Education, under the KNOW program. The authors are indebted to Jarosław J. Panek (Faculty of Chemistry, University of Wrocław, Poland) and to Dariusz Kędziera (Faculty of Chemistry, Nicolaus Copernicus University in Toruń, Poland) for their help in the DFT and NMR calculations.

Supplementary Materials

Click here for additional data file. (5.3MB, pdf)

Supplementary materials can be accessed at: http://www.mdpi.com/1420-3049/20/07/11875/s1.

Author Contributions

J.K. and K.C. designed the research and performed the optimization and NMR calculations. T.R. and M.K.C. performed the NMR experiments and analyzed the resulted data. E.J. performed the statistical analysis and prepared schemes. J.K., T.R. and E.J. wrote the paper. All authors read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Footnotes

Sample Availability: Samples of the compound 1 are available from the authors.

References

  • 1.Ahmad S. Losartan and severe migraine. JAMA. 1995;274:1266–1267. doi: 10.1001/jama.1995.03530160018018. [DOI] [PubMed] [Google Scholar]
  • 2.Stearns R.A., Chakravarty P.K., Chen R., Chiu S.H. Biotransformation of losartan to its active carboxylic acid metabolite in human liver microsomes. Role of cytochrome P450 2C and 3A subfamily members. Drug Metab. Dispos. 1995;23:207–215. [PubMed] [Google Scholar]
  • 3.Lo M.W., Goldberg M.R., McCrea J.B., Lu H., Furtek C.I., Bjornsson T.D. Pharmacokinetics of losartan, an angiotensin II receptor antagonist, and its active metabolite EXP3174 in humans. Clin. Pharmacol. Ther. 1995;58:641–649. doi: 10.1016/0009-9236(95)90020-9. [DOI] [PubMed] [Google Scholar]
  • 4.Dickstein K., Timmermans P., Segal R. Losartan: A selective angiotensin II type 1 (AT1) receptor antagonist for the treatment of heart failure. Expert Opin. Investig. Drugs. 1998;7:1897–1914. doi: 10.1517/13543784.7.11.1897. [DOI] [PubMed] [Google Scholar]
  • 5.Tuccinardi T., Calderone V., Rapposelli S., Martinelli A. Proposal of a new binding orientation for non-peptide AT1 antagonists: Homology modeling, docking and three-dimensional quantitative structure-activity relationship analysis. J. Med. Chem. 2006;49:4305–4316. doi: 10.1021/jm060338p. [DOI] [PubMed] [Google Scholar]
  • 6.Mavromoustakos T., Kolocouris A., Zervou M., Roumelioti P., Matsoukas J., Weisemann R. An effort to understand the molecular basis of hypertension through the study of conformational analysis of losartan and sarmesin using a combination of nuclear magnetic resonance spectroscopy and theoretical calculations. J. Med. Chem. 1999;42:1714–1722. doi: 10.1021/jm980499w. [DOI] [PubMed] [Google Scholar]
  • 7.Latha B., Gunasekaran S., Srinivasan S., Ramkumaar G.R. Computation and interpretation of vibrational spectra on the structure of Losartan using ab initio and Density Functional methods. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014;132:375–386. doi: 10.1016/j.saa.2014.05.017. [DOI] [PubMed] [Google Scholar]
  • 8.Mizera M., Lewadowska K., Talaczyńska A., Cielecka-Piontek J. Computational study of influence of diffuse basis functions on geometry optimization and spectroscopic properties of losartan potassium. Spectrochim. Acta A. 2015;137:1029–1038. doi: 10.1016/j.saa.2014.09.036. [DOI] [PubMed] [Google Scholar]
  • 9.Kujawski J., Doskocz M., Popielarska H., Myka A., Drabińska B., Kruk J., Bernard M.K. Interactions between indazole derivative and magnesium cations—NMR investigations and theoretical calculations. J. Mol. Struct. 2013;1047:292–301. doi: 10.1016/j.molstruc.2013.05.011. [DOI] [Google Scholar]
  • 10.Kujawski J., Bernard M.K., Jodłowska E., Czaja K., Drabińska B. On the interactions of leflunomide and teriflunomide within receptor cavity—NMR studies and energy calculations. J. Mol. Model. 2015;21:2643. doi: 10.1007/s00894-015-2643-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kujawski J., Czaja K., Doskocz M., Bernard M.K., Drabińska B., Kruk J., Myka A. On the interactions of indazole derivative with nucleosides—Toward modeling the cytotoxic activity mechanism. Comput. Theor. Chem. 2015;1059:45–50. doi: 10.1016/j.comptc.2015.02.013. [DOI] [Google Scholar]
  • 12.Zervou M., Cournia Z., Potamitis C., Patargias G., Durdagi S., Grdadolnik S.G., Mavromoustakos T. Insights into the molecular basis of action of the AT1 antagonist losartan using a combined NMR spectroscopy and computational approach. Biochim. Biophys. Acta. 2014;1838:1031–1046. doi: 10.1016/j.bbamem.2013.12.012. [DOI] [PubMed] [Google Scholar]
  • 13.Wolinski K., Hinton J.F., Pulay P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990;112:8251–8260. doi: 10.1021/ja00179a005. [DOI] [Google Scholar]
  • 14.Mennucci B. Polarizable continuum model. WIREs Comput. Mol. Sci. 2012;2:386–404. doi: 10.1002/wcms.1086. [DOI] [Google Scholar]
  • 15.Charisiadis P., Kontogianni V.G., Tsiafoulis C.G., Tzakos A.G., Siskos M., Gerothanassis I.P. 1H-NMR as a Structural and Analytical Tool of Intra- and Intermolecular Hydrogen Bonds of Phenol-Containing Natural Products and Model Compounds. Molecules. 2014;19:13643–13682. doi: 10.3390/molecules190913643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Günther H. NMR Spectroscopy. 2nd ed. John Wiley & Sons; Weinheim, Germany: 1996. [Google Scholar]
  • 17.Bader R.F.W. Atoms in Molecules: A Quantum Theory. Oxford University Press; New York, NY, USA: 1990. The International Series of Monographs on Chemistry, No. 22. [Google Scholar]
  • 18.Bader R.F.W. The Quantum Mechanical Basis for Conceptual Chemistry. Monats. Chem. 2005;136:819–854. doi: 10.1007/s00706-005-0307-x. [DOI] [Google Scholar]
  • 19.Keith T.A. AIMAll. TK Gristmill Software; Overland Park, KS, USA: 2014. version 14.11.23. [Google Scholar]
  • 20.Zhang H., Unal H., Gati C., won han G., Liu W., Zatsepin N.A., James D., Wang D., Nelson G., Weierstall U., et al. Structure of the Angiotensin Receptor Revealed by Serial Femtosecond Crystallography. Cell. 2015;161:833–844. doi: 10.1016/j.cell.2015.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Kellici T.F., Tzakos A G., Mavromoustakos T. Rational Drug Design and Synthesis of Molecules Targeting the Angiotensin II Type 1 and Type 2 Receptors. Molecules. 2015;20:3868–3897. doi: 10.3390/molecules20033868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Hohenberg P., Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964;136:B864–B871. doi: 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  • 23.Gaussian D., Revision A., Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., et al. Gaussian 09 D.01 Program. Gaussian, Inc.; Wallingford, CT, USA: 2009. [Google Scholar]
  • 24.Becke A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
  • 25.Yanai T., Tew D., Handy N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP) Chem. Phys. Lett. 2004;393:51–57. doi: 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  • 26.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  • 27.Eckert F., Klamt A. Fast solvent screening via quantum chemistry: COSMO-RS approach. AlChE J. 2002;48:369–385. doi: 10.1002/aic.690480220. [DOI] [Google Scholar]
  • 28.Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  • 29.Perdew J.P., Burke K., Ernzerhof M. Errata: Generalized gradient approximation made simple. Phys. Rev. Lett. 1997;78:1396. doi: 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  • 30.Head-Gordon M., Pople J.A., Frisch M.J. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1998;153:503–506. doi: 10.1016/0009-2614(88)85250-3. [DOI] [Google Scholar]
  • 31.Cossi M., Rega N., Scalmani G., Barone V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
  • 32.Barone V., Cossi M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A. 1998;102:1995–2001. doi: 10.1021/jp9716997. [DOI] [Google Scholar]
  • 33.Pierens G.K. 1H- and 13C-NMR Scaling Factors for the Calculation of Chemical Shifts in Commonly Used Solvents Using Density Functional Theory. J. Comput. Chem. 2014;35:1388–1394. doi: 10.1002/jcc.23638. [DOI] [PubMed] [Google Scholar]
  • 34.ChemCraft. [(accessed on 20 May 2015)]. Available online: http://www.chemcraftprog.com.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (5.3MB, pdf)

Articles from Molecules are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)

RESOURCES