Application of the fluctuation theorem for noninvasive force measurement in living neuronal axons

Abstract

Although its importance is recently widely accepted, force measurement has been difficult in living biological systems, mainly due to the lack of the versatile noninvasive force measurement methods. The fluctuation theorem, which represents the thermodynamic properties of small fluctuating nonequilibrium systems, has been applied to the analysis of the thermodynamic properties of motor proteins in vitro. Here we extend it to the axonal transport (displacement) of endosomes. The distribution of the displacement fluctuation had three or four distinct peaks around multiples of a unit value, which the fluctuation theorem can convert into the drag force exerted on the endosomes. The results demonstrated that a single cargo vesicle is conveyed by one to three or four units of force production.

INTRODUCTION

One of the technical hurdles in mechanobiology, a growing field of science at the interface of biology and physics, has been the methods to measure force in living cells noninvasively. The force or stress on the outer surface of the cells, or the plasma membrane, can be measured by traction force microscopy (Polacheck and Chen, 2016). Fluorescent protein-based biosensors for force or tension at the cellular levels are also actively being developed using Förster resonance energy transfer (Meng et al., 2008; Meng and Sachs, 2012; Guo et al., 2014). Optical tweezers have been used to measure force exerted on the lipid droplets in cultured cells or in Drosophila embryos (Shubeita et al., 2008; Jun et al., 2014; Mas et al., 2014), but their application to other organelles or subcellular structures is difficult. Stokes’ law can be theoretically used to estimate the drag force on the organelles moving at the velocity v as F = 6πηrv. But the viscosity η and the diameter of the organelle r need to be measured, the latter of which is often difficult for small organelles whose size is close to or below the diffraction limit of the microscope resolution.

A good example that needs force measurements in vivo is the axonal transport of vesicles, which are transported mainly by kinesins from the cell body to the periphery (anterograde) and dynein for the reverse direction (retrograde) (Hirokawa et al., 2009). Although many studies to date have elucidated their biological or functional importance, many physical or biophysical properties are still unclear (Encalada and Goldstein, 2014). For example, there is still controversy regarding the relationship among motor number, velocity, and force (Figure 1A). The in vitro studies of purified kinesin-1 have established that its velocity is around 1 μm/s without external load force. The velocity does not decrease much under low load forces (up to around 2 pN) and decreases with higher load force to zero at around 10 pN, which is called the stall force. The exact value for the stall force of kinesin ranges from 5 to 10 pN depending on the kinesin isoforms and experimental conditions. In this article, however, we assume the stall force of kinesin as 10 pN. Thus, kinesin can carry a micrometer sized bead at around 1 μm/s in vitro, because the drag force on the bead in water is much smaller than 1 pN (blue line in Figure 1A). In contrast, cytoplasm is densely filled with proteins and its viscosity is 1000 times larger than that of water (Wirtz, 2009; Hayashi et al., 2013). Thus, the drag force on the axonally transported vesicle would be about a few piconewtons or more, and its velocity would be slowed down (purple line in Figure 1A). However, the cargo velocity in the axon is often much faster than the maximum velocity in vitro and is as fast as 5 μm/s (Allen et al., 1982; Chiba et al., 2014). Mammalian dynein is even more controversial. Many studies report its maximum force as only around 1 pN (Mallik et al., 2004; Hendricks et al., 2012; Rai et al., 2013), though a few studies report values (5–10 pN) close to that of kinesin (∼10 pN) (Toba et al., 2006; Nicholas et al., 2015; Belyy et al., 2016).

FIGURE 1:

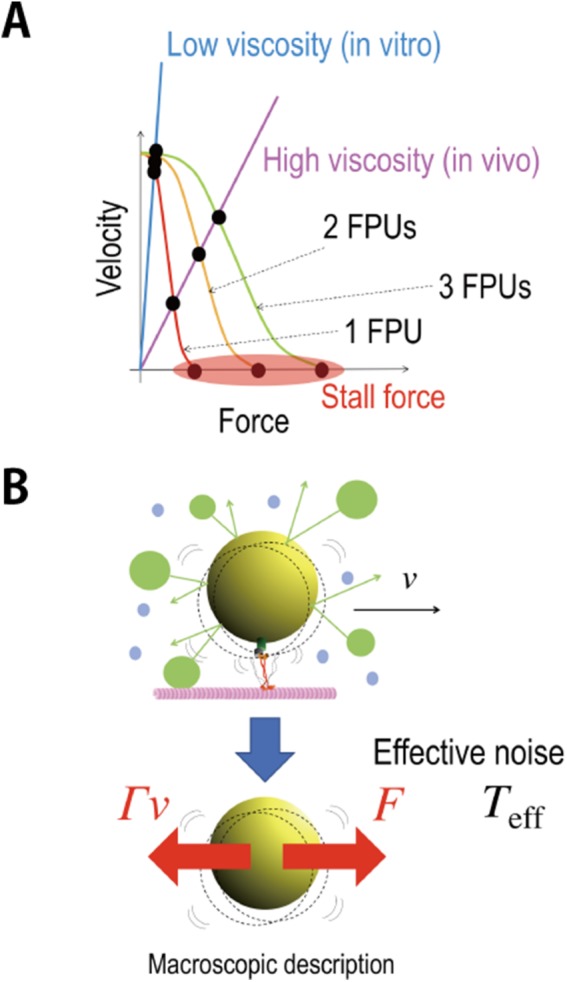
Schematics of the theoretical idea of FT. (A) The schematics of the force–velocity relations for motor proteins (FPUs). The curves represent the case of one FPU (red), two FPUs (yellow), and three FPUs (green). The lines represent the relation Γv = F, where F is a force exerted by motors and v and Γ are the velocity and friction coefficient of a cargo vesicle. The values of drag force for one FPU, two FPUs, and three FPUs are considered to be discrete in the high viscous case (purple line), similarly to the values of stall force. (B) A cargo (yellow) is transported by motors (red) along a microtubule (pink) at a constant velocity (v) (top). Here the dashed circles represent fluctuating movement of the cargo, and the blue and green circles represent water molecules, vesicles, or organelles that collide with the cargo. The cargo fluctuates due to the collision with other vesicles and organelles in addition to thermal noise, while exhibiting directional motion. In the macroscopic description of the cargo transport (bottom), force (F) exerted by motors is balanced by the drag force (Γv). In the macroscopic description, the fluctuation of the cargo is described by the effective temperature (T_eff) representing the additional noise. In this paper, F is estimated from this fluctuation via the FT.

To investigate these questions, we wanted to measure the drag force on axonally transported vesicles. There are several previous reports on the measurement of the force with vesicles or lipid droplets in living cells using optical tweezers. However, those experiments only measured the responses (slowing down or stalling) to the external load force applied by the optical tweezers. The stall force can be measured but it is not the drag force on the vesicle during the transport. To estimate the drag force, here we propose a method using the fluctuation theorem (FT). FT is a new universal law for entropy production in small nonequilibrium systems actively studied in the field of physics, which connects energy dissipation to fluctuation (Ciliberto et al., 2010). In previous studies, for example, we have established that the FT can be applied to estimate molecular energies from the fluctuation property of biomolecules in vitro (Hayashi et al., 2010). This approach enables the estimation of the energy or force from only the passive measurement, the fluctuation of the movement. Thus, it is a fully passive and noninvasive method, potentially suitable for measurements in living cells.

RESULTS

Theory

For a colloidal bead moving at a constant speed (v) in vitro, under highly damped conditions, the motion of center position X(t) can be described by the Langevin equation:

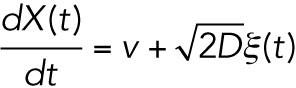(1)

where the second term on the right-hand side represents the stochastic collisions with solvent molecules, where ξ is Gaussian noise with 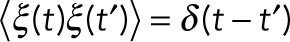, where <> denotes the time average over the time course and D is a diffusion coefficient. It is well known, in near equilibrium, that D in Eq. 1 satisfies the fluctuation-dissipation theorem (Howard, 2001) D = k_BT/γ, where γ is the friction coefficient of the bead, k_B is the Boltzmann constant, and T is the temperature of the environment. Using this relation, Eq. 1 is rewritten as

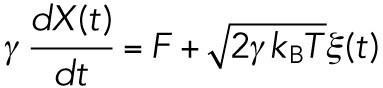(2)

where F is a force defined as F = γ v.

In the case of cargo vesicle transport in cells, these relations cannot be applied directly. There can be more interactions between the vesicle with the surrounding environments than the simple collisions with solvents. Vesicle transport might be hindered by the tethering interaction between the vesicle and the cytoskeleton, by the associating proteins on the microtubule or by the collision with other soluble proteins, cytoskeletons, or organelles. Even in such complex situations, the friction force of the vesicle can be regarded to be proportional to the velocity unless the movement is too fast. This apparent frictional effect is characterized by the effective friction coefficient Γ that includes the interaction effects between the cargo and surrounding environment, so that it would be larger than γ = 6πηr as assumed in the classical Stokes’ law (r is the radius of the cargo and η the viscosity of the cytosol). This assumption was already examined experimentally by tracking the trajectories of the passive tracer beads in the cytoplasm (Wirtz, 2009).

Similarly, the second term on the right-hand side in Eq. 2 should be revised. Since the assumption for Gaussian noise implies that the noise is caused by large numbers of independent interactions, it is not dependent on whether the system is close to the thermal equilibrium or not. In fact, force noise acting on cargo vesicles measured in this study showed the statistical property of Gaussian noise judging from the probability density distributions and the power spectrum densities shown in the results sections below (Figure 2, C and D). For the amplitude of the Gaussian noise, we replace the equilibrium temperature T with an empirical parameter, called effective temperature T_eff, to include the additional noise caused by the complex interactions involved in cargo transport other than thermal noise (see the schematics in Figure 1B). Note that the idea of effective temperature was theoretically studied recently (Hayashi and Sasa, 2004; Cugliandolo, 2011) and was introduced to analyze the nonequilibrium motion of DNA molecules in a single-molecule experiment (Dieterich et al., 2015).

FIGURE 2:

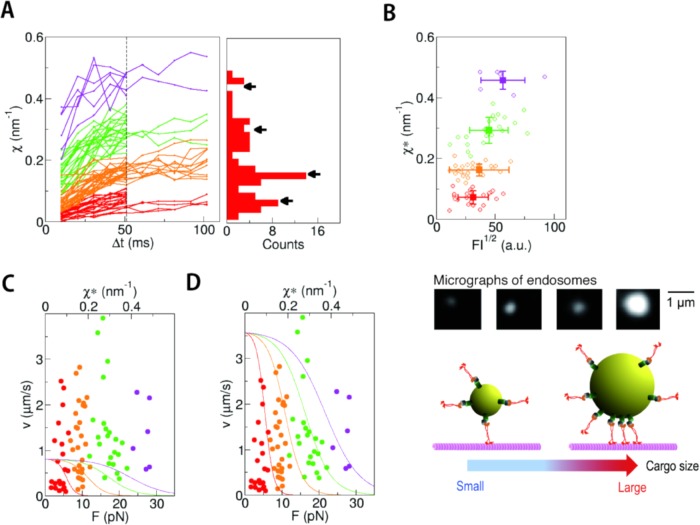
Measurement in the living neuron. (A) Typical view of DiI-stained endosomes in an SCG neuron. In the right bottom panel, a typical two-dimensional trajectory of an endosome during 4 s is shown. (B) Example of the trace of the displacement X(t) of an endosome, which showed a velocity change in the middle of the run event. The direction of movement was set as a plus direction of X. Segments for the analysis (rectangle areas) were determined by fitting the trajectory to the constant velocity movement as detailed under Materials and Methods. (C) Gaussian distribution of displacement ΔX = X(t + Δt)-X(t) in the cases Δt = 10.2 ms (blue), 51.0 ms (pink), and 102 ms (green). (D) Power spectrum of the position X(t) in a constant velocity segment is inversely proportional to the square of the frequency (the dotted line with a slope of –2) (n = 12), which is consistent with the assumption of Gaussian noise. (E) Relaxation of χ. χ^* and τ denote the value of convergence and the time constant, respectively. See also Supplemental Figures S1 and S2 for a detailed analysis of χ.

With these modifications, the movement of a vesicle in the cytoplasm (Figure 1B) can be modeled as

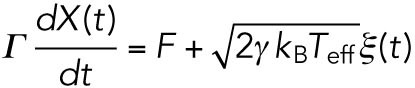(3)

From the stochastic model of Eq. 3, the following fluctuation theorem is derived (Hayashi et al., 2010):

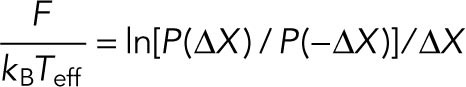(4)

In this article, the quantity on the right-hand side is called the degree of fluctuation χ,

(5)

Then, Eq. 4 becomes

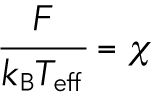(6)

Here, it should be noted that Eq. 3 is a phenomenological macroscopic model. Microscopically, the motion of the vesicle, for example, will be described by a more complex model like

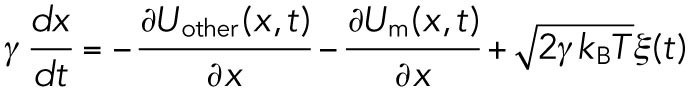(7)

where 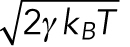is thermal noise acting on the cargo vesicle, U_m is an interaction between vesicle and motors, and U_other is the other interactions acting on the vesicle. Equation 3 corresponds to the coarse-grained model of Eq. 7, and the microscopic effect of U_m and U_other contributes to the effective viscosity Γ, effective noise 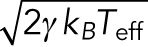, and the drag force F (Hayashi and Sasa, 2004, 2005).

Equation 6 holds for the time scale long enough to be compared with the characteristic time scales for the microscopic interactions U_m and U_other. Hence, the right-hand side of Eq. 6, χ will show a relaxation behavior against the time interval Δt with the analysis for ΔX. The relaxation time constant τ is expected to show dependence on the cycle time of the motor protein, which was confirmed experimentally in the subsequent sections. Therefore, Eq. 6 is modified as follows to reflect that the converged value χ*, instead of the transient values of χ, should be used for the estimation of the drag force:

(8)

Fluctuation measurement of axonally transported vesicles in vivo

We examined the FT (Eq. 8) with a real biological system, the axonal transport of endosomes in supracervical ganglion (SCG) neurons. The endosomes were stained with a membrane-staining dye, 1,1’-dioctadecyl-3,3,3’,3’-tetramethylindocarbocyanine perchlorate (DiI) (Figure 2A). As established previously, most endosomes show linear movement along the axon anterogradely (to the axon terminal) or retrogradely (to the cell body). Although they sometimes show stochastic switching of the velocity or reversal of the direction, the fluctuation analyzed here is the fluctuation of the displacement around a constant velocity. Thus, the segment of unidirectional movement of constant velocity was chosen for the analysis (boxed regions in Figure 2B).

The movement of the endosome was recorded at the rate of 98 frames per second. The position of the endosome was determined as the centroid of the fluorescent spot with the accuracy of 8 nm (see Materials and Methods for details). The degree of fluctuation χ (Eq. 5) was calculated from the distribution P(ΔX) (Figure 2C) of the displacement during the time interval Δt, namely ΔX(t) = ΔX(t + Δt) - ΔX(t) as described above (see Materials and Methods for details and Supplemental Figure S1 for an evaluation of the errors). Here we note that the assumption of Gaussian noise in X(t) assumed under Theory was verified by the Gaussian-like probability density distribution of P(ΔX) (Figure 2C) and the Brownian-noise power spectrum density S(ν) of the position X(t) (Figure 2D).

The degree of fluctuation χ thus calculated showed convergence (χ*) but with a relaxation time (Figure 2E and Supplemental Figure S2A). The relaxation time did show dependency on the enzymatic turnover rate (Supplemental Figure S2, B and C), but the relaxation time was much longer than the enzymatic cycle time (∼10 ms/molecule with saturating adenosine triphosphate [ATP] for kinesin). The microenvironment around the vesicle, especially its viscoelastic nature, would affect the relaxation time as explained under Theory.

Velocity ratio

To validate the FT (Eq. 8), we first searched for the traces that contain two successive constant velocity segments (∼2 s duration for each segment) with different velocities as shown in Figure 2B, because such traces would enable us to test the FT without further estimation of the parameter values.

For each vesicle, its size or surrounding environment of the axon will not change substantially during the few seconds of the run event. Then, the friction coefficient Γ would be same for both before and after the velocity change. The drag forces in the two velocity segments are written as F₁ = Γv₁ and F₂ = Γv₂, respectively, given by Stokes’ law. If the FT (Eq. 8) holds with the same T_eff value for both segments, F₁ = k_BT_effχ₁^* and F₂ = k_BT_effχ₂^*. Their ratio thus gives unity,

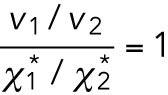(9)

The result (Figure 3) was consistent with this relation, suggesting that the effective temperature would take the same or similar values for each vesicle during the few seconds of the run event. Here it should be noted that the ratio 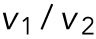(or 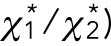is equal to the ratio of the drag forces 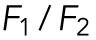and it took values around 1/2, 2, 3, and 5, which suggests the discrete changes of the drag force as discussed below. This discrete behavior was previously reported for organelle transports in living cells (Levi et al., 2006; Shtridelman et al., 2008). Moreover, the proportional relation between v and χ was also examined with the kinesin-1–coated beads in vitro, where the optical tweezers were used to exert external load instead of viscous cytoplasm (Supplemental Figure S3).

FIGURE 3:

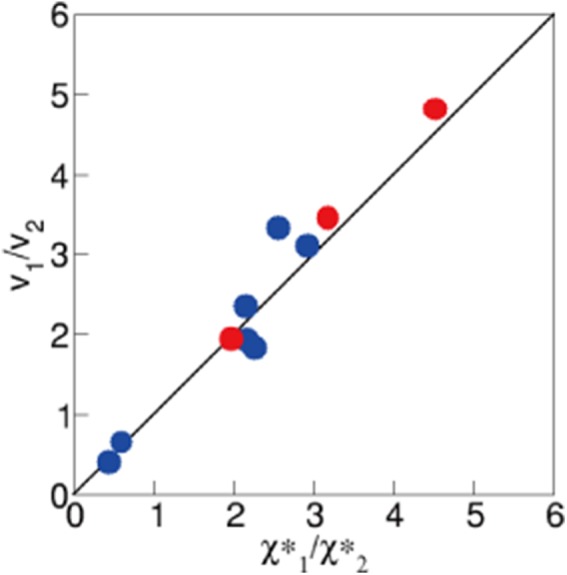
Velocity ratio of axonal endosomes in vivo. Confirmation of the proportional relation between the velocity and the fluctuation (Eq. 9) (n = 3 for anterograde, n = 7 for retrograde from >200 traces). The traces with two successive constant velocity segments with different velocities v₁ and v₂ (see Figure 2B, for example) were analyzed.

Fluctuation measurement for anterogradely transported endosomes in axons

Under the validation of Eq. 9, we then analyzed the remaining traces for the anterogradely transported endosomes with the segments of constant velocity that lasted for longer than 3 s. The measure of the fluctuation χ was calculated for the constant velocity region for each endosome for various intervals Δt from 10 to 100 ms, which confirmed that the time constant for the convergence was around Δt = 50 ms (Figures 2E and 4A). We therefore analyzed the remaining shorter traces that had segments of constant velocity that lasted for ∼2 s, with the interval Δt up to 50 ms.

FIGURE 4:

Measurement of χ for anterogradely transported endosomes in axon. (A) The traces of χ plotted against Δt for anterograde endosomes (n = 79). They were classified into four clusters by k-means clustering (indicated with different colors; see Materials and Methods for the details). The distribution of χ* values (χ at Δt = 51 ms) is shown as a histogram. The positions of the cluster centers are indicated by arrows. (B) The fluctuation χ^* is plotted against the square root of fluorescence intensity (FI), which is a proxy for the radius of the endosome (middle panel). The color of each data point is the same as in the left panels in A, which reflects the number of FPUs. The average and the SD for each cluster are shown with square symbols with error bars. There was a weak correlation between χ^* and (FI)^1/2 (r = 0.40), suggesting a tendency toward the larger endosomes experiencing a larger force with a greater number of FPUs (schema on the bottom). (C, D) For each endosome, the velocity is plotted against χ^*. The data points (circles) are plotted with the same colors as in A. The curves are the results of in vitro measurements of kinesin-1 (Schnitzer et al., 2000) without adjustment of the maximum velocity (C) and after adjustment of the maximum velocity (D).

As summarized in Figure 4A, the plots (79 runs from 76 neurons) appeared to be clustered into several groups. The histogram of the χ values at Δt = 50 ms, the proxy for the convergent value χ*, showed discrete distribution, which was statistically confirmed by the k-means clustering (Materials and Methods). When χ* is approximately proportional to force F (Eq. 8), this discrete distribution of χ* most likely reflects the force-producing unit (FPU) in this system (see the schematics in Figure 1A). Otherwise, the discrete force distribution by the presence of FPU would be obscured.

From the analysis of fluorescence intensities of the endosomes, a weak tendency toward more FPUs on larger endosomes was found (Figure 4B). The number of FPUs would thus not be tightly regulated to compensate for the greater drag resistance for the larger vesicles but would simply reflect the geometric constraints that larger vesicles have more space to accommodate additional FPUs (Figure 4B, bottom panel). It should be noted here that the velocity distribution does not show clear peaks (Supplemental Figure S4), probably reflecting the large variance of Γ due to the various sizes of the axonal endosomes (Figure 4B).

Force–velocity relations for anterogradely transported endosomes in axons

For the anterogradely transported endosomes, the drag force should be balanced with the force produced by the motor protein, most likely kinesin (Figure 1B). Thus, the measured values for the force and the velocity should scatter along the force–velocity relation curve as determined by the mechanochemical properties of the motor protein kinesin.

For the anterogradely transported endosomes, one kinesin dimer molecule would most likely correspond to the anterograde FPU, because the previous biochemical measurement reported that only one to four kinesin dimers are bound to vesicles (Hendricks et al., 2010). On the basis of this assumption, we have compared the mechanical properties of kinesin in vitro and the force–velocity relation of the anterogradely transported endosome. Because the velocity was ∼4 times faster in vivo, the in vitro force–velocity relation of kinesin (Schnitzer et al., 2000) did not match the result in vivo at all (Figure 4C). Better fitting was achieved by increasing the enzymatic turnover rate (Figure 4D), which might suggest the acceleration of the enzymatic reaction due to the macromolecular crowding in the cytoplasm (Ellis, 2001) or some regulatory mechanisms to accelerate the velocity by the scaffold protein that anchors kinesin to the cargo vesicle as suggested from our previous analysis of the APP-transport vesicles (Chiba et al., 2014).

By fitting of the modified force–relation model (Figure 4D) to the experimental data {χ*, v} (Figure 4D), a single value of the effective temperature (Eq. 8) for 79 different endosomes was estimated to be 4200 ± 200 K. This does not literally mean that the temperature of the cytoplasm is 4200 K. Although the exact physical meaning of the effective temperature is still controversial (Hayashi and Sasa, 2004), it is often observed T_eff > T in nonequilibrium systems (Cugliandolo, 2011). The most plausible interpretation would be that the fluctuation process(es) that dominantly determine the drag force are actively driven by using energy 14 times higher than the thermal energy, which might reflect the complex in vivo environment. Here, the free energy obtained by a single ATP hydrolysis is ∼20 k_BT, which would give a reference for the energy scale of active processes in living cells.

Fluctuation measurement for retrogradely transported endosomes in axons

The traces for the retrogradely transported endosomes were similarly analyzed. Traces with the segments of constant velocity that lasted for longer than 3 s were first examined to confirm the time constant for the convergence as ∼50 ms, and then we analyzed the remaining shorter traces that had segments of constant velocity that lasted for ∼2 s (Figure 5A). The plots (119 runs) also clustered into several groups. The discrete distribution of the χ values at Δt = 50 ms (the proxy for the convergent value χ*) was statistically confirmed by the k-means clustering. Thus, the presence of FPU was also demonstrated with retrogradely transported endosomes. The number of FPUs showed a weak positive correlation to the endosome size (Figure 5B) as observed with the anterogradely transported endosomes (Figure 4B), which is consistent with the geometric constraints model (Figure 4B, bottom panel) for the regulation of the number of FPUs on the endosome. Note that the discrete distribution of χ* also is additional experimental support that the effective temperature (Eq. 8) does not vary much among these 119 vesicles from 112 neurons.

FIGURE 5:

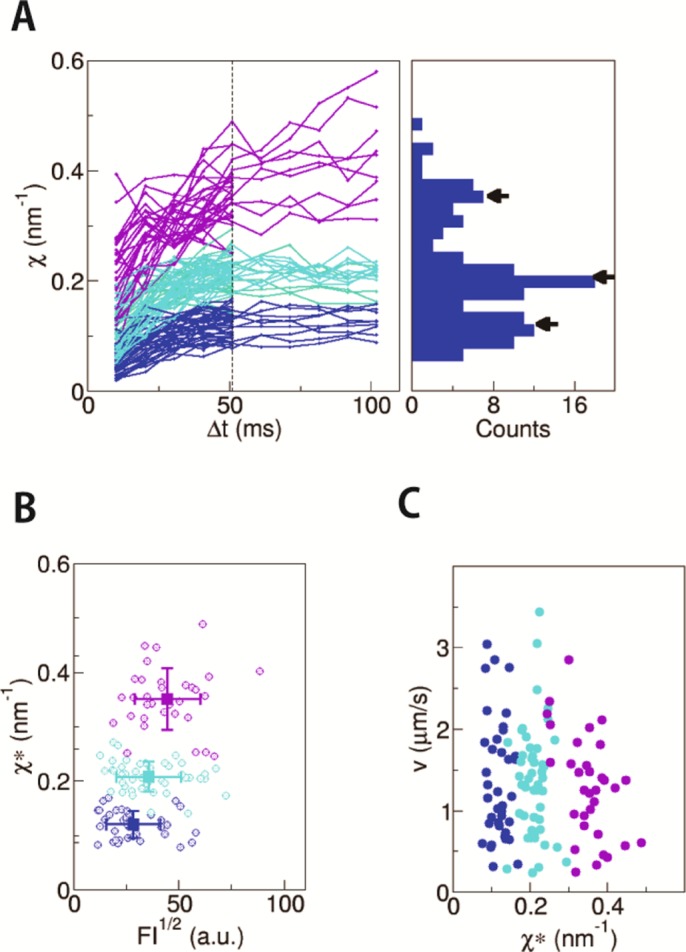
Measurement of χ for retrogradely transported endosomes in axon. (A) The traces of χ plotted against Δt for anterograde endosomes (n = 119). They were classified into three clusters by k-means clustering (indicated with different colors; see Materials and Methods for the details). The distribution of χ* is shown as a histogram. The positions of the cluster centers are indicated by arrows. (B) The fluctuation χ^* is plotted against the square root of fluorescence intensity (FI), which is a proxy for the radius of the endosome. The color of each data point is the same as in the left panels in A, which reflects the number of FPUs. The average and the SD for each cluster are shown with square symbols with error bars. There was a weak correlation between χ^* and (FI)^1/2 (r = 0.33), as observed with anterograde endosomes (Figure 4B). (C) The χ^*–velocity relation. The colors for the data points are the same as in the other panels.

The relation between the fluctuation χ* and the velocity for the retrograde vesicles (Figure 5C) showed similar distribution to the anterograde vesicles (Figure 4C), which would support that the same or similar phenomenological model for kinesin (Schnitzer et al., 2000) used in Figure 4C would be applicable to dynein as well. However, the force-velocity relations, especially the stall force for mammalian dynein in vitro are still controversial. If we assume the same or similar value of the effective temperature for the retrograde vesicles as the anterograde vesicles, then the maximum force of a single dynein FPU would be around 10 pN, roughly same as a single kinesin. This maximum force value is apparently inconsistent with most in vitro studies that report only 1 pN for a single dynein molecule (Mallik et al., 2004; Hendricks et al., 2012; Rai et al., 2013). However, several groups independently reported that dynein can be activated to produce maximum force around 5 pN (Toba et al., 2006; Nicholas et al., 2015; Belyy et al., 2016), and there might be a mechanism to increase the maximum force to 10 pN in the cytoplasm. Thus, it would be difficult at this moment to examine the mechanochemistry parameters for dynein in the phenomenological model Eqs. M4–M6 (see Materials and Methods) and to compare them with the in vitro experiments.

DISCUSSION

In this study, we have demonstrated that the FT is practically useful for the noninvasive force measurement in vivo. The discrete distributions of χ* seen in Figures 4A and 5A along with the results in Figure 3 support that the proportional constant (k_BT_eff) between F and χ* (Eq. 8) does not vary much among ∼200 vesicles analyzed here. The χ*–v relation in Figure 4D fitted well to the force–velocity curve of kinesin in vitro by assuming a single value of T_eff (4200 ± 200 K). Although the physical or mechanistic details that determine T_eff remain unclear, the results imply that the calibration for T_eff would not be necessary for each vesicle or neuron, but a single result of calibration can be applied to other vesicles. In other words, the degree of fluctuation χ can be used as a proxy for the force F in the case of cargo transport in neurons. The degree of fluctuation χ can be measured noninvasively even in living animals and was shown to be very effective for the relative comparison of the force on the synaptic vesicles exerted by UNC-104 kinesin among mutant and wild-type animals (Hayashi et al., 2018).

For the anterograde endosomes, the force value ∼10 pN determined in this study is also consistent not only with the previous in vivo force measurements in macrophages (Hendricks et al., 2012) but also with the microrheology experiments (Wirtz, 2009). The effective viscosity η_eff in this study can be calculated from the force value and other parameter values (the diameter of endosome 2r = 500 nm, and the velocity v = 2 μm/s) to be ∼1000 cP by using the relation 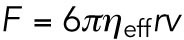. This estimate is 1000 times higher than water but is consistent with the previous measurement in the cytoplasm with tracers of similar sizes to the endosomes (Wirtz, 2009). This 1000 times difference is explained that the effective viscosity includes the effect of the surrounding environments as well as the simple collisions with solvents, as discussed under Theory.

For the retrograde endosomes, the velocity distributions (Supplemental Figure S4) and the size distributions (the distributions of fluorescence intensities) (Figures 4B and 5B) were similar to those of the anterograde endosomes. The effective viscosity would reflect the environment of the axonal cytoplasm, which is common to both the anterograde and the retrograde endosomes. Then, the drag force exerted on the retrograde endosomes would be similar to the anterograde endosomes (Stokes’ law). Namely, the maximum force by a single FPU of dynein would not differ much from kinesin (around 10 pN). This force value is ∼10 times higher than in the previous in vitro studies (Mallik et al., 2004; Hendricks et al., 2012; Rai et al., 2013). Some mechanisms are expected to activate dynein in the cytoplasm. The average number of dynein molecules on a single vesicle (Hendricks et al., 2010) is two times larger than the average number of retrograde FPUs in this study. Two dimers of dynein might serve as a single FPU and produce force in a cooperative and collective manner (Torisawa et al., 2014). Indeed, some dynein adaptors such as BICDR and HOOK3 are recently reported to recruit two dynein dimers as a unit so that the unit can move at faster velocity and produce larger force (Urnavicius et al., 2018). Of course, another possibility not excluded is that only half of the dynein molecules on the endosome might be activated by some other mechanisms to produce force up to 10 pN.

In summary, we have established a FT-based method to estimate the drag force exerted on the vesicles transported in living cells by analyzing only their movement. Unlike other existing methods for force measurement, it is fully passive and noninvasive. We used vital staining with a fluorescent dye for a selective visualization of endosomes, but differential interference contrast or phase-contrast imaging of unstained samples can be used as well. Thus, this noninvasive method would serve as a powerful and versatile tool for basic research in the field of intracellular transport, as well as some potential applications for the examination of the molecular motor functions in clinical samples.

MATERIALS AND METHODS

Reagents

All reagents were purchased from Wako or Sigma-Aldrich, unless otherwise stated.

Primary culture of neurons

Superior cervical ganglions (SCGs) isolated from 3-wk-old ICR mice (male) were enzymatically treated in 0.5% trypsin (Sigma) followed by 2 h treatment with 0.5% collagenase (Worthington). Dissociated cells were rinsed with DMEM/F12 containing 10% heat inactivated bovine serum (Life Technologies) and plated onto a Matrigel (BD-Biosciences)-coated glass-bottom dish (Matsunami). The neurons were cultured for 2–4 d with DMEM/F12 supplemented with 10% heat-inactivated bovine serum and 200 ng/ml 2.5 S nerve growth factor. All the animal experiments were conducted in compliance with the protocol that was approved by Institutional Animal Care and Use Committee, Tohoku University.

Observation of endosomes and image analysis

The neurons were stained for 10 min with 100 nM DiI (DiIC18(3); Life Technologies) and then observed with a fluorescence microscope (IX71; Olympus) equipped with a heating plate (CU-201; Live Cell Instrument). The images of the motile endosomes were obtained with a 100× objective lens (UPlanFL 100×/1.3; Olympus) and an EMCCD camera LucaS (Andor) at 98 frames per second at 37°C. The center position of each endosome was determined from the recorded image using ImageJ (Rasband, 1997), and the displacement from the position in the first frame was calculated for each frame. Here we focused on the displacement along the direction of the motion X(t). The data were collected from 34 preparations (culture dishes). Seventy-nine endosomes from 76 different cells for anterograde and 119 endosomes from 112 different cells for retrograde were investigated. The cells for observation were chosen randomly after visual inspection, and the trajectories with longer than 2 s constant velocity run(s) were selected for the analyses. The constant velocity segment was selected by fitting the trajectory with a constant velocity movement, so that the residual does not exceed the variance perpendicular to the movement. The accuracy of the position measurement was verified with fluorescent beads with a similar size and fluorescent intensity to the endosomes (300 nm latex bead; Polyscience). The SD of the position of the bead tightly attached to the glass surface was 8.4 ± 0.4 nm (five different beads in two independent preparations), which is much smaller than the displacement between frames ΔX (= X(t + Δt)-X(t)) analyzed in this study and would affect the accuracy of the fluctuation measurement by less than 10% CV, within the range of the estimation errors in the fluctuation (Supplemental Figure S1).

Preparation of permeabilized and reactivated neurons

For some experiments, the plasma membrane of the neuron was permeabilized to control the cytoplasmic ATP concentration (Okada et al., 1995). Clarified brain homogenate was used to compensate for the loss of cytoplasmic components after membrane permeabilization. Mouse brain was cleaned in ice-cold phosphate-buffered saline (PBS) and homogenized with three volumes of KHMgE buffer (potassium phosphate 115 mM, HEPES [4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid] 20 mM, MgCl₂ 1 mM, ethylene glycol-bis(2-aminoethylether)-N,N,N’,N’-tetraacetic acid [EGTA] 1 mM, pH 7.4) supplemented with protease inhibitor cocktail (Complete EDTA-free; Roche). The homogenate was clarified by successive centrifugation at 1000 × g 10 min and 100,000 × g 1 h. The brain cytosol thus prepared was aliquoted and snap frozen with liquid nitrogen. The assay buffer was prepared just before use by mixing the brain cytosol with equal volume of KHMgE buffer supplemented with ATP regeneration system (0.125 mM or 0.0125 mM ATP, 10 mM creatine phosphate, 8 U/ml creatine phosphokinase), protease inhibitor cocktail (Complete EDTA-free), and 5 mM β-mercapto ethanol. The neurons were first rinsed with KHMgE followed by 8 min incubation with the assay buffer containing 0.01 mg/ml digitonin. Fluorescent dextran (VECTOR) was used to examine the membrane permeabilization after digitonin treatment. The data were collected from 11 preparations (culture dishes) for [ATP] = 125 μM (62 endosomes from 53 cells) and six preparations (culture dishes) for [ATP] = 12.5 μM (30 endosomes from 23 cells).

Analysis of fluctuation using FT

The value of χ is defined as

(M1)

from the distribution, P(ΔX), of the displacement ΔX = X(t + Δt)-X(t). Since the noise was confirmed to be Gaussian (Figure 2, C and D), P(ΔX) was fitted with a Gaussian function:

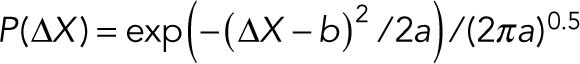(M2)

where the fitting parameters 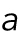and 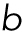correspond to the variance and the mean of the distribution. By substituting Eq. M2 into Eq. M1,

(M3)

Thus, χ was calculated as 2b/a for each P(ΔX) for various interval Δt from 10 to 100 ms. The values for a and b were also estimated from the cumulative Gaussian distribution of ΔX and directly as the sample variance (a = <(ΔX-<ΔX>)²>) and the average (b = <ΔX>). These two estimations provided the same values of a and b within the error of χ (Supplemental Figure S1). The converged value χ* was determined by plotting χ against Δt as shown in Figure 2E (χ* = χ at 51 ms in Figures 4 and 5).

k-means clustering

The χ-Δt plots for the anterograde and retrograde endosomes (Figures 4A and 5A) were classified statistically by using a k-means clustering method using a program package R with a library “cluster.” First, the number of clusters k was determined by calculating Akaike’s Information Criterion (AIC) for χ–Δt plots. In the case of the anterograde χ–Δt plots (Figure 4A), AIC values were –122.1 for k = 2, –134.6 for k = 3, –140.2 for k = 4, and –134.4 for k = 5. In the case of the retrograde χ–Δt plots (Figure 5A), AIC values were –232.3 for k = 2, –246.6 for k = 3, –247.0 for k = 4 and –245.3 for k = 5. From these AIC values along with the Gap statistics, the most probable values of k were determined as k = 4 for anterograde and k = 3 for retrograde, respectively. The initial value for the kth cluster center trajectory χ_c^k was chosen as the kth peak value of χ* (the arrows in Figures 4A and 5A). Each trajectory of χ was classified to the cluster based on the mean square deviation from χ_c^k. Then χ_c^k was renewed as the mean of the trajectories classified to that cluster. This procedure was repeated until convergence.

Analysis of the force–velocity relation

We adopted the widely accepted model of kinesin-1 (Schnitzer et al., 2000) for the analysis of the measured force–velocity relations. In this model, velocity is expressed as the function of ATP concentration as

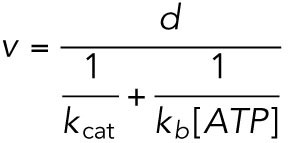(M4)

where d is the step size (= 8 nm). k_cat and k_b are the catalytic turnover rate and the apparent second-order rate constant for ATP binding (= ratio of k_cat and Michaelis-Menten constant K_M). The load (F) dependencies are introduced as

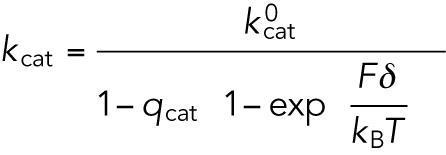(M5)

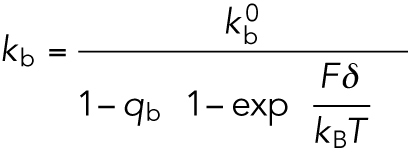(M6)

The values for the parameters k_cat and k_b were taken from the reported in vitro results (Schnitzer et al., 2000): q_cat = 0.0062, q_b = 0.04, and δ = 3.7 nm.

The ATP concentration in the cytoplasm is around 4 mM. Since it is much higher than K_M, which is around 50 μM for both kinesin and dynein, the inaccuracy in the ATP concentration does not affect the results. 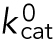was determined from the maximum velocity of endosome observed in our experiments (3.9 μm/s for anterograde). Namely, 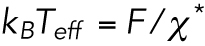= v_max/d (= 488/s).

From the fitting of Eqs. M4–M6 to the experimental data {χ*, v} in Figure 4D, the proportional constant (Eq. 8) between F and χ*

(M7)

was estimated to be 58 ± 3 pN nm (= 14 k_BT). Namely, the effective temperature T_eff was estimated to be 4200 ± 200 K.

Purification of kinesin for in vitro assay

As described previously (Okada and Hirokawa, 1999), a constitutive active dimer construct of mouse kinesin-1 (KIF5C 1–560 amino acids) was subcloned into a plasmid vector pET21B (EMD biosciences). An in vivo biotinylation tag, biotin carbonyl carrier protein (Promega) was inserted to the C-terminus of the construct. The plasmid was introduced into bacterial cell BL21(DE3)RIL (Agilent). The transformant was cultured with 2x YT medium (Bacto Tryptone 16 g/l; yeast extract 10 g/l; NaCl 5 g/l) supplemented with 30 mM phosphate buffer (pH 7.4) at 37°C to mid–log phase (OD₆₀₀ = 1.0). The culture was cooled down to 23°C, and the protein expression was induced by adding 0.1 mM (final concentration) isopropyl β–d-1-thiogalactopyranoside. The bacterial cells were collected 5 h after induction and rinsed with ice-cold PBS) supplemented with phenylmethylsulfonyl fluoride (PMSF).

Then, the bacterial cells were resuspended with five volumes of buffer A (HEPES 50 mM, potassium acetate 500 mM, magnesium acetate 5 mM, imidazole 10 mM, pH 7.4, adjusted with KOH) supplemented with ATP 0.1 mM and the following protease inhibitors: Pefabloc SC 1 mM, leupeptin 20 μM, pepstatin A 10 μM, Nα-p-tosyl-l-arginine methyl ester 1 mM. The bacterial cell wall was solubilized with lysozyme (2 mg/ml). DNase I (10 μg/ml) was added to reduce viscosity by the bacterial genomic DNA. Then bacterial cells were broken by sonication.

The soluble protein was recovered by centrifugation at 20,000 × g for 30 min and was applied to the immobilized metal affinity chromatography column TALON (Takara). The protein was eluted with buffer B (piperazine-N,N′-bis(2-ethanesulfonic acid) [PIPES] 20 mM, imidazole 250 mM, magnesium sulfate 2 mM, EGTA 1 mM) supplemented with ATP 0.1 mM and protease inhibitors. The peak fractions were pooled and stored at –80°C after snap-freezing in liquid nitrogen.

Preparation of microtubules

Tubulin was purified by the high-molarity PIPES buffer method (Castoldi and Popov, 2003) with modifications (Yajima et al., 2012). Porcine brains were cleaned by removing meninges, blood clots, and vessels in washing buffer (PIPES 50 mM, PMSF 5 mM, pH 6.8). They were homogenized in a prechilled Waring blender with PEM buffer (PIPES 100 mM, EGTA 1 mM, MgCl₂ 1 mM, pH 6.8, adjusted with KOH) supplemented with PMSF 0.5 mM, leupeptin 2 µM, and dithiothreitol 0.5 mM. After clarification with centrifugation at 15,200 × g, 60 min, microtubules were polymerized by warming the supernatant to 37°C after supplementation with MgATP 1 mM, MgGTP 0.5 mM, and glycerol. The polymerized microtubules were collected by ultracentrifugation at 100,000 × g 37°C. Then, they were depolymerized in ice-cold P₁₀₀₀EM buffer (PIPES 1000 mM, EGTA 1 mM, MgCl₂ 1 mM, pH 6.8, adjusted with KOH) at 0°C. The supernatant was collected by ultracentrifugation at 100,000 × g, 4°C. The polymerization and depolymerization cycles were repeated four times, and the final supernatant was pooled and stored in liquid nitrogen.

Tetramethyl rhodamine (TMR)-labeled microtubules were prepared as follows. Microtubules were polymerized in PEM buffer supplemented with 1 mM GTP at 37°C. Then, 5-(and-6)-carboxytetramethylrhodamine, succinimidyl ester (Life Technologies) was added at 5–10 molar excess. Labeled microtubules were separated from free dye by ultracentrifugation through glycerol cushion and were resuspended with ice-cold PEM buffer. The microtubules were depolymerized by cooling down the solution to 0°C, and the supernatant was collected by ultracentrifugation at 100,000 × g, 4°C. The labeling efficiency was measured spectroscopically, and the microtubules were stored in liquid nitrogen.

Bead assay

For the bead assay, the carboxy-modified fluorescent 0.5-µm latex bead (Life Technologies) was biotinylated with (+)-biotinyl-3,6,9,-trioxaundecanediamine (Amine-PEG3-biotin, Pierce) using condensation agent DMT-MM(4-(4,6-dimethoxy-1,3,5-triazin-2-yl)-4-methyl-morpholinium). The purified recombinant kinesin dimer was immobilized on the bead surface via streptavidin (Sigma) in assay buffer (PIPES 80 mM, magnesium acetate 5 mM, EGTA 1 mM, ATP 2 mM, casein 0.5 mg/ml, taxol 10 µM, β-mercaptoethanol 10 mM, catalase 0.1 mg/ml, glucose 10 mM, glucose oxidase 0.05 mg/ml, pH 6.8). Diluted, TMR-labeled microtubules were absorbed to the glass surface of the flow cell chamber, and the remaining surface was coated with a biocompatible polymer Lipidure-BL-103 (NOF, Tokyo, Japan). Then, the kinesin-coated beads were injected into the chamber. The optical tweezers instrument is based on the inverted microscope IX2 (Olympus). The beam of a near infrared laser (1064 nm BL-106C; Spectra-Physics) was collimated to fill the back aperture of the objective lens (PlanApo 60×/1.40; Olympus). The bead trapped at the focus was illuminated with green laser (532 nm, 400 mW, Genesis CX; Coherent), and its image was projected to an electron-multiplying charge-coupled device (EMCCD) camera iXon DU-860D-CS0-#BV (Andor). The stiffness of the trap was 0.1 pN/nm. The images were recorded at the speed of 400 frames per second at 22°C. The constant velocity segments (n = 45) used in the analysis (Supplemental Figure S3) were cut from 31 runs from five different bead assays.

Abbreviations used:

ATP

adenosine triphosphate

DiI

1,1’-dioctadecyl-3,3,3’,3’-tetramethylindocarbocyanine perchlorate

FI

fluorescence intensity

FPU

force-producing unit

FT

fluctuation theorem

GFP

guanosine triphosphate