Collective Growth in a Small Cell Network

SUMMARY

Theoretical studies suggest that many of the emergent properties associated with multicellular systems arise already in small networks [1, 2]. However, the number of experimental models that can be used to explore collective dynamics in well-defined cell networks is still very limited. Here we focus on collective cell behavior in the female germline cyst in Drosophila melanogaster, a stereotypically wired network of 16 cells that grows by ~4 orders of magnitude with unequal distribution of volume among its constituents. We quantify multicellular growth with single-cell resolution and show that proximity to the oocyte, as defined on the network, is the principal factor that determines cell size; consequently, cells grow in groups. To rationalize this emergent pattern of cell sizes, we propose a tractable mathematical model that depends on intercellular transport on a cell lineage tree. In addition to correctly predicting the divergent pattern of cell sizes, this model reveals allometric growth of cells within the network, an emergent property of this system and a feature commonly associated with differential growth on an organismal scale [3].

In Brief

Imran Alsous et al. use 3D imaging to quantify collective dynamics of cell sizes in the germline cyst of Drosophila melanogaster, a stereotypically wired network of 16 cells. Their results reveal a spatial pattern of cell-size changes, which can be explained using a mathematical model that correctly predicts allometry in this simple cell network.

RESULTS

A Pattern of Cell Sizes

The female germline cyst arises from a cystoblast that undergoes four sequential mitotic divisions with incomplete cytokinesis. The resulting 16 cells remain connected through intercellular bridges, called ring canals (Figure 1A). The cyst is then enveloped by a layer of somatically derived follicle cells to form an egg chamber. One cell in this cyst differentiates into a transcriptionally inactive oocyte; the other 15 differentiate into polyploid nurse cells that synthesize and transport proteins, mRNAs, organelles, and nutrients to the oocyte throughout its development [4, 5]. The directional transport of material to the oocyte during most of oogenesis depends in part on a polarized network of microtubules that is set up following specification of the oocyte and that extends from the oocyte to the nurse cells through the ring canals, connecting all cells within the germline cyst [6, 7]. Over the course of ~3 days, the egg chamber grows by ~4 orders of magnitude through uptake, accumulation, and redistribution of material among its constituents [8].

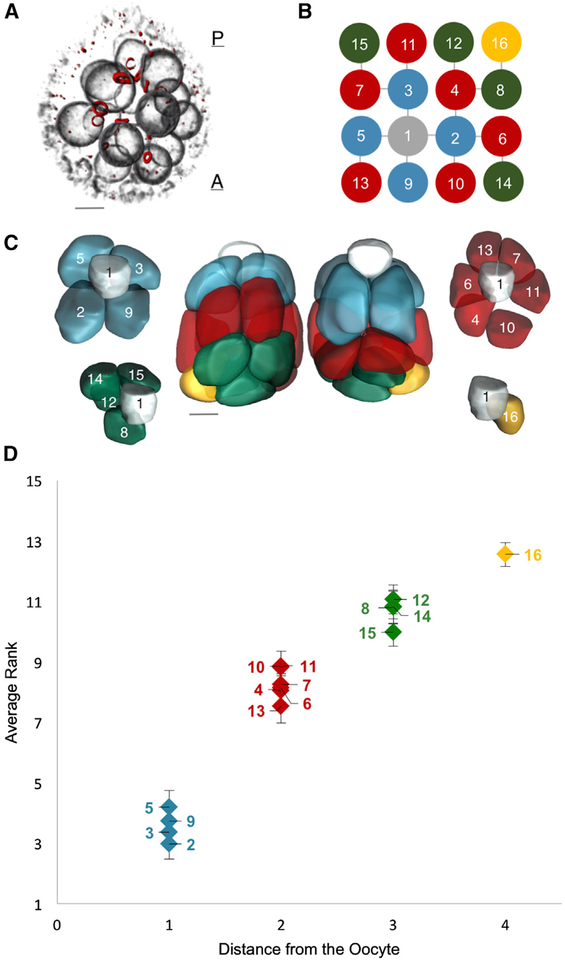
Figure 1. Differential Growth in the Drosophila Egg Chamber.

(A) Schematic representation of the four rounds of synchronous and stereotypic divisions that give rise to the 16-cell egg chamber. Cytokinesis is incomplete, and cells (nodes) remain connected by ring canals (edges). One of the cells with four ring canals becomes the oocyte; the other 15 become nurse cells. (B) Volume renderings of two ovarioles with egg chambers arranged chronologically from youngest (left) to oldest (right). Membranes (gray) and nuclei (red) are fluorescently labeled. Each egg chamber is a cluster of 16 germline cells that are connected as shown in (A) and is encapsulated by an epithelium. Throughout most of oogenesis, egg chambers grow by ~4 orders of magnitude, with unequal distribution of volume among the germ-line cells (yellow arrowheads indicate various pairs of cells of unequal size). Egg chambers also change their global shape from spherical to ellipsoidal. The final cyst size and shape are unobtainable by simple dilation of the younger structure. Scale bar, 10 μm.

One of the most salient features of egg chamber growth is the non-uniform size distribution of the 16 germline cells (Figure 1B). Previous studies noted that the nurse cells closest to the oocyte tend to be larger and proposed that the number of ring canal connections, as well as contact with the follicular epithelium, may affect cell size [9, 10]. However, such observations remained qualitative in nature, and largely unexplained [10–12]. Here we revisit this phenomenon using a combination of three-dimensional (3D) image reconstructions that can uniquely identify and measure the sizes of all cells in egg chambers from all stages of oogenesis prior to nurse cell dumping [13].

We used the fact that the divisions that give rise to the 16-cell cluster are highly regulated and stereotypic, rendering each cell uniquely identifiable within the lineage network (Figures 2A and 2B) [12]. Despite the apparent symmetry of the lineage tree, one of the two cells with four ring canals is readily identifiable as the oocyte by its morphology and posterior location within the egg chamber; this is cell 1. Using 3D confocal images of egg chambers with fluorescently labeled nuclei, cell membranes, and ring canals, we could unambiguously identify all 16 cells and generate membrane-based surface reconstructions of the germline cysts (Figure 2C). These reconstructions revealed that nurse cells are organized into layers dictated by the number of ring canals separating any given nurse cell from the oocyte: arranged from posterior to anterior of the oocyte, the numbers of nurse cells that the layers contain are 4, 6, 4, and 1.

Figure 2. A Layered Arrangement of Cells and an Emergent Pattern of Cell Sizes.

(A) A volume-rendered egg chamber showing its 3D structure, with fluorescently labeled nuclear envelopes (gray) and ring canals (red). The oocyte lies at the most posterior location of the egg chamber, and all nurse cells are relatively more anterior to it. Ring canals are conduits for exchange and transport of products between nurse cells and the oocyte.(B) The ring canal tree, with nodes (cells) colored based on the number of edges (ring canals) from the oocyte (cell 1, gray). The tree’s invariant structure renders each germline cell uniquely identifiable.(C) Color-coded membrane-based reconstruction of a young egg chamber showing front and back views. Also shown is the layered spatial organization of nurse cells separated from the oocyte by one ring canal (2, 3, 5, and 9 in blue), by two ring canals (6, 7, 10, 11, 13, and 15 in red), by three ring canals (8, 12, 14, and 15 in green), and by four ring canals (16 in yellow), away from the oocyte.(D) A plot of each nurse cell’s average nuclear volume rank (1 = largest) as a function of distance from the oocyte across all egg chambers sampled from all stages of oogenesis prior to stage 10 (n = 41), where distance is defined as the number of ring canals separating a given nurse cell from the oocyte. Nurse cells exhibit differential growth, and four groups of nurse cell sizes emerge that correlate with the spatial organization of the cells illustrated in(C). Once the pattern emerges from uniform initial conditions, it persists throughout egg chamber development, prior to stage ten of oogenesis (see also Figures S2 and S4). Number of ring canals does not explain divergent cell size pattern (see also Figure S3).

Error bars indicate SE. Scale bars in (A) and (C), 10 μm.

Our measurements show that nuclear size correlates strongly with cell size across several orders of magnitude (Figure S1). This relationship has been shown to be true in other systems [10, 14, 15]. Consequently, we used nuclear volume, a more easily measurable parameter, as a proxy for cell volume in the nurse cells. For each egg chamber, we obtained a vector of 15 nuclear volumes for each of the nurse cells, labeled 2–16. To normalize for variations in growth among different egg chambers, we ranked each nurse cell within each egg chamber by its nuclear volume. This gave us a vector of 15 rank entries, labeled 1–15, with 1 being largest and 15 smallest. We then calculated the average rank of each nurse cell across all egg chambers.

We found that (1) cells closer to the oocyte rank more highly and (2) four groups of cell sizes emerge that correlate with their layered spatial organization relative to the oocyte. Namely, when ranked by size, cells 2, 3, 5, and 9 are, on average, largest (Figure 2D). These are followed by cells 4, 6, 7, 10, 11, and 13; then by cells 8, 12, 14, and 15; and, finally, by cell 16. This size distribution was observed in both relatively younger and older egg chambers (before and after egg chamber elongation at stage 5) (Figure S2A). Importantly, prior to the encapsulation of the germline cyst by the epithelial sheet, the nuclear volumes of all cells within the cyst are indistinguishable from each other. Thus, starting from uniform initial conditions (Figure S2B), groups of different cell sizes emerge only during growth of the encapsulated 16-cell cyst.

Contrary to previous studies [10, 16], our results indicate that the number of ring canals has no significant effect on the observed pattern of collective cell growth in the egg chamber. For example, even though cells 9 and 16 have one ring canal each, cell 9 is among the four largest cells, and cell 16 is the smallest. Similarly, while cell 4 has 3 ring canals, and cells 10, 11, and 13 have one ring canal each, their average ranks are statistically indistinguishable (Figure S3A). The number of ring canals also fails to explain intra-group size variations, as we did not find a specific distribution of nuclear sizes within each group of cells. For example, contrary to the assertion in [12], cell 9 with its single ring canal is, on average, not the largest cell in the group of four cells closest to the oocyte, and cell 2, with its four ring canals, is not the smallest (Figure S3B). In summary, our results thus show (1) that there is a clear pattern to nurse cell sizes in growing egg chambers; (2) that this pattern correlates with distance from the oocyte, and, consequently, cells grow in groups; and (3) that, once established, the pattern persists throughout egg chamber development.

Mathematical Model

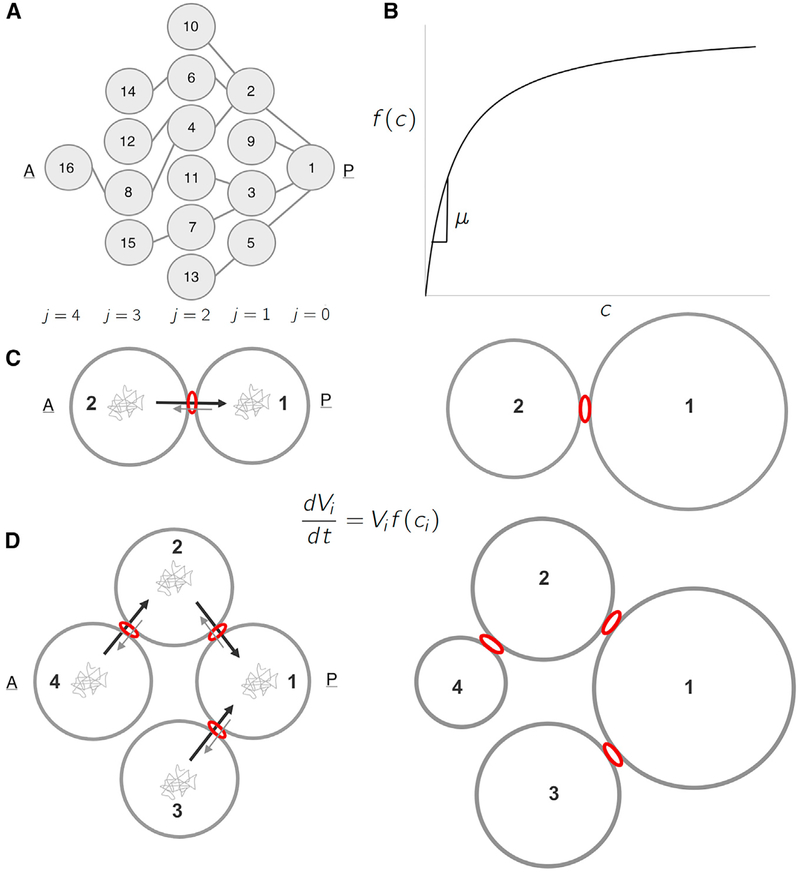
What is the origin of this pattern? As a first step in answering this question, we developed a coarse-grained model whose variables correspond to cell volumes (Figure 3A). Each of the volumes increases according to Monod-like kinetics: proportional to the product of the current cell volume and a monotonically increasing function of the intracellular concentration of some limiting component (Figure 3B):

$$\frac{d{V}_i}{dt}=V_{i}f\left(c_i\right),$$ (Equation 1)

where f(c_i) is a monotonically increasing function of c_i, the intracellular concentration of the limiting component in cell i. We postulate that this component is exchanged among cells comprising the cyst and that this exchange is polarized, such that the probability of being transported through a ring canal connecting any two cells is higher in the direction of the more posterior cell.

Figure 3. A Biophysical Model for Differential Growth and Emergence of Groups.

(A) Schematic representation of the ring canal tree arranged to highlight the anterior nurse cells’ spatial organization as it relates to the posterior oocyte (A, anterior; P, posterior). Each cell (node) is numbered (1–16), and each layer j is labeled (j = 0, 1…, 4). (B) A plot of the specific growth rate, f(c), as a function of concentration, c, showing both the linear regime where f(c) ≈ μc, and the saturated regime.(C) Schematic representation of a 2-cell cluster whose cells are connected by a ring canal. Each cell i of volume V_i grows according to the growth law shown. Diffusing particles of concentration, c_i, in the cells’ cytoplasm that arrive at the ring canal have a higher probability of being transported from an anterior (A) cell to the more posterior (P) cell than in the opposite direction. The result is that two cells, initially of uniform size, will grow at unequal rates, with cell 1 (posterior) getting larger than cell 2 (anterior). (D) Schematic representation of a 4-cell cluster whose cells are connected by ring canals. Again, allowing for polarized transport in the posterior direction, the 4-cell cluster model leads both to differential growth—with cell 1 being largest; followed by cells 2 and 3; and, finally, by cell 4—and to the emergence of 3 groups of cell sizes that correlate with the spatial arrangement of the layers relative to cell 1.

This picture is consistent with the results of particle-tracking studies in growing egg chambers. Specifically, particles in the nurse cells’ cytoplasm move randomly over small distances before they get to the ring canals. Once at a ring canal, micro-tubules then mediate posteriorly directed transport of these particles through the ring canals connecting nurse cells to nurse cells and connecting nurse cells to the oocyte [17–19]. In addition, because there is no physical barrier between adjacent cells within the cyst, particles can also diffuse bi-directionally between the neighboring cells, as demonstrated by photo-bleaching experiments in which fluorescence recovery of an anterior nurse cell is accompanied by loss of fluorescence intensity in the posterior oocyte [20]. We emphasize that the transport of material invoked here is not the rapid mass transport of cytoplasm that occurs as nurse cells empty their contents into the oocyte during nurse cell dumping.

We assume that concentrations within the cell cluster equilibrate rapidly and can therefore be considered at steady state on the much longer timescale of growth of the cyst. This is based on the estimate of the time it takes a particle with diffusivity D to reach a circular window of radius a on the wall of a cell with volume V. This time is given by τ = V/4Da [21]. Using the following lower- and upper-bound estimates for V ≈ 5 – 50μm³, a ≈ 0.5 – 10μm, D ≈ 10μm²/s, we get τ ≈ 1–10 minutes. Growth, on the other hand, occurs over ~3 days. Because of the fast equilibration, the forward and reverse fluxes through any ring canal within the cyst are equal to each other. We found that this model explains both the observed pattern of differential growth and the emergence of groups.

Differential Growth

To explain the origin of differential growth, we start with a two-cell cyst with a single ring canal (Figure 3C). Fast equilibration of the concentrations in the two cells implies that the fluxes between the two cells are balanced:

$$J_{2\to 1}\approx J_{1\to 2}.$$ (Equation 2)

The flux is given by a rate constant multiplied by the intra-cellular concentration of the limiting factor, c_i. The rate constant is a product of the rate constant that describes particle entry into the ring canal and the probability, α; that the particle is transported through a ring canal, either by directional or non-directional transport. In the simplest case, the rate constant for diffusive approach to a ring canal is given by k = 4Da. Then, the fluxes take the following form: J_2→1 = kα_2→1c₂; and J_1→2 = kα_1→2 c₁. Balancing the fluxes, we find that the concentrations in the anterior and posterior cells are related to each other:

$$C_2=\nu C_1,$$ (Equation 3)

where ν = α_1→2/α_2→1, is a parameter that quantifies the asymmetry of transport through the ring canal.

When transport is polarized in the posterior direction, ν < 1. As a consequence, the volume V₁ (t) of the first cell grows faster than the volume V₂ (t) of the second cell. Indeed, since f(c) monotonically increasing, f(c₂) < f(c₁) is Starting with cells of equal size then, two-cell model naturally exhibits differential growth at all times (Figure 3C):

$$\frac{dlog\left(V_2\right)}{dt}<\frac{dlog\left(V_1\right)}{dt}\Rightarrow V_2(t)<V_1(t),$$ (Equation 4)

where d log(V)/dt = (1/V)dV/dt. Thus, differential growth emerges already in a two-cell cyst.

The Emergence of Groups

To understand the emergence of growth in groups, it is sufficient to consider a 4-cell cluster with 3 layers, arranged in increasing distance from the founder cell, labeled cell 1 (Figure 3D). Again, due to fast intercellular equilibration, forward and reverse fluxes through each of the ring canals are balanced:

$$J_{1\to 2}=J_{2\to 1},J_{1\to 3}=J_{3\to 1},J_{2\to 4}=J_{4\to 2}.$$ (Equation 5)

This leads to the following hierarchy for the intracellular concentrations:c₂ = c₃ = νc₁ and c₄ = νc₂ = ν²c₁. Thus, Equation 3 can be generalized to c(j + 1) = νc(j), and for each cell in layer j, the concentration of the limiting factor can be expressed as a function of the concentration in the oocyte, i.e., the founder cell as follows:

$$c(j)={\nu }^j{c}_{1}j=0,1,2.$$ (Equation 6)

When transport is polarized toward the founder cell (ν < 1), we get c₄ < c₃ = c₂ < c₁. Following the same steps leading to Equation 4, we find that, starting with cells of equal sizes, a four-cell cluster exhibits differential growth in which the differences in volumes increase over time and that three groups of cell sizes emerge from uniform initial conditions:

$$V_4\left(t\right)<V_3\left(t\right)=V_2\left(t\right)<V_1\left(t\right).$$ (Equation 7)

Similarly, for the 16-cell cluster, five groups of cell sizes emerge: V₁₆ < V_8,12,14,15 < V_{4,6,7,10,11,13} < V_{2, 3,5,9} < V₁ (STAR Methods). Thus, our model explains the qualitative features of both patterns presented in Figure 2: differential growth and the emergence of groups.

Allometric Scaling in Collective Cell Growth

Differential growth in our model cell clusters appears because a difference in the cellular concentrations of the limiting factor, c, implies a difference in f(c), resulting in a difference in the cells’ specific growth rates. Several of the commonly used growth laws are linear at low concentrations and saturate as the concentrations increase. It is unlikely that the system is in the saturated regime, as that would preclude differential growth. Therefore, we considered what happens in the linear regime. Using our result from Equation 6 and re-writing Equation 1 for each cell in layer j, we get:

$$\frac{dlogV(j)}{dt}=\mu c(j)=\mu {\nu }^j{c}_1.$$ (Equation 8)

Writing these equations for any two cells in the adjacent layers j and j + 1, and taking their ratio, we arrive at:

$$\frac{dlogV(j+1)}{dlogV(j)}=\nu .$$ (Equation 9)

Integrating this equation and using the fact that all cells start from the same initial condition, V(j,t = 0) = V₀, we get:

$$\frac{V(j+1)}{V_0}={\left(\frac{V(j)}{V_0}\right)}^{\nu }.$$ (Equation 10)

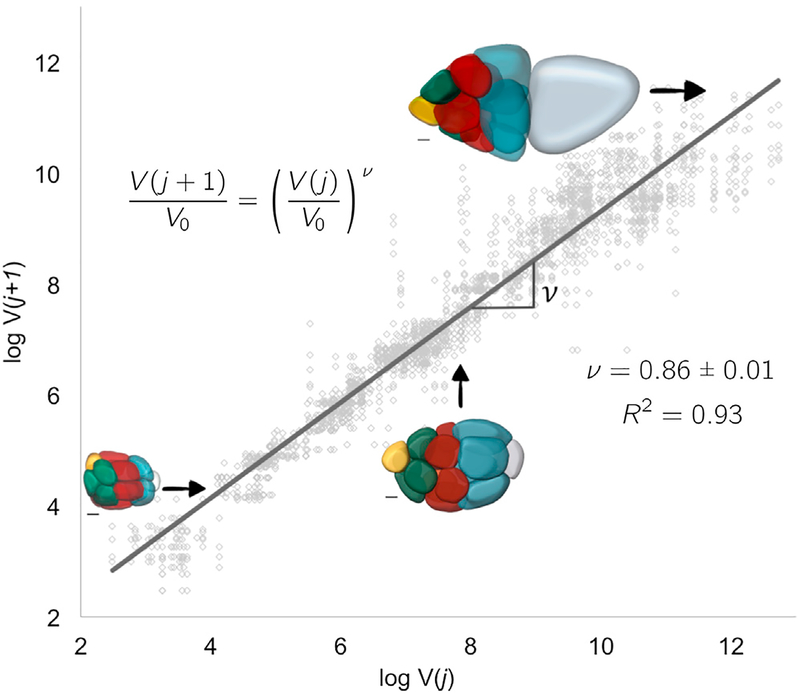
This result predicts a specific quantitative pattern for a qualitative observation, namely, that the pattern of decreasing cell sizes with distance from the oocyte at any moment in time can be quantified with an allometric-type relationship. The only parameter here is ν, which links a process occurring at the molecular scale, transport of an intracellular limiting component, to an observable phenotype, cell size.

To estimate ν, we take the natural logarithm of both sides of Equation 10 to get log $V(j+1)=\nu logV(j)+log\left(V_0^{1-\nu }\right)$, where the value of ν is then given by the slope of the line that best fits through pairs of nuclear volumes of nurse cells from consecutive layers j and j + 1; each egg chamber has 52 such pairs. This leads to ν = 0.86 ± 0.01 and V₀ = 161 ± 2.01 μm³. For this value of ν; transport is polarized, and a growing egg chamber will have four groups of nurse cells that exhibit a posterior-to-anterior gradient of decreasing cell sizes, which is consistent with what we observed experimentally (Figure 4). Thus, in addition to deriving the quantitative relation between volumes of cells from different layers, we also extract the parameter characterizing the extent of polarized transport within the cluster, thus linking a subcellular molecular process to an emergent pattern of collective cell growth.

Figure 4. Allometric Scaling in Collective Cell Growth.

A plot of log V(j + 1) versus log V(j) where j = 1,…, 5. To extract ν, we fit log $V(j+1)=\nu logV(j)+log\left(V_0^{1-\nu }\right)$ to data pairs of nuclear volumes of nurse cells from consecutive layers j and j + 1; each egg chamber has 52 such pairs. The extracted value of ν = 0.86 ± 0.01, is consistent with biased transport toward the posterior oocyte (data from 41 egg chambers). The insets show representative color-coded membrane-based reconstruction of a young, roughly spherical egg chamber (bottom left), an egg chamber beginning to elongate (middle), and an older ellipsoidal egg chamber (top right). Scale bars, 10 μm.

Pattern of Cell Sizes in Mutants

Our model predicts that, in the absence of a polarized transport network, cells in the growing cluster will be of the same size. To test this prediction, we examined mutants that fail to specify an oocyte and set up a polarized microtubule cytoskeleton for transport of oocyte-specific factors. One such mutant is egalitarian (egl) [22, 23]. In egl null mutants, no oocyte is specified, the formation and maintenance of a polarized microtubule network are disrupted, and all 16 cells develop into polyploid nurse cells [6]. In such mutants, oocyte-specific transcripts are evenly distributed throughout the germline cells—a defect that has been shown to correlate with failure to set up and polarize the microtubule cytoskeleton [23, 24]. Perhaps not surprisingly, this phenotype is also observed in egg chambers treated with inhibitors of microtubule assembly [6, 25].

Our own analysis reveals that, although egg chamber development in such mutants is halted midway through oogenesis (prior to yolk accumulation), there are no gross morphological defects and no apparent diminution in the total size of egg chambers when compared to wild-type egg chambers at similar developmental stages (Figure S4A) [22]. However, the group-wise arrangement of cell sizes is absent. In such egg chambers, the average ranks of cells from virtually all groups overlap: for example, cells 9 and 16, the closest and furthest cells from the oocyte, respectively, are, on average, of equal size (Figure S4B). These results suggest that the relative absence of both differential growth and emergence of groups of cell sizes is attributable to the absence of a polarized transport within the cluster.

Our model also explains the pattern of cell sizes observed in mutants that exhibit a rearrangement of cell packing in space, such as mutants in dicephalic (dic): an oocyte is specified, and the lineage tree is unperturbed; however, nurse cells are separated into two clusters that flank both the anterior and posterior sides of the oocyte [26]. Nonetheless, in such mutants, as in wild-type egg chambers, nurse cells closer to either side of the oocyte are larger than those further away and exhibit a gradient of cell sizes predicted by the model.

DISCUSSION

Our work establishes the developing germline cyst as a model of collective dynamics in small cell clusters, in a highly reproducible setting where all cells are uniquely identifiable. We uncovered an emergent pattern of cell sizes and presented a plausible model that captures the most salient features of egg chamber growth and correctly predicts several features of collective growth associated with multicellular systems. However, our model is clearly “a simplification and an idealization, and consequently a falsification” ([27], p. 37) of dynamics in real egg chambers. Future studies can capitalize on the model’s simplicity and include additional features, such as the non-uniform distribution of ring canal sizes, the effects of hormonal regulation, and somagermline interactions [7, 13, 28–30]. It is also critical to identify the limiting factor (or factors) that control cell-size increase in our model. We expect these factors, be they nutrients or organelles (such as ribosomes), to be sensitive to microtubule transport, as genetic and pharmacological perturbations of the microtubule network disrupt the normal pattern of cell sizes [6, 22, 25].

Our model of a small cell cluster displays common features of collective growth on organismal scale: parts diverge in size as the whole system grows, and sizes of the constitutive parts relate allometrically. While such complex spatiotemporal patterns during organismal growth have been documented since Thompson’s and Huxley’s studies [31, 32], the underlying mechanisms have remained largely unclear [3]. Studies in model organisms have suggested two possible classes of mechanisms for differential growth. The first class relies on intrinsic differences between growing parts, such as differential expression of selector genes [33]. The second class relies on interactions between growing parts, such as their competition for resources [34]. While our model for the emergence of a non-uniform distribution of cell sizes in the egg chamber cannot rule out the first class of mechanisms of differential growth, it most closely aligns with the second, presumably resulting from competition between the growing parts for resources and their non-uniform allocation and transport.

STAR+METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Sheep anti-GFP	Wieschaus lab	N/A
Rabbit anti-PTyr	Santa Cruz Biotechnology	Catalog # sc-18182 RRID: AB_670513
Mouse anti-NPC	Abeam	Catalog # ab24609 RRID: AB_448181
Goat anti-Rabbit IgG Alexa-546	Life Technology	Catalog # A11035 RRID: AB_143051
Donkey anti-Sheep IgG Alexa 488	Life Technology	Catalog # A11015 RRID: AB_141362
Goat anti-Mouse IgG Alexa-647	Life Technology	Catalog # A32728 RRID: AB_2633277
Chemicals, Peptides, and Recombinant Proteins
Phalloidin Alexa-647	Life Technology	Catalog # A22287 RRID: AB_2620155
Aqua-Poly/Mount	Polysciences	Catalog # 18606
Experimental Models: Organisms/Strains
Fly: wild type: Oregon R	Bloomington Drosophila Stock Center	Stock number: 5
Fly: Resille-GFP	Wieschaus lab	N/A
Fly: egalitarian: eglwu50	Schüpbach lab	N/A
Fly: egalitarian: eglRC12	Schüpbach lab	N/A
Software and Algorithms
MATLAB	The Mathworks	https://www.mathworks.com/
Imaris	Bitplane	http://www.bitplane.com

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for reagents may be directed to, and will be fulfilled by the Lead Contact, Stanislav Y. Shvartsman (stas@princeton.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Wild-type stock used was Oregon R, and to obtain a better signal of the membranes in germarial egg chambers, GFP-Resille flies were also used. Two egalitarian alleles (egl^wu50 and egl^RC12, kindly provided by Trudi Schüpbach from Princeton University) were crossed to generate a transheterozygote, henceforth referred to as egl throughout. All fly stocks were maintained by standard methods at room temperature, and were grown on a standard cornmeal, molasses, and yeast media. Ovaries used in the study were all dissected from well-fed female flies.

METHOD DETAILS

Immunofluorescence and antibodies

Ovaries from well-fed female flies were dissected and fixed in 4% paraformaldehyde at room temperature for 20 min. Ovaries were then treated and blocked with 0.1% Triton X-100 and 5% NGS in PBS for one hour at room temperature, then stained with a selection of the following primary antibodies at 4°C overnight: sheep anti-GFP (1:1000, a gift from E. Wieschaus, Princeton University), rabbit anti-PTyr (1:500, Santa Cruz Biotechnology), and mouse anti-NPC (1:500, Abcam). Secondary antibodies: Alexa Fluor goat anti-rabbit 546nm, donkey anti-sheep 488nm, and goat anti-mouse 647nm, all diluted 1:300. Phalloidin–Alexa-647 (Life Technology) diluted 1:1000, and DAPI (1:500) were used. Samples were mounted in 50% Aqua-Poly/Mount (Polyscience).

Microscopy

Imaging was performed on a Nikon A1 scanning confocal microscope, using either a 60x or 40x/1.3 NA Plan-Apo oil objective. Z stacks (500 – 1000 nm steps) were acquired in using the 405nm diode laser, 561nm diode-pumped-solid-state (DPSS) laser, a 638nm diode laser, as well as a 488nm Argon-gas laser line.

Cell labeling, size measurements & surface reconstructions

Images were viewed and processed in Bitplane’s Imaris. To label the germ cells from 1–16, z stacks of germline cysts with fluorescently-labeled membranes, ring canals and nuclear envelopes were rendered and then viewed one optical slice at a time. The oocyte was unambiguously identified by its posterior position and four ring canals, and the nurse cells were identified by lineage, i.e., number of ring canals. The nuclear volumes were calculated based on the nuclear diameters, measured at a central z-location for each annotated cell, and the corresponding volume of a sphere. Surface reconstructions of nuclei and cells of labeled egg chambers were generated using Imaris’ Contour Surface tool.

Modeling

Here we describe a mathematical model that explains differential growth and the emergence of the observed pattern of cell sizes in the growing 16-cell germline cluster, shown in Figure 3A.

Each cell is labeled by its number i in the cluster, i = 1,2, …, 16, and each cell layer is labeled by its number j that characterizes the “distance” (the number of connecting ring canals) from a cell belonging to this layer to cell 1 (oocyte), j = 0, 1,…,4. Contacts occur only among cells of neighboring layers.

We model growth, or increase in the cell volume V, according to Monod kinetics, assuming that the volume growth rate is proportional to the product of the current cell volume and a monotonically increasing function of the intracellular concentration of some limiting component. The dynamics of the cell i volume is then governed by the following equation:

$$\frac{d{V}_i(t)}{dt}=V_i(t)f\left(c_i(t)\right)$$ (Equation A.1)

where f(c_i) is a monotonically increasing function of c_i, the concentration of the limiting nutrient in cell i. In the linear regime considered in the present paper, f(c_i) = μc_i, and Equation A.1 reduces to

$$\frac{d{V}_i(t)}{dt}=\mu c_i(t)V_i(t).$$ (Equation A.2)

Since nutrient equilibration among the cells is a fast process, all c_i(t) are proportional to c₁(t). As we will see, the proportionality factor depends on which layer j the cell i belongs to. Thus, the nutrient concentration in cell i belonging to layer j, denoted by $c_i^{(j)}(t)$, can be written as

$$c_i^{(j)}(t)=g_j(\nu )c_1(t),$$ (Equation A.3)

where the proportionality factor g_j(ν) is a function of the parameter ν formally defined below, which characterizes the asymmetry of transport through the ring canal,

$$g_j(\nu )={\nu }^j.$$ (Equation A.4)

Denoting the volume of cell i belonging to layer j by $V_i^{(j)}(t)$ and using Equations A.3 and A.4, Equation A.2 can be written as

$$\frac{d{V}_i^{(j)}(t)}{dt}=\mu {\nu }^j{c}_1(t)V_i^{(j)}(t),$$ (Equation A.5)

This is, in fact, a generalization of Equation 8 from the main text to the case of the 16 cell cluster. We discuss the solution of this equation later, after we provide a derivation of Equations A.3 and A.4.

A. Derivation of Equations A.3 and A.4

The relations in Equations A.3 and A.4 follow from our assumption that all ring canals are identical and from the fact that the net fluxes through each ring canal vanish at equilibrium, since fluxes in the opposite directions compensate each other, as discussed below.

The flux $J_{i\to i\prime }$ from cell i to cell i^′ through the ring canal connecting these cells is given by $J_{i\to i\prime }=k{\alpha }_{i\to i\prime }{C}_i$, where k is the rate constant describing the particle entrance into the canal, and ${\alpha }_{i\to i\prime }$ is the translocation probability, i.e., the probability that a particle entering the canal from cell i passes through and escapes into cell i^′. The transport asymmetry parameter, ν, is the ratio of the translocation probabilities:${\alpha }_{i\prime \to i}/{\alpha }_{i\to i\prime }$. Here, we treat all ring canals as identical, and we have

$$\nu =\frac{{\alpha }_{1\to 2}}{{\alpha }_{2\to 1}}=\frac{{\alpha }_{1\to 3}}{{\alpha }_{3\to 1}}=\frac{{\alpha }_{1\to 5}}{{\alpha }_{5\to 1}}=\frac{{\alpha }_{1\to 9}}{{\alpha }_{9\to 1}}=\frac{{\alpha }_{2\to 4}}{{\alpha }_{4\to 2}}=\frac{{\alpha }_{2\to 6}}{{\alpha }_{6\to 2}}=\frac{{\alpha }_{2\to 10}}{{\alpha }_{10\to 2}}=\frac{{\alpha }_{3\to 7}}{{\alpha }_{7\to 3}}=\frac{{\alpha }_{3\to 11}}{{\alpha }_{11\to 3}}=\frac{{\alpha }_{4\to 8}}{{\alpha }_{8\to 4}}=\frac{{\alpha }_{4\to 12}}{{\alpha }_{12\to 4}}=\frac{{\alpha }_{5\to 13}}{{\alpha }_{13\to 5}}=\frac{{\alpha }_{6\to 14}}{{\alpha }_{14\to 6}}=\frac{{\alpha }_{7\to 15}}{{\alpha }_{15\to 7}}=\frac{{\alpha }_{8\to 16}}{{\alpha }_{16\to 8}}.$$ (Equation A.6)

Flux compensation for the ring canals connecting cell 1 with cells 2, 3, 5, and 9 leads to

$$c_2=\frac{{\alpha }_{1\to 2}}{{\alpha }_{2\to 1}}{c}_1=\nu C_1,c_3=\frac{{\alpha }_{1\to 3}}{{\alpha }_{3\to 1}}{c}_1=\nu C_1,c_5=\frac{{\alpha }_{1\to 5}}{{\alpha }_{5\to 1}}{c}_1=\nu C_1,c_9=\frac{{\alpha }_{1\to 9}}{{\alpha }_{9\to 1}}{c}_1=\nu C_1.$$ (Equation A.7)

Similarly, flux compensation for the ring canals connecting the cells of the first and second layers leads to

$$\begin{array}{lll}{C}_4=\frac{{\alpha }_{2\to 4}}{{\alpha }_{4\to 2}}{C}_2={\nu }^2{C}_1,\hfill & C_6=\frac{{\alpha }_{2\to 6}}{{\alpha }_{6\to 2}}{C}_2={\nu }^2{C}_1,\hfill & C_{10}=\frac{{\alpha }_{2\to 10}}{{\alpha }_{10\to 2}}{C}_2={\nu }^2{C}_1,\hfill \\ C_7=\frac{{\alpha }_{3\to 7}}{{\alpha }_{7\to 3}}{C}_3={\nu }^2{C}_1,\hfill & C_{11}=\frac{{\alpha }_{3\to 11}}{{\alpha }_{11\to 3}}{C}_3={\nu }^2{C}_1,\hfill & C_{13}=\frac{{\alpha }_{5\to 13}}{{\alpha }_{13\to 5}}{C}_5={\nu }^2{C}_1\hfill \end{array}.$$ (Equation A.8)

Next, compensation of fluxes through the ring canals connecting the cells of the second and third layers leads to

$$C_8=\frac{{\alpha }_{4\to 8}}{{\alpha }_{8\to 4}}{C}_4={\nu }^3{C}_1,C_{12}=\frac{{\alpha }_{4\to 12}}{{\alpha }_{12\to 4}}{C}_4={\nu }^3{C}_1,C_{14}=\frac{{\alpha }_{6\to 14}}{{\alpha }_{14\to 6}}{C}_6={\nu }^3{C}_1,c_{15}=\frac{{\alpha }_{7\to 15}}{{\alpha }_{15\to 7}}{C}_7={\nu }^3{C}_1.$$ (Equation A.9)

Finally, the flux compensation for the ring canal connecting cells 16 and 8 leads to

$$C_{16}=\frac{{\alpha }_{8\to 16}}{{\alpha }_{16\to 8}}{C}_8={\nu }^4{c}_1.$$ (Equation A.10)

To summarize, Equations A.7–A.10 show that the relation in Equation A.3 with g_j (ν) given by Equation A.4 is a consequence the balance of fluxes through identical of ring canals.

B. Balancing Fluxes

We start our discussion of flux balance by noting that the time dependence of the number of particles in cell i, denoted by N_i(t), is determined by the rate equation

$$\frac{d{N}_i(t)}{dt}=k\left[\sum _{i\prime }{\alpha }_{i\prime \to i}{c}_{i\prime }\left(t\right)-\left(\sum _{i\prime }{\alpha }_{i\to i\prime }\right)C_i\left(t\right)\right],$$ (Equation A.11)

where the summation over i^′ implies the summation over all cells connected with cell i by ring canals. At equilibrium, dN_i(t)/dt = 0 for all i, and Equation A.11 reduces to

$$\sum _{i\prime }{\alpha }_{i\prime \to i}{c}_{i\prime }\left(t\right)-\left(\sum _{i\prime }{\alpha }_{i\to i\prime }\right)C_i\left(t\right).$$ (Equation A.12)

First, we write this equation for cells 9 – 16, each of which is connected with only one cell,

$${\alpha }_{9\to 1}{C}_9={\alpha }_{1\to 9}{C}_1,{\alpha }_{10\to 2}{C}_{10}={\alpha }_{2\to 10}{C}_2,{\alpha }_{11\to 3}{C}_{11}={\alpha }_{3\to 11}{C}_3,{\alpha }_{12\to 4}{C}_{12}={\alpha }_{4\to 12}{C}_4,{\alpha }_{13\to 5}{C}_{13}={\alpha }_{5\to 13}{C}_5,{\alpha }_{14\to 6}{C}_{14}={\alpha }_{6\to 14}{C}_6,{\alpha }_{15\to 7}{C}_{15}={\alpha }_{7\to 15}{C}_7,{\alpha }_{16\to 8}{C}_{16}={\alpha }_{8\to 16}{C}_8.$$ (Equation A.13)

Multiplying both sides of these equations by the rate constant k, we recover flux compensation for the ring canals connecting cells 9 – 16 with cells 1 – 8, respectively.

Next, we write Equation A.12 for cells 5 – 8, each of which is connected with two cells. Taking into account Equation A.13, we obtain:

$${\alpha }_{5\to 1}{C}_5={\alpha }_{1\to 5}{C}_1,{\alpha }_{6\to 2}{C}_6={\alpha }_{2\to 6}{C}_2,{\alpha }_{7\to 3}{C}_7={\alpha }_{3\to 7}{C}_3,{\alpha }_{8\to 4}{C}_8={\alpha }_{4\to 8}{C}_4.$$ (Equation A.14)

After multiplication of both sides of these equations by k, we recover compensation of fluxes through the ring canals connecting cells 5 – 8 with cells 1 – 4, respectively.

Finally, we write Equation A.12 for cell 2 containing 4 ring canals and cells 3 and 4 containing 3 ring canals, respectively. Taking into account Equations A.13 and A.14, we arrive at

$${\alpha }_{2\to 1}{C}_2={\alpha }_{1\to 2}{C}_1,{\alpha }_{3\to 1}{C}_3={\alpha }_{1\to 3}{C}_1,{\alpha }_{4\to 2}{C}_4={\alpha }_{2\to 4}{C}_2$$ (Equation A.15)

Multiplying both sides of these equations by the rate constant k, we recover flux balance for the ring canals connecting cell 2 with cells 1 and 4, and cell 3 with cell 1.

To summarize, we have shown that forward and backward fluxes through the ring canals balance each other at equilibrium.

C. Solution of Equation A.5

We obtain the time dependence of the volume of cell i separated from cell 1 by j ring canals by integrating Equation A.5 with the initial condition $V_i^{(0)}(0)=V_0$. The result is

$$V_i^{(j)}(t)=V_0\exp \left[\mu {\nu }^j{\int }_0^t{c}_1\left(t^{\prime }\right)d{t}^{\prime }\right]=V(j,t),$$ (Equation A.16)

where we took advantage of the fact that the volumes of all cells belonging to the same layer are equal and denoted this volume for the cells belonging to layer j by V(t,j). The natural logarithm of the ratio of the cell volume V(t,j) to its initial value, V₀, is

$$\text{ln}\frac{V(t,j)}{V_0}=\mu {\nu }^j{\int }_0^t{c}_1\left(t\prime \right)dt\prime .$$ (Equation A.17)

We use this to establish the relation between volumes of the cells belonging to different layers,

$$\text{ln}\frac{V(t,j)}{V_0}=\nu \text{\hspace{0.17em}ln}\frac{V(t,j)}{V_0}={\nu }^j\text{\hspace{0.17em}ln}\frac{V(t,1)}{V_0}.$$ (Equation A.18)

Alternatively, this relation can be written as

$$\frac{V(t,j)}{V_0}={\left[\frac{V(t,j-1)}{V_0}\right]}^{\nu }={\left[\frac{V(t,1)}{V_0}\right]}^{{\nu }^j}$$ (Equation A.19)

This is a generalization of Equation 10 from the main text to the case of the 16 cell cluster.

QUANTIFICATION AND STATISTICAL ANALYSIS

All the statistical details of experiments such as the number of samples used per data point and precision measures (mean ± SEM) are reported in the Figures and Figure Legends. All the measurements reported are of cell volume, obtained as described in STAR Methods. These measurements were all done for individual cells in groups of 16 cells forming a whole egg chamber. The number of samples indicated in all Figure legends, n, refers to the number of whole egg chambers used. The observed relationships between nurse cell identity and volume rank were qualitatively evident and did not require statistical tests. In Figure 4, least square linear regression was performed in MATLAB (MathWorks, Natick, MA) using the regress function to analyze properties of allometric scaling as detailed in the text and provide the confidence interval for ν.

Highlights.

• 3D imaging reveals collective growth of Drosophila nurse cells

• Nurse cells grow in groups, determined by the structure of the cell lineage tree

• Mathematical model of intercellular transport explains the emergence of groups

• The model reveals allometric growth in a small cell network