Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2018 Nov 8;45(21):12023–12031. doi: 10.1029/2018GL079826

Understanding Rapid Adjustments to Diverse Forcing Agents

C J Smith 1,✉, R J Kramer 2, G Myhre 3, P M Forster 1, B J Soden 2, T Andrews 4, O Boucher 5, G Faluvegi 6,7, D Fläschner 8, Ø Hodnebrog 3, M Kasoar 9,10, V Kharin 11, A Kirkevåg 12, J‐F Lamarque 13, J Mülmenstädt 14, D Olivié 12, T Richardson 1, B H Samset 3, D Shindell 15, P Stier 16, T Takemura 17, A Voulgarakis 9, D Watson‐Parris 16
PMCID: PMC6334512  PMID: 30686845

Abstract

Rapid adjustments are responses to forcing agents that cause a perturbation to the top of atmosphere energy budget but are uncoupled to changes in surface warming. Different mechanisms are responsible for these adjustments for a variety of climate drivers. These remain to be quantified in detail. It is shown that rapid adjustments reduce the effective radiative forcing (ERF) of black carbon by half of the instantaneous forcing, but for CO2 forcing, rapid adjustments increase ERF. Competing tropospheric adjustments for CO2 forcing are individually significant but sum to zero, such that the ERF equals the stratospherically adjusted radiative forcing, but this is not true for other forcing agents. Additional experiments of increase in the solar constant and increase in CH4 are used to show that a key factor of the rapid adjustment for an individual climate driver is changes in temperature in the upper troposphere and lower stratosphere.

Keywords: rapid adjustments, radiative forcing, PDRMIP, kernels

Key Points

  • Rapid adjustments affect the Earth's energy balance in different ways for greenhouse gas, aerosol, and solar forcing

  • Radiative kernels and partial radiative perturbations are used to diagnose rapid adjustments from atmospheric and cloud changes

  • Noncloud adjustments agree well between models, whereas cloud adjustments exhibit more spread

1. Introduction

Owing to its expected better correspondence to equilibrium surface temperature change, effective radiative forcing (ERF) has taken precedence over the older definition of stratospherically adjusted radiative forcing (RF) for measuring perturbations to the Earth's radiative energy budget (Boucher et al., 2013; Forster et al., 2016; Myhre et al., 2013; Shine et al., 2003). ERF takes into account the radiative effects of tropospheric and land surface changes to the top of atmosphere (TOA) energy budget, in addition to the stratospheric temperature change, in response to a forcing. Together, these atmospheric and land surface changes are termed rapid adjustments. While there is no formal separation of timescales, rapid adjustments tend to manifest themselves on a period of weeks to months and are distinct from the (generally) slower climate feedbacks, such as the sea ice/albedo, lapse rate, water vapor, and cloud feedbacks, which are driven by the surface temperature response (Sherwood et al., 2015). Therefore, rapid adjustments are usually considered to be part of the forcing (Forster et al., 2013; Gregory et al., 2004).

It has long been known (Manabe & Wetherald, 1975) that an increase in CO2 concentrations cools the stratosphere, which reduces longwave (LW) outgoing radiation, increasing the positive forcing compared to the instantaneous radiative forcing (IRF) of CO2 (the convention in this paper is to report IRF at the TOA). Such knowledge is incorporated into the definition of RF. More recently, it has been acknowledged that CO2 perturbations also change the thermal structure of the troposphere, which leads to changes in water vapor and cloud profiles (Gregory & Webb, 2008). CO2 forcing also drives land‐surface changes due to its effects on plant stomatal conductance (Doutriaux‐Boucher et al., 2009; Richardson et al., 2018). These components all induce their own responses in the TOA energy balance, which are not included in the standard RF framework.

Furthermore, for some forcing agents, stratospheric temperatures do not change in the same way as for CO2 forcing, and tropospheric changes can be more important (Hansen et al., 2005). Aerosols have significant impacts on tropospheric radiative heating rates and many aspects of clouds (Ramanathan et al., 2001), rendering RF as an unsatisfactory method of comparing forcing impacts across greenhouse gases and aerosols (Boucher et al., 2013; Myhre et al., 2013). To date, rapid adjustment analyses have largely been based on CO2 forcing (Andrews & Forster, 2008; Block & Mauritsen, 2013; Chung & Soden, 2015a, 2015b; Gregory & Webb, 2008; Vial et al., 2013; Zelinka et al., 2013) and an investigation across forcing mechanisms has not been made.

2. Methods

2.1. Experiments and Climate Models

In this study we use atmosphere‐only integrations from 11 global climate models (Canadian Earth System Model version 2 [CanESM2], ECHAM6‐HAM2, Goddard Institute for Space Studies E2‐R [GISS‐E2‐R], Hadley Centre Global Environmental Model version 2 Earth System [HadGEM2‐ES], Hadley Centre Global. Environment Model 3 [HadGEM3], Institut Pierre‐Simon Laplace Coupled Model version 5A [IPSL‐CM5A], Model for Interdisciplinary Research on Climate / Spectral Radiation‐Transport Model for Aerosol Species [MIROC‐SPRINTARS], National Center for Atmospheric Research‐Community Earth System Model version 1‐Community Atmospheric Model version 4 [NCAR‐CESM1‐CAM4], NCAR‐CESM1‐CAM5, Max‐Planck‐Institute Earth System Model [MPI‐ESM], and Norwegian Earth System Model 1‐Medium Resolution [NorESM1]) participating in the Precipitation Driver Response Model Intercomparison Project (PDRMIP; Myhre et al., 2017; Samset et al., 2016) for five idealized climate forcing experiments (Table S1 in the supporting information). The experiments are a doubling of CO2 concentrations (2xCO2), tripling of methane concentrations (3xCH4), 5 times sulfate emissions or concentrations (5xSul), 10 times black carbon emissions or concentrations (10xBC), and a 2% increase in the solar constant (2%Sol). One control (base) integration is also performed for each model. Perturbations are made abruptly, and for each model years 6 to 15 of the control and perturbed integrations are used for analysis. For the 5xSul and 10xBC experiments, some models are driven by emissions rather than concentration increases, and aerosol mass loadings depend on the aerosol transport and dynamical schemes within the model. Therefore, the emission‐driven experiments are not necessarily equal in terms of forcing size perturbation with each other or with the concentration‐driven experiments (Figures S1 and S2 in supporting information).

The atmosphere‐only integrations use climatological sea surface temperatures (SSTs) and sea ice. ERF is defined as the difference in TOA flux imbalance between the perturbed and base integrations of each climate model using the same base SST and sea ice climatology in both runs. By fixing the ocean state, any contribution from climate feedback is minimized leaving just the IRF plus the rapid adjustments, which sums to the ERF (Forster et al., 2016). For aerosol experiments, we define IRF as the sum of the direct aerosol effect (RFari) and cloud‐albedo effect (RFaci), whereas adjustments include the semidirect and cloud‐lifetime effects (Boucher et al., 2013). Land surface temperatures are allowed to respond, and feedback from land surface temperature changes, although small, do get aliased into calculations of adjustments (Chung & Soden, 2015b). There is more than one way to define ERF (Gregory et al., 2004; Hansen et al., 2005; Myhre et al., 2013), but we use the fixed‐SST method as fewer model years are needed to minimize the uncertainty in ERF (Forster et al., 2016).

2.2. Radiative Kernel Method

Assuming that rapid adjustments are sufficiently linear and separable, radiative kernels can be used to diagnose adjustments. Radiative kernels describe how the TOA radiative flux changes for a small perturbation in an atmospheric state variable. The kernel technique has generally been used for studies quantifying climate feedback in coupled model integrations (Block & Mauritsen, 2013; Shell et al., 2008; Soden et al., 2008) but is also useful for diagnosing rapid adjustments by applying them to atmosphere‐only integrations (Chung & Soden, 2015a; Vial et al., 2013; Zhang & Huang, 2014).

We can write the ERF resulting from a small perturbation in climate as (Chung & Soden, 2015a)

ERF=IRF+AT+ATs+Aq+Aα+Ac+ϵ, (1)

where Ax is the rapid adjustment x due to atmospheric temperature (T), surface temperature (Ts), water vapor (q), surface albedo (α), and clouds (c), and ϵ is a residual that accounts for nonlinearities. The rapid adjustment due to atmospheric temperature is further broken down into stratospheric and tropospheric contributions, using a tropopause that varies linearly from 100 hPa at the equator to 300 hPa at the poles (Soden et al., 2008). In this study we use radiative kernels from the Bureau of Meteorology Research Centre (BMRC; Soden et al., 2008), Community Climate System Model version 4 (CCSM4; Shell et al., 2008), CESM (Pendergrass et al., 2018), Geophysical Fluid Dynamics Laboratory (GFDL; Soden et al., 2008), HadGEM2 (Smith, 2018), and European Centre for Medium‐Range Weather Forecasts (ECMWF)‐ERA‐Interim/Oslo (Dee et al., 2011; Myhre et al., 2018; Myhre & Stordal, 1997) models.

As cloud adjustments do not typically behave linearly following a perturbation in cloud properties, the adjustments due to clouds are calculated differently. One method is using the difference of all‐sky and clear‐sky kernel decompositions:

Ac=ERF−ERFclr−IRF−IRFclr−∑x∈TqαTsAx−Axclr (2)

where ERFclr and IRFclr refer to cloud‐free ERF and IRF and Axclr are rapid adjustments calculated with clear‐sky kernels. We refer to this as the kernel difference method. IRF and IRFclr are not known precisely from many models, but in some cases an estimate can be made by substituting each model's base and perturbed climatology into an off‐line radiation code and taking the difference in TOA fluxes.

2.3. Monthly Mean Partial Radiative Perturbation Method

The ECMWF‐ERA‐Interim/Oslo kernel did not implement a water vapor kernel, and water vapor and cloud adjustments using this radiation code were computed using a variant of the Partial Radiative Perturbation (PRP) method (Colman et al., 2001; Wetherald & Manabe, 1988), which we denote Monthly Mean Partial Radiative Perturbation (MMPRP) as it uses monthly mean climatologies from each perturbed run. Water vapor and cloud profiles from each experiment are substituted into the control climatology, run through an off‐line radiative transfer model and the difference in TOA fluxes computed compared to the control climatology. As the MMPRP does not require knowledge of the IRF, cloud adjustment calculations are available from more models in the 10xBC and 5xSul experiments than with the kernel difference method. The SW cloud adjustments for 5xSul were further decomposed using the Approximate Partial Radiative Perturbation (APRP) method (Taylor et al., 2007).

Further methodological details describing the radiative kernel, MMPRP and APRP methods are provided in the supporting information (Alduchov & Eskridge, 1996; Collins et al., 2006; Edwards & Slingo, 1996; Huang & Bani Shahabadi, 2014; Manners et al., 2015; Martin et al., 2011; Sanderson & Shell, 2012; Zelinka et al., 2014).

3. Results

3.1. Rapid Adjustments by Forcing Agent

Figure 1 shows the IRF, ERF, and rapid adjustments for each of the five climate forcers. The rapid adjustments to 2xCO2 forcing are positive overall and constitute 30% of the ERF, whereas for 10xBC forcing they are negative and are 107% of the absolute ERF, therefore offsetting more than half of the positive IRF. Rapid adjustments to 2%Sol and 5xSul are slightly negative, whereas they are close to zero for 3xCH4.

Figure 1.

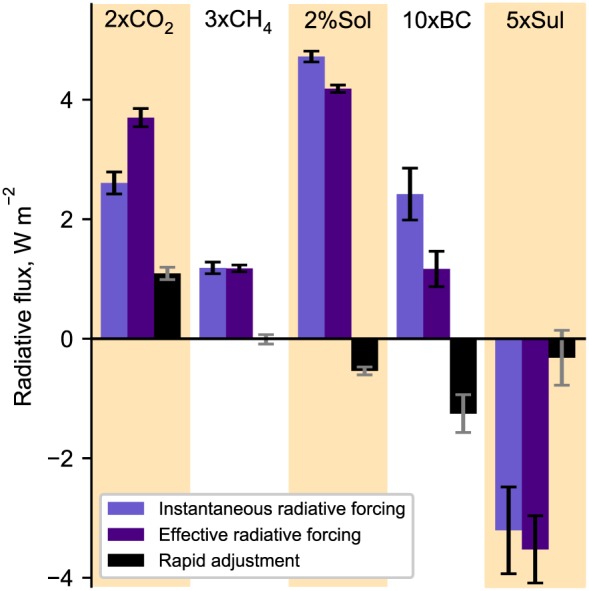
Figure 1

Open in a new tab

Instantaneous radiative forcing, effective radiative forcing, and rapid adjustments for five different climate change drivers. Each bar represents a multimodel mean and each model is given equal weight with up to six different methods of calculating each adjustment for each model (Figure S3 in the supporting information). The error bars are the 95% confidence range weighting each method and model sample equally.

Adjustments are calculated individually for each model and kernel (Figure S3 in the supporting information), and the responses are averaged first over kernels and then over models so that each model has equal weight in Figure 1. In previous work it has been shown that differences in kernel base climatology and radiative transfer are typically minimal (Soden et al., 2008), and differences are only significant where climate perturbations are larger than in this study (Jonko et al., 2012). In general, we find this to be true as interkernel agreement is good except for stratospheric temperature adjustment to 2xCO2 forcing as discussed below. Interkernel agreement is also good for cloud adjustments, although cloud adjustments calculated using MMPRPs differ somewhat from the kernel‐derived methods. For 5xSul we only use cloud adjustments calculated from the MMPRP for Figure 1 except from the NCAR‐CESM1‐CAM4 model, which does not include cloud microphysical changes in its PDRMIP configuration. This is to isolate the component of the cloud lifetime effect (Albrecht, 1989) from the cloud microphysical effect (Twomey, 1977).

The residual term ϵ in equation (1) should be no more than 10% of the ERF for the kernel method to be valid (Shell et al., 2008). For most models and experiments the true IRF is not available as this requires a double radiation call. However, in some situations the shortwave (SW) or LW IRF is known to be 0. This occurs when either SW or LW absorption of a particular species is not present in a model's radiation code. In these cases, any difference between the ERF and the sum of all rapid adjustments is a residual by equation (1). Figure 2 shows the ERF, rapid adjustment, and residual for 10xBC LW, 3xCH4 SW, and 2%Sol LW for those models, which do not include LW absorption of BC or SW absorption of methane in their radiation schemes (no models include LW solar absorption). In each of the three cases it can be seen that the residual term is small, being 6%, 12%, and 2% of the ERF for 10xBC LW, 3xCH4 SW, and 2%Sol LW in magnitude, respectively. The larger multimodel residual in the 3xCH4 SW case is biased by a large relative residual in the HadGEM2 model, whereas residuals in the other four models analyzed are close to 0.

Figure 2.

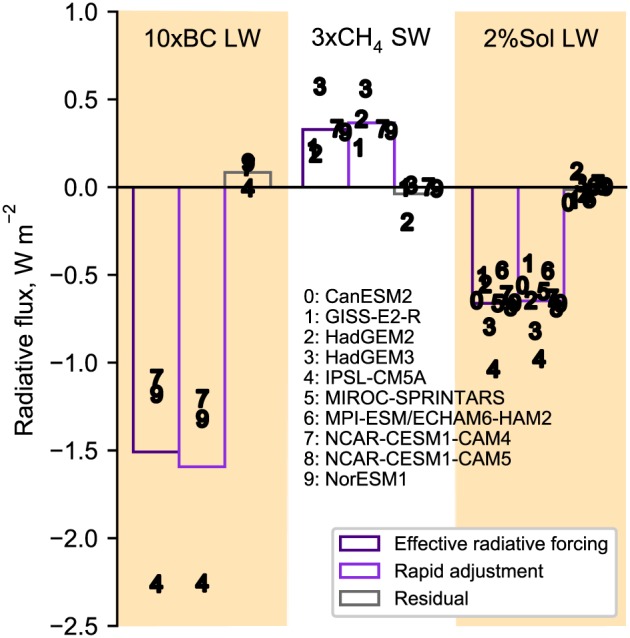
Figure 2

Open in a new tab

Effective radiative forcing, rapid adjustments, and residuals in models where instantaneous radiative forcing is known to be exactly 0. Each point is a multikernel mean for each model and outlined bars show the multimodel means from this subset of models.

Figure 3 shows the contribution to the total rapid adjustment for each atmospheric mechanism. Adjustments normalized by IRF and the mean change in individual model atmospheric profiles are shown in Figures S4 and S5 in the supporting information.

Figure 3.

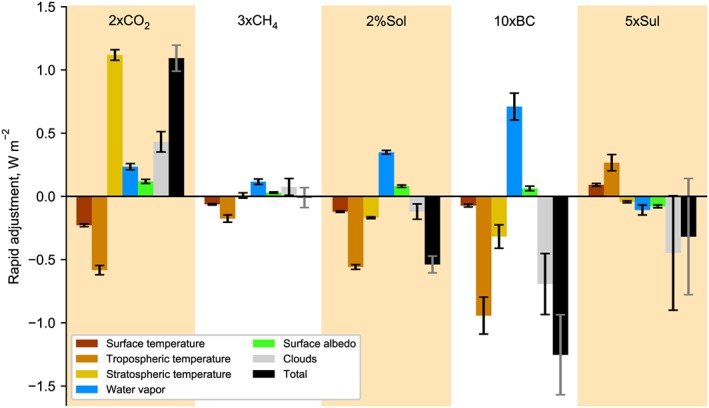
Figure 3

Open in a new tab

Rapid adjustments decomposed by mechanism. The bars represent multimodel means. The error bars are the 95% confidence range weighting each method and model sample equally (see Figure S3 for individual model and kernel responses).

For 2xCO2, the adjustment due to stratospheric temperature change is strong and positive due to stratospheric cooling. The stratospheric cooling is the largest temperature response throughout the atmospheric column and is consistently present in all models. It is a remarkable coincidence that the stratospheric temperature adjustment for 2xCO2 is the same size as the total adjustment, despite the nonnegligible contributions from other adjustments, which sum to 0. This can explain why stratospherically adjusted RF has for a long time been a useful metric for evaluating the energetic effects of CO2 forcing. The larger error bar for the total adjustment reflects the assessment of Myhre et al. (2013) that ERF is expected to be similar to RF for CO2 forcing with a larger uncertainty due to the inclusion of the tropospheric and surface adjustments.

There is some disagreement between kernels for the stratospheric temperature adjustment for 2xCO2, for which the ECMWF‐ERA‐Interim/Oslo kernel projects a stronger adjustment in most models. The reason for this is that the ECMWF‐ERA‐Interim/Oslo kernel has a higher resolution in the stratosphere than the other kernels considered in this study. The ECMWF‐ERA‐Interim/Oslo kernel has 60 model levels with the highest at 0.1 hPa, whereas the other five kernels use the 17 standard pressure levels in CMIP5 (Taylor et al., 2012) with 10 hPa being the highest. The difference is largest in models for which the output is also highly resolved in the stratosphere, such as CanESM2. This additional contribution to the stratospheric cooling accounts for about an additional +0.4 W/m2 allocated to stratospheric adjustment in CanESM2 using the ECMWF‐ERA‐Interim/Oslo kernel compared to other kernels.

Black carbon shows a strong negative total adjustment (Stjern et al., 2017), for which the largest (absolute) negative contributions are tropospheric temperature and clouds. The largest positive adjustment in absolute terms is due to the change in water vapor, which opposes tropospheric temperature changes. The vertical profiles associated with BC forcing show a warming and wetting throughout the atmosphere coupled with a large reduction in cloud fraction, particularly at higher levels. Unlike for 2xCO2, the stratospheric temperature adjustment is negative rather than positive in 10xBC, due to a warming stratosphere (Hansen et al., 1997). The total adjustment is substantially different from the stratospheric temperature adjustment, so RF is not an appropriate measure of ERF for BC forcing. The strong negative adjustment to black carbon forcing indicates that the equilibrium global mean near‐surface temperature response to a black carbon forcing is smaller than indicated by its direct effect. Unlike CO2, BC (and sulfate) mass mixing ratios are spatially variable, and rapid adjustments depend on the location of the aerosol perturbation (Samset & Myhre, 2015). An increase in solar forcing is not distributed equally either, as more solar radiation is received in the tropics, and this zonal asymmetry can drive different circulation responses compared to CO2 (Guo et al., 2018).

In the 2%Sol experiment, the tropospheric temperature adjustment (partially offset by water vapor) also dominates over the stratospheric temperature adjustment. Net cloud adjustments are negative rather than positive for 2%Sol as seen by the change in vertical cloud fraction profile but are smaller in magnitude relative to the IRF than for 10xBC. Again, the rapid adjustment due to stratospheric temperature change does not equal the total adjustment.

The stratospheric temperature adjustment in 3xCH4 shows a much smaller level of change than 2xCO2, as stratospheric temperature changes are much less pronounced. The small stratospheric temperature adjustment could be due to competition between radiative absorption and emission processes in the upper troposphere/lower stratosphere (UTLS; Zhong et al., 1993), unlike for CO2 in which emission from the upper troposphere dominates due to its relatively higher abundance in the atmosphere (Forster et al., 1997; Stocker et al., 2001). Therefore, for 3xCH4, more of the LW emission from the warming troposphere passes through the stratosphere and reaches the TOA. However, overlap with water vapor bands for CH4 is also important. The subset of models with an explicit treatment of SW absorption by methane (CanESM2, MIROC‐SPRINTARS, MPI‐ESM, and NCAR‐CESM1‐CAM5) exhibits a UTLS warming and a negative stratospheric temperature adjustment to methane forcing; the opposite is true for those that do not (Figures S5b and S6 in the supporting information). Inclusion or omission of SW methane absorption also determines whether cloud adjustments are negative or positive. In the multimodel mean, the stratospheric temperature adjustment is similar to the total adjustment, but for the subset of models that either exclude or include SW absorption of methane, they do not agree. This may indicate that ERF also differs from RF for methane.

In 5xSul, noncloud adjustments are generally small in comparison to the IRF, and cloud adjustments, which are larger in magnitude and spread, are described in the following subsection.

In all experiments there is an anticorrelation between tropospheric temperature and water vapor adjustments, which is a result of the Clausius‐Clapeyron relationship. This is shown by observing that the water vapor adjustment is dominated by the adjustment calculated assuming a constant relative humidity for the tropospheric temperature change in each model and experiment (Figure S7 in the supporting information). By decomposing tropospheric temperature responses into Planck and lapse‐rate components, we also show that the model spread in lapse‐rate plus constant relative humidity is smaller than in each of the individual components, reinforcing this anticorrelation and in line with feedback studies (Soden et al., 2008).

3.2. Cloud Adjustments

The cloud adjustments in each model and forcing agent are further split into SW and LW components in Figure 4 using the MMPRP method. Cloud adjustments to CO2 forcing are +0.45 W/m2 on average and all models and methods agree that the net effect is positive, dominated by the SW effect. This is due to a reduction in low‐level and midlevel cloud fraction (also noted in Zelinka et al., 2013), which reduces outgoing SW radiation. There is no agreement between models on the sign of the LW cloud adjustment.

Figure 4.

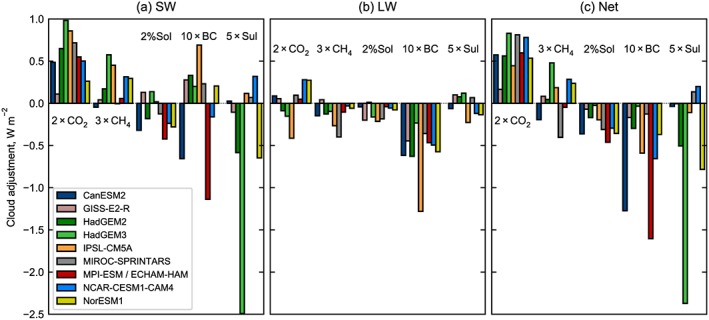
Figure 4

Open in a new tab

Cloud adjustments in each model using the Monthly Mean Partial Radiative Perturbation method. National Center for Atmospheric Research‐Community Earth System Model version 1‐Community Atmospheric Model version 5 (NCAR‐CESM1‐CAM5) is excluded as not all required diagnostics are present.

In 10xBC, a downward shift of clouds occurs. Many competing processes that affect cloud adjustments occur in response to a BC forcing, such as cloud burn off (reduction in clouds), increased convection (increasing clouds), and changes in atmospheric stability, which could increase or decrease clouds depending on the altitude of the BC perturbation (Koch & Del Genio, 2010; Samset & Myhre, 2015). Every model shows a negative LW cloud adjustment to 10xBC, whereas there is no agreement on the sign of SW cloud adjustments. However, those models with a substantial negative cloud adjustment to 10xBC (ECHAM6‐HAM2 and CanESM2) show a large increase in cloud liquid water content in the lower or middle troposphere that is not present in other models, suggesting a possible mechanism.

For 5xSul, there is a large spread in the strength of the cloud adjustment, dominated by the SW effect, which is particularly strong in the HadGEM3 model. Further analysis is undertaken with the APRP method for SW cloud adjustments in the seven models for which diagnostics permit (Figure S8 in supporting information). This shows that the ERF for 5xSul is substantially more negative in HadGEM3 than for other models, driven by a large contribution from the RFaci (RF due to aerosol‐cloud interactions or cloud microphysical effect). The direct aerosol forcing (RF due to aerosol‐radiation interactions, RFari) in HadGEM3 is in line with other models. The APRP highlights the varying strength in RFaci, which ranges from 33% (in CanESM2) to 63% (in HadGEM3) of the ERF in models, which include cloud microphysical changes.

One limitation of the APRP method is that it does not appear to work well with models that do not include interactive cloud microphysical changes in their configurations, such as the apparent positive RFaci in NCAR‐CESM1‐CAM4 and GISS‐E2‐R. Furthermore, the computed SW cloud adjustments with the MMPRP and APRP methods do not agree in magnitude, and the kernel difference method, which is only available in three models due to the availability of double calls, only agrees with the MMPRP where cloud microphysical changes are not included (i.e., in NCAR‐CESM1‐CAM4; Figure S3). The differences obtained with different methods highlight the difficulties in estimating cloud adjustments. A direct estimate of cloud adjustments can be obtained using a cloud kernel (Zelinka et al., 2012) and model output of International Satellite Cloud Climatology Project (ISCCP) simulator diagnostics (Bodas‐Salcedo et al., 2011; Klein & Jakob, 1999; Webb et al., 2001). These diagnostics were not part of the PDRMIP data request and are generally not output by models outside of the CFMIP protocol (Webb et al., 2017). Inclusion of these diagnostics as standard in more models would aid understanding of cloud adjustment mechanisms.

4. Conclusions

Understanding how models respond to different forcing agents is critical to reducing uncertainty in climate‐model projections of the Earth's energy budget and ultimately climate sensitivity (Forster et al., 2016). This work has found that ERF is distinctly different from RF across forcing mechanisms, indicating that for all forcings analyzed rapid adjustments have an important role to play in the quantification of the perturbation of the Earth's energy budget from human activities and the overall heating of the oceans. For CO2 competing tropospheric and land surface rapid adjustment effects cancel, meaning the overall estimates of ERF are similar to the stratospheric temperature adjusted RF. For the other mechanisms tropospheric rapid adjustments significantly alter forcing estimates. Tropospheric temperature (partially offset by water vapor) and cloud changes are the principal sources of adjustment, with stratospheric temperature adjustment playing a lesser role. Clouds have an appreciable effect on the overall forcings, particularly for CO2, BC, and sulfate, and it is shown that intermodel diversity is high and diagnostic methods do not necessary agree. For CH4 the sign of the cloud adjustment, and total rapid adjustment, depends on whether SW absorption of methane is included in the radiation scheme. This highlights the importance of the UTLS region in the radiative balance and has important consequences for model development.

The vertical resolution and truncation height of both the radiative kernel and model output may affect the rapid adjustment due to stratospheric temperature calculated for CO2 forcing. It may be the case that adjustments or climate feedbacks are underestimated using radiative kernels or model output, which is not well resolved in the stratosphere. As radiative kernels have been used extensively for multiple‐CO2 studies or anthropogenic forcing pathways where CO2 is the dominant forcing agent, further work is needed to determine whether this is a significant effect.

In general, noncloud adjustments agree well between methods and models, and radiative kernels provide a robust framework for decomposing ERF into IRF and rapid adjustments. However, cloud adjustments are not consistent between models and methods, particularly for sulfate forcing, and require more understanding. Further modeling work should focus on improving our understanding of cloud adjustments, and output of ISCCP simulator diagnostics as standard in climate models would be beneficial to enable a consistent method of directly estimating these effects. A further progression is to constrain rapid adjustment calculations with observations. A historical reanalysis data set can be used to determine the evolution of rapid adjustments over time. In the present day, satellite and ground‐based stations can be used to observationally constrain the spatial distribution of aerosol concentrations, which would be particularly important for black carbon where the adjustment strength (and possibly sign) is sensitive to the vertical profile of the aerosol.

Supporting information

Supporting Information S1

Click here for additional data file. (1.5MB, docx)

Acknowledgments

C. J. S. and P. F. acknowledge support from Regional and Global Climate Modeling Program of the U.S. Department of Energy Office of Environmental and Biological Sciences under grant DE‐SC0012549 and UK Natural Environment Research Council grant NE/N006038/1. R. J. K. was supported by NASA grant 17‐EARTH17R‐015. D. W. P. acknowledges funding from Natural Environment Research Council projects NE/L01355X/1 (CLARIFY) and NE/J022624/1 (GASSP). G. M., Ø. H., and B. H. S. were funded by the Research Council of Norway, through the grant NAPEX (229778). D. O. and A. K. were supported by the Norwegian Research Council through the projects EVA (229771), EarthClim (207711/E10), NOTUR (nn2345k), and NorStore (ns2345k). O. B. acknowledges HPC resources from TGCC under the gencmip6 allocation provided by GENCI (Grand Equipement National de Calcul Intensif). P. S. acknowledges funding from the European Research Council project RECAP under the European Union's Horizon 2020 research and innovation program with grant agreement 724602 and support from the Alexander von Humboldt Foundation. T. A. was supported by the Met Office Hadley Centre Climate Programme funded by BEIS and Defra. M. K. and A. V. were supported by the Natural Environment Research Council under grant NE/K500872/1. T. T. was supported by the supercomputer system of the National Institute for Environmental Studies, Japan; the Environment Research and Technology Development Fund (S‐12‐3) of the Environmental Restoration and Conservation Agency of Japan; and JSPS KAKENHI grant JP15H01728. Simulations with HadGEM3‐GA4 were performed using the MONSooN system, a collaborative facility supplied under the Joint Weather and Climate Research Programme, which is a strategic partnership between the Met Office and the Natural Environment Research Council. Climate modeling at GISS (D. S. and G. F.) is supported by the NASA Modeling, Analysis and Prediction program and GISS simulations used resources provided by the NASA High‐End Computing Program through the NASA Center for Climate Simulation at Goddard Space Flight Center. The ECHAM6‐HAM2 simulations were performed using the ARCHER UK National Supercomputing Service. The ECHAM‐HAMMOZ model is developed by a consortium composed of ETH Zurich, Max Planck Institut für Meteorologie, Forschungszentrum Jülich, University of Oxford, the Finnish Meteorological Institute, and the Leibniz Institute for Tropospheric Research and managed by the Center for Climate Systems Modeling (C2SM) at ETH Zurich. The HadGEM2 radiative kernels are available from https://doi.org/10.5518/406. For access to PDRMIP model data please see http://www.cicero.oslo.no/en/PDRMIP/PDRMIP‐data‐access.

Smith, C. J. , Kramer, R. J. , Myhre, G. , Forster, P. M. , Soden, B. J. , Andrews, T. , et al. (2018). Understanding rapid adjustments to diverse forcing agents. Geophysical Research Letters, 45, 12,023–12,031. 10.1029/2018GL079826

References

  1. Albrecht, B. A. (1989). Aerosols, cloud microphysics, and fractional cloudiness. Science, 245(4923), 1227–1230. 10.1126/science.245.4923.1227 [DOI] [PubMed] [Google Scholar]
  2. Alduchov, O. A. , & Eskridge, R. E. (1996). Improved Magnus form approximation of saturation vapor pressure. Journal of Applied Meteorology, 35(4), 601–609. [DOI] [Google Scholar]
  3. Andrews, T. , & Forster, P. M. (2008). CO2 forcing induces semi‐direct effects with consequences for climate feedback interpretations. Geophysical Research Letters, 35, L04802 10.1029/2007GL032273 [DOI] [Google Scholar]
  4. Block, K. , & Mauritsen, T. (2013). Forcing and feedback in the MPI‐ESM‐LR coupled model under abruptly quadrupled CO2 . Journal of Advances in Modeling Earth Systems, 5, 691–696. [Google Scholar]
  5. Bodas‐Salcedo, A. , Webb, M. J. , Bony, S. , Chepfer, H. , Dufresne, J.‐L. , Klein, S. A. , Zhang, Y. , Marchand, R. , Haynes, J. M. , Pincus, R. , & John, V. O. (2011). COSP: Satellite simulation software for model assessment. Bulletin of the American Meteorological Society, 92(8), 1023–1043. 10.1175/2011BAMS2856.1 [DOI] [Google Scholar]
  6. Boucher, O. , Randall, D. , Artaxo, P. , Bretherton, C. , Feingold, G. , Forster, P. , Kerminen, V.‐M. , Kondo, Y. , Liao, H. , Lohmann, U. , Rasch, P. , Satheesh, S. K. , Sherwood, S. , Stevens, B. , & Zhang, X. Y. (2013). Clouds and aerosols In Stocker T. F., Qin D., Plattner G. K., Tignor M., Allen S. K., Boschung J., et al. (Eds.), Climate change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (pp. 571–658). Cambridge, UK and New York: Cambridge University Press. [Google Scholar]
  7. Chung, E.‐S. , & Soden, B. J. (2015a). An assessment of direct radiative forcing, radiative adjustments, and radiative feedbacks in coupled ocean–atmosphere models. Journal of Climate, 28(10), 4152–4170. 10.1175/JCLI-D-14-00436.1 [DOI] [Google Scholar]
  8. Chung, E.‐S. , & Soden, B. J. (2015b). An assessment of methods for computing radiative forcing in climate models. Environmental Research Letters, 10(7), 074004. 10.1088/1748-9326/10/7/074004 [DOI] [Google Scholar]
  9. Collins, W. D. , Ramaswamy, V. , Schwarzkopf, M. D. , Sun, Y. , Portmann, R. W. , Fu, Q. , Casanova, S. E. B. , Dufresne, J. L. , Fillmore, D. W. , Forster, P. M. D. , Galin, V. Y. , Gohar, L. K. , Ingram, W. J. , Kratz, D. P. , Lefebvre, M. P. , Li, J. , Marquet, P. , Oinas, V. , Tsushima, Y. , Uchiyama, T. , & Zhong, W. Y. (2006). Radiative forcing by well‐mixed greenhouse gases: Estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). Journal of Geophysical Research, 111, D14317 10.1029/2005JD006713 [DOI] [Google Scholar]
  10. Colman, R. , Fraser, J. , & Rotstayn, L. (2001). Climate feedbacks in a general circulation model incorporating prognostic clouds. Climate Dynamics, 18(1‐2), 103–122. 10.1007/s003820100162 [DOI] [Google Scholar]
  11. Dee, D. P. , Uppala, S. M. , Simmons, A. J. , Berrisford, P. , Poli, P. , Kobayashi, S. , Andrae, U. , Balmaseda, M. A. , Balsamo, G. , Bauer, P. , Bechtold, P. , Beljaars, A. C. M. , van de Berg, L. , Bidlot, J. , Bormann, N. , Delsol, C. , Dragani, R. , Fuentes, M. , Geer, A. J. , Haimberger, L. , Healy, S. B. , Hersbach, H. , Hólm, E. V. , Isaksen, L. , Kållberg, P. , Köhler, M. , Matricardi, M. , McNally, A. P. , Monge‐Sanz, B. M. , Morcrette, J. J. , Park, B. K. , Peubey, C. , de Rosnay, P. , Tavolato, C. , Thépaut, J. N. , & Vitart, F. (2011). The ERA‐Interim reanalysis: Configuration and performance of the data assimilation system. Quarterly Journal of the Royal Meteorological Society, 137(656), 553–597. 10.1002/qj.828 [DOI] [Google Scholar]
  12. Doutriaux‐Boucher, M. , Webb, M. J. , Gregory, J. M. , & Boucher, O. (2009). Carbon dioxide induced stomatal closure increases radiative forcing via a rapid reduction in low cloud. Geophysical Research Letters, 36, L02703 10.1029/2008GL036273 [DOI] [Google Scholar]
  13. Edwards, J. M. , & Slingo, A. (1996). Studies with a flexible new radiation code. I: Choosing a configuration for a large‐scale model. Quarterly Journal of the Royal Meteorological Society, 122(531), 689–719. 10.1002/qj.49712253107 [DOI] [Google Scholar]
  14. Forster, P. M. , Andrews, T. , Good, P. , Gregory, J. M. , Jackson, L. S. , & Zelinka, M. (2013). Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models. Journal of Geophysical Research: Atmospheres, 118, 1139–1150. 10.1002/jgrd.50174 [DOI] [Google Scholar]
  15. Forster, P. M. , Freckleton, R. S. , & Shine, K. P. (1997). On aspects of the concept of radiative forcing. Climate Dynamics, 13(7‐8), 547–560. 10.1007/s003820050182 [DOI] [Google Scholar]
  16. Forster, P. M. , Richardson, T. , Maycock, A. , Smith, C. J. , Samset, B. H. , Myhre, G. , Andrews, T. , Pincus, R. , & Schulz, M. (2016). Recommendations for diagnosing effective radiative forcing from climate models from CMIP6. Journal of Geophysical Research: Atmospheres, 121, 12,460–12,475. 10.1002/2016JD025320 [DOI] [Google Scholar]
  17. Gregory, J. M. , Ingram, W. J. , Palmer, M. A. , Jones, G. S. , Stott, P. A. , Thorpe, R. B. , Lowe, J. A. , Johns, T. C. , & Williams, K. D. (2004). A new method for diagnosing radiative forcing and climate sensitivity. Geophysical Research Letters, 31, L03205 10.1029/2003GL018747 [DOI] [Google Scholar]
  18. Gregory, J. M. , & Webb, M. J. (2008). Tropospheric adjustment induces a cloud component in CO2 forcing. Journal of Climate, 21(1), 58–71. 10.1175/2007JCLI1834.1 [DOI] [Google Scholar]
  19. Guo, A. , Moore, J. C. , & Ji, D. (2018). Tropical atmospheric circulation response to the G1 sunshade geoengineering radiative forcing experiment. Atmospheric Chemistry and Physics, 18(12), 8689–8706. https://www.atmos‐chem‐phys.net/18/8689/2018/. 10.5194/acp-18-8689-2018 [DOI] [Google Scholar]
  20. Hansen, J. , Sato, M. , & Ruedy, R. (1997). Radiative forcing and climate response. Journal of Geophysical Research, 102, 6831–6864. 10.1029/96JD03436 [DOI] [Google Scholar]
  21. Hansen, J. , Sato, M. , Ruedy, R. , Nazarenko, L. , Lacis, A. , Schmidt, G. A. , Russell, G. , Aleinov, I. , Bauer, M. , Bauer, S. , Bell, N. , Cairns, B. , Canuto, V. , Chandler, M. , Cheng, Y. , Del Genio, A. , Faluvegi, G. , Fleming, E. , Friend, A. , Hall, T. , Jackman, C. , Kelley, M. , Kiang, N. Y. , Koch, D. , Lean, J. , Lerner, J. , Lo, K. , Menon, S. , Miller, R. L. , Minnis, P. , Novakov, T. , Oinas, V. , Perlwitz, J. P. , Perlwitz, J. , Rind, D. , Romanou, A. , Shindell, D. , Stone, P. , Sun, S. , Tausnev, N. , Thresher, D. , Wielicki, B. , Wong, T. , Yao, M. , & Zhang, S. (2005). Efficacy of climate forcings. Journal of Geophysical Research, 110, D18104 10.1029/2005JD005776 [DOI] [Google Scholar]
  22. Huang, Y. , & Bani Shahabadi, M. (2014). Why logarithmic? A note on the dependence of radiative forcing on gas concentration. Journal of Geophysical Research: Atmospheres, 119, 13,683–13,689. 10.1002/2014JD022466 [DOI] [Google Scholar]
  23. Jonko, A. K. , Shell, K. M. , Sanderson, B. M. , & Danabasoglu, G. (2012). Climate feedbacks in CCSM3 under changing CO2 forcing. Part I: Adapting the linear radiative kernel technique to feedback calculations for a broad range of Forcings. Journal of Climate, 25(15), 5260–5272. 10.1175/JCLI-D-11-00524.1 [DOI] [Google Scholar]
  24. Klein, S. A. , & Jakob, C. (1999). Validation and sensitivities of frontal clouds simulated by the ECMWF model. Monthly Weather Review, 127(10), 2514–2531. [DOI] [Google Scholar]
  25. Koch, D. , & Del Genio, A. D. (2010). Black carbon semi‐direct effects on cloud cover: Review and synthesis. Atmospheric Chemistry and Physics, 10(16), 7685–7696. https://www.atmos‐chem‐phys.net/10/7685/2010/. 10.5194/acp-10-7685-2010 [DOI] [Google Scholar]
  26. Manabe, S. , & Wetherald, R. T. (1975). The effects of doubling the CO2 concentration on the climate of a general circulation model. Journal of the Atmospheric Sciences, 32(1), 3–15. 10.1175/1520-0469%281975%29032%3C0003%3ATEODTC%3E2.0.CO%3B2 [DOI] [Google Scholar]
  27. Manners, J. , Edwards, J. M. , Hill, P. , & Thelen, J.‐C. (2015). SOCRATES (Suite Of Community RAdiative Transfer codes based on Edwards and Slingo) technical guide. In: Met Office, UK.
  28. Martin, G. M. , Bellouin, N. , Collins, W. J. , Culverwell, I. D. , Halloran, P. R. , Hardiman, S. C. , et al. (2011). The HadGEM2 family of Met Office Unified Model climate configurations. Geoscientific Model Development, 4(3), 723–757. http://www.geosci‐model‐dev.net/4/723/2011/ [Google Scholar]
  29. Myhre, G. , Forster, P. M. , Samset, B. H. , Hodnebrog, Ø. , Sillmann, J. , Andrews, T. , et al. (2017). PDRMIP: A precipitation driver and response model Intercomparison project, protocol and preliminary results. Bulletin of the American Meteorological Society, 98(6), 1185–1198. 10.1175/BAMS-D-16-0019.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Myhre, G. , Kramer, R. J. , Smith, C. J. , Hodnebrog, Ø. , Forster, P. , Soden, B. J. , et al. (2018). Quantifying the importance of rapid adjustments for global precipitation changes. Geophysical Research Letters, 45 10.1029/2018GL079474 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Myhre, G. , Shindell, D. , Bréon, F. M. , Collins, W. , Fuglestvedt, J. , Huang, J. , Koch, D. , Lamarque, J.‐F. , Lee, D. , Mendoza, B. , Nakajima, T. , Robock, A. , Stephens, G. , Takemura, T. , & Zhang, H. (2013). Anthropogenic and natural radiative forcing In Stocker T. F., Qin D., Plattner G. K., Tignor M., Allen S. K., Boschung J., et al. (Eds.), Climate change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (pp. 659–740). Cambridge, UK and New York: Cambridge University Press. [Google Scholar]
  32. Myhre, G. , & Stordal, F. (1997). Role of spatial and temporal variations in the computation of radiative forcing and GWP. Journal of Geophysical Research, 102, 11,181–11,200. 10.1029/97JD00148 [DOI] [Google Scholar]
  33. Pendergrass, A. G. , Conley, A. , & Vitt, F. M. (2018). Surface and top‐of‐atmosphere radiative feedback kernels for CESM‐CAM5. Earth System Science Data, 10(1), 317–324. https://www.earth‐syst‐sci‐data.net/10/317/2018/, 10.5194/essd-10-317-2018 [DOI] [Google Scholar]
  34. Ramanathan, V. , Crutzen, P. J. , Kiehl, J. T. , & Rosenfeld, D. (2001). Aerosols, climate, and the hydrological cycle. Science, 294(5549), 2119–2124. http://science.sciencemag.org/content/sci/294/5549/2119.full.pdf, 10.1126/science.1064034 [DOI] [PubMed] [Google Scholar]
  35. Richardson, T. B. , Forster, P. M. , Andrews, T. , Boucher, O. , Faluvegi, G. , Fläschner, D. , Kasoar, M. , Kirkevåg, A. , Lamarque, J. F. , Myhre, G. , Olivié, D. , Samset, B. H. , Shawki, D. , Shindell, D. , Takemura, T. , & Voulgarakis, A. (2018). Carbon dioxide physiological forcing dominates projected eastern Amazonian drying. Geophysical Research Letters, 45, 2815–2825. 10.1002/2017GL076520 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Samset, B. H. , & Myhre, G. (2015). Climate response to externally mixed black carbon as a function of altitude. Journal of Geophysical Research: Atmospheres, 120, 2913–2927. 10.1002/2014JD022849 [DOI] [Google Scholar]
  37. Samset, B. H. , Myhre, G. , Forster, P. M. , Hodnebrog, Ø. , Andrews, T. , Faluvegi, G. , Fläschner, D. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. , Shindell, D. , Shine, K. P. , Takemura, T. , & Voulgarakis, A. (2016). Fast and slow precipitation responses to individual climate forcers: A PDRMIP multimodel study. Geophysical Research Letters, 43, 2782–2791. 10.1002/2016GL068064 [DOI] [Google Scholar]
  38. Sanderson, B. M. , & Shell, K. M. (2012). Model‐specific radiative kernels for calculating cloud and noncloud climate feedbacks. Journal of Climate, 25(21), 7607–7624. 10.1175/JCLI-D-11-00726.1 [DOI] [Google Scholar]
  39. Shell, K. M. , Kiehl, J. T. , & Shields, C. A. (2008). Using the radiative kernel technique to calculate climate feedbacks in NCAR's community atmospheric model. Journal of Climate, 21(10), 2269–2282. 10.1175/2007JCLI2044.1 [DOI] [Google Scholar]
  40. Sherwood, S. C. , Bony, S. , Boucher, O. , Bretherton, C. , Forster, P. M. , Gregory, J. M. , & Stevens, B. (2015). Adjustments in the forcing‐feedback framework for understanding climate change. Bulletin of the American Meteorological Society, 96(2), 217–228. 10.1175/BAMS-D-13-00167.1 [DOI] [Google Scholar]
  41. Shine, K. P. , Cook, J. , Highwood, E. J. , & Joshi, M. M. (2003). An alternative to radiative forcing for estimating the relative importance of climate change mechanisms. Geophysical Research Letters, 30(20), 2047 10.1029/2003GL018141 [DOI] [Google Scholar]
  42. Smith, C. J. (2018). HadGEM2 radiative kernels. 10.5518/406 [DOI]
  43. Soden, B. J. , Held, I. M. , Colman, R. , Shell, K. M. , Kiehl, J. T. , & Shields, C. A. (2008). Quantifying climate feedbacks using radiative kernels. Journal of Climate, 21(14), 3504–3520. 10.1175/2007JCLI2110.1 [DOI] [Google Scholar]
  44. Stjern, C. W. , Samset, B. H. , Myhre, G. , Forster, P. M. , Hodnebrog, Ø. , Andrews, T. , Boucher, O. , Faluvegi, G. , Iversen, T. , Kasoar, M. , Kharin, V. , Kirkevåg, A. , Lamarque, J. F. , Olivié, D. , Richardson, T. , Shawki, D. , Shindell, D. , Smith, C. J. , Takemura, T. , & Voulgarakis, A. (2017). Rapid adjustments cause weak surface temperature response to increased black carbon concentrations. Journal of Geophysical Research: Atmospheres, 122, 11,462–11,481. 10.1002/2017JD027326 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Stocker, T. F. , Clarke, G. K. C. , Treut, H. L. , Lindzen, R. S. , Meleshko, V. P. , Mugara, R. K. , Palmer, T. N. , Pierrehumbert, R. T. , Sellers, P. J. , Trenberth, K. E. , & Willebrand, J. (2001). Physical climate processes and feedbacks In Houghton J. T., Ding Y., Griggs D. J., Noguer M., van der Linden P. J., Dai X., et al. (Eds.), Climate change 2001: The scientific basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change (Chap. 7, pp. 417–470). Cambridge, UK and New York: Cambridge University Press. [Google Scholar]
  46. Taylor, K. E. , Crucifix, M. , Braconnot, P. , Hewitt, C. D. , Doutriaux, C. , Broccoli, A. J. , Mitchell, J. F. B. , & Webb, M. J. (2007). Estimating shortwave radiative forcing and response in climate models. Journal of Climate, 20(11), 2530–2543. 10.1175/JCLI4143.1 [DOI] [Google Scholar]
  47. Taylor, K. E. , Stouffer, R. J. , & Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society, 93(4), 485–498. 10.1175/BAMS-D-11-00094.1 [DOI] [Google Scholar]
  48. Twomey, S. (1977). The influence of pollution on the shortwave albedo of clouds. Journal of the Atmospheric Sciences, 34(7), 1149–1152. [DOI] [Google Scholar]
  49. Vial, J. , Dufresne, J. L. , & Bony, S. (2013). On the interpretation of inter‐model spread in CMIP5 climate sensitivity estimates. Climate Dynamics, 41(11‐12), 3339–3362. 10.1007/s00382-013-1725-9 [DOI] [Google Scholar]
  50. Webb, M. J. , Andrews, T. , Bodas‐Salcedo, A. , Bony, S. , Bretherton, C. S. , Chadwick, R. , Chepfer, H. , Douville, H. , Good, P. , Kay, J. E. , Klein, S. A. , Marchand, R. , Medeiros, B. , Siebesma, A. P. , Skinner, C. B. , Stevens, B. , Tselioudis, G. , Tsushima, Y. , & Watanabe, M. (2017). The Cloud Feedback Model Intercomparison Project (CFMIP) contribution to CMIP6. Geoscientific Model Development, 10(1), 359–384. [Google Scholar]
  51. Webb, M. J. , Senior, C. , Bony, S. , & Morcrette, J. J. (2001). Combining ERBE and ISCCP data to assess clouds in the Hadley Centre, ECMWF and LMD atmospheric climate models. Climate Dynamics, 17(12), 905–922. 10.1007/s003820100157 [DOI] [Google Scholar]
  52. Wetherald, R. T. , & Manabe, S. (1988). Cloud feedback processes in a general circulation model. Journal of the Atmospheric Sciences, 45(8), 1397–1416. 10.1175/1520-0469(1988)045%3C1397:CFPIAG%3E2.0.CO;2 [DOI] [Google Scholar]
  53. Zelinka, M. D. , Andrews, T. , Forster, P. M. , & Taylor, K. E. (2014). Quantifying components of aerosol‐cloud‐radiation interactions in climate models. Journal of Geophysical Research: Atmospheres, 119, 7599–7615. 10.1002/2014JD021710 [DOI] [Google Scholar]
  54. Zelinka, M. D. , Klein, S. A. , & Hartmann, D. L. (2012). Computing and partitioning cloud feedbacks using cloud property histograms. Part I: Cloud radiative kernels. Journal of Climate, 25(11), 3715–3735. 10.1175/JCLI-D-11-00248.1 [DOI] [Google Scholar]
  55. Zelinka, M. D. , Klein, S. A. , Taylor, K. E. , Andrews, T. , Webb, M. J. , Gregory, J. M. , & Forster, P. M. (2013). Contributions of different cloud types to feedbacks and rapid adjustments in CMIP5. Journal of Climate, 26(14), 5007–5027. 10.1175/JCLI-D-12-00555.1 [DOI] [Google Scholar]
  56. Zhang, M. , & Huang, Y. (2014). Radiative forcing of quadrupling CO2 . Journal of Climate, 27(7), 2496–2508. 10.1175/JCLI-D-13-00535.1 [DOI] [Google Scholar]
  57. Zhong, W. , Haigh, J. D. , & Pyle, J. A. (1993). Greenhouse gases in the stratosphere. Journal of Geophysical Research, 98, 2995–3004. 10.1029/92JD02024 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (1.5MB, docx)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES