Designing bioinspired surfaces for water collection from fog

Abstract

A systematic study is presented on various water collectors, bioinspired by desert beetles, desert grass and cacti. Three water collecting mechanisms including heterogeneous wettability, grooved surfaces, and Laplace pressure gradient, were investigated on flat, cylindrical, conical surfaces, and conical array. It is found that higher water repellency in flat surfaces results in higher water collection rate and inclination angle (with respect to the vertical axis) has little effect. Surfaces with heterogeneous wettability have higher water collection rate than surfaces with homogeneous wettability. Both cylindrical and conical surfaces resulted in comparable water collection rate. However, only the cone transported the water droplets to its base. Heterogeneity, higher inclination and grooves increased the water collection rate. A cone has a higher collection rate per unit area than a flat surface with the same wettability. An array of cones has higher collection rate per unit area than a single cone, because droplets in a conical array coalesce, leading to higher frequency of droplets falling. Adding heterogeneity further increases the difference. Based on the findings, scaled-up designs of beetle-, grass- and cactus-inspired surfaces and nets are presented.

This article is part of the theme issue ‘Bioinspired materials and surfaces for green science and technology’.

1. Introduction

Access to a clean water supply is vital for human health. As such, the United Nations General Assembly explicitly recognizes water as a basic human right [1]. Water scarcity affects more than 40% of the global population and is projected to rise. It is estimated that approximately 800 million people do not have access to clean water [2]. Given the dearth of access to clean water, it is apparent that the current supply of fresh water needs to be supplemented to meet future needs.

All living things require water. Therefore, after some 3 billion years of evolution, many species exhibit efficient solutions to ensure their water security [3,4]. These solutions typically involve species possessing unique chemistry and structuring on or within their body that help to dictate the movement of water.

Figure 1 shows three species that collect water from fog, which include the Namib desert beetle (Stenocara gracilipes), Namib desert grass (Stipagrostis sabulicola) and cactus (Opuntia microdasys). The back of the beetle is comprised of an array of smooth, hydrophilic (water loving) spots which are surrounded by an area covered with microstructured hydrophobic (water fearing) wax [5]. It has been observed that water droplets from the fog accumulate on the spots, grow until they reach a critical size, detach, and then roll/slide down the tilted beetles back to the mouth.

Figure 1.

Inspirations for designing water collecting devices—desert beetle [5], desert grass [6,7] and cactus [8].

The desert grass has longitudinally running grooves, which intercept water droplets from the fog flow, and channel them to the roots [7]. The cactus features small barbs atop of conical spines that help the interception of droplets from the fog flow [8]. The droplets grow on the barbs and then move onto the spine. The curvature gradient resulting in Laplace pressure gradient facilitates the droplet movement. The grooves on the spine help channel the droplets towards the roots. Roughness provided by barbs may result in higher contact angle than that of the spine and may provide surface energy gradient as well. Selected dimensions describing the three species are summarized in table 1. In the three examples discussed here, nature uses heterogeneous wettability, grooves, and/or Laplace pressure gradient, for water collection from fog.

Table 1.

Selected dimensions describing three water collecting species.

water collecting specie	dimensions	references
desert beetle	hydrophilic spot diameter: 0.2–0.5 mm,	Parker & Lawrence [5]
	pitch: 0.5–1.5 mm
desert grass	cross section: C-shaped,	Roth-Nebelsick et al. [7]
	width: approximately 2 mm,
	length: less than 2000 mm,
	groove width: approximately 0.3 mm,
	groove pitch: approximately 0.4 mm
cactus	spine length: approximately 1.5 mm,	Ju et al. [8]
	base diameter: approximately 50 µm,
	tip angle: 10°,
	barbed length: top 1/4th of the spine length,
	groove length: bottom 3/4th of the spine length,
	groove width: approximately 2 µm,
	groove pitch: approximately 20 µm

The water collecting ability of beetle-inspired surfaces has previously been studied [9,10]. Garrod et al. [9] deposited hydrophilic polymers through a mask via plasma deposition onto a superhydrophobic polymer substrate. The beetle-inspired surface collected the most water, followed by superhydrophobic surfaces, while the superhydrophilic surface collected the least. The same trends were confirmed by Bai et al. [10]. They used hydrophilic nanoparticles for superhydrophilicity, coated it with fluorosilane for superhydrophobicity, and followed by UV treatment though a mask to create a beetle-inspired surface. They also studied the effect of various inclination angles—0°, 45° and 85° (0° being perpendicular to the fog flow)—and found the differences to be insignificant. Different spot shapes were also studied, and it was found that star-shaped spots collected more water as compared to the circular spots. The conical shape of the stars provides a Laplace pressure gradient leading to higher water collection.

Water collection by grass-inspired cylindrical surfaces was reported by Azad et al. [11]. Azad et al. [11] used hydrophilic copper wires with a diameter of about 1 mm which were placed vertically. Grooves were created by rubbing the copper wire with sandpaper. The grooved wires were found to collect more water. However, the grooves were made in an uncontrolled manner. No study of grooves on cones currently exists.

Water collection by cactus-inspired conical surfaces was studied by Ju et al. [12] and Chen et al. [13]. Ju et al. [12] used a chemically etched copper conical wire which was aligned parallel to the fog flow. It was found that the higher the tip angle, the higher the water collection. In a study by Ju et al. [14], the conical array was found to collect more water than a flat surface. Heterogeneous wettability on cones was investigated by Chen et al. [13]. They first made a steel cone superhydrophilic by dipping the whole cone in a dopamine solution and then painted the tip with wax to make it hydrophobic. It was found that a heterogeneous wetted cone collected more water than a uniformly hydrophobic cone. A comparison between cylinder and cone shapes does not exist in the literature.

In this paper, a systematic study is presented on various bioinspired water collectors. Heterogeneous wettability, grooved surfaces, and Laplace pressure gradient were investigated on flat, cylindrical, and conical water collectors. The flat surfaces were characterized for their water collection abilities at different wettability, inclination angle and different surface roughness. Cylindrical and conical surfaces, both ungrooved and grooved, were characterized for different inclination angles and wettability. Conical array was also investigated.

2. Experimental method

This section describes various fabrication techniques for different water collectors, wettability characterization and the experimental set-up.

(a). Fabrication

(i). Flat surfaces with homogeneous wettability and beetle-inspired surfaces

Flat surfaces with homogeneous wettability included superhydrophobicity, hydrophobicity, hydrophilicity and superhydrophilicity [4]. Beetle-inspired surfaces consist of superhydrophilic spots over a superhydrophobic background. A spot size of 0.5 mm and a pitch of 1 mm was chosen, which was inspired from the desert beetle's dimensions, as given in table 1. The effect of two surface roughnesses was also investigated, which was introduced by spray coating the surface with nanoparticles and binder. Two sizes of nanoparticles were used, 10 µm and 7 nm, so that the pitch between two nanoparticles asperities can be varied. Fog has water droplets of diameter on the order of 10 µm [15,16] which will interact with the surface according to the surface roughness and surface energy. Therefore, two sizes of nanoparticles were chosen, one comparable to the fog droplet size and one smaller.

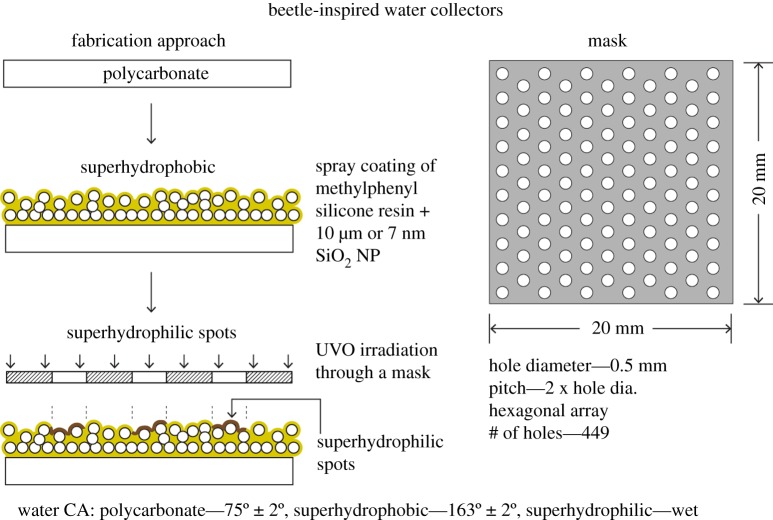
The substrate used was polycarbonate (PC) because it is a tough material and is commonly used in the fabrication of water bottles. PC substrate is hydrophilic. It was made hydrophobic by vapour deposition of fluorosilane (448931, Sigma Aldrich). The 20 mm × 20 mm samples were placed upside down and a droplet of fluorosilane was placed 1 cm below in an enclosure, and left for 30 min [17]. Superhydrophobicity was introduced by spray coating a mixture of hydrophobic silica particles and methylphenyl silicone (SR355S, Momentive Performance Materials) binder on the uncoated PC [18] (figure 2). Two different sizes of particles were used, 10 µm (Aerosil VM2270) and 7 nm (Aerosil RX300). The coating mixture was prepared by mixing 375 mg of the particles and 150 mg of the binder in 30 ml of solvent in an ultrasonifier (Branson Sonifier 450A, Emerson Electric Co., St. Louis, Missouri) for 30 min. The solvent used was 40% tetrahydrofuran (THF, Fisher Scientific) and 60% isopropyl alcohol (IPA, Fisher Scientific). Superhydrophilicity was introduced by treating the PC surface with ultraviolet-ozone (UVO) light. The UVO lamp used was a U-shaped lamp (18.4 W, Model G18T5VH-U, Atlantic Ultraviolet Co.), and the samples were kept directly underneath the light source for 60 min. Superhydrophilic spots were introduced on the superhydrophobic surface by irradiating the spray coated surface using UVO light through a mask; the mask has been shown schematically in figure 2.

Figure 2.

Fabrication of surfaces with heterogeneous wettability for beetle-inspired water collectors.

(ii). Grass- and cactus-inspired surface

The cylindrical and conical water collectors were fabricated using additive manufacturing (3D printing) that allows flexibility in designing and scalability. The machine used was Objet30 Prime, Stratasys, Ltd., Eden Prairie, Minnesota, having an accuracy of about 0.1 mm. The material used was acrylic polymer, RGD720.

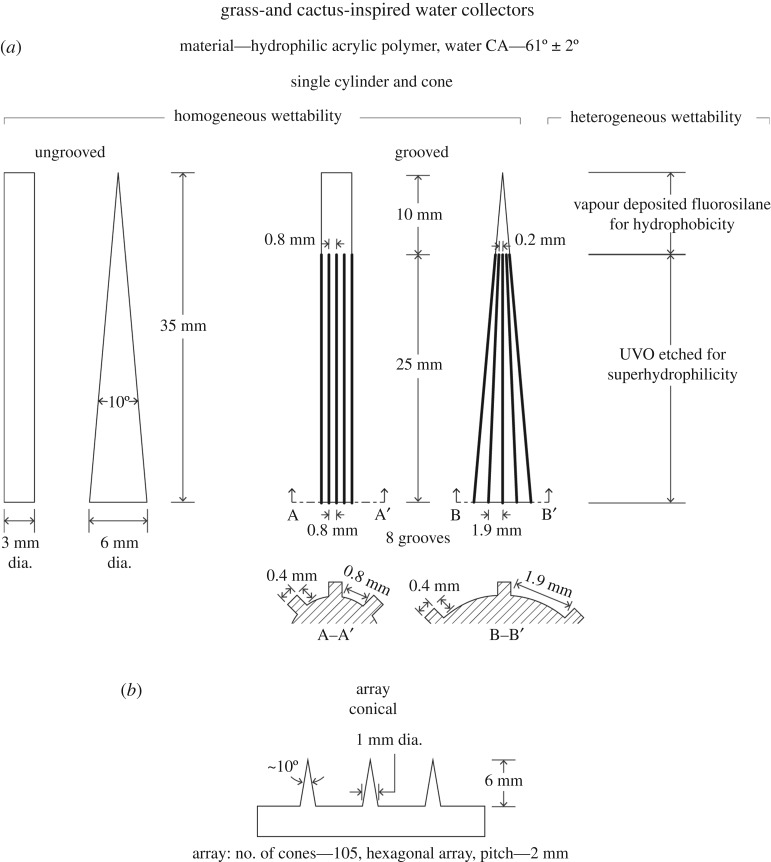
The design of the grass- and cactus-inspired collectors is presented in figure 3. The design was based on the dimensions of natural species, summarized in table 1. As shown in figure 3a, a base cylinder diameter of 3 mm was chosen in an effort to mimic the grass's diameter. The length was chosen to be 35 mm. To keep the surface area and the length constant, the base diameter of the cone, 6 mm, was doubled to that of cylinder, and the tip angle was kept at 10°, as seen in cactus spines. For grooved objects, starting at the base, the grooves were run until 3/4th of the cone's length, similar to the cactus, and the same was applied in the cylinder. Groove width of 0.4 mm and pitch of 0.8 mm were chosen to closely replicate the grass's grooves. The layout of grooves found on a cactus spine being very thin could not be fabricated using the 3D printer. Instead, for the cone, the number of grooves were kept constant.

Figure 3.

Design of 3D printed grass- and cactus-inspired water collectors: (a) cylinder and cone, ungrooved and grooved, and homogeneous and heterogeneous wettability; (b) array with cone.

Heterogeneous wettability in grass and cactus does not exist. It was incorporated in the present study. Heterogeneous wettability in cylindrical and conical surfaces included a hydrophobic tip with a superhydrophilic base. A hydrophobic tip was selected as it can collect more water, and a superhydrophilic base because it can transport the collected water quickly to the base. Superhydrophobic tips are not recommended because droplets will not stick to the surface and will fly away instead because of the low tilt angle. For fabrication, the complete cone was made superhydrophilic under the UVO lamp. The bottom 3/4th was then covered with Teflon tape and the entire object was left for fluorination; afterwards the tape was removed.

For scale-up, a conical surface (20 mm × 20 mm) was designed, as shown in figure 3b. Cones of height of 6 mm and base diameter of 1 mm were chosen with a pitch of 2 mm. Height and width were scaled down dimensions of single cone.

(b). Wettability characterization

Wettability of the surfaces was characterized using contact angles (CA) and tilt angles (TA). The angles were measured using a standard automated goniometer (Model 290, Ramé-Hart Inc.) using 5 µl distilled water droplets which were deposited onto the surfaces. A microsyringe was used for the purpose and the CA was measured by taking a static profile image of the liquid–air interface. The profile was analysed using the DROPimage software. TA refers to the angle of the surface when the droplet just begins to roll off the surface. All angles were averaged over at least five measurements on different areas of the sample and reported as ±σ.

(c). Water collection

(i). Experimental set-up

Figure 4a shows a schematic of the experimental set-up. A commercial humidifier was used to produce a stream of fog onto a surface and collected water was measured in an analytical balance underneath.

Figure 4.

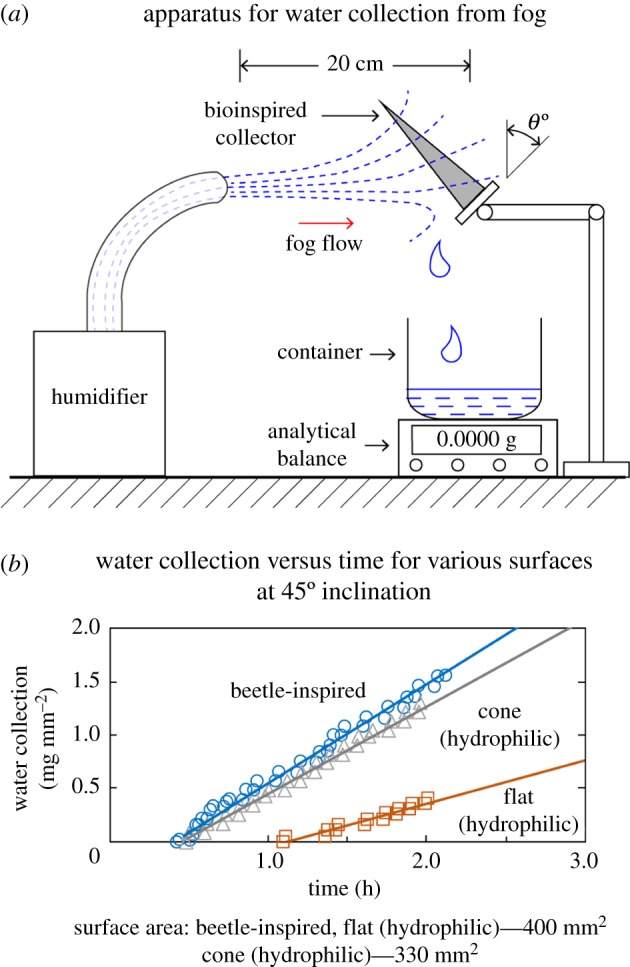
(a) Schematic of apparatus for water collection from fog. A commercial humidifier throws a stream of fog on a bioinspired water collector kept at a distance of 20 cm. The collector is inclined at either 0° or 45° from vertical axis (θ). The collected water is measured by the analytical balance underneath. (b) A representative water collection per unit surface area versus time plot for hydrophilic flat, beetle-inspired (10 µm NP) flat, and hydrophilic cone surfaces at 45° inclination. The slope of each of the curves determines their water collection rate per unit surface area (mg mm⁻² h⁻¹). (Online version in colour.)

Typical wind speed of the fog is reported to be around 1–5 cm s⁻¹ [16]. Therefore, the humidifier (EE-3186, Crane, Itasca, Illinois) which emits fog at about 10 cm s⁻¹ was kept about 20 cm away from the surface. The flow speed was calculated by measuring the volume of water lost over time, and by knowing the diameter of the pipe through which the fog was blown out.

Inclination angles were chosen to be 45° and 0° (flat surface being perpendicular to the fog flow, and cylinder/cone parallel to the fog flow). An inclination angle of 45° was chosen because at 0°, gravity will be a dominating factor with little effect from surface wettability, and at 90° little collection will be observed, since there is no interception of the fog with the surface. Therefore, an angle in between, 45°, was chosen. Also, flat surfaces were characterized at 45° inclination angles in the literature, because the beetles lift their backs up so that the body is at the same angle to the fog flow. An inclination angle of 0° was also included in the study for comparison.

The analytical balance used in the study was B044038, Denver Instrument Company, Bohemia, New York. The minimum weight it could measure was 1 mg. In the experiments, the least weight of collected water measured was about 10 mg. Typical weight range of each collected drop was about 10–60 mg.

(ii). Water collection parameters

For scaling up and comparison purposes, water collection per unit area per unit time is an important parameter. Water collection per unit area was measured as a function of time. Typical water collection per unit area versus time are presented in figure 4b for three different types of surfaces, including beetle-inspired, cone (hydrophilic), and flat (hydrophilic) surface. A minimum of five droplets were allowed to drop which were measured and a straight line was fitted. The slope of the fitted line is water collection per unit area per unit time (mg/mm² h). It is believed to be a more accurate representation of the water collection rate, as compared to the reported studies which calculate the rate from the beginning of the time. The slopes were calculated for three trials; the average and the standard deviation is reported in this study.

There are three parameters by which the collected data can be characterized. First is the initial wait time—the time to get the first droplet in the beaker. Typically, the higher the water collection rate, the lower the initial wait time. The second parameter is the frequency of the droplets dropping (droplets/h), which is the sum of the inverse of the wait time for every droplet except the first droplet. This parameter gives an idea of how fast the surface is collecting water. The third parameter is average weight of the collected droplet (mg). It is the average of every droplet dropped in the beaker. This could be measured since a balance reading was taken before and after the falling of every droplet. This gives us an idea of how heavy are the droplets being collected by the surface. Ideally, high frequency and high average droplet weight per unit area is desired.

(iii). Data correction

There were different methods for mounting the different types of surfaces. The flat surfaces were pasted on a flat surface; therefore, no corrective measures were needed. However, the cylindrical and conical pins were held with a tweezer. The holding site gave the fog an extra nucleation site. It was clear from the trials that a droplet starts at the holding site, grows, and finally drops in the beaker. It was found that additional water collection rate due to that holding site was about 0.08 mg/mm² h, which was subtracted from all the reported data on cylindrical and conical surfaces.

3. Results and discussion

This section presents water collection rates per unit area for flat, cylindrical and conical surfaces. First, water collection data by flat surfaces of various wettability and beetle-inspired surfaces at different inclinations and nanoparticle sizes is presented. This is followed by cylinders and cones of various wettability at different inclination angles. Next, data for flat surfaces, single cones and arrays are compared. Finally, a design for a scaled-up version of a bioinspired water collector is proposed.

(a). Various wettability and beetle-inspired surfaces

Figure 5 shows CA and TA for various surfaces along with their goniometer images. The top row presents the images for surfaces with four homogeneous wettability. The bottom row shows the three characterized homogeneous wettability on the acrylic.

Figure 5.

Wettability characterization of surfaces with various wettability on polycarbonate and acrylic substrates with DI water.

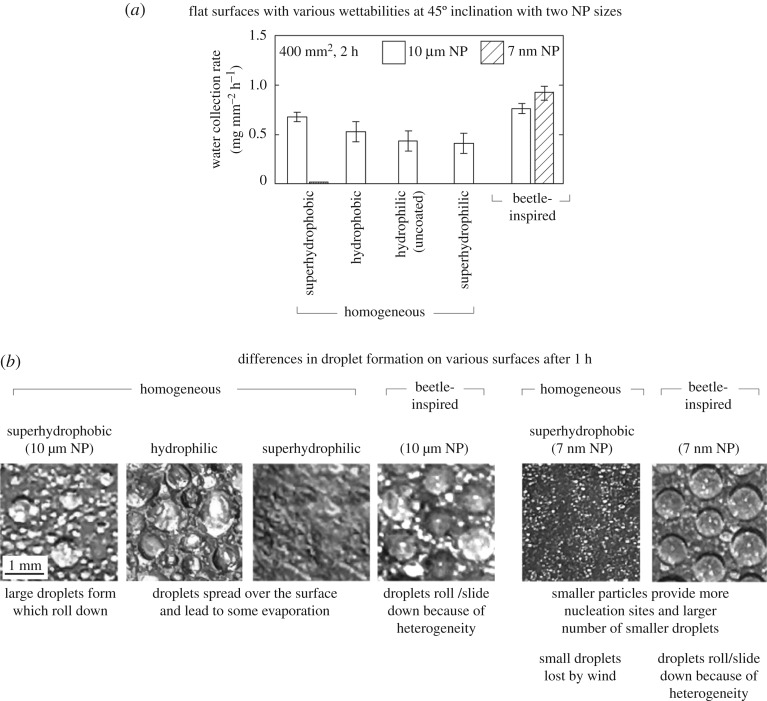
Figure 6a shows water collection rate per unit area of a flat surface at a 45° inclination characterized by various wettability. Superhydrophobic and beetle-inspired surfaces were prepared using 10 µm and 7 nm particles. The superhydrophobic surface and the beetle-inspired surface are the only surfaces affected by the size of the particles. Figure 6b presents differences in droplet formation on different types of surfaces after 1 h.

Figure 6.

(a) Water collection rates per unit surface area for flat surfaces with various wettability at 45° inclination. The wettability includes superhydrophobic, hydrophobic, hydrophilic (uncoated), superhydrophilic, and beetle-inspired surface (which includes 0.5 mm diameter circular superhydrophilic spots surrounded by superhydrophobic surface). The superhydrophobic and beetle-inspired surfaces were created using two different sizes of NP—10 µm and 7 nm. (b) Optical images showing differences in droplet formation on various surfaces after about 1 h.

The data shows that the higher the repellency (higher CA), the higher the water collection. The decreasing order of the water collection rate per unit area on a homogeneous wettability flat surface is superhydrophobic surface using 10 µm, hydrophobic, hydrophilic, and superhydrophilic. This is attributed to the fact that the higher the repellency, the more spherical the droplet shape will be, which results in a lower contact area between the droplet and the surface. Therefore, less heat will be transferred into the droplet and less evaporation will be observed. As shown in the optical images, large spherical droplets are formed on the superhydrophobic surface which roll down. In the case of hydrophilic and superhydrophilic surfaces, the droplets spread across the surface, leading to higher evaporation.

Another observed trend is that a beetle-inspired surface is better than a homogeneous wettability surface. This is because of the heterogeneity; droplets can slide/roll at a faster rate, allowing them to maintain a spherical droplet shape, leading to lesser evaporation.

Next, the effect of smaller particles was investigated. Smaller particles have lower pitch of asperities on the surface as compared to the larger particles which affect the number of nucleation sites. Smaller particles are believed to increase the water collection rate because of more nucleation sites leading to a larger number of smaller droplets coalescing faster. Indeed, there was an increase observed on the beetle-inspired surface, however, the superhydrophobic surface resulted in no water collection at a 45° inclination. This is because of the fact that smaller particles nucleate smaller droplets, as shown in the optical images, which could lead to losing droplets to the wind.

Table 2 summarizes the water collection rate data for various homogeneous wettability and the beetle-inspired surface at the two different inclination angles and at the two different NP sizes. It is clear from the table that there is no significant difference between 45° and 0° inclination angles, except for the superhydrophobic surface using 7 nm particles. This was because there was little water collection as the droplets were not lost to the wind at 0° inclination; instead they fell in the collection beaker.

Table 2.

Summary of water collection rates by flat surfaces with various wettability at two inclination angles and two NP sizes.

		water collection rate (mg mm−2 h−1)
		45°		0°
wettability		10 µm NP	7 nm NP	10 µm NP	7 nm NP
homogeneous	superhydrophobic	0.7 ± 0.1	—	0.5 ± 0.1	0.5 ± 0.1
	hydrophobic	0.5 ± 0.1		0.4 ± 0.1
	hydrophilic (uncoated)	0.4 ± 0.1		0.3 ± 0.1
	superhydrophilic	0.4 ± 0.1		0.3 ± 0.1
beetle-inspired	0.5 mm spot diameter	0.8 ± 0.1	0.9 ± 0.1	0.7 ± 0.1	0.8 ± 0.1

(b). Cylinder versus cone

(i). Homogeneous wettability at 0° inclination angle

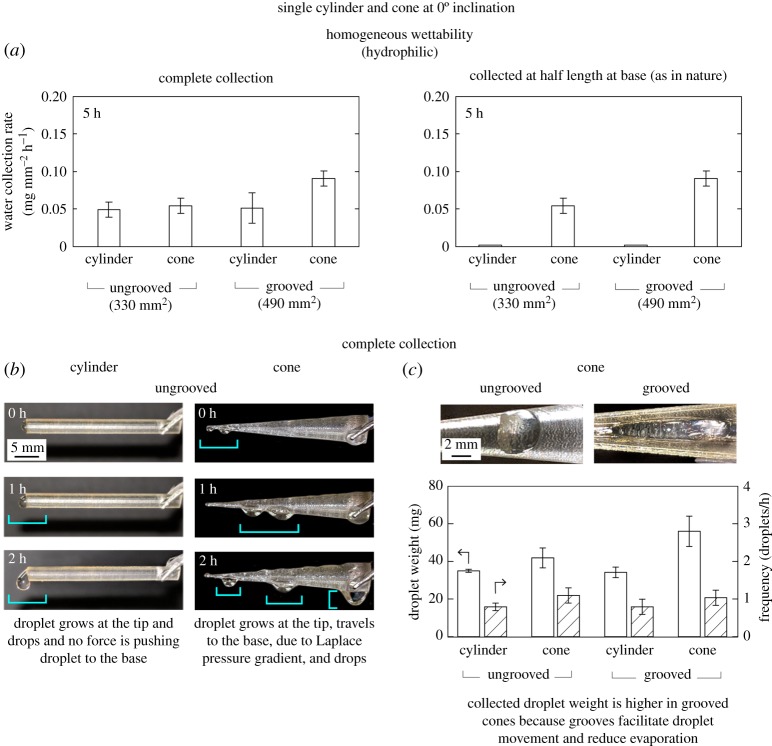
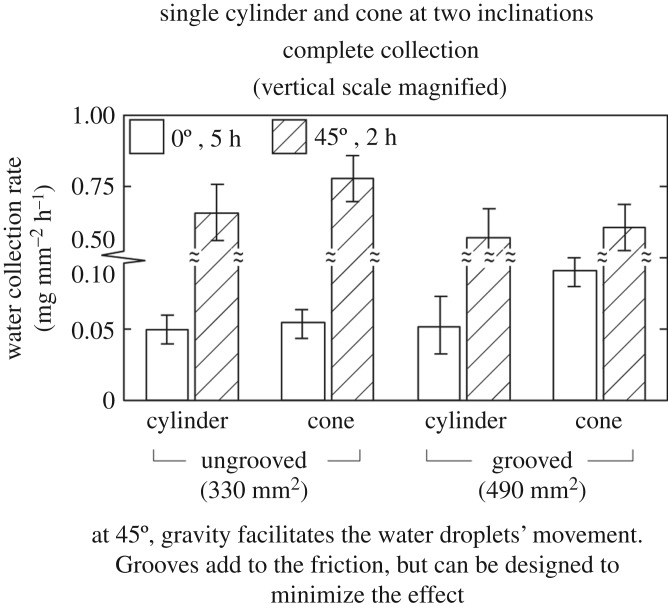
Figure 7a presents the water collection data for a single cylindrical and conical surface, ungrooved and grooved, at 0° inclination angle. The 0° angle was chosen to eliminate the effect of gravity on the movement of the droplets along the length. The left bar chart shows water collection for the complete object. However, in nature, the collected water that matters is that which reaches the base, therefore, the right bar chart presents the water collection rate per unit area at base half-length. Figure 7b presents optical images of droplets growing and moving on a cylinder and a cone at three time steps for complete collection.

Figure 7.

(a) Water collection rates per unit surface area for single cylinder and cone, ungrooved and grooved with homogeneous wettability at 0° inclination. The left side shows the data when water was collected under the entire surface. The right side shows data when the water was collected at the base (as in nature). At the base, a cone collects more water than the cylinder whereas total water collection rates are comparable. Grooved cones have higher collection rates than ungrooved. (b) The optical images show movement of the water droplets on cylinders and cones in complete collection. (c) The top shows optical images of a droplet sitting on an ungrooved cone and a grooved cone; the grooves elongate the droplet. The bottom shows comparison of weights and frequency of droplets in complete collection at the base. Grooved cones collect heavier droplets and frequency of droplets falling is comparable. (Online version in colour.)

Ungrooved. Complete water collection rate per unit area by cylinder and cone was found to be comparable. On the cylinder, water droplets nucleate at the tip, grow, attain a critical size, then fall, as shown in figure 7b. Droplets nucleate at the tip because it intercepts the fog flow perpendicularly. On the rest of the curved surface, little to no droplets were observed since the surface is parallel to the fog flow. The smaller droplets become visible much later; at about the 4-hour mark. Since the droplets are small and sit on the surface for a long time, a significant amount of their volume is lost to evaporation. It is also believed that even if the experiment had been run beyond 5 h, the droplets on the curved surface would not have affected the water collection rate. Therefore, the droplets nucleating at the cylinder's tip are solely responsible for the water collection rate per unit surface area.

The droplets growing at the cylinder's tip do not move along the length, since there is no force acting in that direction. However, this is not the case in cones. Droplets nucleate at the tip, grow and move simultaneously along its length. For a droplet resting on a conical surface, the changing radius results in a pressure difference inside the droplet [19]. The pressure inside the droplet is known as the Laplace pressure, which is given by ΔP = 2γ/(r + h), where γ is the surface tension, r is the radius of the cone and h is the height of the droplet from the centreline of the cone. At a low radius, the droplet shape is hardly deformed by the cone (as r < h) and is near spherical, which implies ΔP = 2γ/h. As the cone radius is increased, h approaches r and the droplet flattens, thus ΔP = γ/r. This flattening results in a Laplace pressure gradient causing droplets to move on a cone from regions of low radius to regions of higher radius. Irrespective of the motion of the droplet, both a cylinder and a cone have similar water collection rates per unit area. In nature, the water collection that matters is at the base only. Therefore, a cylinder does not achieve any water collection. A cone achieves the same water collection that was observed in complete collection. As a result, cones have an advantage over cylinders in directional water collection.

Grooved. The cylinder tip is solely responsible for a cylinder's water collection rate per unit area and there is no force pushing the droplets to its base. Therefore, having grooves on the sides does not affect the water collection, irrespective of complete collection or base collection.

The effect of grooves is measurable on a cone. They result in about twice as much collection as was seen from an ungrooved cone. Figure 7c presents optical images of a droplet on a cone, ungrooved and grooved, and the average weight of collected droplets from the cylinder and cone, ungrooved and grooved. Grooves help in channelling the water droplet to the base, as shown in the optical images. It may seem logical to conclude that the channelling of droplets will increase the frequency of droplets falling. However, that is not the case. Having grooves also increases contact area between a droplet and the surface, resulting in increased friction. Therefore, the frequency of droplets falling remains similar, but the weight of the droplets falling increases by about 30% compared with an ungrooved cone. In other words, heavier droplets move along the length of a grooved cone at a similar velocity to normal droplets on an ungrooved cone.

To summarize, at a 0° inclination angle, in complete collection, cylinders and cones result in similar water collection rate per unit area. For a cylinder, droplets grow at its tip and fall. However, for a cone, the droplets move towards the base due to Laplace pressure gradient and then fall. In nature, the water collection that matters is at the base only. At the base, a cylinder does not result in any water collection and a cone results in the same water collection as was observed in its complete collection. Grooves aid the cones, by increasing the water collection rate per unit area by about a factor of 2.

(ii). Homogeneous wettability at 45° inclination angle

Figure 8 presents the water collection data by a single cylinder and cone, ungrooved and grooved, at a 45° inclination angle. The angle was increased to investigate the water collection abilities of cylinders and cones at an angle. Water collection rate per unit area at 0° has also been included for comparison.

Figure 8.

Water collection rates per unit surface area for single cylinder and cone, ungrooved and grooved, with homogeneous wettability at 0° and 45° inclinations. Objects at higher inclination have higher water collection rates, because gravity is facilitating movement of the droplets. There seem to be no difference between the water collection rates of the cylinders and cones, because gravitational force on the droplets seems to dominate Laplace pressure gradient in movement of the droplets. Grooves seem to add friction force to the movements of the droplets leading to lower water collection rate. However, grooves could be designed to minimize the friction effect.

Ungrooved. At a 45° inclination angle, the entire surface of the cylinder intercepts the fog flow, not just its tip. Droplets nucleate, grow, slide along the length, and drop at the base. Droplets fall at the base because there is gravity (g sinθ) aiding the movement of the droplets towards the base. It was observed, data not reported, that at 45° inclination angle, the frequency of the droplets falling was about 6–8 times higher as compared to the 0° inclination. However aid by gravity did not increase the weight of the droplets falling. The increase in the frequency increased the water collection rate per unit area of a cylinder by about 10 times.

For a cone, there are two forces aiding the droplets to move towards the base: force due to gravity (mg sinθ) and force due to Laplace pressure gradient, ΔP = 2γ/(r + h). As the droplet grows and moves towards the base, the gravitational force is expected to increase as the droplet mass increases and may become large compared to the Laplace pressure gradient.

Grooved. As discussed previously, grooves channel the droplets but increase the friction between a droplet and the surface because of an increase in the contact area [20]. Friction forces decreased the frequency of droplets falling for grooved objects by about 20%. This resulted in a decrease of water collection rate per unit area of about 20%.

To summarize, at a 45° inclination, an increase in water collection rate per unit surface area of about 10 times was observed, as compared to 0° inclination angle. This was because the gravitational force was aiding the movement of the droplets. There was no measurable difference found between the water collection of cylinders and cones, as gravitational force dominates the Laplace pressure gradient present in a cone. Having grooves decreased the water collection rate per unit surface area by about 20%, because they added friction to the moving droplets.

It has been observed that, irrespective of the grooves and inclination angle, a cylinder and a cone have similar water collection rate per unit surface area. However, cones provide the directional water collection and grooves aid cones at low inclination angles.

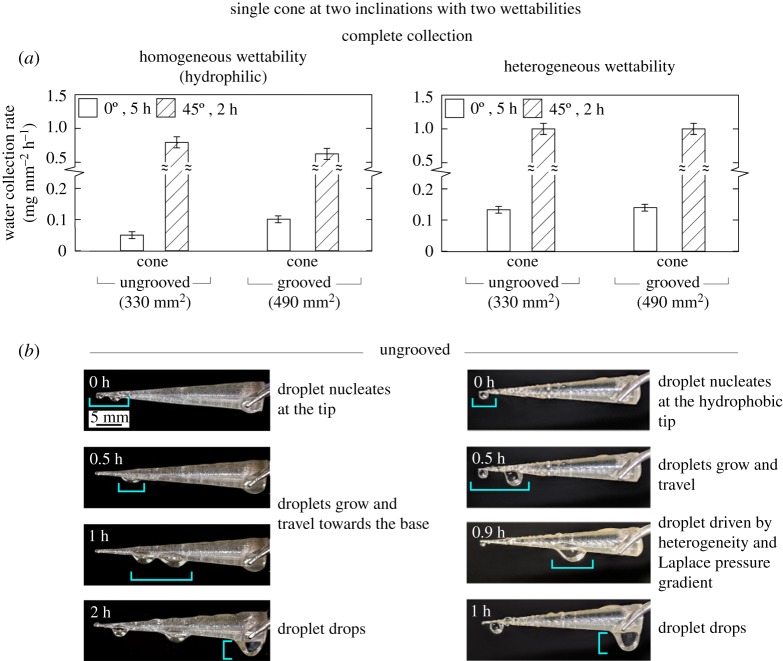
(iii). Heterogeneous wettability of a cone at 0° and 45° inclination angles

A cone, ungrooved and grooved, at 0° and 45° inclination angles was investigated with respect to different wettability. Figure 9 summarizes the water collection by a single cone, ungrooved and grooved, at 0° and 45° inclination angles, having homogeneous and heterogeneous wettability. Figure 9a presents data on water collection rate per unit surface area and figure 9b presents optical images of cones inclined at 0°, at different time stamps.

Figure 9.

(a) Water collection rates per unit surface area single cone, ungrooved and grooved, with homogeneous and heterogeneous wettability at 0° and 45° inclinations. Inclination angle and heterogeneous wettability increase water collection rates. Grooves have little effect. (b) Optical images show movement of water droplets on ungrooved cones with two wettability. The droplet moves faster in case of heterogeneous surface, as compared to the homogeneous surface, because of added surface energy gradient. (Online version in colour.)

Ungrooved. The tip of the cone is hydrophobic. The droplet, nucleating, growing, and moving towards the base, will experience force due to the Laplace pressure gradient, until it reaches the superhydrophilic region. As soon as the droplet touches the wettability change boundary, it experiences force due to surface energy gradient as well. Once the droplet reaches the pure superhydrophilic surface, it spreads out quickly and reaches the base.

This spreading out of droplets is expected to increase the frequency of the droplets falling, which is borne out by the data. At a 0° inclination, it was found (data not reported) that the frequency increased two times as compared to the homogeneous wetted cone. This increased the water collection rate per unit surface area by about 2–3 times, as shown in figure 9a. At a 45° inclination, an increase in the water collection rate per unit area was also observed. However, the increase was not significant because gravity (g sinθ) is also helping to pull the droplets.

Grooved. Adding grooves to the heterogeneity did not help in increasing the water collection rate per unit area, irrespective of the inclination angle. Grooves are known to channel the droplets, and superhydrophilicity spreads the water. It appears that superhydrophilicity is more efficient in transporting the water from the tip to the base.

To summarize, having wettability heterogeneity results in higher water collection rate per unit surface area as compared to a homogeneous wettability cone, ungrooved or grooved. The effect is significant at 0° inclination angle.

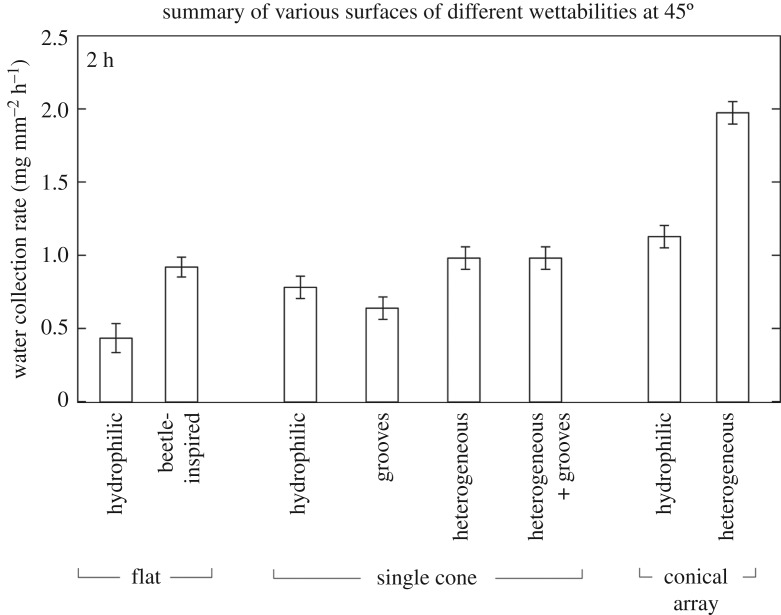
(c). Flat versus cone versus array

In previous sections, homogeneous wetted flat surfaces were compared with beetle-inspired. It was found that the beetle-inspired surface has the highest water collection rate per unit area as compared to all the homogeneous wettability. Inclination angles of 0° or 45° did not have an effect on the water collection by flat homogeneous and beetle-inspired surfaces. Single cylinders were also compared with single cones. It was found that the only advantage cones have over cylinders is directional movement of droplets. In cones, the grooves help in increasing the water collection rate per unit area at 0° inclination angle. The same is true for heterogeneity, irrespective of the inclination angle. And the higher the inclination angle, the higher is the water collection rate per unit surface area.

To compare different shapes, the same inclination angle must be chosen. An inclination angle of 45° was chosen because of high water collection, and comparison between various surfaces including flat, single cone, and conical arrays is made in figure 10. The flat surfaces include hydrophilic and beetle-inspired. Single cones include hydrophilic wetted, with grooves, with heterogeneity, and with heterogeneity and grooves. Data on the conical array with hydrophilic wetted and with heterogeneity is also included.

Figure 10.

Summary of water collection rates for various surfaces, including flat, single cone, and conical array at 45° inclination. Flat surfaces include hydrophilic wetted and beetle-inspired. Single cone surfaces include hydrophilic wetted, with grooves, heterogeneity, with heterogeneity and grooves. Conical array surfaces include hydrophilic wetted and with heterogeneity.

The single hydrophilic cone has a higher water collection rate per unit area than the flat hydrophilic surface. Although they have comparable frequency (droplets per hour), the cone drops heavier droplets as compared to the flat hydrophilic surface. This is believed to occur because the cone intercepts more water droplets from the fog and transports it.

The beetle-inspired surface has higher water collection rate per unit area than the hydrophilic cone. This is mainly because the beetle-inspired surface has higher frequency as compared to the cones. However, the rates of beetle-inspired and cone becomes comparable when the wettability of the cone is switched to heterogeneous. This is because the heterogeneous cone gives higher frequency of droplets as compared to the hydrophilic cone. Grooves do not add to the rate, however, it is believed that grooves could be designed to have a higher rate but with lesser surface area which leads to lesser friction [20].

The water collection rate per unit surface area increases for an array of hydrophilic cones as compared to a single cone. This is because the droplets on the array coalesce with each other, as shown in figure 11, and help in increasing the water collection. It is expected that by further decreasing the pitch, the water collection rate per unit area can be increased further.

Figure 11.

Optical images showing coalescing of droplets in a conical array leading to higher water collection rate per unit area than a single cone.

The water collection rate per unit area goes even higher when the wettability is switched to the heterogeneity. The increase is higher as compared to the increase observed in the single cone. This was an expected trend because in the array there are 105 cones instead of one cone with increased water collection rate per unit area.

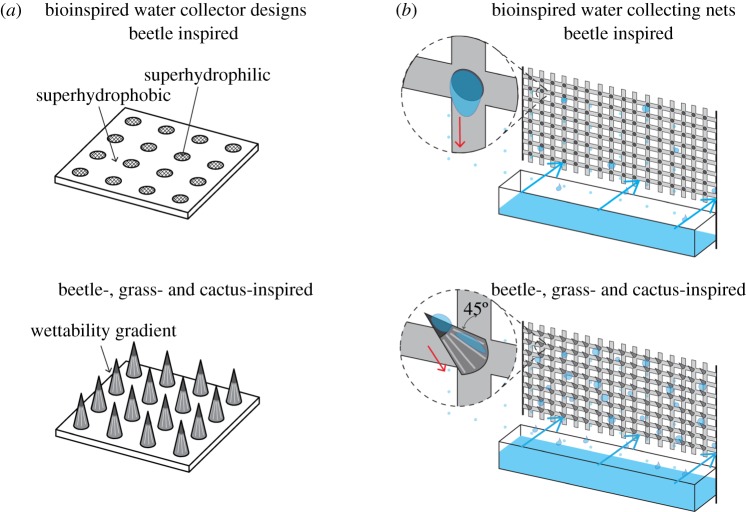
(d). Proposed water collector design

It was shown that the beetle-inspired surface has higher water collection rate per unit area than homogeneous wettable surface. It was also shown that an array of cones have higher water collection rate per unit area as compared to a single cone. The water collection rate per unit area even goes up when the wettability is switched to heterogeneity. The grooves were found to decrease the rate; however, it is believed that dimensions of the grooves could be designed for higher collection. An increase in inclination angle has also been shown to increase the water collection rate per unit area, because gravity facilitates movement of the droplets. Therefore, it is expected that an array of cone with heterogeneity and grooves, inclined at 45°, would have the highest water collection rate per unit area.

Therefore, beetle-, grass- and cactus-inspired water collectors have been designed as shown in figure 12a. Beetle-inspired surface consists of superhydrophilic spots over a superhydrophobic surface. Beetle-, grass- and cactus-inspired surface consists of an array of cones with heterogeneity and grooves. The heterogeneity includes hydrophobic tip and superhydrophilic base. The surfaces can be inclined at 45° to the wind for a high water collection.

Figure 12.

Proposed bioinspired water collector (a) design and (b) nets for scale-up. (Online version in colour.)

A commercially common method for water collection from fog is nets, for example, FogQuest and WarkaWater [3]. For scale-up, nets can be designed from the beetle-, grass- and cactus inspired design, as shown in figure 12b. For beetle-inspired, the junctions of the nets can have superhydrophilic spots. For beetle-, grass- and cactus-inspired, the junction of the nets can have heterogeneous wettable cone with grooves inclined at 45°. The heterogeneity includes hydrophobic tip and superhydrophilic base.

4. Conclusion

A systematic study is presented on various water collectors, bioinspired by desert beetles, desert grass, and cacti. Three water collecting mechanisms, including heterogeneous wettability, grooved surfaces, and Laplace pressure gradient, were investigated on flat, cylinder, and conical surfaces, and conical array. The water collection was made on various surfaces.

The flat surfaces were characterized with various wettability, inclination angle, and two surface roughnesses. It is found that higher water repellency in flat surfaces results in higher water collection rate and inclination angle (with respect to the vertical axis) has little effect. Surfaces with heterogeneous wettability have higher water collection rate than surfaces with homogeneous wettability.

Both cylindrical and conical surfaces resulted in a comparable water collection rate. However, only the cone transported the water droplets to its base. Heterogeneity, higher inclination and grooves increased the water collection rate. A cone has a higher collection rate per unit area than a flat surface with the same wettability. An array of cones has higher collection rate per unit area than a single cone, because droplets in a conical array coalesce leading to higher frequency of droplets falling. Adding heterogeneity further increases the difference.

Based on the findings, scaled-up design of beetle-inspired and beetle-, grass- and cactus-inspired surfaces and nets are presented.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

The financial support for this research was provided by a seed grant no. GOGCAP from the Center for Applied Plant Sciences (CAPS) of The Ohio State University.