Novel muon imaging techniques

Abstract

Owing to the high penetrating power of high-energy cosmic ray muons, muon imaging techniques can be used to image large bulky objects, especially objects with heavy shielding. Muon imaging systems work just like CT scanners in the medical imaging field—that is, they can reveal information inside of a target. There are two forms of muon imaging techniques: muon absorption imaging and muon multiple scattering imaging. The former is based on the flux attenuation of muons, and the latter is based on the multiple scattering of muons in matter. The muon absorption imaging technique is capable of imaging very large objects such as volcanoes and large buildings, and also smaller objects like spent fuel casks; the muon multiple scattering imaging technique is best suited to inspect smaller objects such as nuclear waste containers. Muon imaging techniques can be applied in a broad variety of fields, i.e. from measuring the magma thickness of volcanoes to searching for secret cavities in pyramids, and from monitoring the borders of countries checking for special nuclear materials to monitoring the spent fuel casks for nuclear safeguards applications. In this paper, the principles of muon imaging are reviewed. Image reconstruction algorithms such as Filtered Back Projection and Maximum Likelihood Expectation Maximization are discussed. The capability of muon imaging techniques is demonstrated through a Geant4 simulation study for imaging a nuclear spent fuel cask.

This article is part of the Theo Murphy meeting issue ‘Cosmic-ray muography’.

1. Introduction

Muon imaging techniques are very unique because they can be used to image objects of a very large scale where other techniques often fail. This unique capability of muon imaging is based on the high penetrating power of high-energy muons. Muons are elementary particles, which are similar to electrons but about 207 times heavier. Owing to the heavy mass of muons and the fact that muons do not take part in the strong interaction, muons lose much less energy than almost all of the other particles when passing through matter. Therefore, they can penetrate much deeper. There are two types of muon imaging techniques. The first is muon absorption imaging, and the second is muon multiple scattering imaging. These two techniques are based on the two muon interactions with matter, i.e. energy loss and multiple scattering, respectively. The muon absorption imaging technique can be used to image very large objects such as volcanoes [1], but it can also be used to image relatively smaller objects such as nuclear spent fuel casks [2]. The muon multiple scattering imaging technique can only be used to image relatively small objects, such as shipping containers [3] and nuclear waste containers [4], due to the fact that both the incoming and outgoing muon tracks need to be measured.

Muon imaging requires solving an inverse problem [5]. This is because the characteristic properties of the imaging object cannot be measured directly using the muon imaging system. However, they can be inferred from the effects of the muon interaction with matter, which can be measured directly. In the case of muon absorption imaging, material density can be inferred from the muon flux attenuation; and in the case of muon multiple scattering imaging, the scattering density [3], which is the inverse of the material radiation length and closely related to the atomic number of the materials, can be reconstructed from the muon scattering angle and displacement. There are no simple analytical equations that can be used to calculate the material properties directly from those measured effects for muon imaging. However, the inverse is true, there is a simple relationship between the material properties and the effects, which can be used to predict those measurable effects when the materials' properties of the matter are known. To determine the above relationship is called forward modelling, and the inverse solution can be developed based on the forward model. In the next section, we will introduce the forward models of muon absorption and multiple scattering imaging. In §3, we will discuss some of the popular image reconstruction algorithms, which will be followed by geant4 simulation and experimental results of muon imaging. The final section will summarize the conclusion.

2. The forward models

The forward models of muon imaging are introduced in this section. Before the detailed discussion of the forward modelling, some of the basic but important concepts of muon imaging are discussed. The forward models for the muon absorption and multiple scattering imaging are then outlined.

One of the commonalities between muon absorption and multiple scattering imaging techniques is that both use particle tracking detectors. These tracking detectors are used to measure interaction, or hit, positions of muons, and the trajectory of each muon is constructed from these measured hit positions. At least one pair of tracking detectors is needed for the muon absorption imaging technique, and two pairs of tracking detectors located on opposite sides of the objects are needed for muon multiple scattering imaging. An additional pair of detectors located on the opposite side of the first pair of detectors for a muon absorption imaging system can provide additional information about the muon source, which is very helpful in some situations.

Owing to the lack of a man-made muon source, both the muon absorption and multiple scattering imaging methods rely on cosmic ray muons [6], which are produced in the upper atmosphere by the interactions of primary cosmic rays with the atoms and molecules in the atmosphere. The production of the cosmic ray muon is a random process, therefore the muon trajectory and its production position are randomly distributed. In order to be able to record every muon that is passing through the object, a 2 Pi solid angle coverage is needed for the tracking detector system. However, often, the opening angle of an actual detector system is much smaller than 2 Pi due to various reasons. It is still possible to achieve a 2 Pi coverage by rotating the object inside the detectors or by rotating the detectors around the objects.

Absorption muon imaging is based on the muon flux attenuation, and multiple scattering muon imaging is based on the distribution width of the muon scattering angle. In order to accurately measure the values of these physical effects, a large number of muons is needed, and all these muons should travel along the same path. In reality, the above requirements cannot be met, because the cosmic ray muon source has a very low intensity and each muon takes a random trajectory. As an approximation to the above requirements, muons with similar trajectories can be grouped together to evaluate these effects. Such a group of muons act like a muon quasi-beam. Both the muon absorption and multiple scattering imaging methods measure muon tracks on an event-by-event basis, therefore, it is possible to form muon quasi-beams by using the measured muon tracks. The energy spectrum of each muon quasi-beam should reflect the energy spectrum of the cosmic ray muon. According to the study of Nakamura et al. [6], the cosmic ray muon has a broad energy range, which extends up to TeVs.

The muon flux attenuation is caused by the energy loss of muons in matter. Like all the other charged particles, muons lose energy through ionization, bremsstrahlung, direct pair production and photo-nuclear interactions [6]. At relatively low energies, ionization is the dominant process, while at high energies, the ionization can be ignored, because in this case the determining contributions to energy losses are due to bremsstrahlung and pair production [7]. The energy loss rate (or stopping power) can be approximately treated as a continuously slow varying function of energy. For a low-energy muon, if the matter is thick enough, it will lose all its energy and stop inside the matter.

Let us consider a muon quasi-beam striking matter with a thickness of h. Some low-energy muons lose all their energy and stop inside this matter, while some muons with higher energy pass through the matter, reducing the beam intensity. By counting the muon number registered on the tracking detectors, it is possible to find out the threshold energy if the energy spectrum of the muon source is known. The threshold energy is defined as the energy of a muon that is just sufficient to let the muon pass through the matter. Inversely, if the threshold energy and the energy spectrum of the muons are known, by integrating from the threshold energy to infinity we will be able to predict the muon number that can be detected in a certain period of time. Further, the threshold energy can be related to the stopping power and the thickness of the matter, because if the stopping power and the thickness of matter under study are known, the threshold can be calculated as an integral along the muon path. This can be described as

2.1

Here, E_t is the threshold energy, S(x, E) is the stopping power, which is a function of position and muon energy E, and l is the thickness of the matter.

Equation (2.1) can be used as the forward model for the muon absorption imaging. However, to formulate an algorithm according to this model is very difficult, because the stopping power is not only a function of position but also a slow varying function of muon energy. For some applications, because the variation of the stopping power is very small, an average stopping power S_a(x) can be used to replace the stopping power S(x, E) in equation (2.1), and then it changes into the following format:

2.2

Another way to describe the forward modelling for muon absorption imaging is to convert the threshold energy into a water equivalent length, which is the thickness of water that can cause the same amount of energy loss as the original matter. This was adopted by researchers studying the muon imaging of volcanoes [8] and is similar to the method used for the charged particle energy loss tomography [9]. This relationship can be described as

2.3

Here, W_l is the water equivalent length for the whole muon path, and ρ(x) is the water equivalent length for a unit length of matter at position x, it is a linear integral along the muon path.

When passing through matter, apart from energy loss, muons also suffer from many small elastic Coulomb scatterings from nuclei, which results in repeated changes of the direction of motion of a muon. For each muon event, there are two values that can be measured. These are the scattering angle and the scattering displacement. The scattering angle is the angle between the exiting muon track and the incoming muon track, which is the overall effect of all the small scatterings. The scattering distance is the distance between the expected hit position of the exiting muon and the actual hit position. The multiple scattering of charged particles in matter has been very well studied in the last century, and there are many theories for charged particle multiple scattering. Among them, Moliere theory [10] is the most commonly used. Approximations to the Moliere theory were also developed for practical reasons. The Rossi formula [11] is one of them.

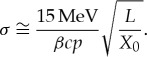2.4

Here, σ is the width of the muon multiple scattering angle distribution, which is roughly a Gaussian distribution with heavy tails. The parameter L is the length of matter, βc is velocity (β = 1), p is the particle momentum in MeV/c, and X₀ is the radiation length of the matter, which can be described by the following equation:

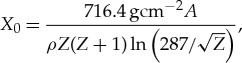2.5

with A the atomic mass, Z the atomic number and ρ the material density.

From equations (2.4) and (2.5), it can be seen that the width of the scattering angle distribution depends on the material radiation length, which is dependent on the atomic number of the material, i.e. materials with higher atomic numbers will typically produce larger scattering angles. Equation (2.4) serves as the basis for muon multiple scattering tomography but is only valid for uniform matter. In practice, we are more interested in mixtures or more complicated structures. There is no strict solution to this problem, but we can use a simple substitution of the radiation length to achieve an approximation. This is because the material's radiation length for compounds or mixtures can be described by using the following equation [6]:

2.6

where X_i is radiation length of the ith component along the muon path, and w_i is the weight of the ith component.

Combining (2.4)–(2.6), we have

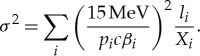2.7

The above equation linked the variance of the muon scattering angle with the radiation length of the matter encountered along each muon's path, which is the forward model for muon scattering imaging.

The scattering displacement can also be used to reconstruct an image. However, the scattering displacement is correlated with the scattering angle. Nevertheless, combining the scattering angle and scattering displacement, a better quality image can be achieved [3].

3. Image reconstruction algorithms

In §2, it has been shown that the forward modelling of muon imaging can be described as a line integral along the muon path, which is similar to the well-studied forward modelling of X-ray CT. Hence, image reconstruction algorithms based on the Radon transform [12] and algorithms based on systems of linear equations [13] can be used directly for muon imaging. However, to use the above-mentioned image reconstruction algorithms, muon quasi-beams have to be formed and muon attenuation or the variance of the scattering angles has to be calculated for each quasi-beam. To keep the statistical error small, the number of muons in each quasi-beam has to be large. There are two ways to increase the muon number for each quasi-beam, one is to increase the angular and spatial bin sizes, and the other is to increase the data collection time. Increasing the bin sizes has a negative effect on the image spatial resolution. On the other hand, due to the fact that the cosmic ray muon rate is relatively low, to gather enough muons to reconstruct a high resolution image is time-consuming. Furthermore, the assumption of a straight muon beam path by the quasi-beam worsens the image spatial resolution even further, because the actual muon paths inside the matter are most likely to be curved due to the multiple scattering effect. Therefore, for applications that require a high spatial resolution, an image reconstruction algorithm not relying on an explicit muon beam is required. Moreover, for some applications, such as imaging a volcano [14], or imaging an underground mineral deposit, where the possible detector deployment locations are limited, special image reconstruction methods are also needed.

Indeed, for multiple scattering imaging, from the very beginning, the Radon transform-based image reconstruction method and the algebraic image reconstruction method were ruled out by this imaging technique developer. Instead, the Point of Closest Approach (PoCA) and the Maximum Likelihood Expectation Maximization (MLEM) image reconstruction methods were developed [3]. The PoCA method treats each of the multiple scattering events as a single scattering event. For a single scattering event, the extensions of the incoming muon track and outgoing muon tracks meet each other at the scattering position, while for a multiple scattering event, the extensions of these two tracks normally do not meet each other. Therefore, the point of closest approach between the incoming and outgoing muon vectors is used as the approximation of the scattering point. Because this method ignores the physical nature of multiple scattering, it only works well for small isolated dense objects. However, due to its simplicity, this method was widely used by many researchers, and there exist several improved versions of the PoCA imaging algorithm.

The MLEM image reconstruction method is the most important method for muon multiple scattering imaging. It does not need to explicitly calculate the scattering angle variance for each muon direction. With this method, the image reconstruction becomes a parameter estimation problem. We have already seen that the scattering angle follows a Gaussian distribution and the width of this Gaussian distribution can be described by equation (2.7). Therefore, the probability to observe the jth muon with a scattering angle θ_j, can be expressed as

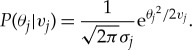3.1

Here, 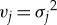is the expected variance of the scattering angle distribution along the jth muon path.

Based on the probability of each single muon, the maximum-likelihood cost function can be expressed as

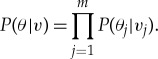3.2

From equations (2.7), (3.1) and (3.2), the image to be reconstructed becomes the parameters of a maximum-likelihood cost function. By maximizing this cost function, images of the object can be estimated. Schultz had used a Newton's method and an EM method to calculate the maximum-likelihood estimator [3]. Both of these methods are iterative image reconstruction methods.

For muon absorption imaging, it is often required to treat the detector as a point and produce a map of areal density of the object, with the horizontal axis being the azimuthal angle, and the vertical axis being the zenith angle. When the detector is far away from the imaging object, the point assumption is approximately true. Because the cosmic muon rate varies with the zenith angle, this density map has to be normalized in order to show the contrast details. This can be achieved by dividing the measured map with a map of the muon source on a pixel-to-pixel basis. Saracino et al. used this method to image underground cavities [15].

One more thing that needs to be mentioned is that both the multiple scattering and absorption imaging benefit a lot from knowing the momentum for each individual muon. However, to measure the momentum of high-energy muons requires very large and costly equipment, which is not possible for most applications. Without knowing the muon momentum, much more data will be needed to achieve the same image resolution for muon multiple scattering imaging. To counter this effect, Perry et al. developed a multigroup method to improve the reconstructed image quality by fitting the muon angle distribution with a multigroup of Gaussian distributions corresponding to different momenta [16]. For muon absorption imaging, low-momentum muons can cause very large quantities of noise because their paths are no longer straight. By knowing the muon momentum, image quality can be improved by filtering away the low-momentum muons.

4. Methods and results

In this section, experimental results and simulated results are shown to demonstrate the capability of muon imaging techniques. All the measurements were carried out by using the prototype detectors developed at the University of Glasgow and its spin-out company, Lynkeos Technology. More details about these detectors can be found in [17,18]. All the simulations were performed using the software toolkit Geant4, which was designed by physicists from CERN for high-energy particle and nuclear applications. A detailed description of Geant4 is reported by Agostinelli et al. [19]. A dedicated muon generator is used to produce muon events, and muons are sampled according to the cosmic ray muon energy spectrum and angular distribution at sea level [20]. The muon energy distribution is described by the Smith & Duller phenomenological model [21]. In the Geant4 simulations, the detector system comprises four tracker modules, two situated on one side and two on the opposite side of the volume under interrogation.

As explained in the previous sections, the Filtered Back Projection (FBP) method [12], in principle, can be used for the image reconstruction using muon data. However, this method was not widely adopted by researchers. There are several reasons that are responsible for this. The first one is that this method needs to have a muon beam in order to be able to calculate the muon beam attenuation and to calculate the scattering angle distribution width. This shortcoming can be accounted for by using a relatively long measuring time. The second reason is that muon imaging techniques are naturally three-dimensional imaging methods, thanks to the random cosmic ray muon source. Therefore, specially designed three-dimensional FBP methods are needed for muon imaging problems, which require extensive research efforts to develop. However, in some special cases, the three-dimensional imaging problem can be reduced to a two-dimensional imaging problem.

A good example for this is vertical nuclear spent fuel casks. Owing to the fact that spent fuel assemblies are very long, spent fuel casks have the same profile at different positions along the vertical direction if we ignore the lid and bottom parts. Therefore, for any muon path, if we shift it in the vertical direction to a new position, then the materials encountered along the new path will be the same as along the original path, therefore the bin size in the vertical direction can be as large as the cask itself. Furthermore, we noticed that for muons with the same azimuthal angle, x- and y-coordinates, but different zenith angles and z-coordinates, their expected water equivalent thickness or the scattering angle variance differ only by a factor of 1/cos(Θ) compared with those values calculated for a horizontal muon beam. If all the muons with the same x- and y-coordinates and the same azimuthal angle are put into the same bin, it is possible to link the expected value with the measurable effect. Hence, a three-dimensional imaging problem can be reduced into a two-dimensional imaging problem, and a two-dimensional FBP image reconstruction algorithm can be used in the image reconstruction. This was already demonstrated by Poulson et al. [2] and Durham et al. [22]. Here, we go one step further by discarding the z-position information from the measured muon hitting positions. In this way, only half of the tracking detectors are required, therefore the cost for a detector system would be greatly reduced.

As an example, a Westinghouse MC-10 cask was simulated. Four planar detector tracker modules were placed on two opposite sides of the cask. The active area of each tracker module is 2.8 × 2.8 m. One layer of 2 mm round fibre arrays placed vertically were used in each of the tracker modules. The MC-10 spent fuel cask has a cylinder shape with a 25 cm thick steel wall. There are 24 slots to hold the spent fuel assemblies in each of the casks. In this simulation, 20 slots were filled with fuel assemblies, and two of them were left empty. Each fuel assembly contains 204 fuel rods, 20 control rod guide tubes and one instrument tube. The fuel rods are filled with UO₂ and surrounded by zirconium alloy cladding. The control rods and instrument tube were simulated with empty cladding, and with no fuel present. The dimensions and geometry of the MC-10 cask and the water pressure fuel assembly used in the simulation were found in [23,24]. The last two slots were filled with fake fuel assemblies, which were made from metallic lead rods. The layout of the fuel bundles in this MC-10 cask is shown in figure 1.

Figure 1.

The layout of the detector system and a MC-10 spent fuel cask.

Because planar detector tracking modules were used in the simulation, in order to cover 360° in the azimuthal angle, 32 tracker positions were used; at each position three million muons (which is equivalent to one day's measurement time) were simulated, then these four trackers were rotated by 11.25° clockwise around the cask centre to the next position. In the data analysis, all the data were put into a grid of quasi-beams according to their azimuthal angle and their distance to a plane that is parallel to the incoming muon beam and through the centre of the cask. An angle step of 2° and a position step of 2 cm were used. Because the vertical position was not measured, the z-coordinate will be set to zero for all muon tracks. This reduced a three-dimensional problem into a two-dimensional one. The scattering angle calculated in this way is not a projected scattering angle, but remains a close approximation to it. Therefore, we can still use it to reconstruct an image.

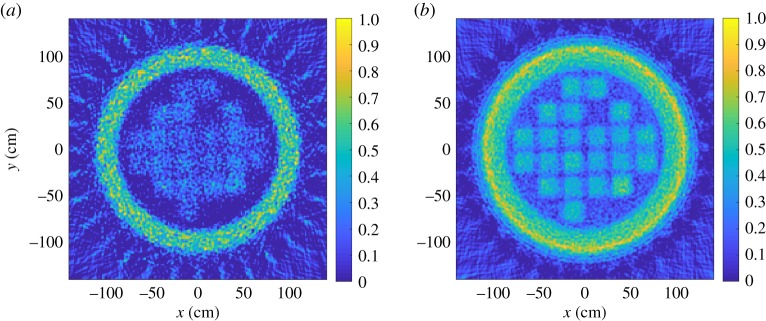
In figure 2, images reconstructed by using the FBP algorithm with only vertical tracking fibres used in the simulation are shown. It can be seen that the major features of the MC-10 cask are correctly reconstructed in both of the multiple scattering and absorption images. The missing fuel assemblies can be clearly identified. The signal ratio between the steel wall and UO₂ in the multiple scattering image and in the absorption image is different. This is because of the different physics behind these two imaging techniques. This feature is very useful for the discrimination of materials. However, the difference between the fake fuel and real fuel is not very obvious in the images reconstructed by the FBP method.

Figure 2.

(a) Image reconstructed using the muon absorption technique, (b) image reconstructed with the multiple scattering technique, with the FBP algorithm.

One drawback the FBP algorithm has is that the size of the muon beam envelope gradually increases from the start towards the end. This is because the muon beam's path is defined by the incoming muon direction, and the muon multiple scattering blows up the beam envelope. The image spatial resolution will be affected by this effect. On the other hand, image reconstruction methods based on the maximum likelihood can use a better estimation of the muon path due to their event-by-event data handling nature, therefore they will have better spatial resolution.

In figure 3, a multiple scattering image reconstructed using the maximum-likelihood method was shown. Only one-fifth of the total data were used for the MLEM image reconstruction. It can be seen, however, that the image spatial resolution is still very high. And also, the fake fuel rod stands out in the MLEM image. But the fins of the cask were not seen in the MLEM image.

Figure 3.

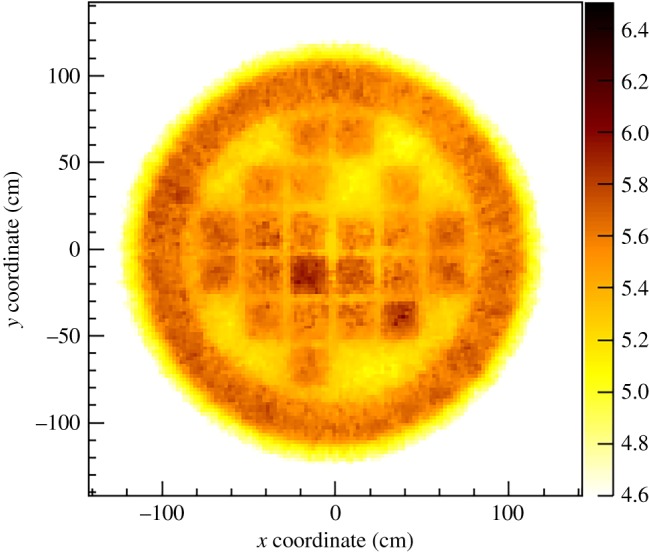
Muon multiple scattering image reconstructed with the MLEM algorithm.

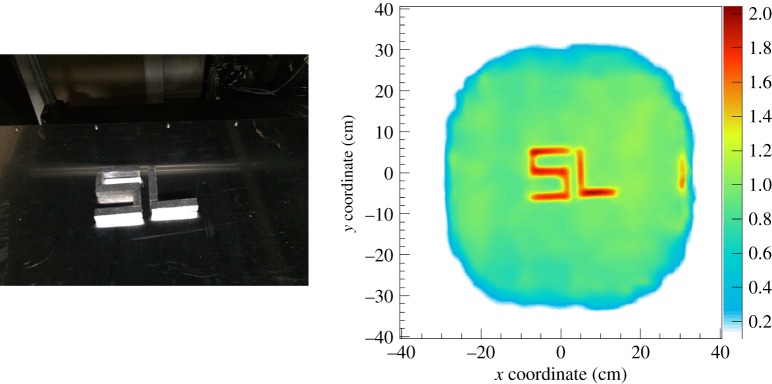
In figure 4, an image of letters ‘SL’ made from lead blocks is shown. On the left is a photo of the lead letters, and on the right is an image reconstructed using the multiple scattering imaging technique. This measurement was performed by using the Glasgow/Lynkeos large prototype detector [18]. The image reconstruction was carried out using a three-dimensional maximum-likelihood method. It can be seen that the letters have been correctly reconstructed. On the right-hand side of the image, the red/orange bar is the edge of a lead brick that is just at the edge of the imaging area. This demonstrated that both the capability of the detector system and also the image reconstruction method are quite high.

Figure 4.

A photo of lead letters ‘SL’, and an image reconstructed with the MLEM algorithm.

5. Conclusion

In conclusion, this paper reviewed the principle of muon imaging techniques. The muon imaging techniques solve inverse problems; the forward modelling of the muon multiple scattering imaging and the muon absorption imaging were presented. Image reconstruction algorithms such as the FBP, PoCA and MLEM were discussed. Geant4 simulation was used to demonstrate the capability of different image reconstruction methods. Images reconstructed from the measured data were also shown.

Data accessibility

Owing to the commercial sensitivity of the proprietary data format and image reconstruction software, both either trade secrets or the Intellectual Property of Lynkeos Technology, the raw data from the results presented in this manuscript cannot be provided.

Authors' contributions

G.Y. developed the image reconstruction algorithm and image reconstruction software; T.C. contributed significantly to the Detector hardware construction and data taking; S.G. and R.A.J. contributed significantly to the data taking and data analysis; M.R. contributed significantly to the DAQ and slow control software design; D.M. contributed significantly to the Geant4 simulation; D.I., R.K. and C.S. conceived of and designed the study of muon images. The paper was written by G.Y. and edited and improved by all co-authors.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was partially supported by the EPSRC and STFC Impact Accelerator Accounts at the University of Glasgow (EP/K503903/1) and by Lynkeos Technology Ltd.