Computational psychiatry of impulsivity and risk: how risk and time preferences interact in health and disease

Abstract

Choice impulsivity is an important subcomponent of the broader construct of impulsivity and is a key feature of many psychiatric disorders. Choice impulsivity is typically quantified as temporal discounting, a well-documented phenomenon in which a reward's subjective value diminishes as the delay to its delivery is increased. However, an individual's proclivity to—or more commonly aversion to—risk can influence nearly all of the standard experimental tools available for measuring temporal discounting. Despite this interaction, risk preference is a behaviourally and neurobiologically distinct construct that relates to the economic notion of utility or subjective value. In this opinion piece, we discuss the mathematical relationship between risk preferences and time preferences, their neural implementation, and propose ways that research in psychiatry could, and perhaps should, aim to account for this relationship experimentally to better understand choice impulsivity and its clinical implications.

This article is part of the theme issue ‘Risk taking and impulsive behaviour: fundamental discoveries, theoretical perspectives and clinical implications’.

1. Introduction

Impulsive behaviour is a core feature of many psychiatric conditions: from the pathognomonic tendency to act without foresight seen in addictive disorders, to the difficulty in suppressing movement once initiated that is characteristic of attention deficit hyperactivity disorder (ADHD), to the thrill-seeking behaviour typical of gambling disorder. While impulsivity is a dimensional symptom that cuts across diagnostic boundaries, it is itself multifaceted. Recently, a panel of experts on impulsivity proposed a taxonomy that broadly divides impulsivity into rapid-response impulsivity, a motoric process characterized by poor inhibitory control, and choice impulsivity, a decision-making process primarily characterized by an inability to delay gratification [1,2]. It is important to note however that, in addition to the delay of gratification, choice impulsivity can also be related to the tendency to make a premature decision without sufficiently evaluating information or considering its accuracy—a process referred to as reflection impulsivity [3]. Consistent with the U.S. National Institute of Mental Health's RDoC initiative [4], this sub-classification of impulsivity has been argued to more closely align with the different neurobiological circuitry that supports each subcomponent process.

Choice impulsivity, in particular, has broad clinical importance. Individuals diagnosed with schizophrenia [5], bipolar disorder [6], impulse control disorders [7], bulimia nervosa [8,9], ADHD [10] and substance use and addictive disorders [11] have all been found to have increased choice impulsivity, while those diagnosed with obsessive compulsive disorder (OCD) and anorexia nervosa may show the converse pattern [12]. The relationship between choice impulsivity and at least a few of these disorders seems to be prospective [13,14], suggesting this subcomponent of impulsivity could have clinical utility as a measurable vulnerability factor for primary prevention.

Choice impulsivity may be assessed with different tools. Certain tasks, such as the information sampling task [15–17] or the information-gathering task [18], report on the inability to fully deliberate and consider solutions to problems (reflection impulsivity) because they index an individual's evaluation of the sufficiency of the information received before making a choice. For the purpose of this opinion piece, we focus on another widely used measure of impatience, which lies at the core of choice theory in economics: delay discounting, which is also referred to as temporal discounting. Temporal discounting is the observation that a reward delivered after a delay is subjectively worth less than the same reward delivered immediately. Temporal discounting can be modelled mathematically in different ways, but all the algorithms capture some form of a discount rate (a notion taken from economics), a constant that captures the idiosyncratic rate of reward devaluation as a function of the delay to reward receipt. The higher this discount rate, the more a delayed reward will be modelled as devalued by waiting; and hence the more likely an individual will be described as foregoing a valuable later outcome in favour of impatiently selecting a smaller but more immediate alternative—the very signature of choice impulsivity. Temporal discounting is usually measured by intertemporal choice tasks in which individuals are specifically asked to decide between smaller–sooner rewards and larger–later rewards. This relatively simple methodology enables rapid and easy measurement of the discount rate in the laboratory, the field and the clinic, with its first applications to psychiatry, and substance addiction in particular, dating back to the late 1990s [19,20]. Its applicability is further supported by its reliability and reproducibility, as several standard tasks have now been shown to yield consistent results in clinical populations [21], a necessary characteristic of a clinical marker.

While separating choice impulsivity from rapid-response impulsivity has received broad translational support, the current disaggregation may still be imperfect [22]. For example, the preference for smaller immediate rewards can, for fairly subtle reasons, also reflect changes in risk-taking or risky behaviour in general, an independent decision construct [23–25]. While individuals colloquially labelled as ‘impulsive’ are more likely to seek and engage in risky situations, it is not clear whether they do so owing to impulsivity or because they exhibit a logically separate and idiosyncratic proclivity to assume risks. Because choices between rewards of different magnitudes are influenced by one's risk attitude, many of the tasks used to measure temporal discount rates necessarily entangle risk attitude and choice impulsivity. Commensurate with this largely theoretical entanglement, a growing number of studies have begun to relate choice impulsivity to pathologically ‘risky’ behaviours, from gambling [26] to suicide [27] and quite prominently to substance use disorders [11], but do not always explore how idiosyncratic risk attitudes and impulsivity, which are both logically and neurobiologically separable, may separately explain the behaviour or pathology of interest.

As with temporal discounting, an individual's general proneness to or avoidance of risky prospects—their risk preference—can also be quantified using simple choice paradigms that are reliable, largely repeatable and well suited to the clinic [28]. Like discount rates, these measures seem to be clinically relevant for many of the same psychopathologies [29–31]. From a theoretical perspective, the economics and finance fields have long acknowledged the possible confounds that risk preferences introduce into the measurement of time preferences and temporal discounting [32–34]. Many studies have explored how individuals' behaviour toward uncertainty technically biases most tools for the measurement of delay discounting [35,36]. This is troubling because, while from an empirical point of view, hundreds of publications employ time preference measures of choice impulsivity, few additionally focus on risk preferences with the goal of disambiguating their contribution to temporal discounting and impulsivity. Even fewer have done so with a focus on individual differences. The result may be a systematic (and unnecessary) confounding of risk attitudes and choice impulsivity in some of the literature.

Here, we review these latter studies and examine how they could, and perhaps should, methodologically impact future studies focused on individual differences in impulsive choice in health and disease. Adding precision to our measures of human (and animal) impulsive choice behaviour, we argue, could help facilitate a more accurate dissection of the neural circuitry that supports this behaviour and its disruption in pathological conditions. Better precision could also translate to better concordance between animal and human measures of the same constructs, aiding the development of more targeted behavioural, pharmacological and other therapeutic interventions. Finally, clinically, a more precise taxonomy of what constitutes ‘impulsive’ and ‘risky’ behaviour may be beneficial for multiple reasons. First, it may contribute to improved diagnosis by facilitating the segregation of disorders with an impulsive decision-making aetiology from those with a risky decision-making aetiology, a clustering that would be obscured by interactions between these two dimensions. This quantitative dimensional approach to psychiatric diagnosis research is being actively explored, with some initiatives coming from the U.S. National Institute of Mental Health [37–39] with the goal of better categorizing healthy and pathological human behaviour. Second, it may help better connect clinical phenomenology to neurobiology, pointing to more specific targets for therapeutic intervention. And finally, it could lay the foundation for personalized medicine in psychiatry, by adding precision to individualized measures of maladaptive behaviour.

2. Temporal discounting formalizations for modelling impulsive choice

The preference for smaller–sooner over larger–later rewards has been an intense topic of research by economists, ethologists, psychologists and neuroscientists for over four decades [34,40–46], but the first formal mention of intertemporal choice dates much further back to at least 1937 [47]. Throughout this rich history, intertemporal choices have been assayed using many different methods and modelled in diverse ways, but almost always by pitting two choice attributes against each other: reward and time. Across the many available measures, preferred choices are always found to be positively correlated with reward amount (I want more) and negatively correlated with delay to reward delivery (I want it sooner). The trade-off between these two attributes is algorithmically formalized by the devaluation or ‘discounting’ of value as a function of delay, hence it is referred to as delay discounting or temporal discounting. Many different formulations of temporal discounting exist in the literature, but the two that have been most widely adopted are exponential discounting and hyperbolic discounting. In the first formulation, it is assumed that delaying or accelerating two dated outcomes by a common amount should not change preferences between the two possible outcomes, and as such a subject's intertemporal preferences are referred to as ‘time-consistent’. When discounting is constant in this way (the subjective value of a reward drops by a constant percentage with each additional unit of time) it can be captured by an exponential decay function where the time constant of the decay is the so-called discount rate:

$$U^t(c_t)=v\cdot {\mathrm{e}}^{-k\cdot t}.$$

This is the most common form of discounting in the economics literature (in which consistency is a desiderata), where U^t(c_t) is the utility U of consumption c at time t and k is the [constant] discount rate by which the value of an outcome v is reduced at time t. In this framework, steep discounting might be said by an economist not to be impulsivity per se, but rather a kind of impatience—a rational, constant degree of preference for immediate outcomes that we perceive in patients to be impulsive in the colloquial sense. However, a significant body of empirical work has shown that this model does not always capture real behavioural data well [32,46,48–52]. Instead, mathematically hyperbolic forms of discounting perform better under many, if not most, real-world conditions [53–56] because humans and other animals are steeper discounters for short delays than for long delays. Some authors have referred to this inconsistency as ‘present bias’ [33,34,46] but this phenomenon is observed irrespective of whether the sooner alternative is in the present or not [57].

Many functional forms for this process that result in a hyperboloid discounting function have been proposed in the literature. The most commonly used in psychology (although alternative forms are used by economists [44,58]) is the one proposed by Mazur (1987) [59]:

$$U^t(c_t)=\frac{v}{1+k\cdot t}.$$

3. Economic theory formalizations of risky choice

All humans and animals also show an idiosyncratic unwillingness to tolerate risk to some degree. If asked to choose between a certain gain and a risky 50% chance of earning more, there is some amount ‘more’ at which any given subject will accept the risk of loss to earn a chance at the larger gain. Just how much more reward one requires to accept a given level of risk varies from subject-to-subject, to some degree between gains and losses ([60], but also see [61]), and also seems to change across the lifespan [62,63].

Most individuals can be described as strongly preferring to avoid risks and these individuals require large gains to entice them to accept offers with more uncertain rewards, a pattern called risk aversion. A smaller group of individuals prefer to engage in risk and accept risky offers even when a certain alternative is of nearly equivalent value. People who behave in this way are referred to as risk seeking. Other individuals are indifferent toward risk—making their decisions based only on the actuarial long-term expected value of the options before them—and are hence called risk-neutral. This relationship between risk (probability) and reward magnitude lies at the heart of essentially all economic theories of choice such as expected utility theory [64,65], rank-dependent utility or prospect theory [66]. As for a sizable range of possible choice options these models are all roughly equivalent, for the purposes of this paper we turn next to expected utility theory explanations of risk preference.

The concept of economic utility, which we will refer to (using the neurobiological convention) as subjective value, was first introduced by Daniel Bernoulli (1738) and hinges on the idea that the subjective well-being (or suffering) derived from a payoff is not precisely equal to the objective size of the gain or loss [67]. Instead, the objective outcome is presumed to be internally and individually processed to yield a subjective experience, in much the way that classical psychophysics relates luminance in the outside world to the percept of brightness. This internal representation of subjective value is assumed to vary from individual to individual (and possibly from context to context).

Economists refer to the mathematical function that, like the Weber Law, maps the objective amount of any reward or punishment (e.g. money) to the subjective well-being derived from obtaining it as the Utility Function. For clarity, we concentrate here on the domain of rewards, or in the language of economics: gains. Consider an individual whose utility function is (like a Weber curve) concave, that is, initial increments in the objective amount of a monetary reward lead to large increments in utility, but subsequent identical increments in reward lead to smaller and smaller increases in utility. Her marginal utility is said to be diminishing as she obtains more money. Now consider what happens when this individual is evaluating two possible options: a certain gain of $100 and a lottery with 50% chance of $200 and 50% chance of $0. Because her marginal utility is decreasing, while the objective expected value of both outcomes is the same (0.5 × 200 = 100), the expected utility of the gamble may be smaller for her than that of the certain payoff because in a subjective sense 200 is less than twice 100. This explains why she might choose to avoid the risky option and chose the safe outcome instead of the lottery despite the fact that to an actuary they are equivalent. Conversely, a risk seeking individual will have a convex utility function, with increasing marginal utility, and therefore will accept many gambles instead of the certain outcome. A risk-neutral individual, who is indifferent to risk, will simply choose the outcome with the largest objective expected value as her mapping between value and utility will be linear. This brief explanation captures how risk preference relates to the shape of the utility function.

Formally, the expected utility can be expressed by

$$E{U}_{(\hspace{0.17em}{p}_1,\dots ,p_n)}=\sum _{i=1}^n{p}_i{U}_i,$$

where a risky prospect is evaluated as the product of the probability of winning p and U_i (the subjective utility of the payoff x_i), rather than the purely objective product of p_i and x_i. As with discounting, the utility function U_i can take many functional forms. One of the most common forms in the literature is the constant relative risk aversion (CRRA), otherwise known as the power utility family of functions [68], of the form:

$$U(x)=x^r,$$

where r captures the curvature of the utility function, and by extension, is a measure of an individual's risk attitude. A ‘risk-neutral’ individual has an r = 1 such that the mapping between value and utility is linear. A ‘risk averse’ individual will have a concave utility function, with diminishing marginal utility, where r < 1. Conversely, a ‘risk seeking’ individual will have a convex utility function, with increasing marginal utility, where r > 1 [69].

The shape of the utility function is of interest to psychiatry because it provides a computational method for quantifying the way in which individuals subjectively value positive or negative outcomes and how this dictates their engagement with, or avoidance of, uncertainty. For instance, while most people are somewhat risk averse, a patient with a phobia may be extremely (pathologically) risk averse [70] and conversely, an individual with a gambling disorder might exhibit risk-loving behaviour [71]. The fact that we can measure the curvature of the utility function using simple choice tasks and that this measure seems to translate to behaviour in realms other than preferences over gambles suggests that this can serve as a potentially powerful clinical tool.

4. Theoretical and empirical separation of risk and time preferences

As alluded to above, traditional approaches to modelling temporal discounting ignore potential nonlinearities in the utility function, and hence individual differences in risk attitude, by computing the discount rate while specifically assuming that subjects are risk neutral. This is particularly problematic as a significant body of work has shown there is wide heterogeneity in the shape of individual utility functions (a diversity in risk preferences) and that, by and large, most individuals exhibit some degree of risk aversion—i.e. concavity in their utility function for most reward types [72].

The theoretical challenge presented by the potentially confounding influence of nonlinear utility upon estimates of the discount rate was originally brought to the general attention of economics and psychology by Frederick et al. in 2002 [33]. Since then, numerous attempts have been made to elicit separable risk and time preferences. In a series of seminal papers [73,74], Andersen and colleagues proposed a measure of the discount function conditional upon utility, first by estimating the r curvature parameter using an independent risk task. Using this methodology, the authors ‘corrected’ their collective estimate of the discount rate of a sample of 253 adult Danes from an annual discount rate of 25.2% to 10.1%, concluding that by ignoring the risk averse preferences of this population, they had overestimated the discount rate (and hence people's choice impulsivity) by a large margin. Similarly, Laury et al. [75] reported a reduction from an annual discount rate of 55.5% to 14.1% after correcting for risk with a different task [75], and Takeuchi [76] showed that imposing linear utility increased the discount rate estimates and resulted in poorer model fits to behavioural data [76].

We note that there have been important contributions on this issue of the separability of time and risk preferences that have proposed solutions outside of the standard expected utility-based approach that we describe here [77]. Primarily, the ordinal certainty equivalent hypothesis [78] and the use of non-expected utility functions [36,79,80] have provided alternative solutions to make risk and time preference parameters identifiable. Andreoni & Sprenger [81], however, approached the separability of risk and time preferences quite traditionally by systematically manipulating risk in an intertemporal choice task [81] and found that preferences differed when both the immediate and delayed rewards were probabilistic relative to when these rewards were certain [82]. They concluded that (1) time preferences are distinct from risk preferences because they change when risk is explicitly present and (2) that utility under risk may be more concave than utility under certainty. This second point is shared by other authors [83–86]. For instance, Abdellaoui and colleagues [87] find differences in the curvature of the utility function for risk and for time preferences measured separately [87]. Other authors suggest that risk must play a role in the evaluation of future choices regardless of time preferences and that this may be accounted for by prospect theory [36,88]. This implies that utility under risk cannot be equated to utility at each time step—instantaneous utility—of a discounting function. This is interesting in light of brain imaging data that we discuss further below showing instead extensive neural overlap in the representation of subjective value for risk and the discounted subjective value, which potentially argues against this perspective. In any case, while these very detailed and advanced debates in the literature are of deep interest, all of these authors focus on the notion that instruments commonly aimed at measuring impulsivity can be entangled with risk-attitude. For this reason, we focus next on a study of how risk preferences can bias estimations of discount rates as they are traditionally explored (using simple binary choice tasks) in many psychology and psychiatry studies, which assumes an equivalence of utility across risk and time as in Andersen et al. [73].

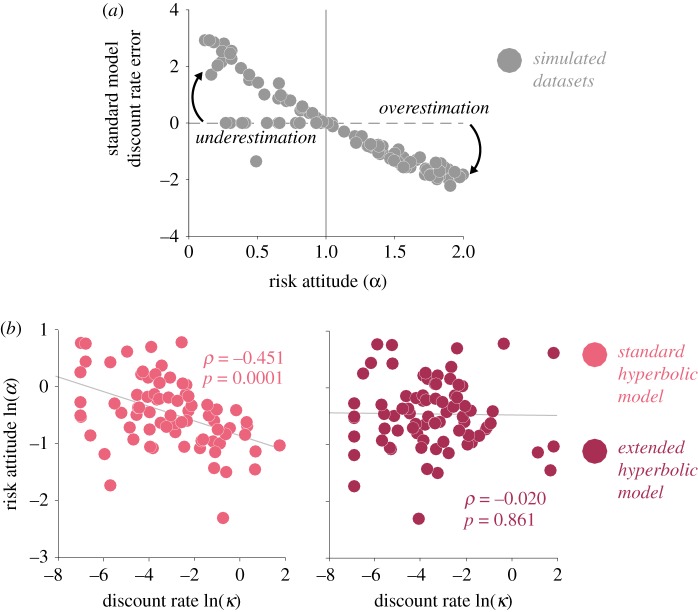
We recently demonstrated that ignoring risk attitudes when estimating individual discount rates not only overestimates these rates, but also introduces a systematic bias, whereby risk averse individuals appear more impulsive while risk tolerant individuals appear less impulsive than they really are [89]. We simulated discounting behaviour using a wide distribution of r curvature values for the utility function and showed that our predicted pattern of bias was matched by the behaviour of a community sample of individuals with diverse risk preferences (figure 1a). Our simple binary choice tasks (designed to separately capture risk and time preferences as in Andersen et al. [73]) have high translational value because they are of the kind that have been employed in studies with other animal species like rodents or non-human primates, unlike the choice lists or convex budget time sets described in the economics literature [90]. Furthermore, they do not require any sophistication or knowledge of finance to complete. Here, we used an independent risk task to estimate the curvature of each subject's utility function. This parameter, which corresponded to the individual's risk attitude, was then imputed into the discount function (exponential or hyperbolic) such that discounting is computed on utility v^r rather than on value v, as in the following equation:

$$U^t(c_t)=\frac{v^r}{1+k\cdot t}.$$

By employing this methodology, we showed that our discounted model accounted better for the behaviour of our real-world sample, and more importantly, we were able to fully decorrelate the estimated discount rate from the estimated risk preference parameter, thus giving us confidence that we can measure dissociable aspects of subjects' decision-making behaviour (figure 1b).

Figure 1.

(a) Bias in estimated discount rate from simulated intertemporal choice data at different levels of risk preference (from risk averse to risk seeking). Bias is computed as the difference between standard hyperbolic model (Mazur [59]) and the extended hyperbolic model (Lopez-Guzman et al. [89]), which discounts utility rather than value. At risk aversion levels (α < 1), the standard model overestimates the discount rate and at risk seeking levels (α > 1), the standard model underestimates the discount rate. (b) Correlation between the natural logarithm of the discount rate (κ) and the natural logarithm of the risk attitude parameter (α) obtained from the standard hyperbolic model (light colour) and the extended hyperbolic model (dark colour). Spearman's ρ and p-value for each correlation are reported. The extended hyperbolic model, which takes risk attitude into account, successfully decorrelates the two parameters. Adapted with permission from [89]. (Online version in colour.)

5. The neural implementation of temporal discounting and risk preference

Numerous studies using functional magnetic resonance imaging (fMRI) in human subjects have examined the neural correlates of intertemporal choice and discounted subjective value [43,91–94], and separately, of risky choice and subjective value modulated by uncertainty [95–99]. A handful have additionally begun to examine how risk preferences and the discount rate might interact at a neural level to drive impulsive choice [100–102].

Early work by McClure and colleagues [86] on the neural basis of intertemporal choice seemed to suggest the engagement of two neural systems in the decision to select a larger later reward, an account some have suggested has to do with the competition between two ‘selves’, one that pushes behaviour towards less patience (i.e. towards the immediate reward) and the other that pushes behaviour towards more patience. This initial conclusion was based on a fairly complex multi-step inference suggesting that one set of brain regions, the ventromedial prefrontal cortex (VMPFC), ventral striatum, and posterior cingulate cortex (PCC), was more active when subjects chose the immediate relative to the delayed options in an intertemporal choice experiment [71,86]. And that yet another set of regions, the dorsolateral prefrontal cortex (DLPFC) and posterior parietal cortex, were active when the subject made a more difficult choice compared to an easier choice.

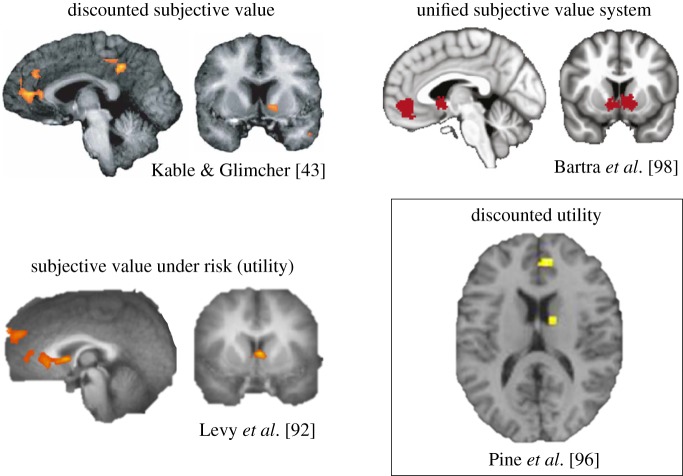
More recent studies agree that a single neural system is used to evaluate both immediate and delayed rewards, with each reward's value determined by how far away in time it is to be received. Kable & Glimcher [43] first tested this idea by estimating individual subjects' discount rates based on the choices they made in an intertemporal choice experiment that included critical elements of the approach used by McClure and colleagues in a nested fashion. The authors then used this estimate to construct what the discounted subjective value of each option on a given trial of the experiment would be for a given subject based on that subject's own discount rate. Using model-based fMRI, this study revealed that activity in a small set of brain regions all previously observed in McClure et al. [86] while subjects chose the immediate rewards, the VMPFC, ventral striatum and PCC, increased (in this case, hyperbolically) exactly as the value of the offer increased—a finding now widely seen as evidence that a single system represents discounted subjective value. In a follow-up study, Kable & Glimcher [57] showed that this was also true in the context of deciding about two delayed rewards (where there could be no ‘present bias’) rather than about a delayed and an immediate reward [57]. In this study, subjects anchored their discounting behaviour to the soonest-possible reward, not simply to the present, and the magnitude of activation in the VMPFC, striatum and PCC was not higher when an immediate reward could be chosen relative to when only a delayed reward could be chosen. Instead, activity in these regions encoded the subjective value of immediate and delayed rewards. Together, these two studies, along with a slew of subsequent work, provide what is now typically seen as unequivocal evidence that the VMPFC, striatum and PCC track discounted subjective value and not simply immediacy, impulsivity or a ‘hot’ response to a reward. While both perspectives—dual-system versus unified system—have found behavioural support, the latter view provides a more parsimonious account (from a neurobiological perspective) of how we might decide about the future. Indeed, further work continues to show that the VMPFC, striatum and PCC are not exclusively or disproportionately more active for immediate rewards. Instead, these regions are thought to form the core of the brain's valuation system, a set of brain regions that track the value of choice options across a variety of decision contexts and reward types—including delayed and risky rewards [98] (figure 2).

Figure 2.

Neural correlates of discounted subjective value, subjective value under risk (or undiscounted ‘utility’) and discounted utility. The three types of value signals are found in the ventromedial prefrontal cortex (VMPFC) and striatum, among other regions. These two regions form the core of the brain's unified subjective valuation system as identified in meta-analytic data. Adapted and reprinted with permission from Kable & Glimcher [43], Levy et al. [92], Bartra et al. [98] and Pine et al. [96]. (Online version in colour.)

A corollary to the unified system view as it pertains to our understanding of the neurobiology of intertemporal choice and the discount rate is that if the same brain system represents individual risk preferences (and hence, the curvature of the utility function) then this prior evidence for discounted subjective value representation might in fact be accounted for by the so-called probability discounting, the notion that all preference for immediate rewards stems from fear that any delay is itself intrinsically risky. As the decision-maker might believe that the probability of acquiring a given reward decreases as delay to its receipt increases, fMRI correlates of discounted subjective value might reflect the influence of probability and subjects' risk preferences rather than delay per se. To address this possibility, a handful of fMRI studies have simultaneously examined subjects’ preferences for risk and delay [99,100], the unique contribution of delay to intertemporal choice holding risk constant [97] and the neural correlates of discounted subjective value adjusted for the curvature of subjects' utility functions [96]. First, what these studies show is that the preference for immediate rewards cannot be fully accounted for by fear of risk, suggesting that it may be possible to isolate the unique contribution of delay on choice at a neural level. Second, while these studies do show overlap in the neural basis of decision-making about delayed and risky rewards, some differences are observed as well. Using a formal conjunction analysis, Peters & Büchel [100] found that, as predicted by the unified system perspective, the same striatal voxels represented the subjective value of delayed and risky rewards, with others showing similar findings in the VMPFC in a larger sample [100]. Interestingly, in this set of studies, differences between delay and risk were observed in the PCC (also typically considered part of the brain's valuation system) and the intraparietal sulcus, which might be related to the episodic memory and future thinking components of intertemporal choice. This finding suggests the activity in these specific brain areas would be more consistent with theories where utility for risk and utility for time are not equivalent [82,87].

In another approach to examining the neural overlap between risk and delay, and similarly, to identifying where their processing might diverge, Luhmann et al. [97] designed a risky choice paradigm where the only difference between two conditions was the amount of time subjects knew they had to wait to receive the outcome of their choice. This allowed the authors to examine the neural correlates of expected value modulated by delay. Brain regions that emerged as common to the immediate and delay conditions included, among others, the VMPFC, insula and PCC. Most notably, regions that emerged as unique to the delay condition included parts of the medial temporal lobe (which, similar to the inferior parietal regions, is implicated in episodic memory) as well as the DLPFC [97].

However, while risk and delay were assumed to be independent and non-interacting in Luhmann et al. [97], this is likely not the case given strong theoretical and empirical evidence to the contrary. To account directly for this interaction, Pine et al. [96] performed a traditional intertemporal choice experiment but, critically, using similar procedures to those described above in Lopez-Guzman et al. [89], incorporated a subject's idiosyncratic utility function curvature into the estimation of his or her discount rate. This allowed the authors to construct, for each subject, a risk preference-adjusted discounted subjective value regressor for their fMRI analyses. Controlling for undiscounted utility (subjective value of the delayed option adjusted for a subject's utility function curvature, but without the effect of delay), the VMPFC and striatum emerged as the only regions that tracked discounted utility (subjective value of the delayed option adjusted for a subject's utility function curvature and the effect of delay) [96]. Interestingly, and providing further support for the unified system perspective, a conjunction analysis again revealed that the same striatal voxels represented undiscounted and discounted utility (with each side of the conjunction statistically controlling for the other; figure 2), further suggesting that this region might support the integration of undiscounted utility and delay to drive temporal discounting. Also of note, as shown behaviourally in Lopez-Guzman et al. [89], the temporal discounting model that best fit the neural data was the modified hyperbolic model, providing converging evidence that the brain implements this particular algorithm [89,96].

In addition to these studies aimed at isolating the neural representation of discounted utility, another interesting line of work aims to test the possibility that there might be distinct sub-circuits within the broader valuation circuit that might independently support risk versus time preferences. These sub-circuits may not be detectable with the resolution of current human neuroimaging techniques but may be amenable to investigation in animal studies. Recent studies indeed suggest impulsive choice as measured by temporal discounting could be subserved by projections from ventral and dorsal striatum to more lateral areas of prefrontal cortex, while risky choice could be subserved by more ventromedial corticostriatal projections—including ventral striatum, medial orbitofrontal cortex, VMPFC and anterior cingulate cortex [102]. However, this work has not yet attempted to account for the interaction between risk and time preferences. Accounting for this interaction could facilitate a more precise dissection of the neurobiology of impulsive choice at the level of sub-circuits and neurotransmitter systems.

6. Implications for psychiatry

Much of the proliferation of time preference measures of impulsive choice in the psychiatric literature is borne out of a heightened interest in the relationship of this construct to unhealthy behaviour [103]. On average, temporal discounting is higher (although distributions overlap) in individuals with substance use disorders including nicotine, alcohol and illicit substances like heroin, cocaine and methamphetamine [11] compared to controls. This finding extends to obesity and overeating [104] and, notably, to risky sexual behaviour [105]. These observations have led several experts to suggest that discount rates could be a transdiagnostic marker of ‘pathological self-control’ [106] and as such could be useful as a predictive measure in at-risk populations [107]. Beyond diagnosis and prognosis, discount rates may also track therapeutic response in addiction [108] and obesity [109]. Recent reports suggest that within some clinical populations, individual differences in discounting could also aid in stratifying patients by their risk for treatment failure, which may prove useful for personalized treatment selection [110]. Perhaps one of the most compelling arguments for the focus on discounting measures in psychiatry is that their neural correlates are now fairly well known, and these behavioural tests can therefore reflect, in a more measurable way, the current biological state of the neurocircuitry that supports them. For example, ample evidence on the functional interaction between the DLPFC and key areas of the valuation network like VMPFC [111–113], indicates DLPFC may modulate the contextual flexibility of value representation for intertemporal choice. Interventions that target the DLPFC could, therefore, strengthen this modulatory effect and be useful therapeutically [114,115]. Having a cheap behavioural readout of this neurobiological effect is thus of great utility to psychiatry.

A key implication of the work discussed here is that the psychological basis of impulsive choice as measured by standard test instruments can be biased by an individual preference for risk. Individuals who are more risk averse can be misidentified as more impulsive if risk attitudes are not measured directly. Fortunately, evidence from neuroimaging and studies of impulse control disorders suggests that risk preferences do not account for the majority of the variance in discount rates—even when the empirical techniques used entangle the two measurements; rather the two appear to be partly independent contributors to impulsive choice. This means that we are not suggesting all results reported in the literature are invalidated by the fact that the measurement techniques used may be confounding risk and time preferences. However, in some particular psychiatric conditions, risk and time preferences may be going in the opposite direction of that predicted by their relationship described here. Pathological gamblers are one clear example of a population that exhibits both steep discounting of delayed rewards and somewhat reduced risk aversion, and these behavioural profiles are supported by both common and distinct neural correlates, as shown by Miedl et al. [99]. In this study, while the subjective value of all reward types and in all subjects was encoded in the brain's valuation system, only encoding of the subjective value of delayed rewards (but not risky rewards) was more pronounced in gamblers than in controls in the VMPFC and striatum. This suggests that our understanding of impulsive behaviour across a range of psychiatric disorders necessitates measurement of both discount rates and the curvature of the utility function (risk preference), among other variables, and their corresponding neural correlates. Measuring only the discount rate can confound interpretation of the primary drivers of why individuals discount delayed rewards at different rates and impulsive choice [116] and can obscure potentially important neurobiological targets for intervention.

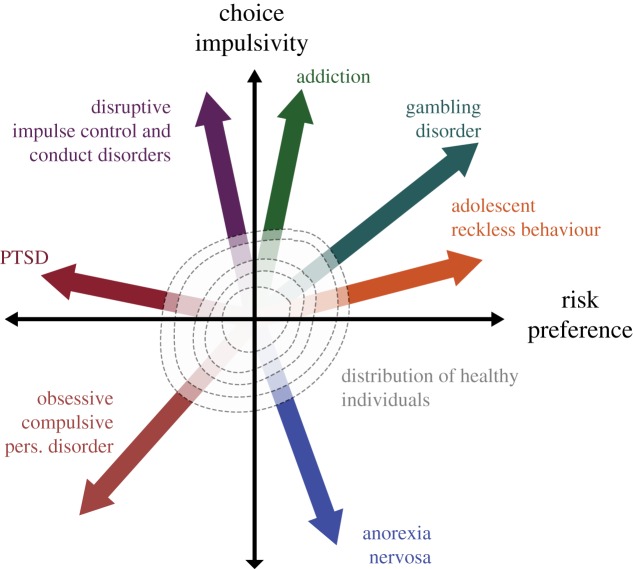
We propose that both time and risk should be thought of in their dimensional nature with respect to their utility in psychiatry (figure 3). For example, individuals with anorexia nervosa exhibit lower discount rates than controls [117], that is, they are perhaps pathologically patient. People suffering from anorexia are described clinically as exhibiting an ‘undue influence of body shape and weight on self-evaluation’ that guides their behaviour towards future goals of achieving a desired improvement, by restricting and titrating their energy intake and being prone to overexert in a constant attempt to lose weight. In this perspective, discounting embodies a behavioural dimension where either extreme is undesirable. The same can be said for attitudes towards risk. Excessive aversion to risk is maladaptive, as most situations in the world carry some level of uncertainty, and an inability to engage with these situations can lead to avoidance and extreme anxiety. Some reports indicate that individuals with anxiety disorders and phobias are more risk averse than controls [118]. On the other side of the spectrum, excessive tolerance or love of risk can obviously also be similarly detrimental, e.g. leading an individual to gamble insensibly [119], or to seek and engage in risky situations like high-risk sexual or drug consumption practices [120,121]. If these dimensions are not fully orthogonalized, that is, if there are unaccounted for interactions between them, this proposed mapping will be distorted, and separability of these disorders may not be readily achievable. Biases introduced in the evaluation of time preferences could thus compromise their true translational utility. Future work focusing on time and risk preference, especially when measured in clinical populations, should be mindful of their interaction.

Figure 3.

Theoretical space spanned by two orthogonal dimensions: choice impulsivity (i.e. discount rate) and risk preference (i.e. risk attitude parameter). Each vector represents a deviation from normality that could correspond to a defined psychiatric disorder. At the origin of this space, we locate a two-dimensional distribution that corresponds to values of choice impulsivity and risk seen in the ‘healthy’ population. PTSD, post-traumatic stress disorder. (Online version in colour.)

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.