Time scales and temperatures of crystal storage in magma reservoirs: implications for magma reservoir dynamics

Abstract

The thermal and therefore physical state of magma bodies within the crust controls the processes and time scales required to mobilize magmas before eruptions, which in turn are critical to hazard assessment. Crystal records can be used to reconstruct magma reservoir histories, and the resulting time and length scales are converging with those accessible through numerical modelling of magma system dynamics. The goal of this contribution is to summarize constraints derived from crystal chronometry (radiometric dating and modelling intracrystalline diffusion durations), in order to facilitate use of these data by researchers in other fields. Crystallization ages of volcanic minerals typically span a large range (10⁴–10⁵ years), recording protracted activity in a given magma reservoir. However, diffusion durations are orders of magnitude shorter, indicating that the final mixing and assembly of erupted magma bodies is rapid. Combining both types of data in the same samples indicates that crystals are dominantly stored at near- or sub-solidus conditions, and are remobilized rapidly prior to eruptions. These observations are difficult to reconcile with some older numerical models of magma reservoir dynamics. However, combining the crystal-scale observations with models which explicitly incorporate grain-scale physics holds great potential for understanding dynamics within crustal magma reservoirs.

This article is part of the Theo Murphy meeting issue ‘Magma reservoir architecture and dynamics’.

1. Introduction

Volcanic eruptions are driven by processes that occur within crustal magma reservoirs, including mixing and differentiation of magmas, transport of volatiles, and assembly and storage of eruptible magma bodies. In addition, crustal magma reservoirs are sites of chemical and physical evolution of magmas resulting in erupted magma compositions, including mixing of mantle-derived magmas with crustal material. Thus, a better understanding of magma reservoir rates and processes has implications for volcanic hazard forecasting, as well as for understanding generation of diverse magma compositions and evolution of the composition of the crust. Reconstructing the processes that operate within crustal magma reservoirs depends in part on developing a better understanding of the time scales of these processes, as different processes may operate at different characteristic time scales. Similarly, the thermal conditions of magma storage and transport are strongly linked to the physical properties of the magma (e.g. crystallinity, liquid viscosity, bulk viscosity) and as such place constraints on the processes operating within crustal reservoirs, and on the time scales over which they occur. Thus time, temperature, and process within magma reservoirs are interconnected, and better information about one aspect can inform each of the others.

Recent work focused on understanding the physical conditions of upper-crustal magma storage has converged around the ‘mush model’ [1–4] in which the reservoir is composed of a relatively small body or bodies of liquid-dominated magma, surrounded by a much larger region of crystal mush (defined as greater than 50% crystalline), grading into sub-solidus plutonic rocks derived from the same magma reservoir. It has long been recognized [5,6] that this upper-crustal mush zone is only the uppermost part of an interconnected series of magma storage regions throughout the crust, which for example Cashman et al. [7] term a ‘trans-crustal magma system’, much of which may also be composed of crystal-dominated magma bodies (see also [8]). Such models are consistent with geophysical imaging of magma reservoirs, most of which indicates small melt fractions (a few per cent to a few tens of per cent; [9–11]) distributed throughout a large region. However, within this broad consensus, many questions remain areas of active research and debate, such as:

• —How long is a crustal magma reservoir active?
• —How long does it take to assemble erupted magma bodies, and how long do they reside in the crust prior to eruption?
• —What are the time scales and processes of mobilization of melts from a mushy reservoir?
• —How are melts extracted from crystal-dominated bodies, and how are they transported and amalgamated to produce liquid-dominated erupted magmas?
• —What are the thermal conditions of long-term storage within a reservoir (‘cold storage’ versus ‘warm storage’) and of storage during final assembly/eruption?

Recent developments in many areas of magma reservoir research, including improvements in spatial resolution and precision of chemical and isotopic analyses of magmatic products as well as laboratory and numerical experimental techniques, have led to rapid growth in our understanding of these topics (many examples of which are included in this volume). In particular, these advances have brought the length and time scales that can be investigated by many different techniques closer together. At the same time, with rapid developments in our understanding within each field, it can be difficult for researchers outside a given sub-discipline to determine what are the solid conclusions and what are inferences suggested by—but perhaps not required by—the data. Therefore, this contribution is aimed at facilitating communication between the petrology/geochemistry and the geophysical/modelling communities, both working on the broad research questions summarized above.

In particular, this paper will focus on summarizing geochemical records of the time scales of magmatic processes that are contained in volcanic crystals, where the time scales are derived from radiometric dating and from modelling intracrystalline diffusion. The differences between these two methods of obtaining time scales, along with comparisons of age and sub-crystal scale compositional data in crystals, provides information about the chemical and thermal evolution of the magma. For example, radiometric ages allow quantification of crystallization ages whereas diffusion modelling constrains storage durations within the magma reservoir, and collectively they can capture processes such as long-term magma storage, mixing, and assembly of erupted magma bodies. The time scales included in these data range from minutes to hours for syn-eruptive magma ascent to years to centuries for magma mixing within the upper crust, to tens of thousands to hundreds of thousands of years of crystal storage and recycling in a long-lived magma reservoir. This paper is focused on time scales of processes within the upper crustal magma reservoir. I will use recent examples from the literature to illustrate different processes and time scales, but this is not intended to be a comprehensive review of the literature, which instead can be found in a number of review papers [12–18]. I will highlight, where possible, biases or assumptions within these approaches to quantifying time scales—for example, the radiometric ages discussed here are biased towards the silicic end of the compositional spectrum, reflecting the prevalence of such compositions in the literature (e.g. [14,17,18]), but the diffusion data are biased more towards the mafic end of the spectrum, due in part to the availability of experimental data on diffusivity (e.g. [15,16]). Whether radiometric or kinetic, the crystal time scale data available in the literature are also biased towards upper-crustal magma systems rather than mid- to lower-crustal magma storage, due to the greater likelihood of sampling crystals from the upper part of the reservoir system. In addition, crystal records by necessity sample the solid material within a reservoir, which will bias these records towards the crystal-rich and therefore colder regions of the reservoir. The overall goal of this paper is to summarize the areas of emerging consensus about processes and time scales within magma reservoirs from the perspective of the crystal records, while also discussing areas of active debate and uncertainty, and then to compare these results to those derived from numerical (or other types of) models of the same magma reservoir processes, in order to highlight areas of fruitful future research.

2. Time scales and temperatures of crustal magma storage

(a). Absolute ages and durations of subsurface magmatic processes

As has been noted for many years, radiometric dates of crystals and time scales from diffusion modelling are sensitive to different variables during magmatic processes (e.g. [7,13,15,19–21]). Radiometric dates record the time since parent–daughter fractionation and the accumulation of radiogenic daughter, corresponding in most cases to the age of crystal growth. In contrast, diffusion of trace elements will start as soon as a chemical potential gradient is established, but the rate of diffusive smoothing of the compositional gradient in response to this chemical potential gradient depends strongly on temperature. Each of these techniques has strengths and weaknesses; for example (with the exception of ⁴⁰Ar-³⁹Ar dating), the radiometric age of crystallization is insensitive to temperature variations that the crystal may have experienced after growth, whereas because the modelled duration of diffusive equilibration is exponentially dependent on temperature, it is a function of the thermal history of the crystal after the compositional gradient was established. On the other hand, radiometric dating of major phases often requires analysis of bulk mineral separates, which averages age variations across zones within crystals or across crystal populations of different ages in the same sample [13,14,17,18]. In addition, each radiometric chronometer has practical limits on the absolute age range that it can resolve, due on the young end to unmeasurably small amounts of ingrown radiogenic daughter, and on the old end to analytical uncertainties propagating into larger absolute uncertainties in older dates. In contrast, the uncertainty in calculated diffusion durations is independent of absolute age, and elements with differing diffusivities in the same crystal can record a range of durations (and a range of magmatic processes, depending on the varying sensitivity of different elements to a given process) within a single sample. Each technique thus provides complementary information about time scales, and combining the results of both techniques in the same crystal populations can provide additional constraints on the thermal history of the magma reservoir [19,22]. In this section, I will summarize the information that these two techniques have provided on durations and rates of processes in the active parts of magma reservoirs that are sampled by eruptions.

(b). Magma mixing and assembly of erupted bodies in shallow plumbing systems

There is abundant evidence that many (or even most) erupted magma bodies are mixtures of multiple silicate liquids and/or crystal populations (e.g. [23]). The time between mixing during assembly of the erupted magma and the eruption itself can be reconstructed if changes in magmatic conditions (e.g. pressure, temperature, volatile abundance, liquid composition) change thermodynamic equilibria during or immediately after mixing. For example, degassing can change mineral–melt equilibria, leading to diffusion of elements into or out of crystals, and mixing (with or without degassing) may trigger crystal growth, producing sharp compositional variations within crystals which then diffusively equilibrate over time [12,15,16]. For most elements used in these studies, diffusion effectively ceases on eruption, due to the abrupt temperature drop. Therefore, modelling the time of diffusive equilibration quantifies the period of time between crystal growth or changing equilibria and eruption. Because studies that target mixing-to-eruption time scales generally focus on the last stages of rim growth, or on diffusion of elements into or out of the crystal at the rim, they typically capture time scales relevant to the most recent magma mixing events. If, as generally assumed, these latest stages of mixing and crystallization take place within shallow magma reservoirs, the modelled durations of storage are relevant to this final location of magma assembly and residence prior to eruptions. In some cases, multiple crystal populations and/or multiple boundaries within each crystal have been investigated, providing additional constraints on the time scales of mixing and transport between different regions within this shallow reservoir (e.g. [24]).

Modelling the time scales of intracrystalline diffusion requires some assumptions, including the initial and boundary conditions (i.e. initial compositional profile, whether the crystal is open to exchange with the external magma or not, etc.), the geometry of the diffusion problem (e.g. one-dimensional (1D) versus two-dimensional (2D) or three-dimensional (3D), crystal shape and orientation), and knowledge of accurate diffusion coefficients for the element and crystal of interest. The diffusion distance is proportional to the duration times the diffusion coefficient $(x\approx \surd Dt)$(e.g. [25]), which means that duration can only be recovered if the diffusion coefficient is known. The accessible time scales and accuracy of diffusion modelling are also limited by the uncertainty in the analytical technique and the spatial resolution, which controls how precisely a concentration profile can be measured. How long diffusion of a given element must have operated in order to be measurable depends both on the spatial resolution of the analytical technique and on the diffusivity of the element (i.e. D).

The initial and boundary conditions are generally not known a priori and must be chosen on a case-by-case basis using a petrological understanding of the system. Common approaches include assuming a perfect initial step function (plagioclase) or initially homogeneous composition (olivine), or using a slow-diffusing element to define the initial shape of the boundary for a faster-diffusing element (e.g. [15,16]). The uncertainty in diffusion duration due to uncertainties in the initial and boundary conditions can be difficult to quantify, but one approach is to model a range of petrologically reasonable initial and boundary conditions to determine the effect on the model diffusion time. The choice of initial condition may not have a large effect on the modelled diffusion times—for example, the difference in model diffusion duration between an initially homogeneous concentration and a step function in concentration near the rim may only be a factor of 1.5 [15]. Boundary conditions can have a larger effect, but for the case of a diffusion of a trace element from a melt into a pre-existing crystal, the assumption that the melt acts as a homogeneous reservoir and that equilibrium is maintained at the crystal interface is reasonably robust except in the case of a slow-diffusing element or rapid crystal growth relative to diffusion (e.g. [15,16]). A note of caution on this general observation, however, is that whether crystal growth was important in producing a particular concentration gradient must be carefully evaluated, which can potentially be done using multiple elements with different diffusivities measured in the same profile [26,27].

One of the most significant uncertainties involved in diffusion modelling is the diffusivity of the element of interest in the crystal of interest, which may vary with pressure, temperature, major-element composition, crystallographic orientation, oxygen fugacity, and other variables in the system [12,16,21]. This uncertainty can be divided into two parts: how well a diffusion coefficient for a particular element in a particular mineral at particular P-T-X-(etc.) conditions is known experimentally given the uncertainties in measurement and extrapolating or interpolating between experimental data, and how well we know the appropriate conditions at which to conduct the modelling. Uncertainties in experimental determinations of diffusion coefficients for a given set of conditions are typically known to within 0.2–0.5 log units (larger when the data have to be extrapolated from experimental conditions), which translates to 0.2–0.5 log units uncertainty in the calculated diffusion times [16]. Owing to the exponential dependence of diffusivity on temperature, the temperature effects can be large [12,15,16]—for example, changing the modelled temperature for diffusion of strontium in plagioclase from 850°C to 750°C changes the modelled duration by approximately an order of magnitude [19].

What can be more difficult to quantify is how uncertainties in knowing the appropriate conditions for modelling affect the overall uncertainty. For example, the exponential dependence of diffusivity on temperature means that knowing the temperature history experienced by a crystal after formation of a modelled compositional profile is critical in calculating accurate diffusion times. However, the true thermal history of a crystal population is rarely known, and for simplicity is most often assumed to be isothermal at the temperature recorded by mineral thermometry (either from the modelled crystals themselves or from other crystals in the same magma). This assumption may be robust in the case of rim growth that precedes eruption by weeks to months and is the last event recorded in the crystals, but it is more likely to be incorrect for profiles further from the crystal rim and/or for crystals which may have had more complicated growth and storage histories (see below).

The extent to which modelling using the simplifying assumption of isothermal diffusion captures the true time scales of diffusion depends on the complexity of the real thermal history. In the case of regular thermal oscillations around a constant mean value, the duration of diffusion can be accurately calculated by assuming isothermal diffusion at the mean temperature [15]. Some simple non-isothermal histories can also be approximated by an isothermal diffusion model at a characteristic temperature that is a function of the peak temperature [15]. In some recent work, non-isothermal diffusion across multiple boundaries within populations of crystals has been modelled, essentially by choosing two or more isothermal steps and solving for combination of durations that reproduce the combined profiles [24,28]. It is also possible to use numerical methods to construct forward models of diffusion during arbitrary thermal histories, in order to explore the magnitude of the effect on diffusion of particular changes in thermal conditions (e.g. [15]). This type of numerical approach can also be useful in assessing the extent to which simultaneous growth and diffusion has modified measured profiles (e.g. [15,26,27]). Petrological modelling (e.g. R-MELTS) can also provide some insights and constraints on intensive variables (e.g. temperature, water content, oxidation state) that can be used to define appropriate conditions for diffusion modelling (e.g. [29,30])

Finally, sectioning effects can lead to substantial inaccuracies in modelled diffusion durations. These arise from the fact that, in practice, compositional variations are typically measured as 1D profiles across random 2D slices of 3D crystals, and profiles are modelled assuming diffusion in one dimension. This can lead to significant inaccuracies compared to considering the full complexity of 3D diffusion, even once the effects of non-isotropic diffusion are accounted for [31,32]. Depending on the location and orientation of the measured profile, such effects can lead to either overestimation or underestimation of the true diffusion time, for example by factors of 0.2–10 for olivine [32]. One implication of these results is that 1D modelling of profiles measured across multiple randomly-oriented crystals would be expected to produce a spread of model diffusion ages of a factor of 5–10, even in the case where all crystals are recording the same duration of diffusion [32]. In cases where one or more of the key variables is poorly constrained, or where factors like crystal growth have played a significant role in nature but are not incorporated into the model, modelled diffusion durations could be inaccurate by as much as 2–3 orders of magnitude. However, hypothetical modelling studies [31,32] allow identification of strategies for choosing profiles to measure and model that can dramatically reduce these inaccuracies, and in the best case scenario—of modelling at least 20 carefully selected profiles from a homogeneous population, where the diffusion coefficients are perfectly known—can recover the true diffusion time with accuracy of approximately 5% and precision of approximately 15–25% relative (with accuracy calculated from the mean diffusion time of all profiles and precision from the standard deviation of the mean modelled durations [32]). Even though the uncertainties in diffusion modelling may seem large, it is important to note that quantifying time scales even to an order of magnitude can in many cases provide useful information. In the well-constrained cases where the models are informed by petrologic data, diffusion modelling can provide critical quantitative information about the durations of magma mixing and storage that is otherwise inaccessible.

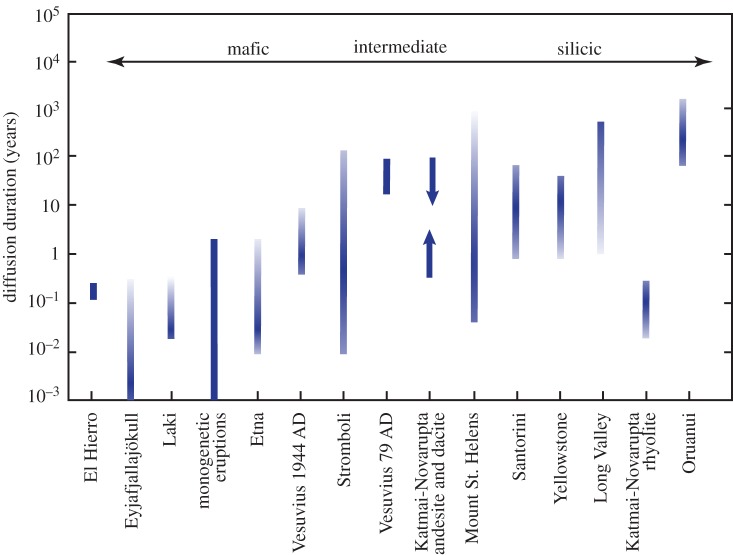
For example, a number of recent papers have focused on the duration of magma storage between mixing or magma extraction from a mush and eruption (figure 1). Most of the intracrystalline diffusion times that have been measured are weeks to months for mafic compositions, with some crystals in each study giving time scales of years. More evolved compositions typically yield diffusion times extending to longer durations, up to centuries or millennia (although an exception to this observation is the Scaup Lake Flow in Yellowstone, WY, which gives diffusion times of decades [26]). However, this observation should be treated as preliminary for two reasons: first, the dataset is limited, and, second, there may be a systematic bias between the measurements made for different compositions. In mafic samples, Fe–Mg interdiffusion in olivine is one of the most common approaches, whereas intracrystalline diffusion of Sr and/or Ba in feldspar is commonly applied to more silicic compositions. The more rapid diffusivity of Fe–Mg in olivine compared to Sr or Ba in feldspar at any given temperature and the higher temperatures characteristic of mafic magmas together will tend to lead to shorter diffusion durations for profiles that are similar length (i.e. resolvable by a given analytical technique). Therefore, additional data are needed in order to test whether the apparent compositional correlation with diffusion durations is a robust feature of volcanic systems.

Figure 1.

Examples of mixing-to-eruption or magma assembly times derived from modelling diffusion equilibration in volcanic crystals. Note that this diagram is a sampling of recent work (weighted towards recent examples) rather than a comprehensive review. Each bar represents a range of modelled diffusion times, with intensity of colour schematically indicating the number of data in that time interval. Bars are solid colour where only a few data exist, and have arrows pointing up or down for minimum and maximum diffusion durations, respectively. Arrow across the top of the diagram schematically indicates magma composition, with mafic eruptions to the left and more silicic eruptions towards the right. The volcanic systems studied are listed along the bottom axis. Data from the following sources: El Hierro, Canary Islands [33]; Vesuvius 1944 AD [34]; Vesuvius 79 AD [35]; Eyjafjallajökull [36]; Laki [37]; monogenetic eruptions [38]; Etna [30,39–41]; Stromboli [24,28]; Katmai-Novarupta [42]; Mount St. Helens [43]; Santorini [44]; Bishop Tuff, Long Valley [27]; Yellowstone [26]; Oruanui, New Zealand [45]. (Online version in colour.)

The modelled times scales reflect diffusion either into or out of a crystal rim, or across internal compositional boundaries in the crystals. This diffusion is interpreted to be driven by changing equilibria caused either by the transport of crystals between environments within the reservoir which have differing conditions (e.g. changing pressure, temperature, oxidation state or composition), and/or by injections of magma into regions of the reservoir where the crystals were stored. However it may have been induced, the change in equilibrium can lead to new growth (typically assumed to be instantaneous compared to the diffusion times) and subsequent diffusional smoothing of compositional profiles between the new and old crystal zones, or to the development of a chemical potential gradient between crystal and surrounding melt that drives diffusion either into or out of the crystal. The temperatures chosen for diffusion modelling are typically eruption temperatures, which are determined either by measurement at the time of eruption or from Fe–Ti oxide temperatures, or are temperatures derived from mineral thermometry (e.g. olivine–liquid Fe–Mg exchange, or two-feldspar thermometry). In some cases (for example, in the case of modelling multiple interior boundaries assuming two or more temperature steps [24,28,44]), temperatures are estimated from petrologic arguments. The assumption of diffusion at or near eruption temperatures is relatively robust in the case of the mafic compositions where the event that caused growth and crystal zoning was closely followed (days to weeks) by eruption, but is more uncertain in the case of crystals which return diffusion durations of centuries to millennia prior to eruptions. In addition, in at least two cases (Long Valley, California, USA, and Yellowstone, Wyoming, USA), discordant diffusion times derived from multiple elements measured in the same profiles suggests that the time scale of crystal growth was significant compared to the diffusivity of the elements modelled [26,27]. Incorporating this effect into the diffusion modelling in each case resulted in time scales that are 1–3 orders of magnitude shorter than those which assume instantaneous growth [26,27]. Growth rates of crystals in natural and experimental systems vary widely between decompression-driven and cooling-driven crystal growth, and have been documented to vary over at least five orders of magnitude [46,47]. As a result, the relative rates of crystallization and diffusion are generally not known a priori, which emphasizes the necessity to consider the effects of crystal growth on profiles used for diffusion modelling and the utility of modelling multiple elements in the same profiles (e.g. [16,21]).

For the mafic systems which have been used for diffusion studies, the durations of diffusion are in many cases interpreted to reflect the time scale between recharge or injection of new magma into the shallow reservoir system, triggering eruption and/or reflecting continued magma supply to the shallow system during an eruption (e.g. [28,38,42,43]). When combined with petrologic modelling, this can lead to reconstruction of detailed information about the waxing and waning of magma flow through chemically distinct regions of the shallow reservoir (e.g. [30,33,37,48]).

The (typically longer) diffusion times measured for intermediate to silicic compositions have been interpreted in a subtly different way. Instead of linking the diffusion time scales to the time between a specific mixing event or activation of a particular region of the magma reservoir, they are more often interpreted to reflect melt extraction from a mush or remobilization of a near-solidus body [26,27,45,49]. In particular, the range of diffusion times for individual crystals in rhyolitic compositions has been interpreted to reflect the duration of assembly of the erupted magma body [27,45], with the longest diffusion duration indicating the onset of assembly and the shortest duration indicating material incorporated into the growing magma body immediately prior to eruption.

In the context of comparisons of geochemical time scale information to geophysical results, a number of these studies have highlighted exciting new avenues for exploring the connections between monitoring data and subsurface processes. For example, several studies have noted that periods of earthquake swarms, large earthquakes or increased gas emissions broadly correlate with the time scales of peaks in diffusion durations measured in individual crystals (e.g. [30,33,35,37–39,43]). This supports the interpretation of the diffusion durations as the timing of mixing events where new magma is injected into a reservoir, although one recent paper proposes that the diffusion durations in olivine from the 2010 Eyjafjallajökull eruption reflect time scales of crystal settling into a mush zone at the base of a sill and subsequent mobilization of the mush prior to eruption [48]. In either case, diffusion durations can provide critical information about the physical processes captured by volcano monitoring signals, which will aid in the use of monitoring data in hazard forecasting.

(c). Crystallization ages and storage durations of crystals within the active magma reservoir

In contrast to the diffusion durations discussed above, which reflect crystal residence in the shallow crust after recharge, crystal movement within reservoirs, or melt extraction events, most radiometric dates record the absolute age of crystal growth. The radiometric chronometers most commonly applied to volcanic crystals are the U-Pb and ²³⁸U-²³⁰Th-²²⁶Ra systems. The results of U-series and U-Pb dating of crystals in young volcanic rocks has been comprehensively covered elsewhere [13,14,17,18,50–53] so I will only summarize the main observations here. First, the volume of material dated, and the resulting averaging of finite durations of crystal growth, is important to consider when drawing conclusions about magma reservoir processes. The volume required for analysis is a function both of the analytical technique employed (e.g. TIMS versus SIMS versus MC-ICPMS) and of the abundances of the measured nuclides in the crystals analysed. For example, accessory phases such as zircon have U abundances that are sufficiently high to allow in situ dating of small volumes of material by ion microprobe or laser-ablation ICPMS (typically spot sizes of approx. 40 µm diameter and approx. 4–5 (SIMS) or approx. 30–50 (LA-ICPMS) µm depth). Concentrations of U and Th are typically orders of magnitude lower in major phases than in accessory phases, requiring analysis of bulk mineral separates (approx. 10 mg to several grams, depending on the mineral and magma composition). This means that individual crystals or even multiple zones within individual crystals can be dated in the case of accessory phases, but dates derived from major phases are averages of hundreds or thousands of individual crystals. For accessory phases, the choice of spot location can then affect the age distribution, and in particular spots placed on polished grain interiors are typically biased towards the older episodes of crystal growth compared to spots on unpolished crystal surfaces, which sample only the outermost few micrometres of crystallization [13,17]. In most cases where spot analyses have been compared to bulk analyses of zircon, the average of interior spot analyses is comparable to the bulk separate date (e.g. [54]). These dates are interpreted to represent crystallization ages, and will be referred to as such in the remainder of the document.

Individual spot ages on zircon for young volcanic rocks typically span a large range—tens of thousands to hundreds of thousands of years—and the average or primary peak in probability density distributions are often tens of thousands of years prior to eruption ages [13,17]. Somewhat surprisingly, this observation holds true for surface analyses as well as interior analyses, although for a given sample, the mean surface age is universally younger than the mean interior age [13]. This indicates that (i) subvolcanic magma reservoirs are active for tens of thousands to hundreds of thousands of years, and (ii) crystals in an individual sample—or even individual crystals—can record much of that history, suggesting that the ‘active’ (i.e. erupting) part of the reservoir incorporates solid material that has been present in the reservoir for up to hundreds of thousands of years. In contrast, less than half of the compiled U-Th ages on bulk mineral separates for major phases are more than 10 kyr older than eruption ages [13], indicating that crystallization of major phases on average captures somewhat later stages of magma storage prior to eruption. This suggests that the earlier phases of major-phase crystallization—which would have been expected on thermodynamic grounds to accompany the earlier stages of accessory mineral crystallization—were not incorporated into the magma bodies that erupted. This in turn suggests a process of efficient segregation of silicate melt (plus entrained small accessory mineral crystals) from a matrix largely composed of major phases. However, a caveat to this interpretation is that in approximately half of the cases where both ²³⁸U-²³⁰Th and ²³⁰Th-²²⁶Ra ages were determined from the same bulk major-phase separates, the two parent–daughter pairs yield discordant ages [13], which is most easily explained as a mixture of zones with different crystallization ages [55]. Thus, the major phases in some cases retain components that likely were crystallizing coevally with the accessory phases, and in some cases do not.

(d). Connecting time scales to thermal conditions of crystal storage

Independent of the details of the radiometric age distributions, a first-order observation is that they are on average orders of magnitude older than the durations of crystal residence derived from diffusion modelling (figure 2). This fundamental observation is not new, and has been interpreted as indicating that the two methods of chronometry are sensitive to different factors (e.g. [7,13,15,19–21]). In particular, diffusion chronometry focuses on elements where diffusion is rapid enough at magmatic temperatures to provide measurable compositional gradients, whereas most radiometric dating relies on elements that are chosen in part because of their low diffusivities in most crystals. As a result, as discussed above, diffusion modelling is highly sensitive to temperature whereas U-series and U-Pb crystallization ages are insensitive to temperature variations. Thus, the combination of the two chronometers in the same minerals can provide information about the temperature history of those crystals. Recently, we have developed a method to exploit this difference in sensitivity in order to quantify the proportion of the total crystal age that is spent at relatively high temperatures in a magma reservoir [19,22]. Although modelling diffusion at eruptive temperatures may be justified when considering the conditions of crystal storage in the weeks to years before eruption, the temperature in dynamic magma reservoirs over many episodes of recharge and/or eruption would likely vary by tens or even a few hundreds of degrees Celsius. In addition, the mush model of magma reservoirs predicts wide variations in crystallinity and temperature across any reservoir even during a single time interval. Therefore, when considering tens of thousands of years of crystal residence, and also considering that crystals in a particular rock may have different crystallization ages and therefore likely different thermal histories, choosing a particular thermal history to model becomes arbitrary. Instead, our approach is to model isothermal diffusion at a broad range of temperatures, and to compare the resulting diffusion durations to absolute durations of crystal storage (from the crystallization ages) in order to place broad constraints on the thermal conditions of crystal residence. These thermal conditions are strongly linked to crystallinity, and are therefore key to reconstructing the physical state of magma storage (e.g. crystal mush versus liquid-dominated magma).

Figure 2.

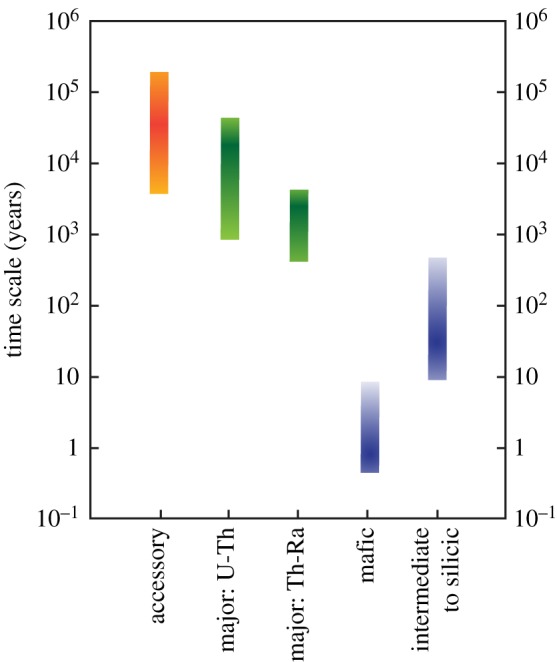
Schematic diagram summarizing time scales from crystal records. Crystallization ages or diffusion durations are plotted according to the technique, crystal, and/or magma composition. Coloured bars show crystal ages or diffusion durations, with colour intensity schematically indicating data density. However, note that the complete compilations for both crystal ages and diffusion data have some longer and shorter times (see [13] for complete crystal age compilation); the bars shown here represent the dominant populations (e.g. main peaks on probability density distributions). U-series or U-Pb crystallization ages from accessory phases (mostly zircon) are shown in orange, U-Th-Ra major phase crystallization ages in green (separated by parent–daughter pair). Diffusion data shown in blue represent a broad summary of the data shown in figure 1. (Online version in colour.)

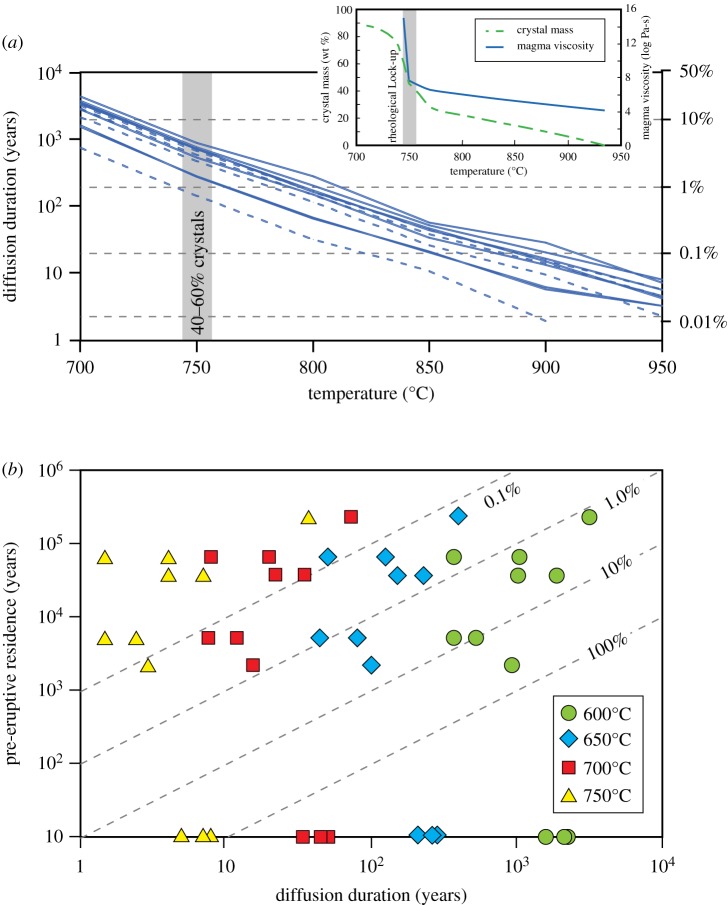
As an example, a case study using recent eruptions from Mount Hood, Oregon, USA, is shown in figure 3 [19]. Figure 3a shows the exponential dependence of modelled Sr diffusion duration on temperature for individual profiles across plagioclase crystals. One approach to interpreting these results is to compare the temperatures to those of important physical transitions within the magma. For example, R-MELTS modelling for the Mount Hood magma (inset to figure 3a) yields crystallinity of approximately 50% at approximately 750°C. This broadly corresponds to the transition from crystals suspended in a silicate liquid to a locked crystal network (although the exact crystallinity of this transition will depend on the small-scale physics of the mush [56]). Because the diffusion modelling was conducted assuming isothermal conditions, any time that the crystals spent at higher temperatures would decrease the diffusion time implied at the modelled temperature, so the model results represent a maximum diffusion duration at or above the model temperature. The bulk plagioclase age for this silicic population of plagioclase in Mount Hood lavas is approximately 126 kyr, although ²³⁰Th-²²⁶Ra ages of the same population that are less than 10 kyr require that some crystallization occurred more recently. Considering this multi-stage history and assuming near-eruption age growth for the young component, the minimum age for the old cores of the crystals is approximately 21 kyr [19,57]. Therefore, these crystals could have spent a maximum of 12% of the total storage duration at or above 750°C using the minimum core age of 21 kyr (figure 3a), and ≪1% of the total storage duration in that temperature interval using the average age of the bulk plagioclase separate. Conversely, the diffusion temperature that reproduces the measured Sr profiles for a diffusion duration of 21 kyr would be between approximately 650–700°C for the individual profiles. Thus, the implication is that these plagioclase crystals spent the majority of their history at near- or sub-solidus temperatures, with only brief excursions to higher temperature.

Figure 3.

Examples of data used to provide constraints on thermal conditions of crystal storage. (a) Modelled durations of diffusion of Sr in plagioclase from Mount Hood (modified from [19]) as a function of model temperature. Solid and dashed blue lines represent profiles across individual crystals for two different samples. Secondary vertical axis and dashed lines show the model diffusion durations as a percentage of the minimum average crystallization age for plagioclase (approx. 21 ka; [19]). Inset shows the relationship between temperature, crystal mass, and magma viscosity from R-MELTS simulations for the Mount Hood magma composition. (b) Comparison of minimum pre-eruptive residence of zircon crystals with modelled diffusion durations for the same zones within the crystals. In the case of three peaks from two crystals, minimum ages were within error of eruption age; diffusion time scales for these are shown along the x-axis. Diffusion time scales for each peak are shown at modelled temperatures of 600°C (green circles), 650°C (blue diamonds), 700°C (red squares), and 750°C (yellow triangles). Diagram is contoured for the percentage of the pre-eruptive residence time that is represented by the diffusion time scales (dashed lines labelled with percentages). Diagram modified from [22].

One factor that could complicate this interpretation is that the crystallization ages are based on bulk separates of thousands of crystals, whereas the diffusion durations are measured on profiles across a much smaller number of crystals. If the crystals containing the diffusion profiles are not representative of the average age of the population, the comparison of diffusion durations to average crystallization age would be invalid. In this particular case, Kent et al. [58] modelled Mg diffusion across 25–50 µm rims on this same population of plagioclase, showing that the rims crystallized within days to weeks of eruption, probably during or immediately after mixing events. However, the profiles measured for Sr diffusion modelling extended 300–800 µm into the crystals, and modelled Sr profiles were not dominated by the most recent crystallization event. In addition, plots of An versus Sr for these crystals show positive correlations for all profiles, instead of the negative correlation expected for equilibrium, and therefore none of the crystals measured had equilibrated internally [19]. Furthermore, Sr concentrations in the cores of the crystals showed wide variations, inconsistent with having equilibrated with the host liquid (or any other liquid of a single composition). Therefore, although the validity of the comparison between bulk crystallization age and diffusion durations must be considered carefully in each case, for Mount Hood crystals this comparison appears robust. Furthermore, preliminary data for other dacitic systems [59,60] show broadly similar patterns, suggesting that—at least for dacitic systems—storage of crystals is dominantly at low magmatic temperatures.

Considering the uncertainty inherent in comparing bulk crystallization ages to individual crystal diffusion durations, it would be ideal to have both measurements in the same crystals. We extended the same conceptual approach to single crystals by coupling U-Th dating of zircon with modelling Li diffusion in profiles measured across the same crystals (figure 3b) [22]. Applying this method to seven crystals from the Kaharoa rhyolite eruption from Okataina Caldera in New Zealand indicates that the analysed crystals spent less than 10% of the time between crystallization and eruption at temperatures above 650°C (a likely lower limit for the solidus temperature) and ≪1% above 750°C (an approximate temperature for the magma mush to liquid transition) (figure 3b). This method is not without its caveats, the most significant of which are: (i) if the peaks in Li concentration which were modelled to provide diffusion time scales were not produced during crystal growth, a comparison of crystallization ages and diffusion times would not yield storage conditions. For the analysed crystals, the shapes of the modelled profiles are inconstant with diffusion in from a crack in the crystal or from a melt inclusion above or below the plane of the measured section [22] but this needs to be carefully evaluated in each case. (ii) Equilibrium partitioning and diffusion of Li in zircon are not fully understood. Melt–zircon partitioning of Li is poorly quantified, but that uncertainty should not affect the modelled diffusion durations as long as there is no compositional dependence in partitioning that would maintain concentration gradients within crystals at equilibrium. Although it has been suggested that diffusivity of Li in zircon is coupled to rare-earth element diffusion [61,62], there is no correlation between REE concentration and Li in the measured crystals [22], and the available experimental data do not show evidence for such coupling [63,64]. It has recently been proposed based on empirical observations that Li may have multiple diffusion mechanisms in zircon [65], and if further experiments document such an effect, applications of this approach would have to take that into account. However, given the available experimental data to date, it appears that Li diffusion in zircon provides an exciting new approach to constraining magma reservoir thermal conditions.

(e). Cold storage or warm storage?

The comparisons of diffusion durations with absolute crystal ages discussed above all suggest that crystals within upper-crustal magma reservoirs spend the vast majority of their lifetimes at relatively cold (less than 750°C) conditions, i.e. ‘cold storage’ [19]. Other recent studies, however, have argued for tens to hundreds of thousands of years of storage under dominantly hotter conditions. These arguments are based on using crystallization ages of zircon coupled with Ti-in-zircon thermometry (‘warm storage’ [66,67]). Thus, the contrasting interpretations of cold or warm storage are based in part on similar observations from zircon, which brings up the question of whether different systems experience different thermal conditions, whether the approaches are capturing different aspects of magma storage, or whether one or more assumptions is not correct.

The interpretation of cold storage is based on the contrast between absolute crystal ages and diffusion durations using compositional profiles measured on the same crystal populations (albeit on a subset of the crystals in the case of plagioclase). Although the exact proportions of time spent in relatively hot conditions compared to cold depends on the temperature history chosen for modelling, the calculations in the studies cited above are set up to maximize the modelled duration of diffusion within a reasonable range of parameters for model temperature, boundary conditions, and initial conditions, and by comparing the diffusion durations to the minimum age (within uncertainty) for the old component of the crystal populations. Therefore, the main ways in which the conclusion of dominantly cold storage in the case of zircon could be wrong are: (i) if the crystals modelled for diffusion were not representative of the crystals used for the age determination, (ii) if the modelled trace-element profiles were late-stage features of the crystals that then would not be comparable to the average crystal ages, or (iii) if the experimental measurements of Li diffusivity in zircon do not apply to the natural conditions (e.g. [65]). We have carefully assessed each of these assumptions based on currently available data [19,22], but our interpretations would need to be re-evaluated if one or more of these assumptions is found to be inaccurate.

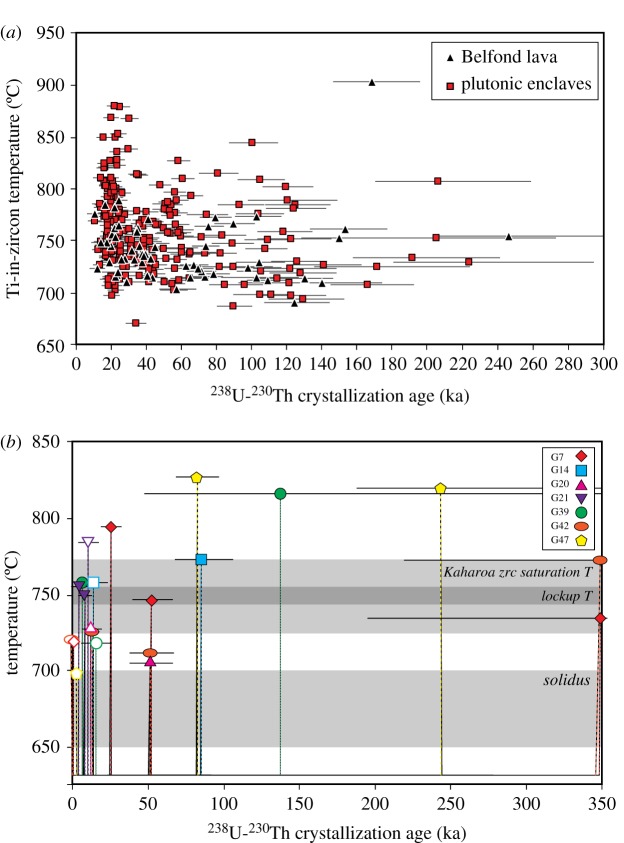
The warm storage interpretations are based on comparing U-Th or U-Pb ages of zircon with Ti-in-zircon temperatures of the same zones within zircon crystals. Owing to the slow diffusion of Ti in zircon, these represent crystallization temperatures for the sampled volume of zircon [68,69]. The argument for tens of thousands to hundreds of thousands of years [66] or even millions of years [67] of warm storage recorded in zircon is based on groups of zircon analyses from individual samples that yield high (greater than 750°C) crystallization temperatures which also have overlapping ages spanning long periods of time [66,67]. The presence of zircon crystallizing at high temperatures indicates that the region(s) of the magma reservoir supplying crystals to the eruptions studied included at least some melt at high temperature in order to allow crystallization. However, given the variations in crystallinity expected across a magma reservoir in the mush model—and the temperature variations implied by those variations—it is not clear how much of the reservoir needs to be at high temperature at a particular time of zircon crystallization. In fact, the zircon datasets presented in each of these studies also include many crystals that yield lower temperatures (less than 750°C) with ages that also overlap with those showing high-temperature crystallization (figure 4a). In addition, these datasets do not require that the presence of high temperature melt at any given location be continuous over the entire span of zircon crystallization ages. SIMS measurements of U-Th and U-Pb crystallization ages for young zircon are relatively imprecise compared to TIMS measurements or to U-Pb on older zircon, which can obscure the details of the crystallization history and therefore thermal history. Modelling of the effect of uncertainty in zircon ages on a measured age versus Ti-in-zircon temperature distribution shows that, given typical analytical uncertainties for SIMS data, it is not possible to resolve multiple short-duration peaks in temperature from an isothermal or monotonic cooling temperature history [70]. Therefore, although the combination of zircon crystallization ages and Ti-in-zircon crystallization temperatures is permissive of protracted high-temperature storage in a magma reservoir, it does not require it. In the one case where zircon age data, Ti-in-zircon crystallization temperatures, and Li diffusion durations all have been measured in the same crystals, the diffusion data preclude a high-temperature near-isothermal history [22] (figure 4b). Other systems could yield different patterns of data, but this case suggests that crystallization temperatures may systematically overestimate average temperatures of storage. Additional work is needed in order to test whether this result is generally applicable to silicic systems.

Figure 4.

Comparison of crystallization ages and Ti-in-zircon temperatures with thermal history derived from also considering diffusion durations. (a) Ti-in-zircon crystallization temperatures versus ²³⁸U-²³⁰Th ages for zircon crystals from the Soufriere Volcanic Center (SVC), Lesser Antilles (redrafted using data in [66]). Dataset includes zircon rim analyses from dacitic eruptions (Belfond lava; black triangles) and cogenetic enclaves of plutonic material (red squares). Error bars shown are 1-sigma. See [66] for additional details. (b) Time–temperature history recorded in the zircon crystals from the Kaharoa eruption, New Zealand, modified from [22]. Each crystal is represented by a different symbol (open symbols represent surface analyses) and all measured ²³⁸U-²³⁰Th ages are plotted with their 1-sigma uncertainties at the corresponding Ti-in-zircon temperature. Points yielding ²³⁸U-²³⁰Th activity ratios within error of secular equilibrium are plotted at 350 ka. The widths of the peaks in temperature correspond to the diffusion durations calculated at 700°C and the temperature between peaks is arbitrarily set below the lowest recorded crystallization temperature. For reference, the grey shaded regions indicate the range of zircon saturation temperatures for the Kaharoa eruption, the estimated rheological lock-up temperature, and the solidus temperature. Note that the zircon saturation temperature is calculated based on the bulk magma composition, and given the diversity of ages and trace-element compositions of zircon in the Kaharoa samples, it is likely that some zircon crystallized in local environments with different zircon saturation conditions. See [22] for additional details.

Other lines of evidence support a model where crystals sample colder regions of the magma reservoir even in silicic systems. For example, Szymanowski et al. [71] combined high-precision U-Pb dating of zircon and titanite with Ti-in-zircon and Zr-in-titanite crystallization thermometry to examine thermal conditions in the Kneeling Nun Tuff (New Mexico, USA). They observed U-Pb dates spanning ca 600 kyr prior to eruption in both phases, but whereas zircon recorded a large range of crystallization temperatures (approx. 850–650°C, corresponding to zircon saturation temperatures to solidus temperatures), titanite records a very restricted temperature range (indistinguishable temperatures at 726 ± 32°C) at near-solidus but super-solidus conditions. They interpret this dataset—and similar data from other large silicic eruptions—to reflect a thermally heterogeneous reservoir, where the core (i.e. eruption-producing) part of the reservoir is maintained at near-solidus conditions and mobilized rapidly prior to eruptions, dissolving low-temperature titanite rims or crystals but preserving the crystals formed at the upper end of titanite crystallization temperatures. Finally, these inferences based on accessory phases are consistent with interpretations of cold storage based on major phases [19]. For example, the interpretation of dominantly cold storage in dacitic systems discussed above is based on crystallization ages and diffusion durations for plagioclase. In addition, a recent ⁴⁰Ar/³⁹Ar study using incremental heating of individual sanidine crystals from the Bishop Tuff [72] showed that while the majority of dates were consistent with a single eruption age (as expected for Ar/Ar dating), there was a tail of older dates that was not attributable to excess Ar. Andersen et al. [72] interpreted this older population to represent crystals stored at low temperatures (less than 475°C) at the margins of the reservoir, mobilized from this subsolidus region and incorporated into the erupted magma body within a few centuries of eruption. Overall, the data from crystal cargo in dacitic to rhyolitic rocks suggests remarkably similar and relatively cold conditions of storage prior to eruptions across intermediate to rhyolitic magma systems.

One note of caution is that the mixing-to-eruption time scales for mafic systems discussed above tend to be shorter than the centuries to millennia of reactivation of near-solidus bodies to produce intermediate or silicic eruptions, and it is possible that mafic magma reservoir systems are on average hotter than more evolved systems. Although mixing-to-eruption times are typically short, it is still possible that the crystals in mafic magmas include cores that had protracted storage in lower-temperature regions of the reservoir. In fact, some crystals in mafic systems do show evidence for derivation from a crystal mush, implying relatively cold storage and rapid remobilization (e.g. [73–76]), or perhaps endogenous development of a crystal mush within a sill over a period of months prior to remobilization [48]. More data are needed in order to test whether mush storage (whether protracted or brief) is generally the case for crystals in mafic systems, and if so to better understand the implications for the long-term thermal conditions in these reservoirs. Whatever the eventual result of a comprehensive study of the thermal conditions of magma storage across magma compositions, it is clear that combining different types of data (e.g. crystallization ages with crystallization temperatures and with constraints on thermal histories from diffusion durations) can be a powerful tool to understand the thermal history of the parts of the reservoir sampled by the crystal cargo, and studies of this nature represent an exciting avenue for future research.

3. Implications for magma storage and remobilization

The main themes resulting from the observations of crystal ages and diffusion durations discussed above are: (i) Crystals brought to the surface by volcanic eruptions preserve diverse crystallization ages, ranging from near-eruption-age to tens of thousands or hundreds of thousands of years, indicating that any single eruption (or even a single hand sample or crystal) samples parts of the magma reservoir that were active over long periods of time. (ii) Crystallization temperatures recorded in a given hand sample (especially from zircon) are also diverse, even when crystallization ages overlap within uncertainties, indicating that the eruption also sampled regions with different thermal histories. Comparison of diffusion durations with crystallization ages and crystallization temperatures (in the one case where all of these data are available for zircon) indicates that while the crystals may have formed at relatively high temperatures, they were stored for most of their history at near- or sub-solidus conditions. (iii) Mobilization of this near-solidus material into the erupted body happens rapidly (within years to decades of eruption, or centuries to millennia at most). (iv) The latest stages of mixing to eruption happen at higher temperatures than the storage temperatures, over time scales that vary from days to centuries, and the duration of post-mixing storage may be related to the erupted composition.

The picture of magma reservoirs that emerges from these data is entirely consistent with the mush model of magma storage, but these data also add a number of useful constraints on the dynamics of these systems. For example, the diversity of crystallization ages and crystallization temperatures within a single eruption (even small eruptions), especially when coupled with observations of compositional heterogeneity within crystal populations (e.g. [27,74,75,77–80]), requires first, that the reservoir overall is diverse in composition at any given time in one location and also over time at a particular location, and, second, that there is a process operating within the reservoir that gathers crystals of diverse origins and ages into localized areas prior to eruptions. Such gathering and mixing could be due to injections of new magma into the system, as has been shown to be effective at mixing crystals in numerical simulations of mafic systems [56,81,82], or to other processes not yet modelled quantitatively.

These data also provide information about the thermal state of magma reservoirs over time. Although it is difficult either from crystallization age-crystallization temperature records or from crystallization ages coupled with diffusion durations to resolve the details of a magma system's thermal history, some thermal histories can be ruled out [19,70]. In particular, for the systems studied to date, protracted (more than a few decades to millennia) storage of crystals at temperatures above approximately 750°C are not consistent with preservation of the trace-element disequilibria between zones within crystals [19,22,70]. This implies that liquid-dominated bodies are transient within magma systems, rather than being maintained for hundreds of thousands of years. One caveat to this argument is that the eruptions studied with this combination of crystal age and diffusion data to date are relatively small-volume and larger bodies may require longer times to generate. However, some studies of diffusion durations alone for crystals from larger eruptions do seem to show relatively short (centuries) assembly times [27,45] which would suggest that even erupted magma bodies on the order of 100s of km³ can be assembled rapidly and are therefore transient features within the shallow reservoir system. The short durations of high-temperature crystal residence also require rapid heating and cooling of the regions where the crystals were stored, including the final mobilization of crystals from near-solidus bodies into the erupted magma [19,22]. This places limits on the size of individual injections and also on the mechanisms of mobilization of crystals from near-solidus bodies.

Thermal models of magma injection into the crust can provide constraints on the magma flux required to generate and sustain magma reservoirs in the crust (and the fraction of melt present within them), and the time scale over which they can be produced and sustained. Numerical models can produce and maintain mush bodies in the crust containing some volume of melt-dominated magma if magma injection rates are over 10⁻⁴ km³ yr⁻¹ to 10⁻² km³ yr⁻¹ [8,83–85]. These models explore the conditions and time scales necessary to produce a mushy magma reservoir in the crust, which likely correspond to the tens to hundreds of thousands of years of activity and crystallization recorded in crystal age distributions. However, such models do not capture the short-duration events that segregate melts, produce mixing events, and produce eruptions (e.g. [86]), and the models average temperatures over larger length scales than would be sampled by growth of crystals.

Other models focus on the mechanisms of mobilization of a mush or of extracting melts from a mush. Processes such as hindered settling or compaction would produce large volumes of crystal-poor melts on time scales of tens of thousands to hundreds of thousands of years (see discussion in [3]), similar to the overall active duration of shallow magma reservoirs, but not rapid enough to be consistent with decades to centuries for remobilization indicated by diffusion data. Simple conductive heating from below to re-melt a crystal mush to the point where it would become mobile would be similarly slow or slower (e.g. [87]) and would also require prohibitively large volumes of underlying magma to supply heat [88]. More recent explorations of melt extraction or mobilization have focused on mechanisms such as gas sparging (transport of volatiles released from underlying magmas through a mush zone, resulting in heating and remelting of the mush to produce crystal-rich magmas), which could potentially produce volumes of less than 1 km³ within weeks, but would require hundreds of thousands of years to produce large volumes (greater than 1000 km³) [87]. A thermomechanical model of mush reactivation, where partial melting causes internal overpressure in the mush, leading to efficient unlocking of the network [89,90] could remobilize thicknesses of mush sufficient to generate approximately 5 km³ of magma in about 0.5 year and thicker mushes (generating greater than 1000 km³ of magma) within a few hundred years. Note that these are minimum remobilization times, which could significantly underestimate the time scales [90]. ‘Unzipping’ of a mush [91] could occur when partial melting of a mush from below creates a buoyant, mobile boundary layer at the base of the mush, triggering overturn on the time scale of months to decades, which would lead to mobilization on time scales similar to the diffusion time scales.

Therefore, a number of models predict mobilization times that are broadly consistent with previous estimates of magma storage times based on diffusion. However, three considerations suggest that more work is needed in order to fully explain the mobilization of magmas in shallow systems. First, time scales of erupted magma assembly for large silicic bodies are at the short end of the mobilization times discussed above for numerical modelling of large bodies, and taking the Li diffusion in zircon results [22] at face value would suggest that heating prior to at least smaller silicic eruptions must take place over years to a few decades at most. For mafic systems, many diffusion results seem to indicate days to weeks for mobilization times. Second, plutonic rocks typically have very low volatile contents, making it potentially very difficult to re-melt sub-solidus material in a magma reservoir because the melting temperatures of dry plutonic rocks are higher than for volatile-bearing rocks (e.g. [92]). And finally, all of these models make simplifications that parametrize the grain-scale physics based on empirical observations, which may not capture the full range of physical behaviour in mush systems (e.g. [93]).

Models which look at the physics of crystal–liquid–volatile interactions at the grain scale in mushes are producing results which can be counterintuitive, but which may be critical for resolving some of these open questions [56,81,82,93–95]. For example, Parmigiani et al. [93] found that gas sparging was likely to be less efficient than previously modelled because of a feedback where partial melting can break up volatile pathways and reduce the efficiency of migration of exsolved volatiles despite increasing the intrinsic permeability of the mush. They also found that bubbles migrate more efficiently through a mush than a crystal-poor melt, which could lead to accumulation of volatiles in a melt-rich body overlying a mush zone [94]. In addition, bubbles can become trapped in a mush in a cooling system, leading to volatile-saturated near-solidus or subsolidus bodies, which could be more easily remelted than had been previously assumed for dry subsolidus bodies [92,94]. Other recent models examining disaggregation of mafic mush systems show that mixing of diverse crystals can be very efficient and rapid [56,81,82]. These studies also suggest that granular materials can exhibit counterintuitive behaviour with respect to rheological lock-up. These studies suggest that the approximately 50% threshold for rheological lockup may be only a crude approximation, and mushes can both remain locked at lower crystal fraction and can be mobile at higher crystal fraction [56]. As these examples show, this new generation of numerical models offers the potential for new conceptual and physical models to compare with the observational constraints on volumes and time scales necessary to produce erupted magma bodies, especially if coupled to models that examine thermal conditions and processes at length scales relevant to the entire reservoir (e.g. [95]).

4. Concluding remarks

Recent advances in micro-analytical techniques and innovations in combining different data types applied to volcanic crystals have resulted in a wealth of new information that is rapidly changing our views of magma reservoir processes. In particular, combinations of crystallization age data, crystallization temperature data, and diffusion durations from crystal populations in volcanic rocks provide important constraints on magma storage and mobilization in upper-crustal reservoirs. These studies mostly suggest that long-term storage conditions recorded in crystals over crystallization histories spanning tens of thousands to hundreds of thousands of years are dominantly cold, with temperatures corresponding to crystal-dominated near-solidus or even sub-solidus conditions (although this view is not universally accepted). In contrast, melt extraction and mobilization of crystal mush to produce the melt-dominated magmas that erupt is rapid—weeks to centuries, or a few millennia at most—requiring very rapid heating and mobilization of the material erupted.

Coupling these constraints on the thermal conditions within magma reservoirs with physical models is one of the foremost challenges and opportunities within the field today. For example, thermal histories determined by crystallization ages coupled with diffusion durations constrain the total time spent at high temperatures, including cooling from initial crystallization temperatures, storage throughout a crystal's lifetime, and any heating during the processes of final assembly of the erupted magma body. In the case of the zircon data in particular, this suggests that individual injections that lead to zircon crystallization are small (so that they can cool rapidly from temperatures of zircon crystallization), storage is dominantly sub-solidus, and that remobilization into the erupted magma body is rapid [22]. These provide concrete constraints on numerical simulations of magma mobilization, which then can provide information on the range of types of mechanisms and parameters that are able to reproduce the observational data.

One important consideration moving forward is that the data discussed here are all derived from crystal records, which would naturally be biased towards the colder (and therefore more crystalline) parts of a magma reservoir. Cold storage of crystals does not preclude the presence of liquid-dominated bodies within the broader magma reservoir, as long as those bodies are not fully coupled thermally with the region where the crystals are stored. This, together with abundant evidence that many—or even most—crystals in volcanic rocks are not in chemical equilibrium with their host liquid (e.g. [23]), suggests that the silicate liquid and crystalline components of erupted magmas may have different origins and different transport and storage histories. In the context of a crustal magma system where multiple reservoirs exist at different depths (e.g. [7,8]), one possibility is that crystal-poor liquids supplied from below (perhaps through extraction from a deeper crystal mush) interact with an upper-crustal mush, remobilizing and incorporating the crystals that carry the records discussed here. This would significantly reduce the thermal and mass-balance requirements for mobilization, because it restricts the volume of near- or sub-solidus material to the volume of crystals in the erupted magma, rather than the entire erupted volume of magma. The combination of these new observational constraints on thermal conditions of storage and time scales of mobilization with a new generation of physical and numerical models which examine processes of heat and mass transfer in crystal mush at the grain scale, offers the potential to make rapid progress in understanding the dynamics of magma reservoirs and the eruptions that they produce.

Data accessibility

No new data were presented in this manuscript.

Competing interests

The author has no financial or non-financial competing interests.

Funding

The development and synthesis of the ideas presented here were supported in part by US NSF awards EAR-0738749, EAR-0838389, EAR-1144945, EAR-1250305 and EAR-1426858 to K.M.C.