The lateral growth and coalesence of magma systems

Abstract

Thermal and mechanical models of magma reservoir growth need to be reconciled with deformation patterns and structural relationships observed at active magma systems. Geophysical observations provide a series of short time-scale snap-shots (10⁰–10² years) of the long-term growth of magmatic bodies (10³–10⁶ years). In this paper, we first review evidence for the growth of magmatic systems along structural features and the associated deformation patterns. We then define three distinct growth stages, (1) aligned melt pockets, (2) coalesced reservoirs, (3) highly evolved systems, which can be distinguished using short-term surface observations. We use two-dimensional thermal models to provide first-order constraints on the time scales and conditions associated with coalescence of individual magma bodies into large-scale reservoirs. We find that closely spaced intrusions (less than 1 km apart) can develop combined viscoelastic shells over time scales of 10s kyr and form laterally extensive mush systems over time scales of 10–100 kyr. The highest temperatures and melt fractions occur during a period of thermal relaxation after melt injection has ceased, suggesting that caldera-forming eruptions may preferentially occur long after the main intrusive activity. The coalescence of eruptible melt-rich chambers only occurs for the highest melt supply rates and deepest systems. Thus, these models indicate that, in most cases, conductive heat transfer alone is not sufficient for a full coalescence of magma chambers and that other processes involving mechanical ruptures and mush mobilization are necessary; individual melt lenses can remain isolated for long periods within growing mush systems, and will only mix during eruption or other catastrophic events. The long-term history of the magmatic system is therefore critical in determining rheological structure and hence short-term behaviour. This framework for the development of magmatic systems in the continental crust provides a mechanical basis for the interpretation of unrest at the world's largest volcanoes.

This article is part of the Theo Murphy meeting issue ‘Magma reservoir architecture and dynamics'.

1. Introduction

(a). Long-term growth of magma bodies

Melt is generated in the lower crust or upper mantle, and transported through the mid-crust along structurally controlled pathways, typically ductile shear zones [1,2]. Magma which rises in discrete, short-lived pulses, stalls at rheological or lithological boundaries in the upper crust [3,4], where it cools and crystallizes forming composite bodies (after [5–7]). In this paper, we adopt the terminology of Bachmann & Bergantz [8] and use the term ‘magma reservoir' to describe a region of partially molten rock with varying proportions of crystal, melt and gas. Localized pockets in which the melt fraction is high enough (greater than 50%) to suspend crystals can be thought of as ‘magma chambers', which are sufficiently mobile to erupt. At low melt fractions (less than 50%), the crystals are in contact forming a rigid or semi-rigid framework with interstitial melt and are referred to as ‘mushes'. The orders of magnitude difference in viscosity between these components creates inherent instabilities: melt segregation likely occurs over time scales of 10³–10⁵ years, whereas instability, re-organization and amalgamation of the high-melt, low-viscosity components occur rapidly in months or years [9–12]. High temperatures within the reservoir alter the rheological and mineralogical properties of the surrounding rock, forming a viscoelastic contact aureole and in some cases partial melting.

Having undergone multiple phases of deformation, the continental crust is typically heterogeneous, with faults and lithological boundaries forming sharp rheological contrasts in a range of orientations. Plutons, which are the fully crystalline remnants of magma reservoirs, are often located on major pre-existing faults, and elongated along them [13,14]. Although a causative relationship is typically inferred, the nature of this relationship is rarely discussed explicitly (e.g. [15,16]). Some studies assume that motion on the fault deforms the weak, magma reservoir (e.g. Donegal [13]), while others show that large batholiths are composite bodies with the individual plutons sequentially emplaced along a preferential alignment (e.g. Adamello [17]; Ardnamurchan [18]). A good illustration of this contrast is given by the Mono Creek Pluton (MCP) and Tuolumne Intrusive Suite (TIS) of the Sierra Nevada batholith (figure 1): the MCP is texturally homogeneous and the internal fabrics are consistent with syn-magmatic NNW-SSE shear, while the TIS consists of a series of at least four compositionally distinct, nested plutons each of which is internally homogeneous and elongated NNW-SSE. These hypotheses are not mutually exclusive but raise an interesting question regarding the nature of the tectonic control: do faults simply act as pathways for magma ascent, or is active deformation important?

Figure 1.

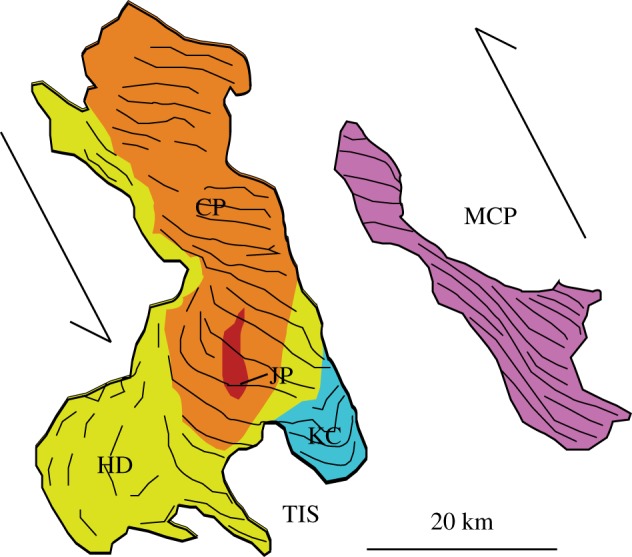
Contrasting internal structure of two NNW-SSE elongated plutons within the Sierra Nevada Batholith. The Tuolumne Intrusive Suite (TIS) is a nested set of elongated plutons (JP, HD, CP and KC), while the Mono Creek Pluton (MCP) is sheared, but internally homogeneous (adapted from [19]). (Online version in colour.)

Plutons are typically longer than they are thick, with small plutons growing laterally and then inflating vertically [20–22]. In plan view, small plutons tend to be circular and form quickly, while larger ones are more elongated and grow over longer time periods [19]. De Saint Blanquat et al. [19] interpret this in the context of active faulting: individual injection events occur sufficiently rapidly that tectonic strain is negligible, whereas the assembly of large plutonic bodies occurs over time scales such that regional tectonic stress fields have the time to deform the growing plutonic body. However, the same observation could be explained if plutonic bodies grow initially by the formation of small magma chambers along a fault, which coalesce into an elongated reservoir that only grows vertically once the surrounding crust is sufficiently hot for ductile deformation. This concept is consistent with the model of Karlstrom et al. [22], which shows that the distribution of size preserved intrusions can be approximated by a reverse-energy cascade model of the merging of small intrusions until irreversible deformation and solidification occur.

The orientation of calderas can be used as a proxy for the shape of the magma reservoir, and the orientation of elliptical calderas can therefore be used to distinguish between the influence of active (e.g. [23]) and pre-existing structures (e.g. [24]). In the East African Rift, for example, many calderas are aligned with the major, pre-existing, cross-cutting faults rather than the current stress field [25,26], suggesting that in this case at least, passive pathways are as important as active strain.

(b). Geophysical evidence

Pressure changes within magma reservoirs can be inferred from surface deformation. Over 220 volcanoes are known to have deformed in the last few decades and while some examples can be attributed to hydrothermal or post-eruption activity, yet more have been linked to magmatic processes [27]. To the first order, the classic ‘volcano deformation cycle' pattern of radially symmetric co-eruptive subsidence and inter-eruptive uplift has been observed at a number of volcanoes with different characteristic lengthscales and time scales [27]. Yet, a recent global review showed that while deformation has a strong statistical link to eruption, only half of all volcanoes that exhibited deformation erupted [28].

High-resolution maps of volcano deformation reveal complexity that was not apparent during the era when volcano geodesy was based on infrequent point measurements (figure 2). The simplest model, that of a point source in an elastic half-space [30], satisfies the observations in a surprisingly large number of cases, but multiple sources, offsets from the vent or time-varying pressure histories are often required (e.g. [31–34]. In other cases, the deformation is asymmetrical and requires complex source geometries, such as ellipsoidal magma bodies or elongated sills (e.g. [35,36]). These observations are consistent with the concept of a magma reservoir composed of a crystalline mush containing multiple lenses of high melt-fraction magma. The time is right to consider the conditions of magma storage, particularly the thermo-mechanical history of the reservoir, when interpreting geodetic signals.

Figure 2.

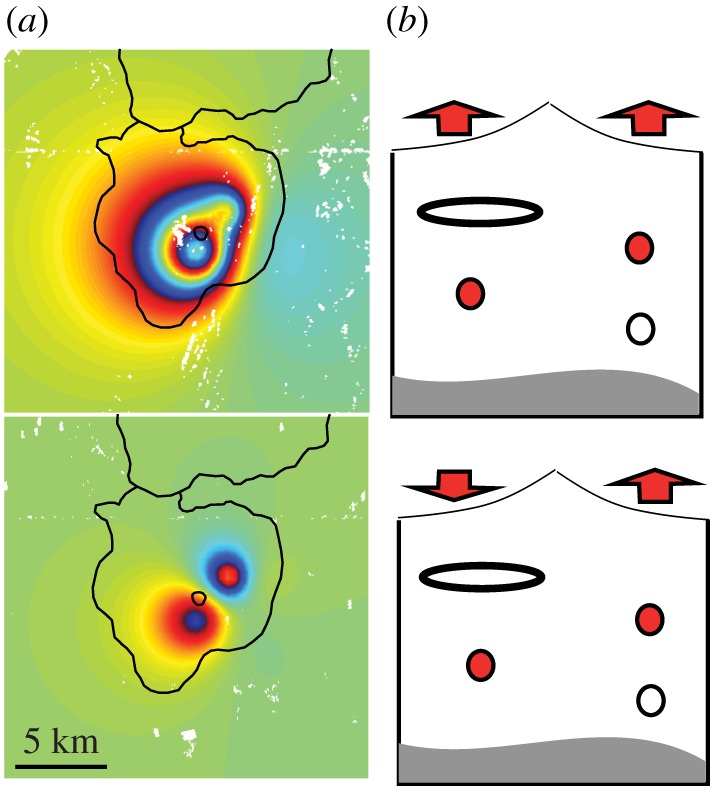
(a) Modelled surface deformation at Paka Volcano. Kenya showing multiple sources of pressurization, consistent with multiple aligned magma chambers. Each coloured fringe corresponds to 2.8 cm of deformation in the satellite line of sight. Circle shows the vent and the black line is the extent of the edifice (with Silali to the north). (b) Schematic E-W cross-section showing approximate location and depth of modelled sources. After [29]. (Online version in colour.)

Large regions (tens of km³) of partial melt (greater than 10%) have been identified at depths of 5–20 km using geophysical methods including seismology, magnetotellurics and gravity (e.g. [37,38]) and references therein). Many of these are asymmetrical with respect to the surface volcanic features, or even offset (e.g. [39–41]). Several mechanisms are consistent with the observation that zones of partial melt are aligned with fault systems (e.g. [42]): (i) the fault zone acts as a pathway for magma ascent, (ii) the magma is accommodated by motion on the fault zone forming a local patch of extension, and (iii) the shape results from the shearing of a weak magma body.

(c). Surface manifestations

Magma, hydrothermal fluids and volcanic gases have low density and viscosity and it is likely that they rise almost vertically, exploiting the most convenient pathway with minimum lateral transport (except in a few cases where there is an impermeable cap near the surface). Thus, the patterns of vents, fumaroles and degassing measured at the surface reflect the lateral extent of the underlying magmatic reservoir [43].

Radial and tangential patterns in the distribution of cones and vents [44,45] or in subsurface intrusions [46–48] can be attributed to the local stress field, which is a superposition of stresses from regional tectonics, topographic load and magma pressure (e.g. [45,49,50]). Caldera systems are typically low relief, so the confining stress caused by the topographic load is small, but cycles of uplift and subsidence are commonly observed (e.g. [51,52]) associated with a radially symmetric but temporally variable stress field [53].

However, in many cases, alignments of cones and vents are associated with shallow faults, which can be attributed to the active regional stress regime (e.g. [54]), inherited basement structures (e.g. [55]) or caldera formation (e.g. [56,57]). Distinction between active and pre-existing faults is complicated by the tendency for older faults to be reactivated by active stress fields (e.g. [58,59]).

(d). Outline

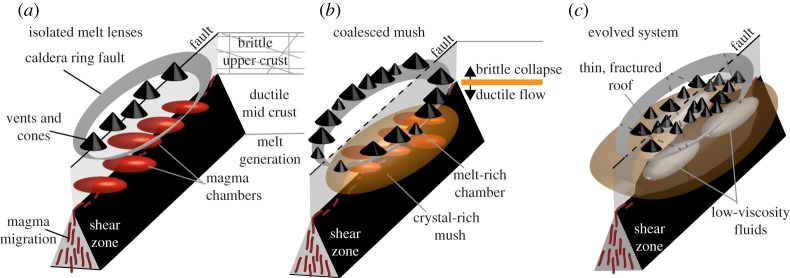
Based on the previous review, we propose a conceptual model of magma reservoir development based on the principle that magma reservoirs grow through short, discrete injections, starting with small, transient magma chambers aligned with faults, which coalesce over time to produce an elongate region of partial melt. According to this conceptual model, the thermal evolution of the reservoir can be subdivided into three distinct phases, each associated with a different reservoir size, shape, gas content and rheology (figure 3). The difference in lateral extent of the magma reservoir mean fluids in the crust above the reservoir would exploit different pathways, causing observable differences in the distribution of volcanic vents, fumaroles and degassing. We identify and discuss modern analogues for each of these stages.

Figure 3.

Conceptual model of the growth of magma reservoirs from (a) isolated melt lenses aligned along a fault to (b) mature reservoirs whose surface characteristics are controlled by a caldera ring fault and finally (c) highly evolved mush systems which undergo frequent internal reorganization. (Online version in colour.)

We then consider the response of the magma system to a fresh input of magma, and conclude that the expected patterns of surface deformation would be distinct. Thus we show that (a) the patterns of surface deformation can be used to infer some aspects of the thermal history of the reservoir and (b) the thermal history of the reservoir must be considered when interpreting patterns of surface deformation. Finally, we develop simple thermal models to investigate the time scales over which closely spaced magma bodies would coalesce, with particular reference to (a) the viscoelastic aureole and (b) the region of partial melt. These thermal models do not involve mechanical processes and thus offer upper bounds on the time scales involved.

2. Conceptual model

(a). Stage 1: aligned melt lenses

Discrete batches of magma rise upward along mid-crustal shear zones forming a line of small magma chambers at rheological or lithological boundaries (figure 3a). Each magma chamber produces individual deformation patterns, which may overlap in space and time. The magmatic and hydrothermal systems are localized above the shear zone, such that magmatic and hydrothermal fluids exploit the shallow extension of the fault as they rise to the surface. Fumaroles and volcanic vents, many of them monogenetic, are thus aligned along the dominant structure.

Examples include Puyehue Cordon-Caulle, Chile, which lies at the intersection of the major trench-parallel strike-slip system, the Liquiñe-Ofqui Fault Zone, (LOFZ) and an old basement structure [55]. Deformation associated with the 2011 eruption indicates the involvement of multiple small magma bodies aligned along this inherited structure [33,60]. Another example, Corbetti, Ethiopia, lies at the intersection of the Main Ethiopian Rift with the Goba–Bonga lineament, which has had a major influence on the tectonic evolution of the rift system [61,62]. Evidence for the influence of the cross-rift structure on the magmatic system comes from a number of directions and a range of time scales: patterns of surface deformation are semicircular, bounded by the fault; seismicity is aligned along the fault, and the distribution of volcanic vents is statistically closer to the line than a random distribution [26]. In both these cases, there is also evidence that a larger magma reservoir is active during different time periods [63–65], suggesting a transition in behaviour towards stage 2.

(b). Stage 2: mature reservoir

The individual chambers coalesce into a large, elongated reservoir containing many small chambers (figure 3b). The large magmatic and hydrothermal systems extend beneath the caldera ring fault, which is exploited as a pathway for rising fluids. Coalescence can take place through a number of mechanisms depending on depth and geometry, for example the brittle collapse of isolated blocks of wall-rock or ductile flow. The deformation pattern is associated with the viscoelastic behaviour of the reservoir, which may be elongated in shape. The behaviour of the individual chambers may be reflected in the time-dependent pressure history. The magmatic and hydrothermal systems are now laterally extensive and the dominant pathway for magmatic and hydrothermal fluids is the caldera ring fault. The result is a ring-shaped edifice, with volcanic vents and fumaroles distributed around the caldera rim.

Examples include Laguna del Maule, Chile, Long Valley, USA, and Aluto, Ethiopia, which demonstrate that the presence of a ring fault controls the surface expression of magmatic systems regardless of their tectonic setting. At Laguna del Maule, postglacial silicic eruptions form a concentric ring around a central lake and in recent years there has been a prolonged pulse of rapid uplift [57,66]. At Long Valley, recent eruptions are concentrated along the caldera and regional fault systems [67] with seismicity along the southern caldera fault [68]. By contrast, multiyear inflation episodes in 1990–1995 and 2011–2014 were driven by a source in the centre of the caldera [69]. At Aluto, Ethiopia, the caldera ring fault acts as the major pathway for degassing, hydrothermal upwelling and magmatic fluids [56,70,71]. Aluto has been subsiding for many years, with occasional pulses of rapid uplift [72,73].

(c). Stage 3: evolved system

Eventually, the large reservoir reorganizes as low-viscosity fluid rise through the crystal-rich mush. Faults and fractures within the extended roof are reactivated and magmatic and hydrothermal fluids exploit these pathways forming volcanic vents and fumaroles distributed across the caldera floor (figure 3c). Owing to the large size of the reservoir and the ability of mush to reorganize internally, fresh magma input does not necessarily result in surface deformation. However, frequent, spatially complex deformation is caused by migration of fluid between sources and phase changes with the mush. Numerous cycles of deformation reactivate local and regional faults and fractures across the highly extended caldera floor. Fluids from the laterally extensive hydrothermal and magmatic systems rise along these pathways leaving volcanic vents and fumaroles distributed across the caldera floor.

The classic example is Yellowstone, USA, which is an evolved magmatic system with frequent deformation, active hydrothermal system and eruptions from vents distributed across the caldera floor [74–76]. Seismic tomography shows that the shallowest portion of the crustal magma reservoir is overlain by a highly fractured, fluid-filled region, suggesting that magmatic fluids (gas, hydrothermal fluids and melt) have migrated to shallower depths along existing fractures [77]. Campi Flegrei, Italy, is an interesting example as it appears to lie at the border between stages 2 and 3. It has experienced multiple pulses of uplift which are attributed to interactions between magmatic and hydrothermal system [78]. Older vents (12–8 kyr) are distributed along the marginal faults of the Neapolitan Yellow Tuff caldera, while younger vents (less than 5 kyr) occur on the caldera floor, which is dissected by reactivation of a number of regional fault systems [79].

(d). Associated deformation

Surface deformation and eruption occur in response to pressure changes within a magma reservoir; thus to understand deformation patterns and the types of precursory activity that might precede eruptions, it is first necessary to understand what causes and controls changes in pressure within the magma reservoir. In the first case, we consider the input of new magma into a spherical reservoir of volume V at a mass injection rate, dM/dt. This causes a viscoelastic response in the crust, plus changes in pressure dP/dt, temperature dT/dt and gas fraction dε_γ/dt [80–83]. Processes of crystallization and exsolution further alter the relative abundance of crystal, melt and gas phases, such that the mixture density evolves with time; for example, significant overpressure can also be generated by ‘second boiling' [84]. To fully describe the thermo-mechanical evolution of the reservoir requires coupled equations for the conservation of mass, water and energy, but here we illustrate the dominant controls on reservoir pressure using the conservation of mass following fresh magma input (following [83]),

$$\frac{\text{d}M}{\text{d}t}=\rho V\left[\frac{\mathrm{\Delta }P}{{\eta }_r}+\left(\frac{1}{{\beta }_m}+\frac{1}{{\beta }_r}\right)\frac{\text{d}P}{\text{d}t}+{\alpha }^{\ast }\frac{\text{d}T}{\text{d}t}+{\rho }^{\ast }\frac{\text{d}{\epsilon }_g}{\text{d}t}\right],$$ 2.1

where β_m and β_r are the compressibility of the magma and reservoir, respectively, the term ΔP/η_r describes the viscous growth in response to an overpressure, ΔP according to the effective viscosity. η_r and α* and ρ*ρ* are coefficients associated with thermal expansion and density defined fully in Degruyter & Huber [83].

For a given mass input, the rate of pressurization is determined by the reservoir size, V, gas content (through magma compressibility, β_c) and reservoir shape (through reservoir compressibility, β_r) [85]. Degruyter et al. [85] only consider spherical chambers, but we note that the compressibility of a spherical cavity is always less than that for an ellipsoidal cavity or penny-shaped crack [86] which leads to a mismatch between chamber and dyke volume for intrusions [87]. Thus we consider reservoir shape, β_r, as a third important control on magma pressurization. Finally, the influence of the viscoelastic shell of changing dimensions can be investigated using the analytical solution for a spherical chamber of radius R₁ within a viscoelastic shell radius of R₂, resulting from a pressure change P [80,88]. At t = 0, the deformation is equivalent to a chamber of radius R₁ embedded in a purely elastic medium and at t → ∞, the deformation pattern approaches that of a magma chamber of radius R₂, thus the effective radius of the chamber increases from R₁ to R₂ with time since the pressure change. Increasing the width of the shell with respect to the chamber radius (R₂/R₁) increases both the characteristic decay time and the magnitude of surface displacement [80,88]. The importance of the viscoelastic response likely depends on the balance between the characteristic viscoelastic time scale (e.g. Maxwell) and the magma flow time scale (e.g. Poiseuille) which are in turn controlled by magma and host rock viscosity and depth [89]. However, the Maxwell time scale for crust with a ‘typical' viscosity on the order of 10¹⁸ Pas is years to decades, compatible with the time scales for geodetically detected volcanic unrest.

This paradigm is most appropriate for describing small, transient reservoirs with a high melt fraction because the mechanisms of multiphase flow operating within an extensive mush, while still poorly understood, are likely to be significantly different. One hypothesis is that magma migrates upwards through a reorganization of melt and mush which does not intrinsically cause any significant volume change [90], and that surface deformation is driven solely by phase changes, particularly gas exsolution and crystallization [9]. However, melt segregation occurs over long time scales (10³–10⁵ years) and over the short time scales associated with unrest (10⁻¹–10¹ years) it is feasible to assume that only the melt and gas components are mobile and that the mush behaves as a viscoelastic medium surrounding the chamber.

Within this framework, the key parameters that determine the response to an intrusion are the size, shape, gas content and thermal aureole of a magma reservoir, which in turn depend on its long-term history of recharge and eruption. From this perspective, the earliest stage of our conceptual model can be further subdivided: (a) where isolated melt bodies intrude cold, elastic crust producing instantaneous deformation, but no viscoelastic response and (b) repeated intrusions have produced a viscoelastic aureole and hence long-term deformation, but these remain spatially independent (figure 4a,b). The second stage of the conceptual model corresponds to a situation where the melt bodies remain separated, but the magma reservoirs have coalesced producing a single long-term signal in response to transient pressure changes in one or more melt lens (figure 4c). Finally, if the melt supply is large enough to overcome the cooling between intrusions, the melt lenses themselves may coalesce to form a single, large magma chamber (figure 4d). Whether or not such a situation is physically plausible is an interesting question, and we will use thermal models to address it in the subsequent sections. However, it seems likely that such a situation would only arise in unusual conditions and not be stable for long periods.

Figure 4.

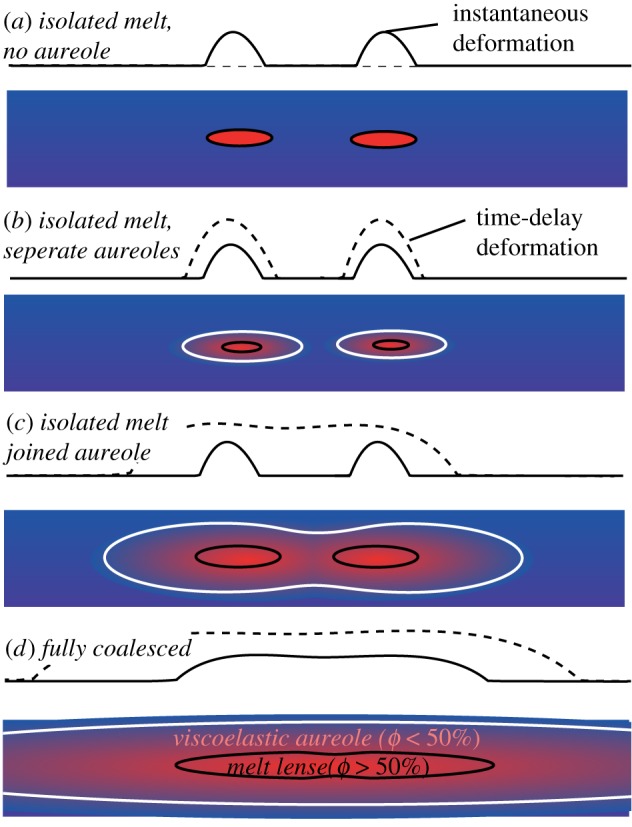
Conceptual model of the coalescence of magma bodies and their viscoelastic aureoles, and the influence on surface deformation. Solid lines show the instantaneous elastic deformation and the dashed lines show the integrated deformation over the longer term, including the viscoelastic response. Numerical models (figure 7) show that stage 4 is rarely achievable at realistic magma fluxes. (Online version in colour.)

3. Numerical models

To fully reproduce the conceptual model described above would require a complex simulation incorporating thermal and mechanical processes within a heterogeneous and fractured crust. Such simulations are beyond the scope of this paper, and would be challenging to interpret in terms of the key processes. Instead, we focus on the temperature field associated with closely spaced intrusions and investigate the time scales over which the viscoelastic aureole and magma reservoir (zone of partial melt) would coalesce through purely thermal processes. This approach implicitly assumes that magma chambers converge when the country rock between intrusions partially melts, and is likely an upper bound on the time scales of coalescence as mechanical links via viscous deformation or hydraulic conduits will be facilitated by increasing temperature and depth.

(a). Thermal modelling

To construct thermal models of the evolution of magma reservoirs, we adapt the finite-difference numerical scheme described by Annen [5]. Heat transfer is calculated by solving the time-dependent heat equation for conduction in a solid medium (3.1), including the latent heat (L) associated with phase changes determined from experimental temperature (T) - melt fraction (X) relationships; ρ, c_p, L, k are density, specific heat capacity, latent heat and thermal conductivity.

$$\rho c_p\frac{\mathrm{\partial }T}{\mathrm{\partial }t}+\rho L\frac{\mathrm{\partial }X}{\mathrm{\partial }t}=k{\mathrm{\nabla }}^{2}T.$$ 3.1

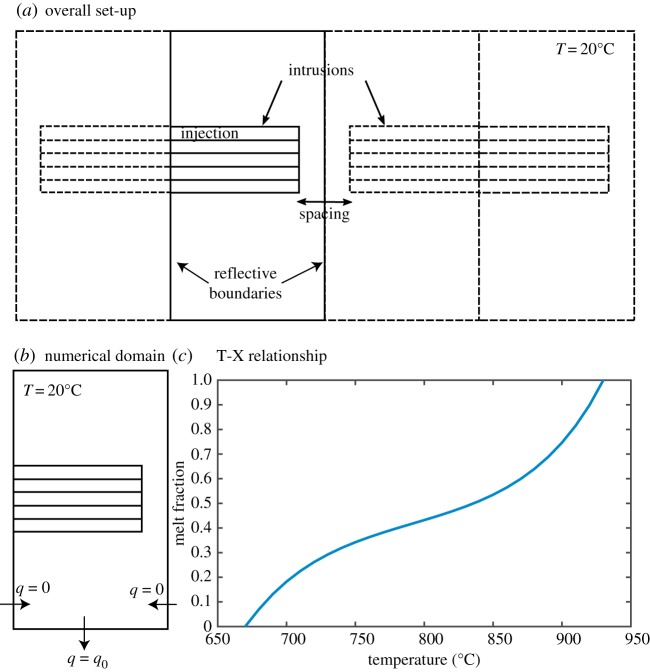
The intrusions, reservoir and surrounding country rock are discretized and the temperature and melt fraction of each cell tracked. The intrusions grow by the accretion of successive sill-like injections (figure 5). Rather than specifying an axisymmetric geometry and using a two-dimensional radial slice as in Annen [5], we use Cartesian coordinates with a reflective boundary condition (figure 5). This means the lateral heat flux out of the system is matched by an incoming flux to simulate the effect of a neighbouring magma body. The disadvantage of this geometry is that it assumes the body is infinitely long in the third dimension and thus does not capture the full three-dimensional shape of the reservoir and hence overestimates the rate of heat transport. Nonetheless, the computational advantages of using a simple geometry enable us to explore the parameter space more fully and investigate the first-order controls and time scales over which melt bodies and their surrounding aureoles coalesce.

Figure 5.

Set-up of the numerical simulations. The numerical domain is outlined with a solid line. The intrusions grow from roof downwards by stacking of sill-like injections. The presence of several intrusions is accounted by imposing a reflective boundary at the right border of the numerical domain. (b) The numerical domain showing boundary conditions. (c)The relationship between melt fractions and temperatures used in the numerical simulation from Caricchi & Blundy [91]. (Online version in colour.)

To explore the range of possible chamber shapes and conditions, it is necessary to explore the parameter space defined by (i) the time-averaged growth rate of the intrusion, (ii) the depth of the intrusions, (iii) the spacing between intrusions. The vertical growth rate of the intrusions is determined by the injection thicknesses and the frequency of injections. Cells with crystal fractions less than 0.5 are considered part of the chamber, and those with temperatures greater than the background geotherm as part of the viscoelastic shell. While ideal for characterising stage 1 of the conceptual model, care must be taken when applying this approach to the dynamics of mush systems, which dominate during stage 3, and operate to some extent, during stage 2.

In this preliminary study, we explore growth rates of 0.1, 0.05 and 0.025 m per year, corresponding, respectively, to injections of 200 m thick emplaced every 2000, 4000 and 8000 years over a total duration of 50 000, 100 000, 200 000 years. At lower growth rates, the magma solidifies between injections and no large magma chamber is generated [92]. Whether higher growth rates are realistic is a debated issue. Regardless of this issue, results tend to plateau at high growth rates and the system behaves as if the whole body of magma was instantaneously emplaced [93]. The exact injection thickness does not affect significantly the results, provided the growth rate is kept constant by adjusting the frequency. After the intrusion has reached a cumulated thickness of 5 km, the system is left to thermally relax during a period of time equivalent to the growth duration. We tested intrusions growing downwards from 5 to 10 km depth, 8 to 13 km depth and 12 to 17 km depth. The horizontal spacing between two intrusions is 0.5, 1 or 2 km. The parameters used in the simulation are reported in table 1. The same properties are used for the intrusion and the country rock. The relationship between melt fraction, X, and temperature, T, is from Caricchi & Blundy [91] and is shown in figure 5:

$$\begin{array}{c}X=1-(a+b.\ast \text{sin}h(c.\ast T^{\mathrm{\prime }}+d))\end{array}$$ 3.2

$$\begin{array}{c}\text{with}{T}^{\mathrm{\prime }}=\frac{T-T_s}{T_l-T_s},\end{array}$$ 3.3

T_s is the solidus at 670°C, T_l is the liquidus at 930°C, a = 5.8213 × 10⁻¹, b = 8.9078 × 10⁻², c = −4.8306 and d = 2.257.

The viscosity prior to melting is given by

$$\eta =A_d\exp \left(\frac{H}{RT}\right),$$ 3.4

A_d, the Dorn parameter, is 10⁹ Pa s [94,95], H, the activation energy of creep mechanism, is 135 000 J mol⁻¹ [96] and R is the perfect gas constant. The viscosity is only calculated in the absence of melt as equation (3.4) is not valid above solidus.

(b). Results

We calculated temperatures, viscosities and melt fractions mid-way between two intrusions, i.e. on the right reflective boundary of the numerical domain (figure 5). We expect the heat flux at this point to be twice that from an individual intrusion at a similar distance. We recorded the time needed for the first melt to appear at this boundary, corresponding to the coalescence of the mush.

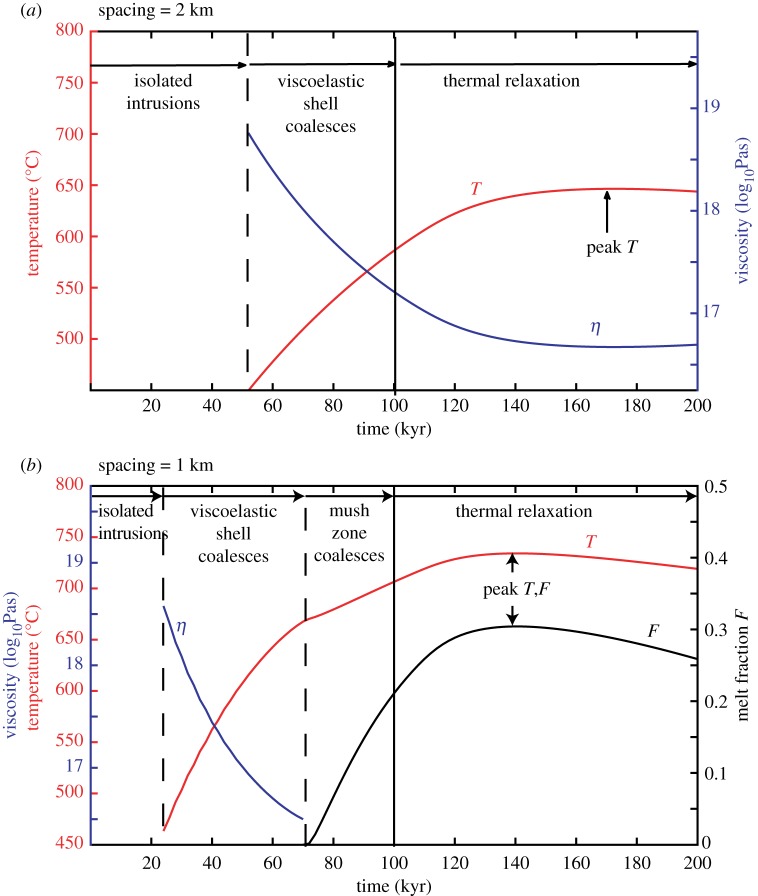
Figure 6 illustrates the evolution of the maximum temperatures and viscosities mid-way between intrusions, for example with spacings of 2 km (figure 6a) and 1 km (figure 6b). In both the cases shown, the intrusions grow downwards from 8 to 15 km depth over 100 kyr. For a spacing of 2 km, the temperature on the reflecting boundary starts to increase after approximately 50 kyr, but does not reach high enough temperatures for melt to form. The viscosity gradually drops from 10¹⁹ Pas, reaching 10¹⁷ Pas after 120 kyr forming a single viscoelastic shell surrounding two distinct mush systems (figure 6a). For a spacing of 1 km, the temperature starts to increase 18 kyr after the first magma injections, and the viscosity drops to 10¹⁶ Pas before the first melt appears on the reflective boundary 71 kyr after the first injection. The temperature and melt fraction peak at 140 kyr, equivalent to 40 kyr after the last injection. The maximum melt fraction is 0.3, which means although the mush system has coalesced, the eruptible melt lenses remain isolated (figure 6b).

Figure 6.

Example of simulation for intrusions growing from 8 to 13 km depth over 100 kyr showing the evolution of the peak temperature, viscosity and melt fraction mid-way between intrusions. The dashed lines mark the first change in temperature and the appearance of melt and the plain line the last magma injection. The viscosity computation is only valid before melt appearance. (a) For a spacing of 2 km in which no melt appears, and (b) for a spacing of 1 km, where melt appears on the boundary approximately 70 kyr after the start of injection. (Online version in colour.)

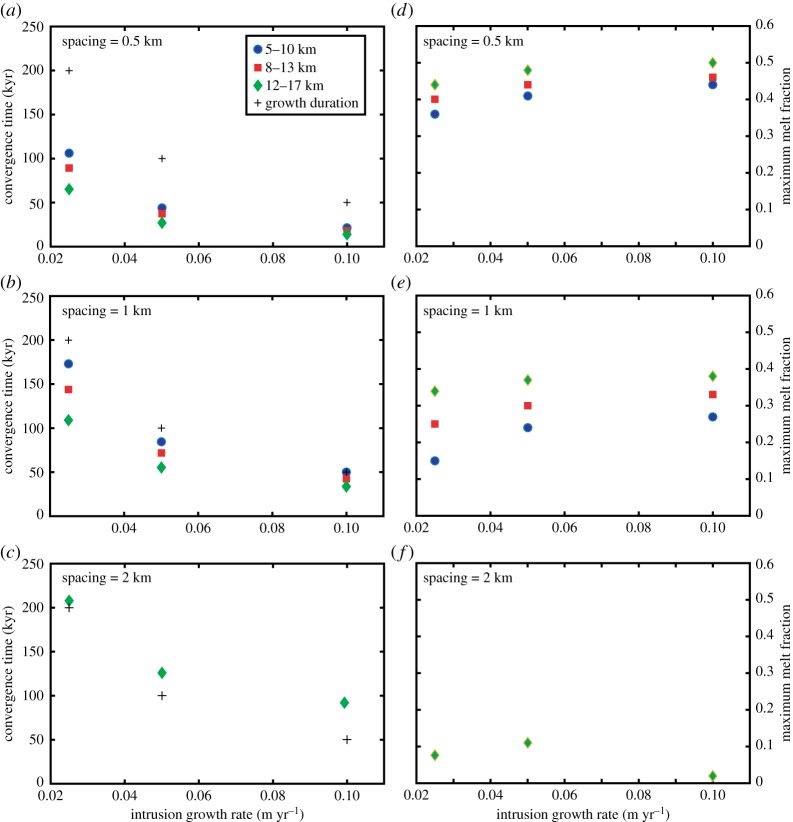
We then compare simulations for a range of magma fluxes, intrusion spacings and depth. As expected, the maximum temperature and melt fraction between the intrusions increases with depth and magma injection rates and hence the time taken for coalescence also decreases (figure 7). Furthermore, when the spacing between the two intrusions decreases, the maximum temperature and melt fraction increase and the time to mush coalescence decreases. This is primarily because the distance between the intrusions and the midway point has decreased. For the largest spacing tested (2 km), the mush zones only coalesce for the deepest experiment (12–17 km), and in this case, coalescence takes place as the system thermally relaxes, after the end of magma injections (figure 7).

Figure 7.

(a–c) Time elapsed between the first injection and mush convergence as a function of intrusion growth rate and emplacement depth. Spacing between intrusions is 0.5 km (a), 1 km (b) and 2 km (c). For an intrusion spacing of 2 km, convergence is obtained only for intrusions growing from 12 to 17 km. For spacing of 0.5 and 1 km, coalescence occurs during the intrusion growth, whereas for a spacing of 2 km, it occurs after the last magma injection. (d–f) Maximum melt fraction mid-way between intrusions as a function of intrusion growth rate and emplacement depth. Spacing between intrusions is 0.5 km (d), 1 km (e) and 2 km (f). For an intrusion spacing of 2 km, melt is present only for intrusions growing from 12 to 17 km. (Online version in colour.)

The convergence of magma chambers (melt fraction ≅0.5) is reached in only one of our simulations—at the closest spacing (0.5 km) and greatest depths (12–17 km) tested. Snapshots of this simulation are shown in figure 8. After 17 kyr, the viscoelastic aureoles have coalesced to produce a single mush system, but the melt bodies remain separated. After 84 kyr, the melt fraction between intrusion is 0.49 and the melt bodies are coalescing into one large magma chamber. Interestingly, this happens 34 kyr after the intrusion has ceased growing.

Figure 8.

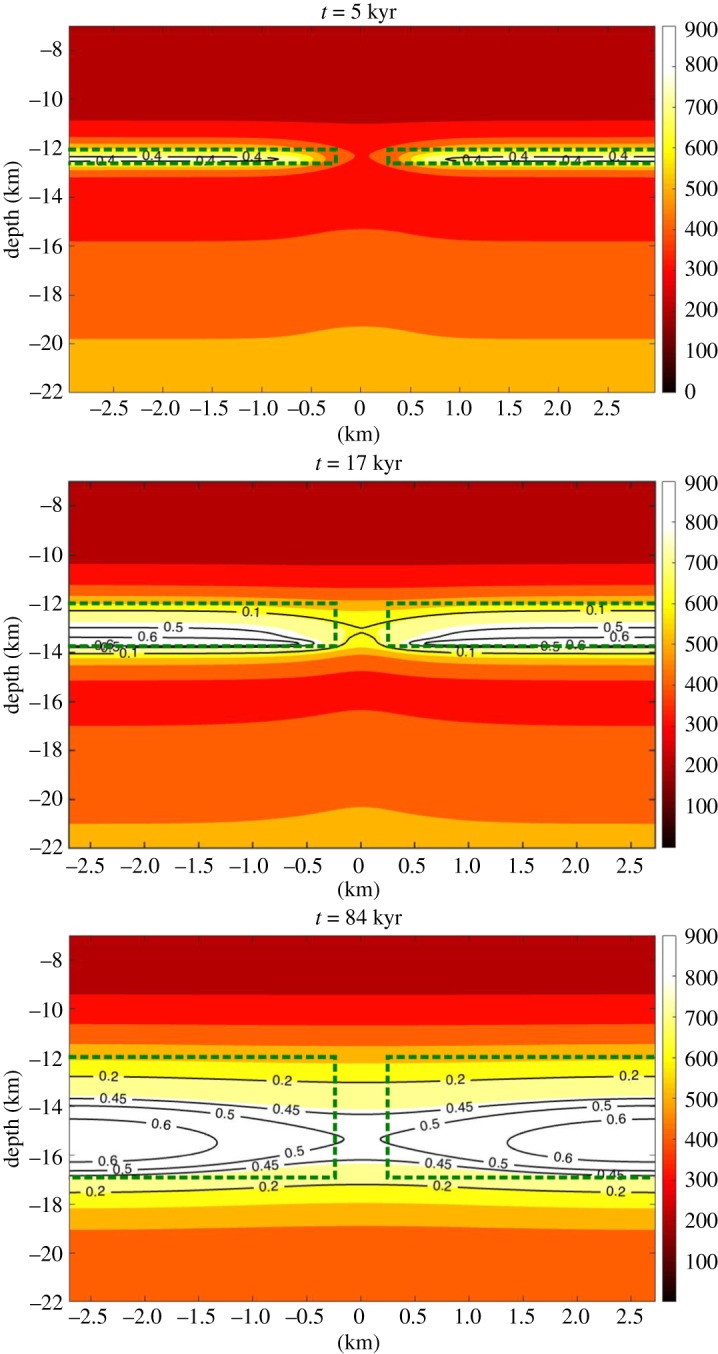
Snapshots at 5 kyr, 17 kyr and 84 kyr after the first magma injection. The intrusions grow downwards from 12 k to 17 km depth over 50 kyr. The spacing between intrusion is 0.5 km. The green dashed lines mark the contour of the intrusions. The temperatures are shown by the colour scale and the melt fraction with the contour lines. At 5 kyr, the intrusions are independent with separate thermal aureoles. At 17 kyr, the mushes converge. At 84 kyr, 34 ky after the last injection, the magma chambers converge. (Online version in colour.)

4. Discussion

The preliminary simulations presented here confirm that our conceptual model of the coalescence between magmatic bodies is plausible. A brief exploration of the physically realistic parameter space suggests that extensive low melt-fraction mush systems can develop over the time scales typical for magma injection, but coalescences of melt-rich lenses is rare if due only to conductive heating and partial melting. An interesting result is that, due to slow heat diffusion, coalescence may happen after the main intrusive episodes, so that major caldera eruptions do not necessary coincide in time with the main intrusive activity. The calculations are limited by the fact that they were two dimensional and did not involve any mechanical processes; no convective processes or fluid migration was considered and we tested only for one type of rock composition and melting behaviour. Nevertheless, our calculations suggest these models have the potential to explain many of the observed features of large magma reservoirs and deserve further exploration.

Within this framework, mushes coalesce and magma chambers converge, when the country rock between intrusions partially melts. The ability of rocks to melt strongly depends on their composition and H₂O content. In the cases presented here, compositions are dacitic and melt appears at 670°C. Moreover, the melting behaviour of injected magma and country rock is similar. In nature, if the country rocks is dehydrated and refractory, mush coalescence would not happen. By contrast, coalescence would be favoured if a hot mafic magma is injected in a wet fertile country rock [97].

For most of the parameter space explored, the melt fraction between the intrusions remained below 0.4, although the wider mush system had coalesced. In a real system, we might expect the size of the magma chambers to be reduced by eruption of mobile, high melt fraction material, while the surrounding immobile mush continues to grow. This suggests individual melt lenses can remain isolated for long periods within growing mush systems, and will only mix during eruptions or other catastrophic events.

In our numerical models, for the melt lenses to coalesce, they must be deep, close to each other, and the magma supply rate must be sufficiently high. In nature, a physical disruption of the mush between the magma chambers could occur at low melt fractions and lead to a merging of the chambers. This disruption can be caused by a tectonic event or by an eruption from one of the chambers and the ensuing magma depressurization (e.g. [98]). The connection of formerly separated melt lenses during caldera forming eruptions has been identified from the petrological and geochemical record of the erupted products [99–101], and from geophysical observations (e.g. [33,102]).

Finally, although these models do not directly assess the structural controls of magma reservoir growth, they clearly demonstrate that mush zones preferentially develop between closely spaced intrusions. Thus growth will be favoured in directions along which structural features cause intrusions to align, and inhibited away from them. Possible mechanisms for such an alignment might include an increase in permeability, stress focusing or active fault motion, but this study does not discriminate between them.

5. Conclusion

We have presented a new conceptual model that integrates short-term observations of volcanic systems, with the long-term growth of magmatic systems. We adopt the premise that systems start as a set of closely spaced, but isolated intrusions which grow and coalesce through thermal diffusion. We identify three distinct stages of coalescence: the viscoelastic shell, the solidus (melt fraction greater than 0) and the eruptible melt (melt fraction greater than 0.5). We explore a two-dimensional numerical model using a reflective boundary condition to simulate the growth of closely spaced reservoirs and track the conditions midway between intrusions. In most simulations, the temperature starts to rise after 10s kyr, indicating that the viscoelastic aureole has coalesced, and the melt fraction starts to rise after 10–100s kyr. The temperature and melt fraction are greatest for deep, closely spaced intrusions at high magma supply rates, and coalescence occurs most rapidly in these conditions. The temperature and melt fraction peak during a period of thermal relaxation suggesting the optimal conditions for caldera-forming eruptions might occur 10s kyr after the magma supply has ceased. For most of the simulations, melt fraction does not reach 0.5, indicating that individual lenses of eruptible magma remain isolated within a larger mush system.

Data accessibility

The code used for the thermal modelling is deposited on runmycode.org.

Authors' contributions

J.B. conceived the conceptual model and wrote the paper with input from C.A. C.A. set up and performed the numerical models.

Competing interests

We declare we have no competing interests.

Funding

C.A. received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 794594. J.B. received funding for the NERC RiftVolc Project NE/L013932/1 and the NERC BGS Centre for the Observation and Modelling of Earthquakes Volcanoes and Tectonics (COMET).