On the hydrodynamics of crystal clustering

Abstract

The formation of crystal clusters may influence the mechanical behaviour of magmas. However, whether clusters form largely from physical contact in a mobile state during sedimentation and stirring, or require residence in a crystal mush, is not well understood. In this paper, we use discrete-element fluid dynamics numerical experiments to illuminate the potential for clustering from both sedimentation and open-system mixing in a model olivine basalt reservoir for three different initial solid volume per cents. Crystal clustering is quantified using both bulk measures of clustering such as the R index and Ripley's L(r) and g(r) functions and with a variable scale technique called Voronoi tessellations, which also provide orientation data. Probability density functions for the likelihood of crystal clustering under freely circulating conditions indicate that there is nearly an equal likelihood for clustering and non-clustered textures in natural examples. A crystal cargo in igneous rock suites exhibiting a dominance of crystal clusters may be largely sampling magmatic materials formed in a crystal mush.

This article is part of the Theo Murphy meeting issue ‘Magma reservoir architecture and dynamics’.

1. Introduction and background

(a). Introduction

The clustering of particles in a moving fluid was first described in the 1940s in the context of industrial applications [1], and has been subsequently described in sedimentology, volcanology and atmospheric transport and has been of significant interest in the chemical processing industry [2]. Clustering is an emergent phenomenon in that it arises from the complex interplay between a hydrodynamic template and a dispersed phase, typically solids, and can manifest multiphase instabilities that have no counterpart in molecular fluids [3]. Even the definition of a cluster will depend on the application; perhaps the most generic definition of a cluster might be that it is a region of elevated particle concentration relative to a random reference state, where particles move as an ensemble. It has been standard practice in material science to differentiate clusters, which result from hydrodynamic processes alone, from orthokinetic agglomerates, which are bonded, jammed or otherwise cohesive arrangements of particles in contact [4]. Our objective here is to exemplify measures of particle clustering from hydrodynamic forces that might occur in magmas. A complete assessment of the formation of crystal agglomerates and their fragmentation (e.g. [5,6]) will be the subject of a future communication. Below, we first describe the general emergence, kinematics and dynamics of clustering. We then describe specific applications to magmatic processes, by consideration of simple examples involving crystal settling and open-system stirring in three idealized basaltic systems.

(b). Geological observations and motivation

There are numerous examples of crystal clustering in the volcanic and plutonic record, but the understanding of how they arise under dynamic conditions is incomplete. The proposition that the mechanical behaviour of magmas may be strongly influenced by crystal clusters [7] and that magmas may often reside in a mushy or crystal-rich state [8], motivates renewed interest in understanding the origins of clustering. In particular, the recognition that many of the ‘crystal clots’ and glomerocrysts found in volcanic rocks may be samples of crystal mush [9–14], while others may originate by hydrodynamic interaction under dilute conditions, commonly referred to as synneusis [15–18]. The textural analysis of plutonic rocks has also motivated an interest in crystal clusters in an effort to better understand cumulate formation, stress transmission and the corresponding magmatic fabric [14,19].

One of the obstacles in the interpretation of complex crystal zoning in crystal clusters is the degree to which clusters originate by repeated magma stirring, and those which form while they reside in a static or near-static crystal mush. Hence, our goal is simply to explore how crystal clusters arise by stirring and sedimentation under plausible geological conditions.

(c). Theoretical overview

In this study, we consider the clustering that may occur as a result of two processes operating simultaneously: sedimentation from the steady acceleration due to gravity, and particle dispersion from non-steady forces arising from fluid circulation caused by an open system intrusion of new magma. Non-cohesive particle clusters can form in either inertial [20] or viscous [21,22] dominated conditions, and by processes related to dissipation from inelastic particle–particle interactions [23,24], hydrodynamic sorting as a function of particle Stokes number (defined below) [25–28], and by particle-wake attraction producing kissing-drafting-tumbling (KDT) and clustering behaviour [29–39]. Individual particles can leave and join clusters intermittently, and clusters can form from systems with initially low particle volume per cents even under viscous conditions [35,39–43]. Particle clustering can give rise to what is termed mesoscale transient structures as manifested in both laboratory and numerical experiments [44–46].

A dilute multiphase system undergoing sedimentation in an otherwise quiescent fluid can manifest clustering. Strong clustering can arise from the progressive unsteadiness associated with the cycle of particle wake formation, asymmetry and shedding [39,47–50]. This, in turn, enhances sedimentation by a wake attraction effect that produces a reduction in drag of trailing particles, and an increase of sedimentation flux by up to an order of magnitude [42,51]. A freely sedimenting system is described by three degrees of freedom, the particle volume per cent, the particle-fluid density ratio and the Galileo number, Ga,

$$Ga=\frac{U_{g}d}{\eta },$$ 1.1

where d is the particle diameter, η the kinematic viscosity and Ug a scaled settling velocity,

$$U_g={\left[\left(\frac{{\rho }_p}{{\rho }_f}-1\right)gd\right]}^{1/2}.$$ 1.2

The Galileo number as defined in (1.1) can be considered as a kind of Reynolds number based on the gravitational settling velocity; we retain the use of Galileo number here to be consistent with the use in [51]. For an isolated particle, it has been observed that a value of Ga equal to around 120 produces steady vertical motion with an axisymmetric wake, and a value of Ga equal to 178 produces steady oblique motion. The onset of strong clustering in a semi-dilute multi-particle system (volume per cent of O(10⁻³)) is associated with values of Ga above 120, reinforcing the notion that non-steady wake behaviour and particle attraction can yield clustering.

Non-dilute sedimenting systems also manifest complex velocity fluctuations even under conditions of low particle Galileo (or Reynolds) numbers, where particle wakes produce fluid channelization and hence clustering [39,43,52–54]. It has been difficult to experimentally resolve and generalize the stochastic nature of local many-body interactions, whether by collisions or by wake unsteadiness at high Ga, or from wake interference effects at low Ga. Significant progress has been made in describing the macroscopic average behaviour of particle sedimentation within the context of traditional notions of hindered settling particle flux [39,53]. Predicting clustering and the role of particle-local wake perturbations, relative to fluid reorganizations and particle crowding that occurs in non-dilute conditions at both high and low Ga, is not yet possible.

Sedimentation in an environment where there is fluid motion arising from far-field forces has also been studied, typically under conditions of near-laminar viscous flow [55–58] or chaotic and formally turbulent flow [26,59–63]. One measure of particle interaction and hence the possibility of clustering is called the dense-dilute threshold D_D [64]:

$$D_D=\frac{t_{c}f}{t_v},t_c=\frac{1}{n\pi U_{\mathrm{RMS}}{d}^2},t_v=\frac{({\rho }_p-{\rho }_f)d^2}{18\mu },$$ 1.3

where t_c is characteristic time between collisions, n the particle number density, μ is the dynamic viscosity, U_RMS the root mean square of the particle speed and t_v is the particle velocity response time. The drag factor, f, is:

$$f=1+0.15{\mathit{\text{Re}}}_p^{0.687}+\frac{0.0175}{1+42500{\mathit{\text{Re}}}_p^{-1.16}},R{e}_p=\frac{U_{g}d}{\eta },$$ 1.4

where Re_p is the particle Reynolds number based on U_g the terminal fall velocity with a kinematic viscosity η; f approaches unity for small values of Re_p as might occur in magmatic conditions. If D_D is less than 1, particles do not have time to respond to the far-field fluid dynamic forces before interacting with another particle, and the multiphase dynamics are dominated by particle–particle interactions. This distinction can be important in establishing regimes of clustering behaviour.

For conditions relevant to magmatic behaviour Burgisser et al. [65] proposed two dimensionless groups to identify when the particle motion was dominated by the non-steady, far-field fluid motion, or by the steady acceleration of gravity associated with sedimentation. The first is the Stokes number, S_T:

$$S_T=\frac{2}{3}{t}_v\frac{\mathrm{\Delta }U}{\delta },$$ 1.5

where ΔU is the characteristic speed change of the fluid over a length scale δ. Particles with a S_T > 1 are decoupled from the flow; buoyancy forces will dominate their behaviour and settling can be described as occurring in a still fluid. The importance of the steady acceleration of gravity relative to the background flow ΔU is given by:

$${\mathrm{\Sigma }}_g=\frac{g{t}_v}{\mathrm{\Delta }U}\left(\frac{{\rho }_p-{\rho }_f}{{\rho }_p}\right),$$ 1.6

where the sign of Σ_g indicates whether particles rise, sink or are neutrally buoyant. The magnitude is a measure of the time scale it takes a particle to settle a characteristic distance over the time scale the far-field velocity has to transport the particle that characteristic distance. At vanishing S_T and Σ_g, the particles circulate as passive tracers.

The dimensionless groups described above give some guidance as to the conditions that might influence clustering. For magmas, the Galileo and Stokes numbers will typically be much less than unity [65], expressing the absence of particle inertia resulting from the control by viscosity. In the absence of fluid circulation and with low Ga, it is unlikely that KDT processes will produce significant clustering in an otherwise dilute fluid [51]. And at low St, clustering is likely to result primarily from an advective gathering of crystals, either in stagnation points, wall boundary layers or along horizons of particle sedimentation. The simulations described below are designed to include all these processes and quantify the resulting clustering.

(d). Objectives of the study

The objectives of this study are to exemplify measures of clustering as might arise in both dilute and dense magmatic systems undergoing simultaneous sedimentation and circulation from open system input. Our focus is on the mobile portion of the multiphase mixture, hence we do not address clustering that occurs in the settled bed. We will consider bulk measures of clustering as discussed in [66–68], as well as Voronoi tessellation, and demonstrate how they recover clustering scales and fabric. We will do this with multiphase, time-dependent numerical simulations that track the trajectory of every particle (the terms crystal and particle are used interchangeably) and hence recover the entire distribution of all particles at every time step. This will allow for the examination of how clustering changes during on-going sedimentation and open-system circulation.

2. Methods

(a). Discrete element method-computational fluid dynamics simulations of an open-system intrusion into an olivine-bearing magma chamber

To develop and exemplify some relevant concepts of crystal clustering caused by hydrogranular processes, we employ the discrete element method combined with computational fluid dynamics (DEM-CFD), a framework we have previously employed and is well described elsewhere in the literature [69,70] (please see electronic supplementary material in [71,72] for a full elaboration of the theory and numerical implementation). Briefly, the DEM-CFD method combines a Eulerian representation of the conservation of mass and momentum balance for the fluid phase, and the motion of a particle of mass m is explicitly solved as a Lagrangian quantity,

$$m\frac{\text{d}}{\text{d}t}\left(\begin{array}{c}v\\ \omega \end{array}\right)=\sum \left(\begin{array}{c}\mathbf{\text{F}}\\ \mathbf{\Gamma }\end{array}\right),$$ 2.1

where t is time and with translational velocity vector v and rotational velocity vector ω subject to force vector F and torque vector Γ. Our application of the DEM-CFD method explicitly resolves particle-sustained frictional contact, collisions, buoyancy, hydrodynamic drag, interphase momentum transfer and implicitly treats lubrication; additional information regarding the governing equations, and the verification and validation procedures can be found in [71,73–75]. The fluid phase is modelled with the usual Navier-–Stokes equation on a cell size that is approximately 2.5 particle diameters. One simplification we make is that the particles are spherical. This will clearly impact the styles of clustering [66,71] and as most crystals only approximate spherical conditions, our results are not intended for direct comparison with geological examples. Nor do we model crystal transport from plumes that might originate at crystal-rich boundary layers [28,76,77]. Rather our aim is to develop and demonstrate a framework for the quantification of clustering that can serve as a proof-of-concept, which can then be extended to the complexity of natural examples in subsequent work.

We present the results from four numerical models. All have the same size of 2.56 m by 1.28 m and initial fluid condition of a reservoir filled with basaltic melt at a temperature of 1290° and an MgO content of 10.76%. The melt phase has the properties of basalt with a viscosity of 0.2 Pa s that was held constant throughout the simulations. The first model is initialized with a continuous (pseudorandom) random distribution of olivine crystals with a uniform diameter of 0.004 m that comprise nine volume per cent, and this system is allowed to settle. This model is referred to as the settling model and will be identified as ‘SM’ in the discussion below. The next three models are initialized with a continuous pseudorandom distribution of one, nine and 20 volume per cent crystals. In these three models, more primitive crystal-free basaltic magma is injected into the domain from the base with a velocity of 0.023 m s⁻¹ with a temperature of 1340° and an MgO content of 12.94%. In these models, crystals are redistributed by the complex interplay of both settling and fluid motion resulting from the new intrusion from below. We will refer to these three as open-system models or ‘OSM’ below. The reader is strongly encouraged to now view the three models designated OSM in the movie file OSM-1.mp4 in the electronic supplementary material.

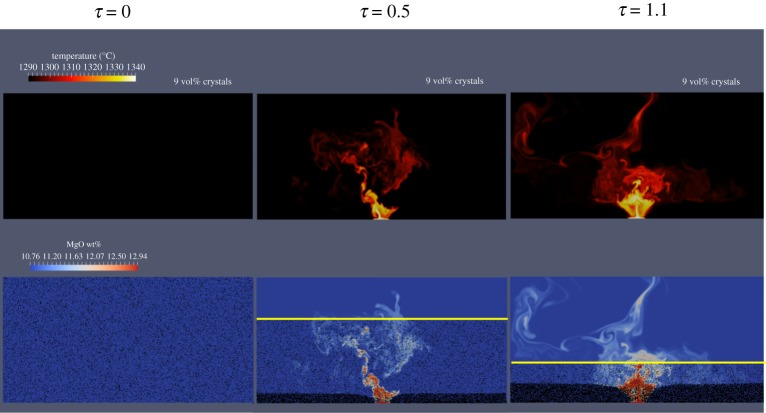
Figure 1 shows the initial nine volume per cent crystals system at three time steps for dimensionless times of τ = 0, 0.5 and 1.1. Dimensionless time τ is defined as

$$\tau =\frac{t}{t^{\ast }},$$ 2.2

where t is time and t* is the time it takes a single particle to settle the vertical height of the domain under conditions of laminar Stokes settling. For our simulation parameters, each increment of τ is 90.332 s of wall-clock time. In figure 1, one can see the progress of sedimentation and the fluid mixing that takes place as a result of the open system intrusion. As crystals accumulate on the floor a so-called mixing bowl is formed where the incoming magma has fluidized crystals arriving from positions initially in the upper portions of the magma reservoir; see discussion in [69,70].

Figure 1.

Three time steps, τ = 0, 0.5 and 1.1, from the initially 9% solid volume per cent of olivine open system model (OSM). The top row shows the changes in the temperature of the multiphase system between the initial temperature of 1290°C and the temperature of the new intruding basalt of 1340°C. The bottom three panels show the particles (olivine crystals) as black points and the background colour is the change in MgO wt% between the initial value of 10.76 and the new intruding value of 12.94. Variations between these reflect mixing of the resident and incoming magma. A yellow line is drawn at the shock front that separates the settling particles and the region of the domain that no longer has particles.

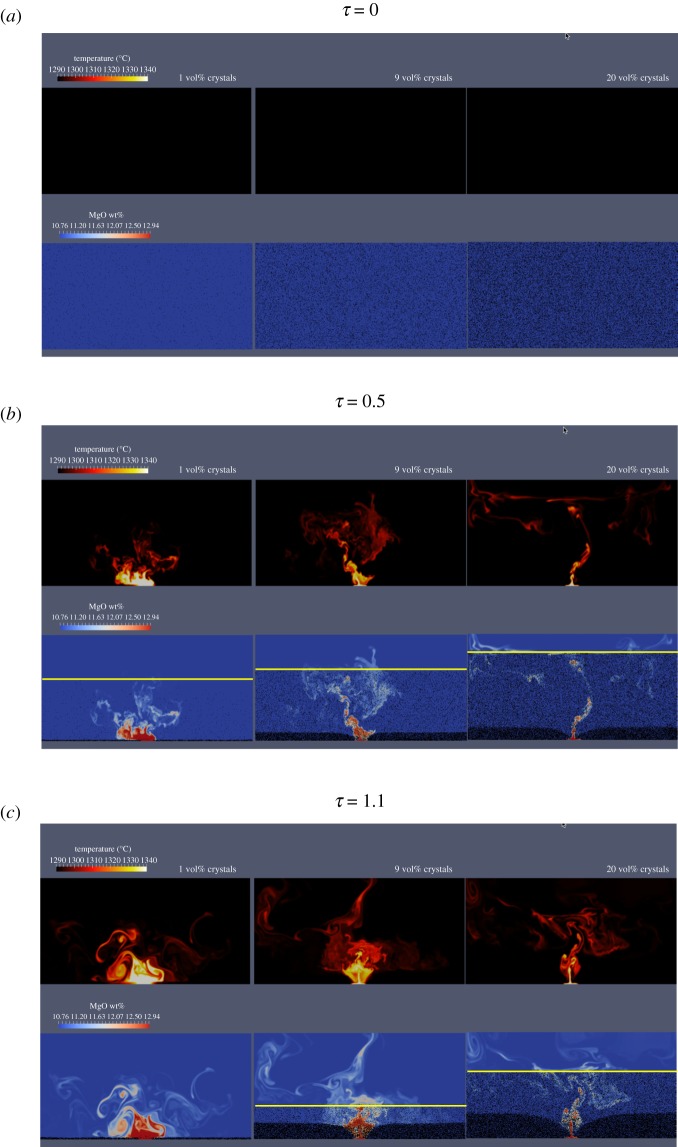
All three initial crystal per cents for the OSM are shown together in figure 2 for three time steps, τ = 0, 0.5 and 1.1 (i.e. 0, 45.166 and 99.365 s of wall-clock time), see movie file OSM-1.mp4. Each time step has two rows, the upper row shows the melt temperature and the bottom row the position of the particles as well as the MgO compositional variation in the melt phase from mixing between the resident and incoming more primitive basalt. As the simulation proceeds for each case, the location of each crystal is tracked creating a time series with position, velocity, and local temperature and melt composition for the entire crystal population. In this study, we are only interested in the dynamics of clustering, and do not consider the evolution of the scalar fields of temperature and composition further. We refer the interested reader to [70] for a discussion of time-dependent scalar field mixing and associated crystal reactions in open-system magmatic events.

Figure 2.

Three time steps, τ = (a) 0, (b) 0.5 and (c) 1.1, from three open system models (OSM) which differ by solid volume per cent. From left to right the solid volume per cents are 1%, 9% and 20%. The three times correspond to those in the text. A yellow line is drawn at the shock front between the settling particles and the region of the domain that no longer has particles in the lower half of figures (b) and (c). The reader is directed to the movie OSM-1.mp4 in the electronic supplementary material.

3. Measures of clustering

In order to discuss the processes that produce clustering in the mobile portion of magmatic systems, there needs to be a means of quantifying the clustering. The domain area within which the mobile portion resides changes with time as particles exit to form a settled bed, and the upper boundary between the region of pure melt and that with settled particles moves downward with time. For example, the yellow horizontal line in figures 1 and 2 is the upper boundary (at those time steps) of the mobile domain, and the lower boundary is the settled bed. So the clustering statistics discussed below are applied within that region, which itself is becoming smaller as settling proceeds.

Several methods of cluster quantification are implemented in this study and discussed below. The first section introduces the R index and two correlation functions, Ripley's L(r) and g(r) functions. These methods have been used to describe the distribution of point arrays and have been used for textural analysis in metamorphic and igneous petrology [7,66,67,78]. The second section introduces the use of Voronoi tessellations for cluster analysis. The Voronoi tessellation has the ability to provide geometric data without predefining length scales [51]. Below we apply these measures of clustering to the simulations described in §2 and discuss the implications for geological applications in §4.

(a). Bulk clustering measures, R, Ripley's K(r), L(r) and g(r) functions

One method that has been used for quantifying crystal clusters is the aggregation index, R [66,67,79]. The R index is the ratio of the mean nearest neighbour distance over the expected value from a spatially continuous random distribution:

$$R=\frac{r_a}{r_E}.$$ 3.1

Here, r_a is the mean nearest neighbour distance, and r_E the expected value. The value of r_E is:

$$r_E=\frac{1}{2\sqrt{\lambda }},$$ 3.2

where λ is the intensity or the total number of points over the total area. Jerram et al. [67] demonstrate how the R value can provide criteria for a collection of objects to be described as ordered, random or clustered. For a system of points of vanishing volume that transition is indexed to a value R equal to unity. However, as discussed in [67] there is no single value of R that discriminates ordered from clustered states in natural materials with finite area. A random distribution of natural grains will always have an R value greater than unity. We have illustrated this in figure 3, which shows the random sphere distribution line (RSDL), that delimits the ordered from clustered states as a function of the solid volume per cent. The interested reader is directed to fig. 5 of [67] for the derivation of the RSDL as a function of solid volume per cent.

Figure 3.

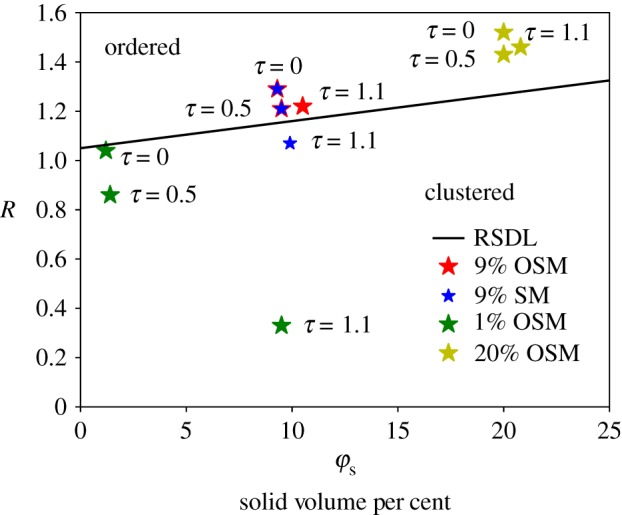
R index as a function of solid volume per cent, φ_s. The black line is the random sphere distribution line (RSDL) from Jerram et al. [67]. The points shown are from τ = 0, 0.5 and 1.1 of the 9% solid volume per cent settling model (SM) and the solid volume per cent of 1%, 9% and 20% open system models (OSM).

The R value of four simulations as a function of solid volume per cent is shown in figure 3, which is a plot of R as a function of solid volume per cent. The RSDL, as developed in [67], is shown dividing the clustered from ordered regions. A number of interesting features are apparent. Firstly, note that the τ = 0 values for the four simulations increasingly depart from the expected ideal RSDL as the solid volume per cent increases. This is a consequence of the fact that our initialization of the domain, which is based on a thinned continuous pseudorandom algorithm, leads to an apparent ordering; that is an artefact. This arises as the domain is progressively initialized with finite area particles; the remaining space induces a filtering such that a truly random choice is moderated by the available locations that can accommodate a particle. Secondly, it is interesting to note that for any individual simulation, there is not a large change in the solid per cent of the mobile region as the simulation proceeds. This is due to the fact that the loss of particles to the settled bed, which should decrease solid per cent, is almost balanced by the reduction in the mobile volume that contains crystals. For example, in figures 1 and 2, the mobile volume is between the horizontal yellow line and the settled bed, and the solid volume per cent stays nearly constant in that region. The fact that the solid per cent does not change markedly as the simulations proceed suggests that there is a local self-similarity or qualitative stationary state in the average mass per cent.

The R value provides a global metric of the clustering in the system but does not provide information on cluster size when clustering is present. To obtain more information about the particle distributions we will use what are called Ripley's K(r), L(r) and g(r) functions [80,81]; the reader is directed to [66] for a more complete presentation. The K(r) function is defined as:

$$K(r)=\frac{E}{\lambda },$$ 3.3

where E is the number of particle centres in a given radial distance, r, from a randomly chosen particle centre. The result of this equation is an area. The more points present within the boundary of the radial distance, the larger the area will be. If the area is larger than the area created by the area of a circle using the radial distance there is clustering, while a smaller area indicates ordering. A complete random spatial distribution of points within the radial distance will yield a K value of πr². The K(r) function is usually expressed in a more useable form as [66]:

$$L(r)=\sqrt{\frac{K(r)}{\pi }},$$ 3.4

where a completely spatially random distribution would yield an L(r) equal to r.

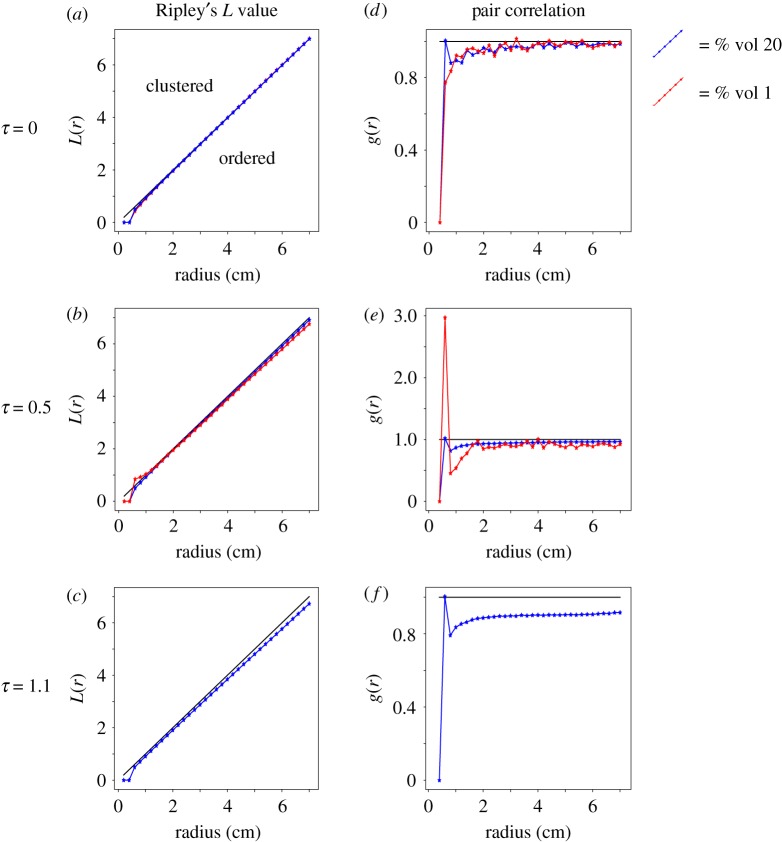
Figure 4 shows the L(r) function for different radius values for the OSM and the SM for the initial 9%, and figure 5 shows the same for the OSM initial 1% and 20% systems. By selecting a random subset of particles from the system and obtaining their L(r) values, one can potentially obtain insight into the particle distribution of the system. However, in this study, we used the average L(r) of all the particles in the system to obtain the average behaviour. We use the average because the system has over 10⁵ particles in several different kinematic regimes. The total number of particles needed to accurately display the particle distribution was not computationally feasible. We calculated the K(r) function for all particles in each system and used the average K(r) values of the individual systems in the L(r) function. The black line in figures 4 and 5 indicates a completely random distribution; the region above the line indicates a clustered distribution, and below the line indicates an ordered distribution. As with the solid per cent versus the R index, there is no significant difference between the L(r) function values for the first two time steps in the 9% OSM and SM systems. In figure 4, for τ = 0, 0.5 both the OSM and SM cases start in the ordered regime and tend to spatial randomness with larger radial distances. For figure 4c, τ = 1.1, there is a bifurcation of the two curves after a radial distance of 0.4 cm. Each radial distance is increased by 0.2 cm, the radius of the particles in the system. In figure 4c, at greater radial distances the OSM tends to a more ordered distribution, while the SM tends to spatial randomness with greater radial distances.

Figure 4.

Ripley's L value (a–c) and pair correlation (d–f) functions for both the open system model (OSM) and settling model (SM) at 9% crystal volume per cent. The results for the OSM and SM were similar for τ = 0 and 0.5 so only the curve of the SM is shown. For τ = 1.1, the maroon line indicates the OSM simulations and the cyan line indicates the SM simulation. The black line represents a random distribution; points above the black line are clustered and points below are ordered. The vertical scale varies between figures.

Figure 5.

Ripley's L value (a–c) and pair correlation (d–f) functions of the open system models (OSM) for a solid volume per cent of 1% and 20%. The 1% OSM is represented by the red lines and the 20% OSM is represented by the blue lines. The vertical scale varies between figures.

Figures 5a–c are L(r) curves for the 1% and 20% systems at τ = 0, 0.5 and 1.1. The OSM 1% and 20% are diverging by τ = 0.5 and the 1% system is clustered with small radial distances, and becomes ordered with greater radial distances. The 20% system is ordered for small radial distances but converges to random with increasing radial distances. In figure 5c, at τ = 1.1 the 20% system starts in the ordered regime, but approaches randomness before increasing to a more ordered state. Figures 5c,f omits the 1% OSM results because by that time step the majority of particles have settled and the clustering analysis gives spurious results.

Another way to represent the clustering is with Ripley's pair correlation function g(r), where:

$$g(r)=\frac{1}{2\pi }\hspace{0.17em}\frac{\text{d}K(r)}{\text{d}r}\left(\frac{1}{r}\right).$$ 3.5

A solution of g(r) = 1 indicates a complete spatial random particle distribution, g(r) > 1 means the distribution is clustered, and a solution of g(r) < 1 means the distribution is ordered. This function assesses the likelihood that a particle centre will be found at or near a specific radial distance of the randomly selected particle centre.

The g(r) function is shown on the right-hand side of figures 4d–f and 5d–f with the same systems considered in the L(r) value as in figures 4a–c and 5a–c. As with the L(r) function, the mean value of K(r) was used to calculate the results for the g(r) function giving the average behaviour of the system. Similar to the L(r) function, the results of the g(r) function do not significantly differ between the first two τ = 0,0.5 in figures 4a,b. However, there is a difference at τ = 1.1 in figure 4f; the OSM strongly tends to an ordered distribution, while the SM maintains a near-random distribution.

The OSM 1% and 20% initial particle per cent systems in figure 5d have similar pair correlations at the initial time step; both start ordered but tend to spatial randomness with increasing radial distance. At τ = 0.5 in figure 5e the 1% system starts in the clustered regime, drops to ordered and then converges to random, while the 20% system starts in the ordered regime and converges to spatially random with distance. At τ = 1.1, in figure 5f the 20% system starts in the ordered regime and tends towards spatial randomness.

(b). Voronoi tessellation as a measure of clustering

Voronoi diagrams are a method to quantify clustering: local cluster size, location and cluster orientation. In the two-dimensional case, Voronoi tessellations are polygons where the area of the polygon is the portion of the domain where the closest particle centre is the particle within the Voronoi polygon [82]. Hence the size and orientation of the polygon is determined by the particle distribution. Figures 6b,c are examples of a Voronoi tessellation from the OSM 0.09 solid volume per cent simulation. The Voronoi polygons are coloured by normalized area. Normalization was achieved by dividing each Voronoi polygon area by the mean Voronoi polygon area of a continuous uniform random distribution of particles, using the same number of particles and area. Particles and their Voronoi polygons around the edges are not included in the calculations below to avoid edge effects. Since we are not interested in clustering associated with the static settled bed, all particles that are in fluid cells with a solid volume per cent greater than 46% were removed.

Figure 6.

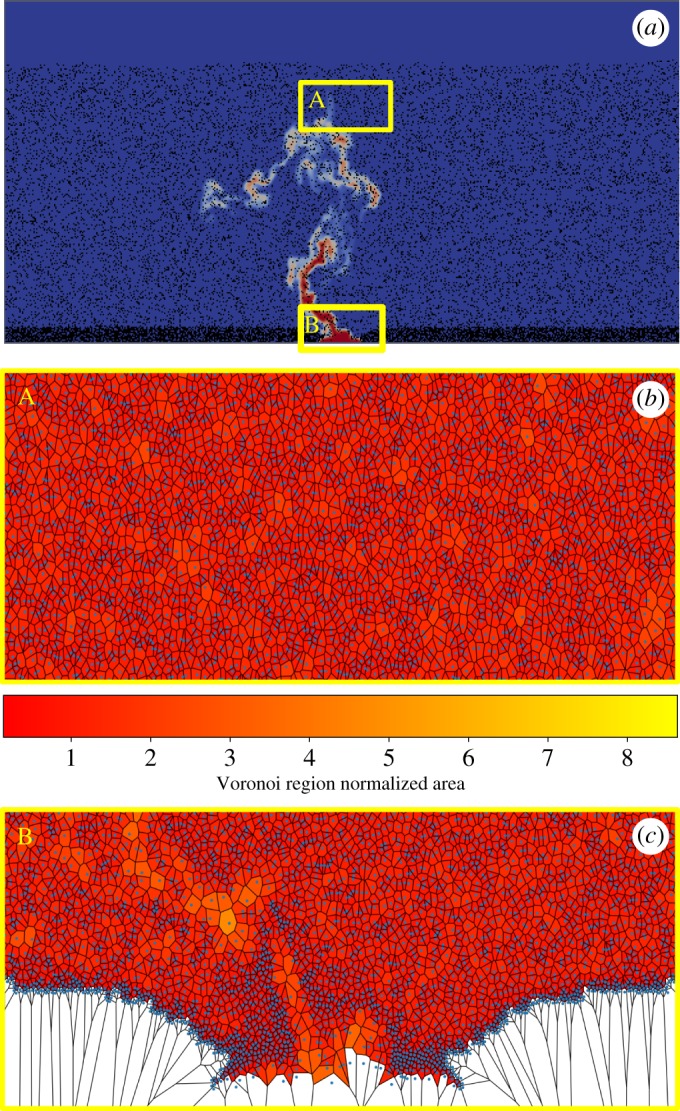
Open system model for τ = 0.3 and Voronoi tessellation for two regions of the settling particles. (a) Snapshot of OSM τ = 0.3 with regions A and B highlighted. (b) Voronoi tessellation for region A. This region was chosen above the new fluid injection site but near the shock front. (c) Region B covers the new fluid injection site. The Voronoi polygons are coloured by polygon area normalized to the mean Voronoi polygon area of a random distribution. An area of 1 indicates a random Voronoi polygon size, areas larger than 1 indicate ordering, and areas smaller than 1 indicate clustering.

Two regions of the settling regime are highlighted in figure 6. Region A is the Voronoi tessellation near the sedimentation shock and region B is the Voronoi tessellation at the mixing bowl. Voronoi polygons in inset A are mostly the same size, as seen by the uniform colour in figure 6b, with a value close to that of the mean polygon area of a continuous uniform random distribution (MCURD). The Voronoi polygons in figure 6c (inset B) are heterogeneous, and are both larger and smaller than MCURD. The sides of the mixing bowl are composed of Voronoi polygons that are smaller than MCURD, while the centre has regions that are larger than MCURD. The settling interface between the settled bed and the particles still settling are Voronoi polygons that are smaller than MCURD.

(i). Voronoi polygon area

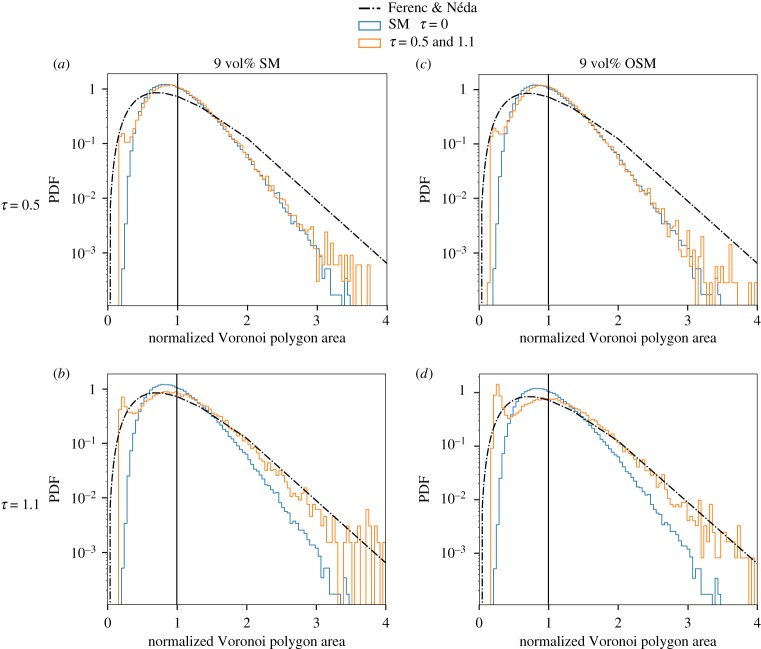
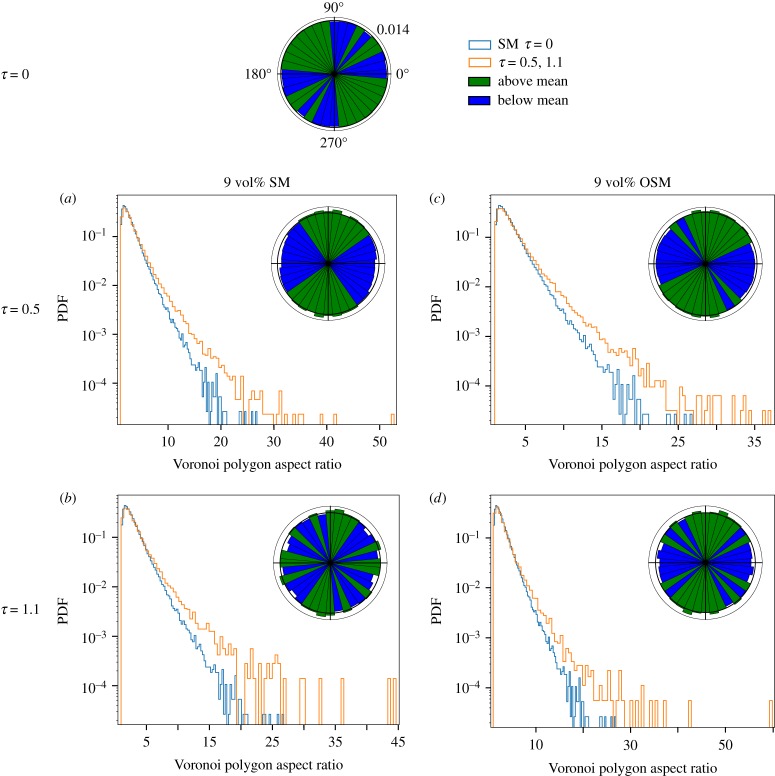
The Voronoi polygon area can also be used to determine if the distribution of the system is random, clustered or ordered. Figures 7a–d are probability density functions (PDF), which are a type of histogram, from the settling system (SM) and the open-system (OSM) for τ = 0, 0.5 and 1.1; τ = 0 is used as a reference for our initial state and is compared on each plot along with an idealized random curve from an equation in [82]:

$$f(a)=\frac{343}{15}\sqrt{\frac{7}{2\pi }}{a}^{5/2}{e}^{-7/2a},$$ 3.6

where a is the normalized area of a random distribution of similar particles and area. The starting condition for the system differs from the truly random curve from [82] in that the PDF has a greater maximum value but a smaller range of Voronoi polygon area. In figure 7a, for SM where τ = 0.5, there is a reduction in the range of Voronoi polygon area, but little change in the maximum value or location of the PDF. The OSM case in figure 7b is similar, indicating that at this time there has been no significant expression of clustering relative to the initial distribution.

Figure 7.

Voronoi polygon area histogram for the settling model (SM) (a,b) and the open system model (OSM) (c,d) at 9% particle volume per cent. The area of each polygon is normalized to the mean area of Voronoi polygons for a continuous uniform random particle distribution. The black chain line shows the ideal random distribution as set forth by Ferenc & Néda [82], the blue line is the histogram from τ = 0 of the SM and the black vertical line indicates unity. The vertical scale varies between figures.

In figures 7b,d, for τ = 1.1, the PDF approaches that of the Ferenc & Néda idealized random curve [82] indicating a shift to a more spatially random distribution of particles. There are two peaks in the PDF, both around 1.

(ii). Voronoi region aspect ratio

The Voronoi polygon area combined with the Voronoi tessellation of the simulation, figure 6, provides insight into distribution and magnitude of clustering. Adding information about the aspect ratio and orientation of the aspect ratio provides additional insights into the kinematic conditions associated with the creation of the clusters. Voronoi polygon aspect ratios were used in [51] to determine if clustering was being produced by synneusis (settling particles). In their study, they used the longest horizontal distance relative to the longest vertical distance to calculate the aspect ratio. It was found in [51] that a horizontal stretching of the aspect ratio indicated vertical particle clustering through settling. Having only the horizontal or vertical component is sufficient when working with a purely settling system, but when considering a more complex system with settling and open-system flow, Voronoi polygon aspect ratio orientations that are oblique to the vertical or horizontal are required.

To obtain the aspect ratios of the Voronoi polygons, we used eigenvectors calculated using a variance/covariance matrix by using the position of the vertices of each region. The eigenvectors were used as proxies for the aspect ratio of the Voronoi polygons. All aspect ratios are calculated by the long axes length divided by the short axes length. In figure 8, the long axis is shown on a rose diagram, to illustrate orientation data. Each bin represents 10 degrees, so there are 36 bins per rose diagram. Figures 8a–d are the PDFs of the aspect ratios and rose diagrams of the Voronoi polygons. The mean of the bins was calculated, and the colours indicate if the value of the bin is above or below the mean. In the figure, green represents above the mean and blue represents those below the mean. Values equal to the mean are displayed with those values below the mean.

Figure 8.

Voronoi region aspect ratio for the settling model (SM) (a,b) and the open system model (OSM) (c,d) at 9% particle volume per cent. The blue histogram is the aspect ratio histogram for τ = 0 of the SM and the orange line is the named system. The rose diagram imbedded in the right corner of each plot shows the orientation of the long axis of the aspect ratio. The green bins are above the mean height of the bins and the blue bins are below the mean height. The rose diagram for τ = 0 has the orientations displayed as well as the value of the inner black circle. Vertical scale for the probability density functions varies between figures.

The initial condition, τ = 0, is shown in the top rose diagram and is the blue curve in all PDFs in figures 8a–d. There is an increase in Voronoi polygon aspect ratio to the initial condition in both the open and settling systems and for τ = 0.5 and 1.1, indicating stretching of the Voronoi polygons. The rose diagram for the initial condition represents our random distribution. Even though the bins are coloured according to their value above or below mean, the bins all have values close to mean. For τ = 0.5, there is a preferred orientation of the Voronoi polygons towards the vertical for both the open and settling systems. In figure 8d, the open system for τ = 1.1, the vertical preferred orientation is maintained, although slightly oblique, but in figure 8c, the settling system there is a horizontal and an oblique preferred orientation.

4. Discussion and Conclusion

We have demonstrated the application of a number of measures that express particle clustering at different scales. The R value produces a single clustering metric at the domain length scale and so expresses a system-wide tendency to order or randomness. The probability density functions of the Voronoi tessellations express a distribution of cluster sizes based on a closest neighbour criteria, as well as statistics of tessellation anisotropy, which is a qualitative expression of the kinematic state of the flow. The L(r), and pair correlation functions express an average of particle distribution as a function of distance.

We first consider the conditions of the settling only (SM) simulation with initially nine volume per cent crystals that are randomly distributed. At τ = 0.5 (figures 7a and 8a), there is no significant change in the clustered state of the system. However, at τ = 1.1 (figures 7c and 8c), there has been an increase in clustering. This change cannot be ascribed to the processes of KDT referred to in §1c, as the Galileo number for the system (equation (1.1)) is approximately 5, which is a factor of 25 smaller than that which would produce wake unsteadiness. Since virtually all conditions of settling in magmas will have very low Galileo numbers this process is unlikely to be important in producing clustering in magmas. The observed clustering can be attributed to the combined effects of ‘hindered settling’ or crowding from the increase in the solid volume per cent in the remaining liquid producing the formation of local fluid channels from the upward-directed fluid return flow. This, in turn, produces a corresponding local increase in particle volume per cent. Thus we expect that clustering from sedimentation alone will be most prevalent in regions near the floor or settling capture-front, where hindered settling enhances particle crowding, which produces a complex return flow and particle transport enhancing clustering.

The combined settling and open-system simulations (OSM) show a more complex pattern of particle transport. Figure 6a shows the initial nine volume per cent particle simulation at a time of τ = 0.3. Figure 6b is the Voronoi tessellation of inset A that is the portion of the system largely dominated by particle sedimentation, while figure 6c is an inset of the lower portion. This figure illustrates two points in the quantification of clustering, firstly that in a dynamic system any bulk metric of clustering as described in §3a will include many scales of heterogeneity and thus may not predict or recover the clustering on a geological sample of size less than the system size. The second point is expressed by figure 6c, centred on a region of strong upwelling. This clearly shows the role of fluid–particle interactions, producing a fluid-rich core region surrounded by a rind or tube of enhanced clustering around the upwelling. Above that extensional flow produces a region with a reduced number of particles. Collectively this is similar to the complexity of mixing, more properly called dispersion, discussed in [70] where a bulk index of mixing (dispersion) suggested good mixing, but a local characterization exposed distinct domains of heterogeneity. This is also expressed by comparison of figures 8b,d. Despite the presence of the flow associated with the new magma input transporting the crystals, there is not a significant difference in the bulk Voronoi polygon aspect ratio. But there is a significant difference in the orientation of the polygons, with a significant contribution to the vertical orientation indicating the presence of an extensional kinematic template (horizontal flattening).

Examination of figures 7b,d at τ = 1.1 leads one to the non-intuitive result that based on bulk measures only, pure settling may produce more clustering than a system with settling and stirring. This reflects the dual nature of open-system stirring, particles are gathered by fluid motion into regions where the local particle per cent exceeds any that might result from simple settling, but at the same time the extensional elements of the fluid flow disperse particles and prevent them from settling. This is in part expected given the values of the Stokes number (equation (1.5)) and settling factor (equation (1.6)) discussed in §1c. For our simulations, the Stokes number is O(10⁻⁴) and the settling factor O(10⁻¹), thus if there is fluid motion associated with open-system input the particles will become almost passive tracers, with a minor ‘drift flux’ velocity associated with the steady acceleration of gravity. Thus clustering in open systems is difficult to generalize and dependent on the details and duration of open system stirring.

While it is desirable to compare the general trends obtained from the numerical experiments directly with natural examples, we do not currently have access to sufficiently characterized geological samples. However, natural examples do reflect some of the general features seen in figures 7 and 8, and we briefly describe one example below.

Plagioclase cluster formation in the Holyoke basalt has been explained as a multistage process involving settling and compaction with a role for upward flow of interstitial melt to act as a source of possible vertical mixing [7,66,83]. We would expect that the cluster distribution in the marginal chill would act as an initial reference, in the same way that the Ferenc & Néda [82] distribution did in this study. The middle unit, which underwent some compaction, might yield Voronoi tessellations with a preferred orientation, with the Voronoi polygons having a similar orientation to the plagioclase chains. If upward flow associated with the compaction from the mush was vigorous enough cluster formation might produce a distribution like that of the OSM in figures 7c,d.

Data accessibility

This article has no additional data.

Authors' contributions

The numerical simulations were performed by J.M.S. and G.W.B., the clustering and Voronoi analyses were done by M.Z.M. All authors contributed to the writing.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by National Science Foundation grant nos. DGE-1256068, EAR-1049884 and EAR-1447266 and access to computational facilities was supported by the National Science Foundation Extreme Science and Engineering Discovery Environment grant no. TG-EAR140013.