Use of Monte Carlo Techniques in Nuclear Medicine

Nuclear medicine has utilized simulations based on Monte Carlo techniques for over 50 years. Over that time, this has involved two main applications: estimations of internal dosimetry based on simplified patient models and investigations into the physical aspects of the instrumentation used in clinical nuclear counting and imaging. As the efficiency of the algorithms and available computing power has evolved, the sophistication of the simulations has also advanced substantially. Monte Carlo approaches are particularly useful when a closed mathematical solution is not possible or when the models become substantially sophisticated. This discussion will have a brief introduction of how Monte Carlo techniques are typically applied in the field of nuclear medicine, its applications in the estimation of internal dosimetry, and, finally, its use in the simulation of radiation detection and imaging. For both dosimetry and instrumentation, the discussion will start with a historical perspective followed by the current advances and challenges in the use of these techniques.

As described in the initial article in this series, Monte Carlo techniques require that well-defined and accurate models of the underlying processes are investigated [1]. In all cases, this involves an accurate model of the interactions associated with the radiations (i.e., x-rays, gamma rays, electrons, positrons, beta particles, and alpha particles) emitted by the radionuclides and radiopharmaceuticals used in nuclear medicine. For photon (x-ray and gamma ray) interactions, this may involve Thomson and Compton scattering, the photoelectric effect, and pair production with the respective probabilities of interaction depending on the energies of the emitted photons and the material with which these radiations interact. For the charged particles (e.g., electrons, positrons, beta particles and alpha particles), it is necessary to model the exchange of energies between these particles and the surrounding media leading to excitation and ionization of atoms in the vicinity of the path of the charged particle. This will require understanding of the stopping power as well as the linear energy transfer and specific ionization rates. In the case of positron interactions, the fate of the resultant 511-keV annihilation photons, will need to be considered. Finally, the nature of the objects within which the radiation is emitted and detected needs to be considered. For example, what is the effective Z number and density of the surrounding material? Where within the patient was the radiation emitted (i.e., within what organs and tissues)? Within what other organs and tissues did the radiation interact before being totally absorbed or leaving the body? If the radiation leaves the body, which may happen with high probability for higher-energy gamma rays, how does it interact within the radiation detector to characterize the detection process (e.g., with respect to energy deposition and, in many cases, spatial distribution)? As a simple example, a single emitted gamma ray is considered. The probability of it interacting within the patient and the type of interaction is sampled using a random or pseudorandom (i.e., a known and reproducible sequence of random numbers) number generator. If it interacts with the body, what was the nature of its energy deposition (i.e., how much energy was within which organs)? If the radiation escapes the body, does it interact with the radiation detector (say a PET scanner), and if so, again what was the nature of the energy deposition? This same process is repeated for millions and more individual photons or “histories” with the end result providing a full picture of the dosimetric or detection process.

The use of Monte Carlo techniques goes back to the very early days of the Medical Internal Radiation Dosimetry (MIRD) Committee of the Society of Nuclear Medicine in the 1960s. According to the MIRD formalism, the radiation dose to the target organ (DT) from radiation emitted from the source organ (S) is given by

$$D_T={\mathrm{\sum }}_S{\stackrel{\sim }{A}}_S{\mathrm{\sum }}_j{\mathrm{\Delta }}_j{\varphi }_j/M_T$$

where Ã_S is the time integrated activity within the source organ, Δ_j is the mean energy of the j_th emitted radiation, ϕ_j is the absorbed fraction of the j^th emitted radiation and M_T is the mass of the target organ [2]. Σ_S and Σ_j indicate summing over all source organs (S) and all emitted radiations (j). The absorbed fraction, ϕ_j, is the fraction of energy from the j^th radiation of the radionuclide emitted from the source organ that is absorbed in the target organ (MIRD 21). Although Ã_S, Δ_j, and M_T can be estimated based on knowledge for the radionuclide that was administered as well as anatomic and physiologic models of the patient, the absorbed fraction is typically estimated through statistical methods such as Monte Carlo. The use of Monte Carlo techniques in the dosimetry of internal emitters started in the 1960s, and, since then, the patient models have evolved from reasonably simple organ models such as cylinders and ellipsoids to today’s realistic, voxel-based phantoms [3]. However, the use of Monte Carlo to estimate the absorbed fraction remains essentially the same (i.e. a very large number of photons or charged particles are followed from the source organ to determine the fraction and the amount of energy deposited within the source organ).

Monte Carlo simulations in nuclear medicine imaging can range from testing the effectiveness of a new detector system to simulating a full imaging study of a new tracer in a human-like phantom, including details like organ dose and detectability [4]. The simulations can guide technology developers to strategies and parameters that will be most effective.

Most imaging simulations start with a digital object—from a simple geometric phantom to a patient-based phantom including major organs and biological motion. For emission modalities such as PET and single-photon emission CT (SPECT), radioactivity is stochastically simulated within the phantom in desired locations, often to imaging metrics such as resolution or signal-to-noise ratios, or can even be placed where a given tracer is expected to travel in a voxelized human. The passage of the decay products is simulated through the phantom material to the point where they reach a detector, according to the underlying physics considerations outlined above.

A digital detector is generated at the crystal level in a precise geometric arrangement—sometimes representing existing scanners, sometimes testing new scanner configurations—and the passage of the detected particles is similarly simulated, including the detection efficiency and the deposited energy distribution. See Figure 1 for an example simulated design of a hypothetical PET scanner.

Figure 1.

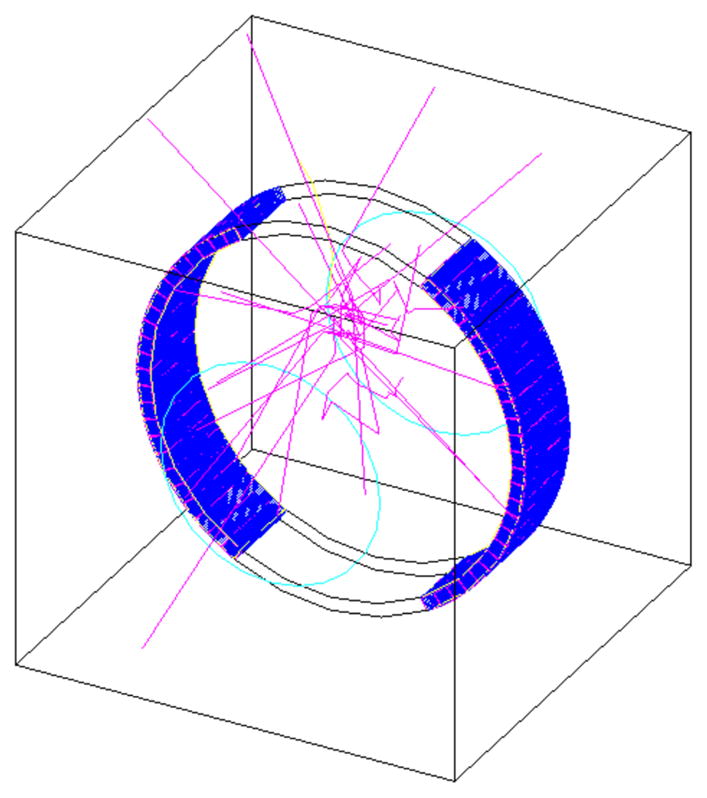
Gate simulation of a partial ring PET system with several photon tracks shown in pink.

Monte Carlo simulations have been used in designing new imaging devices, optimizing imaging protocols, and developing better image reconstruction techniques. Simulations allow researchers to create multiple instances of the same study but with slight variations to determine which parameters result in maximum effectiveness and the associated variance. Because the ground truth is known for the simulations, it is easier to isolate single effects. For instance, scattering in collimators can be simulated and evaluated to determine optimal material, thickness, and spacing for a particular task. The effect of each material and geometric change on final images can be compared with the original input activity distribution. Simulations can also be used in lesion detectability studies, for instance, as a way to determine the minimum dose that can be used, or which reconstruction technique provides the most reliable results.

In the field of CT, PET and SPECT, one of the most popular software packages has been GATE [5], a tool which can numerically simulate everything from the placement of radioactivity to the physics of passing through matter and being detected. It is based on the GEANT4 toolkit for simulating the passage of particles through matter. Another widely used tool is SimSET [6], which is based on physics modeling of photons in matter and was designed specifically for PET and SPECT.

Monte Carlo simulations are often time consuming, because essentially every particle and every physics interaction has to be modeled for millions of particles. Methods to optimize and reduce simulation time are continually under development. Variance reduction techniques, such as truncating time or energy, splitting/Russian roulette, weighting, or forcing collisions, can reduce the number of particles or time needed for a given precision. One of the more recent and promising techniques is the use of GPU for processing the simulations, increasing speeds by up to a factor of 90.

One issue with the development and modification of Monte Carlo simulations in general is the need for validation, either to real measurements, which can be difficult, time-consuming, and expensive, or to existing Monte Carlo code, which can be biased. Another potential limitation in simulation accuracy is the choice of physics parameters (e.g., which photon cross section library) of the chosen simulation software, which can noticeably affect the results. Nevertheless, Monte Carlo simulations are an important tool in the development of medical imaging technology and techniques.