Tinker 8: Software Tools for Molecular Design

Abstract

The Tinker software, currently released as version 8, is a modular molecular mechanics and dynamics package written primarily in a standard, easily portable dialect of Fortran 95 with OpenMP extensions. It supports a wide variety of force fields, including the modern polarizable atomic multipole-based AMOEBA model. The package runs on Linux, macOS and Windows systems. In addition to canonical Tinker there are branches, Tinker-HP and Tinker-OpenMM, designed for use on MPI-parallel distributed memory supercomputers and on state-of-the-art graphical processing units (GPUs), respectively. The Tinker suite also includes a tightly integrated Java-based graphical user interface called Force Field Explorer (FFE), which provides molecular visualization capabilities as well as the ability to launch and control Tinker calculations.

1. Introduction

The Tinker molecular modeling package represents a complete set of software tools for performing a wide range of classical molecular simulations, with special emphasis on biomolecular calculations. This article provides an introduction to some of the features and unique capabilities of the current version of the package, Tinker 8. Recently, specialized branches of the Tinker code have become available for use on large-scale multiprocessor supercomputer systems under MPI (Tinker-HP),¹ and for GPU-based calculations (TinkerOpenMM).² Integration of these codes with the Tinker suite of programs will be briefly discussed, and additional information is available in the original publications describing both Tinker-HP and Tinker-OpenMM. All of the software is available via academic web sites^3–5 and GitHub repositories.^{6, 7}

Tinker originated as a new software package implementing the MM2⁸ and MM3⁹ force fields of Allinger for use in conformational analysis of organic natural products.¹⁰ An early prototype of the software was incorporated as the basis of molecular mechanics calculations in the ChemOffice software package.¹¹ Additional applications used this early pre-Tinker platform for the development of efficient structure optimization algorithms for large molecules¹² and for packing analysis of amino acid side chains in folded protein structures.¹³ Development under the Tinker name began in earnest at Washington University in the mid-1990’s and the first distributed version, Tinker 3.2, was publicly announced and made available in late 1996. A major purpose of the software was, and still is, to provide a modular framework for incorporating existing empirical potentials, as well as design and parameterization of new classical force field models. More recently, Tinker served as the computational engine for the early protein folding simulations done via the Folding@home platform,¹⁴ especially for calculations utilizing implicit solvent models. The Tinker package and its corresponding file formats are interoperable with a variety of molecular modeling and visualization tools, including VMD,¹⁵ PyMol,¹⁶ Jmol,¹⁷ Force Field X,¹⁸ Open Babel,¹⁹ MDTraj,²⁰ MDAnalysis,²¹ ParmEd,²² Molden,²³ VEGA ZZ,²⁴ PACKMOL,²⁵ ForceBalance,²⁶ WebMO,²⁷ and many others. Access to Tinker, including the AMOEBA polarizable multipole force field, is also available from the CHARMM modeling software via the MSCALE interface facility.²⁸

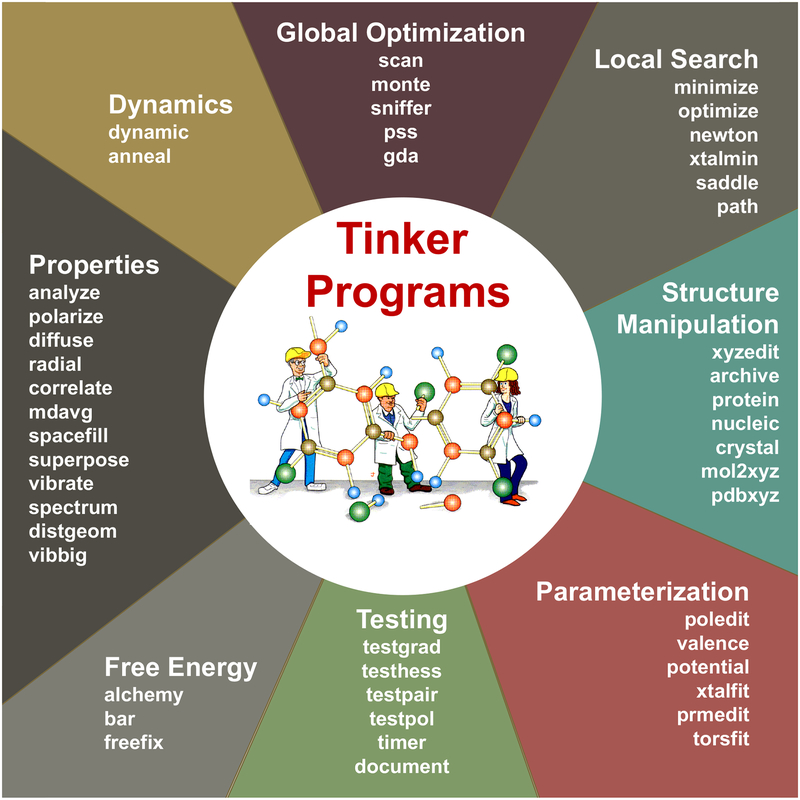
The current Tinker 8 package contains roughly sixty command line programs written in an extended version of Fortran 95, utilizing dynamic memory allocation and OpenMP directives that enable multiprocessing across CPU cores/threads on a shared memory computer system. Figure 1 classifies the individual Tinker programs by basic functionality type. All floating-point computations are performed in full double precision arithmetic. The only hard limits on program size are the allowed number of total atoms and a small number of derived array allocations. The package is distributed with full source code and binary executables for Linux, macOS and Windows operating systems, and dimensioned for a maximum of one million atoms. Systems containing over 20 million atoms have been calculated after rebuilding, and the size is limited only by available memory. The package is designed to enable interactive use via a terminal window, or as background processes controlled via a high-level scripting mechanism. The design goal for the canonical Tinker software is to provide a transparent, modular code base that is easily and directly useable by a broad range of researchers, but efficient enough for application in many production settings.

Figure 1.

Diagram showing the main component programs of the Tinker 8 package, organized into eight functional classes.

In contrast, both Tinker-OpenMM and Tinker-HP are intended to be highly efficient computational engines on their target compute platforms, while maintaining compatibility with canonical Tinker through common coding style, algorithms, file types and general workflows. The Tinker-OpenMM package consists of a branch of the Stanford OpenMM^{29, 30} library with substantial modifications to the AMOEBA plugin, as well as an interface module written in C++ that resides between canonical Tinker and the OpenMM API. It provides a dynamic_omm program that exchanges data between CPU and GPU memory through the library interface and performs molecular dynamics simulations on CUDA-compatible NVIDIA GPUs. TinkerOpenMM supports an increasing subset of Tinker’s energy functions, molecular dynamics integrators, free energy methods, and other features. The current version adds an internal virial implementation for use with barostat techniques, pairwise van der Waals parameters, and is capable of running absolute and relative alchemical calculations with dual topology methods.² Tinker-HP is a new Tinker-compatible MPI-based, massively parallel code for molecular dynamics with an efficient domain decomposition algorithm and analytical polarization solvers. As detailed elsewhere, Tinker-HP is highly scalable across large distributed computer systems containing thousands of nodes and molecular systems containing millions of atoms.¹

2. Features and Organization

File Types and Coordinate Representations

The Tinker files describing a particular molecular system consist of a base name followed by a suffix of three or more characters, e.g., molecule.xyz. Several other file name suffixes are used for various types of output, program control, etc. The most common default Tinker file names are listed in Table 1.

Table 1.

Tinker 8 File Name Suffixes and Descriptions

SUFFIX	Description of File Contents
.xyz	Cartesian coordinates, atom types and connectivity
.int	Internal coordinates as a Z-matrix
.mol	MDL MOL structure compatible with Tinker
.mol2	MOL2 structure compatible with Tinker
.pdb	PDB structure compatible with Tinker
.arc	Structure archive, e.g., MD trajectory
dyn	MD restart information
.hes	Cartesian Hessian matrix
key	Control file with Tinker keywords
tinker.key	Generic keyfile
.err	Current structure at error occurance
.seq	Biopolymer sequence
.vel	Atomic velocities
.ind	Atomic induced dipole moments
.dma	Distributed multipole values
.bar	Window energy values for BAR and FEP
.prm	Force field parameter file
.doc	Detailed parameter descriptions
.end	Requests orderly termination of Tinker program
.vb1, .vb2, .blk	Block iterative vibrational mode files
.001, .002, etc.	“Cycle” files containing sequential structure output

Systems are represented in Tinker as collections of points in space, typically denoting individual atoms or coarse-grained collections of atoms. File representations can contain Cartesian coordinates (.xyz files), full internal coordinates (.int files), torsional angle coordinates or rigid body coordinates. Values are stored in Angstroms and degrees, and output to a precision of 6, 8 or 10 decimal places. Periodic box boundaries are specified in terms of crystallographic lattice lengths (a, b and c) and lattice angles (alpha, beta and gamma). These periodic dimensions are stored as part of the keyword control (.key) file for a calculation or, optionally, as part of the coordinates file itself. Periodic systems, including truncated octahedra, are defined such that the centroid of the box is located at the (0,0,0) coordinate origin.

Software Organization

The majority of the source code of the Tinker package is written in portable Fortran 95 with OpenMP parallelization directives for CPU intensive calculations on shared-memory multiple core systems. The systemwide resources are managed in Fortran modules that make use of dynamic memory allocation and are designed to only represent the current state of the simulation system. The energy specific parameters, e.g. the cubic and quartic coefficients of the fourth-order anharmonic bond potential, are not hard-coded in the source files, thus preserving the flexibility of Tinker in force field development.

The central component of the Tinker package is a modular set of callable routines which (1) manage the package-owned resources, including default initialization, allocation of the dynamic memory, and release of the allocated space, etc., (2) perform molecular mechanical calculations and dynamics simulation on a single set of parameters and atomic coordinates, (3) read in settings from standard input, command line arguments, external files and write out the current state of the system to standard output or external files. These routines essentially work as the underlying application programming interface (API) to build the higher-level routines and programs in the Tinker package. For example, the gradient routine is not only called in multiple integrators but also by various minimization procedures. This design makes creating new routines and new programs easy. A good implementation example is the RESPA integrator. For this integrator the energy and force terms are organized into “fast” and “slow” groups, evaluated on different time scales. Because these energy and force routines are organized as a callable library, RESPA is integrated at a high level by simply toggling these terms on and off.

Keyword Control Mechanism

Every program in the Tinker package is capable of interactively reading arguments from standard input, thus making the program easy to use directly. These interactive inputs are limited to the basic necessities for any given calculation. However, the Tinker programs are not restricted to reading runtime arguments from the command line. Advanced users can set more detailed options via an external configuration (.key) file through a “keyword” mechanism. The keywords not only manipulate the straightforward behavior of the programs, (e.g. whether or not to save the velocities of atoms during a simulation), but also manage default settings (e.g. to change the grid dimension used by PME, as necessary), handle hardware resources (e.g. setting a number of threads for OpenMP, choosing an available GPU card, etc.), and even control library dependency (e.g. switching between underlying FFT algorithms). The current Tinker version implements about 350 keywords, many with multiple options to provide fine-grained control over the behavior of Tinker calculations.

How to Write a Tinker Program

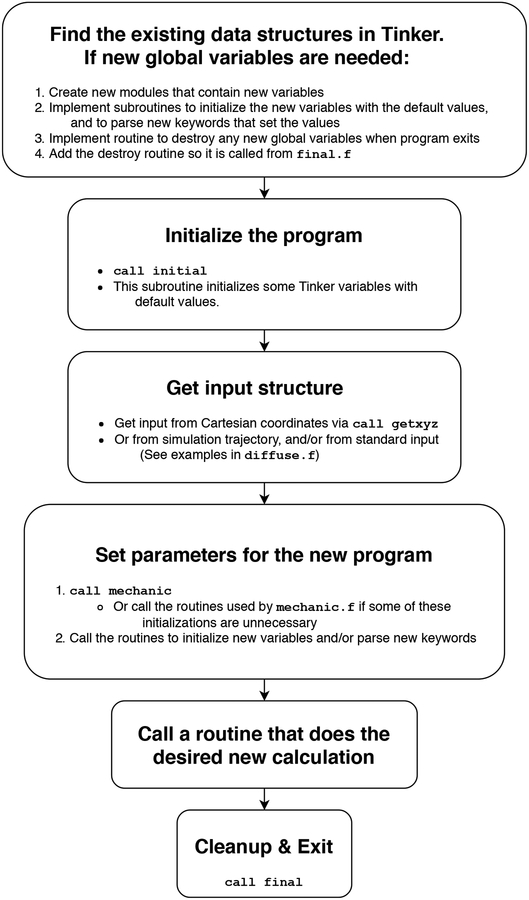
Tinker has an intentionally modular design. In addition to making the code easily understandable, this modularity makes it possible to quickly write new Tinker programs. For most applications, a new program can be initialized, a structure read in, and a molecular mechanics model set up in just three lines of code:

• call initial

• call getxyz

• call mechanic

These steps, shown in more detail in figure 2 allow developers to use Tinker’s existing machinery to quickly set up new types of calculations.

Figure 2.

A schematic procedure illustrating how to construct a new Tinker program.

The first step in writing any new Tinker program is initialization of variables and reading of a molecular structure. If the new program doesn’t require any new global variables, this can be done via the initial and getxyz routines. Initial declares and initializes global variable values that are needed for every Tinker program. Getxyz parses a Tinker Cartesian coordinates file (.xyz) for a molecular system, provided either via command line input or interactively at a user prompt. Once these two routines are called, Tinker is ready to perform operations on the structure. Multistructure “trajectories” can also be read directly as input from Tinker archive (.arc) files.

Once a structure is obtained, the work of setting up a Tinker molecular mechanics calculation is performed by the mechanic routine, which is a self-contained protocol for setting up the potential energy model for a given system. First it assigns connectivity to the structure and obtains a force field parameter file (.prm file). This can be supplied at an interactive prompt, or included in a keyword control file (i.e., a “keyfile”, typically .key) containing Tinker directives or “keywords”. Then mechanic does all the work of setting up the potential energy function. If no keyfile is supplied, the package simply instantiates the contents of the parameter file. If a keyfile is provided, it may optionally contain keywords related to each individual component of the potential energy function and specifying modified or additional parameter values that supersede those in the parameter file. The internal setup for each potential energy term is also highly standardized. For example, the multipole energy, force and Hessian routines, all of which have source files named empole*, have a corresponding initialization routine named kmpole that assigns force field parameters to atoms or groups within the molecular structure. There is a corresponding “k” routine for every potential energy component included in Tinker. Adding an entirely new potential energy function is also straightforward. The developer simply adds the code for the function to the preexisting, empty extra energy and force routines, which have full access to the molecular data structures, and then edits kextra to read in any new parameters or keywords that might be needed for the new potential. Tinker is then set to utilize these routines automatically, and to optionally include them in a force field model.

Providing the tools to easily read in structures and construct models minimizes the work of setting up and debugging Tinker data structures and eases the development of new methods. This modularity, particularly of the potential energy functions, allows developers to quickly alter components of calculations without having to make changes across multiple files. It provides developers the opportunity to create in their own new potential energy terms, force field parameters and keyword control features without having to navigate a maze of source code.

3. Computational Models

Potential Energy Functions

Among the many goals of the Tinker software package, one of the most fundamental is to allow users the ability to explore a wide variety of models. Regardless of whether a user is using new Tinker program they have written or an existing one, every energy-based calculation requires definition of a force field model. To this end, Tinker includes support for a tremendous array of potentials. There are two advantages to the large number of potentials that are included and supported by the package. First, it gives end users the ability to use and compare a wide variety of models for their particular application system. To this end, various Tinker potential terms can be grouped together to replicate several widely used biomolecular force fields such as those from the CHARMM,³¹ Amber³² and OPLS-AA³³ families. The second reason to support a large number of potentials is to expedite the development of new models. Because of the modular nature of the code, researchers can easily incorporate any of the existing potentials in a model. In total there are approximately thirty different potential terms supported in the Tinker package, all with exact analytical energies and Cartesian derivatives, and many with second derivatives. Broadly, the potentials can be divided into intramolecular terms, intermolecular terms and implicit solvent models.

The intramolecular potential energy terms in Tinker can be further subdivided into primary terms and cross terms. The former describe the energetics of simple motions such as bond stretching, angle bending and torsional rotation, while the latter describe coupling between the primary energy terms. The simplest of the primary terms are the bonded potentials. Tinker includes harmonic, anharmonic and Morse bond potentials. The package also has several types of angle bending potentials – harmonic, anharmonic, linear, projected in-plane and Fourier-based angles. Additionally, there are four types of torsion terms included in Tinker. The first is a calculation for a simple torsion defined by four consecutively bonded atoms using a sum of Fourier terms. The second, referred to as a Bell’s “pi-torsion”, computes the torsion around a bond connecting two trigonal centers using the pi-orbital directions at each trigonal center.³⁴ Tinker also includes so-called “improper torsion” terms that define torsionals between nonconsecutively bonded atoms, as used to enforce planarity in the Amber models and many other force fields. Finally, harmonic “improper dihedral” terms can be used to maintain planarity, as in the CHARMM force fields. An additional primary potential term is the direct description of out-of-plane bending. Tinker has thee methods for computing an out-of-plane bending potential. The first two potentials are computed via an out-of-plane angle, using either the Wilson-DeciusCross³⁵ or Allinger³⁶ definitions. A simpler, third method consists of a harmonic term describing the out-of-plane distance of a trigonal atom from the plane defined by its three attached atoms. These primary terms describing the energetics of bonds, angles, torsions, and out-of-plane bends comprise the bulk of most intramolecular energy models a user might like to build or use.

In addition to primary intramolecular potentials, Tinker also supports a variety of intramolecular cross terms. These terms control how the primary energy models are coupled and change as a function of each other. The classic and most basic example of a cross term is the stretch-bend or bond-angle term, which describes how two adjacent ideal bond distances change as a function of the angle between the bonds. Included in Tinker, in addition to a stretch-bend potential, are cross terms for angle-angle, bond-torsion, angle-torsion and torsion-torsion terms as well as a Urey-Bradley³⁷ term. Including these terms in a total potential allows users to build and use sophisticated intramolecular energy models when the application requires it, for example to reproduce vibrational frequencies.

The next broad class of potentials provided by Tinker are intermolecular terms. These can be subdivided into van der Waals (vdW) or repulsion-dispersion interactions, and generalized Coulombic or electrostatic interactions. In order to support a wide variety of models, Tinker includes five different functional forms for van der Waals interactions: a Lennard-Jones 6–12 potential³⁸, buffered 14–7 Halgren potential,³⁹ Buckingham exponential-6 potential,⁴⁰ a Gaussian vdW potential, and the MM3 vdW-hydrogen bond potential.^{41, 42} These functions allow a great deal of flexibility in using and designing models with different representations of short-range interactions between atoms.

The most complex set of potentials included in the Tinker package are the electrostatic interaction potentials. Tinker has the ability to compute simple point charge interactions, but it also implements interactions between higher-order multipole moments. Tinker can treat bondcenter dipole models, permanent atomic multipole models with interactions through quadrupoles, and induced dipole models. The ability to efficiently compute permanent multipole and induced dipole models allows Tinker to run calculations with more advanced models, such as the AMOEBA force field.^43–47 Indeed, much development effort in Tinker has been and continues to be focused on streamlining and modularizing code to implement next-generation force fields with more accurate electrostatic models.

The last major category of potentials in Tinker is continuum models. The most commonly used of these are various implicit solvation models. Tinker includes support for several Generalized Born (GB)⁴² variations including those of Still,⁴³ Onufriev-Bashford-Case,⁴⁸ ACE⁴⁹ and Grycuk,⁵⁰ the Generalized Kirkwood (GK)⁵¹ method for use with polarizable multipoles, accessible surface area-based solvation,⁵² the Hydrophobic Potential of Mean Force (HPMF),⁵³ a novel reaction field method,⁵⁴ and Poisson-Boltzmann (PB)^55–57 solvation models. The GB, GK, surface area and HPMF potentials are all implemented directly in the Tinker code while PB calculations are provided via an interface to the Adaptive Poisson-Boltzmann Solver (APBS) software package.^{58, 59} All of the solvation models in Tinker are implemented to work with advanced electrostatic and induced dipole models. In addition to these solvation models, Tinker also includes surface area and volume calculations with derivatives, which can be used to build or use potentials incorporating these geometric molecular descriptors.

Additionally, Tinker includes two orbital-based models for description of select quantum effects within a classical framework. Simple pi-orbital calculations of the Hückel, Pariser-Parr-Pople, or variable electronegativity self-consistent field (VESCF)⁶⁰ class can be used to scale bond and torsional parameters in conjugated or aromatic systems. Three ligand field models for describing the coordination geometry at transition metal sites within the Tinker package have also been described.^61–63

Although Tinker includes a large number of possible potentials, using them within an energy model is straightforward. The energy and gradient subroutines for each different potential are modular, which is to say they can each be called separately with just one line of computer code. For developers this means it is easy to mix-and-match different potentials in a model or devise new potential as desired. For users this makes it simple way to activate or deactivate individual parts of a model via a single keyword to toggle use of individual potential terms. This makes it easy to manipulate and analyze energy components for complicated structures.

Force Field Models

The wide variety of classical functional forms available in Tinker enables support of a number of existing force fields. From its beginnings Tinker has been intended for use with multiple models. In fact, one of the original goals of the package was to allow users to seamlessly compare energetic models for a given problem or application. To this end Tinker supports the following standard force fields: Amber,^64–68 CHARMM,^69–72 OPLS,^73–78 MM2/3,^{8, 79–83} MMFF,⁸⁴ AMOEBA,^{44–46, 85–87} Dang,^88–97 the so-called “Tiny” force field, and a number of specialized models for water. For many of these force fields, several modifications are provided as complete parameter sets contained within the Tinker distribution.

The force fields available in Tinker span a wide range: from the Tiny force field with generic parameters based on element type and valence for use in optimizing crude structures to the AMOEBA09 small molecule force field containing detailed parameters over finely subdivided atom types and advanced functional forms such as multipolar electrostatics and induced dipole polarizability. The included force fields also span major classes of biomolecules, with parameters to model proteins, nucleic acids, lipids, and small organic molecules. Users should consult the respective literature on each force field before deciding which model might be best suited to their application.

4. Capabilities

Structure Manipulation

In order to generate coordinate files adapted to various software packages and purposes, Tinker provides convenient tools to convert coordinate files into different formats and to manipulate the coordinate file for different calculation purposes, such as building crystal structures, generating periodic boxes etc.

First, Tinker recognizes the Tinker .xyz file format for all calculations. However, other software packages are adapted to coordinate files of other formats. For instance, CHARMM, AMBER and VMD are adapted to PDB files, SYBYL are adapted to MOL2 files and many QM packages such as Gaussian is able to read in internal coordinate files. To allow interoperability, Tinker provides six commands to do the interconversion between different coordinate files. The command pdbxyz takes a Tinker xyz file as input and generates the corresponding PDB file as output. The command xyzmol2 converts a Tinker xyz file to a MOL2 file. The command xyzint converts an xyz file to an internal coordinate file in which the absolute Cartesian coordinates are expressed as relative positions (bond length, bond angle and torsional angle) among atoms. The commands pdbxyz, mol2xyz, and intxyz convert PDB files, MOL2 files and internal coordinate files back to xyz files.

Second, Tinker also provides file-editing tools for the purpose of simulation setup. Most of xyz editing tools are listed as options under the command xyzedit, such as inserting and deleting atoms, changing force field atom types, translating/rotating a system to specified Cartesian or rigid body coordinates or into the inertial frame, appending and merging multiple files, or soaking a second xyz file, creating a periodic boundary box, placing a solute into a periodic solvent box, adding ions to a solvated system, etc. The command superpose is designed to superimpose a pair of structures to at optimal root mean square deviation (RMSD) using a non-iterative quaternion-based algorithm.⁹⁸ Since biomolecules such as nucleic acids and proteins are target systems for many studies, Tinker provides nucleic and protein tools to generate nucleic acid and protein structures respectively according to the sequence information and backbone or side chain torsional angle values. Lastly, the utility crystal utility is designed for manipulation of crystal structures such including generation unit cells from asymmetric units and according to box size, shape and space group.

Local Search and Minimization

Tinker has a number of local minimization algorithms implemented to effectively and efficiently minimize a quantity of interest. Several algorithms are widely used in Tinker in conjunction with a force field to minimize the energy of a molecular structure. The code contains routines for Limited Memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS)^99–101 minimization, Optimally Conditioned Variable Metric (OCVM)^{102, 103} nonlinear optimization, and Truncated Newton Conjugate Gradient (TNCG)^{12, 104} Hessian-based optimization. The LBFGS algorithm is of the nonlinear conjugate gradient class, and as such does not require an analytical Hessian matrix. It uses the BFGS update to update the line search direction at each iteration. The limited memory implementation in Tinker allows this routine to be used for Cartesian minimization of large systems. The OCVM algorithm uses a quasi-Newton methodology without line search to update an approximation to the inverse Hessian at every step. It is particularly effective for optimization of rougher potential surfaces, such as those in torsional space. Lastly, the TNCG algorithm uses a preconditioned truncated conjugate gradient method coupled with direct sparse Hessian evaluation or a finite-difference Hessian approximation to minimize an objective function. The TNCG method converges quadratically once in the vicinity of a local minimum and can optionally find transition states and general stationary points after disabling checks for negative curvature. LBFGS and TNCG use the same line search algorithm, a gradient-based trust region safeguarded parabolic extrapolation, cubic interpolation procedure. To minimize structures, the LBFGS, OCVM and TNCG methods are implemented in the Tinker minimize, optimize and newton programs, respectively. These minimize structures in Cartesian coordinate space. Tinker also contains the corresponding programs, minirot, optirot and newtrot for minimizations in torsional space as well as minrigid and optrigid for minimizations with rigid body groups of atoms.

While TNCG-based optimization methods are easily modified to allow convergence to transition states, the catchment basin is often small and requires a starting structure near to the final transition state. Tinker contains two other methods, saddle and path, that are specifically designed to locate conformational transition states and pathways. Saddle represents a combination of ideas from the Halgren-Lipscomb synchronous transit^{105, 106} and Bell-Crighton quadratic path¹⁰⁷ methods. It takes two endpoint structures as input, and performs an iterative series of maximizations along the connecting path and minimizations orthogonal to the path until the saddle point is located. The path program starts from local minima and uses Lagrange multiplier-based constraints to minimize orthogonal to a series of equally spaced path points, generating a “trajectory” along the interconversion pathway.¹⁰⁸

In addition, Tinker contains an adaptive derivative-free multi-dimensional Nelder-Mead simplex optimization algorithm and a modified Levenberg-Marquardt least squares algorithm combining features of the IMSL BCLSF routine and the LMDER code from Minpack.¹⁰⁹ These methods are used within Tinker for optimization of stochastic objective functions and in force field parameter refinement, respectively.

Global Optimization

Besides the various optimization methods to find local minima of potential energy functions, Tinker also has a number of optimization algorithms to find global minima of the target function. Roughly, these algorithms can be divided into two categories: first, methods that rely on pathway- or trajectory-dependent propagation to overcome the local barriers or to enumerate local minima; second, methods that modify the underlying potential surface while approximating a solution to the equilibrium density distribution. The first category of methods includes simulated annealing,¹¹⁰ generalized gradient descent,^{111, 112} “Jumping-between-Wells”¹¹³ and the Monte Carlo minimization (MCM) method.^{114, 115} The second category of global optimization algorithms includes potential smoothing techniques^116–119 and the related gaussian density annealing (GDA) scheme.¹²⁰

The anneal program is a traditional MD-based simulated annealing code with an optional pre-equilibration phase and several available cooling schedules. It starts from a high temperature at which local energy barriers are easily to overcome. Then the cooling schedule is applied to gradually lower the temperature and coalesce into a low energy local minimum. In the sniffer program, a second order differential equation is designed to enable generalized descent along a trajectory without becoming trapped in the catchment region of any particular minimum. Following a steepest descent propagator, the trajectory is constrained to a minimum that is greater than the predefined energy levels, which is presumed to be the global minimum.^{111, 112, 121} The scan program uses Jumping-between-Wells to locate all the local minima for an input structure by self-consistently following low frequency normal mode search directions from all known minima. The global minimum can be obtained by comparing all the local minima.¹¹³ The monte program implements an MCM protocol which uses Metropolis Monte Carlo exploration of a potential surface where the energy of each point on the surface is remapped to the value of the closest local minimum.¹¹⁴ Potential surface smoothing (PSS) views the original potential energy functional forms as the time zero initial conditions for solution of the diffusion equation. Conformational search is then performed on the smoother surface produced at some finite, nonzero time. The method can be shown to be mathematically equivalent to performing molecular mechanics with “fuzzy” atoms, where the location of each atom is generalized to a Gaussian probability distribution around its most likely position. The pss, pssrot and pssrgd programs implement the PSS idea in terms of Cartesian, torsional and rigid-body representations, respectively. The gda program performs annealing while seeking an approximate solution for the equilibrium density distribution, and can be viewed as a dynamical version of the deterministic potential smoothing methods.

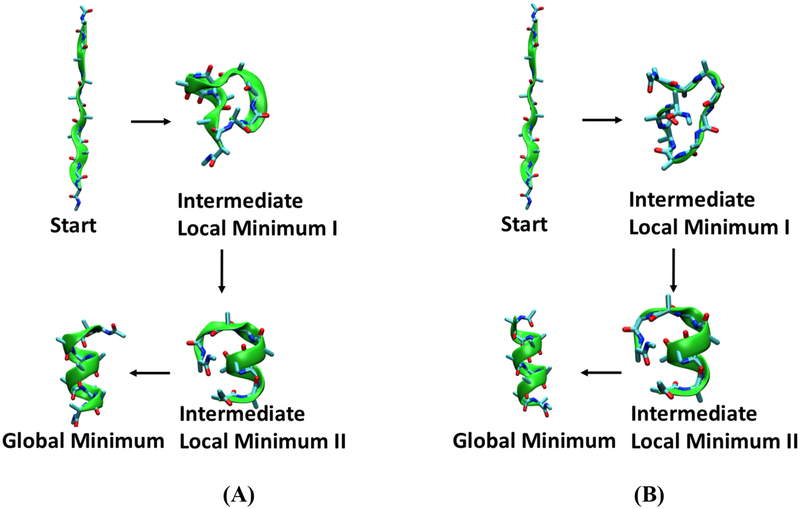
Two examples of the global optimization methods are demonstrated in figure 4 for a gas phase deca-alanine model system in gas phase using the scan and monte programs. Both optimizations start from the same linear structure of Deca-Alanine and eventually reach the same global minimum, the structure of which is a typical a-helix as shown in figure 4A and 4B. The scan method captured 654 intermediate structures while scanning the full potential surface. The monte method generated eight intermediate local minima along its path to the helical structure. Two intermediate structures from each calculation are presented in figure 4A and 4B. Though they follow different paths in moving around the surface, both methods appear to produce find a similar partially optimized structure, shown as intermediate minimum II in figure 4.

Figure 4.

Structural optimization of Deca-Alanine in the gas phase using (A) the scan program and (B) the monte program.

Dynamics Methods

One of the important features for any modern molecular mechanics software package is the ability to perform molecular dynamics (MD). In the past four decades, many of the important contributions of classical empirical potential models have been realized through MD simulations. In Tinker this feature is implemented through the dynamic program: a feature-rich MD engine. In addition to being able to run simulations with any of the force fields included with Tinker, it allows the user a great deal of flexibility in the details of how a simulation is run.

Tinker has the ability to run simulations in any of four traditional statistical mechanical ensembles: Microcannonical (NVE), Cannonical (NVT), Isoenthalpic-Isobaric (NPH) and Isothermal-Isobaric (NPT). For each of these options, where necessary, Tinker can employ a wide variety of integrators, thermostats and barostats. The possible integrators include Velocity Verlet, Beeman,^{122, 123} stochastic,^{124, 125} Nosé-Hoover NPT,¹²⁶ Bussi-Parrinello NPT,¹²⁷ a twostage, multiple time step, reversible Reference System Propagator Algorithm (RESPA)^{128, 129} and a rigid-body integrator.¹³⁰ Most of these integrators have been reviewed extensively in the literature. Two of particular interest, however are the RESPA integrator and the rigid body integrator. The RESPA integrator allows the user to take two separate time steps when propagating molecular dynamics. The first, fast time step is used for fast-changing degrees of freedom such as bond stretching and the second, slow time step is used for the slow-changing, but computationally expensive electrostatics or polarization calculations. The rigid body integrator is unique to Tinker and is based on the original work of Andrey Kutapov and Marina A. Vorobieva (VNIITF, Russian Federal Nuclear Facility, Chelyabinsk). Tinker also includes an implementation of the RATTLE algorithm¹³¹ in order to implement holonomic constraints within velocity Verlet and related integrators. In addition, Tinker contains a stochastic dynamics integrator¹³² employing a series expansion to treat small frictional coefficients,¹³³ and with the ability to scale the friction term based on accessible surface area.¹³⁴

For the constant temperature and pressure ensembles, Tinker includes a variety of thermostats and barostats. The included thermostats are Bussi¹³⁵, Berendsen¹³⁶, Andersen¹³⁷ and Nose-Hoover.^{126, 138} The available barostats are Berendsen,¹³⁶ Bussi-Parrinello¹²⁷ and Monte Carlo.¹³⁹ It should be noted that because Tinker includes an internal virial calculation for every available model potential, the Berendsen barostat may be used with both simple and advanced models. The defaults in Tinker are the Bussi thermostat and Berendsen barostat, but the available thermostats or barostats can be used in any of several combinations with the standard integrators (Verlet, Beeman and RESPA). An active area of development in Tinker is application of an isokinetic scheme that combines a massive thermostat with a multiple time step integrator to achieve ultra-long time steps for the slowly evolving, but computationally expensive, potential terms in a simulation. This method is deemed Stochastic-Iso-NH-RESPA or SIN(R) and it has been demonstrated to achieve outer time steps of up to 100 fs for the AMOEBA water model without loss of model accuracy.^{140, 141}

Properties and Analysis

One of most useful programs in the Tinker package is analyze. It can be used to evaluate a single structure or a multiple-frame file from a simulation. The program is designed to provide everything from general information to detailed atom-level information about the system. Its most basic function is to simply print out the total potential energy broken down into each individual component but can do much more. The analyze program can give information about the force field being used and the parameters for every atom in the system. It optionally outputs a potential energy breakdown by atom, or with details for every interatomic interaction. It can also give the user some basic properties of the system, such as electric moments and principle axes. Analyze calculates the internal virial, numerical and virial-based derivatives of the energy with respect to volume. And lastly it can print the connectivity list and force field parameters used for every atom and interaction. As with many Tinker programs, analyze can take as input either a single structure as an .xyz file, or a multi-frame archive or MD trajectory as a Tinker .arc file. These features not only allow users to evaluate properties for single structures or trajectories, but also to quickly spot and isolate any errors or inconsistencies that might occur.

Tinker implements analytical Hessian computation for many potential functions, and numerical Hessian evaluation for all others. The Hessian is arranged in a sparse matrix with only elements with magnitude greater than a keyword specified cutoff stored. The vibrate program finds the mass-weighted Hessian, and after diagonalization via the diagq routine (Bernard R. Brooks, NHLBI, NIH), produces the normal modes and vibrational frequencies for the input structure. Small multi-frame structure files are also generated to enable visualization of the motion along each mode.

For large structures, such as biopolymers, where full matrix diagonalization is not practical, the vibbig program implements an iterative sliding block diagonalization method that finds the lowest frequencies and corresponding modes with O(N²) computational effort.¹⁴²

In addition to analysis and manipulation of structures, Tinker has a suite of programs designed to assess properties for liquid systems. The diffuse program takes as input an MD trajectory as a .arc file and calculates the self-diffusion coefficient of a homogeneous liquid or subset of atoms from a heterogeneous system. The algorithm employed uses the standard Einstein relation applied to the molecular centers of mass of the liquid. There are also programs to compute the bulk dielectric constant and radial distribution function (radial) starting from an input dynamic trajectory.

Correlate as a general program and formalism for computation of time correlation functions. It has built-in methods to find structural correlation and velocity autocorrelation functions. In addition, users can provide an external routine to compute any structure- or energybased property, and correlate will generate its correlation function. Additionally, the velocity autocorrelation function is used as input to the Tinker spectrum program, which computes the corresponding power spectrum. This suite of programs gives users a set of tools to assess properties from liquid simulations.

Free Energy Calculations

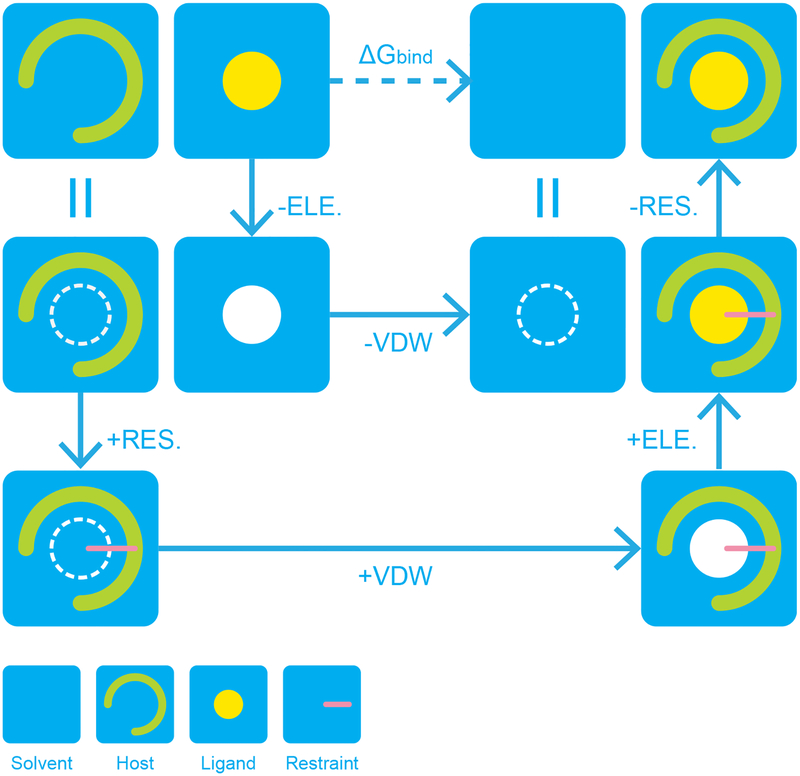
One of the most common applications of molecular modeling is the calculation of binding free energies. To compute the binding free energy of a drug to a protein or solvation free energy of an ion in water, Tinker has methods available. Computation of binding free energies relies on the completion of a thermodynamic cycle, as pictured in figure 5. In order to calculate a free energy, Tinker employs an “alchemical” approach that “disappears” the ligand of interest in the presence and absence of its host. The free energy differences of these processes are calculated using free energy perturbation.

Figure 5.

A typical thermodynamic cycle for the calculation of absolute binding free energy of host and ligand in Tinker. The completely solvated ligand and a solvent box are associated through intermediate states with gradual changes in the order parameters of vdW and electrostatics. While the order parameter of electrostatics affects both intermolecular and intramolecular interactions, the decreasing order parameter of vdW only decouples the ligand from the environment and does not change the intramolecular vdW interaction. A restraint is added to prevent the possible bad contacts and to help sampling.

The majority of the analysis of the free energy difference of the sampled conformations in Tinker package is handled by the bar program. Bar applies the standard Zwanzig’s free energy perturbation (FEP) method¹⁴³ and Bennett’s acceptance ratio (BAR) method¹⁴⁴ for the canonical ensemble. Additionally, the bar program has been extended to process isothermal-isobaric simulations¹⁴⁵ and to estimate the differences in entropy and enthalpy of the samples.¹⁴⁶

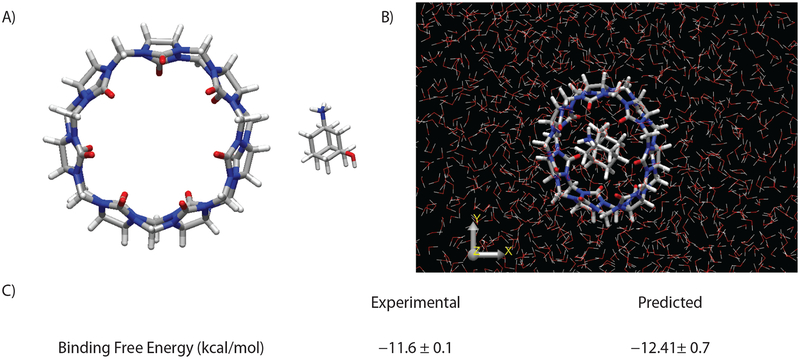
An example of the utility of the dynamic and bar programs is calculation of binding free energies for the SAMPL4 host-guest challenge.¹⁴⁷ We used dynamic to run sampling simulations of the host-guest binding systems over λ-windows to decouple guest electrostatic and van der Waals interactions, and then performed bar free energy perturbation calculations on those trajectories. The results for one particular host-guest pair are shown in figure 3. In addition to prediction of the binding free energy, dynamic trajectory snapshots show the preferred binding pose for this ligand.

Figure 3.

Binding free energy calculation for the model system cucurbit[7]uril and 3-amino-1-adamantanol. (A) Structures of host and guest, (B) Predicted binding pose from dynamic, (C) Experimental and predicted binding free energy.

Testing and Debugging

All of the analysis procedures listed above depend on the validity of the model that goes in to them. Tinker has many built-in utilities to test the correctness of code for new existing and new models. These allow developers to quickly test if a new energy function and its derivatives are consistent. The testgrad and testrot programs check to make sure the analytical potential energy derivatives match those calculated numerically. Testgrad operates in Cartesian space, while testrot computes and checks derivatives with respect to torsional angles. The testhess program takes this the next step by comparing the analytical Hessian against one computed numerically from either gradient or energy values. It can calculate the numerical hessian from either the potential energy or the gradient. Finally, the testpair utility tests methods for determining pairwise neighbor interactions in energy and gradient evaluation. This program compares results and computes timings for energy and gradient evaluations using a double loop, the method of lights or a pairwise neighbor list.

In addition, Tinker includes polarize, a program to compute the molecular polarizability of an individual molecule using either an additive or interactive induced dipole model. In addition to being able to compare with experiment values, computing molecular polarizability gives users an idea of how strongly many-body effects may affect subsequent calculations.

Parameterization Tools

The final set of important utilities in Tinker are a trio of programs designed to parameterize new molecules. The Tinker valence, poledit and potential programs can be used to generate parameters for intra- and intermolecular potential energy functions. The valence program takes a Tinker .xyz file and a Gaussian QM output file and generates a set of parameters for the basic intramolecular potential energy function as well as rough guesses at van der Waals parameters. It can also further refine those intramolecular energy function parameters by fitting to QM calculation results. The poledit program allows users to set and modify atomic multipole models. It can generate multipole parameters obtained from Gaussian Distributed Multipole Analysis (GDMA) output.¹⁴⁸ It is also used to set local coordinate frames for atomic multipole, modify polarizability values, define polarization groups for the AMOEBA model, and average multipole parameters for symmetry-related sites.

Lastly, the potential program can be used for the evaluation and refinement of atomic multipole models. This utility computes the electrostatic potential on a grid of point surrounding a molecule. It can then either compare that potential to another multipole model or QM calculation or fit the multipole model to the QM result. These three parameterization programs are combined in a Python-based, publicly available software package called Poltype.¹⁴⁹ This program is specifically designed to automate the process of generating parameters for the AMOEBA model and has been used extensively to facilitate rapid and reproducible parameterization of new molecules.

5. Algorithms

One of the challenges faced by all molecular modeling packages is efficient calculation on large application systems. Tinker incorporates a number of interesting and novel algorithms to help address computational bottlenecks, including algorithms of for periodic boundary calculations, neighbor list generation, particle mesh Ewald summation for electrostatics, and efficient induced dipole solvers for polarization.

Periodic Systems and Neighbor Lists

To enable modeling of “infinite” systems, four types of periodic box are supported in Tinker. These are orthogonal, monoclinic, triclinic and octahedral, where the octahedral periodic box refers to a truncated octahedron derived from the corresponding cube. When the cutoff of the periodic boundary condition is so large that the neighbors of an atom include at least two images of the same atom, a unique “replica” method is enabled automatically to replicate the periodic box to account for this situation. Tinker provides four internally built neighbor lists whose cutoff distances and list buffers can be configured separately through keywords for the van der Waals, the partial charges, the atomic multipoles and the polarization preconditioner, respectively, to speed neighbor searching as opposed to the naïve double loop method only if the replica method is not enabled. An efficient, OpenMP parallel neighbor list updating mechanism is used to minimize list rebuilding overhead. The Method of Lights¹⁵⁰ can be used to efficiently construct the neighbor lists for the triclinic, monoclinic and orthogonal boxes. Finally, the periodicity code in Tinker is able to handle infinite bonded polymers by tracking valence terms across periodic cell boundaries. This enables correct treatment of the diamond lattice, rubber, graphite, plastics, and similar large repeating systems.

Particle Mesh Ewald Summation

To speed electrostatics and polarization calculations on large systems, Tinker has the ability to use smooth particle mesh Ewald summation (PME) for models including charges, multipoles or induced dipoles. Descended from an original PME code written by Thomas Darden, Tinker 8 gives the user control over the Ewald damping parameter and the allows use of either “tinfoil” or vacuum boundary conditions. The PME module also supports truncated octahedra as a periodic shape and allows performing PME calculations on a non-periodic systems. The current Tinker implementation follows closely the multipole PME version previously described by Sagui, et al.¹⁵¹ The code follows the structure of typical PME software: putting the electrostatic moments onto a spatial grid, performing a Fourier transform, performing the potential and electric field calculations in Fourier space, transforming back to real space, and finally computing the energy and force on every atom. One unique feature of the code is a domain decomposition scheme for putting moments on the grid. This method, developed by David Gohara (Biochemistry, Saint Louis University), parallelizes this step, which otherwise is the rate limiting computational step for large systems. Tinker optionally uses either a refactored 3D version of the public domain FFTPACK Fourier transform code, or the Fast Fourier Transform package FFTW (Fastest Fourier Transform in the West)¹⁵² to perform the forward and backward Fourier transforms necessary for PME calculations.

Polarization Algorithms

One of the defining features of Tinker is its ability to run simulations with force fields that include induced dipole polarization. The foundational idea of such models is that the induced dipole at a given site is proportional to the electric field at that site according to

$${\overrightarrow{\mu }}_i={\alpha }_i{\overrightarrow{F}}_i$$

where μ, α and F represent the induced dipole, the polarizability, and the electric field respectively. In a mutually inducible model, the electric field arises not only from the permanent moments of the systems, but the induced dipoles as well.

$${\overrightarrow{F}}_i={\overrightarrow{F}}_i^{perm}+{\overrightarrow{F}}_i^{ind}$$

This gives rise to the total induction energy,

$$U^{ind}=\frac{1}{2}\sum _i{\overrightarrow{\mu }}_i•{\overrightarrow{F}}_i^{ind}-\sum _i{\overrightarrow{\mu }}_i•{\overrightarrow{F}}_i^{perm}$$

where all that is needed is to solve for the induced dipoles of the system. Tinker has three methods of determining the induced dipoles of a system: Preconditioned Conjugant Gradient (PCG), Optimized Perturbation Theory (OPT) and Extended-Lagrangian/Self Consistent Field (iEL-SCF).

The most straightforward way to obtain the induced dipoles of a system is by requiring a zero residual,

$$R=\left(\frac{dU}{d\overrightarrow{\mu }}\right)=0.$$

which enforces that the change in energy should be zero for an infinitesimal change in the induced dipoles. Solving this system of equations is a flavor of the familiar self-consistent field (SCF) calculation. In Tinker this is done using a preconditioned conjugate gradient algorithm¹⁵³ and is typically able to converge the calculation within 5–6 iterations.

The OPT method^{154, 155} works in a manner similar to PCG, but instead of iteratively lowering the residual, it computes induced dipoles from perturbation theory. In this scheme the exact induced dipoles are expanded in a power series,

$${\overrightarrow{\mu }}_{tot}={\overrightarrow{\mu }}_0+\lambda {\overrightarrow{u}}_1+{\lambda }^2{\overrightarrow{\mu }}_2+\dots +{\lambda }^n{\overrightarrow{\mu }}_n$$

where each order of the perturbation is determined by:

$$\begin{array}{l}{\overrightarrow{\mu }}_0=\alpha {\overrightarrow{F}}^{perm}\hfill \\ \lambda {\overrightarrow{\mu }}_0=\lambda \alpha {\overrightarrow{F}}^{ind\left({\mu }_0\right)}\hfill \\ {\lambda }^2{\overrightarrow{\mu }}_1={\lambda }^2\alpha {\overrightarrow{F}}^{ind\left({\mu }_1\right)}\hfill \\ ⋮\hfill \\ {\lambda }^n{\overrightarrow{\mu }}_n={\lambda }^n\alpha {\overrightarrow{F}}^{ind\left({\mu }_{n-1}\right)}.\hfill \end{array}$$

In this expansion, each order of dipole determined by the one that precedes it. This gives rise to a final energy expression,

$$\begin{array}{l}U=\sum _i{\overrightarrow{\mu }}_i^{OPT}•{\overrightarrow{F}}_i^{perm}\hfill \\ {\overrightarrow{\mu }}^{OPT}=M_0{\overrightarrow{\mu }}_0+M_1{\overrightarrow{\mu }}_1+M_2{\overrightarrow{\mu }}_2+\dots +M_n{\overrightarrow{u}}_n\hfill \end{array}$$

where the M coefficients are parameters that can tuned. Tinker currently has the ability to include up to six terms in this expansion, but it has been shown that including only three is a reasonable approximation that gives a speed boost over traditional PCG.

The final method included with Tinker is the iEL-SCF method.¹⁵⁶ This method minimizes the number of iterations needed in solving the induced dipoles by introducing the Lagrangian,

$$L=\frac{1}{2}\sum _i{m}_i{\dot{\overrightarrow{r}}}_i^2+\frac{1}{2}\sum _i{m}_{\mu ,i}{\dot{\overrightarrow{\mu }}}_i^2-U_{AMOEBA}\left({\overrightarrow{r}}^N,{\overrightarrow{\mu }}_{SCF}^N\right)-\frac{1}{2}{\omega }^2\sum _i{m}_{\mu ,i}{\left({\overrightarrow{\mu }}_{SCF,i}-{\overrightarrow{\mu }}_i\right)}^2$$

where m_i represents the mass of atom i, m_μ,i a fictitious dipole mass and ω the frequency of the harmonic potential that keeps the induced dipoles close to the fully converged SCF solution. By applying Lagrangian equations of motion, one obtains the classical equation of motion plus the equation of motion for the auxiliary degrees of freedom,

$$\begin{array}{l}{m}_i{\ddot{\overrightarrow{r}}}_i=-\frac{\partial U_{AMOEBA}\left({\overrightarrow{r}}^N,{\overrightarrow{\mu }}_{SCF}^N\right)}{\partial {\overrightarrow{r}}_i}\hfill \\ {\overrightarrow{\mu }}_i={\omega }^2\left({\overrightarrow{\mu }}_{SCF,i}-{\overrightarrow{\mu }}_i\right)\hfill \end{array}.$$

To maintain stability, a thermostat is applied to the auxiliary degrees of freedom. This gives the iEL-SCF method the ability to reduce the number of iterations needed to obtain induced dipoles for a system and thus speed up simulations.

In addition to these methods, there are future plans to include at two additional polarization options into Tinker 8. The first is an extension of the iEL-SCF method called iEL0SCF.¹⁵⁷ This method uses the same auxiliary dipoles from the iEL-SCF scheme, but instead of using them as a starting point for SCF, they are used to drive dynamics directly. By avoiding SCF iterations, the iEL-0SCF method does not produce fully converged dipoles but does allow for much faster, stable MD simulations. The second method, already incorporated into the Tinker-HP code base is the Truncated Conjugate Gradient method (TCG).¹⁵⁸ This approach computes a fixed number of iterations of the conjugate gradient algorithm and then corrects for the fact that the residual has not been minimized to zero. By using successive approximations from the conjugate gradient iterations this method avoids needing any parameters as are needed in the previous approximate methods listed. Moreover, by correcting for the lack of zero residual, the TCG method allows for faster computation of analytical induced dipoles than full SCF methods like PCG. Both of these methods are slated for implementation in the next release of Tinker.

Orthogonal Space Random Walk

Besides the typical Free Energy Perturbation (FEP) method, the Orthogonal Space Random Walk (OSRW) free energy calculation method is also implemented in Tinker. Classical FEP methods (BAR, thermodynamic integration, etc.) arbitrarily select an order parameter to sample. The OSRW method is capable of exploring the order parameter as well as the so-called “hidden degrees of freedom” simultaneously.^{159, 160} Due to the complexity of many systems, efficiently sampling the hidden degrees of freedom dominates the accuracy of final free energy computation. Currently, OSRW free energy calculations in Tinker are supported for the NVT ensemble and RESPA integrator, and are restricted to the buffered 14–7 vdW potential where a softcore-modified buffered 14–7 potential is applied as a replacement for the original. Permanent electrostatic interactions are also modified by a softcore treatment, to prevent numerical instability during simulation.¹⁶¹ When using OSRW with AMOEBA, the polarization energy and forces are computed using an interpolation between fully charges/polarizable and decharged/nonpolarizable ligand atoms as described previously.¹⁶² Work is currently underway, in collaboration with Wei Yang (Chemistry, Florida State University) to implement the most recent versions of his orthogonal space tempering techniques into the family of Tinker programs.¹⁶³

The setup of a Tinker keyfile for use of OSRW is straightforward. For instance, to compute the hydration of free energy of small solute in water only four additional keywords are required. First, the keyword LIGAND specifies the atom numbers of the solute for the hydration free energy calculation. The additional Tinker keywords OSRW-ABSOLUTE, DONOLIGANDCONDENSED, DOVAPORELEC specify an absolute solvation energy calculation, the presence of only a single ligand molecule, and use of a gas phase leg in the free energy calculation, respectively.

Distance Geometry

In the context of molecular modeling, distance geometry (DG) is method for generating a structure or structures consistent with an input set of distance constraints.^164,165 A basic DG algorithm takes an object in a high-dimensional mathematical “distance space”, and reduces dimensionality by projecting it into a 3D molecular structure. An early important use of the method involved the generation of protein NMR structural models from short-range NMR NOE distance constraints.¹⁶⁶ However, a more interesting application of distance geometry is to under constrained problems. Given a limited set of upper and lower bound distances between atoms or groups in a molecular system, one would like for a distance geometry algorithm to generate a uniform sampling of all possible structures consistent with the input distance ranges. Tinker 8 contains an efficient method that exhibits excellent sampling properties for under constrained input through extension of standard DG algorithms. First, the Tinker distgeom program uses random partial metrization to update the matrix of upper and lower distance bounds whenever an individual distance value is fixed during structure generation. Only a small predetermined portion of the distance selections are followed by metrization, reducing the computational burden of a nominally O(N⁴) method.¹⁶⁷ Tinker uses a powerful, but relatively little-known, shortest path update algorithm to further reduce the metrization work load.¹⁶⁸ Second, distgeom selects distances between the upper and lower bounds from a Gaussian-like distribution tuned to reproduce reasonable molecule structures, instead of using the traditional flat, uniform distribution.¹⁶⁹ Additional terms are used to enforce local chirality and torsional constraints, and simulated annealing on geometric constraints is used to refine output structures. The resulting Tinker program performs well in NMR applications,¹⁷⁰ and provided good sampling in less constrained situations such as protein structure prediction.¹⁷¹

6. Force Field Explorer

In addition to the suite of command line programs, Tinker also includes a graphical user interface (GUI) called Force Field Explorer or FFE. This program allows users to visualize molecular structures and provides access to many of Tinker’s analysis, search and dynamics methods from a simple, user-friendly interface. This functionality makes FFE useful both as a research tool and as an instructional aid.

Force Field Explorer 8 gives users a powerful, simple and many-featured way to visualize molecular structures. It allows users to model molecules of interest using standard representations (wireframe, ball and stick, etc.). Molecules can be loaded directly from existing Tinker files, or downloaded from the NIH PubChem database,¹⁷² the NCI CACTUS database and the RCSB Protein Data Bank (PDB).¹⁷³ Biopolymers can also be interactively constructed from sequence in various idealized structures. The program also gives users the ability to play back any Tinker molecular dynamics trajectory with the click of a button. In addition to these standard features, FFE also includes tools for force field-specific visualization. It can render a structure using the van der Waals radii specific to the force field being used, or display the partial charges or velocities assigned to each atom of a system. For polarizable force fields, it can display the induced dipoles as a vector at each atom at every time point of a simulation. These features allow users to assess in time and space how force field parameters affect the results of their calculations.

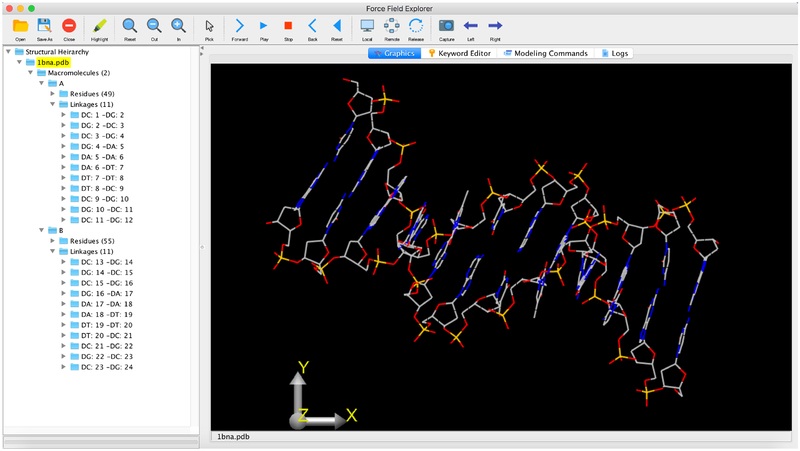
What makes Force Field Explorer a unique tool is that it combines visualization power with the functionality of Tinker. Through the graphical interface, users can run many of Tinker’s analysis, search and dynamics programs. Simple minimizations or MD simulations can be started with the click of a button. The GUI has the ability to directly modify the Tinker key file via a graphical editing facility. By enabling access to the key file, users can quickly and easily change the options for whatever calculation they’re running without touching the command line. As shown in the example of figure 6, FFE’s functionality is laid out in an easy-to-navigate format. This combined with the integration with the full integration of Tinker makes Force Field Explorer useful not only for research, but also educational purposes.

Figure 6.

Force Field Explorer (FFE) displaying the Dickerson dodecamer structure of B-form DNA. The expandable tree structure in the left panel provides access to coordinate and type information at the molecule, residue and atom levels.

Communication between FFE and Tinker is mediated by the Java sockets mechanism. Special versions of Tinker executables built against the FFE interface, allow Tinker calculations to send output to FFE in real time, including coordinates, velocities, induced dipoles, lattice parameters and other variables. Conversely, FFE is able to connect to an already running Tinker job on a remote machine, in order to perform job control tasks, display an MD trajectory interactively, etc.

7. Benchmarks

Six periodic boundary systems of increasing size (from 648 to 174219 atoms) have been constructed as benchmark tests to examine the efficacy of Tinker 8 and Tinker-OpenMM on standard CPU and commodity NVIDIA GPU devices, respectively. The systems reported include: a small water box of 216 AMOEBA water molecules, a larger 500 molecule TIP3P water box, the crystallographic unit cell of the plant protein crambin, a cucurbituril clip host-guest system from the SAMPL5 exercise,¹⁷⁴ a solvated DHFR protein, and a solvated COX-2 protein dimer. The system sizes differ by more than two orders of magnitude. Force fields tested were Amber ff99SB⁶⁸ and AMOEBA. All simulations were performed with a 2 fs MD time step, and throughput is reported in nanoseconds per day in Table 2. We note that hydrogen mass reweighting,¹⁷⁵ which retards high-frequency motions, is a keyword option available in Tinker. Use of this option coupled with tight thermostating enables stable MD trajectories at 4 fs time steps, and yields roughly double the throughput reported in Table 2. As expected, the GPU implementation via Tinker-OpenMM significantly outperforms the reference CPU version of Tinker 8 for production MD calculations.

Table 2.

Tinker 8 CPU and Tinker-OpenMM GPU MD simulation timings in ns/day.^a

			CPUb	GPUc
SYSTEM	POTENTIAL	ATOMS		970	1070	1080Ti
WaterSmall	AMOEBA	648	4.78	61.6	98.4	125.9
WaterBox	TIP3P	1500	14.2	361.7	574.9	671.9
Crambin	AMOEBA	1920	1.12	43.0	64.2	72.0
CBClip	AMOEBA	6432	0.664	20.9	32.5	46.1
DHFR	AMOEBA	23558	0.164	8.62	13.1	20.0
DHFR	Amber ff99SB	23558	1.16	78.4	115.1	204.7
COX-2	AMOEBA	174219	0.0176	1.05	1.67	2.27
COX-2	Amber ff99SB	174219	0.150	10.7	15.3	24.6

^aAll simulations run with 2 fs MD time steps; RESPA integrator and OPT polarization model for AMOEBA, Verlet integrator with constraints used to enforce rigid water and fixed bond lengths to hydrogen for TIP3P and Amber ff99SB potentials.

^bApple Mac Pro with an Intel 6-Core Xeon E5650 Processor running at 2.66 GHz.

^cNVIDIA Maxwell and Pascal Series GTX GPU cards, run via Tinker-OpenMM.

8. Conclusions & Future Development

As has been stressed throughout this report, a defining characteristic of the Tinker molecular mechanics package is its modularity. This intentional design lends itself to straightforward future development and software improvement. There are many unsolved problems requiring advanced energy models and sampling methods yet to be attacked by molecular modeling, and corresponding plans are underway for the future development of Tinker. There are three major projects currently in progress within the Tinker community: acceleration of the existing software, implementation of advanced potentials and sampling algorithms, and integration across the broader Tinker family of codes.

There are a host of problems in molecular biology and elsewhere where advanced models are needed but are computationally too inefficient to be tractable. Simulations of large RNA structures or proteins with significant conformational fluctuations have long been thought to be areas where advanced methods may be required. A future goal of the Tinker package is to make such simulations possible by improving the efficiency of advanced polarizable models. Techniques for speeding the costliest aspect of polarizable force fields, solution of the polarization model itself, are under development for implementation in future versions of Tinker, as are support for current polarizable models including SIBFA¹⁷⁶ and GEM.¹⁷⁷

In addition to efficient software for existing force fields, the Tinker project is developing code that will run the next generation of models. A new class of physics-based potentials is under development that relies less on empiricism than their predecessors. These models attempt to correct for errors that occur at short-range in point change and point multipole force fields because of overlapping charge distributions. Simple models to account for this effect on the electrostatic term of force fields, the so-called charge penetration error, have been recently published^178–180 and corresponding models for polarization, exchange-repulsion and dispersion are under development. These potentials are currently being incorporated into Tinker. We recognize that as computational power continues to grow, and the problems that molecular mechanics models are asked to solve become more demanding, it will be important to ensure that these new models have a home in Tinker.

Importantly, the future development of Tinker is directed toward unifying the code bases of the Tinker family of modeling packages, Tinker, Tinker-HP^{181, 182} and Tinker-OpenMM. Because molecular mechanics simulations of large molecules remain computationally demanding, it is important that the full functionality of Tinker be available to users on a variety of hardware, from large scale CPU-based supercomputers to individual GPUs. The Tinker-HP and Tinker-OpenMM branches are responsible for enabling this high performance; Tinker-HP for massively parallel CPU calculations and Tinker-OpenMM as a CUDA-based GPU implementation. A goal of the Tinker project is to unify the code structure of each of these code packages. This has three major benefits. First, it will bring all of the codes up-to-date with the most efficient methods available. Second, future development of models or methods will be more easily integrated across all three platforms if their structures are unified. Third, it will allow Open Source development of Tinker that can be propagated to the Tinker-HP and Tinker-OpenMM branches. By keeping Tinker-HP and Tinker-OpenMM in step with Tinker development, we can ensure users of access to Tinker functionality regardless of hardware platform.

The Tinker molecular modeling software package is an easy-to-use, easy-to-understand and easy-to-modify set of programs allowing researchers to model molecular systems of interest in a variety of ways. It supports a broad spectrum of classical molecular mechanics models as well as an array of algorithms to efficiently explore the corresponding potential energy surfaces. This is accomplished through a modular code structure that permits users to inspect and manipulate calculation details, and developers to add new functionality quickly. Because it is Open Source and freely available to academics, Tinker 8 provides a community code base in which to test old ideas and investigate new ones. It is our hope that this community-oriented model will continue to advance development of tools that make the Tinker toolbox useful.