Single-cell responses to three-dimensional structure in a functionally defined patch in macaque area TEO

Abstract

Both dorsal and ventral visual pathways harbor several areas sensitive to gradients of binocular disparity (i.e., higher-order disparity). Although a wealth of information exists about disparity processing in early visual (V1, V2, and V3) and end-stage areas, TE in the ventral stream, and the anterior intraparietal area (AIP) in the dorsal stream, little is known about midlevel area TEO in the ventral pathway. We recorded single-unit responses to disparity-defined curved stimuli in a functional magnetic resonance imaging (fMRI) activation elicited by curved surfaces compared with flat surfaces in the macaque area TEO. This fMRI activation contained a small proportion of disparity-selective neurons, with very few of them second-order disparity selective. Overall, this population of TEO neurons did not preserve its three-dimensional structure selectivity across positions in depth, indicating a lack of higher-order disparity selectivity, but showed stronger responses to flat surfaces than to curved surfaces, as predicted by the fMRI experiment. The receptive fields of the responsive TEO cells were relatively small and generally foveal. A linear support vector machine classifier showed that this population of disparity-selective TEO neurons contains reliable information about the sign of curvature and the position in depth of the stimulus.

NEW & NOTEWORTHY We recorded in a part of the macaque area TEO that is activated more by curved surfaces than by flat surfaces at different disparities using the same stimuli. In contrast to previous studies, this functional magnetic resonance imaging-defined patch did not contain a large number of higher-order disparity-selective neurons. However, a linear support vector machine could reliably classify both the sign of the disparity gradient and the position in depth of the stimuli.

INTRODUCTION

The ability to perceive a three-dimensional (3D) world from the two-dimensional (2D) images registered by the two eyes has evolved in different taxa and is present even in more evolved invertebrates such as insects (Nityananda and Read 2017). The frontal placement of the eyes in primates, however, allows them to have a much larger area of overlap of the left and right eye’s visual fields and to use slight position differences in the images impinging on the left and right eye’s retinas as a very strong and unambiguous depth cue. Based on these horizontal binocular disparities between the retinal images of corresponding points on the surface of an object, the primate brain is able to process the depth structure of the object and how far it is located from the fixation plane. The processing of binocular disparities involves both ventral and dorsal visual pathways (Janssen et al. 2017; Verhoef et al. 2016) and begins with disparity-selective neurons in the primary visual cortex (V1) (Cumming and Parker 1999; Ohzawa and Freeman 1986; Poggio and Fischer 1977).

A large number of single-cell and functional imaging studies have investigated the representation of depth structure in end-stage areas of the dorsal and ventral stream in nonhuman primates (Janssen et al. 1999, 2000a, 2001; Srivastava et al. 2009; Theys et al. 2012b; Verhoef et al. 2012; Yamane et al. 2008), yet, relatively little is known about how midlevel areas [located between the early visual areas V1, V2, and V3 and the end-stage areas inferotemporal (ITC) and posterior parietal cortex] represent gradients of binocular disparity. In area MT/V5, neurons respond selectively to linear disparity gradients (Nguyenkim and DeAngelis 2003), and neurons in area V4 in the ventral stream are selective for the 3D orientation of bars (Hinkle and Connor 2001) but not to curved surfaces defined by disparity (Hegdé and Van Essen 2005).

In the rostral lower bank of the superior temporal sulcus (STS), part of area TE, a large fraction of neurons is selective for second-order disparities, as in convex and concave surfaces (Janssen et al. 2000a). This subsector of area TE (termed TEs in previous studies) contains a very detailed representation of 3D structure, with an exquisite sensitivity to small differences in 3D structure (Janssen et al. 2000a) and, in contrast to V1 (Cumming and Parker 1999) and MT/V5 (Krug and Parker 2011), no selectivity for anticorrelated disparities (Janssen et al. 2003). Electrical microstimulation of clusters of TE neurons selective for 3D structure predictably alters perceptual choice in a 3D structure categorization task (Verhoef et al. 2012). However, so far the inputs to these 3D structure-selective TE neurons remain unclear.

Previously, Van Dromme et al. (2016) observed strong fMRI activations related to 3D structure in midlevel areas of the dorsal [posterior intraparietal area (PIP)] and the ventral (area TEO) stream. The latter activation was located on the lip of the lower bank of the STS, which we will term TEOs analogous to TEs (Janssen et al. 2000a). TEO projects, among other regions, to area TE and prefrontal cortex (Webster et al. 1994) and receives feedforward projections from V4 (Ungerleider et al. 2008). Moreover, 3D structure-selective patches of neurons in posterior anterior intraparietal area (AIP) are connected to TEO and TE (Premereur et al. 2015). There is fMRI evidence that a subsector of TEO in the lower bank of the STS is activated more by curved shapes than by rectangular shapes, either in images of real-world natural objects or in artificial stimuli that contain mainly shading to induce the percept of 3D objects (Yue et al. 2014). However, the role of TEO in the disparity-processing network is not clear. The goal of this study was therefore to investigate the single-cell properties of a functionally defined patch in TEO activated more by disparity-defined curved stimuli than by flat stimuli. Remarkably, the strong fMRI activation evoked by curved surfaces in TEO did not contain strong 3D structure selectivity at the single-cell level.

MATERIALS AND METHODS

Surgical procedures and animals.

Two adult male rhesus monkeys (Macaca mulatta, S and R, 6.5–7.5 kg) were used as experimental subjects for fMRI and single-unit extracellular recordings. Both monkeys were first implanted with an fMRI-compatible headpost using dental acrylic and ceramic screws under isoflurane anesthesia (Van Dromme et al. 2016). Monkeys were trained in a passive fixation task and a 3D structure discrimination task previously described (Verhoef et al. 2012). The monkeys were first scanned during passive fixation of curved and flat surfaces, together with control stimuli for each condition (Van Dromme et al. 2016). After the fMRI experiment, a recording chamber was implanted over the left hemisphere of both animals at an angle of ∼45° with the transverse plane to provide easier access to the center of the fMRI activation evoked by curved surfaces [contrast (curved – control) – (flat – control)] located at the posterior part of the IT cortex (Horsley-Clarck coordinates of the center of the grid, 25.8 mm lateral, 0 mm anterior for monkey S and 26.2 mm lateral, 4 mm anterior for monkey R). Animal care and experimental procedures complied with the national and European guidelines (Directive 2010/63/EU) and were approved by the ethical committee of KU Leuven. Structural magnetic resonance imaging (MRI, 0.6-mm slice thickness), using glass capillaries filled with a 1% copper sulfate solution inserted in several grid positions, together with the pattern of gray to white matter transitions, confirmed that the recordings were made in the ventral bank of the posterior part of the superior temporal sulcus, corresponding to area TEO.

Stimuli and task.

The animals were trained to maintain their gaze inside an electronically defined 1° fixation window during the passive fixation task. Horizontal and vertical eye movements were recorded using an infrared camera system sampling at 500 Hz (EyeLink II; SR Research). After a 400-ms fixation period, the stimulus was presented for 600 ms at the fixation point (which remained visible), and, if fixation had been maintained, a drop of juice was given as reward. During training and the single-cell recording experiments, stimuli were presented dichoptically using a double pair of ferroelectric liquid crystal shutters (optical rise/fall time ∼35 µS; Displaytech) operating at a frequency of 60 Hz each and synchronized with the vertical retrace of the display monitor (120 Hz, 20-in. P46 fast-decay phosphor; Vision Research Graphics), at a viewing distance of 86 cm (Srivastava et al. 2009). Stimulus luminance measured behind the shutters (operating at 60 Hz) was 0.8 cd/m² with no measurable cross talk between the images presented to the two eyes. Both monkeys showed excellent stereopsis as demonstrated in an earlier 3D structure categorization test in which concave and convex surfaces at different disparity coherences (ranging from 40 to 100% coherence) had to be discriminated by means of eye movements to the left or right (Verhoef et al. 2012).

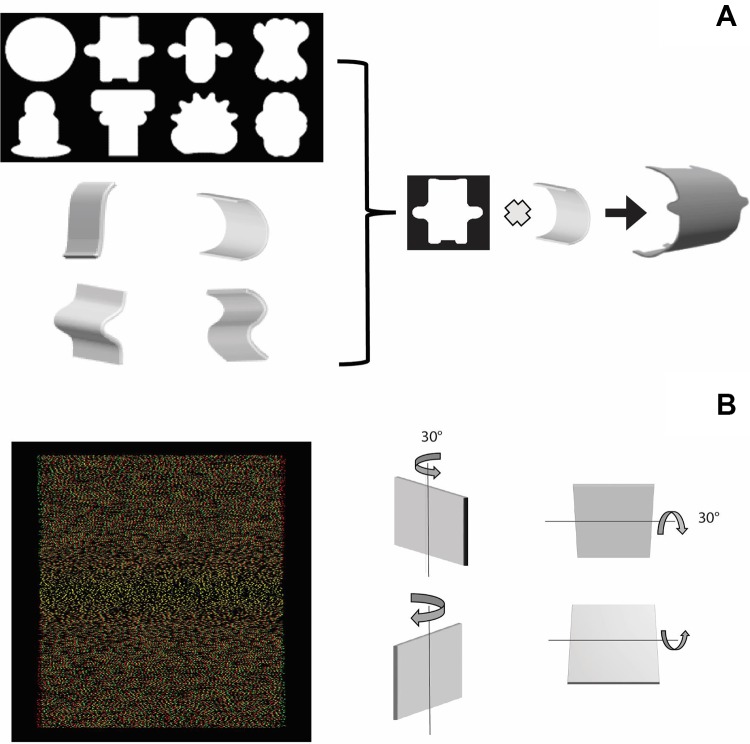
The stimulus set was identical to our previous study (Alizadeh et al. 2018) and consisted of 32 pairs of disparity-defined curved surfaces together with eight planar surfaces (first-order stimuli). The first-order stimuli (Fig. 1A) were presented in two different sizes (8.3° and 18.7°) and consisted of squares with linear disparity gradients either along the vertical or horizontal axis of the stimulus (50% dot density). The surfaces in which disparity varied along the vertical axis (30° rotation along the horizontal axis) could have the top either tilted toward (profile A) or away (profile B) from the observer. Similarly, the surfaces in which disparity varied along the horizontal axis could have the right side toward (profile A) or away (profile B) from the observer. The two profiles were derived from the same monocular images by simply interchanging the images presented to each eye. To avoid texture-density cues in surfaces with disparity variations along the horizontal axis, we randomly removed dots with each change in disparity, as in previous studies (Janssen et al. 2001). The curved (second-order) surfaces (Fig. 1B) were constructed by combining four pairs of depth profiles (half-sine, inclined, Gaussian, S shape) with eight 2D shapes, filled with a 50% density random-dot pattern. The combination of a 2D contour and a depth profile generates a 3D stimulus. The two members of each 3D surface pair used the same two monocular images, since interchanging the monocular images between eyes yielded two 3D surfaces that differed only in the signs of their disparity gradients (convex surfaces become concave and vice versa). The curved surfaces measured 6.6° vertically, dot size was 2 arcmin, and stimulus contrast was 4.6 (ΔI/I, where I is intensity). In the case of the curved stimuli, disparity varied only along the vertical axis of the stimulus.

Fig. 1.

Stimuli. A: 2-dimensional contours (top) and 3-dimensional profiles (bottom) used to create curved (2nd-order) surfaces defined solely by gradients of binocular disparity along the vertical axis of the shape. The icon on the far right is a rendering of the perceived stimulus. No perspective or shading information was present in the stimuli used in this experiment. B: random-dot stereogram of a planar surface with the top part tilted toward the observer (red in front of left eye in anaglyphs). Planar surfaces were either rotated along the horizontal axis (disparity variation along the vertical axis of the surface) or rotated along the vertical axis (disparity variation along the horizontal axis).

fMRI experiment: scanning procedures and stimuli.

All scanning procedures have been described in Van Dromme et al. (2016). We trained monkeys S and R to sit in a sphinx position inside an MRI-compatible plastic chair, which was placed inside the horizontal bore of the magnet. Stimuli were projected using a digital projector (Barco 6300 LCD) on a translucent screen positioned 57 cm in front of the monkey. A pair of red/green stereoglasses was placed in front of the monkey’s eyes to provide dichoptic presentations of the stimuli. We used a 3.0-Tesla full-body scanner (Trio; Siemens), and a radial transmit-only surface coil and custom-built eight-channel phased-array receive coil were positioned closely around the monkeys’ heads. A contrast agent (monocrystalline iron oxide nanoparticle; Feraheme, AMAG Pharmaceuticals) was injected to enhance the signal-to-noise ratio and spatial selectivity of the MR signal (Zhao et al. 2006). We used a gradient-echo single-shot T2-weighted echo-planar imaging sequence (40 horizontal slices, TR = 2 s, TE = 17 ms, 1.25 mm isotropic). A pupil/corneal reflection tracking system (Iscan, operating at 120 Hz) was used to monitor the position of one eye. Monkeys were required to maintain fixation on a dot on the center of the screen within a 1.5° electronically defined window.

We used a 2-by-2 block design with factors curvature (curved vs. flat) and disparity (stereo vs. control). In the curved stereo condition, we presented a subset of the curved surfaces [four 2D shapes combined with three pairs of depth profiles (Van Dromme et al. 2016)] at two positions in depth (at −0.25° and +0.25°). In the flat stereo condition, we presented flat surfaces (with the same 2D contours as the curved stimuli) at 12 positions in depth such that the disparity content (i.e., the sum of all disparities) was identical to the one in the stereo curved condition. The curved-control and flat-control conditions consisted of the presentation of one of the monocular images of the corresponding stereo conditions to both eyes simultaneously (zero disparity).

Single-cell experiment.

During all single-unit recording sessions, eye position signals from both eyes, neural activity, and photocell pulses were digitized and processed at 20 kHz on a digital signal processor (DSP, C6000 series; Texas Instruments). We recorded extracellular neural activity by means of tungsten microelectrodes (1 MΩ; FHC). After amplification (1,000 times), the signal was passed through an analog bandpass filter (500–5,000 Hz) and then sent to the digital signal processor. Single-unit activity (spikes) was discriminated on-line on the DSP using a dual-time window discriminator and displayed using LabView and custom-made software.

The search test consisted of 32 curved stimuli (8 different shape contours combined with 4 different 3D profiles) in addition to 8 planar surfaces (linear disparities in 2 sizes as described above). We collected at least six unaborted trials per condition (median = 8) during the search test. If a unit was well-isolated and responsive to at least one of the stimuli in the search test, two curved surfaces with identical 2D contours (but different depth profiles) were selected on the basis of the responses observed in the search test (one stimulus to which the neuron fired strongly and one less-effective stimulus). We presented each 3D surface and its counterpart obtained by exchanging the monocular images between the eyes binocularly, and the monocular images of the same stimuli, to the left and the right eye separately (disparity test). The most effective stimulus was labeled the preferred 3D surface; the other member of that pair (with identical 2D contour but opposite depth profile) was termed the nonpreferred 3D surface. Stimuli were presented at the center of the display (at the fixation point) and at the middle position, in depth (mean disparity = 0). Because all four different profiles of the planar stimuli were presented in the search test, if a cell responded to any of these four conditions, we tested the neuron with two pairs of the planar stimuli in the disparity test as well.

If a neuron showed significant response differences between the members of a pair of 3D surfaces that could not be accounted for by the sum of the monocular responses (judged after plotting the data and calculating a t-test on the responses), the pair of 3D surfaces evoking the strongest selectivity was studied further in the position-in depth test (PID test). However, during the recording sessions, we tried to record neural responses to both profiles systematically in the PID test. In this test, the preferred and the nonpreferred stimuli were displayed at five positions in depth at the fixation point. The average disparity varied from −0.5° (near) to +0.5° (far), which was a wider range than the disparity amplitude in the stimulus (0.65°). Because the disparity in the stimulus varied between −0.83° and −0.18° for the extreme near position in depth, and between +0.18º and +0.83° for the extreme far position in depth, the stimulus consisted entirely of either near or far disparities at the extreme positions in depth. For the position-in-depth test, it was critical to measure changes in vergence angle after stimulus onset, since vergence eye movements tracking the stimulus in depth could potentially reduce the variation in the mean disparity of the test. Therefore, we measured the positions of both eyes in all tests and analyzed the changes in eye position in the PID test. At the beginning of every recording session, we calibrated the eye position signal by presenting the fixation point (without the stimulus) at two positions on the horizontal meridian 4° from the center of the display.

We measured the receptive fields of the neurons by presenting the preferred stimulus with a size of 3.7° at 35 positions on the screen (on a 7 × 5 grid), spaced 3.83° apart on the horizontal axis and 4.26° on the vertical axis, covering an area of 17° × 23° around the fixation point (receptive field test). Each stimulus was presented for 400 ms during passive fixation.

Data analyses.

The analysis of the fMRI data has been described by Van Dromme et al. (2016). Briefly, depth-structure sensitivity was defined as a significant interaction (1-tailed, P < 0.05 family-wise error rate corrected for multiple comparisons on the entire brain) between the factors curvature (curved or flat) and disparity (stereo or control) in the block design. This interaction is equivalent to the contrast [(curved stereo – curved control) > (flat stereo – flat control)], i.e., areas that are more activated by curved surfaces (compared with their controls) than by flat surfaces (compared with their controls) at different disparities. (We did not investigate areas that were more activated by flat surfaces compared with curved surfaces.) Both monkeys showed significant fMRI activation related to depth-structure sensitivity in the lip of the posterior STS in TEO, which was then used to guide the implantation of the recording chamber.

Data analysis was performed using MATLAB 2015b (Mathworks). We calculated net neural responses by subtracting the mean firing rate in the 300 ms immediately preceding stimulus onset from the mean firing rate between 40 and 540 ms after stimulus onset.

In the disparity test, a two-sample t-test was applied to the responses elicited by the two members of each pair of 3D stimuli to assess disparity selectivity (average number of trials per condition = 20). We also calculated a nonparametric statistic (Mann-Whitney U-test) on the same responses. To verify that the observed selectivity did not reflect selectivity for the monocular images, we calculated a stereo difference index (SDI) (Srivastava et al. 2009): $\text{SDI=}\frac{D_{stereo}-D_{mono}}{D_{stereo}+D_{mono}}$ in which D_stereo represents the response difference between preferred and nonpreferred 3D surface in the stereo condition, and D_mono represents the difference in the sum of the responses to monocular presentations of the same images. If the SDI was >0.5, the stereo selectivity was considered to arise from binocular rather than monocular mechanisms (Srivastava et al. 2009). To quantify the degree of stereo selectivity, we calculated a stereo selectivity index (SSI) on the responses to the 3D surface pair yielding the highest selectivity as follows: $\text{SSI}=\frac{{\text{R}}_{\text{B}}-{\text{R}}_{\text{W}}}{{\text{R}}_{\text{B}}}$, in which R_B is the response to the best 3D surface, and R_W is the response to the worst 3D surface. Population response latencies were calculated by identifying the first of three 20-ms time bins in which the population response to the preferred 3D surface was significantly higher than in the preceding time bin (paired t-test, P ≤ 0.01). The population latency of the neural selectivity was likewise computed as the first of three 20-ms time bins in which the population response to the preferred 3D surface significantly exceeded the response to the nonpreferred 3D surface (paired t-test, P ≤ 0.01). These t-statistics were used for consistency with previous studies (Janssen et al. 2000a; Srivastava et al. 2009; Theys et al. 2012b). However, we also calculated nonparametric statistics (Mann-Whitney U-tests). In addition, we computed the response latency for each individual neuron using the Poisson cumulative distribution (Janssen et al. 2008).

In a manner similar to previous studies (Janssen et al. 2000a; Srivastava et al. 2009; Theys et al. 2012b), we presented the preferred and nonpreferred surface at five positions in depth. As a criterion for position-in-depth tolerant 3D shape selectivity, we required that the response to the nonpreferred 3D surface should never significantly (t-test, P < 0.05) exceed the responses to the preferred 3D surface at any position in the position-in-depth test.

We constructed receptive field (RF) maps using cubic 2D interpolation of the net responses measured in the RF test. The size of the RF was defined as the square root of the area for which responses were ≥50% of the maximum response.

Similar to our previous work (Alizadeh et al. 2018), in order to assess which 3D information can be reliably extracted from neuronal activity in area TEO, we used a linear support vector machine classifier [SVM, the neural decoding toolbox version 1.0.4, http://www.readout.info/ (Meyers 2013)]. We used the position-in-depth test data of 20 disparity-selective neurons tested with curved stimuli. These selected neurons showed significant (t-test, P < 0.05) response differences between the concave and convex surfaces at least at one of the five positions in depth. We selected cells with at least 20 trials per condition. For each neuron, data from 20 trials from each of the 10 conditions (PID test, consisting of either a pair of concave/convex profiles at 5 positions in depth, so 2 × 5 = 10 conditions) were randomly selected. For each of these trials, 500 ms of neural activity after stimulus onset from all neurons (irrespective of response latency) were combined to create a pseudopopulation response vector for PID tests with curved stimuli. This procedure resulted in 20 × 10 data points in a 20-dimensional space. These pseudopopulation vectors were grouped into 20 splits of data, with each split containing one pseudopopulation response vector for each of the 10 stimuli. Nineteen of these splits were used to train the pattern classifier (linear SVM), whereas the remaining one was used to test the performance of the classifier (20-fold cross-validation). A z-score normalization was applied before sending data to the classifier. Classification was performed for the sign of the disparity gradient, irrespective of position in depth, and the position-in-depth of the stimuli, irrespective of curvature sign, separately. Chance level was estimated by running the classifier 1,000 times with the stimulus labels randomly shuffled, with permutation of the order of neurons and the selection of trials for training and testing. All classification accuracy values presented in this paper are the zero-one loss function results (proportion of correct predictions), and the SE is expressed as the SD across 100 resample runs. To assess how well the 3D structure information (sign of the disparity gradient) at a given mean disparity value generalized across position in depth, we trained the classifier with a concave/convex pair at one position in depth and tested on each of the other positions in depth independently.

RESULTS

fMRI activations related to 3D structure sensitivity in area TEO and recording sites.

We scanned two monkeys (R and S) during presentation of curved and flat surfaces at the center of the screen (127 and 130 runs for R and S, respectively). The contrast [(curved stereo – curved control) – (flat stereo – flat control)] yielded robust (P < 0.05 corrected) and bilateral activations in the lower bank of the posterior STS of both animals (Fig. 2). This activation was located at the posterior border of TEO, anterior to the ascending limb of the inferior occipital sulcus (Boussaoud et al. 1991) but posterior to the posterior middle temporal sulcus (PMTS), (Fig. 2B). This region may correspond to area OTd (Kolster et al. 2014). In line with previous findings in F5a (Theys et al. 2012b), PIP (Alizadeh et al. 2018), and AIP (Srivastava et al. 2009), these activations may suggest a sensitivity to higher-order disparities.

Fig. 2.

Functional magnetic resonance imaging (fMRI) results and recording positions. A: significant activation related to depth structure (interaction between the factors curvature and disparity) in area TEO of monkey S, plotted on a coronal section of the monkey’s own anatomical MRI. B: a sagittal section of monkey S showing the recording area containing the most selective neurons. C and D: recording positions with disparity-selective neurons in monkeys R and S plotted on a horizontal section. A, anterior; P, posterior.

To verify that the significant interaction effect in TEOs was indeed caused by stronger fMRI responses to curved than to flat surfaces, we plotted the percent signal changes (compared with the baseline fixation condition without a visual stimulus) evoked by the four conditions in TEOs, and for comparison also in the caudal intraparietal sulcus (cIPS) and in the anterior IPS (aIPS; Fig. 3). Curved surfaces did evoke stronger responses than all flat surfaces (flat stereo condition and both control conditions) in TEOs. However, in cIPS and aIPS, flat stimuli evoked much less activations compared with TEOs.

Fig. 3.

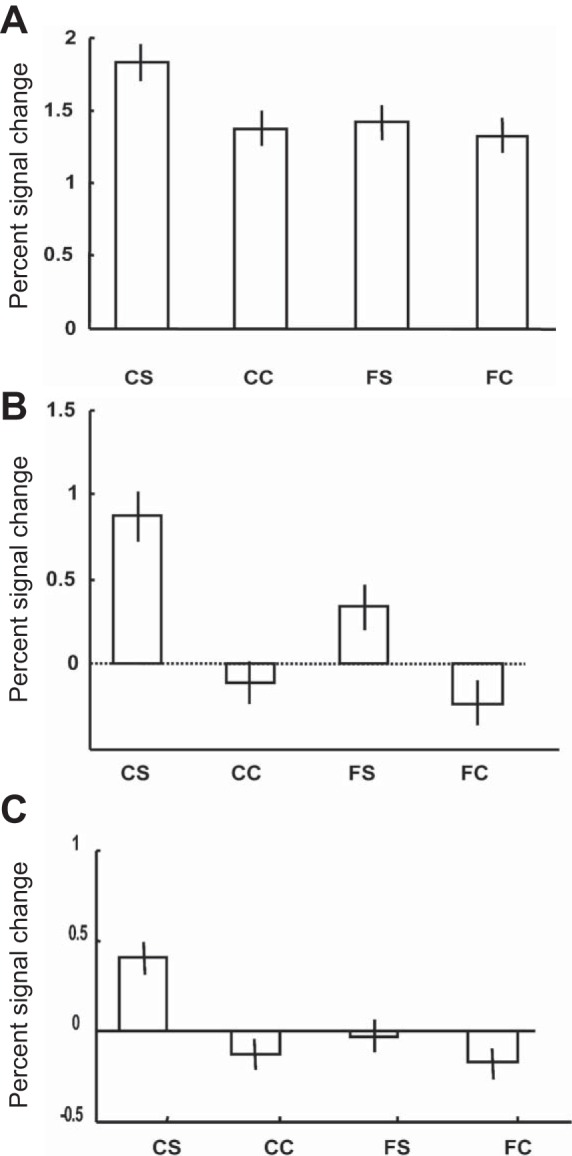
Percentage signal change in the functional magnetic resonance imaging (fMRI) experiment. A: caudal intraparietal sulcus. B: anterior IPS (aIPS). C: TEOs. CS, curved stereo; CC, curved control (monocular); FS, flat stereo; FC, flat control (monocular).

Guided by these fMRI activations, we implanted a recording chamber over TEO. Figure 2, C and D, shows the recording positions mapped on the fMRI activations on horizontal sections through the posterior STS. Because the STS makes an ∼45° angle with respect to the horizontal plane, some recording positions may appear to have been targeting the white matter, but extrapolation of the recording tracks verified that we did reach the lower bank of the STS as the electrode was lowered. We also obtained an anatomical MRI with an electrode in one of the recording positions (more posterior to the section shown in Fig. 2A), which confirmed that we targeted the lip of the lower bank of the posterior STS. We recorded in 12 grid positions in monkey S and 25 grid positions in monkey R, spanning an area of 5 mm in the anterior-posterior direction in monkey S and 8 mm in monkey R. Note that the fMRI activations posterior from the recording sites were located in the area V4 complex (Kolster et al. 2014).

Disparity selectivity of single neurons in a functionally defined patch in TEO.

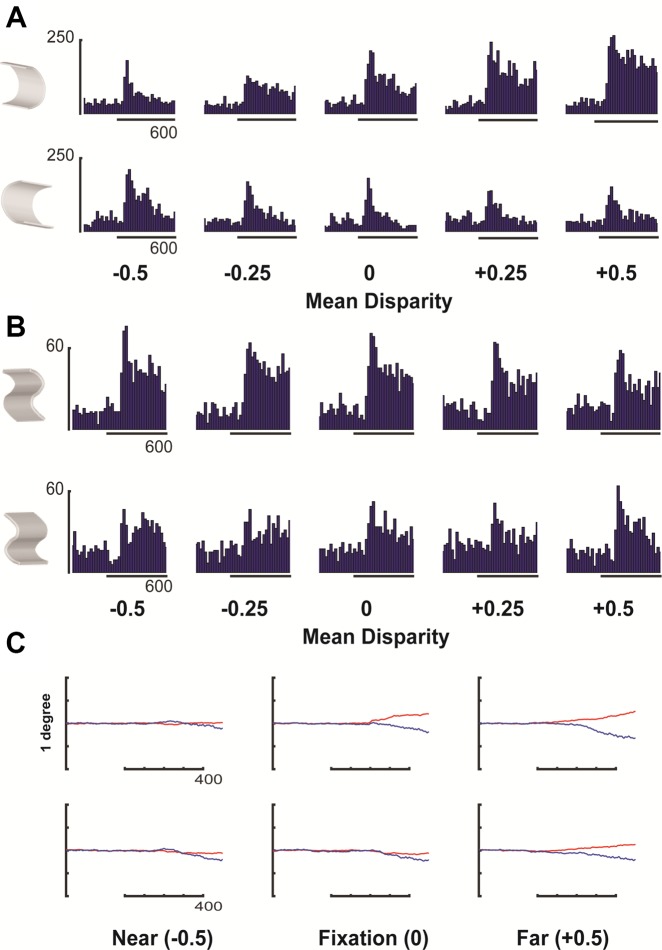
In total, we recorded the activity of 533 neurons in two monkeys (the same animals as in the fMRI experiment), 168 of which (31.5%, 89 in monkey R and 79 in monkey S) were responsive to the random dot patterns. The example neuron in Fig. 4A fired strongly (83 spikes/s on average) to the concave cosine profile and significantly (P < 0.001, t-test) less to the convex counterpart (SSI = 0.73). The monocular responses could not account for this selectivity (SDI = 1.0). This neuron was also significantly selective for the Gaussian shape pair (with the same 2D shape contour, P < 0.001).

Fig. 4.

Disparity selectivity in area TEO. A: peristimulus-time histogram (PSTH) of an example TEO neuron tested with curved stimuli in the stereo condition (“stereo”) and in the monocular conditions (“left eye” and “right eye”). The horizontal bar indicates the duration of stimulus presentation. B: average population response (±SE) to preferred (blue) and nonpreferred (red) curved surfaces of all disparity-selective TEO neurons (n = 20) to the curved stimuli. Broken lines indicate the monocular responses (black, preferred right eye; green, nonpreferred right eye; cyan, preferred left eye; purple, nonpreferred left eye).

Only a small fraction of TEO neurons tested with curved surfaces (20/168 or 12% based on a t-test, and 10/168 using Mann-Whitney U-test, P < 0.05; 13/89 in monkey R and 7/79 in monkey S) showed significant response differences that could not be explained by the monocular responses, as in the example neuron in Fig. 4A. The average population response of those neurons is shown in Fig. 4B. Although the visual response of these neurons was robust (average net response to the preferred 3D surface equaled 40.1 spikes/s), the selectivity (i.e., the response difference between preferred and nonpreferred surface) was relatively weak (average SSI = 0.6). During the first 200 ms after stimulus onset, the response to the monocular presentations was almost as strong as the response to the preferred 3D surface. Similarly, the latency of the visual population response was 90 ms, but the latency of the neural selectivity was as high as 150 ms (first of three consecutive 20-ms bins with significant response differences between preferred and nonpreferred surface, paired t-test). The median response latency, calculated for every individual responsive neuron, averaged 83 ms (Poisson statistic). With the use of a nonparametric statistic (Mann-Whitney U-test), the population response latency was 70 ms, and the selectivity latency equaled 90 ms. Normalizing the responses of each neuron to the peak activity and then averaging across neurons yielded a very similar response profile (data not shown).

Response variations for different 3D surfaces do not necessarily imply selectivity for gradients of disparity (Janssen et al. 2000b). To evaluate this higher-order disparity selectivity, we tested TEO neurons with 3D surfaces presented at five different positions in depth (PID test). The example neuron in Fig. 5A (the same neuron as in Fig. 4A) failed to preserve its selectivity for the concave profile across positions in depth, since the neuron preferred the concave profile at the middle (0° mean disparity) and far (+0.5° mean disparity) positions while preferring the convex profile at the near position (−0.5°). Therefore, this neuron was deemed zero order. Figure 5B shows a second example neuron in which the response to the (nonpreferred) convex profile never significantly exceeded the response to the (preferred) concave profile at any position in depth. In accordance with previous studies (Janssen et al. 2000b), this neuron was deemed higher order, albeit with weak selectivity. As in previous studies (Srivastava et al. 2009), vergence eye movements could not account for the neural responses, since the eyes remained stable during the first 50–250 ms after stimulus onset (Fig. 5C) although neural selectivity was already present. Moreover, the average deviation of the eyes (0.10°) was much smaller than the range of disparities in the test. In total, we ran a PID test in 38 TEO neurons, 2 of which were tested with both planar and curved surfaces. Out of these, 33 were tested with curved stimuli, and 7 were tested with planar stimuli. None of the cells tested with planar surfaces showed higher-order disparity selectivity, whereas only 4 neurons tested with curved surfaces were higher order. The average normalized response of all neurons to curved stimuli tested in the PID test (Fig. 6A) shows that the population of TEO neurons we investigated only showed selectivity at the center position in depth. In contrast to area TEs (Janssen et al. 1999), AIP (Srivastava et al. 2009; Theys et al. 2012a), F5a (Theys et al. 2012a), and PIP (Alizadeh et al. 2018), no significant response differences were present at any of the other positions in depth tested.

Fig. 5.

Position-in-depth test, example neurons. A: peristimulus-time histograms (PSTHs) of the example neuron (the same neuron as in Fig. 3) in the position-in-depth test with a pair of curved stimuli. The preferred (row on top) and nonpreferred (row on bottom) stimuli were presented at 5 different positions in depth (−0.5° indicates near disparities, whereas +0.5° indicates far disparities). Same conventions as in Fig. 3. B: PSTH of a 2nd-order neuron in the position-in-depth test with curved surfaces. C: average horizontal eye position traces (red, right eye; blue, left eye) at three positions in depth (near, fixation plane, and far) recorded together with the example neuron. The vertical scale bar on the left indicates 1°.

Fig. 6.

Position-in-depth (PID) test, population graphs. A: average response of all disparity-selective neurons (n = 20) responding to curved stimuli in the PID test. The preferred (blue line) and the nonpreferred (red line) stimuli were presented at 5 different positions in depth (−0.5° indicates near disparities, whereas +0.5° indicates far disparities). B: comparison between the average response to the preferred and nonpreferred curved stimuli (red line) and the response to the flat stimuli (black line) at three positions in depth (***P < 0.001).

To relate our single-cell data to the fMRI activations, we compared the average responses to curved surfaces at the three middle positions in depth (the same range as used in Van Dromme et al. 2016) with the responses to flat surfaces at the same positions in depth for all visually responsive TEO neurons tested with curved and flat surfaces (n = 30; Fig. 6B). The mean response to curved and planar stimuli across the three positions in depth was significantly higher than that to flat stimuli (paired t-test, P < 0.001). The same analysis on the responses of all disparity-selective TEO neurons yielded a virtually identical result (data not shown). With the caveat that we did not search for responsive neurons using flat stimuli (which may have introduced a bias in the selection of neurons), the population of TEO neurons that we tested may have contributed to the stronger fMRI activation for curved surfaces than for flat surfaces at different positions in depth.

RF of the visually responsive TEO neurons.

We mapped the receptive fields of 48 visually responsive TEO neurons (of which 19 were disparity selective) with the preferred stimulus (diameter 3.7°, to avoid overlap between neighboring positions) at 35 positions at the center of visual field (covering a 17° × 23° area around the fixation point, spacing 3.8°) and at the fixation plane (center position in depth). Figure 7A shows an example RF of a disparity-selective TEO neuron, with a maximum response (115 spikes/s) at the fixation point (RF size = 4.6°). This neuron was weakly inhibited when the stimulus appeared further from the center of the screen. The neuron shown in Fig. 7B represents a non-disparity-selective TEO neuron with a somewhat larger RF size (6.83°) centered at the fixation point and inhibitory responses at higher eccentricities. The RF size of all TEO neurons tested varied between 3.68° and 10.46° (mean 6.03°), and the eccentricity of the RF center varied between −12.9° and 8.2° (negative values indicate ipsilateral and positive values indicate contralateral, mean eccentricity = −0.99°, the absolute eccentricity varied between 0° and 12.9°, mean = 2.21°). We did not observe any significant differences between the RF size and the mean eccentricity of the populations of disparity-selective and nonselective neurons (t-test, P = 0.84 for size and P = 0.39 for eccentricity). Figure 7C shows the average normalized RF of all TEO neurons recorded. Overall, only 16 out of 47 neurons tested (34%) had their RF maximum at an eccentricity >1.86°. The size of the population RF was 5.67°, and the average maximal response was measured at 0.26° from the fixation point. The RF results demonstrate that the lack of 3D structure selectivity we observed in TEO was not because of misalignment of the stimulus with respect to the RF. Overall, we did not observe significant clustering of disparity-selective neurons. In total, 74% of the neurons in monkey R and 84% of the neurons in monkey S displayed foveal receptive fields (RF centers at an eccentricity of <3°). Moreover, our results confirm the largely foveal representation in this part of inferotemporal cortex (Kolster et al. 2014).

Fig. 7.

Receptive fields (RFs) of TEO neurons. A: example RFs of a disparity-selective neuron. B: example RF of a visually responsive neuron (nonstereo). C: population RF of all visually responsive TEO cells tested (n = 47).

Decoding of 3D structure and position in depth.

To determine whether the population of 20 disparity-selective TEO neurons (both zero order and second order, all neurons showed selectivity at least at one position in depth) contains reliable information regarding second-order disparities (convex – concave) across positions in depth, we used a linear SVM classifier (see materials and methods). We classified both the sign of the disparity gradient (concave vs. convex) and the position in depth of the stimulus based on the responses of these neurons. For determining the sign of the disparity gradient, we randomly selected trials from all five different positions in depth and used concave/convex as labels. For the classification of position in depth, we combined the responses to convex and concave and used five labels corresponding to each of the five positions in depth in the test. The classifier performed well above chance level for both the sign of the disparity gradient (0.839 ± 0.08 correct, chance level = 0.5 ± 0.04, P < 0.001; Fig. 8A) and the position-in-depth of the stimulus (0.388 ± 0.05 correct, chance level = 0.21 ± 0.02, P < 0.001; Fig. 8B). In addition, we tested whether the classifier could reliably categorize the sign of the disparity gradient at different positions in depth when trained at one position in depth (generalization analysis). Figure 8C summarizes the results of this generalization analysis. At the most extreme positions (−0.5° and +0.5°) and at the center position, the classifier only generalized to one neighboring position in depth. However, at the −0.25° and +0.25° positions (same range as in the fMRI experiment), the classifier also generalized to other positions in depth.

Fig. 8.

Classification analysis results of disparity-selective TEO neurons. A: classification accuracy of a population of 20 disparity-selective neurons for the sign of curvature. B: classification accuracy for position in depth. C: generalization analysis showing significant results for −0.25 to +0.25 mean disparity (*P < 0.05, **P < 0.01, and ***P < 0.001). ns, Not significant.

DISCUSSION

We combined the fMRI block-design results with invasive single-cell recordings and advanced analysis methods to address the properties of neurons in area TEO. Despite the strong fMRI activations evoked by curved surfaces compared with flat surfaces, we observed in a part of area TEO, only a very low proportion of the neurons showed disparity selectivity, and an even lower fraction was higher order. However, the average response to curved surfaces was significantly higher than that to flat surfaces irrespective of the mean disparity of the stimulus, indicating that these TEO neurons distinguished between curved and flat but not between different signs of curvature. TEO neurons in this fMRI patch generally had small and foveal receptive fields. The results of the classification analysis showed that a sample of disparity-selective TEO neurons contains reliable information about the sign of the disparity gradient and, albeit to a lower degree, about the position in depth of the stimulus.

Single-unit recording is constrained by several factors, including time, anatomical locations practically available for recording (recording sites are accessed through a grid system with 1-mm spacing between grid positions), and other factors (e.g., a potential bias toward larger neurons). Bearing that in mind, we tried to cover a large fraction of the TEO activation. Previously, Uka et al. (2000) reported a large number of disparity-selective neurons in the inferior temporal cortex of macaque covering the more dorsal parts of areas TE and TEO, the latter possibly partially overlapping with our TEOs on the lip of the STS. Verhoef et al. (2016) measured significant fMRI activations related to binocular disparity in TEO, but this activation was located more medially within the STS. We focused on the fMRI activations elicited by curved surfaces on the lip of the STS and tried to target the center of the activations. Despite all of the limitations of single-cell recordings, the likelihood of missing all disparity-selective clusters in two monkeys seems to be very low.

The use of a functional localizer is well established in several domains [such as for color, motion, bodies, or faces (Conway and Tsao 2006; Popivanov et al. 2012; Sunaert 2006; Tsao et al. 2003; Vanduffel et al. 2002)]. Unlike other mapping studies that generally use the same parameters in the single-cell study as in the fMRI study, we compared the sum of the activations to all curved stimuli (both concave and convex) with those evoked by flat stimuli containing the same disparities while, in the single-cell experiment, we searched for neurons using only curved stimuli and tested whether the neurons discriminated between, for example, concave and convex. In essence, the fMRI localizer was correct, since TEO neurons did respond significantly more to curved surfaces compared with flat surfaces across different positions in depth. The pattern of percent signal changes in the fMRI experiment confirmed that TEOs responded more to curved surfaces compared with flat surfaces but also revealed differences compared with the posterior parietal cortex. In TEOs, all flat stimuli evoked strong activations (but curved surfaces were stronger), whereas in cIPS and aIPS, flat surfaces evoked much less activations. Importantly, the use of the fMRI localizer has been successful in predicting the existence of higher-order disparity selectivity in other brain areas in the past (Alizadeh et al. 2018; Theys et al. 2012a; Van Dromme et al. 2015).

It should also be noted that the low temporal resolution of fMRI does not allow determining how long after stimulus onset the neural selectivity emerged. In our study, the weak disparity selectivity emerged 150 ms after stimulus onset, which is much later than in AIP (Srivastava et al. 2009) or TEs (Janssen et al. 2000a).

We did not record local field potentials in this study. Because the fMRI signal may in some cases correlate better with γ-activity than with single-neuron responses (Logothetis et al. 2001), it is possible that the γ-band responses in TEOs may have been selective for curved surfaces, which may have been detected in the fMRI and thereby caused the apparent discrepancy between the fMRI and the single-unit results. However, even if the input to TEOs (the local field potential) would have contained reliable 3D structure selectivity, the output of TEOs (the action potentials) contained very little neural selectivity for 3D structure at the level of individual neurons.

In our study, we also observed strong activation in area V4. Whereas disparity tuning of V4 neurons is well documented (Hinkle and Connor 2001, 2002; Tanabe et al. 2005), second-order disparity selectivity is virtually absent (Hegdé and Van Essen 2005). Notably, previous studies reported that a substantial proportion of visually responsive neurons in V4 are tuned to a wide range of disparities (−2° to 2°) (Tanabe et al. 2005) and to relative disparities (Hegdé and Van Essen 2005), potentially contributing to the strong fMRI activations we observed in area V4. Overall, second-order disparity selectivity appears to be largely absent in the ventral stream up to the level of TEOs. It should be noted that, despite the virtual absence of neural selectivity for the sign of 3D structure (concave vs. convex) in TEO, our population of neurons did discriminate between curved and flat surfaces. Therefore, it is possible that the neural representation in TEO is a first step toward more elaborate sign-specific representations higher in the visual system.

Our single-cell results are important for the interpretation of a series of previous studies on the network involved in the processing of 3D structure from disparity. The part of area TE in the rostral lower bank of the STS, which was previously termed TEs, hosts a very detailed representation of 3D structure with strong selectivity for small disparity discontinuities and the sign of curvature and rejecting anticorrelated disparities, similar to 3D surface perception (Janssen et al. 2000b, 2003). Moreover, electrical microstimulation in TEs predictably alters the perceptual report of monkeys when categorizing 3D structure [convex vs. concave (Verhoef et al. 2012)]. On the other hand, area AIP contains a coarser but also faster (shorter latencies) representation of 3D structure (Srivastava et al. 2009), and reversible inactivation of area CIP impacts the 3D structure-related activation in AIP and in TEs but not those in TEO (Van Dromme et al. 2016).

It could be argued that, despite the very weak disparity selectivity we measured in TEOs, our SVM analysis showed that, at the population level, these TEO neurons contain significant information about 3D structure that could be extracted at the next level in the hierarchy (in our case TEs). The neural representation of 3D structure in PIP contains very reliable first-order information that generalized across all positions in depth and at least some second-order 3D information (Alizadeh et al. 2018). In TEOs, however, the SVM could extract reliable information about the sign of the disparity gradient that was generalizable across neighboring positions in depth (−0.25° to +0.25°). It is important to emphasize that the results of the SVM analysis merely imply the presence of 3D structure information in the pattern of firing rates of a population of TEO neurons, without necessarily any selectivity at the single-neuron level. Given that the neural selectivity for 3D structure is even higher in TEs, one can expect much higher classification accuracies in this area. Hence, it seems unlikely that the sophisticated and detailed 3D structure information emerges in a single step between TEOs and TEs. Additional processing within TEs or between TEOs and TEs appears to be necessary. This interpretation is corroborated by published data on the difference between TEO and TE with respect to size tolerance (Hikosaka 1999). Although size tolerance is stronger in TE compared with TEO, the degree of size tolerance overlaps considerably between the two areas, and a small proportion of TEO neurons even shows size tolerance similar to the one observed in TE. In contrast, we did not observe any robust 3D structure selectivity in TEO.

The fMRI activation elicited by curved surfaces in TEOs may not be a major source of 3D structure selectivity for area TEs, whereas area AIP, which is anatomically connected to TEs (Borra et al. 2008; Premereur et al. 2015), contains a very robust representation of 3D structure. Although previous studies and our observations do not exclude a role for TEO input to TEs (e.g., for the detection of disparity discontinuities), our results strongly suggest that substantial additional processing is necessary between TEOs and TEs. Assuming that second-order disparity selectivity arises from pooling the responses of first-order disparity-selective neurons, one would expect to observe first-order neurons in TEOs. However, we did not observe any first-order disparity selectivity in TEOs, in contrast to PIP (Alizadeh et al. 2018). Therefore, our study leaves open two possibilities. Either 3D structure information from AIP arrives in TEs, where it is further elaborated and refined for 3D object recognition and categorization. Consistent with this hypothesis, which remains to be tested directly, both anatomical and functional evidence suggests that visual information travels from posterior parietal cortex to TEs, but not or much weaker in the opposite direction (reviewed in Janssen et al. 2017). Unpublished observations in our group also demonstrate that electrical microstimulation of any of the 3D structure patches in the ITC does not activate AIP, whereas microstimulation of posterior AIP induces strong activation in ITC [both in TEO and in TE, (Premereur et al. 2015), E. Premereur and P. Janssen, unpublished observations]. Alternatively, the detailed 3D structure representation in TEs arises from multiple computational steps between TEOs and TEs. The latter possibility would imply that the computation of 3D structure in the ventral stream would progress differently compared with the dorsal stream, where consecutive processing stages encode zero-order disparity (V3 and V3A), then first-order disparity (PIP and CIP), and finally second-order disparity (AIP). Obviously, a reversible inactivation of TEOs during fMRI would provide crucial evidence to disentangle these two hypotheses. A significant effect of TEO inactivation on the 3D structure-related activation in area TE would indicate a substantial contribution of TEOs to the 3D structure network, whereas the absence of such an effect would suggest that TEOs have no role in the processing of 3D structure defined by disparity.

Here, we reported the results of our single-unit recording investigations in area TEO of the inferior temporal cortex of the macaque, which is activated by disparity-defined curvature in contrast to flat stimuli. Although fMRI is a powerful and invaluable tool for obtaining a map of activations, our results suggest that any conclusion about the specific selectivity of individual neurons in the activated brain areas should be drawn with caution and emphasize the necessity of more direct measurements of neuronal selectivity (such as extracellular recordings) in the regions of interest.

GRANTS

This work was supported by Fonds voor Wetenschappelijk Onderzoek Vlaanderen, Program Financing (PFV/10/008), IUAP VII/11 and Odysseus Grant G.0007.12.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.-M.A. and P.J. conceived and designed research; A.-M.A. and I.C.V.D. performed experiments; A.-M.A. and I.C.V.D. analyzed data; A.-M.A. and P.J. interpreted results of experiments; A.-M.A. prepared figures; A.-M.A. and P.J. drafted manuscript; A.-M.A. and P.J. edited and revised manuscript; P.J. approved final version of manuscript.