Are you thinking what I’m thinking? Synchronization of resting fMRI time-series across subjects

Abstract

We describe BrainSync, an orthogonal transform that allows direct comparison of resting fMRI (rfMRI) time-series across subjects. For this purpose, we exploit the geometry of the rfMRI signal space to propose a novel orthogonal transformation that synchronizes rfMRI time-series across sessions and subjects. When synchronized, rfMRI signals become approximately equal at homologous locations across subjects. The method is based on the observation that rfMRI data exhibit similar connectivity patterns across subjects, as reflected in the pairwise correlations between different brain regions. We show that if the data for two subjects have similar correlation patterns then their time courses can be approximately synchronized by an orthogonal transformation. This transform is unique, invertible, efficient to compute, and preserves the connectivity structure of the original data for all subjects. Analogously to image registration, where we spatially align structural brain images, this temporal synchronization of brain signals across a population, or within-subject across sessions, facilitates cross-sectional and longitudinal studies of rfMRI data. The utility of the BrainSync transform is illustrated through demonstrative simulations and applications including quantification of rfMRI variability across subjects and sessions, cortical functional parcellation across a population, timing recovery in task fMRI data, comparison of task and resting state data, and an application to complex naturalistic stimuli for annotation prediction.

Introduction

Resting fMRI (rfMRI) is being increasingly used to study brain connectivity and functional organization (Arslan et al., 2017). In particular, rfMRI has been used extensively to measure functional connectivity between different brain regions (Horwitz, 2003; Langs et al., 2014; Smith et al., 2011; Smitha et al., 2017; van den Heuvel and Hulshoff Pol, 2010). It is also used for longitudinal studies of brain development and is being explored as a diagnostic biomarker in cross-sectional studies for various neurological and psychological diseases and conditions (Redcay et al., 2013). Large-scale connectivity information derived from rfMRI can be used to delineate functional regions (Arslan et al., 2017). By extension, identification of multiple contiguous areas, each of which exhibits distinct connectivity to the rest of the brain, can be used to define a functional parcellation of the entire cerebral cortex (Amunts et al., 2007; Sporns et al., 2005).

Since rfMRI data reflect spontaneous brain activity, it is not possible to directly compare signals across subjects (Iraji et al., 2016). Instead, comparisons make use of connectivity features, typically computed from pairwise correlations of the rfMRI time-series between a point of interest and other locations in the brain (Fan et al., 2016). For analysis of cerebral cortex, it is common to compute a feature vector at each location on a tessellated representation of the cortex as the correlation from that vertex to all other vertices. For cortically mapped fMRI data, this approach results in a V dimensional feature vector at each vertex, where V is the number of vertices in the tessellated representation of the cortex. This results in a high dimensional feature (correlation) matrix of size V × V. Not only is the computational cost of working with this correlation matrix high but, since in most cases the number of time samples T is much smaller than V, the matrix is singular and dimensionality reduction should be used to identify a less redundant and more robust feature vector. Another limitation of working with the spatial correlation is that this approach does not preserve anytemporal information so that studies of network dynamics are not directly possible.

Correlation-based analysis can be used for cortical parcellation at either the subject or group level (Wig et al., 2014). Embedding techniques have also been described to define a functional atlas (Langs et al., 2014) or for function-based inter-subject registration (Nenning et al., 2017) using rfMRI data, but again these methods are based on the use of spatial correlation. An alternative approach that uses the original data, rather than its correlation, for inter-subject comparisons is group independent component analysis (ICA) (Calhoun et al., 2009). Group ICA concatenates rfMRI data from multiple subjects and represents the data as a summation of independent spatial or temporal components. In this way, common networks across subjects can be identified. To make use of data from multiple subjects, it is common to concatenate data based on a fixed anatomical correspondence across subjects. This can limit the ability to identify individual differences with respect to the group independent components.

Another recent technique for inter-subject comparison is hyperalignment (Haxby et al., 2011) which aligns multi-subject brain data in a high-dimensional functional space. This method was used to build a common model of the ventral temporal cortex that captures visual object category information. Hyperalignment maps data from multiple subjects into a common space using a Procrustes fit that computes an orthogonal transform which maps each subject to a common reference subject across a set of voxels. The more recent extensions of this work (Guntupalli et al., 2016; Guntupalli and Haxby, 2017) define connectivity hyperalignment, which minimizes distance between target regions in different subjects based on connectivity vectors computed for each subject. While both forms of hyperalignment share the use of orthogonal transforms with the BrainSync transform we describe below, they differ in the use of spatial or connectivity features in place of the direct application of an orthogonal matrix to the time series as we describe.

The SMIG (Small Memory Iterative-Group PCA) approach (Hyvärinen and Smith, 2012) uses rotations to find the optimal approximation of fMRI data for a group of subjects in terms of a set of group spatial patterns (a matrix) and an associated set of time series matrices (one per subject). SMIG iteratively solves this problem by alternating between updating the spatial patterns and the time series matrices, with the latter computed under an orthogonality constraint. The resulting approximation is effectively the PCA of the group data, but computed without the need to directly decompose the entire concatenated set of data. The method has similarities to the BrainSync transform in the sense that the fMRI data are effectively aligned across subjects in order to compute the spatial patterns. The goal of SMIG is to find a common (reduced dimensionality) representation which can be used, for example, to perform a group-level parcellation (Smith et al., 2014). In contrast, the orthogonal BrainSync transform also aligns data across subjects, but in such a way that all of the information in the original data are retained so that we can, for example, compute individual parcellations while still exploiting similarities in the data, as described below.

Here we describe BrainSync, a novel transform for inter-subject comparison of fMRI signals in which a transformation is applied that allows direct comparison of time-series across subjects. We represent normalized (zero mean, unit norm) rfMRI time-series data as a set of labeled points on the hypersphere. We then describe an orthogonal transformation that makes the rfMRI data from two subjects directly comparable. The BrainSync transform retains the original signal geometry by preserving the pairwise geodesic distances between all pairs of points on the hypersphere while also temporally aligning or synchronizing the two scans (Joshi et al., 2017). This synchronization results in an approximate matching of the time-series at homologous locations across subjects. The synchronized data can then be directly pooled to facilitate large-scale studies involving multiple subjects from cross-sectional as well as longitudinal studies. We show applications of BrainSync to rfMRI as well as illustrate how it can be used for task fMRI through examples involving motor function and annotation prediction.

Materials and methods

We assume we have rfMRI and associated structural MRI data for two subjects. Our goal is to synchronize the rfMRI time-series between these two subjects, although the method extends directly both to multiple sessions for a single subject or synchronization across multiple subjects. Our analysis below assumes that the rfMRI data has been mapped onto a tessellated representation of the mid-cortical layer of the cerebral cortex. The cortical surfaces for the two subjects must also be non-rigidly aligned and resampled onto a common mesh, as can be achieved using FreeSurfer (Fischl, 2012) or BrainSuite (Shattuck et al., 2002).

Denote the cortically mapped rfMRI data for the subjects as matrices X and Y, each of size T × V, where T represents the number of time points and V is the number of vertices in the cortical mesh, with V≫T. Corresponding columns in X and Y represent the time-series at homologous locations in the two brains. The data vectors in each column in X and Y are normalized in pre-processing to have zero mean and unit norm.

The BrainSync transform

Since the time-series at each vertex is of unit norm, we can represent each column of X and Y as a single point on the unit hypersphere ${\mathbb{S}}^{T-1}$ of dimension T − 1T

Let $\overrightarrow{x}$ and $\overrightarrow{y}$ represent time-series from two points in the brain. Then the inner product of $\overrightarrow{x}$ and $\overrightarrow{y}$ yields the Pearson correlation ${\rho }_{\overrightarrow{x}\overrightarrow{y}}$ between them. Distance between points on the hypersphere depends only on the correlation between their respective unit-length vectors, so that highly correlated time-series will appear as tight clusters of points. Distance between clusters on the hypersphere will reflect the degree of correlation between their respective time-series. The inverse cosine of ${\rho }_{\overrightarrow{x}\overrightarrow{y}}$ gives the geodesic distance between the points on the hypersphere. The squared Euclidean distance between them is given by ${(\overrightarrow{x}-\overrightarrow{y})}^2=2-2{\rho }_{\overrightarrow{x}\overrightarrow{y}}$ and so is also solely a function of ${\rho }_{\overrightarrow{x}\overrightarrow{y}}$. It therefore follows that if two subjects have similar connectivity patterns to each other, then both intra- and inter-cluster distances are similar, resulting in a similar configuration of points on the hypersphere for the two subjects. In other words, we would expect the patterns for two subjects to differ from each other primarily by a rotation and/or reflection of one hypersphere with respect to the other. With this picture in mind, we compute an orthogonal transformation (rotation and/or reflection) that will map the data from one subject onto that of the other based on the following result (Boutin and Kemper, 2004):

Let ${\overrightarrow{x}}_1,\cdots ,{\overrightarrow{x}}_V$ and ${\overrightarrow{y}}_1,\cdots ,{\overrightarrow{y}}_V$ be points in ${ℝ}^T$.If $\Vert {\overrightarrow{x}}_i-{\overrightarrow{x}}_j\Vert =\Vert {\overrightarrow{y}}_i-{\overrightarrow{y}}_j\Vert ,\forall i,j\in \{1,\cdots ,V\}$, then there exists a rigid motion (O, t) such that ${\overrightarrow{x}}_i=O{\overrightarrow{y}}_i+t,\forall i\in \{1,\cdots ,V\}$, where O is a T × T orthogonal matrix and $t\in {ℝ}^T$, representing rotation/reflection and translation respectively. Since in our case the points are on a hypersphere ${\mathbb{S}}^{T-1}$, we can exclude the translation and apply a strict orthogonal transformation.

The orthogonal transform O^s that synchronizes the two data sets, X and Y, is chosen to minimize the overall squared error:

$$O^s= \text{argmin}{ }_{\text{O}\in \text{O}(\text{T})}\left|\right|X-OY|{|}_F^2$$

where O(T) represents the group of T × T orthogonal matrices and || · ||_F represents the Frobenius norm. Given the high dimensionality of the surface vertices (V ≈ 32,000) relative to the number of time samples (T ≈ 1,200) in the data analyzed below, the problem is well-posed and can be solved using the Kabsch algorithm (Kabsch, 1976). Following the derivation in (Sorkine, 2009), we first form the T × T cross-correlation matrix XY^t , where trepresents the transpose operator, and then compute its singular value decomposition (SVD): XY¹ = UΣV^t. The optimal orthogonal matrix is then given by:

$$O^s=U{V}^t$$

The synchronized data is given simply by Y^s = O^sY. Note that all the steps in the computation involve relatively small amounts of memory and are computationally inexpensive since we form and decompose the T × T temporal cross-correlation matrix that is much smaller than the V × V spatial cross-correlation. Cross-subject synchronization can be computed in a few seconds on a regular desktop PC.

To illustrate the behavior of the BrainSync transform, we applied this orthogonal transformation to data from a pair of rfMRI data sets from the Human Connectome Project (HCP) database described and explored more extensively below. Fig. 1 shows a single frame from the video M1 (supplemental material) depicting the sample subject, reference and synchronized subject data plotted on the cortical surface. Fig. 2 shows an example of the time-series before and after BrainSync for the same vertex for the two subjects. While the synchronization makes the time courses of the two datasets similar, individual variation is retained after the transformation as manifested in the differences in spatial activation patterns between the reference and synchronized subject data. This is to be expected and is an important feature of the proposed transform: the BrainSync transform aligns the components of the spatiotemporal data that are common (with respect to their representation in the hypersphere) but will also retain any individual differences. The impact of synchronization can be seen more clearly in the video M1 (supplemental material). We note that the transformation is not restricted to be a simple nonlinear scaling or a permutation of the time series. Rather, the transformed time series values at a particular vertex at each point in time are, in general, a linear function of the values at all time points at that vertex.

Fig. 1.

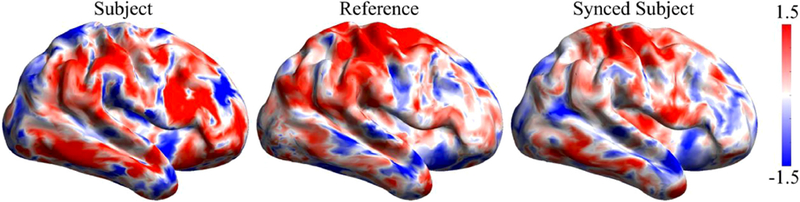
A single frame from the animation of synced data is shown. (left) subject, (middle) reference and (right) subject synchronized to reference. An animation showing the dynamic changes in these data is included in video M1 (supplemental material).

Fig. 2.

Representative time-series for two subjects for a single cortical location before and after synchronization from a subject to the reference subject.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.058.

To illustrate the concept of BrainSync, we performed the following experiment. We used rfMRI data resampled onto the cortical surfaces for three subjects, denoted as subject 1, subject 2 and reference, with T = 1200 time samples per vertex (see Section 2.3 for details of the rfMRI data used). For illustrative purposes, we need to reduce dimensionality to ${ℝ}^3$ so that we can plot the data on the ${\mathbb{S}}^2$ sphere. We considered data from only three locations: cingulate, motor cortex and visual cortex. We projected this data onto the ${ℝ}^3$ subspace corresponding to the three largest singular values in the data matrix for each subject and renormalized to unit length. Only three regions were considered for this illustration so that embedding to three dimensions is possible. This data is of sufficiently low rank that we can indeed see the clustering of points on the sphere (Fig. 3 (a)). Fig. 3 (b) shows the result of applying the BrainSync orthogonal transformation from the two subjects to the reference in the original T = 1200 -dimensional space, and then mapping back to the unit sphere using the same projection onto ${ℝ}^3$ as used to generate the result in Fig. 3 (a). We included two subjects in this example, one for which the orthogonal matrix was a pure rotation (determinant = 1) and the other that included a reflection (determinant = − 1). The transformed data represented on the sphere for both subjects is now very similar to that of the reference. Note that the dimensionality reduction to three dimensions using PCA was performed only for the purposes of illustration and visualization. BrainSync does not require dimensionality reduction and was not performed for any of the applications presented in this paper.

Fig. 3.

Illustration of the BrainSync concept: (a) Data from motor (red), cingulate (green) and visual (blue) areas was considered. Representation of this data on a hypersphere is depicted. Dimensionality reduction was performed using PCA. (b) Three datasets (reference and two subjects) from these areas was used as input to PCA. Dimensionality of the data was reduced to 3D and renormalized to generate the mapping to the sphere. Application of BrainSync to the two subjects relative to the reference results in a configuration of data on the sphere similar to that for the reference dataset. Subject 1 requires only rotation while subject 2 requires rotation and reflection for synchronization.

Properties of the BrainSync transform

The BrainSync transform has some interesting as well as useful properties. It is an orthogonal transform and hence invertible. Orthogonality also ensures that the spatial correlation structure (brain connectivity) contained in the original data is preserved. Because of this property, the ‘synchronization’ performed by BrainSync transformation can be interpreted as a lossless transformation of the original data such that the brain connectivity patterns are preserved, and the data can be compared across subjects using the regular Euclidean metric and Fro-benius norms. The transformation is unique due to the uniqueness of the SVD used to compute the transform (assuming no repeated singular values in XY^t = UΣV^t). It can be shown that the transform is inverse-consistent (Christensen and Johnson, 2001), i.e. switching the reference X and subject Y results in a transform which is the inverse of 0^s, and results in the same cost. The transformation is not necessarily associative, i.e. if X is synchronized to Y using the transformation O₁ and Y is synchronized to Z using O₂, then the transformation O₃ that synchronizes X to Z is not necessarily equal to O₂ O₁. However, it can be shown that if instead of considering O₂ that synchronizes Y to Z, we consider Õ₂ that synchronizes O₁X to Z, then we have the equality O₃ = Õ₂O₁. This property shows that synced data can be used as a surrogate for the original data.

Due to the lack of associativity, the results of a multi-subject study using BrainSync will depend on the choice of reference subject to which all others are synced. However, we expect that these differences will be small if the reference subject’s connectivity is representative of the population in the study. A simple strategy of using the reference with smallest average distance to the rest of the subjects in the study population is used in Section 4.2 below. Since the BrainSync transform is fast, performing all possible pairwise synchronizations in a given study population will also typically be computationally tractable.

Since X and Y are normalized, and due to the properties of Frobenius norm and trace operators, the minimization of the Frobenius norm $||X-OY|{|}_F^2$ is equivalent to the maximization of Trace(X^t (OY)) = Trace((OY)^tX). The left-hand side is proportional to spatial correlation, i.e. the sum of the spatial dot products of the X images and the transformed Y images. On the other hand, the right-hand side is the temporal correlation, which is the sum of the temporal dot products of the X time series and the transformed Y time series. Therefore, the optimization of the cost function leads to maximization of both spatial and temporal correlations.

Note that the group of T × T orthogonal transformations is represented by matrices with det = ±1. The rotations in higher dimensions are defined as the transformations represented by matrices with det = + 1, while combinations of rotations and reflections are represented by matrices with det = − 1. For the BrainSync transform we observed both cases with equal frequency. The group of orthogonal transformations has two connected components corresponding to matrices with det +1 and −1 respectively. Luckily this does not present a problem when solving the optimization problem to find the orthogonal transform since a closedform solution exists and an iterative search is not required.

Data description and preprocessing

We used the minimally preprocessed (ICA-FIX denoised) resting fMRI data from 40 randomly selected subjects (all right-handed, age 26–30, 16 male and 24 female), which are publicly available from the Human Connectome Project (HCP) (Barch et al., 2013; Glasser et al., 2013; Smith et al., 2013; Van Essen et al., 2013; Woolrich et al., 2001). These data were acquired for four independent resting fMRI sessions (LR_1, LR_2, RL_1, RL_2) of 15 min each (TR = 720ms, TE = 33.1ms, 2 mm × 2 mm × 2 mm voxels) with the subjects asked to relax and fixate on a projected bright cross-hair on a dark background. Here we use the LR_1 sessions and the LR_2 sessions to evaluate the performance of BrainSync. The pre-processing pipeline includes processing of T1W images of each subject using FreeSurfer (Fischl, 2012) for identification of cortical surfaces and co-registration of the surfaces to a common atlas. These surfaces were then registered to a common standard cortical surface mesh (32K Conte-69). rfMRI data were corrected for acquisition artifacts and subject to a non-aggressive spatiotemporal clean up (Glasser et al., 2013). The time-series data were then linearly resampled onto the mid-cortical surfaces generated by FreeSurfer and then transferred to the grayordinate representation defined by the 32K Conte-69 surface (Glasser et al., 2013). The 15 min of scan time with TR = 720ms resulted in 1200 time samples per voxel. From the available grayordinate data, we extracted only the data corresponding to the cortical surface.

The task-related results presented below are based on the task-localizer data also made available by the HCP. Task-based fMRI data (Barch et al., 2013) were obtained for the same 40 subjects in language processing and motor strip mapping task domains. To identify regions of language processing, subjects perform an interleaved math and story task. In the motor category, subjects are told to move certain parts of the body (tongue and left/right hand) to identify the functional areas associated with the respective movement. For the motor tasks, HCP also provides the task timing blocks that indicate the start and stop times for each task.

The other dataset we used for this work is available from the Study-forrest project (http://studyforrest.org) and centers around the use of the movie Forrest Gump, which provides complex sensory inputs that are reproducible and rich with real-life-like content and contexts (Labs et al., 2015). The dataset encompasses fMRI scans, structural brain scans, eye-tracking data, and extensive annotations of the movie. We considered phase II (Hanke et al., 2016) of the study that involves audio-visual stimuli resulting from the subject watching and listening to the movie while whole brain fMRI scans were acquired using a 3T scanner. An annotation dataset is also available with the imaging data in which a total of 12 observers independently annotated emotional episodes regarding their temporal location and duration. For this preliminary investigation, we use only the ‘face’ annotation (presence of faces in the video).

We processed the Studyforrest fMRI datasets using the fcon1000 pipeline (Mennes et al., 2013) that uses a combination of FSL and AFNI. The pre-processing for functional data included deobliquing, motion correction, skull stripping; rigid coregistration to structural images and then to MNI space; nuisance signal (white matter and CSF) removal; 3D spatial smoothing (FWHM = 2.35 mm); global mean removal; temporal bandpass filtering (0.005 Hz-0.1 Hz); and removal of linear and quadratic trends. Processing of the structural MPRAGE data was performed using BrainSuite (Shattuck et al., 2002). BrainSuite includes a multi-step cortical modeling sequence. These steps include skull-stripping; tissue classification; labelling of cerebrum, cerebellum, and brainstem; white matter mask generation; topology correction; white matter surface generation; pial surface generation. This is followed by a surface constrained volumetric registration sequence (Joshi et al., 2012) that performs labelling and coregistration of the subject to a standard atlas. The fMRI data were then resampled onto the Brainsuite cortical surface representation using linear interpolation. To map this dataset to a common space with the HCP datasets we then registered this surface data to the 32K Conte-69 surface using FreeSurfer and FSL.

We performed additional downsampling of the HCP and Studyforrest surface fMRI data to ~11K vertices using Matlab’s ‘reducepatch’ function. We then applied denoising to the fMRI data using nonlinear temporal non-local means (tNLM) filtering (Bhushan et al., 2016). In contrast to traditional local Gaussian filtering, tNLM filtering reduces noise in the fMRI data without spatial blurring between regions of different functional specializations. To achieve this, tNLM uses the weighted average of data in a large neighborhood surrounding each vertex where the weights are chosen adaptively depending on similarities between the fMRI time series at the vertices. Specifically, the tNLM filtered fMRI signal f (s, t) at vertex s and time t is expressed as $f(s,t)=\frac{1}{{\sum }_{r\in N(s)}w\left(s,r\right)}\sum _{r\in N(s)}w(s,r)d(r,t)$ where d(s, t) is the original unfiltered signal, N(s) is a vertex neighbourhood of s, and the weights are given by $w\left(s,r\right)=\text{exp}\left(-\frac{\frac{1}{T}||d(s)-d(r)|{|}^2}{h^2}\right)$. We chose the parameter h = 0.72 and a neigh-bourhood N(s) consisting of all vertices no more than 11 edges from s, based on the recommendations in (Bhushan et al., 2016). Unless otherwise stated, all data used in the results presented below are based on tNLM-filtered data.

Finally, we normalized the filtered resting fMRI time-series at each vertex to zero mean and unit norm by subtracting the mean of the time-series for each vertex and scaling by the corresponding norm of the zero-mean time-series.

Simulation and experimental studies of the properties of the BrainSync transform

Effect of scan length on synchronization

Since the BrainSync transform is based on the hypothesis that brain networks are similar across subjects, we expect performance to improve with number of samples T. For larger T, estimation of the sample correlation matrices become more accurate, and therefore more similar across scans or subjects.

In order to test how well the synchronization works for different scan lengths, we considered rfMRI scans X and Y from different subjects, each of size T × V. Each of these scans were truncated to shorter time lengths t and renormalized. The truncated scans, denoted by X_t and Y_t, were synchronized using BrainSync to produce the orthogonal transformation O_t, such that O_tY_t becomes similar to X_t. The correlation ρ_t = X_t·Yt between truncated scans was computed before and after synchronization and averaged over the cortex. We considered 40 distinct pairs of subjects for the cross subject comparison. For the within-subject case, we synchronized two sessions of each subject, for a total of 40 subjects, and averaged correlation over the cortex. The plots in Fig. 4 show mean correlation and standard deviation across subjects for different time lengths T.

Fig. 4.

Average correlation over the cortex before and after synchronization, as a function of number of time samples (TR = 0.72 s), for (left) within subject across two sessions; (right) across subjects. Mean and standard deviations across subjects are shown as line plots and shaded areas respectively.

While synchronization of signals continues to improve with longer scans, BrainSync achieves close to the maximum correlation at around 5 min (T ≈ 400). The shaded regions denoting standard deviations in the ‘after synchronization’ cases are generally very small indicating consistency of the result across subjects.

Permutations of vertices

The transform that synchronizes the rfMRI data across scans is based on the assumption that the brain networks in the two brains are similar to each other, although they are not required to be identical. To test if this hypothesis is required for synchronization to work, and to ensure that the synchronization is not simply due to the data being low-rank, the following statistical comparison was performed.

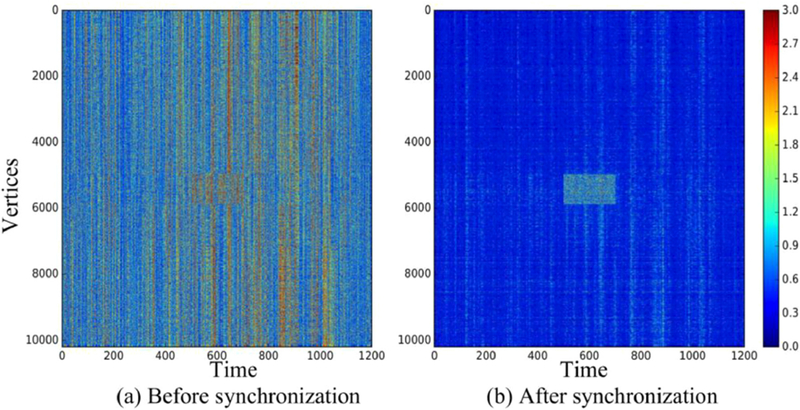
Data (tNLM filtered) for two subjects X and Y was synchronized and the pairwise correlation between their corresponding points on the cortical surface was computed. It can be seen in Fig. 5 (b) that the pairwise correlations were high after synchronization across most of the brain, compared to the low correlation that we obtain before the signals are synced (Fig. 5 (a)). Next, we performed a random permutation of the rows of the data matrix of X. This operation results in a permuted data matrix X^p that has the same singular value structure as X, however the correlation with Y will be different since the permutation destroys the vertex correspondence. The permuted data X^p was then synchronized to Y using BrainSync. The correlations after permutation was low before syncing (Fig. 5 (c)), and remained relatively low after syncing (Fig. 5 (d)) relative to the unpermuted case (Fig. 5 (b)). To test for statistical significance, we repeated the permutation procedure 1000 times to generate correlation maps similar to (d). These maps form a null distribution for the case where we would not expect meaningful synchronization. The positive correlation after transformation of the permuted data can be explained by the observation that the BrainSync transform will always attempt to maximize correlations, resulting in some degree of positive correlation even for data that do not satisfy our underlying assumption of common networks. Furthermore, even after permutation we would still expect some degree of (random) correspondence between the two brains, particularly for the larger networks that occupy a significant fraction of the cerebral cortex. To determine whether the results for synchronization of the original (unpermuted) correlations in (b) are significant they were tested against the null distribution. The p-values were corrected for multiple comparison using the Benjamini-Hodgeberg false discovery rate (FDR) procedure (Benjamini and Hochberg, 1995) (Fig. 5 (e)). This test showed significance throughout the cortex with p-values close to zero at almost all points on the cortex. This result confirms that the high correlation after syncing seen in Fig. 5 (b) is not simply due to low rank structure, and is consistent with our hypothesis that it is the underlying common spatial correlation patterns across subjects that allows alignment of data across subjects.

Fig. 5.

BrainSync for two subjects. Each map shows the cross-correlation between time-series from homologous locations in the two subjects as follows: (a) before synchronization, (b) after synchronization. The spatial ordering of the vertices for the second subject were then randomly permuted and the cross-correlation recomputed: (c) before synchronization, (d) after synchronization; (e) the random permutations were repeated 1000 times to generate a null distribution of the correlations and the correlation map in (b) was tested against this null distribution to test for significance. The resulting p-values, corrected for multiple comparisons using FDR, were close to zero throughout the cortex, except at a few points, as shown in (e).

Detection of localized differences between scans

We performed a test to study the ability of BrainSync to identify and localize, both spatially and temporally, deviations in activity and connectivity from resting behavior. This may occur for example as a subject transition from ‘resting’ to performing a specific task, and back again. Deviations may also be caused by pathology such as inter-ictal spiking in an epileptic subject. For this test, we used two sessions of resting data from a single subject. A block of white Gaussian noise was added to the spatiotemporal data matrix for one scan scaled so that the full-time series for each affected vertex had unit norm. The resulting datasets were synchronized to each other. The residual error after synchronization shows that the resting signal in the two datasets was relatively well synchronized while the noise block is clearly not, Fig. 6. This simulation illustrates the potential for BrainSync to localize differences between scans, both spatially and temporally.

Fig. 6.

Absolute value of difference between two scans of rfMRI data from two sessions of a single subject. A noise block is added in one of the scans as can be seen at the central region of the images, (a) difference before syncing; (b) difference after syncing. After syncing, the region in which the two scans are qualitatively different is clearly visible.

Applications to in-vivo data

Application 1: quantifying variability of rfMRI across a population

To investigate within-subject variability, we computed the correlation at each vertex between two sessions in the same subject after synchronization and averaged the result over all 40 subjects, Fig. 7 (a). To compute between-subject variability, we performed pairwise synchronization for all 40 × 39/2 = 780 pairs. We then computed the between- subject correlations at each vertex after synchronization, averaged over all pairs and plotted the result as the maps shown in Fig. 7 (b).

Fig. 7.

Average correlation between resting fMRI time series at each vertex after applying BrainSync: (a) across two sessions within the same subject, averaged over 40 subjects; (b) across subjects, averaged over all pairs and two sessions.

Within-subject variability across sessions reveals that most of the brain exhibits repeatable patterns of correlation, which lead to accurate syncing. Examples of areas with lower correlation include the temporal lobe and medial frontal cortex, possibly due to lower signal amplitudes (and hence lower signal to noise ration) from these regions. Across subject correlations are lower than within-subject correlations as might be expected. Nevertheless, the regions showing higher correlations are similar to those found within individuals.

For additional insight, we computed the mean and standard deviation (s.d.) of the between-subject correlations, both for tNLM filtered and unfiltered data. For this study, we first computed the Fisher-z transform to normalize the correlations, then computed mean and s.d. of the transformed data over all pairs of subjects, Fig. 8. Histograms for each of the four cases, computed across the cortex, are shown in Fig. S1 (supplemental material). These results show low correlation before synchronization, with or without tNLM filtering. We also see that without filtering, the post-sync correlations are lower than for the filtered data. This follows from the fact that tNLM filtering tends to reinforce components in the time series that are strongly correlated with those at other vertices, as described in (Bhushan et al., 2016). Without filtering, correlations will be considerably lower, as they are when computing rfMRI correlations between vertices in a single subject.

Fig. 8.

Mean and standard deviation maps for between subject correlation of resting fMRI before and after applying BrainSync, and with and without tNLM filtering. Maps are shown after computing correlation across all pairs of subjects, taking Fisher-z transform of the correlations and averaging across all subject pairs.

Application 2: cortical parcellation

Parcellations of the human cerebral cortex representing cyto-, myelo-or chemo-architecture are helpful in understanding the structural and functional organization of the brain (Amunts et al., 2007; von Economo and Koskinas, 1925). Resting fMRI has been used for identification of contiguous areas of cortex that exhibit similar functional connectivity to define a functional parcellation (Arslan et al., 2017; Sporns et al., 2005). One major problem in using rfMRI for single subject parcellation is that the amount of data from an individual is usually not sufficient to reliably parcellate the cerebral cortex brain into a large number of regions (Arslan et al., 2017; Rubinov and Sporns, 2010). An alternative approach is to pool data across subjects, although this typically requires definition of an anatomical correspondence across subjects which results in a single group parcellation that does not account for individual functional differences. A second challenge that arises in both single subject and group parcellations, is that the feature vectors used for parcellation are often defined by the correlation from each surface vertex to all other vertices (Fan et al., 2016). These are very high dimensional so that down-sampling is commonly used to make the problem tractable (Iraji et al., 2016). Recent approaches have been described that use graph theory and constrained optimization to accelerate group parcellation while preserving individual characteristics (Chong et al., 2017; Wang et al., 2015), but computational cost remains high and there is a dependence on parameters used to define the underlying statistical models.

Here we explore the use of BrainSync for parcellation. Since Brain- Sync makes data across subjects directly comparable, this synchronized data itself can be used as a feature vector for parcellation, and since its dimension is equal to the number of time samples, it is significantly smaller than the correlation-based feature vectors just described. Our approach is straightforward: we first select a representative subject (see below) and sync all other subjects to that subject. We then treat the synced time series at each vertex as the feature vector for that subject and vertex. Finally, we jointly parcellate the data for all subjects using k-means clustering (MacQueen, 1967; Thirion et al., 2014) with one feature vector per vertex in each subject.

For joint parcellation, we used two sessions of 15min scans for the 40 subjects. Let B_l,m represent the T × V data matrix for the l^th subject and m^th scan, all synchronized to the reference. A data matrix was then generated as B = [B_1,1,B_1,2, B_2,1,B_2,2, …,B_40,2] as illustrated in Fig. 10 (b). This matrix has size T × (2 × 40 × V) with T being the dimension of the feature vector. The k-means algorithm was then applied to cluster the data into k = 17, 40 and 100 clusters. In other words, each vertex in each of the 40 × 2 brain scans were separately assigned to one of the k clusters. Note that since the time series are synchronized across scans, k-means clustering can treat the time series themselves as a feature vector and produce a label vector of size 2 × 40 × V. We do not enforce any spatial prior or topological constraint on the labels and the clustering does not make use of the vertex position, so that the time series from corresponding vertices in different subjects and scans are treated independently.

Fig. 10.

(a) The rfMRI data from N = 40 subjects, 2 sessions each, was temporally concatenated to generate a 2NT × V data matrix, as shown on the left. This data matrix was input to k-means clustering, with feature vector of dimension 2NT and k = 100, to generate a single common parcellation for all brains. (b) The BrainSync’ed data were arranged as T × 2NV matrix and input to k-means clustering with a feature vector of size T to jointly produce an individualized parcellation of each subject, as shown in Fig. 11.

We choose a reference as the most representative subject across the population of 40 subjects. To do this, we performed pairwise synchronization of the rfMRI data for all 40 × 39/2 = 780 possibilities. After synchronization, the residual RMS error e = X − OY_F was computed between each pair and used as a measure of dissimilarity. We then chose the subject with the minimum average distance to all other subjects. To visualize the distance between subjects we entered the pairwise errors into a 40 × 40 distance matrix where the (i, j)^th entry indicates the distance between subject i and j. We then used the multidimensional scaling (MDS) algorithm (Torgerson, 1952) and reduced the dimensionality of the data to two for visualization of relative distances between all subjects (Fig. 9).

Fig. 9.

Result of applying MDS (multidimensional scaling) to the synchronized data to identify the (circled) representative subject who has the smallest average distance to all other subjects in terms of the error e = X − OY_F.

For comparison, we applied two alternative approaches. In the first, we produce a single parcellation by stacking the unsynchronized data for each vertex label from each subject as illustrated in Fig. 10 (a). In this case the data matrix is of size (T × 2 × 40) × V where (T × 2 × 40) is the dimension of the feature vector. We then applied the k-means clustering method to label each of the V vertices. We also applied k-means clustering to each data set separately, i.e. to data matrices of size T × V, with feature vector size T, for each of the 40 × 2 data sets.

The single group parcellation for K = 100 is shown in Fig. 10 (a) and sample parcellations for two subjects, two sessions each, are shown in Fig. 11 using individual clustering and joint BrainSync-based clustering. For comparison of results we used the Hungarian algorithm (Kuhn, 1955) for label matching between individual results, the joint labelling, and the BrainSync results. Note that for BrainSync-based clustering, corresponding regions are automatically identified across subjects since the same k clusters are used to label all subjects.

Fig. 11.

Representative individual parcellation results (k = 100) for two subjects, two sessions each. Upper row: each brain parcellated separately; lower row: joint parcellation using the synchronized time-series.

The individual parcellations (Fig. 11 top row) vary significantly, even for the same subject for two different scanning sessions. In contrast, the individual parcellations produced using BrainSync transformed data (Fig. 11, bottom row) show similar results for different sessions of the same subject, even though the clustering algorithm treated the two data sets as equivalent to those from separate subjects. In other words, the assignment of each vertex to one of the k clusters was done independently for the two sessions for each subject. The BrainSync data shows differences in labelling between the two subjects shown in Fig. 11, but also closer similarity to the joint parcellation result from the fully concatenated data in Fig. 10(a) than we see in the individual parcellation results in the top row of Fig. 11.

To quantify performance, we computed the Adjusted Rand Index (ARI) (Hubert and Arabie, 1985) between all pairs of subjects and scans and report both within-subject and across-subject similarity by averaging across subjects and sessions respectively in Table 1. ARIs were computed for both the individual and BrainSync-based parcellation. Table 1 shows substantially higher within and between subject consistency when labelling using all synchronized data, than when labelling each subject and session separately. In Table 1 we also compare the individual and BrainSync parcellations to the single group parcellation result. Again, the BrainSync results show significantly closer similarity to the group result than do the individual parcellations.

Table 1.

Adjusted Rand Indices: mean(s.d.) for different number of clusters (k) for group, individual and BrainSync-based parcellation.

ARI	Individual k = 17	BrainSync k = 17	Individual k = 40	BrainSync k = 40	Individual k = 100	BrainSync k = 100
Within subject	0.79(0.05)	0.95(0.03)	0.48(0.13)	0.94(0.02)	0.42(0.12)	0.93(0.03)
Across subjects	0.68(0.11)	0.91(0.04)	0.46(0.15)	0.91(0.03)	0.32(0.16)	0.90(0.03)
Compared to group parcellation	0.69(0.12)	0.93(0.03)	0.49(0.14)	0.92(0.03)	0.33(0.17)	0.91(0.04)

We emphasize that there is no spatial prior or across subject similarity constraint used for the BrainSync-based clustering. Because the data are synchronized across subjects and sessions, k-means clustering automatically produces label correspondence across subjects. The fact that the clusters are made up of one or more contiguous regions for both the individual and group results arises in part from the filtering effects of tNLM, which emphasizes temporal similarity when filtering the data. This property is also shown in (Bhushan et al., 2016) for parcellation of tNLM filtered data based on normalized cuts.

One way to interpret these results is that the data for each subject forms a constellation on the hypersphere of the signal space. We are effectively parcellating this pattern on the hypersphere into k regions. The constellations for individual subjects are too sparse to be successfully parcellated individually as the boundaries for a single subject are poorly defined. However, when the constellations of all the subjects are aligned by rotations/reflections of their signal space hyperspheres, they can be pooled to successfully to perform a joint clustering of all subjects simultaneously while still retaining individual differences.

Applications to task fMRI

Contrasting task vs rest

We applied BrainSync for direct comparison of resting and task fMRI. For this purpose, we synced motor activity (tongue movement) with resting data from the HCP database for the same subject. At each point on the brain, the correlation between synced task and resting data was computed (Fig. 12). Despite the fact that we are comparing task and resting data, much of the brain can still be synchronized. Exceptions for the motor task (Fig. 12 (b)) include the face-region of primary motor cortex and portions of the default mode network (DMN). This result is consistent with the idea that we would expect increased motor activity and decreased default mode activity during the motor task. Similarly, for the language task (Fig. 12 (a)), we see reduced synchronization between task and rest in language-related and DMN areas.

Fig. 12.

Task data: Correlation between resting and synchronized (a) language task, (b) motor tongue task time-series.

Predicting timing information

To further investigate the behavior of BrainSync, we considered two sessions of task data for a single subject. This task data involved a block design with different motor tasks involving tongue, right and left feet as well as hand motion in different timing blocks. While the two sessions involved identical tasks and involved all of these motor actions, their timing blocks were different. Here, we demonstrate the ability of the BrainSync transform to predict the timing blocks of the second session given the timing blocks of the first session. The first session’s rfMRI was synchronized to the second and the resulting orthogonal transformation O^s then applied to the T × 1 time-series that defines the timing blocks for the first session. Since the data used for computing the BrainSync transform are BOLD fMRI signals, the time-series denoting the timing blocks were first convolved with a hemodynamic response function (HRF) modelled using a double gamma distribution (Steffener et al., 2010). The function we used as the HRF h(t) is given by $h(t)=t^5\frac{\text{exp}(-t)}{\Gamma (6)}-t^{15}\frac{\text{exp}(-t)}{6\Gamma (16)}$. As shown in Fig. 13, the rfMRI synchronization matrix O_s allows us to estimate the task timing of the second session from the first with relatively high accuracy.

Fig. 13.

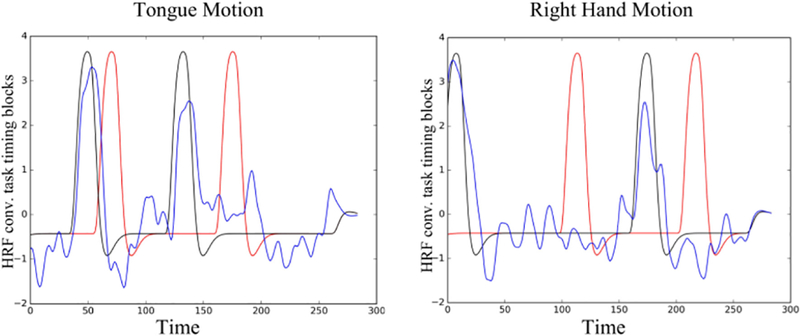
Task data timing recovery: (a) red: HRF convolved timing blocks for session 1; black: HRF convolved timing blocks for session 2; and blue: timing for session 1 after applying the orthogonal transformation predicted by BrainSync to timing blocks for (left) tongue and (right) right hand motor tasks.

Application to Studyforrest data

To investigate the applicability of the BrainSync transform to tasks involving self-paced activities and naturalistic stimuli, we used the Studyforrest dataset (Labs et al., 2015). The data description and our preprocessing are detailed in Section 2.3. For two segments of this data, our goal was to predict annotations of the second segment based on the annotations of the first segment. Here, we consider only the ‘face’ annotation. In order to generate the annotations, 12 raters watched the movie annotating with +1 when a full face was present, 0 for no face. The annotations were then averaged across the 12 raters and smoothed temporally by Gaussian smoothing with a standard deviation of 5 s. Two segments of data were considered. The first segment of fMRI data was synchronized to the second and the resulting BrainSync transform then applied to the annotations of the first segment to predict the annotation of the second. This process was repeated using the data from 8 subjects to predict the annotations for one, which were then averaged. The annotations from the two segments and the predicted annotations are shown in Fig. 14. The correlation of annotations from segment 1 and 2 before synchronization was 0.02. Averaging the predicted annotation over 8 subjects resulted in a correlation of 0.51 with the human rater values averaged over the 12 independent raters.

Fig. 14.

Face annotation from segment 1 (blue); from segment 2 (red); and predicted annotation (black).

Discussion

We have described a novel method for synchronization of rfMRI data across subjects and scans. By exploiting similarity in correlation structure across subjects we are able to transform the time-series so that they become highly correlated across subjects. This synchronization process bears similarity to rigid image registration. In the case of structural comparisons, spatial alignment of images makes cross-subject and longitudinal studies easier by providing approximate point-wise correspondences in space. Similarly, BrainSync facilitates functional comparisons: temporal alignment (synchronization) provides an approximate point-wise correspondence in time.

Pointwise comparisons of fMRI data

The BrainSync transform gives us a unique ability to perform direct pointwise comparisons (in time and space) between time-series data from resting fMRI scans across multiple sessions and subjects. As shown in Fig. 8, pointwise comparisons of unsynced data result in low correlation and high variation (mean = 0.05, s.d. = 0.21) uniformly throughout the brain when computed across all pairs of 40 subjects in a normal population. With BrainSync, significantly higher correlation and lower variance (mean = 0.35, s.d. = 0.16) is achieved throughout the brain. Additional filtering using tNLM results in even higher correlations and lower variance (mean = 0.82, s.d. = 0.08) indicating that denoising with tNLM helps improve synchronization. We see slightly higher variance in the primary visual cortex which may be indicative of the differences of subject behaviors within the scanner (Martinez-Conde et al., 2004). Subjects were asked to fixate on a cross on the screen and avoid blinking (Glasser et al., 2013). Adherence to this task may be difficult and we suspect that subjects may have had differences in eye movement affecting the dynamic BOLD activity in the visual cortex. The pointwise study of mean and variance of inter-subject correlations could be used to investigate individual or group differences in connectivity. Comparison of correlation of an individual synced to each of a set of control subjects could be used to identify regions of abnormal connectivity associated, for example, with epileptogenic networks. This approach would be conceptually similar to measures of local functional connectivity density (Tomasi and Volkow, 2010). Similarly, group-wise comparisons could be used to identify connectivity differences between groups. The utility of pointwise comparisons is again demonstrated in Section 4.3.1 where we detect regional differences between task and rest by synchronizing resting and task fMRI within a single subject. Fig. 12 b shows differences between motor and default mode areas when comparing motor task to rest. For the language task, Fig. 12 a, there are clear differences in Wernicke and Broca’s areas as well as visual and medial prefrontal cortex, which is consistent with the areas identified by (Barch et al., 2013; Binder and Desai, 2011) for this task.

Group level analysis

Synchronized data can be easily pooled to increase the amount of information to perform group-level analysis when information from a single subject is sparse. We demonstrate the utility of pooled data in a population-based joint parcellation of the cerebral cortex using synchronized rfMRI data. As seen in Fig. 11, the boundaries detected within a single subject across different scanning sessions are inconsistent, indicating the information obtained from a single session to be too limited for consistent and reliable cortical parcellation. This discrepancy increases when compared across subjects. The joint-parcellation facilitated by using synchronized time-series data was able to detect more consistent boundaries between homologous regions. Small differences can still be seen across subjects, potentially reflecting individual differences in functional specialization (Amunts et al., 1999). Standard group-level analysis using anatomically coregistered data will retain large-scale common features within a group but may lose unique features of individual subjects. Conversely, BrainSync can exploit connectivity similarities across subjects, while retaining individual variations since we do not constrain cluster labels to be consistent across subjects with respect to the anatomical alignment.

These potential benefits extend to studies of dynamic connectivity. A sliding window approach is the most common method of investigating dynamic functional connectivity (Damaraju et al., 2014; Hindriks et al., 2016). However, this approach only allows for measures of dynamic connectivity to be computed within a single subject and single session since dynamic activity in spontaneous ‘resting’ periods will be different for each individual and session. Syncing time-series data, however, should bring common patterns of correlated activity into temporal alignment, potentially allowing pointwise analysis of dynamic connectivity across subjects for a more robust group level analysis.

Utility of orthogonal transformation

In Section 4.3, we demonstrate the ability to perform synchronization of resting with task fMRI and also between two task data sets, even when the timing of the task blocks was different. The resting to task synchronization, Fig. 12, shows regions in which the task-related signal differs from resting activity. We can also use the computed orthogonal matrices to synchronize time series associated with the BOLD signal, Fig. 13. This ability to predict task block timing from the synced data, as we demonstrate for the motor task, has potential applications where task variables cannot be directly controlled in the experimental design. For example, self-paced or other cognitive studies in which event timing cannot be directly measured.

The application to the Studyforrest data was able to use the synchronized data to predict the presence of faces in the video, Fig. 14. The ‘face’ time series for segment 2 was computed by the BrainSync transformation of the corresponding time series for segment 1, with the orthogonal matrix computed from their respective BOLD fMRI data sets. The correlation of 0.51 with the average over 12 independent rater annotations indicates the potential for BrainSync-based temporal alignment to make inferences about stimulus or emotional content from measured fMRI data provided a training fMRI data set with known content timing is available. Our attempts to predict emotional content (‘love’, ‘fear’, ‘happiness’) from the same data set were less successful and not reported here since to date our analysis has been restricted to the cortical surface and does not include the amygdala, which would be expected to play a major role in responses to these factors. Currently, machine learning approaches are being applied to predict brain activity based on stimuli and vice versa (LaConte et al., 2005). Extensions of BrainSync may be able to contribute in this area.

The hyperalignment technique (Haxby et al., 2011; Guntupalli et al., 2016; Guntupalli and Haxby, 2017) has some similarity to our approach, in that both techniques estimate an orthogonal transform. But the goal of the hyperalignment is to match spatial or connectivity patterns by an orthogonal transform. Time synchronization is not performed so the original timing is unaltered. BrainSync, in contrast generates a T × T orthogonal matrix and aims for temporal alignment of the signal. A combination of hyperalignment and BrainSync may be able to perform a joint spatiotemporal alignment.

Since the transformation is orthogonal, correlations in the original data are preserved and the transform is invertible. The BrainSync transform is fast, requiring only seconds on a laptop and has computational complexity O(T³)+ O(T²V). One of the implicit assumptions in this work is that the rfMRI signal is stationary in the sense that correlation patterns are preserved over time. Our results show good correspondence of signals over the 15-min windows used in this analysis. However, even within a 15-min period we would expect to see variations in the activity of different networks, and it would be interesting to explore whether BrainSync is able to enhance our ability to identify and characterize these dynamic changes in network activity.

Limitations and future directions

Synchronization of time-series data become better with an increasing number of time points and decreasing noise. The goodness of fit after synchronization in Fig. 4 indicates that 5 min of acquisition (with TR = 0.72 secs) produces close to the minimum error, relative to longer time courses. Syncing of shorter time courses should probably be avoided since the error increases rapidly below this limit.

By considering all possible pairs after syncing across subjects (Section 4.1), we avoid bias towards any individual. However, in the parcellation study (Section 4.2) we sync to a single individual in order to produce a feature vector of a reasonable size (T = 1200). To reduce bias, we select the most representative subject based on a distance measure as described above. However, since we are syncing everyone to a single subject, the results may tend to emphasize differences in that individual from the population. The recursive scheme described in (Guntupalli et al., 2016), in which results are averaged across subjects as alignment is performed, could be adapted as a means of avoiding this bias. More generally, we could reformulate the optimization problem to compute the orthogonal transform that minimize the average error in the fit of each subject to all others. This may avoid the bias problem, but would lead to a more complex problem without the simple closed form unique solution we obtain for the pairwise case.

We have not explored the robustness of BrainSync to technical challenges including differences in image acquisition parameters, field strength, and manufacturer, which may affect the analysis of multi-center data. Further testing will be required to investigate this issue.

Conclusion

The BrainSync transform¹ allows direct comparison of time-series data between homologous points of registered brains and has a wide range of possible applications. The main contribution of this work is to define, we believe for the first time, a method for rotating time series so that spontaneous brain activity can be synchronized across different scans from the same subject and also between scans from different subjects. Our results indicate that when combined with tNLM filtering, we are able to achieve correlations of 0.8, averaged across the brain, between the synchronized resting time series across subjects at homologous locations. Because the transformation retains the temporal information in each data set we are able to explore dynamic aspects of data, which would not be possible when using the spatial correlation matrix. For example, we show that block-design functional task data can be synchronized, either to each other or to resting data. By applying the estimated orthogonal matrices to time series representing either the task timing (e.g. for motor activity) or stimulus content (e.g. presence of faces in a movie), we were also able to predict the timing of these events from the fMRI data. Potential applications include identification of group and individual differences in connectivity, individualized functional parcellation, studies of dynamical connectivity, and inference of event timing and emotional responses from fMRI data.

Appendix A. Supplementary data

Supplementary data related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.01.058.