Borrowing of strength from indirect evidence in 40 network meta-analyses

Abstract

Objective:

Network meta-analysis (NMA) is increasingly being used to synthesize direct and indirect evidence and help decision makers simultaneously compare multiple treatments. We empirically evaluate the incremental gain in precision achieved by incorporating indirect evidence in NMAs.

Study Design and Setting:

We performed both network and pairwise meta-analyses on 40 published datasets of multiple-treatment comparisons. Their results were compared using the recently proposed borrowing of strength (BoS) statistic, which quantifies the percentage reduction in the uncertainty of the effect estimate when adding indirect evidence to an NMA.

Results:

We analyzed 915 possible treatment comparisons, from which 484 (53%) had no direct evidence (BoS = 100%). In 181 comparisons with only one study contributing direct evidence, NMAs resulted in reduced precision (BoS < 0) and no appreciable improvements in precision (0 < BoS < 30%) for 104 (57.5%) and 23 (12.7%) comparisons, respectively. In 250 comparisons with at least two studies contributing direct evidence, NMAs provided increased precision with BoS ≥ 30% for 166 (66.4%) comparisons.

Conclusion:

Although NMAs have the potential to provide more precise results than those only based on direct evidence, the incremental gain may reliably occur only when at least two head-to-head studies are available and treatments are well connected. Researchers should routinely report and compare the results from both network and pairwise meta-analyses.

1. INTRODUCTION

In the recent fifteen years, network meta-analysis (NMA) has been frequently applied in evidence-based medicine to inform the relative benefits and harms of various treatments [1–3]. The fundamental idea is to simultaneously synthesize both direct and indirect evidence from all available studies of all related treatment comparisons, and thus to provide better decision making than conventional pairwise meta-analysis that separately and directly compares each pair of treatments [4–8]. Specifically, to compare two treatments A and B, the clinical studies that include both treatment groups provide the direct evidence for this comparison. However, such evidence may be sparse, especially when the two treatments are newly developed or when no financial incentive supports conducting head-to-head trials [9, 10]. Alternatively, more studies may be available to compare A or B with another common comparator, say C, which may be placebo or some well-established drugs. Consequently, these studies of A vs. C and B vs. C provide the indirect evidence for the comparison between A and B [11, 12]. The three treatments A, B, and C form an evidence loop (cycle) in the network. Because conventional pairwise meta-analysis can only use the direct evidence, NMA is expected to produce more precise evidence for decision making by using information from all studies [13]. For example, in a systematic review of 12 new-generation antidepressants [14], the pairwise meta-analysis estimated the odds ratio of escitalopram vs. fluoxetine as 1.23 with 95% confidence interval (0.87, 1.74), suggesting insufficient evidence for differential effects, while the NMA estimated it as 1.32 with 95% credible interval (1.12, 1.55), providing improved precision and indicating a significant difference between the two antidepressants in efficacy.

Comparing the results from an NMA with those from separate pairwise meta-analyses is critical for assessing the quality of evidence [15]. However, many NMAs were found to be inappropriately performed and inadequately reported [16–21]. Only a few NMAs explicitly compared the results produced by NMAs with those produced by conventional pairwise meta-analyses and showed how much indirect evidence was gained from NMAs [18]. Without such information and knowledge of the improved precision, NMAs may not be justified considering their complex statistical procedures [22, 23] and additional assumptions (e.g., transitivity and consistency for treatment comparisons) [6, 19, 24]. In addition, NMAs may complicate assessment of publication and reporting bias given that unpublished results may differentially occur in certain treatment groups in certain studies under diverse missingness scenarios [25–27]. In contrast, plenty of methods are available to test and adjust for such bias in pairwise meta-analyses [28–33]. Moreover, the publication and reporting bias in one treatment in an NMA may affect the ranking of all treatments, leading to completely wrong conclusions for decision making [34].

Recently, the borrowing of strength (BoS) statistic was proposed to quantify how much evidence (incremental precision) is gained in a multivariate meta-analysis (including NMA) [35–37]. It can be interpreted as the percentage reduction in the uncertainty of the effect estimate of a treatment comparison that benefits from the indirect evidence in an NMA. This empirical study uses the BoS statistic to explore the benefits of incorporating indirect evidence in NMAs.

2. METHODS

2.1. Borrowing of strength in NMA

The BoS statistic is defined as BoS = (1 − E) × 100%, where E is the ratio of the variance of the treatment effect estimate using an NMA to that using the direct evidence, representing the efficiency gained from the NMA [35, 36]. An NMA is often performed through Bayesian hierarchical models and researchers usually report the posterior median with a 95% credible interval (CrI) for each treatment comparison. Therefore, under the Bayesian framework, the efficiency E can be equivalently calculated as the squared ratio of the CrI length using the NMA (denoted as L_NMA) to that using the direct evidence (denoted as L_direct), because the CrI length roughly indicates uncertainty. Specifically, the BoS statistic can be calculated as $\mathrm{BoS}=\left(1-L_{\mathrm{NMA}}^2/L_{\mathrm{direct}}^2\right)\times 100\%$ for treatment comparisons in the NMA.

2.2. Data source

We extracted 45 NMAs with binary outcomes from a total of 58 NMAs investigated by Trinquart et al. [38], which were originated from the datasets collected by Veroniki et al. [39] and Bafeta et al. [17, 18]. Datasets that originally used extensions of the classical NMA model (e.g, models for competing-risk outcomes and evidence inconsistency) were excluded [38]. Also, we excluded 5 NMAs that addressed similar questions and had overlapping studies [40–44]. Finally, we obtained 40 NMAs which evaluated a variety of conditions with important morbidity, including rheumatoid arthritis, stroke, cancer, chronic hepatitis B infection, depressive disorder, vertebral fractures, major cardiovascular events, etc. Table S1 in the Supplementary Material describes the NMAs in terms of the number of studies, treatments, direct comparisons, and patients. Figure S1 depicts their geometry.

2.3. Statistical analysis

The included studies in a systematic review are likely heterogeneous because they were conducted at different places using different clinical methods on different populations [45–49]. Therefore, regardless of the original methods used in the 40 NMA datasets, we used a Bayesian random-effects NMA model to account for the heterogeneity between studies [5]. We assumed that the between-study variances τ² were equal for all treatment comparisons in each NMA, and the correlation coefficient between each pair of comparisons within each study was 0.5 [5, 50]. Informative log-normal priors suggested by Turner et al. [51] were used for the between-study variances τ²; Table S1 in the Supplementary Material shows the specific prior for each dataset. Also, direct and indirect evidence was assumed to be consistent. These assumptions greatly reduced model complexity and have been frequently adopted in similar studies [52]. We applied the NMA model for each dataset and obtained the 95% CrI of the odds ratio of each treatment comparison. All odds ratios were used on a logarithmic scale when calculating the BoS statistics.

When a treatment comparison was directly given by at least two studies, we applied a Bayesian pairwise meta-analysis model to calculate the 95% CrI based on the direct evidence of each comparison [53], instead of using the traditional frequentist inverse-of-variance or DerSimonian–Laird method [54]. This Bayesian pairwise meta-analysis can be viewed as a special case of the Bayesian NMA model when a network contains only two treatments. Also, it used the same informative log-normal prior for the between-study variance as in the corresponding NMA. By conducting the analyses under the same Bayesian framework, we can fairly compare the results produced by the pairwise meta-analysis and the NMA.

The BoS statistic was computed for each treatment comparison and classified into three mutually exclusive scenarios (Table 1). In the first scenario (no direct evidence exists), the NMA estimate was entirely derived from indirect evidence. The CrI of the direct estimate can be considered as (−∞, +∞) leading to efficiency E = 0 and thus BoS statistic = 100%. In the latter two scenarios, the BoS statistics were strictly less than 100% because direct evidence must have a portion of contributions, no matter how small, to overall evidence. Of note, in these scenarios, the BoS statistics may be negative because the random-effects NMA incorporated the between-study variance, which was assumed common across the network, in the effect estimate; thus the total variation of a specific effect estimate in the NMA was not necessarily smaller than the variation of the direct estimate (from a single study or pairwise meta-analysis) [35]. Negative BoS statistics indicated reduced precision in NMAs compared to using only direct evidence, and suggested iatrogenic rather than beneficial effects of NMAs.

Table 1.

Interpretation of the borrowing of strength (BoS) statistic.

Case	Interpretation
General case	The percentage reduction in the uncertainty (imprecision or variance) of the effect estimate of a treatment comparison that benefits from indirect evidence in an NMA; i.e., it can be conceptualized as (indirect evidence) / (direct evidence + indirect evidence) × 100%.
For a treatment comparison not directly given by any studies	The effect estimate is entirely informed by indirect evidence, so the BoS statistic is conceptually 100%.
For a treatment comparison directly given by only one study	Only a single study contributes direct evidence, so the BoS statistic reflects the comparison between the NMA and the single study.
For a treatment comparison directly given by at least two studies	A pairwise meta-analysis of multiple studies contributes to direct evidence, so the BoS statistic reflects and comparison between the NMA and the pairwise meta-analysis.

Moreover, we explored the relationship between the networks’ geometry and their BoS statistics. We roughly classified the 40 networks into well-connected ones and sparsely-connected ones. A network was considered sparsely-connected if at least 1/3 of its treatments were not contained in any evidence loop; otherwise, it was considered well-connected. We compared the BoS statistics in the two groups of networks using Wilcoxon rank sum test (assuming the independence of the BoS statistics), instead of the t-test, because some treatment comparisons had outlying BoS statistics. In addition, we investigated how the results from NMAs and those based on only direct evidence led to different go/no-go decisions regarding treatment comparisons. A treatment comparison was considered significantly different if the CrI of its odds ratio did not contain 1.0.

The Bayesian analyses were implemented using the Markov chain Monte Carlo (MCMC) algorithm via the R package “rjags” [55]. The results were based on three Markov chains, each having 200,000 iterations after a 50,000-run burn-in period with thinning rate 2 for reducing sample autocorrelations. The convergence of all Markov chains was checked according to their trace plots.

3. RESULTS

3.1. Distribution of BoS statistic

In the 40 datasets, there were 915 possible treatment comparisons; 484 comparisons had no direct evidence, so their BoS statistics were 100%. Among the remaining 431 comparisons with direct evidence, 181 were directly given by only one study, and 250 were directly given by at least two studies.

Figure 1 presents the histogram of the BoS statistics of all treatment comparisons. Among the 250 comparisons directly given by at least two studies, the BoS statistics of 9 comparisons (3.6%) were larger than 90%, those of 25 comparisons (10.0%) fell within the range of 80%–90%, 30 (12.0%) within 70%–80%, 29 (11.6%) within 60%–70%, 24 (9.6%) within 50%–60%, 21 (8.4%) within 40%–50%, and 28 (11.2%) within 30%–40%. In other words, the uncertainty of effect estimates was reduced by at least 30% when using NMAs for the majority of these comparisons (66.4%). Also, the BoS statistics of 48 (19.2%) treatment comparisons were between 0 and 30%, and those of 36 (14.4%) comparisons were below zero.

Figure 1.

Histogram of borrowing of strength statistics in the 40 datasets

However, among the 181 treatment comparisons directly given by only one study, the BoS statistics of 104 comparisons (57.5%) were below zero, indicating that NMAs provided less precise effect estimates than their corresponding single studies. Also, 23 comparisons (12.7%) had the BoS statistics between 0 and 30%. In other words, precision was not appreciably improved by using NMAs for the majority of comparisons (70.2%) with only one study contributing to direct evidence. Also, because the BoS statistics of many comparisons (especially those directly given by only one study) were below zero and even more comparisons without any direct evidence massed at BoS statistics = 100%, the histogram in Figure 1 shows a U-shaped distribution.

3.2. Network connectivity and BoS statistic

Figure 2 presents the BoS statistic of each treatment comparison in each dataset. The unfilled points represent the comparisons directly given by only one study, and the filled points represent those directly given by at least two studies. The plot shows only the BoS statistics between 0 and 100%; the number of comparisons whose BoS statistics < 0 in each dataset is specified in Figure 2.

Figure 2.

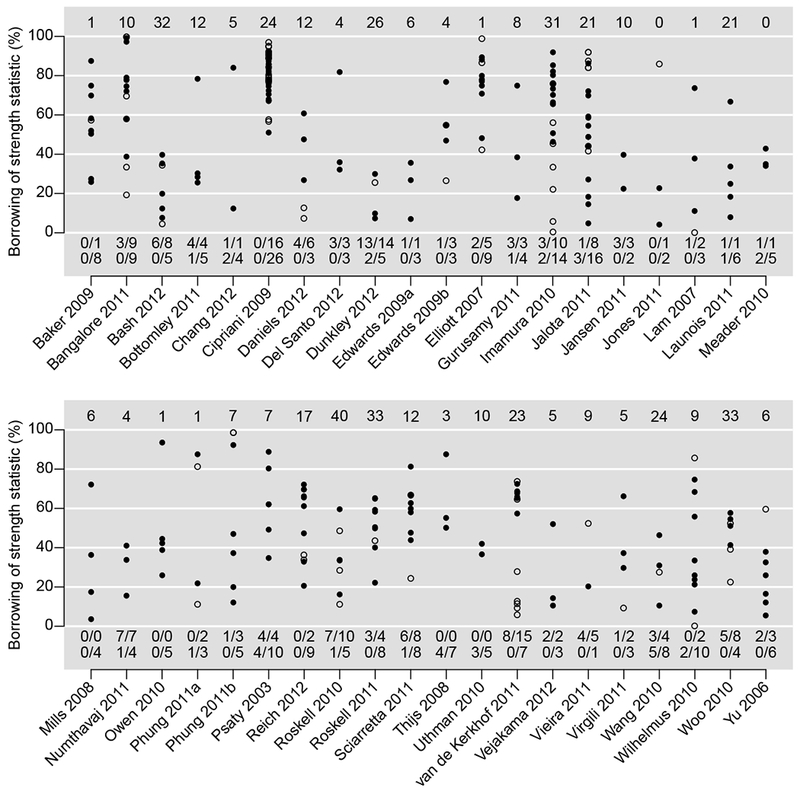
Borrowing of strength (BoS) statistics in percentage in each dataset. The number at the top is the number of comparisons without any direct evidence (BoS statistics = 100%) in each dataset. The unfilled/filled points represent comparisons directly given by only one study/at least two studies. The numbers of such comparisons having BoS statistics < 0 are shown in the first/second line at the bottom in each dataset.

Referring to the treatment networks in Figure S1 in the Supplementary Material, the BoS statistics in Figure 2 were closely related to the networks’ geometry. For example, in the network of Cipriani 2009 [14], a total of 12 treatments were compared, and 42 treatment comparisons had direct evidence, among which 26 were directly given by at least two studies and 16 were directly given by a single study. As the treatments were connected very well in the network, they formed many evidence loops and thus the NMA improved effect estimates dramatically. The BoS statistic of each comparison in this network was larger than 50%.

On the other hand, if some treatments were connected sparsely in a network, then the NMA might not be very beneficial for the effect estimates. For example, in the network of Roskell 2010 [56], the number of treatments was 11, which was similar to that in the network of Cipriani 2009 [14]. However, only 15 treatment comparisons had direct evidence, and the evidence loops were much fewer than those in Cipriani 2009. Only five comparisons (2 vs. 1, 3 vs. 2, 7 vs. 2, 8 vs. 2, and 11 vs. 2) were directly given by at least two studies, and the remaining ten comparisons were directly given by only one study. The sparsely-connected network led to negative BoS statistics for eight comparisons. Similarly, in the network of Vieira 2011 [57], although six treatments were compared, there was only one evidence loop formed by treatments 3, 5, and 6. The five treatment comparisons 6 vs. 1, 5 vs. 3, 6 vs. 3, 6 vs. 4, and 6 vs. 5 were directly given by only one study; four of them had negative BoS statistics.

Among all 40 NMAs, 24 were considered well-connected, while the remaining 16 were considered sparsely-connected; see Table S1 in the Supplementary Material. Figure 3(a) presents the boxplots of the BoS statistics of comparisons directly given by only one study among the sparsely- and well-connected NMAs, and Figure 3(b) presents those given by at least two studies. Both plots indicate that the BoS statistics in the well-connected NMAs were noticeably higher than those in the sparsely-connected NMAs. Their differences were statistically significant; P-values were < 0.001 in both Figures 3(a) and 3(b).

Figure 3.

Boxplots of borrowing of strength (BoS) statistics of comparisons directly given by only one study (left panel) and at least two studies (right panel) among sparsely- and well-connected network meta-analyses. The left panel shows only comparisons with BoS > −600%, and the right panel shows only those with BoS > −100%. In the sparsely- and well-connected network meta-analyses, 5 and 6 comparisons directly given by only one study had BoS < −600%, respectively, and 8 and 4 comparisons directly given by at least two studies had BoS < −100%, respectively.

3.3. Decisions made by direct evidence and NMAs

Table 2 presents the number of significant and non-significant treatment comparisons based on direct evidence and NMAs. For comparisons with no direct evidence, their significance could be informed only by NMAs; 158 of them were significant, while the remaining 326 comparisons were non-significant. For comparisons with only one study contributing direct evidence, NMAs changed the decisions of non-significant difference to significant difference in only 16 comparisons, while they implied non-significant differences in 25 comparisons that were significantly different based on the single study. For treatment comparisons with at least two studies contributing direct evidence, NMAs improved the non-significant comparisons based on pairwise meta-analyses to be significantly different in 34 comparisons. The differences of 11 comparisons were significant based on pairwise meta-analyses but were no longer significant when using NMAs.

Table 2.

Significant differences of treatments comparisons based on their 95% credible intervals.

Treatment comparisons with no direct evidence:
		Network meta-analysis
		Non-significant difference	Significant difference
Direct evidencea	Non-significant difference	326	158
	Significant difference	0	0
Treatment comparisons with only one study contributing direct evidence:
		Network meta-analysis
		Non-significant difference	Significant difference
Direct evidenceb	Non-significant difference	84	16
	Significant difference	25	56
Treatment comparisons with at least two studies contributing direct evidence:
		Network meta-analysis
		Non-significant difference	Significant difference
Direct evidencec	Non-significant difference	107	34
	Significant difference	11	98

^aFor treatment comparisons with no direct evidence, tde credible intervals provided by tde direct evidence are considered as (−∞,+∞), so all results are non-significant.

^bThe single study is tde only source of tde direct evidence.

^cThe pairwise meta-analysis provides tde direct evidence.

4. DISCUSSION

4.1. Main findings

Clinicians, policymakers, and funding agencies require effect estimates that warrant high certainty for go/no-go decisions regarding the adoption/funding of evidence-based treatments, particularly when there are competing interventions available. Imprecision is a key domain of certainty in evidence [58, 59], while NMAs may be touted to improve precision. Our findings provide an important caveat regarding the specific circumstances under which these touted benefits may occur. This empirical study has investigated the benefits of incorporating indirect evidence in NMAs through applying the recently proposed BoS statistics to 915 treatment comparisons. We have shown that NMAs improved the effect estimates for most treatment comparisons by dramatically improving their precision (i.e., producing narrower CrIs) compared with conventional pairwise meta-analyses, but only when the comparisons were sufficiently connected in networks and had at least two head-to-head studies. However, NMAs either reduced or failed to appreciably improve precision for most treatment comparisons with only one study contributing direct evidence. The performance of NMAs depended greatly on the networks’ geometry and having well connected loops.

4.2. Practical implications

We implemented the popular Bayesian random-effects model with a common between-study variance for all treatment comparisons [4, 5]. Although this model effectively accounted for heterogeneity between different studies, incorporating too many insufficiently-compared treatments in the network may not be beneficial for an NMA. Consider an NMA containing N studies on a total of K treatments. Under the assumption of evidence consistency, researchers are interested in estimating K − 1 “basic” treatment comparisons (e.g., 2 vs. 1, 3 vs. 1, …, and K vs. 1) and thus they can use them to impute all remaining comparisons (e.g., obtaining 3 vs. 2 from 2 vs. 1 and 3 vs. 1). The common between-study variance also needs to be estimated to assess heterogeneity. Consequently, the NMA model estimates K parameters using N studies, so each parameter has N/K studies on average. If K₁ new treatments are added to the network and each is investigated by only one study, then the total number of studies becomes N + K₁, while the number of parameters to be estimated in the NMA model becomes K + K₁. The average number of studies for each parameter becomes (N + K₁)/(K + K₁), which is always smaller than N/K given that N > K.

For example, to investigate the effect of bisphosphonates in the prevention of vertebral fractures, Jansen et al. [60] collected N = 5 studies that compared K = 3 treatments, i.e., placebo, alendronate, and risedronate. In the sub-network consisting of these three treatments, the NMA had 1.67 studies, which were already limited, to estimate one parameter on average. The whole network contained additional K₁ = 3 treatments (i.e., etidronate, ibandronate, and zoledronic acid); each was compared in only one study (see Figure S1). The average number of studies for each parameter in the NMA further reduced to only 1.33. Having too few studies per parameter may lead to very imprecise estimates with large variances. Therefore, the treatments that were investigated in few studies may not help an NMA produce more precise effect estimates, and they need to be carefully investigated in future NMAs.

4.3. Strengths and limitations

We used informative priors suggested by Turner et al. [51] for the between-study variances in both pairwise and network meta-analyses. These priors were derived based on many meta-analyses in the Cochrane Database of Systematic Reviews. They may help avoid unreasonably large estimates for the heterogeneity variances, especially when the number of studies is small. Currently, however, many published Bayesian pairwise and/or network meta-analyses used non-informative priors. Their results may have much wider CrIs than those produced by informative priors.

This study has some limitations. First, the BoS statistic was used to quantify the improvement in precision that benefitted from indirect evidence, while this statistic only assessed the effect estimates in terms of their precision (i.e., their CrI length); it did not reflect the change of bias in the effect estimates due to incorporating indirect evidence. On the one hand, under the assumption of evidence consistency, NMAs have been shown to reduce potential bias (e.g., caused by selective reporting) by borrowing information across treatments [61–63]. On the other hand, NMAs may yield biased effect estimates due to inclusion of studies not satisfying the consistency assumption. If only a few direct head-to-head studies are available, it is infeasible to validate the required NMA assumptions. Methods to assess the risk of bias in an NMA, especially that from indirect evidence, need to be developed as future work.

Second, the random-effects NMA model in this study assumed a common between-study variance for all treatment comparisons and assumed consistency between direct and indirect evidence. In some cases, the extent of heterogeneity for different comparisons may dramatically differ, so an unstructured variance-covariance matrix may be more proper to account for such differences [64]. However, this adds more parameters into the NMA model and increases model complexity, and it may lead to larger variances for the estimated parameters. Researchers may evaluate the tradeoff between model complexity and model fitting on a case by case basis via the deviance information criterion in the Bayesian framework [65]. In addition, this article assumed evidence consistency for all 40 NMAs. If the direct and indirect evidence for certain comparisons was significantly inconsistent, the different sources of evidence may need to be analyzed separately, possibly leading to larger variances and lower BoS statistics. For example, we applied an inconsistency model suggested by Dias et al. [66] to the dataset Del Santo 2012 [67]. This model is also called an “unrelated mean effects” model, which still assumes a common between-study variance across the network but treats all comparisons in the network as separate, unrelated, basic parameters; therefore, it does not require the assumption of evidence consistency. Table S2 in the Supplementary Material presents the BoS statistics based on both consistency and inconsistency NMA models. It shows that BoS statistics of all comparisons dramatically reduced without using evidence consistency.

Third, the MCMC chains did not converge well for a few treatment comparisons associated with antithrombin III in Gurusamy 2011 [68], non-dihydropyridine calcium-channel blocker in Vejakama 2012 [69], and placebo in Woo 2010 [70], possibly because all these treatment groups had zero or few events. Their Bayesian effect estimates may be improved by incorporating information from external sources such as cohort studies [71].

In summary, this study revealed that NMAs can increase the precision of most, but not all, treatment comparisons, provided that at least two head-to-head studies are available for a comparison. The increase in precision should not be taken for granted. NMAs may not provide better effect estimates for insufficiently-compared treatments, and may even reduce precision relative to single-study estimates. Researchers should routinely compare the results produced by NMAs and pairwise meta-analyses.

WHAT IS NEW?

Key finding

• More than half of the comparisons in the 40 network meta-analyses are not supported by direct evidence

• In comparisons with only one study contributing direct evidence, most of the time (57.5%) adding indirect evidence to the network does not increase precision; in comparisons with at least two studies contributing direct evidence, most of the time (66.4%) adding indirect evidence to the network greatly improves precision (borrowing of strength statistic ≥ 30%).

• Network geometry that shows well-connected loops of treatments leads to more gain of precision when indirect evidence is added.

What this adds to what is known

• Network meta-analysis is supposed to increase precision; however, this is not always the case.

What are the implications? What should change now?

• Researchers should routinely report and compare the results of both network and pairwise meta-analyses and be aware of the potential impact of including insufficiently-compared treatments in a network.