Estimation of brain functional connectivity from hypercapnia BOLD MRI data: validation in a lifespan cohort of 170 subjects

Abstract

Functional connectivity MRI, based on Blood-Oxygenation-Level-Dependent (BOLD) signals, is typically performed while the subject is at rest. On the other hand, BOLD is also widely used in physiological imaging such as cerebrovascular reactivity (CVR) mapping using hypercapnia (HC) as a modulator. We therefore hypothesize that hypercapnia BOLD data can be used to extract FC metrics after factoring out the effects of the physiological modulation, which will allow simultaneous assessment of neural and vascular function and may be particularly important in populations such as aging and cerebrovascular diseases. The present work aims to systematically examine the feasibility of hypercapnia BOLD-based FC mapping using three commonly applied analysis methods, specifically dual-regression Independent Component Analysis (ICA), region-based FC matrix analysis, and graph-theory based network analysis, in a large cohort of 170 healthy subjects ranging from 20–88 years old. To validate the hypercapnia BOLD results, we also compared these FC metrics with those obtained from conventional resting-state data. ICA analysis of the hypercapnia BOLD data revealed FC maps that strongly resembled those reported in the literature. FC matrix using region-based analysis showed a correlation of 0.97 on the group-level and 0.54±0.10 on the individual-level, when comparing between hypercapnia and resting-state results. Although the correspondence on the individual-level was moderate, this was primarily attributed to variations intrinsic to FC mapping, because a corresponding resting-vs-resting comparison in a sub-cohort (N=39) revealed a similar correlation of 0.57±0.09. Graph-theory computations were also feasible in hypercapnia BOLD data and indices of global efficiency, clustering coefficient, modularity, and segregation were successfully derived. hypercapnia FC results revealed age-dependent differences in which within-network connections generally exhibited an age-dependent decrease while between-network connections showed an age-dependent increase.

1. Introduction

Functional connectivity (FC) mapping is widely used to estimate spontaneous neural activity in the human brain (Biswal et al., 1995; Fox et al., 2005; Smith et al., 2009) and has made a major impact in cognitive and clinical neuroscience (Cole et al., 2010; Greicius et al., 2003; Lerman et al., 2014; Matthews et al., 2006). The FC signal is based on the principle of neurovascular coupling in that spontaneous fluctuations in neural activity are thought to cause a corresponding change in hemodynamic parameters such as cerebral blood flow and oxygenation, which can be measured by Blood-Oxygenation-Level-Dependent (BOLD) MRI signals. FC mapping is typically estimated from BOLD MRI data when the participant is at rest and not performing any explicit task.

FC mapping has also been conducted using data during tasks, for example task-evoked fMRI data (Cole et al., 2014; Fair et al., 2007). It is therefore plausible that FC mapping can also use BOLD data acquired during physiological tasks (King et al., 2018; Liu et al., 2017; Xu et al., 2011). In particular, the assessment of vascular and functional parameters in the same spatial framework is important for conditions in which both neural and vascular function may be compromised, such as aging and cerebrovascular diseases. One of the most important vascular measures relevant to fMRI signal is the vessel’s dilatory capacity, cerebrovascular reactivity (CVR), which can be measured by collecting MRI images during interleaved hypercapnia and normocapnia periods (Liu et al., 2018). Importantly, since both CVR and FC are based on the analysis of BOLD EPI images, it may be feasible to estimate both parameters from the same data set.

We have recently demonstrated the proof-of-principle that FC can be obtained from BOLD data collected under gas-inhalation challenge, by regressing out the gas effects from BOLD signal and subjecting the residual BOLD time-course data to FC analyses (Liu et al., 2017). Using a group independent component analysis (ICA) method, several FC networks were delineated from the gas-inhalation MRI data. However, there has not been a comprehensive comparison to quantify the group-level and individual-level consistency of FC results obtained from hypercapnia BOLD MRI data relative to those obtained from conventional resting-state BOLD data.

In this study, we aim to provide a systematic comparison between hypercapnia FC and resting-state FC in a lifespan cohort of 170 healthy subjects ranging from 20–88 years old. Each subject received both a hypercapnia and a resting BOLD scan. We first examined two commonly used FC indices, specifically data-driven, ICA based analysis (Beckmann et al., 2005; Nickerson et al., 2017) and model-based correlation matrices (Hagmann et al., 2008). For the computation of correlation matrices, we used automatic, atlas-based regions-of-interest (ROIs) instead of hand-drawn ROIs in order to minimize rater dependence. Furthermore, topological organizations of brain networks, e.g. graph theoretical metrics (Achard et al., 2006; Sporns et al., 2004; Wig et al., 2011), were investigated using the hypercapnia BOLD data. Consistency between hypercapnia and resting-state FC results were studied on both group and individual levels. In addition, age effects on FC were studied in this lifespan cohort and the results were compared between hypercapnia and resting-state data.

2. Materials and methods

2.1. Participants

A total of 170 healthy adult subjects (51.0±20.0 years old, 65 males and 105 females) were recruited from the Dallas Lifespan Brain Study, which is a longitudinal study of cognitive aging using multimodal imaging tools and cognitive assessment (Park et al., 2012). All study procedures were reviewed and approved by the Institutional Review Boards at The University of Texas at Dallas and The University of Texas Southwestern Medical Center. Each participant provided written consent before participating in the study.

The participants did not report any pulmonary, respiratory, neurologic, or psychiatric disorders according to self-completed questionnaires. None of the participants had asthma. All participants were considered free of mild cognitive impairment or dementia. The lowest mini-mental state exam (MMSE) score of the participants was 26.

2.2. MRI experiment

All MR imaging was performed on a 3T Philips Achieva scanner with an 8-channel head coil. Each participant received a resting-state FC scan, which was followed by a hypercapnia CVR scan after repositioning to attach the CO₂ delivery apparatus. The hypercapnia CVR scan consisted of interleaved breathing of room-air and CO₂-enriched air (5% CO₂ ,21% O₂, and 74% N₂) in 1-minute blocks, while BOLD images (TR=2000 ms, TE=25 ms, flip angle=80°, FOV=220×150 mm, 43 interleaved axial slices per vol ume, 3.5/0 mm (slice-thickness/gap), in-plane resolution=3.4×3.4 mm) were continuously acqu ired. End-tidal CO₂ (EtCO₂), CO₂ concentration in the lung and thus approximating arterial CO₂ levels, was recorded throughout the CVR scan using a capnograph device (Capnogard, Model 1265, Novametrix Medical Systems, CT). Heart rate was recorded using a physiological monitor (MEDRAD, Pittsburgh, PA). Other details of the CVR procedure is described previously (Lu et al., 2014; Lu et al., 2011). The total number of image volumes in the CVR data used was 154 and corresponds to 5.2 minutes of scan time. The resting-state FC scan was performed using identical BOLD imaging parameters and the scan duration of 5.2 minutes, matching that of the CVR data. In addition to these BOLD scans, a T1-weighted magnetization-prepared rapid gradient-echo sequence (MPRAGE) was performed for anatomic reference and image registration (TR=8.1 ms, TE=3.7 ms, shot interval 2100 ms, flip angle=12°, FOV=204× 256 mm, 160 slices with 1×1×1 mm³ voxels).

2.3. Image processing

The BOLD data first underwent standard pre-processing steps including slice timing correction, realignment, normalization to Montreal Neurologic Institute (MNI) standard brain space via MPRAGE image, and spatial smoothing using a Gaussian filter with a full-width half-maximum of 4mm.

The post-processing of hypercapnia CVR data followed the steps outlined in Fig. 1. The EtCO₂ time course was synchronized with BOLD time series to account for the time it took for CO₂ to travel from the lung to the brain. The synchronization was conducted by shifting the EtCO₂ time course one TR at a time and calculating the cross-correlation coefficient between EtCO₂ and whole-brain averaged BOLD time course. The shift that corresponds to the maximum correlation coefficient was considered the optimal shift. General linear regression between the BOLD time course and the shifted EtCO₂ time course was used to compute CVR map, as reported previously (Liu et al., 2018). Next, we factored out the hypercapnia effect on BOLD signals on a voxel-by-voxel basis by regressing BOLD time series against the shifted EtCO₂ time course, yielding the residual image series. The residual image series were detrended and bandpass-filtered to 0.01 – 0.1 Hz to retain the low-frequency fluctuation components, which then underwent the FC analyses described below.

Fig. 1:

Flowchart of data processing steps to estimate functional connectivity metrics from hypercapnia BOLD MRI data.

As an additional procedure to reduce motion effects, the image series also underwent the scrubbing process in which image volume manifesting a displacement of 0.4 mm or above relative the prior frame was discarded (Cocchi et al., 2016). In addition, the frames acquired immediately prior and immediately after each of these frames were also discarded to account for temporal spread of artifactual signal resulting from the temporal filtering in the low-frequency functional signal (Chan et al., 2014). Following motion scrubbing discussed above, any participant with less than 75 frames of remaining data was removed from subsequent analysis. Out of the 170 participants enrolled, 150 participants had hypercapnia and resting-state BOLD images that met the criteria and these data sets were used in the final analysis.

2.4. Computation of FC indices

2.4.1. ICA FC indices

A dual-regression ICA was performed using the MELODIC toolbox (FMRIB Analysis Group, Oxford University) (Filippini et al., 2009) and in-house script. As the first step of the ICA analysis, group ICA was performed on the datasets of all participants to obtain the group-level components. Age was not included in this analysis. The number of independent components (ICs) was set as 30 based on previous literature (Iraji et al., 2016). Next, using the group-level components as the spatial predictors, we estimated BOLD time courses of each network (i.e. component) on an individual level. Finally, the BOLD time courses were used as regressors to extract individual-level FC networks, while using whole brain signal, white matter signal, CSF signal, and six rigid-body head motion corrections as nuisance covariates. The Z-score map of each FC network was obtained.

To examine the spatial consistency between FC networks obtained from hypercapnia BOLD and those from resting-state BOLD, we calculated spatial Pearson cross-correlation for each network on a subject-by-subject basis. Although we have a total of 30 networks in our data, our report will primarily focus on 10 FCs that have the most well-defined functional relevance according to previous literatures (Cole et al., 2010; Sala-Llonch et al., 2015; Smith et al., 2009), with the other FCs showing in supplemental materials.

To better interpret the differences between hypercapnia and resting-state data, we sought to also determine the variations of our resting-state data itself. The resting-state scan was only performed once in the main study, thus it was not possible to evaluate the reproducibility of the resting data. However, 39 of these participants (age 53.7±18.4 years old) were recruited back for another MRI session, in which two resting-state scans using identical imaging parameters were performed in this new session, with a break and repositioning in-between. We then computed spatial correlation between these repeated resting-state scans that were acquired in the same session.

2.4.2. Functional connectivity matrix

Once each data set was normalized into the MNI space, they were parcellated into 114 regions ROIs based on the work of (Yeo et al., 2011). These ROIs were grouped into 17 FC networks (Fig. 5a). Cross-correlation coefficient was calculated between each pair of ROIs, after factoring out the nuisance parameters and motion parameters. The correlation coefficient values were converted to z-scores using a Fisher-z transform. Z-scores of all ROI pairs then formed a symmetric 114 × 114 functional connectivity matrix.

Fig. 5:

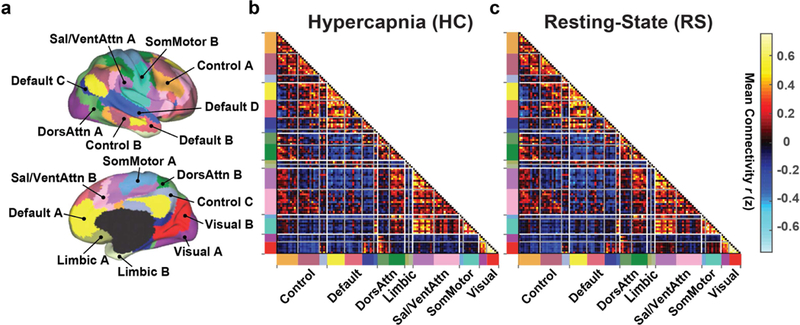
Group-averaged FC matrix organized by resting-state networks. (a) The brain was parcellated into 114 regions grouped into 17 networks (Yeo et al., 2011). (b) Averaged FC matrix derived from hypercapnia data. (c) Averaged FC matrix derived from resting-state data. Hot and cool colors in the matrix represent positive and negative correlations, respectively. The colors along the horizontal and vertical axes in (b) and (c) match those in (a) and indicate different networks.

2.4.3. Graph measures: global efficiency, clustering coefficient, modularity, segregation

Using graph theory implemented in Brain Connectivity Toolbox (Rubinov and Sporns, 2010) and in-house MATLAB scripts, we computed the following four measures for each subject. Global efficiency quantifies the overall (positive, i.e. a threshold of 0) connectivity across different regions in the brain. Clustering coefficient of a brain region indicates the extent to which the region is involved in triangular connections. The global clustering coefficient is simply the average of all 114 ROIs. Modularity quantifies the degree to which the brain ROIs are grouped into mutually separate networks with minimal or negative relationships between them. Both positive and negative connections were used in the computation of the modularity index (Rubinov and Sporns, 2011). The segregation index is computed as the difference between within-network correlations and between-network correlations (Wig, 2017).

2.5. Age effect

Given the age span of our cohort, we also examined FC differences across age and compared the results between hypercapnia and resting-state data.

To characterize age differences in FC matrix, we first reduced the FC matrix size from 114×114 to 17×17 by averaging entries belonging to the same network. Linear regression analysis was then performed in which the network-wise FC was used as the dependent variable and age was the independent variable. Due to the large number of comparisons, a false-positive-rate (FDR) adjusted p-value of 0.05 or less is considered significant. Similarity between hypercapnia and resting-state results was determined by Dice coefficient (Craddock et al., 2012). In addition, we also investigated the age dependence of the graph measures and compared between hypercapnia and resting-state results.

3. Results

3.1. Assessment of displacements in the images

The motion scrubbing process resulted in 19 hypercapnia and 3 resting-state data sets disqualified from further analysis, 2 of which were from the same participants. In the remaining 150 participants, the hypercapnia data had 135.6±20.2 frames (mean±SD) on average and the resting-state had 147.8±13.5 frames. For the frames survived, the frame-averaged displacement was 0.17±0.04 mm in the hypercapnia data, which was significantly greater (p<0.001) than that in the resting-state data (0.11±0.04 mm).

3.2. Physiological data

A typical EtCO₂ time course during the hypercapnia scan is illustrated in Fig. 2a, showing a modulation of EtCO₂ with hypercapnia blocks. The corresponding whole-brain BOLD time course is shown in Fig. 2b. Heart rate during room-air and CO₂ breathing periods were 65.5±10.1 and 66.7±9.7 beats-per-minute (bpm), respectively. There was a small, but significant (p<0.001) increase in heart rate. Breathing rate during room-air and CO₂ breathing periods were 11.8±3.1 and 12.1±3.0 breaths-per-minute (brpm), respectively, again with a significant (p<0.001) increase.

Fig. 2:

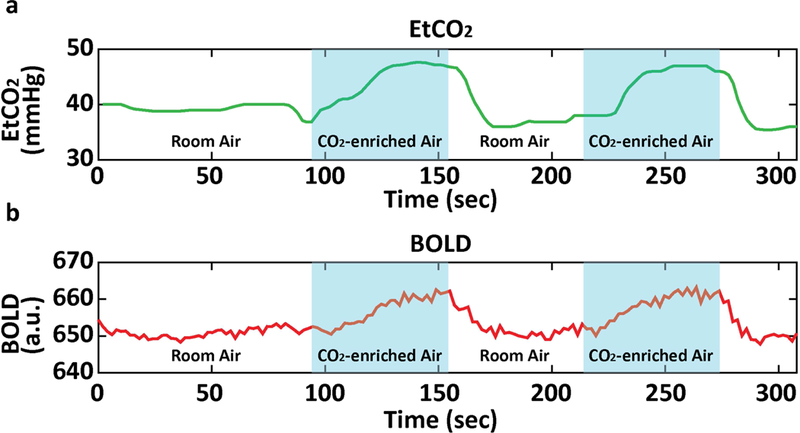
Representative data of (a) EtCO₂ and (b) whole-brain BOLD signal as a function of time.

3.2. ICA results

Fig. 3 depicts 10 group-level independent components identified from the hypercapnia and resting-state BOLD data. The putative functional assignments of these components are listed in Table 1, based on the criteria established in (De Luca et al., 2006; Lerman et al., 2014; Smith et al., 2009). Visual inspection suggested that the functional connectivity maps obtained from hypercapnia and resting-state BOLD data were highly consistent. Group-level ICA maps showed a spatial correlation of 0.85±0.11 between hypercapnia and resting-state results across the 10 components. Supplemental Fig. S1 shows the ICA maps of all 30 components. Their spatial correlations are plotted in Supplemental Fig. S2.

Fig. 3:

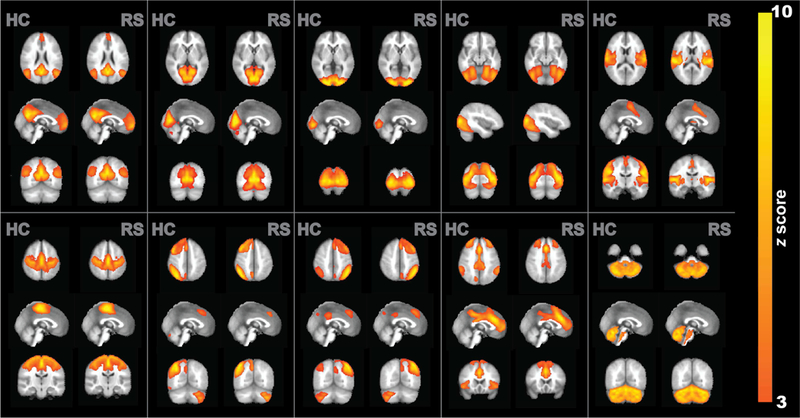
Group-level ICA results using hypercapnia and resting-state data. Ten representative component maps are shown. Each map is shown in three orthogonal orientations. The color map indicates z statistic after thresholding at Z=3.

Table 1.

Anatomical regions and functional network assignments of 10 group-level independent components identified from resting-state (RS) and hypercapnia (HC) BOLD images

	Anatomical Regions	RS	HC	Putative Network
IC 1	Posterior cingulate cortex Bilateral angular gyrus Ventromedial prefrontal cortex/Rostral ACC	○	○	Default Mode Network (DMN)
		○	○
		○	○
IC 2	Calcarine fissure	○	○	Primary Visual (V1)
IC 3	Prestriate cortex	○	○	Secondary Visual (V2)
IC 4	Associative visual cortex	○	○	High-order Visual (V3+V4+V5)
IC 5	Auditory cortex Supplementary motor area Sensorimotor cortex	○	○	Auditory +Sensory Association
		○	○
			○
IC 6	Sensorimotor cortex Secondary somatosensory area Supplementary motor area	○	○	Sensorimotor
		○	○
		○	○
IC 7	Right inferior frontal gyrus Right middle temporal gyrus Right Parietal cortices	○	○	Right Executive Control Network (RECN)
		○	○
		○	○
IC 8	Left inferior frontal gyrus Left middle temporal gyrus Left parietal cortices	○	○	Left Executive Control Network (LECN)
		○	○
		○	○
IC 9	Anterior cingulate/Paracingular Dorsolateral prefrontal cortex Precuneus Supramarginal gyrus	○	○	Salience
		○	○
		○	○
			○
IC 10	Cerebellum	○	○	Cerebellum

Fig. 4 shows individual-level spatial consistency between hypercapnia and resting-state ICA maps for the 10 components described above. It can be seen that there is a moderate level of consistency between the results. Among the components investigated, Default Mode Network (DMN) revealed the highest correlation (0.51±0.12), while cerebellum showed the lowest correlation (0.30±0.13). When averaged across all 10 networks, the correlations between hypercapnia and resting-state IC maps were 0.38±0.14.

Fig. 4:

Summary of individual-level spatial correlations between hypercapnia and resting-state ICA maps (green bars). Ten different components are shown. Also shown are correlations between two repetitions of resting-state ICA maps (red bars) in a sub-sample (N=39).

To interpret these spatial correlations between hypercapnia and resting-state results in the context of normal variations across resting-state data, we also examined such correlations between two repetitions of resting-state data (red bars, Fig. 4). It can be seen that the resting-vs-resting correlation is slightly higher than the resting-vs-hypercapnia correlation. In two of the networks, auditory and sensorimotor ICs, this difference was statistically significant (paired t-test, FDR-corrected p<0.05). When averaged across all networks, the correlations between two repeated resting-state results were 0.43±0.14, which is 13% greater (p=0.002) than the hypercapnia-vs-resting correlations.

We further compared ICA-derived Z-score maps between hypercapnia and resting-state networks using voxel-wise paired t tests. A very small fraction of voxels in the brain (1.4±1.6%) revealed a significant difference (FWE corrected p<0.05), in which approximately half (0.73%) showed resting-state maps having a higher sensitivity than hypercapnia and the other half (0.64%) showed hypercapnia maps having a higher sensitivity than resting-state. The voxel-wise difference maps (in terms of Z-scores) between hypercapnia and resting-state ICA networks are displayed in Supplemental Fig. S3).

3.3. FC matrix results

Fig. 5b shows averaged FC matrix obtained from the hypercapnia BOLD data, with the 114 brain regions grouped by networks (Fig. 5a). For comparison, resting-state FC matrix is also shown (Fig. 5c). Consistent with voxel-wise ICA results shown above, FC matrix exhibited a strong similarity between hypercapnia and resting-state results (r=0.97). The FC matrix also revealed general features reported in previous literatures that regions within the same network manifested high correlations whereas regions of different network tended to show low or anti-correlations (Betzel et al., 2014; Yeo et al., 2015). On an individual level, correlations between hypercapnia and resting-state FC matrices were r=0.54±0.10. We further investigated whether there is an association between the hypercapnia-vs-resting correlation coefficient and head motion, and found that individuals with a larger mean image displacement revealed a lower correlation (p<0.001) (Supplementary Fig. S4). The resting-vs-resting correlations were 0.57±0.09.

Aside from examining the spatial consistency between hypercapnia and resting FC matrices, we also investigated their potential differences in absolute connectivity values. Each within-network and between-network FC was examined and significant (FDR-corrected p<0.05) differences were observed in several connections (Supplementary Fig. S5). 24 connections revealed a lower connectivity in hypercapnia relative to the resting state, while 17 connections showed a higher connectivity in hypercapnia data.

3.4. Graph-based indices

We next investigated the hypercapnia-vs-resting correlations of graph-based network metrics. Fig. 6a displays scatter plots of global efficiency, clustering coefficient, modularity, and segregation indices across individuals. As can be seen, there exists a significant correlation between hypercapnia and resting-state results in all indices examined. The r values for these associations were 0.51, 0.31, 0.72, and 0.70 for global efficiency, clustering coefficient, modularity and segregation, respectively (p<0.001 for all). Furthermore, the data points were distributed around the unity line with slopes of 1.00, 1.00, 0.90, and 0.95 for global efficiency, clustering coefficient, modularity, and segregation, respectively. Bland-Altman plots of these measures are displayed in Fig. 6b.

Fig. 6:

Consistency in graph-theory FC measures between hypercapnia and resting-state BOLD data. (a) Scatter plots for global efficiency, clustering coefficient, modularity, and segregation. (b) Bland-Altman plot for these measures. Each dot represents data from one subject.

For reference, the r values for resting-vs-resting scatter plots were 0.54, 0.43, 0.72, and 0.72 for global efficiency, clustering coefficient, modularity, and segregation, respectively.

3.5. Age effects on FC indices

Age-related differences were observed in the hypercapnia FC data (Fig. 7a). Out of the 17 diagonal entries in the FC matrix, i.e. within-network connections, 12 showed a significant (FDR-corrected p<0.05) age-decrease and none showed an age-increase. As a reference, in the resting-state data (Fig. 7b), 11 within-network connections were found to decrease with age and none showed an increase. The Dice coefficient between hypercapnia and resting-state age effects was 0.87. Similar to these FC matrix results, ICA results also showed an age-decrease in within-network connectivity.

Fig. 7:

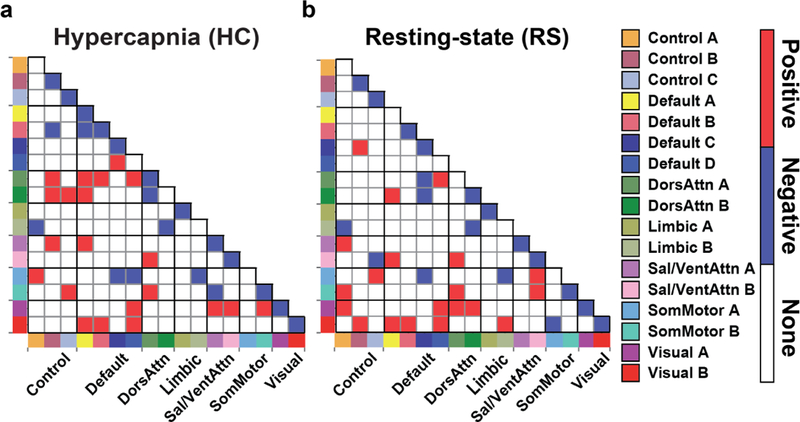
Age-related differences in FC. (a) hypercapnia derived age-change in FC and (b) resting-state derived age change in FC. Red color indicates age-increase (FDR corrected p<0.05); blue color indicates age-decrease. The colors along the horizontal and vertical axes indicate different networks, which are specified by the labels on the right-hand side.

For the off-diagonal entries, i.e. between-network connections, 21 connections exhibited age-increase while 9 revealed a decrease. For resting-state data, the entry number was 20 and 8, respectively. The Dice coefficients between hypercapnia and resting findings were 0.39 and 0.47 for age-increase and decrease effects, respectively.

For graph-based indices, modularity and segregation revealed an age-dependent decrease (FDR-corrected p<0.001 for all) (Fig. 8c and d). Surprisingly, the efficiency index showed an age-dependent increase (FDR-corrected p<0.001 for both) (Fig. 8a and b). These age effects were observed in both hypercapnia and resting-state data. Clustering coefficient did not reveal an age difference.

Fig. 8:

Graph-theory based FC measures as a function of age. (a) global efficiency. (b) clustering coefficient. (c) modularity. (d) segregation. Left panels: results from hypercapnia data. Right panels: results from resting-state data.

4. Discussion

Functional connectivity mapping and cerebrovascular reactivity imaging are traditionally considered two different sub-modalities of MR imaging, and generally require separate scans (Golestani et al., 2016b). In view of substantial overlaps between the acquisitions of these two techniques, e.g. both using BOLD sequence, it is desirable to derive both maps from the same data set thereby saving previous scan time. Furthermore, simultaneous and registration-free measurements of voxel-by-voxel FC and CVR images allow interpretation of brain functional signal in the context of localized cerebral vascular properties, especially because functional MRI signal is based on vascular responses. The present study showed that CVR MRI data can be used to compute ICA-based FC maps, region-based connectivity matrices, and graph-theory based network properties, and validated the results in a large cohort of 170 participants.

BOLD MRI signal can be modulated by multiple neural and physiological factors. Because the amplitude of each factor is generally small, e.g. <3%, it is generally accepted that the effects of these factors can be considered additive. For example, some literature in the functional MRI field has suggested that the effects of neural activity and cardiac and respiratory modulation are additive and that they can be separated by linear regression (Birn et al., 2006; Chang et al., 2009; Chang and Glover, 2009). Others have suggested that regressing out task-evoked fMRI signal can allow the use of the residual signal for functional connectivity analysis (Fair et al., 2007; Ganger et al., 2015). Similarly, a recent study has demonstrated that the influence of CO₂, O₂, and spontaneous neural activity on the BOLD signal is approximately additive and that three separate parametric maps can be derived from the same BOLD dataset (Liu et al., 2017). The present study extended these earlier findings and conducted a comprehensive investigation of the feasibility and validity of extracting FC from CO₂-inhalation MRI data.

The present study observed that the spatial correlation of FC matrix between hypercapnia and resting-state data was 0.54 for individual-level data of 5.2 minutes. This is considered moderate. To further evaluate the source of the variation, we calculated spatial correlation between two repeated resting-state fMRI using identical imaging parameters and scan duration as the hypercapnia MRI, which revealed a value of 0.57. Therefore, it appears that much of the variation we observed between hypercapnia and resting-state data was due to measurement noise, rather than systematic differences between the two data sets. Indeed, upon reducing the noise by averaging the FC matrix over 150 participants, the spatial correlation between hypercapnia and resting-state results improved to 0.97. The slightly low consistency in hypercapnia-vs-resting comparison (correlation coefficient=0.54) relative to the resting-vs-resting comparison (correlation coefficient=0.57) may be attributed to the fact that there tends to be a greater amount of motion in the hypercapnia data, presumably due to the breathing task. This notion is supported by the inverse correlation between FC spatial consistency and image displacement (Supplementary Fig. S4). We further point out that some of the variations in the test-retest data may be attributed to physiological fluctuations in brain states including circadian rhythm, and advanced analysis approaches such as connectivity domain analysis (Iraji et al., 2016) could be used to mitigate these variation sources. In general, the test-retest reproducibility of FC results observed in the present study is within the typical range reported in the literature (Noble et al., 2017; Zuo et al., 2010).

It is important to point out that CO₂ may have an effect on neural activity thereby affecting functional connectivity. Indeed, several previous studies including some from our group have shown that continuous, long-duration (e.g. 5 minutes) inhalation of CO₂ can reduce brain activity (Golestani et al., 2016a; Marshall et al., 2015; Thesen et al., 2012; Xu et al., 2011), which is thought to be associated with metabolic acidosis effects of CO₂. However, the present study uses intermittent CO₂ inhalation (as opposed to continuous CO₂) and a substantially shorter CO₂-breathing duration (1-minute blocks). Our results suggest that there are negligible differences between functional connectivity results using this type of breathing protocol and resting-state fMRI. Therefore, in patients with no respiratory, lung disease, or acidosis conditions, the hypercapnia BOLD is expected to provide comparable FC results to resting-state BOLD.

To further demonstrate that FC indices obtained from hypercapnia BOLD data can reveal important information about brain function, we examined the age dependence of these indices. We found that within-network FCs tend to decrease while between-network FCs increase with age (Betzel et al., 2014; Chan et al., 2014). This is consistent with the notion that functional divisions of the brain networks become less distinct as we age (Park et al., 2004; Park et al., 2012; Song et al., 2014). It was also noted that the age effects detected by hypercapnia and resting-state data were not completely consistent (Fig. 7), in that some connectivities only showed an age dependence in one but not the other dataset. Upon further investigation, we found that the connectivities that revealed age dependence in only one of the datasets generally had a lower statistical index (i.e. F value=10.9±3.7) compared to those that revealed age dependence in both datasets (13.2±3.9). Thus, the discrepancy between hypercapnia and resting-state age effects is likely because the age effects in those connectivities are not strong. Our graph-based measures revealed that the brain’s modularity and segregation decreased significantly with age (Brier et al., 2014; Cao et al., 2014; Chan et al., 2014). An intriguing observation is that the efficiency index was found to increase with age. A possible explanation is that the efficiency index reflects the interconnections of all brain regions in the brain, thus the increased between-network connections may have contributed to this overall increase especially given that there are many more between-network connections than within-network ones. These age effects were also observed when using the resting-state data, as shown in a previous report (Chan et al., 2014).

The present work also has several limitations. First, our study only considered static functional connectivity patterns. We did not investigate how the dynamic features of hypercapnia FC results could be different from that of resting-state FC (Bassett et al., 2011). This is relevant because our hypercapnia data were acquired with a breathing paradigm of one-minute CO₂ inhalation interleaved with one-minute blocks of room air breathing. It is possible that FC could vary within the scan duration in accordance with the inhaled gas type. A second limitation is that the study is based on the assumption that the effects of CO₂ and brain spontaneous neural activity on the BOLD signal are linear and additive. Previous investigations in the context of physiological corrections of fMRI signal, influence of task in FC results, and the effects of CO₂ and O₂ on BOLD signal have suggested that this is generally valid (Chang and Glover, 2009; Liu et al., 2017). However, it is expected that some non-linearity between different BOLD modulating factors will still be present. Finally, in our FC analyses, we used a low-pass filter of 0.01–0.1Hz in accordance with the majority of previous literature (Fox and Raichle, 2007; Liang et al., 2012). However, some recent reports have suggested the use of 0.01–0.25Hz (Vij et al., 2018). We have tested the use of 0.01–0.25Hz in our analyses and the results were generally consistent with those using 0.01–0.1Hz filter. These topics merit further investigation.

5. Conclusions

Hypercapnia CVR MRI data contains signal modulations from both CO₂ inhalation and spontaneous neural activity. By factoring out the CO₂ effects, the residual signals can be used to compute ICA-based functional connectivity maps, region-based functional connectivity matrix, and graph-based network properties. The hypercapnia FC results exhibited excellent agreement with resting-state FC results. Both also revealed highly consistent patterns of age-related differences. Hypercapnia BOLD MRI has the potential to provide concomitant assessment of functional and vascular parameters in a single scan.

Abbreviation:

BOLD

Blood-Oxygenation-Level-Dependent

CVR

Cerebrovascular reactivity

FC

Functional connectivity

ICA

Independent component analysis

ROIs

Regions-of-interest

EtCO₂

End-tidal CO₂

MPRAGE

Magnetization-prepared rapid gradient-echo sequence

MNI

Montreal Neurologic Institute

ICs

Independent components

FDR

False-positive-rate