Global-scale dispersal and connectivity in mangroves

Significance

Mangroves are of considerable ecological and socioeconomical importance; however, substantial areal losses have been recorded in many regions, driven primarily by anthropogenic disturbances and sea level rise. Oceanic dispersal of mangrove propagules provides a key mechanism for shifting distributions in response to environmental change. Here we provide a model framework for describing global dispersal and connectivity in mangroves. We identify important dispersal routes, barriers, and stepping-stones and quantify the influence of minimum and maximum floating periods on simulated connectivity patterns. Our study provides a baseline to improve our understanding of observed mangrove species distributions and, in combination with climate data, the expected range shifts under climate change.

Abstract

Dispersal provides a key mechanism for geographical range shifts in response to changing environmental conditions. For mangroves, which are highly susceptible to climate change, the spatial scale of dispersal remains largely unknown. Here we use a high-resolution, eddy- and tide-resolving numerical ocean model to simulate mangrove propagule dispersal across the global ocean and generate connectivity matrices between mangrove habitats using a range of floating periods. We find high rates of along-coast transport and transoceanic dispersal across the Atlantic, Pacific, and Indian Oceans. No connectivity is observed between populations on either side of the American and African continents. Archipelagos, such as the Galapagos and those found in Polynesia, Micronesia, and Melanesia, act as critical stepping-stones for dispersal across the Pacific Ocean. Direct and reciprocal dispersal routes across the Indian Ocean via the South Equatorial Current and seasonally reversing monsoon currents, respectively, allow connectivity between western Indian Ocean and Indo-West Pacific sites. We demonstrate the isolation of the Hawaii Islands and help explain the presence of mangroves on the latitudinal outlier Bermuda. Finally, we find that dispersal distance and connectivity are highly sensitive to the minimum and maximum floating periods. We anticipate that our findings will guide future research agendas to quantify biophysical factors that determine mangrove dispersal and connectivity, including the influence of ocean surface water properties on metabolic processes and buoyancy behavior, which may determine the potential of viably reaching a suitable habitat. Ultimately, this will lead to a better understanding of global mangrove species distributions and their response to changing climate conditions.

In recent decades, climate change has affected the distribution of species in both the terrestrial (1) and marine (2) environment. Although the majority of studies on species’ distributional changes have focused on climatic drivers, there is an increased recognition of the importance of dispersal (i.e., the movement or transport of organisms or their offspring away from their source to a settlement site) (3, 4). Limited dispersal efficiency and the presence of physical barriers may prevent species from tracking shifts in suitable habitat as climate changes, increasing the risk of extinction (5). In contrast, long-distance dispersal (LDD) events allow for the large-scale exchange of individuals between populations and the colonization of unoccupied habitats (6). However, while knowledge of local dispersal can be obtained with various methods such as release–recapture techniques, quantifying LDD remains challenging due to the difficulty of making observations over vast spatial scales (7). This is particularly the case in coastal and marine habitats, such as coral reefs, seagrass, and mangroves, where dispersal and connectivity [i.e., dispersal followed by successful establishment (4, 8)] are modulated by ocean currents that promote LDD (9–12) and allow for global-scale connectivity over decadal timescales (13). Connectivity in these systems is commonly examined based on genetic differentiation or the sharing of alleles or haplotypes, along with the use of numerical ocean models (14–16). In contrast to genetic studies, which help identify the spatial scale of dispersal and reveal patterns of connectivity, numerical models provide insight into physical dispersal processes and can help with identifying biophysical factors that control distributional shifts. Such insight is also important for aligning conservation strategies and prioritization with anticipated ecological consequences (17). However, while biophysical models (i.e., models incorporating both physical and biological factors) with various degrees of sophistication were previously used to quantify connectivity and examine biogeographic patterns in coral reefs (18–21) and seagrass species (9, 22), the application of state-of-the-art numerical ocean models and Lagrangian methods (23), which can simulate individual particle trajectories, remains largely unexplored for mangrove ecosystems (24).

Mangroves are halophytic woody plants, found in the intertidal zones of tropical and subtropical shorelines (25). They have received much attention due to their exceptional ecological and societal value (26, 27) and their high susceptibility to climate change (28). For example, mangroves support a wide range of ecosystem services such as providing breeding ground and nursery habitat in support of coastal and marine fisheries, shoreline protection, and carbon sequestration (29, 30), with an estimated value of $194,000 ha⁻¹ y⁻¹ (31). Nevertheless, mangroves have been heavily impacted by land use conversion (32) and are facing several climate change-related threats, including sea level rise (33); mangrove range shifts following climate perturbations have already been observed on several continents (34–36), stressing the need to quantify potential LDD in these systems.

Mangroves produce buoyant seeds and fruits (hereafter referred to as “propagules”) (25) that allow for dispersal via ocean currents within and between populations and for biological connectivity when establishment is successful. These propagules exhibit distinct floating periods (FPs) ranging from days to several months (37–39), and often float for 1 to 5 wk before developing roots for anchoring (37). This so-called obligate dispersal period (ODP) can increase the potential dispersal of propagules by postponing establishment (25). Altogether, these properties determine the timescales over which viable propagules can be transported into a suitable settlement habitat. Therefore, in combination with prevailing ocean currents, propagule FPs determine the spatial scale of dispersal (6) and modulate the genetic structure and global biogeography of mangrove species (40–42).

Global mangrove biogeography is characterized by two primary hot spots of species diversity [i.e., the Indo-West Pacific (54 mangrove species) and the Atlantic–East Pacific (17 mangrove species)], with few shared species (25). Using allelic frequency data obtained with genetic markers, the African and American continents and large distances spanning the Atlantic, Indian, and Pacific Oceans have been recognized as important land and ocean dispersal barriers, respectively (40, 41, 43). However, conflicting viewpoints exist regarding the effectiveness of these barriers in hindering dispersal (42). For example, other genetic studies have found evidence for transoceanic mangrove propagule dispersal across the Atlantic (40, 43, 44), Indian (45), and Pacific Oceans (45, 46). Despite the potential for numerical ocean models to simulate propagule transport at these spatial scales and complement observational records derived from genetic studies, no previous attempts have been made to estimate connectivity patterns for mangroves globally.

Here we use a high-resolution (∼4-km horizontal grid spacing), eddy- and tide-resolving numerical ocean model to simulate mangrove propagule trajectories for up to a period of 1 y, with hourly releases over the entire biogeographical range of mangroves. We identify the dominant oceanic routes and spatial scales of simulated propagule transport and test whether dispersal across previously assumed dispersal barriers is likely, accounting for complexity and spatiotemporal variability in both coastal and large-scale ocean currents. Anticipating future biological data, an idealized approach was used instead of a species-specific parameterization, and the >36 million modeled trajectories were constrained with a maximum floating period (maxFP); we then tested a variety of maxFP values that lie within the range of values reported in the literature. To represent the magnitude and direction of potential connectivity between habitats, we generated global connectivity matrices by grouping the settlement cells based on widely used biogeographic units (province level) presented by Spalding et al. (47). By placing our modeling results in this context, we provide a framework that allows for the identification of oceanic processes that connect biogeographic regions. Our criterion for successful settlement was satisfied when simulated propagules reached a wet model grid cell adjacent to land after a specified minimum floating period (minFP) had occurred. Hence, the minFP prevents rapid stranding near the release location and ensures the potential for LDD events (i.e., potential colonizers). Cumulative density functions of the dispersal path length and great circle distance were then used to quantify retention in ocean surface currents and to evaluate the sensitivity of dispersal distance to minFP and maxFP.

Results

Simulated Propagule Transport.

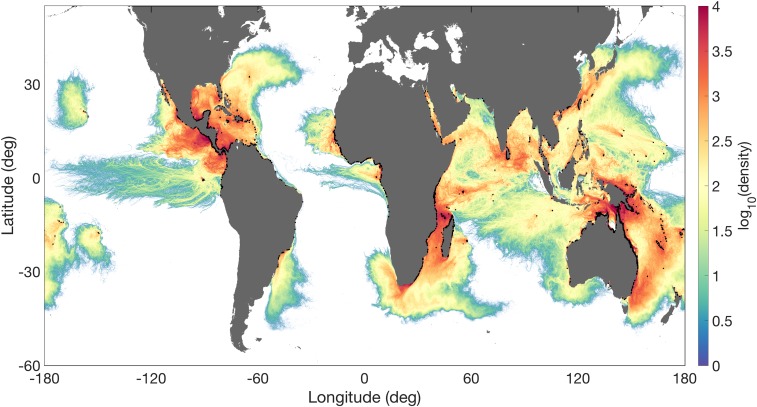
The highest trajectory densities are found in the Mozambique Channel in the western Indian Ocean region and near the Indo-West Pacific and Atlantic-East Pacific (Fig. 1 and SI Appendix, Fig. S1), corresponding to the highest density of release locations and the two primary hot spots for mangrove species [Indo-West Pacific: 54 mangrove species; Atlantic-East Pacific: 17 mangrove species (25)]. Simulated propagule transport exhibits a dominant along-coast component (i.e., high trajectory densities near the coast) in many regions. No dispersal is observed between mangrove populations on either side of the American and African continents or between southwest and southeast Australia (SI Appendix, Fig. S2). For simulated propagules with a maxFP of 12 mo, sporadic LDD events occur across the Atlantic, Indian, and Pacific Oceans (SI Appendix, Fig. S1B). In contrast, for a maxFP of 6 mo (Fig. 1) and 1 mo (SI Appendix, Fig. S1A), these ocean basins form effective barriers for dispersal. For shorter maxFPs, islands and island groups such as the Galapagos, Hawaii, and French Polynesia in the Pacific Ocean and the Reunion, Mauritius, Maldives and Chagos island groups in the Indian Ocean become increasingly isolated (Fig. 1 and SI Appendix, Fig. S1; see also Fig. 2 and SI Appendix, Fig. S3). Other islands, such as Bermuda, remain connected, even for a maxFP of 1 mo. Simulated propagules released in the western Indian Ocean region are transported around the southern tip of Africa into the South Atlantic via the shedding of Agulhas rings and filaments; however, the retroflection of the Agulhas Current (48) returns the majority of simulated propagules to the south Indian subtropical gyre.

Fig. 1.

Simulated mangrove propagule trajectory density across the global ocean. Trajectories were generated using velocity fields from a high-resolution ECCO2 ocean model simulation. Particles were released hourly for an entire year (1 April 2011 to 1 April 2012) for three different maxFP values (6 mo shown here; 1 mo and 12 mo are shown in SI Appendix, Fig. S1). Trajectories were aggregated on a 1/24° × 1/24° grid. Solid black circles along coastlines indicate the release locations used from the MRDH (80). White represents zero density.

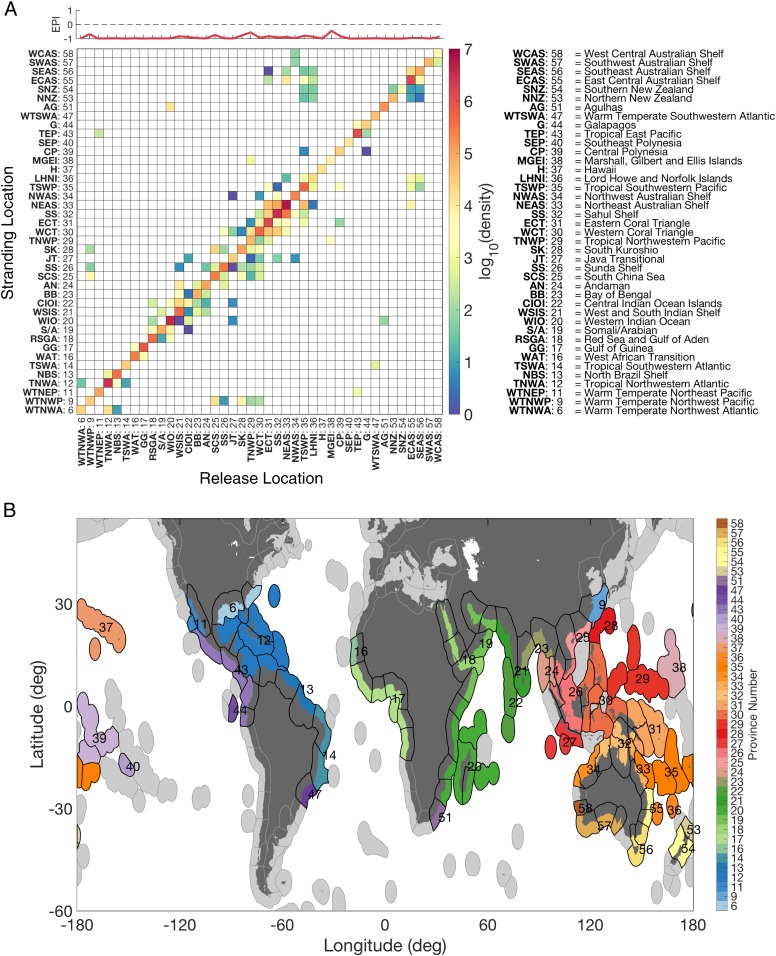
Fig. 2.

Global connectivity matrix. (A) The matrix shows the simulated connectivity between release (x axis) and predicted stranding (y axis) locations for propagules with a minFP of 5 d and a maxFP of 6 mo. To obtain a biogeographic framework and a tool for ocean-wide conservation planning, the release and stranding locations were binned using the marine provinces from Spalding et al. (47). Province numbers and abbreviations are shown on the axes. Above the matrix, the EPI = [(remote stranding − self-stranding)/(remote stranding + self-stranding)] is a measure of the relative importance of self-stranding and export of particles to remote provinces. (B) Global map showing the provinces (color code) and corresponding number for geographical interpretation of the connectivity matrix. Black contours show the ecoregion boundaries within each province; shades of gray show provinces without mangroves.

Connectivity Matrices.

High densities along the diagonal indicate dominant connectivity within provinces (we use the term “self-stranding” to indicate dispersal events whereby simulated propagules do not leave their native area, here called a province). This self-stranding component typically becomes more pronounced for shorter maxFPs (Fig. 2 and SI Appendix, Fig. S3). No connectivity is observed between populations on either side of the American and African continents; these landmasses function as effective dispersal barriers. For simulated propagules with a maxFP of 12 mo (SI Appendix, Fig. S3B), westward-flowing equatorial currents allow for efficient transoceanic dispersal. For example, simulated propagules released in the Gulf of Guinea (GG; see province abbreviations on connectivity matrices axes) are transported across the Atlantic Ocean via the South Equatorial Current to coastal sites within the Tropical Southwestern Atlantic (TSWA), the North Brazil Shelf (NBS), and the Tropical Northwestern Atlantic (TNWA). No direct exchange is found between American and West Pacific sites, but for a maxFP of 6 mo (Fig. 2A) and 12 mo (SI Appendix, Fig. S3B), connectivity matrices suggest that simulated propagules released in the Tropical East Pacific (TEP) can reach the Galapagos Islands (G) (and vice versa), which in turn are connected with Central Polynesia (CP). When extending the maxFP to 12 mo, simulated propagules originating from the Galapagos Islands can also reach Southeast Polynesia (SEP), the Marshall, Gilbert, and Ellis Islands (MGEI), the Eastern Coral Triangle (ECT), and the Tropical Northwestern Pacific (TNWP) (SI Appendix, Fig. S3B). From there, potential connectivity exists with the Sunda Shelf (SS) and Northeast Australian Shelf (NEAS), along with other provinces in the Indo-West Pacific region (but not for maxFP of 1 mo). Similarly, for maxFP of 6 mo and 12 mo, the Indian South Equatorial Current connects the Java Transitional (JT) with the Western Indian Ocean (WIO) and the Central Indian Ocean Islands (CIOI) (Fig. 2A and SI Appendix, Fig. S3B), and weakly with the Agulhas (AG) for a maxFP of 12 mo (SI Appendix, Fig. S3B). Our results suggest reciprocal connectivity between Western Indian Ocean locations and Indo-West Pacific sites via locations in the Arabian Sea, the CIOI, the West and South Indian Shelf (WSIS), and the Bay of Bengal. No LDD events across these ocean basins are observed for simulated propagules with a maxFP of 1 mo (SI Appendix, Fig. S3A). The semienclosed nature of the Indian Ocean and the associated ocean currents ensure connectivity among most provinces in the western Indo-Pacific realm (see figure 2A in ref. 47 for marine realms). While this connectivity weakens for a 1-mo maxFP, high connectivity is still observed in the southern Indo-West Pacific mangrove hot spot for all maxFP values considered. No connectivity is found between southwest [West Central Australian Shelf (WCAS) and Southwest Australian Shelf (SWAS)] and southeast Australian [Southeast Australian Shelf (SEAS)] locations. To further investigate particle export to remote provinces and the relative importance of self-stranding, we computed an export potential index (EPI) (Fig. 2A). The highest EPI was found in TNWP and MGEI.

Dispersal Distances.

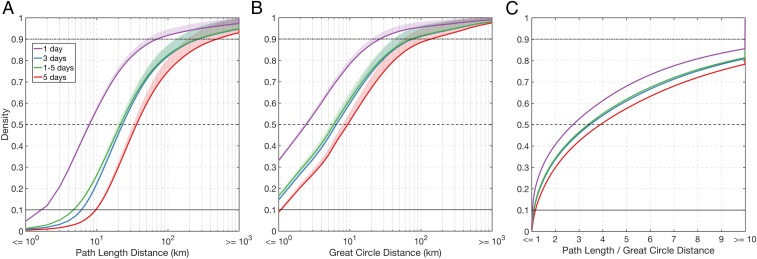
Cumulative density functions (CDFs) of simulated dispersal distances demonstrate that stranding primarily occurs within less than 50 km from the release site (>80% of the 1-d minFP simulated propagules and >90% of the 5-d minFP simulated propagules; see Fig. 3B), with dispersal distance being sensitive to minFP and maxFP. We found that minFP controls the density of short-distance dispersal events (Fig. 3 A and B); increasing minFP shifts the CDF distribution along the horizontal axis (i.e., toward longer distances). For example, roughly 50% of the simulated propagules strand within 10 km when having a 5-d minFP; however, this portion increases to nearly 80% for simulated propagules with a 1-d minFP (Fig. 3B). Similarly, the density of simulated propagule stranding events shifts along the vertical axis (shaded envelope) and shows the importance of maxFP in determining the number of successful LDD events (Fig. 3 A and B). The ratio between the path length and great circle distance highlights the effect of retentive ocean processes, such as tides and eddies, on propagule trajectories. The path length is 3–4 and 10 times larger than the great circle distance for roughly 50% and 20–30% of the simulated trajectories, respectively.

Fig. 3.

CDF for dispersal distances. The CDFs show the fraction of simulated mangrove propagule dispersal trajectories with (A) a path length and (B) a great circle distance shorter than or equal to a specific value. Colors represent CDFs for different minFPs in the model [i.e., 1 d (purple), 3 d (blue), 5 d (red), and a Monte Carlo simulation which generated random values between 1 and 5 d (green)]. The shaded envelope shows the density range for maxFP values between 1 mo (upper edge of shaded envelope) and 12 mo (thick line), with 1 mo, 3 mo, 6 mo, 9 mo, and 12 mo tested. CDFs of propagules with shorter minFPs are shifted toward smaller spatial scales compared with CDFs of propagules with longer minFPs. In the range of tens to hundreds of kilometers, the CDF densities increase for a maxFP of 1 mo compared with 12 mo. (C) CDF of the ratio between path length and great circle distance.

Discussion

Our numerical approach enabled the modeling and identification of mangrove dispersal routes, barriers, and stepping-stones, as well as connectivity between biogeographic regions globally, supporting findings from phylogenetic and population genetic studies. Modeled dispersal patterns and distances reveal dominant along-coast propagule transport (Figs. 1–3 and SI Appendix, Figs. S1–S3). This component may control coastal connectivity and (along with variations in habitat quality) spatial gradients in genetic diversity and likely reflects the anisotropy of coastal transport due to the presence of coastal boundaries and conservation of potential vorticity (49). Additionally, we found that the path length is 3 to 4 times larger than the associated great circle distance for 50% of the trajectories and an order of magnitude larger for 20% of the simulated dispersal events. These results support previous work suggesting that retentive ocean processes such as tides, mesoscale eddies, and fronts have the ability to modulate the transport of marine and coastal species (4, 50, 51) and hence influence the potential for particles to reach suitable habitats within their viability period (VP). Therefore, the use of ocean models that explicitly resolve these processes increases the realism of simulated propagule transport and connectivity. Interestingly, we found that the spatial scale of simulated propagule transport is highly sensitive to minFP and maxFP. In our simulations, the minFP strongly controls the number of stranding events (density shift along the horizontal axis) within ∼1–50 km of the release location, while the maxFP (shaded envelope) determines the number of simulated dispersal events exceeding 50 km (Fig. 3). We anticipate that our findings will help future research agendas quantify the relevant biophysical factors that determine mangrove dispersal and connectivity. For example, the influence of ocean surface water properties (such as temperature, salinity, and biogeochemistry) on metabolic processes and buoyancy behavior (52) should be investigated, as it may regulate minimum and maximum floating periods and the potential of viably reaching a suitable habitat (ref. 53 and references therein).

We found evidence for dispersal barriers such as the American and African continents, which were previously recognized from phylogenetic and population genetic studies (41, 42, 54). These findings also indicate that mangrove populations on both sides of the American and African continents are isolated over the timescales considered here. This absolute separation precludes range expansion, mangrove community shifts, or genetic introgression. Hence, the lack of propagule exchange causes both sides of these continents to be on a divergent genetic and ecological trajectory for mangrove species and communities. Although simulated propagules are transported westward around the tip of South Africa, the retroflection and termination of the Agulhas Current (48) prevent connectivity between East and West African populations. In previous work, the effectiveness of ocean basins in reducing connectivity was expected to depend on taxon-specific dispersal capabilities (41). Our results suggest that for propagules with a 1-mo maxFP, ocean basins act as effective dispersal barriers (SI Appendix, Fig. S1A). However, for propagules with longer maxFP (SI Appendix, Figs. S1B and S3B), coastal and open-ocean processes allow for transport over hundreds to thousands of kilometers (Fig. 3 and SI Appendix, Fig. S2). FPs of several months have been reported for wide-ranging Avicennia and Rhizophora species (37), and propagules of Avicennia marina (Forsk.) Vierh. were found to be viable for up to 7 mo (55). These FPs and VPs exceed the floating and competency durations reported for other marine taxa, facilitating “extreme” LDD events. For example, empirical competence and survival duration for scleractinian coral larvae (which, unlike mangrove propagules, develop during dispersal) are typically a few days to weeks, with a maximum of roughly 130 d (56). For a 1-y maxFP, our findings provide evidence for trans-Atlantic dispersal; this agrees with previous observational studies reporting close genetic affinity between West African and South American populations of Avicennia germinans L. (44, 54). and Rhizophora mangle L. (46, 54). Similarly, our model simulations support genetic evidence for contemporary gene flow between Australian and Pacific lineages and populations across the Pacific (45, 46). We find no direct connection between American and western Pacific regions (45). However, for a 6-mo maxFP and, particularly, a maxFP of 12 mo, simulated propagule trajectories suggest propagule supply from mangrove communities on the Pacific coast of Central America and northern South America to the Galapagos Islands, which in turn are connected to coastal and insular sites in the western Pacific (SI Appendix, Figs. S1B and S3B). While it is unclear whether direct exchange between American and West Pacific populations occurs for a maxFP > 12 mo, our simulations suggest that scattered Pacific islands (e.g., Galapagos, Polynesia, Micronesia, and Melanesia) provide stepping-stones that allow for trans-Pacific dispersal. For a maxFP of 6 mo and 12 mo, we found that these islands, along with TNWP and MGEI, exhibit elevated EPI. A higher EPI was also found for CIOI when using a maxFP of 12 mo. For a shorter FP of 1 mo, connectivity with these islands is strongly reduced, along with a decrease in EPI. Notably, like for corals (19), simulated propagule transport reveals a complete isolation of the Hawaiian Islands, where mangroves were introduced by humans during the early 1900s to stabilize mudflats (57). Furthermore, our model results confirm previous explanations for the presence of mangroves in Bermuda (the northernmost limit of mangroves and a latitudinal outlier), where the warm Gulf Stream system provides suitable growth conditions and supplies propagules from the US Gulf region (58, 59).

Our simulations demonstrate the potential for direct (i.e., not stepping-stone) connectivity between coastal regions in the JT and WIO (Fig. 2A and SI Appendix, Fig. S3B) via the Indian South Equatorial Current, suggesting that the Indian Ocean does not function as a present-day dispersal barrier for propagules with FP > 6 mo. Locations in the WIO may also receive propagules from Australia (SS, NEAS, and NWAS) via the JT, supporting previous findings that revealed a close relationship among Kenyan and Australian Rhizophora mucronata Lam. populations, with R. mucronata from Kenya being nested in the Australian clade (45). In contrast, the Indian Ocean has been considered an effective historical and present-day dispersal barrier based on species composition (East African mangrove communities are a subset of more species-rich mangroves in the east Indian Ocean and beyond) (42) and genetic evidence for A. marina across its range: a high number of unique alleles in each of the distant populations from South Africa, United Arabic Emirates, India, and the Malaysian-Australasian region (60). Floristic impoverishment is also shown in the infrageneric and infraspecific pattern of Avicennia in the Indian Ocean and Indo-West Pacific (61). Indeed, compared with Rhizophora, the much smaller Avicennia propagules are generally considered poorer long-distance dispersers (45), and for a FP of 6 mo or shorter, our results show strongly reduced connectivity across the Indian Ocean. However, connectivity across the Indian Ocean might also be established in a stepping-stone manner. For example, we found evidence for reciprocal potential gene exchange between WIO and Indo-West Pacific sites via the Arabian Sea and Gulf of Bengal, as suggested previously by Duke (41) (Fig. 2A and SI Appendix, Fig. S3B). This two-way exchange most likely reflects the seasonally reversing monsoon currents south of India and Sri Lanka and the eastern and central Arabian Sea (62). Overall, these results may help explain the distribution of mangrove species in the Indian Ocean region, such as R. mucronata (e.g., refs. 45 and 63), A. marina (60), and Xylocarpus granatum J. Koenig (64). Although we did not observe direct connectivity between East African and Australian populations, the directionality of transport via the subtropical gyre (SI Appendix, Fig. S1B) renders such connectivity likely for a FP > 12 mo and/or under particular ocean and wind conditions, as suggested from an experiment with plastic drift cards (65). High connectivity in the southern part of the Indo-West Pacific was found for all maxFP values considered (Fig. 2 and SI Appendix, Fig. S3), suggesting that the geography of the southern Indo-West Pacific, with its numerous islands and close proximity to vigorous ocean currents, may increase gene flow between populations and contribute to the high species richness and diversity observed in the region (25).

In summary, our simulations provide a tool that can be used to complement data from phylogenetic and population genetic studies (40–46, 54, 60, 61, 63, 64) and aid us in better understanding the role of contemporary ocean currents in driving mangrove biogeography. The framework provided in this study can be readily paired with climate data, allowing for a better understanding of potential interactions between biological and climate factors that modulate the response of mangrove systems to climate variability (34–36). We note that our model was not parameterized to represent taxon-specific biological information such as specific propagule characteristics [e.g., empirically determined variations in FP and VP (37–39, 55) and windage (66)], but considered values that represent a generic mangrove species. Additionally, we did not take into account other factors such as fecundity (67), predation (68), propagule retention in the landscape matrix (69), the timing of propagule release (70, 71), niche availability (72), and postdispersal processes (73, 74). These factors may control the abundance of potential emigrants and the likelihood of successful connectivity. Ultimately, quantifying these parameters and estimating their spatial and temporal variability for various mangrove species will allow for improved modeling efforts and reduce the uncertainty of estimated population connectivity (75).

Materials and Methods

Ocean Model.

The ocean surface currents used as input for our particle-tracking model were obtained from a mesoscale and tide-resolving configuration of the Massachusetts Institute of Technology general ocean circulation model (MITgcm). The model has a horizontal grid spacing of ∼4 km and vertical grid spacing of 1 m near the surface to better resolve surface currents (SI Appendix, Fig. S4). The simulation was initialized from a data-constrained global ocean solution provided by the Estimating the Circulation and Climate of the Ocean, Phase II (ECCO2, see ref. 76; www.ecco2.org/) project. Model bathymetry is a blend of the Smith and Sandwell (77) global seafloor topography, Version 14.1 and, south of 60°S, the International Bathymetric Chart of the Arctic Ocean (78). Surface boundary conditions were taken from the 0.14° European Centre for Medium-Range Weather Forecast atmospheric analysis starting in 2011. The ocean simulation includes tidal forcing, allowing for an improved representation of coastal ocean dynamics. The high spatial and temporal resolution of the ocean model resolves mesoscale eddies, which can strongly affect dispersal and connectivity of marine organisms (4, 50, 51). A more complete description of our ocean simulation is given in Rocha et al. (79).

Particle Release.

Particles were released over the full biogeographical range of mangroves using data from the Mangrove Reference Database and Herbarium (MRDH, see ref. 80; www.vliz.be/vmdcdata/mangroves/). Since coordinates in the database (11,706 in total) may represent different species, duplicate locations were removed. Particles were released hourly at 4,165 coastal grid cells over a 1-y period [1 April 2011 (0 h) to 1 April 2012 (0 h); i.e., 8,785 time steps in total], yielding >36 million release events. Due to the model resolution and land mask, release locations situated on land were shifted to the closest wet grid cell. The model was not parameterized to represent species-specific differences in the timing of propagule release; therefore, the model output represents an upper bound for this parameter [i.e., near-continuous (hourly) releases over the full 1-y period]. Although variation in the timing of propagule release is likely to alter estimates of dispersal and connectivity patterns (70), a species-specific approach is not currently possible due to the lack of adequate data (71). In addition, while factors such as fecundity, predation, and propagule retention in the landscape matrix may control the abundance of potential emigrants, we stress that quantifying the relative contributions of these factors to the dispersal process is beyond the scope of this study.

Particle Trajectories.

Particle trajectories were computed using Lagrangian particle tracking, allowing for the advection of simulated propagules via ocean surface currents. The particle-tracking method computes particle trajectories at hourly time steps by linearly interpolating zonal and meridional ocean surface velocities. The trajectories were time stepped using a first-order Euler method, which was chosen over higher-order methods since it is computationally inexpensive, the integration time step is short (1 h), and the surface velocity fields are not known to sufficient accuracy to justify higher-order methods. The model domain covers longitudinal and latitudinal ranges of 180°W to 180°E and 57°N to 70°S, respectively. Simulated propagules were tracked over 1 y (8,760 h), which was the maxFP considered, yielding a dataset of more than 32 × 10¹⁰ longitude-latitude data points over all release times (8,785) and locations (4,165). Vertical motion was neglected in computing trajectories. While this may be important for active animal larvae with behavioral traits such as vertical migration (4, 75), mangrove propagules are buoyant and generally remain on the ocean surface.

Dispersal Patterns and Connectivity Matrices.

From the Lagrangian particle trajectories, global dispersal trajectory density maps were generated by aggregating all modeled particle trajectories on an ∼4-km resolution grid (i.e., the native grid resolution) for a range of maxFPs: 1 mo (SI Appendix, Fig. S1A), 6 mo (Fig. 1), and 12 mo (SI Appendix, Fig. S1B). For this aggregation, particle trajectories were selected at 12-h time steps to reduce computation time. We stress that in contrast to the connectivity matrices (below), no stranding condition or minFP was employed when generating particle trajectory density maps. Mangrove propagule VPs and FPs reported in the literature range from less than 2 wk to ≥7 mo among mangrove taxa (38, 39, 55, 81). However, the duration of most field experiments may be too short to reliably depict the variation and maximum values for these properties; therefore, FP and VP remain largely undocumented for most mangrove species, hampering a species-specific analysis. While our approach is idealized, the goal of this study was to provide a first-order representation of potential dispersal and global connectivity patterns in mangroves.

Estimates of potential connectivity (exchange of simulated propagules between sites) were obtained by evaluating whether or not a particle had stranded within the respective maxFP. We did not allow for multiple potential settlement locations. Simulated propagules were considered stranded after first reaching a wet grid cell adjacent to a land grid cell and satisfying the minFP condition. If multiple land grid cells surrounded the wet grid cell, the first wet cell encountered by the algorithm was used. The stranding condition was evaluated at 4-h time steps to reduce computation time. Connectivity matrices represent the magnitude and direction of potential dispersal between locations and were computed for simulated propagules with a 5-d minFP and a 6-mo (Fig. 2A), 1-mo (SI Appendix, Fig. S3A), and 12-mo (SI Appendix, Fig. S3B) maxFP. While the minFP value used in this study is arbitrary, it lies within the ODP (i.e., minimum time to extend and produce roots) values reported in the literature (38, 55). However, the 5-d minFP was particularly chosen with respect to the scope of this study, i.e., to maximize the potential of LDD and avoid rapid stranding near the release sites. Nevertheless, to further explore the role of this parameter we conducted a sensitivity test using a range of minFP values (see Cumulative Density Functions section).

To obtain a biogeographic framework and a tool for ocean-wide conservation planning, we bin averaged release locations (x axis) and stranding locations (y axis) in all connectivity matrices (Fig. 2A and SI Appendix, Fig. S3) using data from a global biogeographic system for coastal and shelf areas: the Marine Ecoregions of the World (MEOW; see ref. 47). This nested system covers 12 realms, 62 provinces, and 232 ecoregions (47). To aggregate our results, the province scale was chosen over the ecoregion scale to ensure readability of the connectivity matrices. Since many of the provinces in the MEOW classification are beyond the spatial range that is relevant for mangrove connectivity (e.g., Arctic regions), the MEOW database was reduced by considering only those provinces (41 in total) that overlap with the global range of mangroves as represented by the MRDH data (i.e., those containing release locations considered in this study).

For all 41 biogeographic province units, we computed an EPI, which is a measure of the relative importance of self-stranding and particle export to remote provinces (Fig. 2A and SI Appendix, Fig. S3). Self-stranding events represent occasions when simulated propagules strand within the same province unit in which they were released. The EPI of a province is defined as the number of simulated propagules released in that province that strand remotely minus the number of self-stranding events divided by the sum of these two components: (remote strand − self-strand)/(remote strand + self-strand). Hence, EPIs of −1 and 1 reflect 100% self-stranding and 100% export, respectively.

Cumulative Density Functions.

For each combination of minFP and maxFP, we derived CDFs for trajectory path length (Fig. 3A) and great circle distance (Fig. 3B), as well as the ratio of both distances (Fig. 3C). The path length can strongly differ from the great circle distance and provides a measure of ocean processes that may facilitate retention. Since the minFP considered in our stranding definition (i.e., 5 d) is arbitrary and may influence the probability distribution of dispersal distances, we incorporated a sensitivity test by calculating CDFs for a range of minFP values: 1 d, 3 d, 5 d, and a Monte Carlo simulation which generated random values between 1 and 5 d. In addition, we also tested the sensitivity of the CDFs to the maxFP using the following values: 1 mo, 3 mo, 6 mo, 9 mo, and 12 mo (Fig. 3 A and B, shaded envelope). To compute the CDFs, we integrated probability density functions; path length and great circle distances were computed in 1-km bins (Fig. 3 A and B), and we binned the ratios by 0.01 (Fig. 3C).