Analysis of heart rate signals during meditation using visibility graph complexity

Abstract

In the dynamics analysis of heart rate, the complexity of visibility graphs (VGs) is seen as a sign of short term variability in signals. The present study was conducted to investigate the possible impact of meditation on heart rate signals complexity using VG method. In this study, existing heart rate signals in Physionet database were used. The dynamics of the signals were then studied both before and during meditation by examining the complexity of VGs using graph index complexity (GIC). Generally, the obtained results showed that the heart rate signals were more complex during meditation. The simple process of calculating the GIC of VG and its adaptability to the chaotic nature of the biological signals can help in estimating the heart rate complexity in meditation.

Introduction

A numbers of biological signals show the cellular events which exhibit the alteration of physiological systems after short time. One of the most important examples of these signals is the heart rate signals. Therefore, heart rate signals have been the focus of many research studies for a long time (Patidar et al. 2015; Li et al. 2015; Alvarez-Estevez and Moret-Bonillo 2016). Actually, there is need for the present increased interest in heart rate (HR) analysis since a great amount of information is embedded in the time series of heart rate signals; for example, these information were found to be directly linked with the heart health and can be used to diagnose some cognitive and central nervous system pathologies causing cardiac diseases (Costa-Neto et al. 2008; Yun et al. 2015; Hascoët et al. 2016). In addition, the study of these signals has been shown to be a valuable non-invasive technique for explaining the role of Autonomic Nervous System (ANS) branches in the regulation of the cardio-circulatory system. It was also shown that the heart coherence can be a cardiac marker for the meditation states and it is strongly associated with heart rate variability (HRV) (Kim et al. 2013). Therefore, the focus of the present study is on the physical effects of meditation on heart-rate dynamics. Several studies have investigated the HR dynamics changes during meditation (Peng and Henry 2004; Sarkar and Barat 2008; Jiang et al. 2013). The initial HR analysis which is based on statistical indexes was replaced by more sophisticated analyses capable of giving more information out of the signals.

Although, spectral analysis is mainly approved as an initial method for HR analysis, it is accurately assumed that it suffers different sources of noise because it is a heart rate series. This method has also been challenged for non-stationary signals analysis. In some signals, the spectrum includes a wide range of frequencies as well as spurious harmonics which are not often considered during analysis using conventional methods. For example, in Fourier spectral analysis which is based on linear super-positions of trigonometric functions, additional harmonic components which are available in most biological non- stationary time-series like HR, may produce a deformed wave profile. These deformations are known as the consequence of non-linear contributions. Therefore, with respect to the results, to apply conventional and standard methods to the analysis of a time series like HR in which non-stationary and non-linear components induce spurious harmonic components makes little sense (Sarkar and Barat 2008; Conte et al. 2009).

In psychobehavioral research, a major challenge encountered is the biological and behavioral system complications and the fact that complex systems can be modeled in a mathematical manner (Mumtaz et al. 2017; Dasdemir et al. 2017; Lehrer and Eddie 2013; Nasrolahzadeh and Haddadnia 2014) and the complex changes in bio-systems is evaluated using nonlinear dynamical analysis (Pu et al. 2016). In the analysis of the heart rate signals, nonlinear methods have been implemented to calculate heart rate indices because the dynamics of the cardiac system are chaotic (Goshvarpour and Goshvarpour 2013).

In the recent years, many researchers used nonlinear methods for quantitative assessment of meditation effects on biological time series such as electroencephalogram (EEG), electrocardiographam (ECG), and HR signals (Goshvarpour and Goshvarpour 2012; Goshvarpour et al. 2012).

Recently, a powerful approach was devised by combining time series analysis and complex network theory, and the approach successfully overcomes the major drawbacks of the classical methods of time series analysis (Donner et al. 2011; Nunez et al. 2012; Donne and Donges 2012).

Within this theoretical approach, there is a new simple method that converts a time series to a graph and it is called visibility graph (VG), with a structure which has been shown to be related to fractality (self-similarity) and complexity of the time series (Lacasa et al. 2008). Since the quantification of complexity and self-similarity of a graph does not need many nodes in the graph when a time series is converted to a graph, then the computation of its complexity does not need many time samples (Tang et al. 2013).

VGs have been given great attention, because they can represent the properties of a signal without redundancy and information overlap between the graphs and they are highly robust to noise (Sanz-Lobera et al. 2015).

VGs have been used widely in different types of applications, such as biological signals analysis and they have yielded promising results (Bhaduri and Ghosh 2015; Dong and Li 2010; Li and Dong 2011). Ahmadlou et al. (2010) developed a method for the diagnosis of Alzheimer’s disease using VG analysis of 19-channel EEGs time series and their four sub-bands. Shao (2010) constructed the VG for the heartbeat intervals time series from five healthy subjects and five congestive heart failure (CHF) patients. These patients showed that the assortative coefficient could be used as a basis for the diagnosis and prognosis of CHF. In another study (Mohammadpoory et al. 2017), weighted VG entropy was proposed for the detection of ictal, interictal, and healthy group in automatic epileptic seizure application and 97% high accuracy was obtained. Bhaduri et al. studied the effects of meditation on HR time series using VG methods. They used the power of scale freeness of VG for complexity analysis of the cardiac dynamics during meditation (Bhaduri and Ghosh 2016).

The present study was conducted to investigate the cardiac dynamics during meditation using VG complexity. In this study, HR complexity is estimated using the Maximum eigenvalue of the adjacency matrix of the VG during and before meditation (Ahmadlou et al. 2010; Kim and Wilhelm 2008).

This paper is outlined as follows: in the next section, the datasets used is briefly described and then, the methods and quantification analysis implemented are explained. The simulation results and performance analysis on datasets are presented. Finally, discussion and conclusions are dealt with.

Methods

Data selection

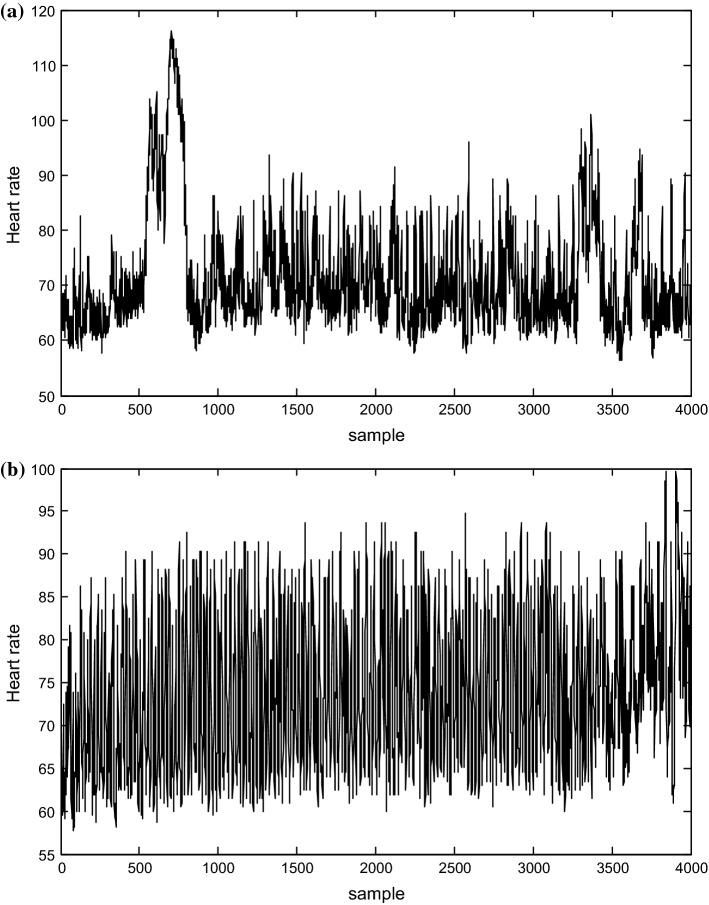
In this study, the heart rate signals of subjects before and during meditation, available at the Physio-Bank, were analyzed (Peng et al. 1999). Figure 2 shows the two types of signals.

Fig. 2.

Heart rate time series from C1 a before meditation, and b during meditation

Specific meditative techniques and Chinese Chi meditation were used for the analysis. Chi meditators were considered to be at an advanced level of meditation training (mean meditation experience of 7 years). The participants were all graduate and post-doctoral students. They were relatively novice in their practice of Chi meditation, because most of them just started meditation practice about 1–3 months before the start of the present study.

A Holter recorder was used to record the heart rate signals from 8 Chi meditators, 5 women and 3 men (age range 26–35, with a mean age of 29 years). The meditators were neither on any medication nor suffer from any specific heart diseases or psychological disorders. They were generally in good health. The meditators wore a Holter recorder for about 10 h while doing their everyday activities. At approximately 5 h into the recording, each of them practiced 1 h of meditation. During these sessions, the Chi meditators sat quietly, listening to the taped guidance of the master. The meditators were instructed to breathe spontaneously while visualizing the opening and closing of a perfect lotus in the stomach. The meditation session lasted for about 1 h. After the heart signals were recorded, with a sampling rate of 360 Hz, the necessary analyses were performed on them offline. The start time and end time of the meditation were separately marked with the event marks (Peng et al. 1999).

Visibility graph

VG method is considered to be a powerful technique for time series analyses. VG analysis based computational method which maps a time series into a graph was proposed recently (Nunez et al. 2012; Lacasa et al. 2008). In the literature (Lacasa et al. 2008; Lacasa et al. 2009), it was suggested that visibility graph analysis could be used for almost all types of time series. Also, graph theory methods can be used to develop techniques to quantify long-range fractality and dependency in time series. Within this framework, periodic series are transformed into regular graphs, random series into random graphs, and fractal series into scale-free graphs. In a similar manner, the present study attempts to analyze the characteristics of time series using this new approach.

VG of the time series $\text{x}{\left(\text{t}\right)}_{\left(\text{t}=1,\dots ,\text{n}\right)}$ is developed in the following condition:

Let the ith node of the graph, a_i, corresponds to the ith point of the time series, x_i. Then, the two vertices (nodes) of the graph, a_m and a_n, are connected via an edge if and only if:

$${\text{x}}_{\text{m}+\text{k}}<{\text{x}}_{\text{n}}+\left(\frac{\text{n}-\left(\text{m}+\text{k}\right)}{\text{n}-\text{m}}\right)\left({\text{x}}_{\text{m}}-{\text{x}}_{\text{n}}\right)\forall \text{k}\in {\text{Z}}^{+};\text{k}<n-m$$ 1

Figure 1 shows how a time series x Fig. 1a is converted into its VG Fig. 1b. As shown in Fig. 1, a_i is the first node of the graph corresponding to x_i. The gray line between x_i and x_j in Fig. 1a shows that x_i and x_j can see each other. If and only if x_i and x_j can see each other. The corresponding vertexes of the VG, a_i and a_j, connect together via a bidirectional edge. The time series is characterized with a degree sequence in VG. Therefore, some dynamical features of the time series, such as complexity and self-similarity, hidden in the signal may be specified in the structure of the resulting VG (Lacasa et al. 2008, 2009).

Fig. 1.

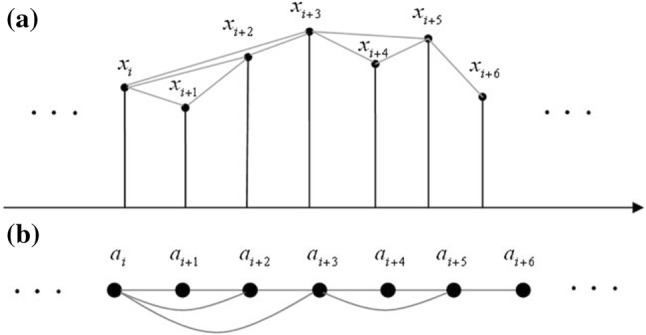
The method for converting a time series {x_i}, shown in (a), into its visibility graph with node sequence {a_i} shown in (b). Each gray line shows that the two connected points can see each other

Complexity of VG

The complexity and fractality (self-similarity) of a time series can be achieved by calculating its VG complexity which is similar to fractal dimension (FD) computation, without constructing the state space which requires a large number of sampling points. In this study, graph index complexity (GIC) methods are evaluated for measuring VG complexity (Lacasa et al. 2008; Tang et al. 2013; Ahmadlou et al. 2010).

Graph index complexity (GIC)

In this study, GIC (Kim and Wilhelm 2008) is implemented as a measure of complexity of a graph for heart rate signals during meditation. If ${\lambda }_{\mathit{max}}$ is the largest eigenvalue of the adjacency matrix of a graph with n nodes, GIC can be expressed as follows:

$${\text{C}}_{{\mathrm{\lambda }}_{\text{max}}}=4\text{c}\left(1-\text{c}\right)$$ 2

where

$$c=\frac{{\mathrm{\lambda }}_{\text{max}}-2cos\left(\mathrm{\pi }/\left(\text{n}+1\right)\right)}{\text{n}-1-2cos\left(\mathrm{\pi }/\left(\text{n}+1\right)\right)}$$ 3

where ${\text{C}}_{{\mathrm{\lambda }}_{\text{max}}}$ can be shown to alter between 0 and 1 because the following inequality is true for all unweighted bidirectional graphs (Kim and Wilhelm 2008):

$$2cos\left(\frac{\mathrm{\pi }}{\text{n}+1}\right)\le {\mathrm{\lambda }}_{\text{max}}\le \text{n}-1$$ 4

The more complex the graph’s structure is, the larger $C_{{\lambda }_{\mathit{max}}}$ will be. In this study, the VG index complexity is used as a measure to investigate the VG.

Results

Figure 2 shows the heart rate signals of subject C1, before and during meditation. The meditation signals become more complex as shown in this figure.

In this study, the parameters described in the previous section were calculated for the heart rate data before and during meditation.

On this note, first time series were windowed using non-overlapped rectangular windows. Two epoch lengths were used for the analysis: 500 points and all points in each time series. Then, these epochs were converted to VGs and GIC values were calculated.

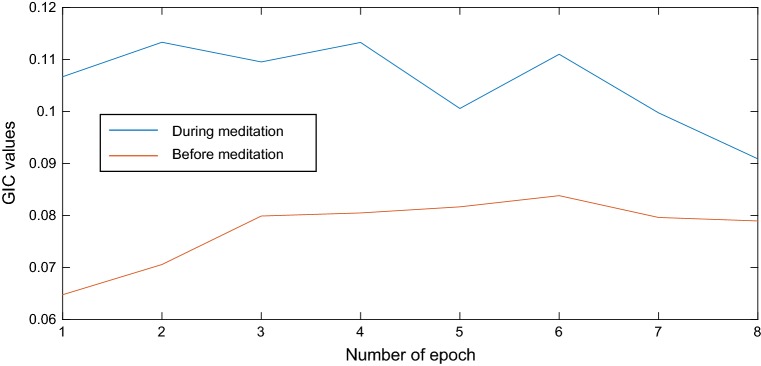
Figure 3 shows the GIC values for 500 points epoch and subject C1, during and before meditation.

Fig. 3.

The GIC values for 500 points epochs and subject C1: before versus during meditation

As shown, GIC values increased during meditation and it means HR time series became more complex during meditation.

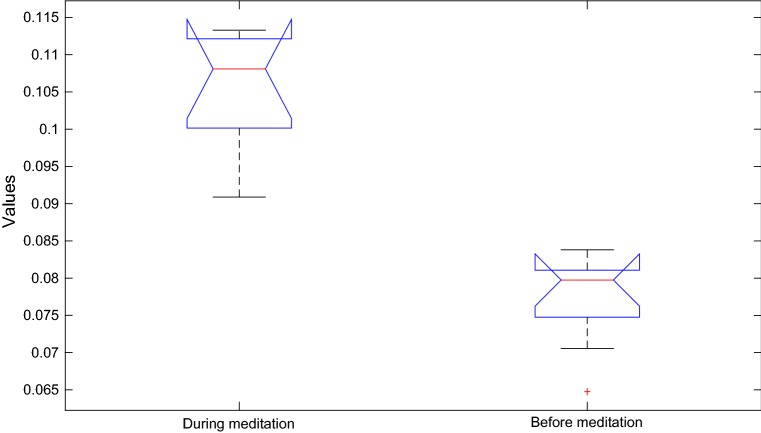
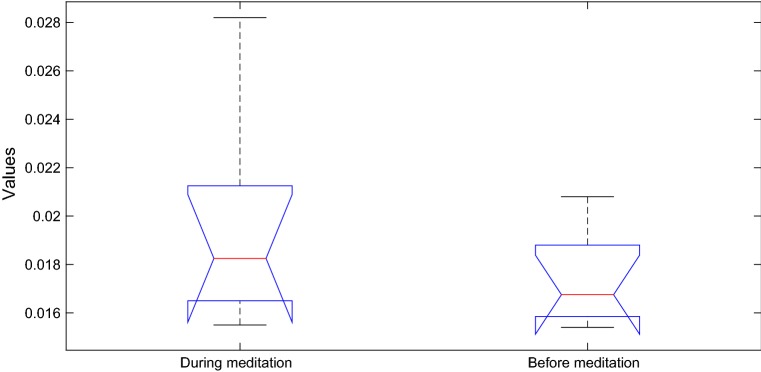
The box plots of GIC values for 500 points epoch and subject C1, before and during meditation are as shown in Fig. 4. This figure shows that the two groups are significantly different in terms of GIC values of VG.

Fig. 4.

Box plot of of GIC values of 500 points epochs and subject C1: before versus during meditation

Figure 5 shows GIC mean values for each subject, during and before meditation for 500 points epochs. As can be seen, GIC mean values increased during meditation for all subjects. Two horizontal lines show the mean of GIC values for all subjects and it can be seen they are not close together.

Fig. 5.

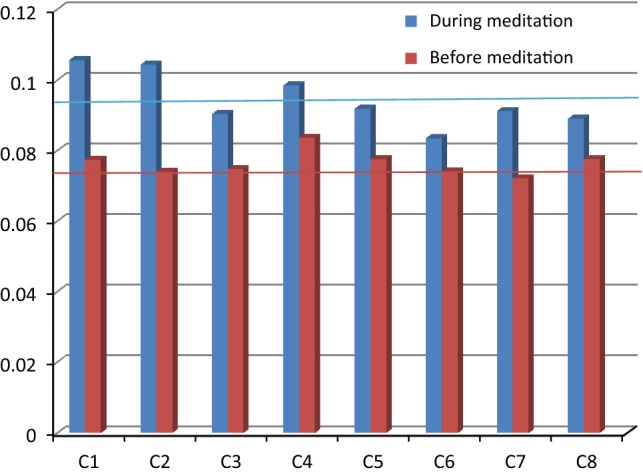
The mean values of GIC for each subject for 500 points epochs: before versus during meditation (red horizontal line is the mean of all GIC values before meditation and blue horizontal line is the mean of all GIC values during meditation). (Color figure online)

One-way analysis of variance (ANOVA) test was used to determine the P values for GIC values of the two groups (before and during meditation). Table 1 shows the P value obtained using ANOVA test. P value less than 0.01 shows GIC values are significantly different between the two groups. As can be seen, except for subject C6, P values are less than 0.01 for all subjects.

Table 1.

The P value obtained by the ANOVA testfor each subject and 500 points epochs: before versus during meditation

Subjects	P values
C1	0.000001
C2	0.00001
C3	0.004
C4	0.002
C5	0.007
C6	0.027
C7	0.0006
C8	0.003

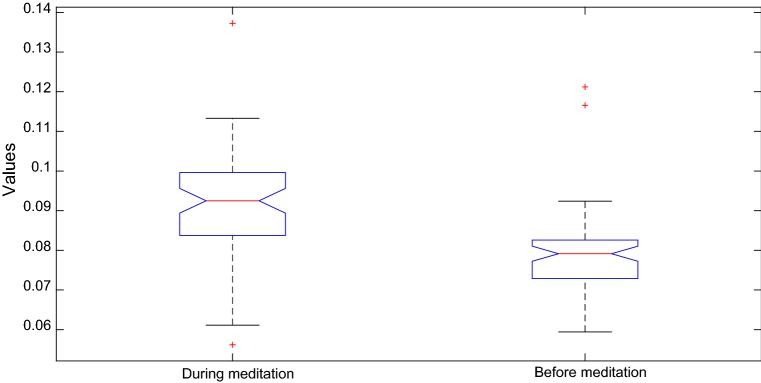
Figure 6 shows the box plot of all GIC values for all 500 points epochs and all subjects, during and before meditation. P value is 0.0005 for these GIC values.

Fig. 6.

The box plot of all GIC values for all 500 points epochs and all subjects: before versus during meditation

Figure 7 shows GIC values for each subject, during and before meditation for all points in each time series. As can be seen, GIC values increased for all subjects during meditation. Two horizontal lines show the mean of GIC values for all subjects and it can be seen they are close together.

Fig. 7.

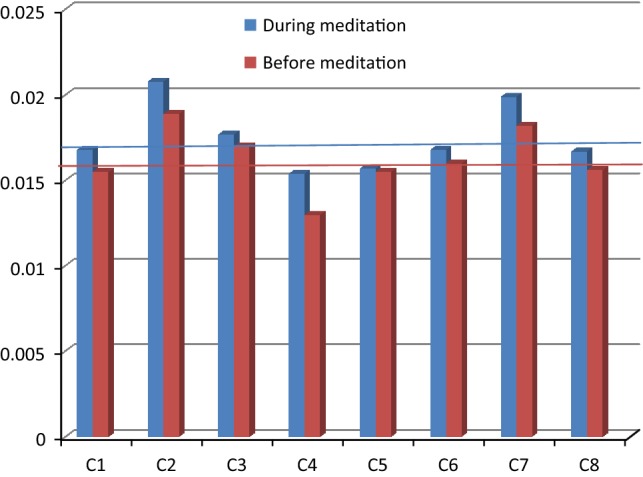
GIC values for each subject, during and before meditation for time series all points in each time series (red horizontal line is the mean of all GIC values before meditation and blue horizontal line is the mean of all GIC values during meditation). (Color figure online)

Figure 8 shows the box plot of all GIC values for all points in each time series and all subjects, during and before meditation. P value is 0.2 for these GIC values.

Fig. 8.

The box plot of all GIC values for all points in each time series and all subjects: before versus during meditation

Discussion

The present study focused on an innovative method using VG quantification analysis, which can identify the maximum eigenvalue of the adjacency matrix of a graph as a measure of complexity. The heart rate signals of eight subjects during special psycho-physiological state were analyzed. To the best of our knowledge, the present study is the first study where the GIC of VG has been used with the aim of evaluating the effect of eigenvalue of the adjacency matrix of a graph on the complexity of the heart rate signals during meditation.

It was observed that the VG contains important information about the dynamics of the system under study and the GIC increased during meditation. However, the length of the analyzed time series affects the results. Two epoch lengths were considered for the analysis of HR time series using the VG method. First 500 points epochs were used for VG construction and then all points in each time series were used. The results showed that for the 500 points epochs, GIC was significantly increased during meditation (Fig. 5). Then, HR complexity increased during meditation and P values showed that meditation has significant effects on GIC values (Table 1). For all points in each time series case, the results also showed that GIC values increased during meditation for all the subjects. As shown in Figs. 5 and 7, GIC values are more different in 500 points data than all the point cases, when compared. This difference is rational since the HR signal is non-stationary (Toledo et al. 1998). Recent studies confirmed that there is a natural background of chaos and complexity in the human body and lack of chaos and complexity can lead to an abnormal function such as seizure, congestive heart failure and some other dysfunctions (Bhaduri and Ghosh 2016). Adeli et al. (2007) showed in the case of epileptic seizure, EEG signals are less chaotic and complex than the normal state. Bhaduri et al. (2017) showed HR signals are also less complex and chaotic in congestive heart failure case than the normal state. Maity et al. (2015) showed consistent increase of multi-fractal spectra in EEG time series or increase of degree of complexity can be a parameter for quantification of well-being and an improved therapy.

According to last studies, meditation with a wider spectra leads to better functions of the body and can correct some abnormal functions and health problems (Hernández et al. 2018; Fingelkurts et al. 2015; Travis et al. 2018).

Bhaduri and Ghosh (2016) proposed PSVG and multi-fractal detrended fluctuation analysis for quantitative evaluation of HR dynamics during meditation and showed that HR time series become more complex during meditation. Therefore, the results of this research are in agreement with the results of the present study. Moreover, the present method is fast and easy.

The results suggest that the VGs analysis of the heart rate signals can display good information, giving additional insight into the formation of cardiac signals in different psychological states (before and during meditation). Moreover, the results appear robust and can be significantly interpreted in terms of characteristic properties of the underlying time series. As can be observed from the study of the resulting graph attributes as a function of time, slight changes were observed in the dynamical attributes of the time series under study. Generally, it seems that VG analysis enjoys great potentials for future applications to heart rate data.

Conclusion

In this paper, a novel VG-based method was presented for the extraction of discriminative information from the complex networks structure with the aim of evaluating heart rate dynamics during meditation. Recently, VG algorithm was introduced as a simple but powerful algorithm to convert time series into graphs while preserving the dynamic characteristics such as complexity. GIC measure was used for VG complexity assessment. Generally, the present results showed that the GIC values increased during meditation. Therefore, HR signals become more complex during meditation. As observed from the last researches, meditation has positive effects on the quality of life. Therefore, this can be due to the fact that increase in the degree of complexity can be a parameter for quantification of well-being and hence an improved therapy.

Conclusively, the findings of the present study suggest that as a sensitive tool for the study of complex systems, the VG quantification analysis using complexity measures can play an important role in analyzing the heart rate signals during meditation.