Skip to main content
PMC home page
Frontiers in Neuroscience logoLink to Frontiers in Neuroscience
. 2019 Jan 14;12:1055. doi: 10.3389/fnins.2018.01055

Test-Retest Reliability of Diffusion Measures Extracted Along White Matter Language Fiber Bundles Using HARDI-Based Tractography

Mariem Boukadi 1,2, Karine Marcotte 3,4, Christophe Bedetti 1, Jean-Christophe Houde 5, Alex Desautels 3,6, Samuel Deslauriers-Gauthier 7, Marianne Chapleau 1,2, Arnaud Boré 1, Maxime Descoteaux 5, Simona M Brambati 1,2,*
PMCID: PMC6339903  PMID: 30692910

Abstract

High angular resolution diffusion imaging (HARDI)-based tractography has been increasingly used in longitudinal studies on white matter macro- and micro-structural changes in the language network during language acquisition and in language impairments. However, test-retest reliability measurements are essential to ascertain that the longitudinal variations observed are not related to data processing. The aims of this study were to determine the reproducibility of the reconstruction of major white matter fiber bundles of the language network using anatomically constrained probabilistic tractography with constrained spherical deconvolution based on HARDI data, as well as to assess the test-retest reliability of diffusion measures extracted along them. Eighteen right-handed participants were scanned twice, one week apart. The arcuate, inferior longitudinal, inferior fronto-occipital, and uncinate fasciculi were reconstructed in the left and right hemispheres and the following diffusion measures were extracted along each tract: fractional anisotropy, mean, axial, and radial diffusivity, number of fiber orientations, mean length of streamlines, and volume. All fiber bundles showed good morphological overlap between the two scanning timepoints and the test-retest reliability of all diffusion measures in most fiber bundles was good to excellent. We thus propose a fairly simple, but robust, HARDI-based tractography pipeline reliable for the longitudinal study of white matter language fiber bundles, which increases its potential applicability to research on the neurobiological mechanisms supporting language.

Keywords: dMRI, tractography, tractometry, test-retest, language

Introduction

The characterization of the brain and language network and its development, disruption, and changes over time represents one of the central themes of cognitive neuroscience. Diffusion magnetic resonance imaging (dMRI)-based tractography has been proven to be a valuable tool for the in vivo identification of white matter (WM) fiber bundles involved in language and the extraction of measures of their micro- and macro-structural characteristics. However, the ability of this tool to reproduce the same language fiber bundles’ morphology and micro- and macro-structural characteristic measurements when dMRI data is acquired twice from the same participant under the same conditions (i.e., test-retest reliability), has yet to be clearly demonstrated. In fact, while test-retest reliability has already been reported for other neuroimaging techniques that are usually employed in evaluating longitudinal changes in the language brain network (such as resting state and task-based functional MRI, voxel-based morphometry, and cortical thickness; e.g., Jovicich et al., 2009; Zhang et al., 2011; Braun et al., 2012; Birn et al., 2013; Powers et al., 2013; Lin et al., 2015; Seiger et al., 2015; Wang et al., 2016; Madan and Kensinger, 2017; Zhang et al., 2017), test-retest reliability of dMRI-based tractography has received comparatively less attention. This represents a first necessary step to validate the use of this approach in longitudinal studies on language.

It is increasingly accepted that WM associative fiber bundles play a crucial role in mediating the transfer of information among specialized language brain areas, distributed along two main processing streams, namely the dorsal and ventral streams (Hickok and Poeppel, 2000, 2007; Saur et al., 2008; Poeppel et al., 2012; Dick et al., 2014). The central and most widely studied WM fiber bundle of the dorsal stream is the arcuate fasciculus (AF), putatively connecting Broca’s and Wernicke’s territories (Catani and Thiebaut de Schotten, 2012). The AF has been suggested to play a central role in the processing of phonological information and complex syntax in both language production and comprehension (Duffau et al., 2002, 2003; Friederici et al., 2006; Brauer et al., 2011, 2013; Wilson et al., 2011). The major fiber bundles of the ventral stream are the inferior longitudinal fasciculus (ILF), the inferior fronto-occipital fasciculus (IFOF), and the uncinate fasciculus (UF). Their specific contribution to language processing is still a matter of debate. Both the ILF and IFOF are bundles of long association fibers originating in the occipital lobe (Dick et al., 2014). The ILF connects occipital and temporal lobes, while the IFOF connects the occipital and frontal lobes (Catani and Thiebaut de Schotten, 2008; Thiebaut de Schotten et al., 2012; Dick et al., 2014). Both of these bundles have been suggested to play a key role in semantic processing, more specifically in reading and naming (Duffau et al., 2005, 2014; Duffau, 2008; Turken and Dronkers, 2011; Gil-Robles et al., 2013; Han et al., 2013). The UF is a long-range association fiber bundle connecting the anterior temporal lobe with the orbital and polar frontal cortex (Thiebaut de Schotten et al., 2012). While the role of this bundle in language is still controversial, it has been suggested to support semantic retrieval (Lu et al., 2002; Grossman et al., 2004; Catani and Mesulam, 2008) and simple syntactic operations (e.g., processing of phrases) (Friederici et al., 2006).

The use of advanced probabilistic fiber tracking based on high angular resolution diffusion imaging (HARDI) has proven to be particularly suitable for the reconstruction of fiber bundles with complex configurations (i.e., crossing, kissing, or fanning fibers), such as language-related fiber bundles (Alexander et al., 2002; Tuch et al., 2002; Tournier et al., 2012b; Descoteaux, 2015; Farquharson and Tournier, 2016; Jeurissen et al., 2017; Maier-Hein et al., 2017). Up until recently, diffusion tensor imaging (DTI) tractography based on dMRI data has been considered a standard tool for the in vivo reconstruction of fiber bundles. However, it has been demonstrated that DTI fails to adequately represent the complex architecture of WM fibers in the brain (Frank, 2001; Alexander et al., 2007; Behrens et al., 2007; Descoteaux et al., 2007, 2009; Jeurissen et al., 2010; Prckovska et al., 2012; Descoteaux, 2015). Standard DTI analysis can represent only one fiber population per voxel, whereas about 66% to 90% of voxels contain a complex fiber configuration (Descoteaux and Deriche, 2008; Jeurissen et al., 2010; Jeurissen et al., 2014). HARDI has been introduced to mitigate some of DTI’s limitations in WM areas with a complex geometry (Alexander et al., 2002; Tuch et al., 2002; Tournier et al., 2012a; Descoteaux, 2015; Farquharson and Tournier, 2016). HARDI measures the diffusion signal along 60 or more gradient directions taken on the sphere in q-space (Descoteaux, 2015). HARDI-based reconstruction techniques such as constrained spherical deconvolution (CSD) aim to estimate the distribution of different fiber orientations within a voxel using a mathematical object known as the fiber orientation distribution function (fODF) (Seunarine and Alexander, 2009). As opposed to the tensor, the fODF allows the estimation of more than one fiber population per voxel, which allows better characterization of WM in regions with a complex architecture (Côté et al., 2013; Descoteaux, 2015).

The combination of micro- and macro-structural measures allows a more comprehensive analysis of WM fiber bundle characteristics. Microstructural properties of bundles reconstructed with tractography are usually inferred from the extraction of different scalar metrics, such as fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD). These measures are sensitive to different fiber properties such as axonal ordering, myelinization, and density (Jones et al., 2013). Although the specific interpretation of these measures is still a matter of debate, they are routinely used in both fundamental and clinical neuroscience studies to provide insights into WM fiber bundles’ profile (Tournier et al., 2012b). The development of CSD based on HARDI data allows the estimation of the number of fiber orientations (NuFO) using the number of local maxima of the fiber orientation distribution (FOD) (Dell’Acqua et al., 2013). NuFO indicates the number of distinct fiber orientations in each voxel, thus providing valuable information on WM complexity. Interestingly, NuFO maps are highly consistent across individuals, which could represent a sensitive marker of age-related changes in WM complexity among healthy populations or changes observed in clinical populations (Dell’Acqua et al., 2013). Macrostructural measures provide complementary information regarding the morphology of the bundles, which includes the volume of the fiber bundles and the mean length of streamlines (MLS) (Girard et al., 2014).

While there is growing interest in the use of tractography and tractometry in longitudinal studies to investigate language-related fiber bundles’ changes over time (e.g., Forkel et al., 2014; Lam et al., 2014; Mandelli et al., 2016; Takeuchi et al., 2016; Asaridou et al., 2017; Chow and Chang, 2017), the test-retest reliability of HARDI-based tractography and tractometry for language-related fiber bundles has yet to be demonstrated. Test-retest reliability refers to the reproducibility of a measure repeated twice for the same participant (Berchtold, 2016). In order for an instrument to be used to detect a change, it has to be able to distinguish between a real change in individuals and a random variation due to the measurement instrument itself (Guyatt et al., 1987). This entails that one of the most crucial aspects to look at when assessing the reliability of a method for longitudinal designs is the test-retest reliability of measurement instruments (Berchtold, 2016). To date, most studies have not integrated reproducibility assessment of their diffusion measures and fiber bundles. This is a critical issue because different factors may affect intra-subject reproducibility such as imaging acquisition parameters (e.g., Jones, 2004; Bisdas et al., 2008; Gao et al., 2009), tractography pipelines (Wang et al., 2012; Kristo et al., 2013; Cousineau et al., 2017), and subject physiological noise (e.g., Pfefferbaum et al., 2003; Farrell et al., 2007). Previous studies have provided evidence of good to excellent test-retest reliability for other methods of analysis of dMRI data, such as tract-based spatial statistics (TBSS), region-of-interest (ROI)-based approaches, and DTI-tractography (Ciccarelli et al., 2003; Heiervang et al., 2006; Danielian et al., 2010; Vollmar et al., 2010; Magnotta et al., 2012; Wang et al., 2012; Cole et al., 2014). However, the test-retest reliability of HARDI-tractography and tractometry has received less attention. Promising evidence of test-retest reliability of this approach comes from the work of Besseling et al. (2012), Kristo et al. (2013) and Cousineau et al. (2017). These studies have demonstrated the overlap of WM fiber bundles reconstructed by means of HARDI-based tractography and the reproducibility of their micro- and macro-structural measures, based on dMRI data obtained from healthy subjects in separate MRI acquisition sessions. Even though these studies were crucial in determining the potential of this approach in longitudinal studies, the only language-related bundle included in all of them is the AF which yielded conflicting results. Thus, the test-retest reliability of HARDI-tractography and tractometry in the main language-related fiber bundles remains to be validated.

In order to fill this gap, the aim of the present study is to assess test-retest reliability of the reconstruction, as well as the micro- and macro-structural characteristics of the major WM fiber bundles associated with language processing reconstructed using probabilistic HARDI-tractography. To this aim, we have collected dMRI data from a sample of healthy individuals at two time-points, one week apart, and reconstructed major WM fiber bundles supporting language functions within the left and right hemispheres (AF, ILF, IFOF, and UF). We expect that no measurable changes in the micro- and macro-structural characteristics of the tracts under study would be observed in that short time period. The test-retest reliability of the fiber bundles’ morphology was obtained by calculating, for each subject, the spatial overlap between each tract’s reconstruction at the two time-points as proposed in Cousineau et al. (2017). Additionally, macro-structural characteristics such as volume and MLS, as well as mean microstructural measures such as the tensor-based metrics FA, MD, RD, AD, and the FOD-based measure NuFO (Dell’Acqua et al., 2013) were extracted for each bundle and their reproducibility was assessed.

Materials and Methods

Participants

Eighteen right-handed cognitively unimpaired participants (age: M = 64.61 y.o. ± 7.99; education: M = 16.16, ± 3.42 years; 9 women, 9 men) with no history of psychiatric or neurological conditions were scanned at two time-points, one week apart. The study was approved by the research ethics committee of the Center intégré universitaire de santé et de services sociaux du Nord-de-l’Ile-de Montréal (Project #MP-32-2018-1478) and written informed consent was obtained from all participants.

Image Acquisition

The diffusion MRI protocol was acquired using a Skyra 3T MRI scanner (Siemens Healthcare, United States) at the radiology department of Hôpital du Sacré-Coeur of Montreal. At each of the two scanning occasions participants underwent the same acquisition sequence. One high resolution 3D T1-weighted (T1w) image (TR = 2200 ms, TE = 2.96 ms, TI = 900 ms, FOV = 250 mm, voxel size = 1 mm × 1 mm × 1 mm, matrix = 256 × 256, 192 slices, flip-angle = 8) was acquired using a Magnetization Prepared Rapid Gradient Echo (MP-RAGE) sequence. A diffusion weighted imaging (DWI) sequence was also acquired (TR = 8051 ms, TE = 86 ms, FOV = 230 mm, voxel size = 2 mm × 2 mm × 2 mm, flip angle = 90°, bandwidth = 1698; EPI factor = 67; 68 slices in transverse orientation) with one image (b = 0 s/mm2) and 64 images with non-collinear diffusion gradients (b = 1,000 s/mm2) in a posterior-anterior (PA) acquisition, as well as two additional images (b = 0 s/mm2): one in a PA acquisition, namely in the same direction as the diffusion gradients, and the other in an anterior-posterior (AP) acquisition, namely in the opposite direction of the diffusion gradients.

dMRI Data Analysis

All analysis steps were conducted using the Toolkit for Analysis in Diffusion MRI (TOAD) pipeline1.

Pre-processing

Pre-processing steps included denoising, motion/eddy/distortion corrections, upsampling, registration, segmentation and parcellation, and masking. First, DWI was noise-corrected using overcomplete local principal component analysis (PCA) using the Matlab toolbox DWI Denoising Software (Manjo et al., 2013) The FMRIB Diffusion toolbox EDDY of FSL 5.0.11 (publicly available neuroimaging software2) (Jenkinson et al., 2012) was used to correct all images for subject movement, eddy-currents, and susceptibility-induced distortions using AP-PA images. Gradient directions were corrected corresponding to motion correction parameters (motion for each subject at each timepoint is reported in the Supplementary Material). T1w images were processed with Freesurfer’s pipeline 6.0.0 (Dale et al., 1999; Desikan et al., 2006) for segmentation and parcellation of gray and WM into anatomical regions. DWI was upsampled to 1 mm isotropic resolution using a trilinear interpolation (Girard and Descoteaux, 2012; Raffelt et al., 2012; Smith et al., 2012; Tournier et al., 2012a; Dyrby et al., 2014) and the segmented and parcellated T1w was registered to the DWI using FMRIB’s linear registration tool (FLIRT) from FSL. This step allowed us to carry out anatomically constrained tracking (ACT) (see next section for further details). Finally, a mask image was obtained from the segmented T1w image and served to seed streamlines on the gray matter-white matter interface (Tournier et al., 2012a).

Tractography

Fiber orientation distribution functions (fODFs) were estimated using CSD. A whole-brain tractogram was computed using MRtrix3’s probabilistic tractography algorithm with ACT3 (Tournier et al., 2012a). ACT uses the T1w (i.e., the segmented anatomical image obtained from Freesurfer) to limit potential false-negatives (i.e., no-connections) and improve WM coverage in general (Guevara et al., 2011; Girard and Descoteaux, 2012; Smith et al., 2012; Girard et al., 2014; Mori and Tournier, 2014). The AF, ILF, IFOF, and UF were reconstructed from the tractogram using the White Matter Query Language (WMQL) (Wassermann et al., 2016). WMQL is a user-friendly method to carry out WM bundle extraction from tractography in a nearly automatic way. It allows us to consistently define bundles across subjects without manually specifying regions of interest. It consists in writing queries with the WMQ language describing the WM bundles to be reconstructed using anatomical definitions from Freesurfer’s Desikan-Killiany atlas. In order to be able to extract the fiber bundles using the written queries, Freesurfer’s gray and WM parcellation was overlaid on the tractogram. The queries were then automatically interpreted by tractography tools. The queries used to reconstruct the fiber bundles are presented in the Supplementary Material. Outlier streamlines were then removed from each tract using a tract-filtering algorithm (Côté et al., 2015). The following diffusion and bundle measures were extracted along each fiber bundle for each participant: FA, MD, AD, RD, NuFO (Dell’Acqua et al., 2013), volume, and MLS. All tractography steps were performed in native space since non-linear normalization with diffusion MRI data requires local reorientations and warping which affects the gradient table at every voxel (bval/bvec) (Vollmar et al., 2010). Bringing the T1-w image into native diffusion space with linear affine registration and using the Freesurfer parcellation in this space is more robust (Girard et al., 2014, 2015).

Statistical Analysis

Test-retest analyses were carried out in two steps. First, we used the weighted dice similarity coefficient (wDSC) to determine the degree of overlap between the reconstructed fiber bundles at Times 1 and 2 as in Cousineau et al. (2017). DSC is a statistical metric that ranges between 0 and 1 and is used to assess the degree of overlap between two volumes (Dice, 1945). The wDSC is a variation of this metric and gives more weight to voxels with more streamlines. This is important to take into account considering the fact that WM bundles have more streamlines in their middle than in the extreme portions (Cousineau et al., 2017). In the two previous studies which used this measure to assess the test-retest reliability of CSD-based reconstruction of WM tracts (Besseling et al., 2012; Cousineau et al., 2017), the minimum value of Dice was 0.70. Therefore, this value was used as the acceptable threshold for a good wDSC in our study. The wDSC was computed using the following formula from Cousineau et al. (2017):

D(Wi, Wj)=Σv′ Wi,v′+Σv′ Wj,v′Σv Wi,v′+Σv Wj,v

where Wi and Wj, respectively, represent the bundles at Time 1 and Time 2, and v′ represents the voxels from the two reconstructions of the bundles (Wi and Wj) that overlap.

To do so, T1-weighted images in diffusion space taken at Time 1 were registered linearly to anatomical images taken at Time 2 (i.e., seven days later) for each subject with Advanced Normalization Tools (ANTs), version ≥ 2.1 (Tustison et al., 2014)4. Transformation matrices were applied to all Time 1 bundles using TractQuerier’s tract_math tool (Wassermann et al., 2016). Once the two fiber bundles of each subject were in the same space, wDSCs were computed with the tractometry pipeline from the Sherbrooke Connectivity Imaging Lab (SCIL) http://scil.dinf.usherbrooke.ca/?lang=fr. The right UF bundle could not be reconstructed in one participant. Analyses were therefore conducted with a sample of 17 participants for that bundle.

In a second step, we combined two complementary analyses, the intra-class correlation coefficient (ICC) and the Bland-Altman plots to assess the test-retest reliability of each of the measures extracted in each reconstructed fiber bundle. The intra-class correlation coefficient (ICC) (Shrout and Fleiss, 1979; McGraw and Wong, 1996) is a widely used statistical approach to assess agreement in test-retest reliability studies in different fields, including neuroimaging (e.g., Zhang et al., 2011; Braun et al., 2012; Birn et al., 2013; Duda et al., 2014; Duan et al., 2015). The ICC is calculated from an analysis of variance and can be broadly defined as the ratio of between-subject variance to the total variance (including within-subject variance and residue) (Berchtold, 2016). ICC values range from 0 to 1 and can be categorized into four levels of test-retest reliability: excellent (ICC > 0.75), good (ICC = 0.60 to 0.74), fair (ICC = 0.40 to 0.59), and poor (ICC < 0.40) (Fleiss, 2003). ICC estimates and their 95% confidence intervals were calculated using SPSS version 25 based on a single measurement, absolute-agreement, two-way mixed-effects model. The formula used for computing this ICC (McGraw and Wong, 1996) is as follows:

MSR−MSEMSR+(k−1)MSE+kn(MSC−MSE)

where MSR is the mean square for rows, MSC is the mean square of columns, MSE is the mean square for error, k is the number of measurements, and n is the number of subjects.

We also created Bland and Altman plots which provide a visual assessment of the agreement of the two time-points (test and retest) of each measure in all four fiber bundles bilaterally (Bland and Altman, 1999). The created graphs are scatter plots with the Y axis representing the difference between the measurements at the two timepoints and the X axis representing the mean of these measures. Good agreement between measurements at two time-points exists if 95% of the data falls within ± 2 standard-deviations of the mean of differences.

Results

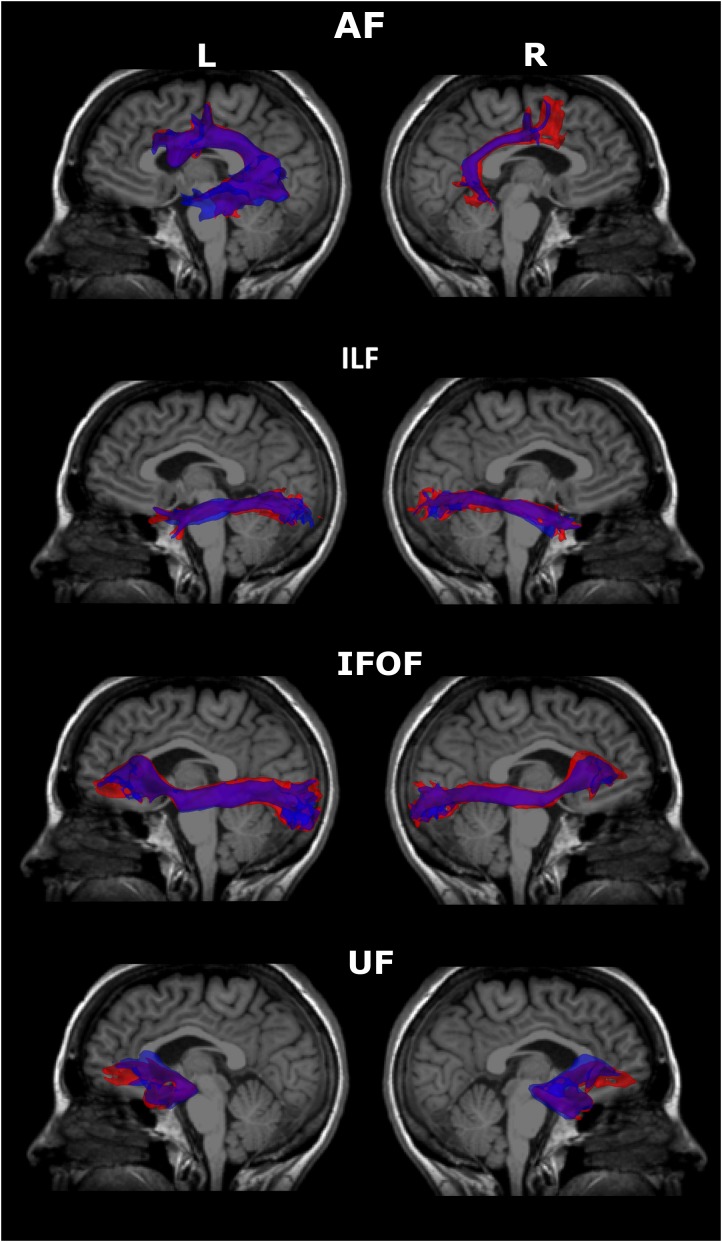
The degree of overlap was good for all four reconstructed fiber bundles (AF, ILF, IFOF, and UF, bilaterally) between Time 1 and Time 2, with wDSC values ranging between 0.71 and 0.87 (values for each fiber bundle are reported in Table 1). Figure 1 illustrates the bundle overlap for a representative subject. One must note that the figure reflects the raw bundle overlap rather than the weighted overlap represented by the wDSC which gives more weight to voxels with more streamlines.

Table 1.

wDSC values, ICC estimates and their 95% confidence intervals for all measures and fiber bundles.

wDSC FA
 AD
 MD
 RD
 NuFO
 Volume
 MLS
ICC CI ICC CI ICC CI ICC CI ICC CI ICC CI ICC CI
AF
Left 0.86 0.89∗∗∗ 0.61–0.96 0.91∗∗∗ 0.78–0.97 0.91∗∗∗ 0.79–0.97 0.92∗∗∗ 0.81–0.97 0.62∗∗ 0.22–0.84 0.83∗∗∗ 0.61–0.93 0.71∗∗∗ 0.37–0.88
Right 0.83 0.85∗∗∗ 0.65–0.94 0.71∗∗∗ 0.38–0.88 0.86∗∗∗ 0.67–0.95 0.89∗∗∗ 0.73–0.96 0.68∗∗ 0.33–0.87 0.79∗∗∗ 0.52–0.92 0.87∗∗∗ 0.68–0.95
ILF
Left 0.79 0.78∗∗∗ 0.52–0.91 0.95∗∗∗ 0.86–0.98 0.95∗∗∗ 0.86–0.98 0.88∗∗∗ 0.70–0.95 0.50∗ 0.05–0.78 0.79∗∗∗ 0.53–0.91 0.84∗∗∗ 0.62–0.94
Right 0.71 0.86∗∗∗ 0.67–0.94 0.88∗∗∗ 0.70–0.95 0.90∗∗∗ 0.75–0.96 0.89∗∗∗ 0.73–0.96 0.56∗∗ 0.14–0.81 0.75∗∗∗ 0.46–0.90 0.89∗∗∗ 0.65–0.96
IFOF
Left 0.84 0.87∗∗∗ 0.70–0.95 0.89∗∗∗ 0.72–0.96 0.84∗∗∗ 0.62–0.94 0.83∗∗∗ 0.60–0.93 0.62∗∗ 0.22–0.84 0.70∗∗∗ 0.14–0.90 0.70∗∗ 0.35–0.88
Right 0.87 0.85∗∗∗ 0.65–0.94 0.92∗∗∗ 0.79–0.97 0.86∗∗∗ 0.66–0.94 0.84∗∗∗ 0.62–0.94 0.63∗∗ 0.25–0.85 0.58∗∗ 0.12–0.83 0.69∗∗ 0.33–0.87
UF
Left 0.78 0.62∗∗ 0.22–0.84 0.85∗∗∗ 0.65–0.94 0.83∗∗∗ 0.60–0.93 0.76∗∗∗ 0.45–0.90 0.61∗∗ 0.21–0.83 0.71∗∗∗ 0.38–0.88 0.68∗∗ 0.33–0.87
Right 0.83 0.74∗∗∗ 0.42–0.90 0.82∗∗∗ 0.58–0.93 0.80∗∗∗ 0.52–0.92 0.77∗∗∗ 0.48–91 0.69∗∗ 0.32–0.87 0.41∗ −0.08–0.74 0.82∗∗∗ 0.56–0.93
Open in a new tab

AF, arcuate fasciculus; ILF, inferior longitudinal fasciculus; IFOF, inferior fronto-occipital fasciculus; UF, uncinate fasciculus; FA, fractional anisotropy; AD, axial diffusivity; MD, medial diffusivity; RD, radial diffusivity; NuFO, number of fiber orientations; MLS, mean length of streamlines; wDSC, weighted dice similarity coefficient; ICC, Intra-class correlation coefficient estimates; CI, 95% confidence intervals of the ICC. ∗p < 0.05; ∗∗p < 0.01; ∗∗∗p < 0.001.

FIGURE 1.

FIGURE 1

Open in a new tab

Overlapped 3D volume representations of the reconstructed fiber bundles at the two scanning time-points in a representative subject. Please note that these do not reflect the wDSC values. Blue = time 1, red = time 2, purple indicates the overlap. AF, arcuate fasciculus; ILF, inferior longitudinal fasciculus, IFOF, inferior fronto-occipital fasciculus; uncinate fasciculus; L, Left; R, Right.

Table 1 shows the ICC estimates, their 95% confidence intervals, and p values of the diffusion measures of interest, namely FA, MD, RD, AD, NuFO, volume, and MLS. FA, AD, MD, RD, and MLS measures showed consistently good to excellent test-retest reliability (ICCs = 0.62–0.95) across all four WM fiber bundles, bilaterally. Volume showed fair reliability in the right IFOF and UF (ICC = 0.41–0.58), and good to excellent reliability in all other bundles. NuFO showed the lowest reliability; test-retest reliability was fair in the ILF bilaterally and good in all other bundles.

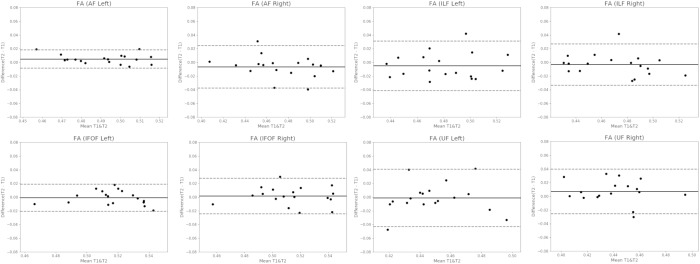
In Figure 2, we only present the Bland and Altman plots created for the FA measure for the sake of brevity and clarity. Bland–Altman analysis showed high reproducibility (95% CI = 0.019, −0.01 for the left AF; 0.025, −0.04 for the right AF; 0.03, −0.04 for the left ILF; 0.03, −0.03 for the right ILF; 0.02, −0.02 for the left IFOF; 0.03, −0.02 for the right IFOF; 0.04, −0.04 for the left UF; and 0.2, −0.2 for the right UF) with little difference (mean difference = 0.005 for the left AF, −0.006 for the right AF, −0.004 for the left ILF, −0.003 for the right ILF, −0.0008 for the left IFOF, 0.002 for the right IFOF, 0.001 for the left UF, and 0.03 for the right UF). A total of 88% (right AF, left and right UF) to 94% (Left AF, left and right ILF, left and right IFOF) of data points were within these limits. The 6 other plots are reported in the Supplementary Material. All plots were consistent with the ICC analyses.

FIGURE 2.

FIGURE 2

Open in a new tab

Bland-Altman Plots for the FA metric in all four fiber bundles, bilaterally. The Y axis represents the mean difference between the measurements at the two timepoints and the X axis represents the mean of these measures. The upper and lower dashed lines represent the two limits of agreements at ± 2 standard-deviations of the mean of differences (i.e., the 95% confidence interval). The solid line represents the mean of the differences between the two timepoints. The dots represent the individual subjects. FA, fractional anisotropy; AF, arcuate fasciculus; ILF, inferior longitudinal fasciculus; IFOF, inferior fronto-occipital fasciculus; UF, uncinate fasciculus; T1, time 1; T2, time 2.

Discussion

The aim of this study was to demonstrate the test-retest reliability of the reconstruction and micro- and macro-structural characteristics of major WM language fiber bundles using probabilistic CSD-tractography based on HARDI data. The dMRI data were obtained on a group of healthy subjects at two timepoints, spanning one week. First, the results demonstrated that all the reconstructed fiber bundles have a good overlap between the two timepoints. Secondly, tract-specific measures usually used in studying microstructural WM characteristics, such as FA, MD, RD, and AD, as well as the macrostructural measure MLS showed good to excellent test-retest reliability in the AF, ILF, IFOF, and UF, bilaterally. Volume, another macrostructural property, showed good to excellent reproducibility for some fiber bundles (AF, ILF, as well as the IFOF, and UF in the left hemisphere) but only fair reproducibility for others (IFOF and UF in the right hemisphere). NuFO showed good test-retest reliability for all fiber bundles, except the ILF which showed only fair test-retest reliability. Our results agree with and, at the same time, critically expand on previous studies that investigated the test-retest reliability of probabilistic CSD-tractography (Besseling et al., 2012; Cousineau et al., 2017). These results represent a first necessary validation protocol for longitudinal studies in research in the cognitive neuroscience of language. Assessing test-retest reliability of the reconstruction of fiber bundles and of their micro- and macro-structural measures is of paramount importance for the use of this approach in longitudinal studies, as it allows to ascertain that the observed variations truly reflect the changes that may take place in WM over time and are not due to the variability inherent to dMRI data processing, instead (Cousineau et al., 2017).

Diffusion MRI tractography is presently the only method that allows the reconstruction of WM fiber bundles in vivo. For this reason, in the last decades it has gained tremendous popularity in the field of neuroscience and its potential to map the human connectome is widely recognized. In the last years, an increasing number of big data initiatives has been developed in order to collect longitudinal dMRI data in healthy individuals with the ultimate goal to describe the changes of dMRI over the lifespan and to link these changes to cognitive performance (Howell et al., 2017). In order to fully benefit from the potential of longitudinal dMRI data, it is necessary to demonstrate the test-retest reliability of dMRI-based tractography. The present work provides critical information to investigate two important questions. When we obtain dMRI data in two separate acquisition sessions one week apart in the same subjects, using probabilistic CSD-tractography with ACT and tractometry based on HARDI data, can we 1) reconstruct overlapping WM language fiber bundles? and 2) extract similar micro-and macro-structural measure values?

Regarding the first question, our data seem to provide an affirmative response. The obtained wDSC values determining the degree of overlap of the bundles reconstructed at the two timepoints using probabilistic CSD-tractography ranged between 0.71 and 0.87. Based on the minimum value (0.70) of Dice found in the two studies which used this metric to assess the test-retest reliability of CSD-based reconstruction of WM tracts (Besseling et al., 2012; Cousineau et al., 2017), our wDSC values indicate that all the fiber bundles investigated in the present study have good test-retest reliability. In addition, our wDSC values are consistent with the values obtained in previous studies aimed at validating test-retest reliability of probabilistic CSD-tractography in other fiber bundles, such as the cingulum, optic radiation, and the corpus callosum (Besseling et al., 2012; Cousineau et al., 2017). We also report excellent overlap for the AF and IFOF, which is consistent with Cousineau et al. (2017) who used a similar tractography pipeline. The overlap obtained in our study is greater than what has been reported by Besseling et al. (2012) in which, in order to reconstruct the AF, they only used seed and target ROIs. Considering the complex anatomy of the AF, a tractography method allowing the use of more specific anatomical priors, as we did in the present study, might improve the reconstruction of this complex tract and thus allow for a better reproducibility of its morphology.

Our study also confirms the reproducibility of tensor metrics and MLS. Test-retest reliability of tensor metrics (FA, MD, RD, and AD) has been previously studied using DTI-based tractography (Ciccarelli et al., 2003; Heiervang et al., 2006; Danielian et al., 2010; Vollmar et al., 2010; Wang et al., 2012; Buchanan et al., 2014). However, studies using this approach have not always reported satisfactory results. For example, in one study, poor test-retest reliability was observed with AD across all studied fiber bundles (Danielian et al., 2010), whereas others reported tract-specific variability of the reproducibility of FA and MD (Wang et al., 2012). There are several sources of variability in diffusion MRI that can affect the test-retest reliability of tractography or the measures of WM structural characteristics (Danielian et al., 2010). These include, but are not limited to, partial volume effects introduced by the DTI model, bad anatomical priors, as well as potential inter- and intra-rater reliability of ROI placement in seed-based approaches for tractography (Wakana et al., 2007; Danielian et al., 2010; Cousineau et al., 2017). In the present study, we used an approach that attempts to reduce variability from these sources by using HARDI-based state-of-the-art tracking algorithms based on ACT and probabilistic tracking algorithms which have the potential to yield fuller, longer bundles that better reach the cortex (Mori and Tournier, 2014; Maier-Hein et al., 2017), novel approaches to extract the bundles from the tractogram (i.e., WMQL), as well as good anatomical priors (Conturo et al., 1999; Catani et al., 2002; Hagmann et al., 2003; Huang et al., 2004; Wakana et al., 2007). Using this approach, we were able to demonstrate good to excellent reliability of all tensor-based metrics which are the microstructural measures most commonly used in dMRI studies on language, and MLS, a macrostructural measure, in all language fiber bundles. This represents an important step towards the validation of this approach in the longitudinal study of language fiber bundles. On the other hand, the test-retest reliability of NuFO was less than good in some tracts. To the best of our knowledge, no previous study has investigated the test-retest reliability of this measure. Our results seem to encourage further longitudinal validation of this measure before adopting it in longitudinal studies. Additionally, our results for the volume, another macrostructural measure, were consistent with previous studies that reported inconsistent test-retest reliability for this measure across fiber bundles, using probabilistic CSD-tractography (Besseling et al., 2012) or DTI-based tractography (Wang et al., 2012).

Even though the present results are very promising, particularly for the tensor metrics and MLS, future studies should be designed in order to confirm our findings. First, these results should be reproduced in larger groups. Secondly, the use of CSD allows to resolve multiple fiber orientations at reasonable angles with a properly data-driven response function at lower b-values and 64 directions as in the present study (Tournier et al., 2007; Descoteaux et al., 2009; Raffelt et al., 2012). Nevertheless, utilizing multi-b-value sequences, such as b = 1000 s/mm2, b = 2000 s/mm2, b = 3000 s/mm2, or b = 1000 s/mm2, and b = 3000 s/mm2, could help to interpret the differences obtained in the present study by considering other available measures, such as intracellular, extracellular, and isotropic volume (Raffelt et al., 2012).

Conclusion

In conclusion, in an era where initiatives to collect dMRI longitudinal data are multiplying and fiber tracking is considered one of the most popular tools to follow changes in the language network over time, the question of test-retest reliability of dMRI tractography is of paramount importance. Our study provides critical evidence indicating the test-retest reliability of probabilistic CSD-tractography. As in previous studies which demonstrated test-retest reliability of TBSS or DTI-tractography (e.g., Kitamura et al., 2013; Forkel et al., 2014; Poudel et al., 2015), the present results support the use of probabilistic CSD-tractography to study language fiber bundles in longitudinal studies in healthy and clinical populations interested in language related fiber bundles.

Author Contributions

MB drafted the manuscript, contributed to the design of the study, reviewed the literature, and collected, analyzed, and interpreted the data. SB and KM designed the study, contributed to data collection, supervised data analysis and interpretation, and contributed to the drafting of the manuscript. MD contributed to the design of the study and to the development of the tractography pipeline. AD contributed to the design of the study and MRI data acquisition. CB and MC helped with the data analysis. CB, MD, AB, J-CH, and SD-G developed the tractography pipeline. All authors revised the final version of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the participants who accepted to take part of this study. We also would like to thank Pamela Ross, Audrey Borgus, and Amélie Brisebois for their valuable assistance with the recruitment and testing of participants. We also thank the radiology team at Hôpital du Sacré-Coeur de Montréal (HSCM) for their support with the scanning of participants.

Funding. This work was supported by doctoral awards from the Canadian Institutes of Health Research – Frederick Banting and Charles Best Canada Graduate Scholarships and the Fonds de Recherche du Québec – Santé (FRQS) in partnership with Heart and Stroke Foundation – Québec to MB (Grant Number: N.A.). SB and KM hold a Career Award from FRQS (Grant Number: N.A.). This work was also supported by grants from Réseau Québécois de la Recherche sur le Vieillissement (RQRV) to SB (Grant Number: N.A.), Heart and Stroke Foundation of Canada to SB and KM (Grant Number: G-16-00014039), the National Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant Program (Grant Number: RGPIN-2015-05297) and the institutional Université de Sherbrooke Research Chair in Neuroinformatics to MD (Grant Number: N.A.).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2018.01055/full#supplementary-material

Click here for additional data file. (1.7MB, pdf)
Click here for additional data file. (667.3KB, DOCX)
Click here for additional data file. (664.1KB, DOCX)

References

  1. Alexander A. L., Lee J. E., Lazar M., Field A. S. (2007). Diffusion tensor imaging of the brain. Neurotherapeutics 4 316–329. 10.1016/j.nurt.2007.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alexander D. C., Barker G. J., Arridge S. R. (2002). Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data. Magn. Reson. Med. 48 331–340. 10.1002/mrm.10209 [DOI] [PubMed] [Google Scholar]
  3. Asaridou S. S., Demir-Lira O. E., Goldin-Meadow S., Small S. L. (2017). The pace of vocabulary growth during preschool predicts cortical structure at school age. Neuropsychologia 98 13–23. 10.1016/j.neuropsychologia.2016.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Behrens T. E. J., Berg H. J., Jbabdi S., Rushworth M. F. S., Woolrich M. W. (2007). Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? NeuroImage 34 144–155. 10.1016/j.neuroimage.2006.09.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berchtold A. (2016). Test-retest: agreement or reliability? Methodol. Innovat. 9 1–7. 10.1177/2059799116672875 [DOI] [Google Scholar]
  6. Besseling M. H., Jansen J. F., Overvliet G. M., Vaessen M. J., Braakman H. M., Hofman P. A., et al. (2012). Tract specific reproducibility of tractography based morphology and diffusion metrics. PLoS One 7:e34125. 10.1371/journal.pone.0034125 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Birn R., Molloy E., Patriat R., Parker T., Meier T., Kirk G., et al. (2013). The effect of scan length on the reliability of resting-state fMRI connectivity estimates. NeuroImage 83 550–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bisdas S., Bohning D. E., Besenski N., Nicholas J. S., Rumboldt Z. (2008). Reproducibility, interrater agreement, and age-related changes of fractional anisotropy measures at 3T in healthy subjects: effect of the applied b-value. AJNR 29 1128–1133. 10.3174/ajnr.A1044 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bland J. M., Altman D. G. (1999). Measuring agreement in method comparison studies. Stat. Methods Med. Res. 8 135–160. 10.1177/096228029900800204 [DOI] [PubMed] [Google Scholar]
  10. Brauer J., Anwander A., Friederici A. D. (2011). Neuroanatomical prerequisites for language functions in the maturing brain. Cerebral Cortex 21 459–466. 10.1093/cercor/bhq108 [DOI] [PubMed] [Google Scholar]
  11. Brauer J., Anwander A., Perani D., Friederici A. D. (2013). Dorsal and ventral pathways in language development. Brain Lang. 127 289–295. 10.1016/j.bandl.2013.03.001 [DOI] [PubMed] [Google Scholar]
  12. Braun U., Plichta M. M., Esslinger C., Sauer C., Haddad L., Grimm O., et al. (2012). Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. NeuroImage 59 1404–1412. 10.1016/j.neuroimage.2011.08.044 [DOI] [PubMed] [Google Scholar]
  13. Buchanan C. R., Pernet C. R., Gorgolewski K. J., Storkey A. J., Bastin M. E. (2014). NeuroImage Test – retest reliability of structural brain networks from diffusion MRI. NeuroImage 86 231–243. 10.1016/j.neuroimage.2013.09.054 [DOI] [PubMed] [Google Scholar]
  14. Catani M., Howard R. J., Pajevic S., Jones D. K. (2002). Virtual in vivo interactive dissection of white matter fasciculi in the human brain. NeuroImage 17 77–94. 10.1006/nimg.2002.1136 [DOI] [PubMed] [Google Scholar]
  15. Catani M., Mesulam M. (2008). The arcuate fasciculus and the disconnection theme in language and aphasia: history and current state. Cortex 44953–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Catani M., Thiebaut de Schotten M. (2008). A diffusion tensor imaging tractography atlas for virtual in vivo dissections. Cortex 44 1105–1132. 10.1016/j.cortex.2008.05.004 [DOI] [PubMed] [Google Scholar]
  17. Catani M., Thiebaut de Schotten M. (2012). Atlas of Human Brain Connections. New York, NY: Oxford University Press. [Google Scholar]
  18. Chow H. M., Chang S.-E. (2017). White matter developmental trajectories associated with persistence and recovery of childhood stuttering. Hum. Brain Mapp. 10.1002/hbm.23590 [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ciccarelli O., Parker G. J. M., Toosy A. T., Wheeler-Kingshott C. A. M., Barker G. J., Boulby P. A., et al. (2003). From diffusion tractography to quantitative white matter tract measures: a reproducibility study. NeuroImage 18 348–359. 10.1016/S1053-8119(02)00042-3 [DOI] [PubMed] [Google Scholar]
  20. Cole J. H., Farmer R. E., Rees E. M., Johnson H. J., Frost C., Scahill R. I., et al. (2014). Test-retest reliability of diffusion tensor imaging in huntington’s disease. PLoS Curr. 6 1-20. 10.1371/currents.hd.f19ef63fff962f5cd9c0e88f4844f43b [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Conturo T. E., Lori N. F., Cull T. S., Akbudak E., Snyder A. Z., Shimony J. S., et al. (1999). Tracking neuronal fiber pathways in the living human brain. Proc. Natl. Acad. Sci. U.S.A 96 10422–10427. 10.1073/pnas.96.18.10422 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Côté M. A., Garyfallidis E., Larochelle H., Descoteaux M. (2015). “Cleaning up the mess: tractography outlier removal using hierarchical quickbundles clustering,” in Proceedings of the ISMRM Vol. 23 Toronto, 2844. [Google Scholar]
  23. Côté M. A., Girard G., Boré A., Garyfallidis E., Houde J. C., Descoteaux M. (2013). Tractometer: towards validation of tractography pipelines. Med. Image Anal. 17 844–857. 10.1016/j.media.2013.03.009 [DOI] [PubMed] [Google Scholar]
  24. Cousineau M., Jodoin P., Garyfallidis E., Côté M., Morency F. C., Rozanski V., et al. (2017). A test-retest study on Parkinson ’ s PPMI dataset yields statistically signi fi cant white matter fascicles. NeuroImage 16 222–233. 10.1016/j.nicl.2017.07.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Dale A. M., Fischl B., Sereno M. I. (1999). Cortical surface-based analysis. NeuroImage 194 179–194. 10.1006/nimg.1998.0395 [DOI] [PubMed] [Google Scholar]
  26. Danielian L. E., Iwata N. K., Thomasson D. M., Kay M. (2010). Reliability of fiber tracking measurements in diffusion tensor imaging for longitudinal study. NeuroImage 49 1572–1580. 10.1016/j.neuroimage.2009.08.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dell’Acqua F. D., Simmons A., Williams S. C. R., Catani M. (2013). Can spherical deconvolution provide more information than fiber orientations? Hindrance modulated orientational anisotropy, a true-tract specific index to characterize white matter diffusion. Hum. Brain Mapp. 34 2464–2483. 10.1002/hbm.22080 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Descoteaux M. (2015). “High angular resolution diffusion imaging (HARDI),” in Wiley Encyclopedia of Electrical and Electronics Engineering, ed. Webster J. G. (Hoboken, NJ: Wiley; ). [Google Scholar]
  29. Descoteaux M., Angelino E., Fitzgibbons S., Deriche R. (2007). Regularized, fast, and robust analytical Q-ball imaging. Magn. Reson. Med. 58 497–510. 10.1002/mrm.21277 [DOI] [PubMed] [Google Scholar]
  30. Descoteaux M., Deriche R. (2008). Mapping neuronal fiber crossings in the human brain. SPIE Newsroom. 22158128 [Google Scholar]
  31. Descoteaux M., Deriche R., Knösche T. R., Anwander A. (2009). Deterministic and probabilistic tractography based on complex fibre orientation distributions. IEEE Trans. Med. Imaging 28 269–286. 10.1109/TMI.2008.2004424 [DOI] [PubMed] [Google Scholar]
  32. Desikan R. S., Ségonne F., Fischl B., Quinn B. T., Dickerson B. C., Blacker D., et al. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage 31 968–980. 10.1016/j.neuroimage.2006.01.021 [DOI] [PubMed] [Google Scholar]
  33. Dice L. R. (1945). Measures of the amount of ecologic association between species. Ecology 26 297–302. 10.2307/1932409 [DOI] [Google Scholar]
  34. Dick A. S., Bernal B., Tremblay P. (2014). The language connectome: new pathways, new concepts. Neuroscientist 20 453–467. 10.1177/1073858413513502 [DOI] [PubMed] [Google Scholar]
  35. Duan F., Zhao T., He Y., Shu N. (2015). Test-retest reliability of diffusion measures in cerebral white matter: a multiband diffusion MRI study. J. Magn. Reson. Imaging 42 1106–1116. 10.1002/jmri.24859 [DOI] [PubMed] [Google Scholar]
  36. Duda J. T., Cook P. A., Gee J. C. (2014). Reproducibility of graph metrics of human brain structural networks. Front. Neuroinform. 8:46. 10.3389/fninf.2014.00046 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Duffau H. (2008). The anatomo-functional connectivity of language revisited. New insights provided by electrostimulation and tractography. Neuropsychologia 46 927–934. 10.1016/j.neuropsychologia.2007.10.025 [DOI] [PubMed] [Google Scholar]
  38. Duffau H., Capelle L., Sichez N., Denvil D., Lopes M., Sichez J.-P., et al. (2002). Intraoperative mapping of the subcortical language pathways using direct stimulations. An anatomo-functional study. Brain 125(Pt 1), 199–214. 10.1093/brain/awf016 [DOI] [PubMed] [Google Scholar]
  39. Duffau H., Gatignol P., Denvil D., Lopes M., Capelle L. (2003). The articulatory loop: study of the subcortical connectivity by electrostimulation. Neuroreport 14 2005–2008. 10.1097/01.wnr.0000094103.16607.9f [DOI] [PubMed] [Google Scholar]
  40. Duffau H., Gatignol P., Mandonnet E., Peruzzi P., Tzourio-Mazoyer N., Capelle L. (2005). New insights into the anatomo-functional connectivity of the semantic system: a study using cortico-subcortical electrostimulations. Brain 128 797–810. 10.1093/brain/awh423 [DOI] [PubMed] [Google Scholar]
  41. Duffau H., Moritz-Gasser S., Mandonnet E. (2014). A re-examination of neural basis of language processing: proposal of a dynamic hodotopical model from data provided by brain stimulation mapping during picture naming. Brain Lang. 131 1–10. 10.1016/j.bandl.2013.05.011 [DOI] [PubMed] [Google Scholar]
  42. Dyrby T. B., Lundell H., Burke M. W., Reislev N. L., Paulson O. B., Ptito M., et al. (2014). Interpolation of diffusion weighted imaging datasets. NeuroImage 103 202–213. 10.1016/j.neuroimage.2014.09.005 [DOI] [PubMed] [Google Scholar]
  43. Farquharson S., Tournier J.-D. (2016). “High angular resolution diffusion imaging,” in Diffusion Tensor Imaging, eds W. Van Hecke, Emsell L., Sunaert S. (New York, NY: Springer; ), 383–406. 10.1007/978-1-4939-3118-7 [DOI] [Google Scholar]
  44. Farrell J. A. D., Landman B. A., Jones C. K., Smith S. A., Prince J. L., Van Zijl P. C. M., et al. (2007). Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5T. J. Magn. Reson. Imaging 26 756–767. 10.1002/jmri.21053 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Fleiss J. L. (2003). “The measurement of interrater agreement,” in Statistical Methods for Rates and Proportions, eds Fleiss J. L., Levin B., Paik M. C. (New Jersey, NY: John Wiley & Sons Inc.), 598–626. [Google Scholar]
  46. Forkel S. J., De Schotten M. T., Dell’Acqua F., Kalra L., Murphy D. G. M., Williams S. C. R., et al. (2014). Anatomical predictors of aphasia recovery: a tractography study of bilateral perisylvian language networks. Brain 137 2027–2039. 10.1093/brain/awu113 [DOI] [PubMed] [Google Scholar]
  47. Frank L. R. (2001). Anisotropy in high angular resolution diffusion-weighted MRI. Magn. Reson. Med. 45 935–939. 10.1002/mrm.1125 [DOI] [PubMed] [Google Scholar]
  48. Friederici A. D., Bahlmann J. R., Heim S., Schubotz R. I, Anwander A. (2006). The brain differentiates human and non-human grammars: functional localization and structural connectivity. Proc. Natl. Acad. Sci. 103 2458–2463. 10.1073/pnas.0509389103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Gao W., Zhu H., Lin W. (2009). An unified optimization approach for diffusion tensor imaging technique. NeuroImage 44 729–741. 10.2217/nnm.12.167.Gene [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Gil-Robles S., Carvallo A., Jimenez M. D. M., Gomez Caicoya A., Martinez R., Ruiz-Ocaña C., et al. (2013). Double dissociation between visual recognition and picture naming: a study of the visual language connectivity using tractography and brain stimulation. Neurosurgery 72 678–686. 10.1227/NEU.0b013e318282a361 [DOI] [PubMed] [Google Scholar]
  51. Girard G., Descoteaux M. (2012). “Anatomical tissue probability priors for tractography,” in Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI’12) - Computational Diffusion MRI Workshop, Nice, 174–185. [Google Scholar]
  52. Girard G., Fick R., Descoteaux M., Deriche R., Wassermann D. (2015). AxTract: microstructure-driven tractography based on the ensemble average propagator. Inf. Proc. Med. Imaging 24 675–686. 10.1007/978-3-319-19992-4_53 [DOI] [PubMed] [Google Scholar]
  53. Girard G., Whittingstall K., Deriche R., Descoteaux M. (2014). Towards quantitative connectivity analysis: reducing tractography biases. NeuroImage 98 266–278. 10.1016/j.neuroimage.2014.04.074 [DOI] [PubMed] [Google Scholar]
  54. Grossman M., McMillan C., Moore P., Ding L., Glosser G., Work M., et al. (2004). What’s in a name: voxel-based morphometric analyses of MRI and naming difficulty in Alzheimer’s disease, frontotemporal dementia and corticobasal degeneration. Brain 127 628–649. 10.1093/brain/awh075 [DOI] [PubMed] [Google Scholar]
  55. Guevara P., Duclap D., Rivière D., Cointepas Y., Poupon C., Mangin J. (2011). “Accurate tractography propagation mask using T1-weighted data rather than FA,” in Proceedings of the 19th Scientific Meeting International Society for Magnetic Resonance in Medicine, Montreal, QC. [Google Scholar]
  56. Guyatt G., Walter S., Norman G. (1987). Measuring change over time: assessing the usefulness of evaluative instruments. J. Chron. Disord. 40 171–178. 10.1016/0021-9681(87)90069-5 [DOI] [PubMed] [Google Scholar]
  57. Hagmann P., Thiran J. P., Jonasson L., Vandergheynst P., Clarke S., Maeder P., et al. (2003). DTI mapping of human brain connectivity: statistical fibre tracking and virtual dissection. NeuroImage 19 545–554. 10.1016/S1053-8119(03)00142-3 [DOI] [PubMed] [Google Scholar]
  58. Han Z., Ma Y., Gong G., He Y., Caramazza A., Bi Y. (2013). White matter structural connectivity underlying semantic processing: evidence from brain damaged patients. Brain 136 2952–2965. 10.1093/brain/awt205 [DOI] [PubMed] [Google Scholar]
  59. Heiervang E., Behrens T. E. J., Mackay C. E., Robson M. D., Johansen-Berg H. (2006). Between session reproducibility and between subject variability of diffusion MR and tractography measures. NeuroImage 33 867–877. 10.1016/j.neuroimage.2006.07.037 [DOI] [PubMed] [Google Scholar]
  60. Hickok G., Poeppel D. (2000). Towards a functional neuroanatomy of speech perception. Trends Cogn. Sci. 4 131–138. 10.1016/S1364-6613(00)01463-7 [DOI] [PubMed] [Google Scholar]
  61. Hickok G., Poeppel D. (2007). The cortical organization of speech processing. Nat. Rev. 8 393–402. 10.1038/nrn2113 [DOI] [PubMed] [Google Scholar]
  62. Howell B. R., Styner M. A., Gao W., Yap P. T., Wang L., Baluyot K., et al. (2017). The UNC/UMN baby connectome project (BCP): an overview of the study design and protocol development. NeuroImage 185 891–905. 10.1016/j.neuroimage.2018.03.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Huang H., Zhang J., van Zijl P. C. M., Mori S. (2004). Analysis of noise effects on DTI-based tractography using the brute-force and multi-ROI approach. Magn. Reson. Med. 52 559–565. 10.1002/mrm.20147 [DOI] [PubMed] [Google Scholar]
  64. Jenkinson M., Beckmann C. F., Behrens T. E. J., Woolrich M. W., Smith S. M. (2012). FSL. NeuroImage 62 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
  65. Jeurissen B., Descoteaux M., Mori S., Leemans A. (2017). Diffusion MRI fiber tractography of the brain. NMR Biomed. 10.1002/nbm.3785 [Epub ahead of print]. [DOI] [PubMed] [Google Scholar]
  66. Jeurissen B., Leemans A., Tournier J.-D., Jones D. K., Sijbers J. (2010). Estimating the Number of Fiber Orientations in Diffusion MRI Voxels: a Constrained Spherical Deconvolution Study. Available at: http://cds.ismrm.org/protected/10MProceedings/files/573_808.pdf [Google Scholar]
  67. Jeurissen B., Tournier J. D., Dhollander T., Connelly A., Sijbers J. (2014). Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage 103 411–426. 10.1016/j.neuroimage.2014.07.061 [DOI] [PubMed] [Google Scholar]
  68. Jones D. K. (2004). The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a monte carlo study. Magn. Reson. Med. 51 807–815. 10.1002/mrm.20033 [DOI] [PubMed] [Google Scholar]
  69. Jones D. K., Knösche T. R., Turner R. (2013). White matter integrity, fiber count, and other fallacies: the do’s and don’ts of diffusion MRI. NeuroImage 73 239–254. 10.1016/j.neuroimage.2012.06.081 [DOI] [PubMed] [Google Scholar]
  70. Jovicich J., Czanner S., Han X., Salat D., Van Der Kouwe A., Quinn B., et al. (2009). MRI-derived measurements of human subcortical, ventricular and intracranial brain volumes: reliability effects of scan sessions, acquisition sequences, data analyses, scanner upgrade, scanner vendors and field strengths. NeuroImage 46 177–192. 10.1016/j.neuroimage.2009.02.010.MRI-derived [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Kitamura S., Kiuchi K., Taoka T. (2013). Longitudinal white matter changes in Alzheimer’s disease: a tractography-based analysis study. Brain Res. 1515 12–18. 10.1016/j.brainres.2013.03.052 [DOI] [PubMed] [Google Scholar]
  72. Kristo G., Leemans A., Raemaekers M., Rutten G. J., De Gelder B., Ramsey N. F. (2013). Reliability of two clinically relevant fiber pathways reconstructed with constrained spherical deconvolution. Magn. Reson. Med. 70 1544–1556. 10.1002/mrm.24602 [DOI] [PubMed] [Google Scholar]
  73. Lam B. Y. K., Halliday G. M., Irish M., Hodges J. R., Piguet O. (2014). Longitudinal white matter changes in frontotemporal dementia subtypes. Hum. Brain Mapp. 35 3547–3557. 10.1002/hbm.22420 [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Lin Q., Dai Z., Xia M., Han Z., Huang R., Gong G., et al. (2015). A connectivity-based test-retest dataset of multi-modal magnetic resonance imaging in young healthy adults. Sci. Data 2:150056. 10.1038/sdata.2015.56 [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Lu L. H., Crosson B., Nadeau S. E., Heilman K. M., Gonzalez-Rothi L. J., Raymer A., et al. (2002). Category-specific naming deficits for objects and actions: semantic attribute and grammatical role hypotheses. Neuropsychologia 40 1608–1621. 10.1016/S0028-3932(02)00014-3 [DOI] [PubMed] [Google Scholar]
  76. Madan C. R., Kensinger E. A. (2017). Test–retest reliability of brain morphology estimates. Brain Inf. 4 107–121. 10.1007/s40708-016-0060-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Magnotta V. A., Matsui J. T., Liu D., Johnson H. J., Long J. D., Bolster B. D., et al. (2012). MultiCenter reliability of diffusion tensor imaging. Brain Connect. 2 345–355. 10.1089/brain.2012.0112 [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Maier-Hein K. H., Neher P. F., Houde J. C., Côté M. A., Garyfallidis E., Zhong J., et al. (2017). The challenge of mapping the human connectome based on diffusion tractography. Nat. Comm. 8:1349. 10.1038/s41467-017-01285-x [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Mandelli M. L., Vilaplana E., Brown J. A., Hubbard H. I., Binney R. J., Attygalle S., et al. (2016). Healthy brain connectivity predicts atrophy progression in non-fluent variant of primary progressive aphasia. Brain 139(Pt 10), 2778–2791. 10.1093/brain/aww195 [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Manjo V., Concha L., Buades A., Collins D. L. (2013). Diffusion weighted image denoising using overcomplete local PCA. PLoS One 8:e73021. 10.1371/journal.pone.0073021 [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. McGraw K., Wong S. (1996). Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1 30–46. 10.1037/1082-989X.1.1.30 [DOI] [Google Scholar]
  82. Mori S., Tournier J.-D. (2014). Introduction to Diffusion Tensor Imaging and Higher-Order Models. Oxford: Academic Press. [Google Scholar]
  83. Pfefferbaum A., Adalsteinsson E., Sullivan E. V. (2003). Replicability of diffusion tensor imaging measurements of fractional anisotropy and trace in brain. J. Magn. Reson. Imaging 433 427–433. 10.1002/jmri.10377 [DOI] [PubMed] [Google Scholar]
  84. Poeppel D., Emmorey K., Hickok G., Pylkkänen L. (2012). Towards a new neurobiology of language. J. Neurosci. 32 14125–14131. 10.1523/JNEUROSCI.3244-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
  85. Poudel G. R., Stout J. C., Domínguez D. J. F., Churchyard A., Chua P., Egan G. F., et al. (2015). Longitudinal change in white matter microstructure in huntington’s disease: the IMAGE-HD study. Neurobiol. Dis. 74 406–412. 10.1016/j.nbd.2014.12.009 [DOI] [PubMed] [Google Scholar]
  86. Powers J. P., McMillan C. T., Brun C. C., Yushkevich P. A., Zhang H., Gee J. C., et al. (2013). White matter disease correlates with lexical retrieval deficits in primary progressive aphasia. Front. Neurol. 4:212. 10.3389/fneur.2013.00212 [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Prckovska V., Descoteaux M., Poupon C., ter Haar Romeny B. M., Vilanova A. (2012). “Classification study of DTI and HARDI anisotropy measures for HARDI data simplification,” in New Developments in the Visualization and Processing of Tensor Fields, (Berlin: Springer; ), 1–23. [Google Scholar]
  88. Raffelt D., Tournier J., Rose S., Ridgway G. R., Henderson R., Crozier S., et al. (2012). Apparent fibre density: a novel measure for the analysis of diffusion-weighted magnetic resonance images. NeuroImage 59 3976–3994. 10.1016/j.neuroimage.2011.10.045 [DOI] [PubMed] [Google Scholar]
  89. Saur D., Kreher B. W., Schnell S., Kümmerer D., Kellmeyer P., Vry M.-S., et al. (2008). Ventral and dorsal pathways for language. Proc. Natl. Acad. Sci. U.S.A. 105 18035–18040. 10.1073/pnas.0805234105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  90. Seiger R., Hahn A., Hummer A., Kranz G. S., Ganger S., Küblböck M., et al. (2015). Voxel-based morphometry at ultra-high fields. A comparison of 7T and 3T MRI data. NeuroImage 113 207–216. 10.1016/j.neuroimage.2015.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Seunarine K. K., Alexander D. C. (2009). “Multiple fibers: beyond the diffusion tensor,” in Diffusion MRI: From Quantitative Measurements to in Vivo Neuroanatomy, 2nd Edn, eds Johansen-Berg H., Behrens T. E. J. (London: Academic Press; ), 105–123. [Google Scholar]
  92. Shrout P. E., Fleiss J. L. (1979). Intraclass correlations: uses in assessing rater reliability.1. Shrout PE, Fleiss JL: intraclass correlations: uses in assessing rater reliability. Psychol. Bull. 86 420–428. 10.1037/0033-2909.86.2.420 [DOI] [PubMed] [Google Scholar]
  93. Smith R. E., Tournier J., Calamante F., Connelly A. (2012). Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage 62 1924–1938. 10.1016/j.neuroimage.2012.06.005 [DOI] [PubMed] [Google Scholar]
  94. Takeuchi H., Taki Y., Hashizume H., Asano K., Asano M., Sassa Y., et al. (2016). Impact of reading habit on white matter structure: cross-sectional and longitudinal analyses. NeuroImage 133 378–389. 10.1016/j.neuroimage.2016.03.037 [DOI] [PubMed] [Google Scholar]
  95. Thiebaut de Schotten M., Dell’Acqua F., Valabregue R., Catani M. (2012). Monkey to human comparative anatomy of the frontal lobe association tracts. Cortex 48 82–96. 10.1016/j.cortex.2011.10.001 [DOI] [PubMed] [Google Scholar]
  96. Tournier J. D., Calamante F., Connelly A. (2012a). MRtrix: diffusion tractography in crossing fiber regions. Int. J. Imaging Syst. Technol. 22 53–66. 10.1002/ima.22005 29845009 [DOI] [Google Scholar]
  97. Tournier J. D., Masterton R. A. J., Seitz R. J. (2012b). “Imaging techniques provide new insights,” in Stroke Rehabilitation: Insights from Neuroscience and Imaging, ed. Carey L. M. (New York, NY: Oxford University Press; ), 35–53. [Google Scholar]
  98. Tournier J. D., Calamante F., Connelly A. (2007). Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. NeuroImage 35 1459–1472. 10.1016/j.neuroimage.2007.02.016 [DOI] [PubMed] [Google Scholar]
  99. Tuch D. S., Reese T. G., Wiegell M. R., Makris N., Belliveau J. W., Wedeen V. J. (2002). High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn. Reson. Med. 48 577–582. 10.1002/mrm.10268 [DOI] [PubMed] [Google Scholar]
  100. Turken A. U., Dronkers N. F. (2011). The neural architecture of the language comprehension network: converging evidence from lesion and connectivity analyses. Front. Syst. Neurosci. 5:1. 10.3389/fnsys.2011.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  101. Tustison N. J., Cook P. A., Klein A., Song G., Das S. R., Duda J. T., et al. (2014). Large-scale evaluation of ANTs and FreeSurfer cortical thickness measurements. NeuroImage 99 166–179. 10.1016/j.neuroimage.2014.05.044 [DOI] [PubMed] [Google Scholar]
  102. Vollmar C., Muircheartaigh J. O., Barker G. J., Symms M. R., Thompson P., Kumari V., et al. (2010). Identical, but not the same: intra-site and inter-site reproducibility of fractional anisotropy measures on two 3. 0 T scanners. NeuroImage 51 1384–1394. 10.1016/j.neuroimage.2010.03.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
  103. Wakana S., Caprihan A., Panzenboeck M. M., Fallon J. H., Perry M., Gollub R. L., et al. (2007). Reproducibility of quantitative tractography methods applied to cerebral white matter. NeuroImage 36 630–644. 10.1016/j.neuroimage.2007.02.049 [DOI] [PMC free article] [PubMed] [Google Scholar]
  104. Wang H., Jin X., Zhang Y., Wang J. (2016). Single-subject morphological brain networks: connectivity mapping, topological characterization and test-retest reliability. Brain Behav. 6 1–21. 10.1002/brb3.448 [DOI] [PMC free article] [PubMed] [Google Scholar]
  105. Wang J. Y., Abdi H., Bakhadirov K., Diaz-arrastia R., Devous M. D. (2012). A comprehensive reliability assessment of quantitative diffusion tensor tractography. NeuroImage 60 1127–1138. 10.1016/j.neuroimage.2011.12.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
  106. Wassermann D., Makris N., Rathi Y., Shenton M., Kikinis R., Kubicki M., et al. (2016). The white matter query language: a novel approach for describing human white matter anatomy. Brain Struct. Funct. 221 4705–4721. 10.1007/s00429-015-1179-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  107. Wilson S. M., Galantucci S., Tartaglia M. C., Rising K., Patterson D. K., Henry M. L., et al. (2011). Syntactic processing depends on dorsal language tracts. Neuron 72 397–403. 10.1016/j.neuron.2011.09.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  108. Zhang H., Chen X., Zhang Y., Shen D. (2017). Test-retest reliability of “high-order” functional connectivity in young healthy adults. Front. Neurosci. 11:439 10.3389/fnins.2017.00439 [DOI] [PMC free article] [PubMed] [Google Scholar]
  109. Zhang H., Zhang Y.-J., Duan L., Ma S.-Y., Lu C.-M., Zhu C.-Z. (2011). Is resting-state functional connectivity revealed by functional near-infrared spectroscopy test-retest reliable? J. Biomed. Optics 16 67008–67009. 10.1117/1.3591020 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1.7MB, pdf)
Click here for additional data file. (667.3KB, DOCX)
Click here for additional data file. (664.1KB, DOCX)

Articles from Frontiers in Neuroscience are provided here courtesy of Frontiers Media SA

RESOURCES