Conformations of an RNA Helix-Junction-Helix Construct Revealed by SAXS Refinement of MD Simulations

Abstract

RNA is involved in a broad range of biological processes that extend far beyond translation. Many of RNA’s recently discovered functions rely on folding to a specific conformation or transitioning between conformations. The RNA structure contains rigid, short basepaired regions connected by more flexible linkers. Studies of model constructs such as small helix-junction-helix (HJH) motifs are useful in understanding how these elements work together to determine RNA conformation. Here, we reveal the full ensemble of solution structures assumed by a model RNA HJH. We apply small-angle x-ray scattering and an ensemble optimization method to selectively refine models generated by all-atom molecular dynamics simulations. The expectation of a broad distribution of helix orientations, at and above physiological ionic strength, is not met. Instead, this analysis shows that the HJH structures are dominated by two distinct conformations at moderate to high ionic strength. Atomic structures, selected from the molecular dynamics simulations, reveal strong base-base interactions in the junction that critically constrain the conformational space available to the HJH molecule and lead to a surprising re-extension at high salt. These results are corroborated by comparison with previous single-molecule fluorescence resonance energy transfer experiments on the same constructs.

Introduction

RNAs perform complex biological functions in cells and viruses ranging from gene expression (1, 2, 3, 4) through enzymatic activities (5, 6, 7, 8). This wide array of functions is partially enabled by RNA’s intrinsic flexibility, which provides ready access to different conformations (9, 10, 11). As a direct result of structural studies that elucidate RNA conformations (12, 13, 14, 15), there has been increasing interest in pharmaceutical applications for functional RNA molecules (16, 17, 18, 19). Because of RNA’s hierarchically organized structures, identifying the roles of individual RNA structural elements has been an effective lens for visualizing RNA folding pathways (20). In this spirit, we have been exploring the salt dependent conformations of a simple RNA system containing two short duplexes joined by a single strand of RNA: an RNA helix-junction-helix (HJH) construct.

Naively, one might expect a continuous change in the conformation of this model system as a function of increasing [KCl] because both the screening length of the ionic cloud around the helices and the linker stiffness decrease with added salt (21). Surprisingly, previous studies of the HJH system by single-molecule fluorescence resonance energy transfer (smFRET) showed a nonmonotonic energy transfer (E_FRET) with increasing KCl concentrations (22), suggesting that the dyes attached to the two helices do not report a continuous molecular collapse as the salt concentration increases (23). From FRET studies carried out with different constructs, we arrived at the following qualitative explanation of the measured salt dependence: repulsion between helices determines conformations at low salt, junction sequence determines conformation at high salt, and these effects compete at moderate (close to physiological) salt.

A quantitative interpretation of FRET data is challenging if multiple, interconverting conformations of a flexible system simultaneously contribute to the signal. The energy transfer efficiency, E_FRET, represents a temporal average over all the conformations visited during a measurement. Multiple states in an ensemble cannot be distinguished if the duration of one FRET event (10–100 μs) exceeds the typical dwell time of a state. Thus, additional measurements are required to assess the makeup of the structural ensemble and, for the HJH construct, to explain the measured nonmonotonic trends.

The global size, shape, and composition of this HJH construct make it a suitable system to study by small angle x-ray scattering (SAXS) and all-atom molecular dynamics (MD) simulations. SAXS reports global structural properties such as radius of gyration (R_g), pair-distance distribution function (P(r)), and maximal distance of atom pairs (D_max). The SAXS profile is largely determined by the relative position and orientation of the more electron-dense, rigid RNA helices (24, 25), which dominate the measured scattering signal. In addition, this simple HJH construct is also an ideal target for MD simulations. However, because there are numerous uncertainties in simulations, including force fields and sampling convergence, verification of MD results and enhancements of their accuracy as needed are essential. This is especially critical for RNA, for which force-field inaccuracies are well documented (26, 27, 28).

The accurate coupling of experiments and simulations for ensemble determination is a major goal for structural biology studies (29). Empirical energies are used in conjunction with simulations to find conformations that satisfy experimental, chemical, and geometrical constraints. In typical applications, terms that penalize deviations from experimental values are added to the simulation force fields, and simulations are conducted to find minimal energy or free-energy structures (30). MD simulations are especially needed when the experimental data are sparse and not complete enough to determine a tight set of conformations, but even sparse data can still be used to bias the MD simulations toward more consistent shapes. Of course, a goal in the MD field is to create increasingly reliable simulations and to make progress in force-field parametrization and enhanced sampling techniques. Ideally, simulations will provide useful information on the system geometry and behavior even without the experimental input.

An intermediate mode of coupling between experiment and simulation is to conduct simulations without an experimental bias but to use experimental data to select a subset of the MD structures that is consistent with the empirical observations. A disadvantage of this procedure is that significant flaws in MD setup will be hard to correct, i.e., no or a very few structures will be obtained that satisfy the experimental observables. This result may significantly reduce the statistics and the reliability of the proposed approach. The advantage of using MD without bias is that the same simulations can be used for a variety of tasks, can help to interpret more than one experiment, and can potentially predict other observables that can be probed in future experiments. We use this type of approach in this manuscript, employing an ensemble optimization method (EOM) (31) to couple MD and SAXS data. To assess the feasibility of the selected models, we compute a FRET signal from the selected structures and compare with additional measurements. EOM was introduced and recently used to investigate and interpret the folding dynamics of a small RNA (32).

We use unbiased MD simulations to generate structures for further experimental refinement by requiring agreement with measured SAXS data. In this way, we identify the conformational ensembles in which three-dimensional helix placement best recapitulates our measurements. The known orientation of these helices provides strong geometrical constraints on the junction conformations, which in turn are further constrained by interactions between its bases. The combination of SAXS and MD allows the junction conformations to be inferred.

Our results reveal a surprising salt dependence of the HJH: a bimodal, as opposed to continuous, distribution of structures is found, implying similar complexity to other RNA junction systems (33, 34). An extended state reemerges at high salt as a result of strong stacking interactions between uracil bases. Such an extension is not immediately evident from the FRET results, but with the deeper understanding of the smFRET experiment described here, including careful consideration of the ensemble nature of HJH, the SAXS and FRET results are consistent, validating our refinement scheme.

Materials and Methods

RNA HJH construct

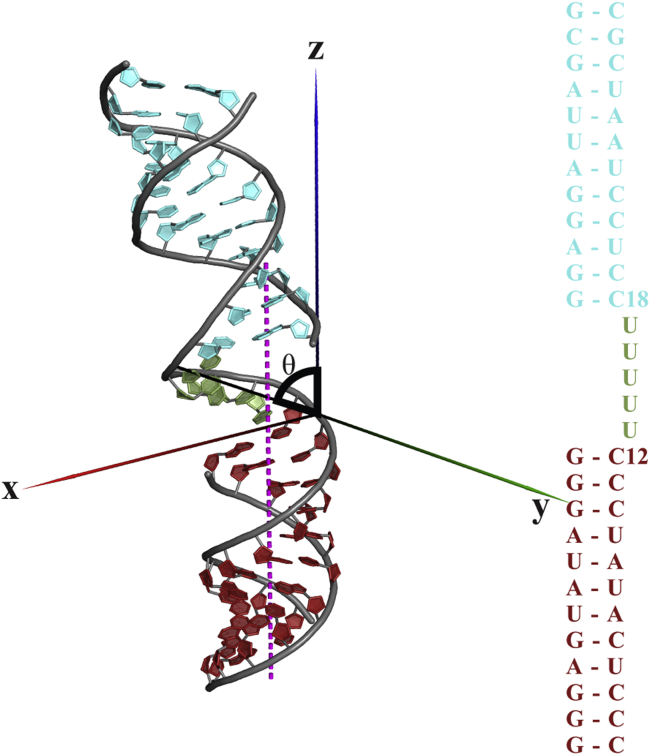
The RNA HJH contains two 12 based-paired RNA duplexes linked by a short chain of rU₅, shown in Fig. 1. The molecule is constructed by pairing a 29-nucleotide backbone with two complementary 12-nucleotide oligonucleotides at the ends. The long backbone has the same mixed sequence as in (22), CCC UAU ACU CCC UUU UUC CUC CUA AUC GC.

Figure 1.

HJH RNA construct and its sequence. The HJH molecule comprises three basic RNA elements: two 12-bp-long duplexes shown in dark and light colors, linked by an rU5 junction. The junction vector is defined by a bending angle θ between the z axis and the line joining the phosphorus atoms of C12 and C18. To see this figure in color, go online.

Sample preparation

RNA molecules were purchased desalted, protected, and high-performance-liquid-chromatography-purified from Dharmacon (Lafayette, CO). 400 μL of deprotection buffer was added to three tubes of single-stranded RNA molecules individually. The mixtures were incubated at 60°C for 30 min. All three strands were reconstituted in the annealing buffer, 10 mM potassium 3-(N-morpholino) propanesulfonic acid buffer containing 100 mM KCl and 20 μM EDTA at pH 7 using Amicon 3 kDa 0.5 mL Ultra Centrifugal Filters (EMD Millipore, Billerica, MA). 130.6 nmole of three single-stranded RNA molecules was mixed together in 200 μL annealing buffer, annealed at 92°C for 2.5 min, slowly cooled in air for 15 min to ∼35°C, and further cooled in a water bath for another 15 min to room temperature. The solution was then concentrated, and HJH construct molecules were separated from unannealed single-stranded RNA molecules by an Amicon 10 kDa 0.5 mL Ultra Centrifugal Filter. The concentrated HJH sample was divided into five aliquots for buffer exchange in 30, 50, 100, 200, and 500 mM KCl with 10 mM potassium 3-(N-morpholino) propanesulfonic acid and 20 μM EDTA. Different volumes of buffer were added to bring the volume to 30 μL for SAXS measurements.

SAXS

The SAXS measurements were conducted at the Cornell High Energy Synchrotron Source (CHESS) beamline G1 using an EigerX 1M detector (Dectris AG, Switzerland) with a sample-to-detector distance of ∼1.7 m. The SAXS curves were integrated and averaged from three sets of 20 images with 10-s exposure. To achieve the optimal sample concentration without interparticle interference, 40, 80, 120, 160, and 200 μM samples were measured under all conditions. No evidence of interparticle interference was found. We selected a final RNA concentration of 80 μM with reasonable sample consumption and good SAXS signal/noise ratio without systematic interparticle interference or aggregation (see Supporting Materials and Methods; Fig. S4). The momentum transfer q is defined as q = (4π/λ) × sin(2θ/2), where λ is the x-ray wavelength and 2θ is the scattering angle. Data were collected over a q range from 0.011 to 0.295 Å⁻¹. The SAXS curves were normalized by the number of photons measured at the beamstop to account for varying beam intensity. Buffer-subtracted curves were scaled to account for any slight variations in sample concentration. We used home-written MATLAB (The MathWorks, Natick, MA) scripts for the data analysis.

EOM for SAXS

In solution, flexible molecules visit a large number of conformations. A single SAXS profile reports the time-averaged scattering curve from the different instantaneous molecular states within the measurement period. The ensemble optimization method (31, 35) fits a SAXS profile using a sum of individual states in an ensemble:

$$\begin{array}{c}\frac{1}{N}\end{array}\sum _{i=1}^N{I}_i\left(q\right)=I_{exp}\left(q\right),$$ (1)

where I_i(q) is the theoretical scattering profile of the i^th state and N is the total number of states in an ensemble or the size of an ensemble. We built multiple structural pools from MD simulations that contain plausible structures and used CRYSOL (36) to compute the theoretical scattering curves for each conformation. We did not populate the structures with ions because the increase in scattering due to the presence of these low Z partners is smaller than the error in the EOM fits (see Supporting Materials and Methods; Fig. S5). A genetic algorithm can be applied to choose different conformations from the large pool, forming an ensemble that best fits the experimental SAXS profile by minimizing

$${\chi }^2=\frac{1}{K-1}\sum _{j=1}^K{\left(\frac{\mu I\left(q_j\right)-I_{exp}\left(q_j\right)}{\sigma \left(q_j\right)}\right)}^2,$$ (2)

where I and I_exp are the ensemble and experimental SAXS profiles with K data points at certain q_j, respectively, whereas σ and μ are the experimental error and scaling constant. The genetic algorithm is implemented using the program GAJOE 2.1 (35). We used a maximal ensemble size of N = 20, different numbers of generations, and genetic algorithm cycles based on the size of pools. Constant subtraction was enabled because of different baselines of the experimental and theoretical SAXS profiles. The models chosen by GAJOE from all genetic algorithm cycles comprise the “all cycle” ensemble, and many of them are highly degenerate. The degeneracy and large ensemble size result in the difficulty of identifying the representative models. One way to significantly reduce the ensemble size is to extract models from the best genetic algorithm cycle with the smallest χ². It turns out that the models from the “best cycle” consistently reproduce the properties of the ensemble from “all cycles.” In the rest of the study, the term “ensemble” refers to the ensemble from “all cycles” if not otherwise stated. It is known that ensemble size might introduce uncertainties in the results (37), but in our case and implementation, varying ensemble sizes only yield more degenerate conformations or more selections of the same conformations. Our results hold for different ensemble sizes tested. Clustering analysis (see Supporting Materials and Methods; Figs. S1 and S2) was done to combine similar and degenerate models.

A significant challenge associated with this type of approach involves the potential for overfitting the data. Although we exercise care to use the smallest possible ensemble size that minimizes χ², we do not expect to retrieve identical results for each cycle of fitting. Instead, we seek (and find) plausible solutions consisting of clusters of similar structures that equally well recapitulate our experimental measurements. As an essential check on our findings, we validate the results of the EOM selection against an independent experimental measurement, in this case FRET.

MD simulations details

We used the Nucleic Acid Builder web server (38) to create the structure of the HJH construct in the canonical A-form, in which the 5′ and 3′ ends of the junction were respectively linked to the 3′ end of the first helix (H1) and the 5′ end of the second helix (H2). Initially, the complex was aligned along the positive z-direction. The diameter and length of H1 and H2 were ∼21 and 41 Å, respectively, in their idealized A-form. The HJH construct was solvated in a rectangular periodic box measuring 85 × 85 × 145 Å³ (3) of an aqueous solution containing monovalent K⁺ ions. The dimensions of the box were determined such that the ion cloud of the HJH construct does not overlap with their periodic images for any global conformations. The box contains ∼103,000 atoms.

Simulations were performed at eight different KCl concentrations: 30, 50, 75, 100, 200, 300, 500, and 900 mM. These target values were selected in accordance with those examined in the experiments, except for 30 mM. Below this concentration, the number of ions is too scarce for the given system size to provide reasonable statistics. An additional 50 K⁺ ions were added to the system to ensure the overall charge neutrality, which is a prerequisite for our electrostatic potential calculations. K⁺ and Cl⁻ ions were initially distributed in the solvent, randomly replacing water molecules.

Force fields were adopted from previous MD studies on isolated RNA duplexes (39, 40). The bonding and nonbonding terms were obtained by AMBER f99 (41) and OPLSAA (42), respectively. Water molecules were modeled with the TIP3P (transferable intermolecular potential with three points) force field (43) with appropriate parameters for ion-water interactions (44) and ion-nucleic acid interactions (45).

We conducted MD simulations using the molecular package MOIL (46, 47). The periodic lengths were slightly contracted to reproduce the experimental water density at every corner of the simulation box. To reduce the necessary size of the system, H1 was fixed to its initial position to maintain the idealized A-form by means of the harmonic constraint with a force constant of 10 kcal mol⁻¹ Å⁻² throughout the simulation. However, both H2 and the junction were mobile without any conformational constraint. The long-range electrostatic forces were computed using the smooth particle mesh Ewald method (48) with 64 × 64 × 128 grid points. The cutoff radius for van der Waals interactions and for the real-space component of the electrostatic forces was set to 10.0 Å. The water molecules are constrained to be rigid with a symmetric matrix implementation of the SHAKE algorithm (49, 50). At each ionic concentration, a production simulation of 640–670 ns was run at constant volume and temperature (300 K) using velocity rescaling. Configurations were saved every 1 ps for analysis.

Structural pool construction by MD

The construction of structural pools is crucial in the sense that the pools should consist of realistic structures and cover as many states as possible in the conformational space. We use the structures from MD simulations to populate the pool as follows. Initially, pools were constructed from simulations at different [KCl], ranging from 30 to 900 mM. Each of these pools contains 2000–3000 structures. For a second pool, we obtained the structures from longer simulations carried out for 600 ns after equilibration. A third and larger pool of 22,540 structures was constructed by combining all the smaller pools from 200 ns simulations. This step prevents potential bias or inaccuracy from the salt dependence of MD simulations. The size of each pool is shown in Table 1. For a direct comparison of MD results and experimental data, we calculate the time-averaged theoretical SAXS curve by averaging all the computed scattering profiles of all the models for each condition. We also computed the χ² value using Eq. 2 to determine the quality of fit.

Table 1.

Number of Models in Different Searching Pools

[KCl] (mM)	All-Salt Pool	Subpool: 200 ns	Subpool: 600 ns
30	22,540	2970	12,857
50		2984	13,225
100		2980	13,014
200		2823	12,773
500		1944	12,930

Probabilistic ensemble and smFRET

To correlate the experimental smFRET measurements with results of the SAXS-derived ensembles, we need to simulate the E_FRET of the ensemble. We take the following experimental variables into account. First, the experimental E_FRET was measured using freely diffusing molecules on a confocal microscope with focal volume of ∼10⁻¹⁵ L. The average residence time of a single HJH molecule in this volume is on the order of μs, whereas the structural fluctuations of the two RNA duplexes occur on timescales between tens and hundreds of nanoseconds. Therefore, the HJH molecule samples many different conformations while diffusing through the focus. Second, because of the probabilistic nature of fluorescent energy transfer described by binomial distribution (51), the efficiency, E_FRET, cannot simply be averaged across different conformations in an ensemble. We will show in the next paragraph that interchanging compact (high-FRET) and extended (low-FRET) states do not contribute equally to the measured FRET efficiency. Lastly, with this picture in mind, not every state in the ensemble is sampled because of a finite number of events in a measurement. A single FRET measurement may reflect contributions from tens of conformational states, and some conformations may not be sampled through thousands of FRET measurements. In contrast, dominant conformations would be visited more often.

For a highly flexible molecular system whose dwell time in a given state is shorter than the diffusion time through the focal volume, high-FRET states more significantly contribute to the measured number of acceptor photons than low-FRET states. The measured E_FRET value is therefore larger than a simple, equally weighted average. For example, consider a measurement M from a two-state system with equally populated low-FRET (l, E_low = 0.3) and high-FRET (h, E_high = 0.7) states. If we record $E_{FRET,exp}=16/30\cong 0.533$ with 16 acceptor photons and 14 donor photons under the assumption of ideal dyes and measurement, the Bayes theorem suggests that this measurement is more likely to be generated by a high-FRET conformation diffusing through focal volume with the conditional probability

$$Pr\left(h\text{|}M\right)=\frac{Pr\left(M\text{|}h\right)Pr\left(h\right)}{Pr\left(M\right)}=84.5\%.$$ (3)

With an E_FRET value that just slightly exceeds 0.5, this measurement reflects conformations that are strongly biased (more than five times more possible) toward the high-FRET state. Moreover, we can compute the expected value of E_FRET if this two-state system spends equal amounts of time in each state while passing through the focal volume. For a given number of donor photons, the high-FRET state, on average, will contribute more than twice the number of acceptor photons emitted by the low-FRET state. Therefore, measurements of such a rapidly interchanging system overestimate E_FRET and are biased toward high-FRET states: in a (rapidly exchanging) ensemble measurement containing both extended and compact states, the molecules appear more compact than they really are because a FRET event with sufficient acceptor photons more likely originates from high-FRET states.

Considering these characteristics of smFRET experiment and the highly flexible HJH system, we formulate the following to simulate E_FRET from a SAXS-derived structural ensemble. We start with a random FRET burst size based on the burst size distribution (BSD) for an exponential decay:

$$BSD\left(\text{x}\right)=\frac{1}{s}{e}^{-\frac{x-t}{s}},$$ (4)

where $x\in \mathbb{N}$ is the number of photons in a burst and x ≥ t. Here, t = 30 is the typical threshold of the FRET burst size and s = 3 is the characteristic decay constant measured directly from experiments. During the time of a single FRET measurement, HJH visits N interconverting states in the focal volume, and each state contributes A_i acceptor photons, according to a binomial distribution, B(n, p) with (n, p) = (BS_i, E_FRET,i):

$$A_i\sim B\left(B{S}_i,E_{FRET,i}\right),$$ (5)

where A_i is the number of acceptor photons emitted by state i, whereas BS_i and E_FRET,i are the burst size and energy-transfer efficiency for state i, respectively. The value E_{FRET, i} is calculated using the average distance between two labeled bases, R_i, in (22) using $R_0=52\mathrm{\AA }$.

$$E_{FRET,i}=\frac{1}{1+{\left(\frac{R_i}{R_0}\right)}^6}$$ (6)

The probability of getting exactly A_i acceptor photons is

$$\text{Pr}\left(A_i\right)=\mathrm{Pr}\left(A_i;B{S}_i,E_{FRET,i}\right)=\left(\begin{array}{c}B{S}_i\\ A_i\end{array}\right){\left(E_{FRET,i}\right)}^{A_i}{\left(1-E_{FRET,i}\right)}^{B{S}_i-A_i}.$$ (7)

Here, we assume that the transition time between different states of HJH is negligible and donor excitation rates are constant. The resultant E_FRET of this single FRET event can be calculated as follows:

$$E_{FRET}=\frac{{\sum }_{i=1}^N{A}_i}{{\sum }_{i=1}^{N}B{S}_i}.$$ (8)

It is interesting to note that the number of visited interconverting states, N, follows a similar exponential decay as BSD(x) because the more time a molecule spends in the focal volume, the larger the burst size and the number of visited states are. In our calculation, we use a total of 1500 FRET events, which is a typical number in a smFRET experiment with good statistics. The distribution of the calculated E_FRET is fitted by a normal distribution, whose center is then interpreted as the E_FRET of the ensemble.

Results

Raw SAXS data

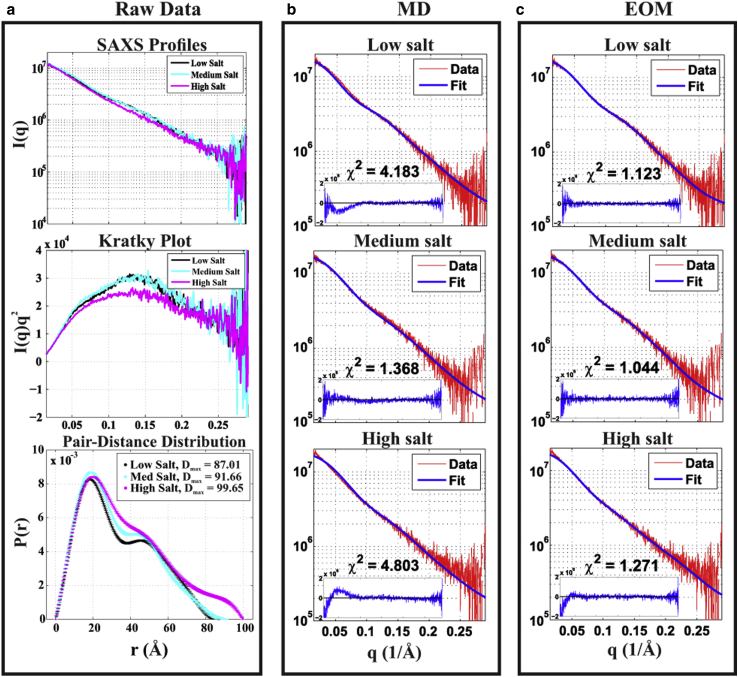
Conformational changes of the HJH in different [KCl] are detectable by SAXS. Fig. 2 a shows the raw SAXS data by reporting scattering intensity as a function of q (top); the Kratky plots of Iq² vs. q (middle), which emphasize scattering at higher q; and the pair distance distribution, P(r), computed by the ATSAS data analysis package (52) (bottom). P(r) provides a real-space interpretation of scattering data. The SAXS data were acquired at [KCl] ranging from 30 to 500 mM. Three characteristic points are shown in the figure: low (30-mM), medium (100-mM), and high (500-mM) KCl. Scattering profiles for the HJH at low and medium salt are different, as viewed in the Kratky plots and Holtzer plots (Fig. S3); however, a small change in P(r) near 40 Å suggests conformational variations. More significant changes are observed at high [KCl]. Because more pronounced peaks in Kratky plots are associated with more compact molecular conformations, the diminution of the peak at 500-mM KCl indicates that the HJH molecule is extended relative to its low salt conformations. Such a counterintuitive result is further supported by the salt-dependent P(r) curves. At high salt, the maximal pair distance $D_{max}=99.65\mathrm{\AA }$, as compared with 87.5 at lower salt. Thus, the raw SAXS data reveal unexpected HJH global properties, but they are challenging to interpret.

Figure 2.

Comparison of raw SAXS data with predictions from the full (600-ns) MD pool and EOM refinements of that pool. (a) The raw SAXS profiles, the Kratky plot, and the pair distance distribution function. The Kratky plot of high salt suggests that HJH in high (500-mM) [KCl] is more extended than in low (30-mM) and medium (100-mM) [KCl]. The right two panels show the comparison with SAXS data of (b) MD and (c) EOM predictions, using residuals and χ² to evaluate the quality of the fits. The MD method fits the data best at medium salt and is improved, in all cases, by experimental refinement using EOM.

Fitting SAXS data with full, 600-ns MD pool

To gain insight into the ensemble of molecular conformations present, we refer to MD models. As a first step, we compare each experimental SAXS profile with the MD prediction from the longer, 600-ns simulation at the corresponding [KCl]. The theoretical SAXS profiles of all the MD models were computed by CRYSOL (36) and subsequently averaged. Fig. 2 b directly compares the profiles computed from MD to the SAXS data. The χ² and fitting residuals are shown at the bottom of each plot. The logarithmic y axis highlights more subtle features of the curves. The MD models fit the SAXS data well at medium [KCl] with χ² of 1.368, with only a small mismatch in the mid-q regime (q = 0.1–0.15 Å⁻¹). In contrast, at low and high salt, agreement with MD-computed profiles is good only in the middle of the measured q-range, resulting in large values of χ². The disagreement in the higher-q (q > 0.15 Å⁻¹) regime is significant in identifying the conformational ensemble because the separation range between the two helices occurs on the length scales of tens of Å, which contributes to the scattering in this q range.

Fitting SAXS data with EOM refinement of 600-ns MD pool

Following recent studies showing the success of ensemble methods in describing highly flexible single-stranded nucleic acids (53) and DNA bulges (54), we further improved the fitting to the SAXS data by guiding a selection of a subset of the MD models using an EOM. The resulting curves, χ², and fitting residuals are shown in Fig. 2 c. For low and high [KCl], the ensemble selection significantly improves the fit to the data. Most of the χ² contribution comes from the relatively large residuals at q < 0.05 Å⁻¹ and q > 0.25 Å⁻¹. With the higher-quality EOM fits and smaller ensemble at each [KCl], we can visualize the conformations that populate the ensemble at salt concentration.

Optimizing the MD pools for EOM

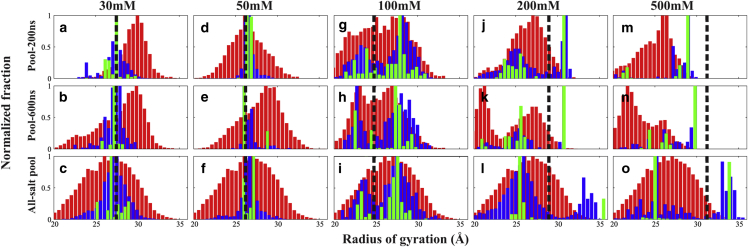
Encouraged by the improvements to the fits shown in Fig. 2, we explored the use of different structural pools as input to the EOM algorithm to ensure that all relevant conformations are represented. Fig. 3 presents these comparisons, in which each structure is parameterized by its radius of gyration, R_g. The top two rows show a comparison using the pools generated by the two different simulation lengths: 200 and 600 ns. The latter pool was used to generate the data shown in Fig. 2. The R_g distribution of the full pool (containing all structures from the MD simulation of a given length at a given condition) is shown in red, whereas the distribution of structures in the EOM-selected ensembles of “all cycles” and “best cycle” are shown in blue and green, respectively. The black dashed lines represent the experimental R_g values.

Figure 3.

Distribution of radii of gyration (R_g values) of all structures at different [KCl] using Subpool-200 ns (a,d,g,j,m), Subpool-600 ns (b,e,h,k,n) and All-salt pool (c,f,i,l,o). The black dashed lines indicate the experimental R_g values of 27.5, 26.5, 24.7, 29.0, and 31.4 Å for 30–500 mM KCl concentrations. The gray histograms show the R_g distribution of all structures in each pool, under the quoted condition, whereas the darker and lighter histograms show the distributions from the “all-cycle” and “best-cycle” EOM analysis, respectively. Each distribution is normalized by the maximal number of counts. To see this figure in color, go online.

At low salt, the full MD pool for both simulations contains broad distributions of structures, centered at ∼30 Å. The EOM-selected ensembles are centered at 26.5 Å (Fig. 3, a, b, d, and e). Near physiological salt conditions, [KCl] ∼100 mM, the longer (600-ns) simulation predicts a bimodal R_g distribution. This trend is mirrored and enhanced in the selected ensembles despite a slight shift of the peak positions (Fig. 3, g and h). Thus, the MD prediction of two peaks is borne out by the selection algorithm. The MD simulations perform well (as assessed by the χ² metric) near physiological salt at which the force fields are extensively used (55, 56). At [KCl] = 200 mM, the peaks shift further apart in the pool, and a very compact state emerges in the longer simulation, with R_g = 21 Å. Interestingly, the EOM-selected ensemble also includes conformations with a larger R_g (Fig. 3, j and k). At high salt, [KCl] = 500 mM, the two peaks in the MD pool smear out, implying a broad distribution of structures from compact to extended. In contrast, the EOM procedure specifically selects the most extended models (Fig. 3, m and n). This selection is concerning because models with R_g > 30 Å are absent from the corresponding MD pools. The algorithm therefore chooses the most extended models available. This discrepancy raises the question of potentially flawed ensembles if the pool fails to cover the required conformational spaces. To account for this possibility, we created a third, large pool, the “all-salt pool” that includes every model from all the 200-ns MD simulations. Results of EOM selection from this pool are shown in the bottom row of Fig. 3, c, f, i, l, and o.

Interesting trends are observed when the larger, all-salt pool is used. Although the same pool is used for all data sets, distinct conformational ensembles are selected at different [KCl]. In most cases, the overall structural features of the refined ensembles are consistent with those selected from the smaller pools at each value of [KCl]. There is one notable exception: structures with larger R_g in the ensembles at higher salt (Fig. 3 o). As discussed above, these structures are absent from the smaller MD simulation pools.

HJH subtleties at different KCl concentrations

To ensure that all possible structures are represented, we focused the remainder of our analysis on comparison of experimental data with structures from the all-salt pool. From Fig. 3, c and f, at [KCl] = 30 and 50 mM, the R_g distribution of the ensemble shifts slightly from 27 to 26 Å. The narrower R_g distribution at [KCl] = 50 mM allows a better definition of the ensemble because it favors some conformations with specific values of R_g.

At [KCl] = 100 mM (Fig. 3 i), the bimodal nature of the ensemble suggests that the HJH construct adopts two distinct conformations with R_g values centered at 23 and 27.5 Å. The coexistence of two states is not readily ascertainable from either the previous smFRET study or the Guinier analysis (57) because of data averaging during collection and processing.

As [KCl] increases to 200 mM (Fig. 3 l), we observe a further splitting of the distribution with peaks at R_g = 25 and 34 Å. Note that the maximal possible R_g for the HJH construct is 35.5 Å, corresponding to a structure that has the central lines of H1 and H2 aligned and the junction in an A-form conformation. This extended conformation is the starting state of the MD simulations. The wide R_g distribution centered at 26 Å shows that there are still many different possible conformations for HJH molecule because of structural variations. However, the selection is quite narrow at high R_g. There are two possible explanations for these narrow peaks. First, the all-salt pool may still fail to cover the full conformational space, forcing the EOM algorithm to select only from a small number of conformations near the extended states. Second, the narrow peak may result from a restricted conformational space or the inability of HJH to explore some conformationally nearby structures once the HJH molecule is extended.

At the highest [KCl] (Fig. 3 o), two competing conformations exist: the extended state, R_g = 34 Å, and compact state, R_g = 25 Å, which resemble the states populated at [KCl] = 200 mM. The difference lies in the increased population of the extended states. Although very few extended conformations are present in the all-salt pool, EOM consistently selects those states over tens of thousands of competing conformations to improve the fit. To summarize, consistent with the results of (22), the HJH has three distinct conformational regions depending on the salt concentration. This ensemble picture provides critical insight into the structures present.

Base stacking at high KCl concentrations

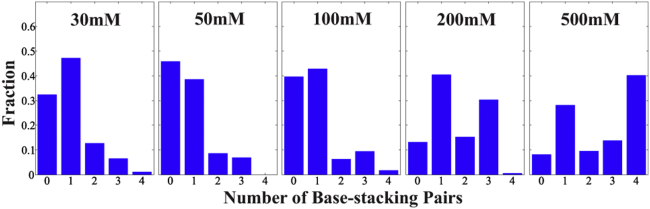
An examination of structures present in the all-salt pool but absent from the high-salt pool allows a straightforward visualization of the states that are missing in the latter. The high-salt MD simulations do not predict extended states with R_g > 35 Å, whereas our analysis indicates that these states are significantly populated. These extended conformations appear at the earliest time points of the simulations but are eliminated by equilibration. They are present in the all-salt pool only because they persist in simulations at lower [KCl]. The structures of the junctions within these extended states are all similar: they display stacking of uracil 13 (U13) and 17 (U17) on top of cytosine 12 (C12) and 18 (C18), respectively (see Fig. 1) Although the base-stacking in uracil was not seen in some studies (58, 59) and the stacking free energy for uracil is assumed to be negligible in some MD force fields (60, 61), ionic strength is often not considered, and it is known that stacking interactions between uracil and other nucleobases play a role in some systems (21, 62). Previous studies, on the other hand, revealed that the junctions contribute significantly to RNA folding and conformations (63). The C12-U13 and U17-C18 base-stacking interactions lock the mobile helix (H2) in place and the global conformation is determined by the junction. Base stacking at high [KCl] also impacts the compact structures. The R_g of the “bent” state increases because of specific junction conformations and arrangement of the helices. The broad distribution at [KCl] = 200 mM implies conformational variation of the bent state because of the flexibility of the rU₅ junction. However, at 500 mM KCl, the low-R_g state has a narrower distribution because the helices and junction conformations are locked in place as a result of increased stacking interaction in the rU₅ bases and reduced flexibility. Fig. 4 shows the number of base-stacking pairs in the region of C12–18 at different [KCl]. The fraction of stacked bases increases at high salts and peaks at 500 mM KCl. In summary, at higher salt, base stacking of uracil-cytosine (junction to helix) appears first and is followed by uracil-uracil stacking within the junction, resulting in very different conformational ensembles.

Figure 4.

Number of base-stacking pairs in the junction (C12–18) within an ensemble at different [KCl]. Below [KCl] = 100 mM, the number of base-stacked pairs is small and mostly results from immobilization of C12 and (therefore) the highly constrained positions of U13. As [KCl] increases to 200 mM and beyond, the number increases significantly: two and three pairs are seen in 200 mM, whereas most of the bases are stacked along the junction at 500 mM. To see this figure in color, go online.

The ensemble and smFRET measurement

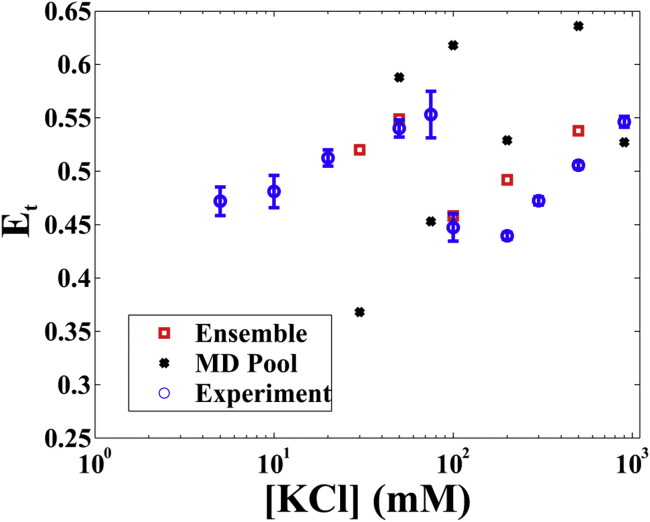
The nonmonotonic behavior measured in the smFRET experiments can now be explained by the SAXS-derived HJH ensemble. Fig. 5 shows the simulated E_FRET values of the ensembles (red), the simulated E_FRET values of the 600-ns MD pools (black), and the experimental values (blue), using the methods described above. The simulated E_FRET of the ensemble matches the experimental measurements well at low and medium [KCl] and accurately reflects the trend at high [KCl], providing corroboration for the ensembles refined by SAXS profiles. Moreover, the large deviation of calculated E_FRET of the MD pool from the experimental values indicates that the SAXS refinement of the MD models is essential to accurately describe the HJH structures in KCl solutions.

Figure 5.

The calculated E_FRET of structures from the EOM-selected “all-cycle” ensemble as well as the full MD pool are plotted with the experimental data smFRET data (22). The error bars are the standard deviations of at leaset two independent measurements. The EOM-selected ensembles more closely capture the smFRET measurements. To see this figure in color, go online.

Discussion

Our model system, the HJH RNA construct, contains two 12-bp helices linked by a single-stranded junction containing five uracil nucleotides. In the SAXS measurement, the x-ray photons are mostly scattered by the two electron-dense helices rather than the junction. However, the effect of the junction is pronounced because it constrains the orientations of the helices. Thus, it can be inferred if the placement of the helices is determined. Models from MD simulations are used to bridge the gap between the helical locations (extractable from a low-resolution SAXS measurement) and junction conformation. In the last section, we showed that experimental refinement of the MD results by EOM is required to recapitulate the SAXS profiles and to reveal notable features of the ensembles. Importantly, data from previous smFRET experiments are also well described by the EOM-selected ensemble, providing independent validation.

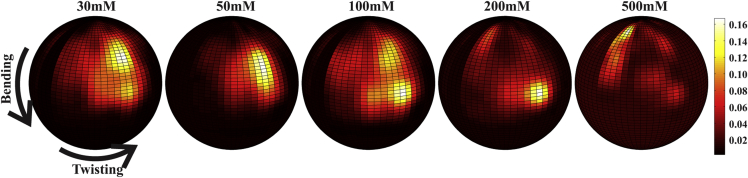
The existence of a selected set of atomically detailed models allows us to extend our analysis beyond the distribution of R_g shown in Fig. 3. Quantification of the model structures in terms of bending and twisting angles of the junction provides two axes for enhanced visualization of the results (34). The junction vector is defined as the phosphate-to-phosphate direction from C12 to C18, as shown in Fig. 1. We use the phosphorus atom of C12 as the new origin and the direction of central line of H1 as +z at x = x₀ > 0, y = 0. The polar angle and azimuthal angles, (θ, φ), represent the bending and twisting angles of the junction using the spherical coordinate convention. Fig. 6 shows the spherical density for the bending and twisting angles of junction in the selected EOM ensembles at different [KCl]. The shifting location of the hot spot indicates the trends with increasing [KCl]: the junctions are extended at low salt, adopt two distinct (extended and bent) conformations at [KCl] = 100 mM and a more fully bent conformation at 200 mM, and finally revert to extended conformations at high salt.

Figure 6.

The spherical densities of the junction bending and twisting angles for structures in the optimized ensembles, shown as a function of [KCl]. The density of structures is indicated using the scale at right, with higher density regions indicated by a brighter “hot spot.” Motion of the hot spot is clearly seen, underscoring the observed structural transitions. Below ∼200 mM KCl, the angles increase. At high salt, an unexpected hot spot appears at small angles, reflecting extended states and stacked bases along the junction. To see this figure in color, go online.

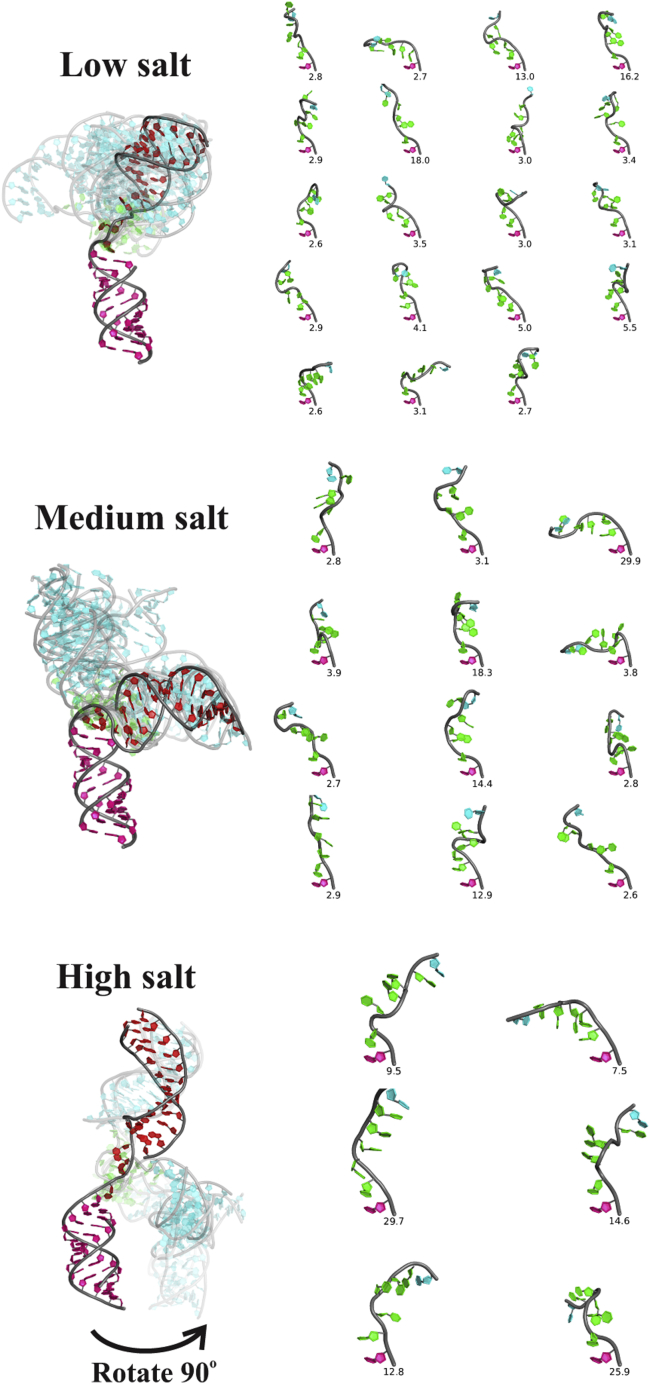
The visualization is important because there are many cases in which a single macromolecular property such as R_g or D_max might not necessarily distinguish different conformations. Two very distinct conformational ensembles may have similar values of these parameters. Care must be taken in interpreting EOM results because many of the conformations have very similar arrangements of helices as well as junction conformations. Thus, we use the clustering algorithm described in the Supporting Materials and Methods to categorize the geometries of the HJH construct. We extract the representative conformations present in any given ensemble that occur with frequencies beyond a threshold that is set to be the average of frequencies plus two SDs. Additional representative conformations with different thresholds are shown in Figs. S5–S9. The representative conformations at three different salt concentrations are shown together on the left of Fig. 7, with H1 (magenta) aligned for all models. The dominant conformation is shown in red, and the others are in transparent cyan. The transparency is inversely correlated with frequency: the more frequent, the less transparent. Moreover, the junctions C12-rU₅-C18 are also shown on the right, labeled with the percentages observed.

Figure 7.

Representative conformations of HJH in different [KCl] regimes: low (30 mM), medium (100 mM), and high (500 mM). The dominant conformation is shown in red, whereas other competing conformations are shown in transparent cyan, based on the detected frequencies in the ensemble. The junction conformations are shown on the right (C12-UUUUU-C18), with a label reflecting the percentage observed. This figure was generated by PyMOL (Schrödinger LLC, New York, NY) using home-written Python scripts. To see this figure in color, go online.

Extended at low salt

At low salt ([KCl] = 30 mM), the HJH molecules are mostly extended with ∼15–25° of bending (Figs. 6 and 7). The junction conformations do not display specific base arrangements or geometries, and the junction itself is almost always extended. Three possible interactions determine the HJH conformation: electrostatic interactions, stacking of the junction bases, and coaxial stacking of the two duplexes. First, at these low salt concentrations, the negative charges of phosphates in the backbones of H1 and H2 are not locally screened because of the small number of K⁺ ions. Thus, repulsive forces between H1 and H2 pull them apart, leaving the junctions in indefinite, nonstructured extended states. The observed lack of ordering in the junction suggests that the strength of base-stacking interactions is negligible compared with this repulsion. The flexibility of the junction in such an extended state remains unknown. A direct measurement could be carried out to establish a persistence length (21, 64) or to determine an orientation correlation function (53), but these analyses are challenging to implement for the HJH construct. Finally, although the coaxial stacking appears in many RNA systems, the stacked helices are usually found in the middle of other RNA structures, which impose a strict limitation on the available space for the duplexes. In the HJH, the helices are not constrained by other RNA elements. Considering minor end-fraying effects on the 12th and 18th Watson-Crick GC basepairs at both ends of the junction, coaxial stacking can also be excluded (65). The extension results in the large separation between H1 and H2, which echoes the previous smFRET study.

Bimodal jump at medium salt

As [KCl] increases, the component structures in the ensemble begin to change. The HJH molecule favors the two different conformations as shown in Figs. 6 and 7. Extended and bent states are observed with R_g of 27 and 23.5 Å (see Fig. 3 i). The dominant conformation, shown in red, contains the 90°-bent junction, comprising almost 30% of the ensemble. The rest of the conformations are relatively straight, resembling those found at low [KCl]. No backbone geometries are consistent with base stacking; therefore, these interactions appear to be negligible. The closer separations between helices observed in the bent state but absent in the low [KCl] ensembles is consistent with the greater local screening. These two states are most easily seen in the 600-ns MD simulations. The two peaks correspond to different states: “extended” versus “bent.” Some RNA systems show multiple states under the physiological salt conditions (66). The approximately equal contribution of both states indicates that the conformational landscape of this HJH has two or more readily accessible shallow local minima.

Locked conformations at high salt

Unexpected conformations become populated at higher salt concentrations. One would expect that electrostatic repulsion would be strongly screened, resulting in the broadest range of conformations (23) because helices are freer to explore a larger three-dimensional space. However, the selected structural ensemble at the bottom of Fig. 7 suggests a richer story. For clarity of visualization, the structures are rotated 90° counterclockwise to show the bent states. Some structures are in the antiparallel bent states, in which most of the nucleobases in the junction are involved in base stacking with neighbors, while the dominant state is extended. From the junction conformations shown on the right, the most frequent conformation has all the bases stacked with either C12 or C18. The stacking interactions between uracil bases and cytosine bases lock the junction into a specific form, placing the H1 and H2 in parallel extended conformations. Although some antiparallel bent states also populate the ensemble, extended states with R_g of 34.5 Å are dominant (Fig. 3 o), corresponding to HJH structures with coaxially aligned helices and A-form junction conformation. These extended states do not appear in the MD simulations at high salt. The equilibration eliminates a few starting conformations. MD force fields only suggest the antiparallel bent states in the later time points of simulations. It is relatively unlikely for these states to unfold back to their initial conformations (coaxially aligned helices) in the MD simulations without adequate base interactions. Interestingly, the latest, revised force field parameters for RNAs predict unconventional base-stacking patterns of rU₄ (28), but further experimental confirmation is required.

Finally, the locations of ions in the MD simulations provide some insight into the cause of uracil-uracil and uracil-cytosine base-stacking interactions: there is a strong association of counterions with O2 and O2′ in the uracil that takes place when the nucleobases stack. The counterions neutralize the negative charges on O2 and O2′, reducing the local electrostatic repulsion between the adjacent bases. The weaker base-stacking interactions of uracil in some of the previous work might be due to the exclusion of counterions or the pairing and burying of bases inside the duplex (60, 61). The exposure of the uracil bases to the solvent environment makes possible counterion binding to O2 and O2′, which are two hot spots for local strong electrostatic repulsions. In addition, the hydrophobic effect increases with added salt in solutions (67). The uracil bases are also in direct contact with the ion environment. The π stacking interactions thus become stronger, locking the adjacent nucleobases in place. These interactions not only facilitate the specific base arrangements but also determine the backbone geometries. In contrast to conformations found at low and medium [KCl], the junction stiffens and constrains the two duplexes.

Conclusions

In summary, we used SAXS and MD to extend an earlier smFRET study of a flexible RNA HJH construct. We compare the MD-generated structures and use a genetic algorithm to optimize a solution ensemble, obtaining the best fit to our experimental SAXS profiles. The resulting ensembles suggest three distinct conformational regimes: indefinite extended at low, bimodal states at medium, and parallel-antiparallel states at high [KCl] due to specific base alignment of rU₅. Association of ions to neutralize local electronegativity and enhanced hydrophobic effect explain the observed base stacking. Finally, the calculated E_FRET from ensembles also agrees with the experimental data. We demonstrate that the combination of SAXS and MD reveals multiple macro- and microscopic properties of small RNA molecules and uniquely enables the visualization of conformational ensembles.

Author Contributions

Y.-L.C. and L.P. designed and carried out experiments. T.L. and R.E. designed and carried out MD simulations. All authors contributed to writing the manuscript.

Editor: David Lilley.