Abstract
rain-Wide and Genome-Wide Association (BW-GWA) study is presented in this paper to identify the associations between the brain imaging phenotypes (i.e., regional volumetric measures) and the genetic variants (i.e., Single Nucleotide Polymorphism (SNP)) in Alzheimer’s disease (AD)rain-Wide and Genome-Wide Association (BW-GWA) study is presented in this paper to identify the associations between the brain imaging phenotypes (i.e., regional volumetric measures) and the genetic variants (i.e., Single Nucleotide Polymorphism (SNP)) in Alzheimer’s disease (AD)B. The main challenges of this study include the data heterogeneity, complex phenotype-genotype associations, high-dimensional data (e.g., thousands of SNPs), and the existence of phenotype outliers. Previous BW-GWA studies, while addressing some of these challenges, did not consider the diagnostic label information in their formulations, thus limiting their clinical applicability. To address these issues, we present a novel joint projection and sparse regression model to discover the associations between the phenotypes and genotypes. Specifically, to alleviate the negative influence of data heterogeneity, we first map the genotypes into an intermediate imaging-phenotype-like space. Then, to better reveal the complex phenotype-genotype associations, we project both the mapped genotypes and the original imaging phenotypes into a diagnostic-label-guided joint feature space, where the intra-class projected points are constrained to be close to each other. In addition, we use ℓ2,1-norm minimization on both the regression loss function and the transformation coefficient matrices, to reduce the effect of phenotype outliers and also to encourage sparse feature selections of both the genotypes and phenotypes. We evaluate our method using Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, and the results show that our proposed method outperforms several state-of-the-art methods in term of the average Root-Mean-Square Error (RMSE) of genome-to-phenotype predictions. Besides, the associated SNPs and brain regions identified in this study have also been shown in the previous AD-related studies, thus verifying the effectiveness and potential of our proposed method in AD pathogenesis study.
Index Terms: Brain-Wide and Genome-Wide Association (BW-GWA) study; Single Nucleotide Polymorphism (SNP); Magnetic Resonance Imaging (MRI); Alzheimer’s disease (AD); feature selection; sparse regression model; ℓ2,1-norm minimization
I. INTRODUCTION
ALZHEIMER’S disease (AD) is the most common form of dementia that often affect individuals over 65 years old, which strongly impacts human’s thinking, memory and behavior [1], [2], [3], [4], [5], [6], [7], [8]. This disease always progresses along a temporal continuum, initially from a normal control (NC) stage, subsequently to mild cognitive impairment (MCI) and eventually deteriorating to AD. According to a recent report from Alzheimer’s Association [9], the total estimated prevalence of AD is expected to be 60 million worldwide over the next 50 years, thus gaining growing attention in clinical research.
In recent years, a large number of neuroimaging studies [10], [11], [12], [13] have been done to investigate the associations between the AD and the brain structural or functional changes [14], [15], [16], [17], [18], [19]. Besides, some genome studies have also been done to understand the genetic causes of AD [20], while some genome-wide association (GWA) studies focus on identifying the genetic variations that affect the brain structures and functions [21], [22], [23]. Most of the GWA studies are based on the massunivariate linear model, which fixes one variable (e.g., imaging phenotypes) while performing regression analysis using the other variables (e.g., genetic variations). However, as one genotype is probably associated with multiple imaging phenotypes (e.g., one gene may affect the cortical thickness of several brain regions) and one imaging phenotype is also probably associated with multiple genotypes (e.g., the cortical thickness of one brain region could be influenced by multiple genetic variations), the association between genotypes and phenotypes is actually a complex many-to-many relationship. Therefore, univariate analysis of conventional GWA studies is not sufficient to address the complex phenotype-genotype relationship. Consequently, more and more attentions have been given to multivariate analysis of the imaging genetic, i.e., Brain-Wide Genome-Wide Association (BW-GWA) study [24], [25], [26], which can simultaneously identify the genetic variations and imaging phenotypes that are associated with each other in AD study.
The aim of BW-GWA study is to evaluate the influence of genetic variations on brain structures and functions, so that we can better understand the complex neuropathology of the disease (e.g., AD), from genetic variants, to cellular processes, to brain structure and function, and to the symptoms of memory and cognitive impairment. This kind of study is highly desirable in clinical applications, as it enables the researchers to monitor the progression of AD starting from its origin. That is, such study may provide vital information on how the AD-related genes interact with other non-genetic factors, which is important to possibly slow down the progression or even prevent the occurrence of AD.
However, the BW-GWA study is challenging, primarily due to the high-dimensional genotypes (e.g., Single Nucleotide Polymorphisms: SNPs) and the heterogeneity between the genotypes and the neuroimaging phenotypes (e.g., Region-Of-Interest (ROI)-based features in Magnetic Resonance Imaging (MRI) data). To address the high-dimensional data issue, some studies regarded this imaging genetic study as a feature selection problem [27], [28], [29], [30], e.g., to select SNPs that are most correlated with the imaging phenotypes. For instance, Wang et al. [30] proposed a group sparse multitask regression model to predict the neuroimaging measures using the most related SNPs. This method focused on selecting the most relevant SNPs, while the neuroimaging measures were preselected based on prior knowledge. Vounou et al. [31], [32] proposed to use a sparse reduced-rank regression model and a sub-sampling strategy to select a subset of SNPs that are most associated with the multivariate phenotypes. Zhu et al. [24] developed a structured sparse low-rank regression model to investigate the associations between the imaging phenotypes and the genotypes. In addition, considering that the neuroimaging phenotypes are often measured over time, the longitudinal profile should provide increased power for identifying the associated genotypes. Following this line of research, Wang et al. [33] presented a temporal structure learning model that used the longitudinal genotype-phenotype interrelations to predict the phenotypes, while Wang et al. [29] presented a task-correlated longitudinal sparse regression model to identify longitudinal imaging markers that are associated with the ADrelevant SNPs. In summary, to address the high-dimensionality issue in imaging genetic study, the current approaches project the SNP data into a lower dimensional space via different sparsity constraint and/or low-rank constraint methods.
However, there are still several limitations in the current BW-GWA studies. First, the existing methods seldom consider the data heterogeneity between the genotypes and the imaging phenotypes. For instance, the conventional methods [24], [29], [33], [34] often simply adopt a linear regression model using the imaging phenotypes and the genotypes as the responses and the input variables, respectively, without considering the heterogeneity between these two data modalities. Second, the current methods also lack of consideration of complex associations between the genotypes and the imaging phenotypes. For example, most of the current methods [30], [33], [32], [24] only focus on finding the associated SNPs for a subset of neuroimaging phenotypes, or finding the associated neuroimaging phenotypes for a subset of SNPs, without simultaneously exploit the many-to-many associations between the SNPs and the imaging phenotypes. Third, the issue of phenotypes outliers is seldom considered in the existing studies. Many current BW-GWA methods [30], [33], [32], [24], [35] use squared Frobenius-norm loss function in their linear regression models, i.e., , where X2 and X1 denote the SNPs and the MRI phenotype data, respectively, and W2 is the learned weight matrix that reflects the relations between the SNPs and the imaging phenotypes (as shown in Fig. 1). However, since not all the brain regions (phenotypes) are AD-related, using squared Frobenius-norm loss function to measure the reconstruction error of all the phenotypes (i.e., ) is vulnerable to those non-AD-related phenotypes (outliers) [24], [33]. Fourth, the valuable diagnostic label information is also often ignored in the previous studies [30], [32], [36]. As the main aim of BW-GWA study for AD is to find the associations between genotypes and phenotypes for AD study, the efficient usage of diagnosis label information may improve the learning performance in BW-GWA study [37].
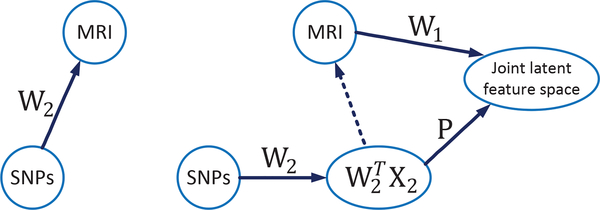
Fig. 1.
Comparison of the basic framework and our proposed framework in BW-GWA study. (Left) The basic framework: It projects the genotypes (e.g., SNPs, denoted as X2) into brain imaging phenotypes (e.g., MRI data, denoted as X1). A sparse weight matrix W2 (e.g., with ℓ2,ℓ1,1 or ℓ2,1-norms regularization) can be learned to reflect the relationships between SNPs and MRI. (Right) Our proposed framework: We first learn a weight matrix W2 to intermediately transform the raw SNP data to the imaging phenotypes space. Then, we project the transformed SNP data (which is imaging-phenotype-like) and the MRI phenotype data into a disease label guided joint latent feature space via the orthogonal projection matrix P and the transformation matrix W1, respectively. The feature selection for SNP and MRI phenotypes is achieved by imposing sparsity constraints on W1 and W2, respectively.
In this paper, we address the above limitations by proposing a BW-GWA method that simultaneously selects the associated genotypes and imaging phenotypes, while considering the data heterogeneity, phenotype outliers, and diagnostic label information. We achieve this by proposing a novel joint projection and sparse feature learning algorithm, which projects the genotypes and the imaging phenotypes into a diagnostic-label-guided joint latent feature space, while at the same time employs a sparse regression model to find the associations between these two data modalities. In Fig. 1, we show the overview of our framework as well as how it is different from typical framework of the conventional BW-GWA studies. Specifically, to alleviate the negative influence of the data heterogeneity, we first map the genotypes (i.e., SNPs) to the neuroimaging-phenotype-like space. Then, we project the mapped genotypes (which is now imaging-phenotype-like) and the imaging phenotypes into a joint latent feature space. We also introduce the diagnostic label information to constrain the projected data to have small intra-class distance in this joint feature space, which will consequently enhance the disease discriminability of the projected data in terms of their disease labels. In addition, to select only a subset of genotypes and phenotypes that are associated with each other, we impose a ℓ2,1 -norm regularizer on the transformation matrix that maps the phenotypes to the joint latent space (i.e., W1 in Fig. 1), and also on the transformation matrix that maps the genotypes to the intermediate phenotypes space (i.e., W2 in Fig. 1). The ℓ2,1 -norm regularizer has been widely used to encourage group sparsity (e.g., row-wise sparsity, where each row is corresponding to one genotype or phenotype index), which in our case, is used to select the associated phenotypes and genotypes. Besides, in order to address the issue of phenotype outliers, we use a ℓ2,1 -norm (instead of the conventional squared Frobenius-norm) based loss function in our proposed method.
We evaluate our method using the genetic and MRI data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). More specifically, we learn our model by using the SNPs as genotypes, and the ROI-based volumetric measures of the MRI data as phenotypes in this BW-GWA study. We use the learned model to predict the imaging phenotypes by using the selected associated SNPs, and the experimental results show that our proposed model outperforms the state-of-the-art methods in term of the average Root-Mean-Square-Error (RMSE) of genotype-to-phenotype predictions.
The rest of this paper is organized as follows. We describe materials and data preprocessing steps in Sec. II, introduce our model in Sec. III, present the experimental results in Sec. IV, and conclude our study in Sec. V.
II. MATERIALS AND IMAGE DATA PREPROCESSING
A. Subjects
We use the public ADNI dataset [38] to verify the performance of our proposed framework. The ADNI dataset was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and nonprofit organizations with a five-year public private partnership. In this study, we used 737 ADNI-1 subjects, including 171 AD, 362 MCI, and 204 NC subjects, as described in [39].
B. Neuroimaging Data Preprocessing
We used the ROI-based MRI features as phenotypes in this study. We first downloaded ADNI preprocessed 1.5T MR images from the ADNI website 1. The structural MR images were collected by using a variety of scanners with protocols individualized for each scanner. To ensure the quality of all images, ADNI had reviewed these MR images and corrected them for spatial distortion caused by B1 field inhomogeneity and gradient nonlinearity. After that, following the previous studies [40], [41], [42], we processed these neuroimaging data and extracted the ROI-based features. Specifically, for each MR image, we processed it by using the following steps: anterior commissure-posterior commissure (AC-PC) correction by using MIPAV software2, intensity inhomogeneity correction by using N3 algorithm [43], brain extraction by using a robust skull-stripping algorithm [44], cerebellum removal, tissues segmentation by using FAST algorithm in FSL package [45] to obtain three main tissues (i.e., white matter (WM), gray matter (GM), and cerebrospinal fluid), and registration to a template [46] by using HAMMER algorithm [47]. We then dissected the images into 93 regions-of-interest (ROIs) by using the labeling information from the template [46], and used the gray matter tissue volumes, one from each ROI, as the MRI features of a subject. Finally, we have 93 ROI-based MRI features, or phenotypes, for each subject.
C. Genetic Data Preprocessing
We used SNPs as genotypes in this study. The SNP data were genotyped using the Human 610-Quad BeadChip [48]. According to the AlzGene dataset 3, only SNPs that belong to the top AD gene candidates were selected after the standard quality control and imputation steps. The Illumination annotation information was used to select a subset of SNPs [49], and the dimensionality of the processed SNP data is 3123 in this study.
III. METHODOLOGY
A. Basic Notations
In this paper, we denote matrices, vectors, and scalars as boldface uppercase letters, boldface lowercase letters, and normal italic letters, respectively. For a matrix , where d and n denote the feature dimension and the number of samples, respectively, we use and to denote its Frobenius-norm and ℓ2,1-norm, respectively, where xij is the (i,j)-th element (i.e., i-th row and j-th column) of the matrix X. In addition, we use Xi and Xj to denote the i-th row and the j-th column of X, respectively, and use XT and Tr(X) to denote the transpose and the trace operator of the matrix X, respectively.
B. Joint Projection Learning and Sparse Regression Model
Let and denote the feature matrices for MRI (ROI-based features) and SNP data, respectively, where n is the number of samples, and d1 and d2 denote their corresponding numbers of feature variables. We can use linear regression to model the relationship between the MRI phenotypes and the SNP genotypes, i.e.,
| (1) |
where is a coefficient matrix. With Eq.(1), we can project the SNP data into the MRI feature space. Furthermore, assuming that only certain SNPs are associated with the brain imaging features, we impose a group sparsity constraint (i.e.,ℓ2,1-norm) on W2 in Eq. (1), and obtain the following objective function
| (2) |
where λ is the regularization parameter to balance the contributions of the reconstruction error (i.e., the first term in Eq. (2)) and the regularizer (i.e., the second term). The ℓ2,1-norm regularizer has been widely applied in multi-task feature learning [50], [51], [52], [53] to impose row sparsity (i.e., many all-zero rows) on the matrix of interest. Given that where is the i-th row of W2, the minimization in Eq. (2) will enforce only certain rows of W2 to be non-zero. Thus, by ranking , the first k(k ≪ d2) highest magnitude of would be corresponding to the top k SNPs that are associated with the neuroimaging phenotypes.
In addition, some studies have shown that the first term in Eq. (2) is more vulnerable to the row-wise outliers of X1 [54], which, in our case, are the phenotype outliers. This is because the “square” of the squared Frobenius-norm will magnify the reconstruction errors of the phenotype outliers, and cause them to dominate the minimization of the objective function. One solution to address this issue is to replace the squared Frobenius-norm of the fidelity term with the ℓ2,1-norm, which has been shown to be robust to row-wise outliers [54]. Thus, by adopting ℓ2,1-norm to measure the reconstruction error, we obtain
| (3) |
In summary, the ℓ2,1 -norm is used for both the data fidelity term and the regularization term in Eq. (3), where its usage in fidelity term is to increase its robustness to phenotype outliers, while its usage in regularization term is to sparsely select SNPs that are associated with the ROI-based MRI phenotypes.
However, as shown in many works [2], [3], [16], [17], [20], not all the ROI-based MRI features are related to AD, since AD mainly affects brain regions that are related to memory and cognitive functions. Similarly, we would also expect that the SNPs that are associated with AD would only affect certain brain regions only. Thus, features in X1 that are not useful for the AD diagnosis should be removed, and only certain features in X1 should be used as targets in Eq. (3) to find the associated SNPs. But how should we select features in X1 for BW-GWA study? The simplest selection method perhaps is using the disease label as target and X1 as regressors in sparse regression, to select the most discriminate features in X1. Then, the proposed Eq. (3) can be subsequently used to find the associated SNPs. However, such 2-step approach is sub-optimal in BW-GWA study, as it ignores the complex pathogenesis of the disease and the intercorrelated relationship among the genetic variations (SNPs), imaging phenotypes and the disease labels. In this study, we would like to jointly select the associated SNPs and imaging phenotypes by exploiting the disease label information and its relationship with SNPs and imaging phenotypes. To achieve this, we first assume there exists a joint latent feature space for X1 and X2, i.e., a space which is guided by the disease label and thus closer to the disease labels. We further assume that, under different transformation matrices and , the feature matrices X1 and X2 are respectively mapped to the same latent feature space , i.e.,
| (4) |
where denotes the regularizer that involves W1 and , e.g., l2,1-norm regularizer that encourages group sparsity for these two matrices, such as . However, there is an issue with this formulation, i.e., both the genotypes and phenotypes are assumed to be directly correlated with H, which could be untrue. Let us consider a special case of H, which is the corresponding disease label, and then Eq. (4) would end up selecting the discriminate SNPs and ROI-based neuroimaging features. But SNPs as genotype features are much less sensitive to the disease labels (or diagnostic performance) than the neuroimaging features [55], and thus should have taken a longer path to reach the joint latent feature space, as shown in Fig. 1. Accordingly, we redefine the objective function in Eq. (4) as follows,
| (5) |
where is a projection matrix, is an identity matrix, and the orthogonal constraint PTP = I ensures P to be a basis transformation matrix. In Eq. (5), we compute the latent feature space H to help us find the genotype-phenotype associations, but this H is not really used in analysis. Thus, by omitting the explicit computation of the joint feature matrix H, we propose to use a simplified alternative of Eq. (5), as follows,
| (6) |
Remarks.
The projection matrix P and the coefficient matrix W2 in Eq. (6) are used to map the genomic features to the joint latent space, to assist us in finding the associations between the SNPs and the neuroimaging phenotypes. Also note that, although we do not compute the latent feature representation H explicitly, the two modality data (X1 and X2) are still implicitly transformed into the joint feature space through the learning of W1, W2, and P. Furthermore, as shown in Fig. 1 and Eq. (6), the proposed model takes several measures to address the heterogeneity between the high-dimensional SNPs and the low-dimensional ROI-based MRI phenotypes. Specifically, it first maps the SNPs to an intermediate imaging-phenotype-like space via W2, and then projects both the imaging-phenotype-like features (from genotypes) and the original imaging phenotypes into a joint latent feature space.
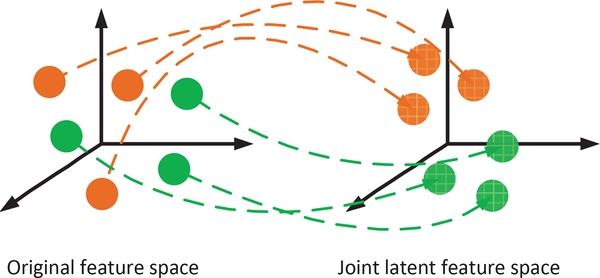
So far, the label information is still not exploited in Eq. (6). Inspired by [37], to learn a more meaningful joint latent feature space, in this study, we use linear discriminant analysis strategy to encourage compactness of intra-class samples in the joint latent feature space, as shown in Fig. 2. For example, for MRI data, if the i-th sample (X1)i and the j-th sample (X1)j are belonged to the same class (i.e., disease label), we would like to have their projections and to be closer to each other. Similar criterion can also be applied to the samples from the SNP data. Based on these criteria, the regularizer in Eq. (6) is given as,
| (7) |
where and are the corresponding Laplacian matrices for X1 and X2, respectively. The Laplacian matrix is defined as L1 = D1 − S1 [56], [57], where is the degree matrix, in which its i-th diagonal element is given as , and is the similarity matrix defined as
| (8) |
where y((X1)i) denotes the corresponding label value for the sample (X1)i. Similar formulation is also used to obtain the Laplacian matrix L2.
Fig. 2.
Illustration on how the label information is used in this BW-GWA study. The brown and green balls denote samples with different labels, where samples with the same color have the same labels. The dashed blue arrows denote the projection of the original features into the joint feature space. We constrain the samples with the same labels to be close to each other in the joint feature space by using symmetric normalized Laplacian operations (Eq. (7)).
Finally, by combining Eqs. (3), (6), and (7), we have the following final objective function,
| (9) |
where R(X1,X2,W1,W2,P) is given by Eq. (7), and β, γ, λ1 and λ2 are the regularization parameters. To ease the comprehension of the proposed formulation in Eq. (9), we have summarized the main notations in Table I. The properties of our proposed formulation are also summarized below.
TABLE I.
The main notations used in our proposed formulation in Eq. (9)
| Notation | Size | Description |
|---|---|---|
| X1 | d1 × n | Feature matrix for MRI data |
| X2 | d1 × n | Feature matrix for SNP data |
| W1 | d1 × h | Mapping matrix, it is used to map MRI features to a joint feature space |
| W2 | d2 × d1 | Mapping matrix, it is used to map SNP features to MRI feature space |
| P | h × d1 | Projection matrix |
| L1 | n × n | Laplacian matrix |
| L2 | n × n | Laplacian matrix |
| n | Number of subjects | |
| d1 | Dimension of MRI features | |
| d2 | Dimension of SNP features | |
| h | Dimension of the joint feature space | |
| β,γ,λ1,λ2 | Regularization parameters | |
The first term, i.e., , is a reconstruction term (or data fidelity term) which is mainly used to find the association between the SNP and MRI data. All the other terms are used to improve the reconstruction error of this term for the testing samples, for AD study. Looking from another angle, it can also be regarded as an intermediate-level feature learning for the SNP data, i.e., to first map the SNP data to a neuroimaging-feature-like space (i.e., ), before using the orthogonal projection matrix P to further project the mapped data into the label-guided joint latent feature space. This intermediate feature learning for the SNP data is also reasonable as it is high dimensional and less discriminative to the disease label than the neuroimaging data. Besides, we use ℓ2,1-norm regularizer for this term (rather than the popularly used Frobenius norm) to alleviate the issue about feature outliers [54], [58].
The second term, i.e., , is a joint feature projection term, to project the SNPs and the MRI phenotypes into a joint latent feature space, and assist the association study. We further utilize the diagnostic label information when learning the joint feature projection, by adding the Laplacian regularizer in the third term, so that the intra-class samples (i.e., diagnostic cohort) will be close to each other in the joint feature space.
We use ℓ2,1-norm regularizer to impose row-wise sparsity (i.e., all zero-value rows) on W1 and W2. As each row in W1 and each row in W2 corresponds to one ROI-based neuroimaging feature and one SNP, respectively, the row sparsity implies the selection of associated ROIs and SNPs. In addition, we do not impose ℓ2,1-norm on P, but rather use the orthogonal constraint to avoid the trivial solution, which has been used widely in many computer vision and machine learning applications [59].
C. Optimization
The objective function in Eq. (9) simultaneously learns W1, W2 and P. Since it is not jointly convex with respect to all the variables (i.e., W1, W2 and P), we can update each of these variables by fixing other variables iteratively. More specifically, we adopt the Augmented Lagrange Multiplier (ALM) [60] to solve the optimization problem specified in Eq. (9). We have provided the detailed optimization steps in Supplementary Materials of this manuscript.
IV. EXPERIMENTAL RESULTS AND ANALYSIS
In this section, we used ADNI dataset to evaluate our method. We evaluated our proposed method by using the associated SNPs to predict the MRI imaging phenotypes. Besides, using our proposed method, we also identified the subset of SNPs that are associated with AD-related imaging phenotypes and vice versa.
A. Experimental Setup
In order to verify the effectiveness of our proposed method, we compared it with some state-of-art methods, including Ridge Regression (RR) [61], Group-sparse Feature Selection (GFS) [30], sparse feature selection with a ℓ2,1 -norm regularizer (L21) [62], Structured-sparse Low-rank Regression model (SLR) [24], and Robust Feature Selection via joint ℓ2,1 -norm (RFS) [63]. For clarity, we also describe the details of these comparison methods below:
Ridge Regression (RR) [61]. RR employs a least square loss function to exploit the association between SNPs and MRI data (e.g., ROIs).
Group-sparse Feature Selection (GFS) [30]. GFS employs two types of regularizers, i.e., one that considers the group level structural information within the SNP data, and another that considers the sparsity among the SNP groups.
Sparse feature selection with a ℓ2,1 -norm regularizer (L21) [62]. L21 employs a least square loss function in combination with a ℓ2,1 regularizer to exploit the association among the features.
Structured-sparse Low-rank Regression model (SLR) [24]. SLR projects SNP data to MRI data (e.g., ROIs) via BAT, and the ℓ2,1 -norm is respectively imposed on both matrices A and B. SLR does not consider the phenotype outliers and label information in its formulation.
Robust Feature Selection via joint ℓ2,1 -norm (RFS) [63]. RFS imposes the ℓ2,1 -norm on both the loss function and the regularization term. But, it does not consider label information.
We also summarize the objective functions of all the comparison methods in Table II, where X1 and X2 denote the MRI phenotypes and the SNP data in our study, respectively. In summary, the objective functions of all the comparison methods consist of two parts, i.e., the reconstruction term and the regularization term. It is worth noting that the RFS method is the degraded version of our method, i.e., when we only adopt the genotype-to-phenotype linear regression model without using the joint latent space, as in Eq. (3).
TABLE II.
The objective functions for all the comparison methods.
| Method | Objective function |
|---|---|
| RR | |
| GFS | |
| L21 | |
| SLR | |
| RFS | minW ||WTX2–X1||2,1 + λ1 ||W||2,1 |
We used a 5-fold nested cross-validation to select the optimal regularization parameters for our method, i.e., β, γ, λ1 and λ2. Similarly, we also used the same method to select the optimal parameters for all the competing methods in this study. The best parameter values are determined by searching in the range of {10−3,10−2,...,102,103}. In addition, we empirically searched the value for the parameter h in the range of {10,20,...,80}. Based on our empirical results, we found that the RMSE performance of our proposed model is stable for the value of parameter h in the range of {20,...,60}. Thus, we empirically set the parameter h to 30 as its default parameter value. Finally, we used the Root-Mean-Square-Error (RMSE) of the genotype-to-phenotype predictions as our evaluation method.
After training our method using the training data, we obtained the coefficient matrix for the SNPs (W2), where each of its row corresponds to a SNP. We sorted the l2-norm of each row of W2, and selected the top {10,20,...,250} SNPs (that correspond to the largest row-wise l2-norm of W2) to predict the imaging phenotypes of the testing SNP data. For each method, we conducted five random repetitions of the 5-fold cross-validation experiments, and reported the average results as the final result. In addition, we also investigated how the selections of SNPs and ROIs are affected by the disease labels, as different disease labels would affect the implicitly learned joint latent feature space. Thus, we performed experiments using different combinations of disease label cohorts (called as tasks, for simplicity) as guidance, including AD/NC, MCI/NC, and AD/MCI/NC.
B. Performance Comparison
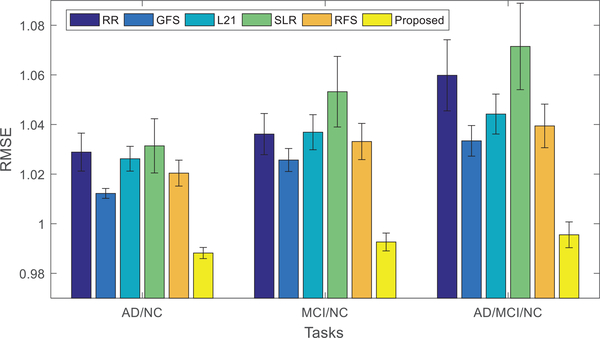
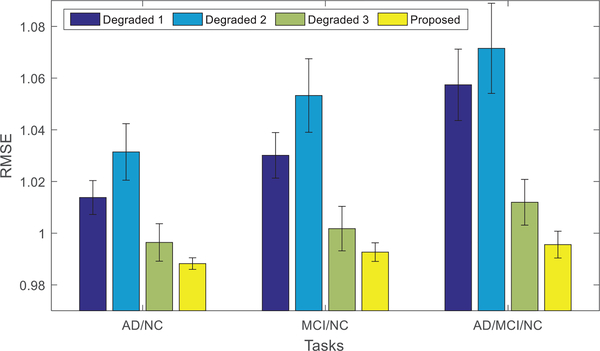
Fig. 3 shows the performances of all the comparison methods, using 3 different disease cohort combinations (i.e., tasks). The mean (bar height) and standard deviation (error bar) of the RMSE values of the comparison methods are shown. It can be easily observed that our proposed method consistently outperforms other state-of-the-art methods in all tasks, both in terms of mean and standard deviation. This can be explained by a few advantages of our proposed method as follows.
Fig. 3.
Performance comparison using different methods and different subsets of data (i.e., task or disease cohort combination). The mean of the root mean square errors (RMSE) obtained from the experiments of each method is plotted. Lower RMSE indicates better performance. In addition, the standard deviations of RMSE are also shown in the figure as error bars.
Our method adopts the ℓ2,1 -norm to model the reconstruction loss, which can effectively reduce the effects of phenotype outliers. The advantage of ℓ2,1 -norm over Frobenius-norm in modeling the reconstruction error can be seen by comparing the results given by RFS and L21 in Fig. 3. Note that, RFS and L21 methods only differ in their reconstruction terms, where RFS uses the ℓ2,1 -norm while L21 uses the Frobenius-norm, as shown in Table II. The results in Fig. 3 demonstrate that RFS is better than L21. However, as RFS only simply projects the SNP data to MRI data without considering label information, it performs inferior to our proposed method.
Our method projects the SNP and MRI data into a joint feature space, with the guidance from diagnostic label information. Note, diagnostic labels provide extra information for learning the joint feature space, which in turn helps the selection of associated SNP and MRI phenotypes.
C. Identification of Top Selected SNPs
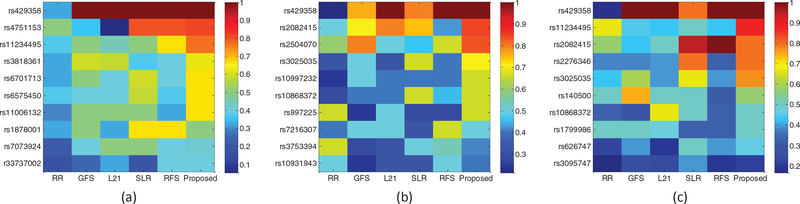
Fig. 4 shows the normalized selection frequency of the top 10 selected SNPs by using our method and all the comparison methods. From Fig. 4, we have the following observations:
Most methods include APOE-rs429358 as one of the top 10 associated SNPs, indicating its strong association with MRI phenotypes. In the literature, APOE-rs429358 has been shown to be highly correlated with the atrophy patterns of the entire cortex as well as medial temporal regions (including amygdala, hippocampus, and parahippocampal gyrus) in AD [64], [65], [33]. It is worth noting that, although APOE-rs429358 is one of the well-known major AD risk factors, it is not always selected by other comparison methods (i.e., with the normalized selection frequency less than 1), whereas our proposed BW-GWAS method always selects this SNP (i.e., with the normalized selection frequency being one) in all the three tasks. This is probably due to the fact that we have utilized disease label information in our association study, which make the results more related with AD and useful for AD study.
For AD/NC task, the top selected SNPs are from ApoE gene (e.g., rs429358), PICLAM gene (e.g., rs11234495), CR1 gene (e.g., rs3818361, rs6701713, r33737002), SERPINA13 gene (e.g., rs6575450), SORCS1 gene (e.g., rs7073924), etc. For MCI/NC task, the top selected SNPs are from ApoE gene (e.g., rs429358), CTNNA3 gene (e.g., rs997225, rs10997232, rs2082415), VEGF gene (e.g., rs3025035), etc. For AD/MCI/NC task, the top selected SNPs are from ApoE gene (e.g., rs429358), PICLAM gene (e.g., rs11234495), VEGF gene (e.g., rs3025035), SORL1 gene (e.g., rs2276346), etc. These findings are consistent with the existing GWA studies in [24], [66], [55], [67], [28], [68], [69]. Specifically, the ApoE gene and SORCS1 gene have been shown to have significant relationship with AD and MCI [66], [24], the VEGF gene has been shown to have greater risk for sporadic AD [67], and the PICALM gene affects AD risk primarily by modulating production, transportation, and clearance of β-amyloid peptide [70].
We also found some new associated SNPs that are worthy for further investigation, including TFAM gene (e.g., rs11006132), EBFs gene (e.g., rs4751153), ESR1 gene (e.g., rs2504070), BCR gene (e.g., rs140500). For example, some studies have investigated that the TFAMgene encodes the mitochondrial transcription factor A to control the transcription, replication, damage sensing, and repair of mitochondrial DNA (mtDNA), and lots of mutations in mtDNA have been found in the brains of patients with late-onset Alzheimer’s disease [71]. In other words, these SNPs are associated with the ROI-based MRI phenotypes, which could be helpful in AD pathogenesis.
Fig. 4.
Normalized selection frequency of the top 10 selected SNPs for six different methods using data from three different tasks: (a) AD/NC, (b) MCI/NC, (c) AD/MCI/NC.
In brief, that our main findings are consistent with the findings in the literature, has not only verified the effectiveness of our proposed method, but also justified our results. Besides, our method has also found other new associated SNPs that are worthy for further investigation in AD pathogenesis study.
D. Identification of Top Related ROIs
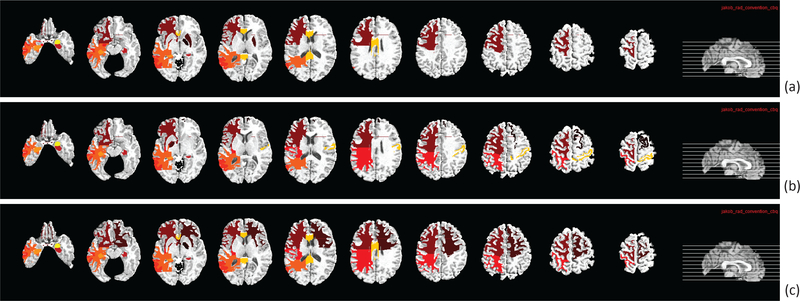
We are also interested in identifying the brain regions (i.e., ROIs) that are most associated with the top selected SNPs in this BW-GWA study. In our experiments, the most frequently selected ROI-based features in cross-validation experiments are regarded as the most AD-associated brain regions. These top ROIs and the associated SNPs are important as they can become potential biomarkers and genotypes for pathogenesis study and AD diagnosis. In our model, we can select the ROIs that are most associated with the selected SNPs by ranking for MRI data, where denotes the l2-norm of the i-th row in W1, and 93 is the total number of ROI features in MRI data. Fig. 5 shows the top ten ROIs by using our proposed method for different disease cohort combinations. Specifically, for AD/NC task, the top selected ROIs are frontal lobe WM left, hippocampal formation right, middle temporal gyrus left, temporal lobe WM left, hippocampal formation left, corpus callosum, and amygdala right. For MCI/NC task, the top selected ROIs are globus palladus left, hippocampal formation right, parietal lobe WM left, middle temporal gyrus left, hippocampal formation left, postcentral gyrus right, and amygdala right. For AD/MCI/NC task, the top selected ROIs are globus palladus right, frontal lobe WM right, hippocampal formation right, parietal lobe WM left, temporal lobe WM left, hippocampal formation left, and amygdala right. These findings are consistent with those reported in many AD diagnostic studies [72], [41], [16], [17], [73] and also genome-wide association studies [24], [33], [37]. Thus, the ROIs selected by our proposed method are considered trustworthy.
Fig. 5.
The top ten selected ROIs from MRI data by using our proposed method and the subsets of data from three different disease cohort combinations (i.e., classification tasks): (a) AD/NC, (b) MCI/NC, and (c) AD/MCI/NC.
E. Validation of Key Components
Experimental results so far have clearly demonstrated the effectiveness of our proposed method, as it can obtain lower RMSE by using a subset of SNPs to predict the MRI data. There are three key components in our proposed method, including 1) phenotype outliers robustness via the ℓ2,1 -norm of the data fidelity term, 2) the joint projection into a common feature space, and 3) the label guiding feature projection/selection. In the following text, we will verify the effectiveness of these three key components in our method. First, we use F-norm to replace the ℓ2,1 -norm in Eq. (9), so that the first term is changed to while the other terms remain unchanged; this model is denoted as “Degraded 1”. Second, if we do not project the two modalities into a joint latent feature space, the proposed model can be further degraded to
| (10) |
Remarks.
Without projecting the two modalities into a joint feature space, it will remove the joint projection term in Eq. (11). Besides, without P and W1, the term for label-guided feature selection can be automatically removed. In this case, our proposed method is degraded into RFS method, and it is denoted as “Degraded 2”.
Third, if we do not use label information in our method, i.e., removing symmetric normalized Laplacian operation for guiding feature selection, we can obtain another degraded model denoted as “Degraded 3”, with its objective function described as
| (11) |
Fig. 6 shows the RMSE performance comparison of our proposed method and the three degraded models. From Fig. 6, it can be clearly seen that our proposed method performs better than its degraded counterparts (without one of the key components).
Fig. 6.
The average RMSE of our method and three degraded versions of our proposed methods (where lower RMSE indicates better performance).
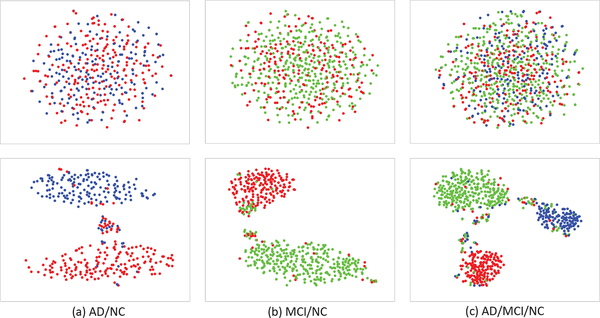
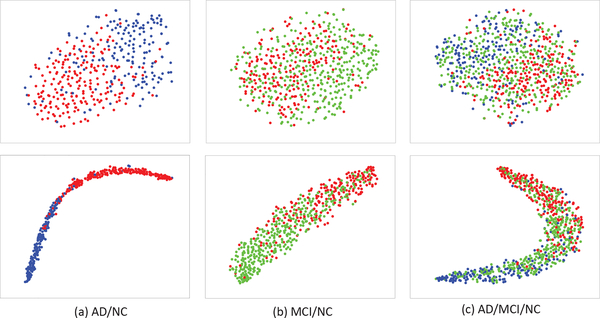
In addition, in order to evaluate the effectiveness of Laplacian regularizer (i.e., the third term in Eq. 9) in encouraging the intra-class sample compactness and class separation when learning the label-guided joint feature space, we define an intra-inter class distance ratio as separation measure. More specifically, we use the ratio of mean intra-class squared distance to mean inter-class squared distance. Intuitively, if our Laplacian regularization is effective, we will have smaller distance among intra-class samples and larger distance between two class centes after the joint feature projection, resulting smaller intra-inter class distance ratio. We show the detailed computation steps for this separation measure as Algorithm 1 in Table III. Table IV shows the comparison results, i.e., intra-inter class distance ratios before and after the joint feature projection, using MRI and SNP data from different disease cohort combinations. As expected, all the ratios have decreased after the joint feature projection. Furthermore, as a qualitative measure, we also visualize the sample distributions before and after the joint feature projection in Fig. 7 and Fig. 8, by using t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm [74]. From Fig. 7 and Fig. 8, it can be seen that the intraclass samples become closer after the joint feature projection, for both the SNP and MRI data. In conclusion, we have quantitatively and qualitatively showed that our label-guided joint feature space has closer intra-class samples and better label separation, compared with the original feature space.
TABLE III.
Algorithm 1 The detailed steps for computing an intra-inter class distance ratio as a separation measure. The Smaller ratio denotes higher intra-class compactness and label separation.
| Input:Feature matrix X and the number of class C. |
|
Step 1: Compute the mean feature vector for the i-th class, i.e., where xij denote the j-th sample from the i-th class, and Ni is
the number of samples in the i-th class; Step 2: Compute the mean intra-class squared distance (i.e., intra-class variance) for the i-th class, i.e., , and then compute the mean intra-class variance, i.e., ; Step 3: Compute the mean inter-class squared distance, i.e., , where is the mean of the class means; Step 4: Compute the intra-inter class distance ratio, i.e., ; |
| Output: Intra-inter class distance ratio r. |
TABLE IV.
Comparison of intra-inter class distance ratios before and after the joint feature projection for the MRI and SNP data.
| Tasks | MRI | SNP | ||
|---|---|---|---|---|
| Before | After | Before | After | |
| AD/NC | 1.5867 | 0.3036 | 9.2221 | 0.3198 |
| NC/MCI | 2.9566 | 0.8053 | 11.4125 | 0.3601 |
| AD/MCI/NC | 4.3203 | 1.2392 | 17.9856 | 0.7740 |
Fig. 7.
Visualization of sample distributions (based on t-SNE [74]) before (top row) and after (bottom row) the joint feature projection, using the SNP data from different disease cohort combinations (Red: NC, blue: AD, and green: MCI).
Fig. 8.
Visualization of sample distributions (based on t-SNE [74]) before (top row) and after (bottom row) the joint feature projection, using the MRI data from different disease cohort combinations (Red: NC, blue: AD, and green: MCI).
Besides, from Fig. 7 and Fig. 8, it seems that SNP data are more separable in the joint feature space, compared with the MRI data. This is interesting, as genotype features (of SNP data) should be much less sensitive to the disease labels than the neuroimaging features (of MRI data). This is probably due to the fact that the points in Fig. 7 consist of samples from all the data in the training and testing sets, and the more separable samples in the joint feature space are mostly coming from the training set. In other words, SNP data are kind of “overfitting” to the label in the joint feature space. In contrast, although MRI data seem less separable than the SNP data in the joint feature space, they have less “overfitting” issue, as we can still observe a drop in intra-inter class distance ratio for the testing samples, when we examine further. Nevertheless, this “overfitting” issue did not affect much on the performance of our proposed method, as shown in Fig. 6, since we are focusing on BW-GWA study, not classification.
Further, we have computed the intra-inter class distance ratio in the neuroimaging-feature-like space for SNP data. The results for three disease cohort combinations (i.e., AD/NC, MCI/NC, and AD/MCI/NC) are 0.3218, 0.3655, and 0.7819, respectively. This means that the disease cohort separation has also been significantly improved for the neuroimaging-feature-like space of SNP data. However, when compared these results with the results in Table IV, the intra-inter class distance ratios are only slightly improved after joint feature projection. The small improvement of intra-inter class distance ratio from the neuroimaging-feature-like space to the joint feature space could be explained by the fact that the learning of W2 is intrinsically guided by the label information. As the label-guided joint feature space and the SNP to MRI projections are learned together, the label information could guide the learning of W2, which consequently improves the disease cohort separation in the neuroimaging-feature-like space for SNP data.
V. CONCLUSION
In this paper, we propose a novel joint projection learning and sparse regression model to study the associations between the genetic variations (characterized by SNPs) and neuroimaging phenotypes (characterized by ROI-based GM volumetric features). Guided by label information of each subject, our proposed method can uncover the interrelation between genetic data and brain image phenotypes, and find the most associated SNPs and ROIs. We achieve these by projecting the genetic variations and neuroimaging phenotypes into a joint latent feature space, where the samples with same labels are constrained to be close. In this joint latent feature space, the heterogeneity between the SNP and MRI data is reduced, as they are much closer to each other in the disease label space. Thus, their correlation can be exploited more effectively. Furthermore, our main objective term to find the associations between the SNPs and neuroimaging phenotypes, if looks from another angle, is equivalent to first intermediately map the SNP data into a neuroimaging-like feature space, before introducing an orthogonal projection matrix to project the mapped SNP data to the joint feature space. The intermediate mapping of SNP data is necessary to alleviate the high dimensionality and less discriminative issues of the SNP data. The orthogonal property of the projection matrix, on the other hand, enables a more efficient solution for our objective function. The experimental results have validated the effectiveness of our proposed method when compared with some state-of-the-art methods, in terms of RMSE value of the reconstruction errors between the mapped SNP and MRI data. Besides, we have also verified the effectiveness of the key components in our proposed method, i.e., 1) the use of ℓ2,1 -norm to overcome the phenotype outliers, 2) the mapping to the joint feature space, and 3) the use of label information in guiding feature projection and feature selection, by comparing our proposed method with its degraded counterparts (without one of the key components in our proposed method). Furthermore, the selected associated SNPs and ROIs are also consistent with the findings in the literature, confirming the effectiveness of our proposed method. In conclusion, our proposed method is able to identify important associated SNPs and ROIs for future pathogenesis of AD and possibly also other neuropsychological diseases.
Supplementary Material
Acknowledgments
This research was supported in part by NIH grants EB006733, EB008374, EB009634, MH100217, AG041721 and AG042599.
Footnotes
Contributor Information
Tao Zhou, Department of Radiology and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA (taozhou.dreams@gmail.com)..
Kim-Han Thung, Department of Radiology and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA (henrythung@gmail.com)..
Mingxia Liu, Department of Radiology and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA (mxliu@med.unc.edu)..
Dinggang Shen, Department of Radiology and Biomedical Research Imaging Center, University of North Carolina, Chapel Hill, NC 27599 USA, and also with the Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, Republic of Korea (dgshen@med.unc.edu).
REFERENCES
- [1].Lin D, Cao H, Calhoun VD, and Wang Y, “Sparse models for correlative and integrative analysis of imaging and genetic data,” Journal of Neuroscience Methods, vol. 237, pp. 69–78, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Thung K-H and et al. , “Neurodegenerative disease diagnosis using incomplete multi-modality data via matrix shrinkage and completion,” NeuroImage, vol. 91, pp. 386–400, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Liu M and et al. , “Inherent structure-based multiview learning with multitemplate feature representation for Alzheimer’s disease diagnosis,” IEEE Trans. Biomed. Eng, vol. 63, no. 7, pp. 1473–1482, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wee CY, Yap PT, and et al. , “Resting-state multi-spectrum functional connectivity networks for identification of mci patients,” PloS one, vol. 7, no. 5, pp. e37828, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Thung KH, Yap PT, and et al. , “Conversion and time-to-conversion predictions of mild cognitive impairment using low-rank affinity pursuit denoising and matrix completion,” Medical image analysis, vol. 45, pp. 68–82, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Zhang Y, Zhang H, and et al. , “Inter-subject similarity guided brain network modeling for mci diagnosis,” in International Workshop on Machine Learning in Medical Imaging Springer, 2017, pp. 168–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zhou L, Wang Y, and et al. , “Hierarchical anatomical brain networks for MCI prediction: revisiting volumetric measures,” PloS one, vol. 6, no. 7, pp. e21935, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Thung Kim-H., Yap P-T, and Shen D, “Multi-stage diagnosis of Alzheimer’s disease with incomplete multimodal data via multi-task deep learning,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, pp. 160–168. Springer, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Alzheimer’s Association, “2015 Alzheimer’s disease facts and figures.,” Alzheimer’s & dementia: the journal of the Alzheimer’s Association, vol. 11, no. 3, pp. 332, 2015. [DOI] [PubMed] [Google Scholar]
- [10].Thung K-H, Adeli E, Yap P-T, and Shen D, “Stability-weighted matrix completion of incomplete multi-modal data for disease diagnosis,” in International Conference on Medical Image Computing and Computer-Assisted Intervention Springer, 2016, pp. 88–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Zhang Y and et al. , “Hybrid high-order functional connectivity networks using resting-state functional mri for mild cognitive impairment diagnosis,” Scientific Reports, vol. 7, no. 1, pp. 6530, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhou T and et al. , “Feature learning and fusion of multimodality neuroimaging and genetic data for multi-status dementia diagnosis,” in International Workshop on Machine Learning in Medical Imaging Springer, 2017, pp. 132–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Thung K-H, Yap P-T, Adeli-M E, and Shen D, “Joint diagnosis and conversion time prediction of progressive mild cognitive impairment (pMCI) using low-rank subspace clustering and matrix completion,” in MICCAI. NIH Public Access, 2015, vol. 9351, p. 527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Fan Y, Rao H, Hurt H, and et al. , “Multivariate examination of brain abnormality using both structural and functional mri,” NeuroImage, vol. 36, no. 4, pp. 1189–1199, 2007. [DOI] [PubMed] [Google Scholar]
- [15].Zhang C, Adeli E, Zhou T, Chen X, and Shen D, “Multi-layer multi-view classification for Alzheimer’s disease diagnosis.,” in AAAI, 2018. [PMC free article] [PubMed] [Google Scholar]
- [16].Convit A, De Asis J, and et al. , “Atrophy of the medial occipitotemporal, inferior, and middle temporal gyri in non-demented elderly predict decline to Alzheimer’s disease,” Neurobiology of Aging, vol. 21, no. 1, pp. 19–26, 2000. [DOI] [PubMed] [Google Scholar]
- [17].Misra C, Fan Y, and Davatzikos C, “Baseline and longitudinal patterns of brain atrophy in MCI patients, and their use in prediction of shortterm conversion to AD: results from ADNI,” NeuroImage, vol. 44, no. 4, pp. 1415–1422, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Liu M, Zhang J, Yap P-T, and Shen D, “View-aligned hypergraph learning for Alzheimer’s disease diagnosis with incomplete multimodality data,” Medical Image Analysis, vol. 36, pp. 123–134, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Liu M and et al. , “Relationship induced multi-template learning for diagnosis of Alzheimer’s disease and mild cognitive impairment,” IEEE Trans. Med. Imaging, vol. 35, no. 6, pp. 1463–1474, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Petrella JR, Coleman RE, and Doraiswamy PM, “Neuroimaging and early diagnosis of Alzheimer’s disease: a look to the future,” Radiology, vol. 226, no. 2, pp. 315–336, 2003. [DOI] [PubMed] [Google Scholar]
- [21].Price AL, Patterson NJ, and et al. , “Principal components analysis corrects for stratification in genome-wide association studies,” Nature Genetics, vol. 38, no. 8, pp. 904, 2006. [DOI] [PubMed] [Google Scholar]
- [22].Nalls Mike. A. and et al. , “Large-scale meta-analysis of genome-wide association data identifies six new risk loci for Parkinson’s disease,” Nature Genetics, vol. 46, no. 9, pp. 989–993, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Morris GP and et al. , “Population genomic and genome-wide association studies of agroclimatic traits in sorghum,” Proceedings of the National Academy of Sciences, vol. 110, no. 2, pp. 453–458, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Zhu X, Suk H-I, Huang H, and Shen D, “Structured sparse low-rank regression model for brain-wide and genome-wide associations,” in International Conference on Medical Image Computing and Computer-Assisted Intervention Springer, 2016, pp. 344–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Medland S, Jahanshad N, Neale B, and Thompson P, “Whole-genome analyses of whole-brain data: working within an expanded search space,” Nature Neuroscience, vol. 17, no. 6, pp. 791–800, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Huang M and et al. , “Fvgwas: Fast voxelwise genome wide association analysis of large-scale imaging genetic data,” NeuroImage, vol. 118, pp. 613–627, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Shen L, Kim S, and et al. , “Whole genome association study of brain-wide imaging phenotypes for identifying quantitative trait loci in MCI and AD: A study of the ADNI cohort,” NeuroImage, vol. 53, no. 3, pp. 1051–1063, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Harold D and et al. , “Genome-wide association study identifies variants at CLU and PICALM associated with Alzheimer’s disease,” Nature Genetics, vol. 41, no. 10, pp. 1088–1093, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Wang H and et al. , “From phenotype to genotype: an association study of longitudinal phenotypic markers to Alzheimer’s disease relevant SNPs,” Bioinformatics, vol. 28, no. 18, pp. i619–i625, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Wang H and et al. , “Identifying quantitative trait loci via group-sparse multitask regression and feature selection: an imaging genetics study of the ADNI cohort,” Bioinformatics, vol. 28, no. 2, pp. 229–237, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Vounou M, Nichols TE, and et al. , “Discovering genetic associations with high-dimensional neuroimaging phenotypes: a sparse reduced-rank regression approach,” NeuroImage, vol. 53, no. 3, pp. 1147–1159, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Vounou M, Janousova E, and et al. , “Sparse reduced-rank regression detects genetic associations with voxel-wise longitudinal phenotypes in Alzheimer’s disease,” NeuroImage, vol. 60, no. 1, pp. 700–716, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Wang X, Yan J, Yao X, and et al. , “Longitudinal genotype-phenotype association study via temporal structure auto-learning predictive model,” in International Conference on Research in Computational Molecular Biology Springer, 2017, pp. 287–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Wang H and et al. , “Identifying disease sensitive and quantitative trait-relevant biomarkers from multidimensional heterogeneous imaging genetics data via sparse multimodal multitask learning,” Bioinformatics, vol. 28, no. 12, pp. i127–i136, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Bralten J and et al. , “Association of the Alzheimer’s gene SORL1 with hippocampal volume in young, healthy adults,” American Journal of Psychiatry, vol. 168, no. 10, pp. 1083–1089, 2011. [DOI] [PubMed] [Google Scholar]
- [36].Batmanghelich N and et al. , “Joint modeling of imaging and genetics,” in International Conference on Information Processing in Medical Imaging. NIH Public Access, 2013, vol. 23, p. 766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Hao X, Yao X, and et al. , “Identifying multimodal intermediate phenotypes between genetic risk factors and disease status in Alzheimer’s disease.,” Neuroinformatics, vol. 14, no. 4, pp. 439–452, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Jack CR et al. , “The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods,” Journal of Magnetic Resonance Imaging, vol. 27, no. 4, pp. 685–691, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].An L and et al. , “A hierarchical feature and sample selection framework and its application for Alzheimer’s disease diagnosis,” Scientific Reports, vol. 7, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Shi F, Yap P-T, and et al. , “Altered structural connectivity in neonates at genetic risk for schizophrenia: a combined study using morphological and white matter networks,” Neuroimage, vol. 62, no. 3, pp. 1622–1633, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Zhang D, Shen D, and ADNI, “Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer’s disease,” NeuroImage, vol. 59, no. 2, pp. 895–907, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Thung K-H, Wee C-Y, Yap P-T, and Shen D, “Identification of progressive mild cognitive impairment patients using incomplete longitudinal MRI scans,” Brain Structure and Function, vol. 221, no. 8, pp. 3979–3995, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Sled JG, Zijdenbos AP, and Evans AC, “A nonparametric method for automatic correction of intensity nonuniformity in MRI data,” IEEE Trans. Med. Imaging, vol. 17, no. 1, pp. 87–97, 1998. [DOI] [PubMed] [Google Scholar]
- [44].Wang Y et al. , “Knowledge-guided robust MRI brain extraction for diverse large-scale neuroimaging studies on humans and non-human primates,” PloS one, vol. 9, no. 1, pp. e77810, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Zhang Y and et al. , “Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm,” IEEE Trans. Med. Imaging, vol. 20, no. 1, pp. 45–57, 2001. [DOI] [PubMed] [Google Scholar]
- [46].Kabani NJ, “3D anatomical atlas of the human brain,” NeuroImage, vol. 7, pp. P–0717, 1998. [Google Scholar]
- [47].Shen D and Davatzikos C, “Hammer: hierarchical attribute matching mechanism for elastic registration,” IEEE Trans. Med. Imaging, vol. 21, no. 11, pp. 1421–1439, 2002. [DOI] [PubMed] [Google Scholar]
- [48].Saykin A and et al. , “Alzheimer’s disease neuroimaging initiative biomarkers as quantitative phenotypes: Genetics core aims, progress, and plans,” Alzheimer’s & dementia, vol. 6, no. 3, pp. 265–273, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Bertram L et al. , “Systematic meta-analyses of Alzheimer’s disease genetic association studies: the alzgene database,” Nature Genetics, vol. 39, no. 1, pp. 17–23, 2007. [DOI] [PubMed] [Google Scholar]
- [50].Wang J, Wang Q, and et al. , “Multi-task diagnosis for autism spectrum disorders using multi-modality features: A multi-center study,” Human brain mapping, vol. 38, no. 6, pp. 3081–3097, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Argyriou A, Evgeniou T, and Pontil M, “Convex multi-task feature learning,” Machine Learning, vol. 73, no. 3, pp. 243–272, 2008. [Google Scholar]
- [52].Wang H, Nie F, and Huang H, “Multi-view clustering and feature learning via structured sparsity.,” in ICML, 2013, pp. 352–360. [Google Scholar]
- [53].Zhu X, Suk H-I, Wang L, Lee S-W, and Shen D, “A novel relational regularization feature selection method for joint regression and classification in AD diagnosis,” Medical image analysis, vol. 38, pp. 205–214, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Wong WK and et al. , “Low-rank embedding for robust image feature extraction,” IEEE Trans. Image Process, vol. 26, no. 6, pp. 2905–2917, 2017. [DOI] [PubMed] [Google Scholar]
- [55].Peng J, An L, Zhu X, Jin Y, and Shen D, “Structured sparse kernel learning for imaging genetics based Alzheimer’s disease diagnosis,” in International Conference on Medical Image Computing and Computer-Assisted Intervention Springer, 2016, pp. 70–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Cai D, He X, and ey al., “Graph regularized nonnegative matrix factorization for data representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 8, pp. 1548–1560, 2011. [DOI] [PubMed] [Google Scholar]
- [57].Zhou T and et al. , “Graph regularized and locality-constrained coding for robust visual tracking,” IEEE Trans. Circuits Syst. Video Technol, vol. 27, no. 10, pp. 2153–2164, 2017. [Google Scholar]
- [58].Jiang W and et al. , “The ℓ2,1 -norm stacked robust autoencoders for domain adaptation,” in AAAI, 2016, pp. 1723–1729. [Google Scholar]
- [59].Zhang C, Hu Q, Fu H, Zhu P, and Cao X, “Latent multi-view subspace clustering,” in CVPR, 2017, vol. 30, pp. 4279–4287. [Google Scholar]
- [60].Bertsekas DP, Constrained optimization and Lagrange multiplier methods, Academic Press, 2014. [Google Scholar]
- [61].Hoerl AE and et al. , “Ridge regression: applications to nonorthogonal problems,” Technometrics, vol. 12, no. 1, pp. 69–82, 1970. [Google Scholar]
- [62].Argyriou A, Evgeniou T, and Pontil M, “Multi-task feature learning,” NIPS, vol. 19, pp. 41, 2007. [Google Scholar]
- [63].Nie F and et al. , “Efficient and robust feature selection via joint ℓ2,1 norms minimization,” in NIPS, 2010, pp. 1813–1821. [Google Scholar]
- [64].Pereira J, Cavallin L, and et al. , “Influence of age, disease onset and ApoE4 on visual medial temporal lobe atrophy cut-offs,” Journal of Internal Medicine, vol. 275, no. 3, pp. 317–330, 2014. [DOI] [PubMed] [Google Scholar]
- [65].Risacher S, Kim S, Shen L, and et al. , “The role of apolipoprotein E (ApoE) genotype in early mild cognitive impairment (E-MCI),” Frontiers in Aging Neuroscience, vol. 5, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Chiappelli M and et al. , “VEGF gene and phenotype relation with Alzheimer’s disease and mild cognitive impairment,” Rejuvenation Research, vol. 9, no. 4, pp. 485–493, 2006. [DOI] [PubMed] [Google Scholar]
- [67].Del R, Scarlato M, Ghezzi S, and et al. , “Vascular endothelial growth factor gene variability is associated with increased risk for AD,” Annals of Neurology, vol. 57, no. 3, pp. 373–380, 2005. [DOI] [PubMed] [Google Scholar]
- [68].Osoegawa K and et al. , “Identification of novel candidate genes associated with cleft lip and palate using array comparative genomic hybridization,” Journal of Medical Genetics, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Busby V and et al. , “α-T-catenin is expressed in human brain and interacts with the wnt signaling pathway but is not responsible for linkage to chromosome 10 in Alzheimer’s disease,” Neuromolecular Medicine, vol. 5, no. 2, pp. 133–146, 2004. [DOI] [PubMed] [Google Scholar]
- [70].Xu W, Tan L, and Yu J, “The role of picalm in Alzheimer’s disease,” Molecular Neurobiology, vol. 52, no. 1, pp. 399–413, 2015. [DOI] [PubMed] [Google Scholar]
- [71].Alvarez V, Corao AI, and at al., “Mitochondrial transcription factor A (TFAM) gene variation and risk of late-onset Alzheimer’s disease,” Journal of Alzheimer’s disease, vol. 13, no. 3, pp. 275–280, 2008. [DOI] [PubMed] [Google Scholar]
- [72].Zhu X, Suk H, Lee S-W, and Shen D, “Subspace regularized sparse multitask learning for multiclass neurodegenerative disease identification,” IEEE Trans. Biomed. Eng, vol. 63, no. 3, pp. 607–618, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Fox N and Schott J, “Imaging cerebral atrophy: normal ageing to Alzheimer’s disease,” The Lancet, vol. 363, no. 9406, pp. 392–394, 2004. [DOI] [PubMed] [Google Scholar]
- [74].Maaten LV and Hinton G, “Visualizing data using t-sne,” Journal of Machine Learning Research, vol. 9, no. Nov, pp. 2579–2605, 2008. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.