Conformational Dynamics in the Core of Human Y145Stop Prion Protein Amyloid Probed by Relaxation Dispersion NMR

Abstract

Microsecond to millisecond timescale backbone dynamics of the amyloid core residues in Y145Stop human prion protein (PrP) fibrils were investigated by using ¹⁵N rotating frame (R_1ρ) relaxation dispersion solid-state nuclear magnetic resonance spectroscopy over a wide range of spin-lock fields. Numerical simulations enabled the experimental relaxation dispersion profiles for most of the fibril core residues to be modelled by using a two-state exchange process with a common exchange rate of 1000 s⁻¹, corresponding to protein backbone motion on the timescale of 1 ms, and an excited-state population of 2%. We also found that the relaxation dispersion profiles for several amino acids positioned near the edges of the most structured regions of the amyloid core were better modelled by assuming somewhat higher excited-state populations (~5–15%) and faster exchange rate constants, corresponding to protein backbone motions on the timescale of ~100–300 μs. The slow backbone dynamics of the core residues were evaluated in the context of the structural model of human Y145Stop PrP amyloid.

Table of Contents Graphic

Backbone dynamics in the core of Y145Stop human prion protein amyloid fibrils are investigated by using ¹⁵N rotating frame relaxation dispersion solid-state NMR. Protein backbone motions on timescales ranging from ~0.1 to 1 ms and excited-state conformer populations ranging from ~2 to 15% are detected for the different core residues, and evaluated in the context of the structural model of Y145Stop human prion protein amyloid.

1. Introduction

Transmissible spongiform encephalopathies, a family of fatal neurodegenerative conditions that includes Creutzfeld-Jakob disease in humans and ‘mad cow’ disease, involve the conformational rearrangement of an a α-helical brain prion protein from its native cellular form (PrP^C) to a pathogenic misfolded amyloid-like form (PrP^Sc).^[1–2] Although not currently understood at the atomistic level, the three-dimensional structures adopted by the PrP^Sc aggregates appear to be intimately linked to prion toxicity and ease of disease transmission.^[3–5]

The C-terminally truncated human Y145Stop prion protein variant (huPrP23–144), which is associated with a hereditary PrP cerebral amyloidosis,^[6] has previously been shown to display in vitro the key features of mammalian prion propagation including strain variability and cross-seeding barriers.^[7] Remarkably, mouse PrP23–144 amyloid generated from recombinant protein has also recently been found to trigger transmissible prion disease in mice.^[8] To gain atomic level structural insights into PrP23–144 amyloid propagation we have carried out a series of solid-state nuclear magnetic resonance (NMR) studies for a set of homologous recombinant proteins corresponding to the human, mouse and Syrian hamster amino acid sequences as well as related mutants.^[9–15] These studies concluded that huPrP23–144 fibrils consist of two protofilaments, where each protofilament contains a structured compact core region of ~30 amino acids (aa) spanning residues ~112–141 with parallel in-register β-sheet architecture and a large dynamically disordered ~90-residue N-terminal tail domain.

Interestingly, these experiments also revealed considerable variations in the NMR spectral intensities suggestive of the presence of conformational dynamics for multiple core residues, with the backbone signals for residues Y128 and M129 located in a flexible loop segment roughly in the middle of the core region not detectable at all in conventional solid-state NMR spectra recorded at temperatures exceeding approximately −20 °C.^[9–10] Additional experiments designed to probe the backbone one-bond ¹⁵N-¹H^N, ¹³Cα−¹Hα and ¹⁵N-¹³CO/¹³Cα dipolar couplings revealed uniformly high dipolar order parameters (S ~ 0.9–1) for all the amyloid core residues consistent with the presence of only small-amplitude motions of the different bond vectors around their equilibrium positions on the sub-μs timescale. In contrast, considerable variations in transverse spin relaxation rates were observed for the backbone ¹H, ¹³C and ¹⁵N nuclei, suggestive of the presence of slower motions, on the timescale of ~0.1–1 ms, for the core residues.^[10] A more detailed analysis of these slower motions could not be performed, however, since the initial experiments were conducted on fully protonated fibril samples at moderate (~10 kHz) magic angle spinning (MAS) rates, where considerable residual ¹H-¹H dipolar couplings contribute significantly to the decay of spin coherences, partially masking the dynamics-induced relaxation.

Recent advances in solid-state NMR methodology, including the availability of fast MAS probes combined with protein deuteration and proton spin dilution as well as proton detection for enhanced sensitivity,^[16–22] have enabled the detailed investigation of backbone dynamics for a variety of proteins and protein assemblies in the solid phase over a wide range of timescales^[23–29] including the slow μs-ms motions that are of interest for huPrP23–144 amyloid fibrils in the present study. Of particular utility in the context of characterizing these μs-ms motions in a residue-specific manner are multidimensional rotating frame (R_1ρ) relaxation dispersion (RD) experiments^[29–34] for amide ¹⁵N nuclei as a function of the spin-lock radiofrequency (RF) field strength spanning both the low-field (or Bloch-McConnell) regime^[31] and the near rotary resonance (v_RF ≈ v_MAS)^[30−31] regime, where both ¹⁵N-¹H dipolar couplings and ¹⁵N chemical shift anisotropy are effectively recoupled under MAS.^[35] In the Bloch-McConnell regime, these RD experiments provide information about the modulation of isotropic ¹⁵N chemical shifts due to the μs-ms protein backbone dynamics, while the near rotary resonance RD (NERRD) measurements report on the angular fluctuations of the ¹⁵N-¹H^N bond vectors on this timescale.

Here we employ the above ¹⁵N RD experiments to investigate, in residue-specific fashion, the μs-ms timescale motions in the amyloid β-core of huPrP23–144 fibrils. Analysis of these data is used to extract the key motional parameters including the exchange rate, the minor conformer population and the amplitude of angular motions.

2. Results and Discussion

All experiments were performed using huPrP23–144 amyloid fibrils generated from uniformly ²H,¹³C,¹⁵N-labeled protein that was back-exchanged in a 1:1 mixture of H₂O and D₂O as described in the Experimental Section. The resulting 50% ¹H incorporation at the exchangeable amide proton sites in combination with rapid sample spinning at 40 kHz frequency, provides sufficient suppression of residual ¹H-¹H dipolar couplings to enable quantitative measurements of residue-specific ¹⁵N R_1ρ rate constants for a broad range of spin-lock fields with high-resolution and sensitivity by using ¹H detection.

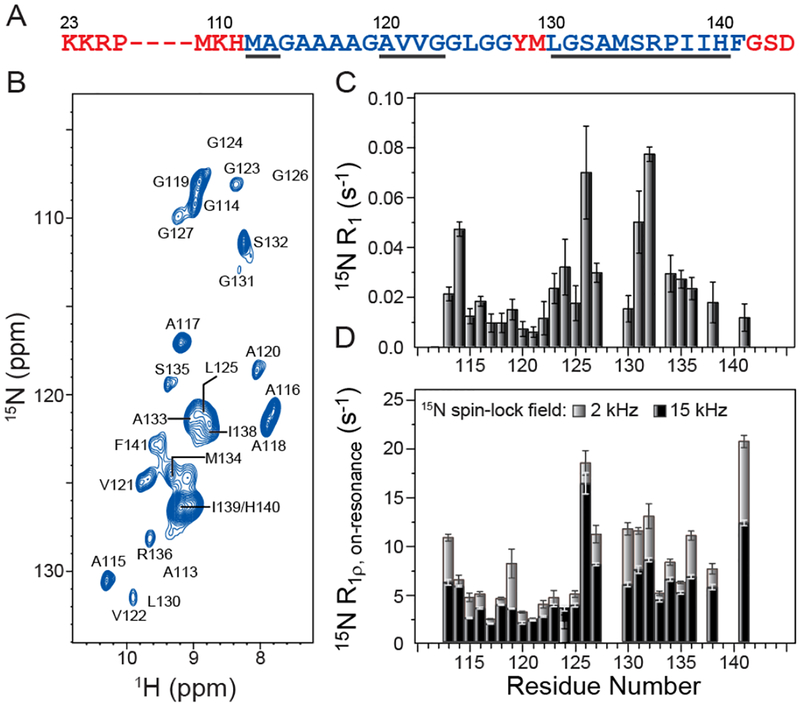
The 2D ¹⁵N-¹H cross-polarization spectrum shown in Figure 1B shows that the vast majority of the cross-peaks for individual residues are well-resolved, with typical ¹H linewidths of ~0.1–0.15 ppm indicative of high degree of sample homogeneity and effective suppression of homonuclear ¹H-¹H dipolar couplings. The assignments of the ¹⁵N-¹H correlations in this spectrum could be readily performed by recording a pair of 3D hCANH and hCONH spectra^[36] (Supporting Information (SI) Figure S1) and taking advantage of the previously reported ¹⁵N, ¹³Cα and ¹³CO chemical shift assignments.^[9]

Figure 1.

(A) Amino acid sequence of huPrP23–144, with the most rigid amyloid core residues shown in blue. The dynamically disordered N- and C-terminal residues and two flexible residues located within the core region, which are not detectable in conventional solid-state NMR experiments, are shown in red. Regions with the highest β-strand propensity predicted by TALOS-N^[37] based on backbone ¹³C and ¹⁵N chemical shifts are underlined. (B) 2D ¹⁵N-¹H chemical shift correlation spectrum of amyloid fibrils generated from ²H,¹³C,¹⁵N-labeled huPrP23–144 back-exchanged in a 1:1 mixture of H₂O and D₂O. The spectrum was recorded in 2 h at 800 MHz ¹H frequency, 40 kHz MAS rate, and sample temperature of ~10 °C. Due to large variations in resonance intensities, for clarity the cross-peaks are drawn with the lowest contour at 75 times the rms noise level. The locations of cross-peaks for residues A113, G124, G126, and L130, for which the signal-to-noise is below this threshold, are indicated. (C) Residue-specific ¹⁵N R₁ values determined using the pulse sequence shown in SI Figure S2B. (D) Residue-specific ¹⁵N R_1ρ values determined using the pulse sequence shown in SI Figure S2A with ¹⁵N spin-lock fields of 2 kHz or 15 kHz as indicated.

To rapidly assess the extent of microsecond timescale motions for the huPrP23–144 amyloid core residues, we measured the residue-specific ¹⁵N R_1ρ rate constants for ¹⁵N spin-lock fields of 2 and 15 kHz using the pulse sequence shown in SI Figure S2A. Additionally, in order to account for off-resonance effects in the ¹⁵N R_1ρ experiments (see Experimental Section), ¹⁵N longitudinal relaxation (R₁) rate constants were determined using the pulse sequence shown in SI Figure S2B. The residue-specific ¹⁵N R₁ and ¹⁵N R_{1ρ, on-resonance} values are shown in Figure 1C and 1D, respectively. These data indicate that both the ¹⁵N R₁ and ¹⁵N R_1ρ rate constants are generally smallest for the least solvent-exposed hydrophobic core residues (aa ~115–125),^[15] while larger relaxation rate constants are observed for most of the remaining residues, particularly those located near the N- and C-terminal edges of the amyloid core region and bracketing the flexible region (aa ~127–130) within the core. Importantly, the ¹⁵N R_1ρ values for many of the core residues recorded with the 2 kHz spin-lock field were found to be considerably larger than the corresponding values recorded with the 15 kHz field (on average the ¹⁵N R_{1ρ, on-resonance} values were ~8 s⁻¹ and ~5.5 s⁻¹ for the 2 kHz and 15 kHz spin-lock fields, respectively). This residue-specific relaxation dispersion is strongly indicative of the presence of slow protein backbone motions throughout the huPrP23–144 amyloid core. It is also quite remarkable that, relative to one another, the residue-specific ¹⁵N transverse relaxation (R₂) rate constants obtained for the fully protonated huPrP23–144 amyloid in our earlier work^[10] are in reasonable qualitative agreement with the ¹⁵N R_1ρ values determined in the present study. Note, however, that the former R₂ rate constants were a factor of ~10–20 larger due to the incomplete averaging of ¹H-¹H dipolar couplings, while the current R_1ρ data are largely free of deleterious dipolar dephasing effects.

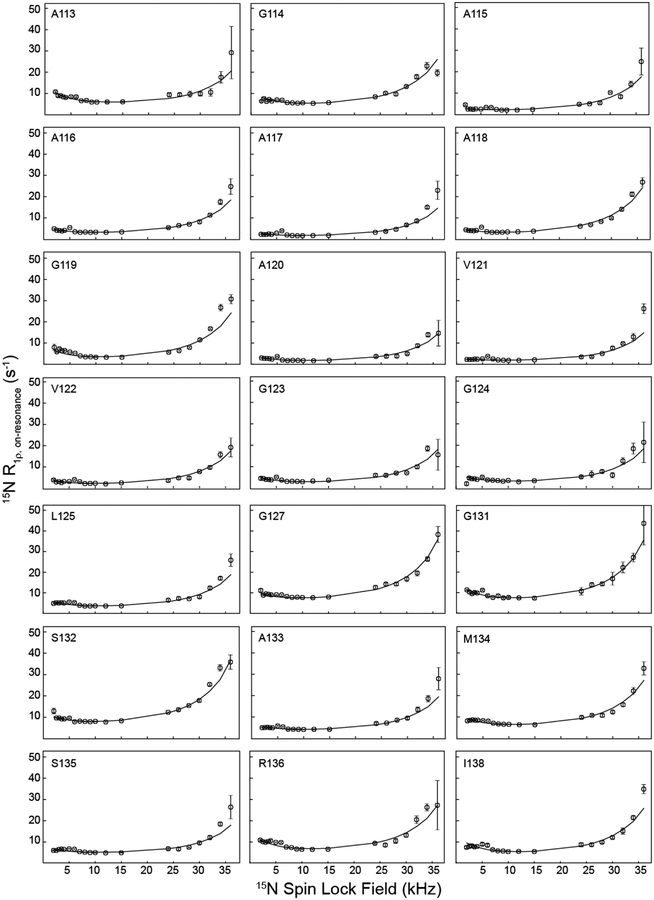
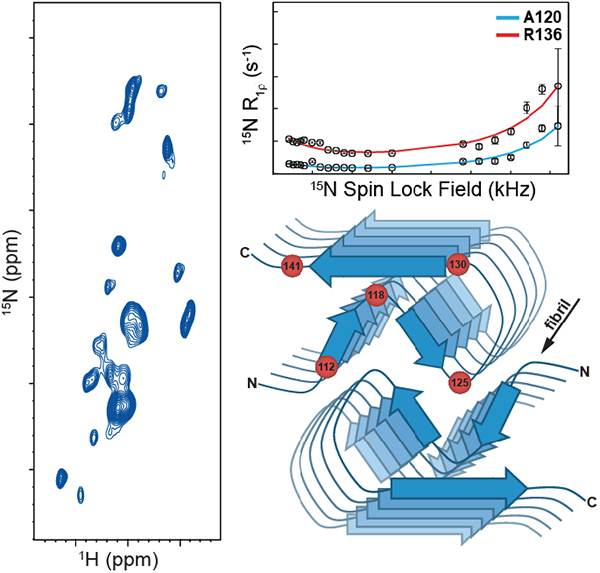
Having established the existence of slow protein motions in the core of huPrP23–144 fibrils, in order to gain a more comprehensive insight into these motions we recorded complete residue-specific ¹⁵N R_1ρ RD profiles at 40 kHz MAS rate spanning the Bloch-McConnell (2–15 kHz ¹⁵N spin-lock field) and near n = 1 rotary resonance (24–36 kHz ¹⁵N spin-lock field) regimes. Figure 2 shows these complete RD profiles for most of the huPrP23–144 amyloid core residues, with representative relaxation trajectories for individual residues at different spin-lock fields shown in SI Figures S3 and S4. Overall, the experimental data are of high quality owing to the use of ¹H detection, with relatively small uncertainties in the ¹⁵N R_1ρ values extracted for different spin-lock fields. Inspection of the experimental data in the 2–15 kHz spin-lock field regime reveals prominent ¹⁵N R_1ρ RD effects for some of the residues (e.g., A113, L130 and F141) but rather subtle ones for most others, especially the hydrophobic core aa ~115–125, making it difficult to extract accurate motional parameters from this regime alone. Interestingly, we also observe that virtually all residues display considerable broadening of the n = 1 rotary resonance condition as the ¹⁵N spin-lock field is increased from 24 to 36 kHz, due to reorientation of the amide ¹⁵N CSA and ¹⁵N-¹H dipolar coupling tensors, suggestive of the presence of μs-ms timescale motions throughout the sequence.^[31]

Figure 2.

Residue-specific ¹⁵N R_1ρ RD profiles for huPrP23–144 amyloid fibrils at 800 MHz ¹H frequency. Experimental data are shown as open circles, and numerical fits used to extract the global exchange rate and minor excited-state population, as well as site-specific parameters Δω and α (c.f., Figure 3) are shown as solid lines. RD profiles for residues G126, L130, and F141, which were not fit as well by the global exchange model, are shown in SI Figure S5 along with individual residue-specific fits. RD profiles for residues I139 and H140 could not be obtained due to insufficient resolution in the 2D ¹⁵N-¹H spectrum.

To gain more quantitative insight into the huPrP23–144 amyloid backbone dynamics we performed a multi-parameter numerical fit of the ¹⁵N R_1ρ data for the entire range of spin-lock fields investigated. Briefly, numerical simulations of ¹⁵N R_1ρ relaxation in the presence of a dynamic two-state model were used to generate in silico RD profiles as a function of the exchange rate constant (k_ex), population of the minor, excited-state conformer (p_B), and residue-specific chemical shift difference (Δω) and angular amplitude (α) parameters. A grid search of these computed RD profiles was then performed to identify the best-fits to residue-specific experimental RD data (see Experimental Section). While fits of particularly high quality could be obtained by modeling the ¹⁵N R_1ρ RD profiles for individual residues one-by-one with completely independent values of k_ex and p_B (in addition to the residue-specific Δω and α parameters), we instead opted for a simpler, more physically-relevant motional model where RD profiles for all residues are fit simultaneously to a single, global excited-state population and exchange rate. This treatment of the data yielded best-fit k_ex and p_B parameters of 1000 s⁻¹ and 2%, respectively, with reasonable quality fits for the vast majority of the residues as seen in Figure 2 (i.e., for these residues the improvement in χ² between experimental and calculated RD profiles obtained via independent fitting vs. by using the global exchange model was statistically insignificant). Note that the exchange rate of 1000 s⁻¹ obtained by the global fitting of the complete RD profiles for all huPrP23–144 residues is considerably lower than the lowest spin-lock field (2 kHz) that was practically attainable in our experiments, due to coherent contributions to R_1ρ that can become dominant at sufficiently low spin-lock field amplitudes.^[38] Given that the largest modulations of ¹⁵N R_1ρ in the low-field Bloch-McConnell regime are expected for exchange rates that are on the order of the spin-lock field, this provides a rationale for why relatively small RD effects were observed for many residues in the 2–15 kHz regime and also underscores the importance of utilizing RD data over a wide range of spin-lock fields spanning both the Bloch-McConnell and near rotary resonance regimes in order to reliably identify protein backbone motions occurring on the ~ms timescale.

Figures 3A and 3B, respectively, show plots of the Δω and α values as a function of residue number extracted from the global fit of the ¹⁵N R_1ρ RD profiles with k_ex = 1000 s⁻¹ and p_B = 2%. As noted above, these parameters report on the structural differences between the major and minor states undergoing exchange via the isotropic ¹⁵N chemical shift difference (Δω) and the angle between the ¹⁵N-¹H bond vectors (α) in the two states. While both of these parameters display some scatter for individual residues, we note that most of the hydrophobic amino acids (aa ~115–125) tend to have the smallest Δω (~3 ppm or less), while Δω exceeds ~3.5–4 ppm for many of the remaining residues. These trends in Δω show a reasonable correlation with the extracted residue-specific α values, where most residues in the region ~115–125 have α in the ~10–15° range while most other residues appear to have larger angular fluctuations (α ~ 15–25°). Altogether, these results imply that the most restricted millisecond timescale motions occur for the most solvent-protected residues ~115–125 found in the hydrophobic core of the fibril^[15] (Figure 3C), while the more solvent-exposed residues located at the edges of the amyloid core, the C-terminal β-strand and the adjacent partly flexible loop exhibit larger amplitude dynamics on this timescale. Finally, we note that for three residues (G126, L130 and F141) the comparison of χ² values for individual fits versus the global fit using an F-test revealed a statistically significant improvement with the individual fits. The global and individual fits as well as the fit parameters for these residues are shown in SI Figure S5. While the values of Δω and α obtained with both fits were comparable overall, the individual residue fits yielded considerably higher minor state populations (p_B ~ 5–15%) and exchange rates (k_ex ~ 3000–7500 s⁻¹) relative to the global fit. Given that all three residues are located near the most flexible regions of the huPrP23–144 amyloid core, including the C-terminus (F141) and loop preceding the C-terminal β-strand (G126 and L130) it is feasible that these amino acids are associated with somewhat faster backbone motions (on a timescale of hundreds of microseconds) and elevated excited state populations compared to the remaining amyloid core residues.

Figure 3.

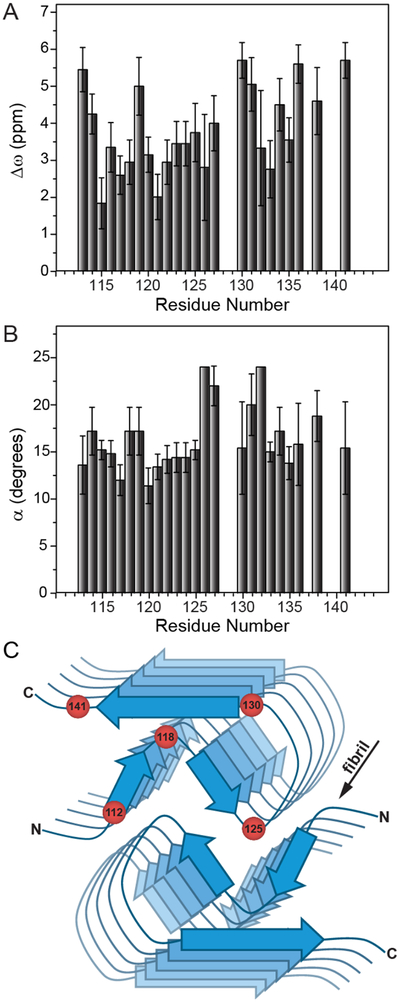
Plots of residue-specific (A) Δω and (B) α values extracted from the global fit of ¹⁵N R_1ρ RD profiles for huPrP23–144 amyloid with k_ex = 1000 s⁻¹ and p_B = 2%. The residue-specific Δω and α values and uncertainties shown in the plots correspond to the average and standard deviation for these values obtained from a set of 10 calculated RD profiles having the lowest χ² to the experimental data. Note that the α values obtained for residues 126 and 132 using the global fit were near the edge of the grid for that parameter, and consequently no error bars are reported for these two residues. (C) Schematic structural model of the huPrP23–144 fibril with approximate locations of several amino acid residues indicated by red spheres.

3. Concluding Remarks

In summary, we have carried out a detailed analysis of slow protein backbone motions in the β-core of huPrP23–144 amyloid fibrils by using solid-state NMR ¹⁵N R_1ρ RD measurements over a wide range of spin-lock fields. The residue-specific RD profiles spanning both the Bloch-McConnell and near rotary resonance regimes could be modelled for most of the amyloid core residues by assuming a common exchange rate of 1000 s⁻¹, corresponding to protein backbone dynamics on the timescale of 1 ms, and a 2% excited-state population. Additionally, several residues located near the edges of the most structured segments of the huPrP23–144 fibril core, including G126, L130, and F141, were found to exhibit somewhat faster exchange, corresponding to backbone motions on the timescale of ~100–300 μs, and higher excited-state populations on the order of 5–15%.

While it remains unclear whether the slow μs-ms timescale motions occurring for residues located throughout the huPrP23–144 fibril core have any biological consequence, taken together with earlier reports of extensive motions on multiple timescales for other protein fibrils,^[27] our findings further underscore the notion that, in spite of their ordered nature, amyloids can be highly dynamic entities. The presence of these μs-ms protein backbone dynamics in huPrP23–144 amyloid is also consistent with our earlier observation of significant amide hydrogen-deuterium exchange taking place for many residues within the parallel-in-register β-sheet regions on timescales as short as several hours.^[15] One hypothesis is that these slow backbone motions in huPrP23–144 amyloid originate in the partly flexible loop region (aa ~126–129) as well as the N- and C-terminal amyloid core edges around residues 112 and 141, respectively, and propagate into the more structured regions of the β-core. This hypothesis is further supported by the finding that the solvent-exposed residues appear to undergo somewhat larger amplitude motions relative to the more solvent-protected hydrophobic residues located in the interior of the fibril.

4. Experimental Section

4.1. Sample Preparation

Overexpression of uniformly ²H, ¹³C, ¹⁵N−labeled huPrP23–144 using M9 minimal media containing ²H,¹³C-glucose (2 g/L) and ¹⁵N-ammonium chloride (1 g/L) in D₂O and protein purification were carried out as described previously.^[13] The purified lyophilized protein was dissolved in excess 1:1 H₂O:D₂O mixture at a concentration of 60 μM and incubated at room temperature for 1 h. The completeness of the amide hydrogen-deuterium exchange was quantified by comparing 1D ¹H NMR spectra for the 50% back-exchanged huPrP23–144 sample and a fully protonated reference sample of identical concentration. The protein solution was then concentrated to 400 μM using a 3 kDa molecular weight cutoff Amicon centrifugal filter device, and amyloid fibril formation was initiated by adding potassium phosphate pH 6.4 buffer in 1:1 H₂O:D₂O to a final concentration of 50 mM. Fibrils were routinely characterized using atomic force microscopy to confirm sample homogeneity,^[13] washed with two aliquots of 50 mM potassium phosphate pH 6.4 buffer in 1:1 H₂O:D₂O, and centrifuged directly into a 1.9 mm Bruker zirconia rotor. The rotor was sealed using slow-setting epoxy glue to prevent potential sample dehydration during the experiments.

4.2. NMR Spectroscopy

Solid-state NMR studies were performed on an 800 MHz Bruker Avance III HD spectrometer equipped with a 1.9 mm ¹H-¹³C-¹⁵N MAS probe. The MAS rate was set to 40 kHz, the effective sample temperature was maintained at ~10°C, and all experiments utilized low-power pulse sequences and ¹H detection for optimal sensitivity.

To establish the resonance assignments in 2D ¹⁵N-¹H spectra, which served as the basis for residue-specific ¹⁵N spin relaxation measurements described below, 3D hCONH and hCANH spectra were recorded using the pulse sequences of Pintacuda and co-workers^[36] and analyzed in combination with available ¹⁵N, ¹³Cα and ¹³CO chemical shifts.^[9] Briefly, for magnetization transfer these experiments employed ¹H-¹³C’/¹³Cα cross-polarization (CP) with 4 ms duration and a linear ramp on the ¹H channel, ¹³C’/¹³Cα−¹⁵N double-quantum SPECIFIC CP^[39] with ¹⁵N and ¹³C field strengths of ~30 kHz and ~10 kHz, respectively, and a tangent ramp on the ¹³C channel, and ¹⁵N-¹H CP with 0.6 ms duration and a linear ramp on the ¹H channel. Water suppression was achieved immediately prior to the ¹⁵N-¹H CP by using a series of long ¹H pulses with xy-phase alternation,^[40] ~18 kHz field strength and total duration of 300 ms. The indirect ¹⁵N and ¹³C’/¹³Cα dimensions utilized 5 ms of evolution with XiX ¹H decoupling.^[41] Additionally, during ¹³C’/¹³Cα evolution the one-bond ¹³C’−¹³Cα J-couplings were suppressed by using a frequency-selective rSNOB pulse^[42] with 250 μs duration applied at the ¹³C’ or ¹³Cα frequency as appropriate, and in both the ¹³C’/¹³Cα and ¹⁵N dimensions the ¹³C-¹⁵N J-evolution was suppressed by applying a 180° pulse on the ¹⁵N and ¹³C, respectively. The direct dimension consisted of 30 ms of ¹H evolution with WALTZ-16 ¹⁵N decoupling.^[43]

The residue-specific ¹⁵N R_1ρ relaxation rate constants were determined in a pseudo-3D manner by using the pulse scheme in Figure S2A, with 14 ms of ¹⁵N evolution in the indirect dimension and most of the remaining key parameters identical to those noted above for the 3D hCONH and hCANH experiments. The experiments employed ¹⁵N spin-lock fields ranging from 2 to 36 kHz, with the RF field amplitudes calibrated as described previously.^[31] For ¹⁵N spin-lock field strengths up to 15 kHz, a series of ¹⁵N-¹H correlation spectra was recorded for spin-lock durations of 1, 5, 25, 50, 75, 100, 125 and 150 ms. For spin-lock field strengths between 24 and 36 kHz durations of 1, 2.5, 5, 10, 20 and 30 ms were used (note that the 30 ms spin-lock duration was omitted for the highest, 36 kHz, ¹⁵N field strength to stay within the probe duty cycle limits for the 2 s recycle delay that was utilized). Additionally, in order to correct for off-resonance effects in the ¹⁵N R_1ρ measurements, the residue-specific ¹⁵N R₁ were determined using the pulse scheme in Figure S2B with relaxation delays of 0.00001, 1, 3 and 5 s.

4.3. Data Analysis

All NMR data were processed using NMRPipe.^[44] Resonance assignments were established by analyzing the spectra in SPARKY,^[45] and nmrglue^[46] was used to extract the peak volumes in the series of 2D ¹⁵N-¹H spectra and perform data fitting to decaying single exponentials in order to obtain the residue-specific ¹⁵N R_1ρ and ¹⁵N R₁ rate constants. The “on-resonance” ¹⁵N R_1ρ values, corrected for off-resonance effects, were then calculated according to the following equation: R_{1ρ, on-resonance} = R_1ρ/sin² θ - R₁/tan² θ, where θ = arctan(ω₁/Ω) with ω₁ and Ω being the spin-lock field strength and resonance offset, respectively.

Numerical simulations of the residue-specific ¹⁵N R_1ρ RD profiles in the entire 2 to 36 kHz range of spin-lock fields were performed using in-house programs within the GAMMA simulation library^[47] akin to previously described work.^[48] A two-spin (¹H-¹⁵N) system was generated in Liouville space and duplicated for the two exchanging states, connected by the exchange rate constants. The evolution of spin coherence under the ¹⁵N spin-lock RF field of varying strength was simulated by a stepwise time integration of the Liouville-von Neumann equation with standard powder averaging. The ¹⁵N R_1ρ values were obtained by a numerical fit of the obtained coherence decay profiles, assuming a mono-exponential decay. While in general relaxation decays in spinning solids are not mono-exponential,^{[34, 49]} the data analysis scheme employed here, where both experimental and simulated data are treated identically and fitted to mono-exponential functions, nevertheless allows for quantitative comparison.

The above simulations of ¹⁵N R_1ρ as a function of ¹⁵N spin-lock field strength were repeated on a 4D grid by systematically varying the following parameters: (1) the population of the minor excited state (p_B), (2) the exchange rate between the states (k_ex), (3) the ¹⁵N chemical shift difference between the exchanging states (Δω) and (4) the angular change of the ¹H-¹⁵N dipolar and ¹⁵N CSA tensors between the exchanging states (α; for a graphical representation see Fig. 17 of ref. ^[49]). Note that the simulated R_1ρ profiles exhibit – on top of the exponential decay – periodic oscillations due to dipolar recoupling, which become quite significant especially near the n = 1 rotary resonance condition. This has also been noted in earlier studies,^[34] and is experimentally not observed here because the distribution of RF fields in the coil dampens this effect.^[34] No attempt to account for the inhomogeneity of the spin-lock RF field was attempted in our simulations due to the heavy computational load that would be required for such calculations. For comparison with experimental R_1ρ profiles, a vertical offset in R_1ρ, which accounts for relaxation from other sources than the two-site exchange model, was also included, and the best-fit to the experimental data was obtained via a systematic grid-search on the basis of the χ² value. As noted in the Results and Discussion section, simulations of the experimental ¹⁵N R_1ρ RD profiles were performed both by using independent p_B and k_ex values for each residue and by assuming a common p_B and k_ex for all residues. To assess whether the improvement in fit quality obtained by independently fitting the data for individual residues was statistically significant, an F-test was used to compare the residue-­specific χ² values obtained with the global vs. independent fitting procedure.