Population Shift Mechanism for Partial Agonism of AMPA Receptor

Abstract

α-amino-3-hydroxy-5-methyl-4-isoaxazolepropionic acid (AMPA) ionotropic glutamate receptors mediate fast excitatory neurotransmission in the central nervous system, and their dysfunction is associated with neurological diseases. Glutamate binding to ligand-binding domains (LBDs) of AMPA receptors induces channel opening in the transmembrane domains of the receptors. The T686A mutation reduces glutamate efficacy so that the glutamate behaves as a partial agonist. The crystal structures of wild-type and mutant LBDs are very similar and cannot account for the observed behavior. To elucidate the molecular mechanism inducing partial agonism of the T686A mutant, we computed the free-energy landscapes governing GluA2 LBD closure using replica-exchange umbrella sampling simulations. A semiclosed state, not observed in crystal structures, appears in the mutant during simulation. In this state, the LBD cleft opens slightly because of breaking of interlobe hydrogen bonds, reducing the efficiency of channel opening. The energy difference between the LBD closed and semiclosed states is small, and transitions between the two states would occur by thermal fluctuations. Evidently, glutamate binding to the T686A mutant induces a population shift from a closed to a semiclosed state, explaining the partial agonism in the AMPA receptor.

Introduction

The α-amino-3-hydroxy-5-methyl-4-isoaxazolepropionic acid (AMPA) receptor is a member of the ionotropic glutamate receptor (iGluR) family, which mediates excitatory neurotransmission throughout the central nervous system (1, 2). AMPA receptors play a crucial role in fast excitatory transmission, and the change in the number of AMPA receptors in nerve membranes relates to synaptic plasticity, that is, learning and memory (3, 4). AMPA receptor dysfunction is associated with numerous neurological disorders such as epilepsy, amyotrophic lateral sclerosis, and Alzheimer’s disease (5). The receptors are assemblies of four identical subunits each organized into three domains: the amino-terminal domain, the ligand-binding domain (LBD), and the transmembrane domain (TMD). The LBD consists of the D1 and D2 lobes and forms a clamshell shape. The ligand-binding site resides in its cleft region (Fig. 1 A) (6). Recently, the structures of the full-length GluA2 receptor have been determined by X-ray crystallography (7, 8) and cryoelectron microscopy (cryo-EM) (9, 10, 11), which reveal that the structural mechanism of iGluR gating (12) involves agonist-induced cleft closure at the LBD, a conformational change transmitted by LBD-TMD linkers to open the channel gate, and the resulting influx of ions.

Figure 1.

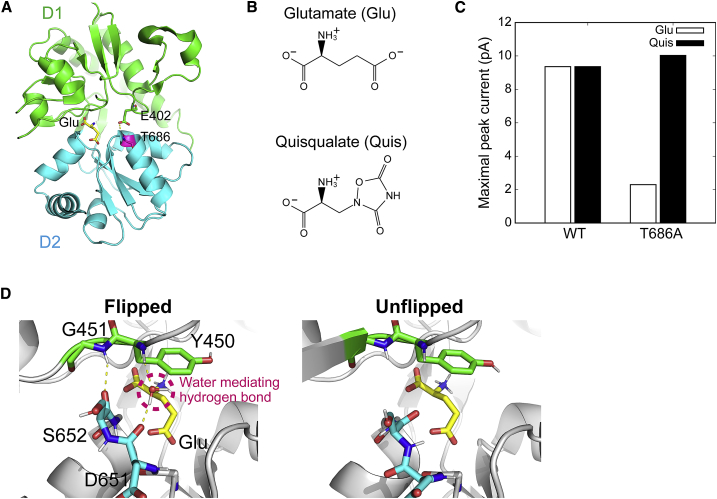
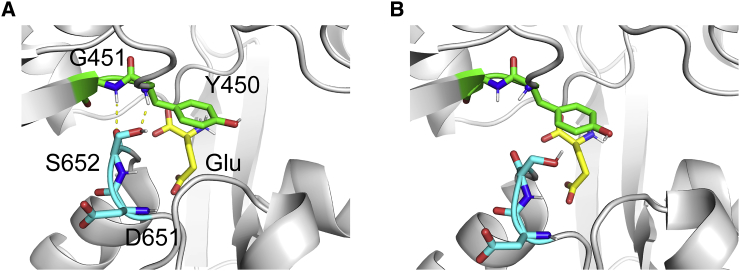
Structure of ligand-binding domain (LBD) and effect of T686A mutation on agonist efficacy. (A) A cartoon representation of the LBD of GluA2 with glutamate (Glu). The bound Glu, E402, and T686 are shown in stick representation. The D1 and D2 lobes are colored green and cyan, respectively. The glutamate and T686 are colored yellow and magenta, respectively. A yellow dashed line represents hydrogen-bonding interaction. (B) Chemical structures of Glu and Quis. (C) Maximal peak currents induced by channel opening upon ligand binding. These data are taken from the experimental results of Zhang et al. (19). (D) Flipped and unflipped conformations of the peptide backbone of D651 and S652. Yellow dashed lines represent hydrogen-bonding interactions. To see this figure in color, go online.

Full agonists exhibit maximal channel activation with accompanying complete LBD cleft closure, whereas partial agonists close the cleft to lesser extents depending on ligand size, which correlates with submaximal channel activation (6, 13). Earlier studies suggested that the degree of channel activation depends on the residence time of the completely closed conformation of the LBD cleft (14, 15, 16, 17). In the case of partial agonists, complete closure of the LBD cleft is less frequent, and channel opening is less probable. Partial agonists are useful for clarification of the molecular mechanism of iGluR gating because they provide the insights into the relationship between structure and function.

The closed conformation of the LBD is stabilized by a number of ligand-protein and D1-D2 interlobe hydrogen bonds. Disruption of the cross-cleft interaction between T686 and E402 significantly increases half-maximal effective concentration values for two agonists, glutamate (Glu) and quisqualate (Quis) (Fig. 1 B), and speeds recovery from desensitization (18). Zhang et al. (19) have investigated the effects of mutating T686 to alanine by observing the agonist-evoked current in patches containing wild-type (WT) GluA2 channels and comparing them with those of the T686A mutant. In patches expressing WT channels, Glu and Quis produced similar peak currents, whereas in T686A channels, Glu yields only 20% of the current evoked by Quis (Fig. 1 C), suggesting that Glu acts as a partial agonist for the T686A mutant. X-ray crystallography data show that WT and T686A mutant LBD structures are similar in structure: the root mean-square displacement (RMSD) between Glu-bound WT (Protein Data Bank (PDB): 1FTJ (6)) and Glu-bound T686A (PDB: 3B6Q (19)) is 0.30 Å, and that between Glu-bound T686A and Quis-bound T686A (PDB: 3B6T (19)) is 0.14 Å. Thus, the crystal structures do not provide insight into differences in glutamate efficacy. The stability of the LBD closed state may be decreased by the mutation. Alternatively, the Glu-bound T686A mutant may have intermediate or hidden inactive states. Neither of these possibilities can be easily attainable by X-ray crystallography.

Free energies associated with ligand binding and ensuing conformational changes, which underlie the physical processes behind receptor function, are often difficult to access experimentally. Molecular dynamics (MD) simulations can be extremely helpful here. For example, simulations have provided the free-energy landscapes governing GluA2 LBD cleft closure upon binding a variety of ligands and revealed key interactions in the cleft associated with different closure states (20, 21). Similarly, the free-energy landscapes for GluN1–3 LBDs of N-methyl-D-aspartate receptors characterized their conformational spaces (22) and explained their partial agonism (23).

In our study, we investigated the effect of the T686A mutation on GluA2 LBD bound with Glu or Quis by performing MD simulations. This study would contribute toward a general understanding of the molecular mechanism underlying the partial agonism at AMPA receptors. We calculated the free-energy landscapes corresponding to the opening/closing of the cleft using the replica-exchange umbrella sampling (REUS) method (24). In REUS simulations, exchange of replicas allows the system to escape local minima, accelerating convergence of the free-energy calculation. The peptide bond between D651 and S652 of GluA2 LBD can adopt one of two conformations: flipped and unflipped. In the flipped conformation, a direct hydrogen bond forms between S652 and G451, and a water-mediated hydrogen bond forms between D651 and Y450. In the unflipped conformation, the backbone carbonyl atoms of D651-S652 are rotated away from the D1 lobe (Fig. 1 D), preventing the formation of hydrogen bonds. Crystal structures of the apo state and those with bound antagonist or partial agonist are mainly observed in the unflipped conformation, whereas those with bound full agonists exist in the flipped conformation, although the unflipped conformation is also observed in some cases. In this study, we examined both the conformations. Starting from the LBD conformation, and estimating the effects of cleft closure on the displacement of LBD-TMD linkers, we found a semiclosed state in addition to the closed state for the Glu-bound T686A mutant, whereas only a closed state was observed for the other complexes. The semiclosed conformations are in good agreement with the most stable conformation of a partial agonist (S)-4-AHCP-bound WT. Based on these results, we construct a molecular mechanism for LBD closing and channel opening.

Methods

Modeling of proteins and ligands

The Gaussian 09 program (25) was used to optimize the geometries and calculate the electrostatic potentials at the Hartree-Fock/6-31G^∗ level for Glu, Quis, and (S)-4-AHCP. The atomic partial charges were obtained by the restrained electrostatic potential approach (26). The remaining parameters for the ligands were determined by the general Amber force field (27) using the antechamber module of Amber Tools 16 (28).

The LBDs of Glu-bound WT, Quis-bound WT, Glu-bound T686A mutant, and Quis-bound T686A mutant were used. The complexes are hereafter referred to as WT-Glu, WT-Quis, T686A-Glu, and T686A-Quis, respectively. The atomic models for WT and T686A mutant of the ligand-bound GluA2 LBD monomers were constructed from the following X-ray crystal structures: PDB: 1FTJ (6) (WT-Glu), 1MM6 (29) (WT-Quis), 3B6Q (6) (T686A-Glu), and 3B6T (19) (T686A-Quis). “Flipped” models were constructed from 1FTJ chain C, 1MM6 chain A, 3B6Q chain A, and 3B6T chain A for the respective systems. The “unflipped” model of WT-Glu was constructed from 1FTJ chain A. Because there are no crystal structures in the “unflipped” conformation for WT-Quis, T686A-Glu, and T686A-Quis, we built the unflipped conformation for these models using the loop-modeling routine of the MODELER program (30). For the loop modeling, the D651-S652 conformation from 1FTJ chain A was used as a template. Missing amino acid residues and side-chain atoms were also added in MODELER. Crystallographic waters were included in our models. The same procedure as described above was used to construct the model of WT-(S)-4-AHCP using PDB: 1WVJ chain A (31). The Amber ff99SBildn force field (32) was used for protein and ions, and the TIP3P (transferable intermolecular potential with three points) model (33) was used for water molecules. Water molecules were placed around the complex model with an encompassing distance of 10 Å. The systems include roughly 17,000 water molecules. Na⁺ and Cl⁻ ions were added to maintain physiological salinity (150 mM) and to neutralize the system. Molecular graphics images were generated using PyMOL (34).

MD simulations

All simulations were performed using the GENESIS program (35, 36). A cutoff length of 9.0 Å without any smoothing functions was employed for Lennard-Jones interactions, whereas long-range electrostatic interactions were calculated using the smooth particle mesh Ewald summation method (37). All bonds involving hydrogen atoms were kept rigid using the SHAKE (38) and SETTLE (39) algorithms. A time step of 2 fs was used for integration. Each system was first equilibrated in the NPT (isobaric-isothermal) ensemble, maintaining the temperature and the pressure at 300 K and 1 atm, respectively, using the Bussi thermostat and barostat (40). After NPT equilibration, a 100-ns NVT (isochoric-isothermal) equilibration at 300 K was performed. To retain the closed conformation during equilibration, the ${\xi }_1$ and ${\xi }_2$ distances were restrained to their values in the crystal structure by employing a harmonic potential with a force constant of 1 kcal/mol/${\text{Å}}^2$. ${\xi }_1$ describes the distance between the centers of mass (COMs) of L479-I481 in the D1 lobe and S654-T655 in the D2 lobe. ${\xi }_2$ describes the distance between the COMs of L401-S403 in the D1 lobe and T686-A687 in the D2 lobe. After NVT equilibration, a 500-ns production run of conventional MD was performed without any restraints under NVT conditions using the Bussi thermostat (41). The equilibrated systems were also used as starting structures for subsequent REUS simulations.

REUS

100 windows were used for REUS by employing ${\xi }_1$ and ${\xi }_2$ as the reaction coordinates to describe the opening/closing of the LBD monomer. All REUS simulations were performed under NVT conditions with the Bussi thermostat (41). The windows were spaced 0.6 Å along ${\xi }_1$ from 8.0 to 13.4 Å and 0.6 Å along ${\xi }_2$ from 7.0 to 12.4 Å. Harmonic restraints were used at each window using a force constant of 4 kcal/mol/${\text{Å}}^2$. The initial coordinate for each window was constructed from the equilibrated structure by gradually changing ${\xi }_1$ and ${\xi }_2$. Exchanges between neighboring windows were attempted every 5,000 time steps (10 ps) and were accepted or rejected according to a Metropolis criterion. Each window was simulated for 10 ns, that is, 1 μs in total. After sorting resulting trajectories into the specified windows, the multistate Bennett acceptance ratio (MBAR) method (42) was used to reconstruct the free-energy landscape and to obtain the weight of each snapshot.

Analysis of conformational distributions using the MBAR

The probability distribution in $\left({\xi }_1,{\xi }_2\right)$ from all windows were unbiased and recombined using MBAR (42). MBAR also enables us to calculate the weight factor for each snapshot obtained by REUS simulations. The relative free energies of replicas are calculated by iteratively solving the following equation:

$${\hat{f}}_i=-\frac{1}{\beta }\ln \sum _{j=1}^{N_{\text{window}}}\sum _{ns=1}^{N_j}\frac{\exp \left[-\beta E_i\left(X_{ns}^{\left[j\right]}\right)\right]}{{\sum }_{k=1}^{N_{\text{window}}}{N}_k\exp \left[\beta \left({\hat{f}}_k-E_k\left(X_{ns}^{\left[j\right]}\right)\right)\right]},$$

where $i$, $j$, and $k$ are the window indexes. $\beta =1/\left(k_{\text{B}}T\right)$ is the inverse of the simulation temperature $T$, and $k_{\text{B}}$ is the Boltzmann constant. ${\hat{f}}_i$ and$E_i$ are the free and potential energies in the ith window, respectively. $N_{\text{window}}$ is the number of windows, $N_j$ is the number of snapshots in the trajectory of the jth window, and $X_{ns}^{\left[j\right]}$ is the nsth coordinate of the jth window. The weight factor for each snapshot in the unbiased state, W₀, is calculated using ${\hat{f}}_k$ according to the following:

$$W_0\left(X_{ns}^{\left[j\right]}\right)=\frac{1}{C}\frac{\exp \left[-\beta E_0\left(X_{ns}^{\left[j\right]}\right)\right]}{{\sum }_{k=1}^{N_{\text{window}}}{N}_k\exp \left[\beta \left({\hat{f}}_k-E_k\left(X_{ns}^{\left[j\right]}\right)\right)\right]},$$

where C is a normalization constant, and $E_0$ is the potential energy in the unbiased state. A two-dimensional histogram of some quantities $x_1\left(X_{ns}^{\left[j\right]}\right)$ and $x_2\left(X_{ns}^{\left[j\right]}\right)$ at values $\left(x_1,x_2\right)$ in the unbiased state can be obtained using the following:

$$H\left(x_1,x_2\right)=\sum _{j=1}^{N_{\text{window}}}\sum _{ns=1}^{N_j}{W}_0\left(X_{ns}^{\left[j\right]}\right)Q\left(x_1,x_2,X_{ns}^{\left[j\right]}\right)\text{and}$$

$$Q\left(x_1,x_2,X\right)=\{\begin{array}{cc}1,& \left|x_1\left(X\right)-x_1\right|<\mathit{\Delta }{x}_1/2\mathrm{and}\left|x_2\left(X\right)-x_2\right|<\mathit{\Delta }{x}_2/2\\ 0,& \mathrm{otherwise}\end{array},$$

where $\mathit{\Delta }{x}_1$ and $\mathit{\Delta }{x}_2$ are bin widths for $x_1$ and $x_2$, respectively. The free energy at $\left(x_1,x_2\right)$ can be calculated by $-k_{\text{B}}T\ln H\left(x_1,x_2\right)$.

Calculation of inter-LBD distance and its distribution

LBD conformations obtained by REUS simulations were superposed on the crystal structure of the full-length GluA2 (PDB: 3KG2 (43)) by fitting the Cα atoms of V394-M407, Y420-I488, and Y732-T767 in the D1 lobe of chain B to preserve the back-to-back dimer interfaces. A copy of such conformation was also superposed on chain D, which is positioned opposite to chain B using the same atoms for fitting. The distribution and the free-energy landscape for the inter-LBD distance ${\xi }_3$ were calculated using MBAR as described above. ${\xi }_3$ is defined as the distance between the COM of the Cα atoms of the linker residues (G630 and T631) of chain B and that of chain D. For simplicity, we assume that the LBD conformations in chains B and D are identical, such that binding of a ligand closes each LBD to the same extent in the different protomers.

Calculation of water occupancy map

A map of water occupancy was calculated using the Volmap plugin in visual molecular dynamics (44). Volmap creates an occupancy map at each grid point. Each grid point was set to either 0 or 1, depending on whether it contains water oxygen atoms. The resolution of the grids was set to 0.5 Å. The fractional occupancy of each grid point was calculated by averaging 500-ns conventional MD simulations. High-occupancy regions (above 80%) were visualized using the volume visualization feature in PyMOL. In the MD trajectory of the unflipped T686A-Glu, the LBD conformation changed from the semiclosed state to the closed state roughly at halfway through the 500-ns simulation. The first and second halves of the trajectory were used for calculations of water occupancy maps for the semiclosed and closed states, respectively.

Calculating the average structure of the LBD semiclosed state

Average structures of the semiclosed state of the unflipped T686A-Glu and WT-(S)-4-AHCP were calculated using the GENESIS analysis tool set as follows. First, we determined the ranges of ${\xi }_3$ and ${\xi }_4$, which include the semiclosed basin in the free-energy landscape shown in Figs. 5 C or 7 B. The ranges were identified as $56\AA <{\xi }_3<62\AA$ and $7.8\AA <{\xi }_4<10\AA$ for unflipped T686A-Glu and $56\AA <{\xi }_3<63\AA$ and $7.5\AA <{\xi }_4<10\AA$ for WT-(S)-4-AHCP. The probabilities of each snapshot at each of the regions were obtained using MBAR. Then, the 100 most probable structures were selected based on the obtained probability distribution, and their coordinates were averaged without their weights.

Figure 5.

Free-energy landscapes of the GluA2 LBD along $\left({\xi }_3,{\xi }_4\right)$. (A) Definition of a reaction coordinate related to hydrogen-bonding interactions between the D1 and D2 lobes. ${\xi }_4$ describes the distance between the COMs of Y450-G451 in the D1 lobe and D651-S652 in the D2 lobe. ${\xi }_1$ is also shown for comparison with ${\xi }_4$. The free-energy landscapes along ${\xi }_3$ and ${\xi }_4$ for flipped (B) and unflipped (C) conformations are shown. White circles represent the corresponding crystal structures. A white triangle represents the average structure of the semiclosed state. The red dashed arrow on the landscape for T686A-Glu represents the direction along the reduced coordinate ${\xi }_{34}=0.26{\xi }_3-0.74{\xi }_4$. To see this figure in color, go online.

Figure 7.

(A) The chemical structure of a partial agonist, (S)-4-AHCP. (B) The free-energy landscape along ${\xi }_3$ and ${\xi }_4$ for the complex of wild-type (WT) GluA2 and partial agonist (S)-4-AHCP. A white circle and a white triangle represent the corresponding crystal structure and the structure averaged over the semiclosed state, respectively. (C) The superposition of the averaged conformation of the T686A-Glu (magenta) onto that of the WT-(S)-4-AHCP (cyan). The RMSD of two averaged conformations is 0.28 Å. To see this figure in color, go online.

Results

Free-energy landscapes of LBD bound with Glu or Quis

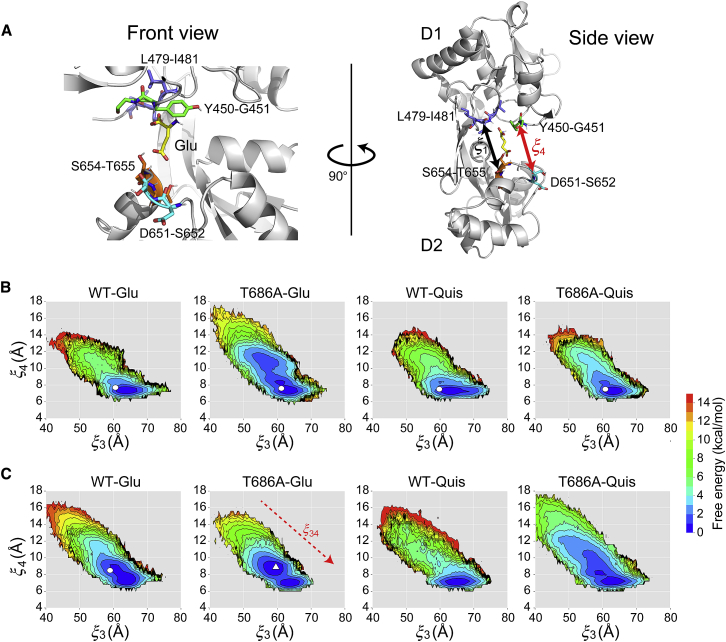
To elucidate the effect of the T686A mutation on LBD bound with Glu or Quis, we calculated the free-energy landscapes with respect to cleft opening/closing for WT-Glu, WT-Quis, T686A-Glu, and T686A-Quis. Following Lau and Roux (20, 21), we used two interlobe distances, ${\xi }_1$ and ${\xi }_2$, to describe cleft closure of the LBD monomer (Fig. 2 A). The free-energy landscape for each complex was calculated using REUS (24) by employing ${\xi }_1$ and ${\xi }_2$ as reaction coordinates. The free-energy landscapes reconstructed from REUS simulation data are shown in Fig. 2, B and C. To understand the effect of the flipped/unflipped conformations, we calculated free-energy landscapes for both conformations.

Figure 2.

Free-energy landscapes of the GluA2 LBD along $\left({\xi }_1,{\xi }_2\right)$. (A) The reaction coordinates used in the REUS simulation. ${\xi }_1$ describes the distance between the COMs of L479-I481 in the D1 lobe and S654-T655 in the D2 lobe. ${\xi }_2$ describes the distance between the COMs of L401-S403 in the D1 lobe and T686-A687 in the D2 lobe. The free-energy landscapes along ${\xi }_1$ and ${\xi }_2$ for flipped (B) and unflipped (C) conformations are shown. White circles represent the corresponding crystal structures. To see this figure in color, go online.

For flipped conformations (Fig. 2 B), the free-energy landscapes of WT-Glu and WT-Quis complexes have narrow and deep basins, whose minima are located near corresponding crystal structures. The value of ${\xi }_2$ in the minimum is slightly larger than that in the crystal structure possibly because of packing in the crystal. In contrast, for the T686A-Glu, ${\xi }_2$ in the global minimum is significantly larger than in the crystal structure probably because no hydrogen bond between E402 and T686 is formed, and E402 is favorably hydrated and distant from T686. The landscape of T686A-Glu has a local minimum around $\left({\xi }_1,{\xi }_2\right)=$ (12 Å, 12 Å), which is similar to that of the apo crystal structure. However, this local minimum is shallow, and its free energy is ∼7 kcal/mol greater than that of the global minimum, suggesting that its contribution is not significant. The landscape of T686A-Quis features a broad basin along ${\xi }_2$ with a minimum that largely deviates from the crystal structure, similarly to T686A-Glu.

For unflipped conformations (Fig. 2 C), the free-energy landscapes of all combinations of ligand and proteins are similar to those of the respective flipped conformations. The minimum in each landscape is located near that of the corresponding flipped GluA2, but the gradient along ${\xi }_1$ is shallower in the unflipped landscapes. This is because the hydrogen bonds between Y450-G451 and D651-S652 cannot be formed in the unflipped conformation (Fig. 1 D), thus weakening the interlobe interactions along ${\xi }_1$.

In both the flipped and unflipped conformations, the T686A mutation changes the position and the breadth of the minimum along ${\xi }_2$ compared to the WT. However, the value of ${\xi }_1$ at the minimum is almost the same as that of the crystal structure, implying that the LBD cleft near the ligand-binding site remains closed. The effect of the T686A mutation cannot explain the experimental observations using the landscapes of ${\xi }_1$ and ${\xi }_2$. Thus, a different approach or using other order parameters should be considered.

Effects of cleft closure on channel gate opening

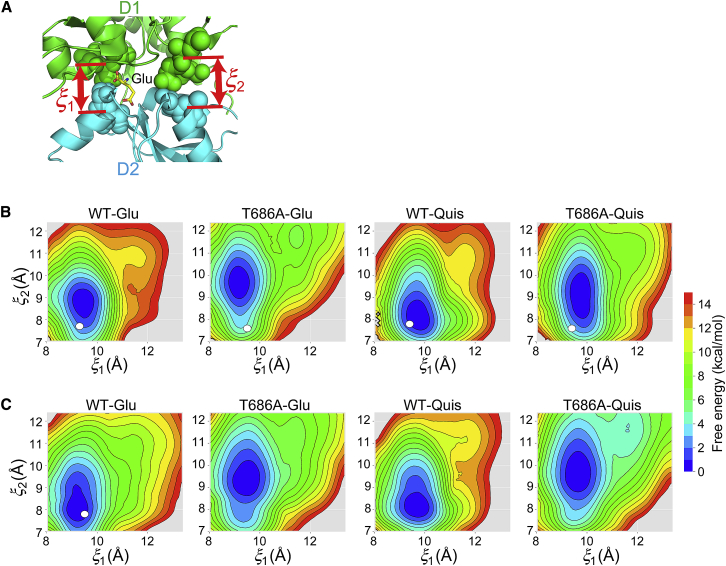
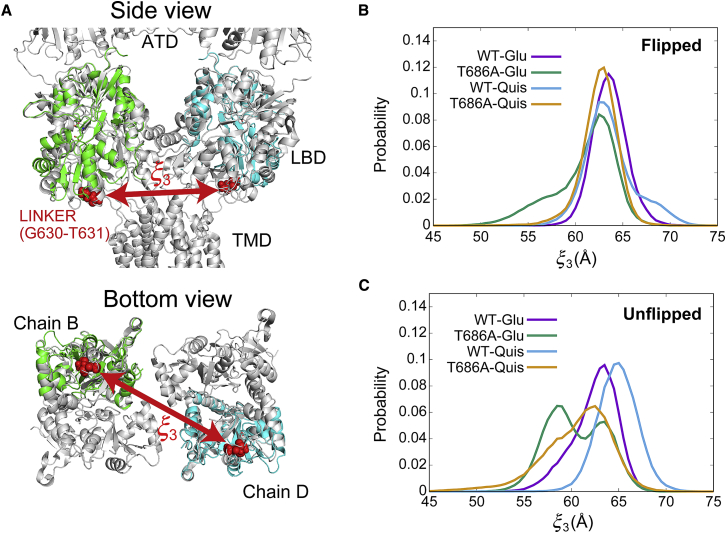
To clarify how the conformational change of the LBD affects channel opening, we calculated the distribution of distances between LBDs from different chains in the full-length GluA2 receptor. Following Lau and Roux (21), we superposed each LBD conformation obtained by our REUS simulations on the full-length GluA2 crystal structure (43) (Fig. 3 A). We measured the distribution of the inter-LBD distance ${\xi }_3$, which is defined as the distance between the linker residues of chains B and D. The linker residues connect the LBD to the TMD and transmit the conformational change. When the inter-LBD distance becomes larger upon ligand binding and cleft closing, it is expected that the probability of channel gate opening will increase. The distributions of ${\xi }_3$ are shown in Fig. 3, B and C.

Figure 3.

Probability distributions of inter-LBD distance. (A) The distance ${\xi }_3$ between the COMS of linker residues, G630 and T631, of two LBDs. The LBD conformations (green and cyan) obtained from the REUS simulation are superposed on the crystal structure of the full-length AMPA receptor (gray; PDB: 3KG2). The inter-LBD distance distributions for flipped (B) and unflipped (C) conformations are shown. To see this figure in color, go online.

In the case of the flipped conformation (Fig. 3 B), all complexes have a single peak around ${\xi }_3=$ 63 Å. This value is slightly larger than 60.6 Å of the flipped LBD crystal structure of WT-Glu (1FTJ chain C). For unflipped conformations (Fig. 3 C), WT-Glu, WT-Quis, and T686A-Quis also have a single peak. In contrast, T686A-Glu displays two peaks located around ${\xi }_3=$ 58 and 63 Å. ${\xi }_3=$ 58 Å is relatively close to that of the unflipped WT-Glu in the crystal structure (${\xi }_3=$ 59.0 Å; 1FTJ chain A). Considering that the X-ray structures correspond to the active state of the channel, we infer that the peak at ${\xi }_3=$ 63 Å corresponds to the channel open state. In the other state (${\xi }_3=$ 58 Å) observed in the unflipped T686A-Glu, the displacement of the linker residues is smaller, which would weaken the force pulling the helices in the TMD, thereby impeding channel opening in this state.

We characterized the two peaks in the unflipped T686A-Glu by the relative positions of residues in the flip region (Fig. 4). In the peak located around ${\xi }_3=$ 63 Å, residues D651-S652 come close to residues Y450-G451, allowing the formation of two hydrogen bonds between S652 and backbone atoms of Y450 and G451. This conformation is also observed in other unflipped complexes. In the peak located around ${\xi }_3=$ 58 Å, residues D651-S652 move away from Y450 to G451, and the residues are hydrated by surrounding waters. The interlobe distance becomes larger so that the cleft slightly opens, and the distance between linker residues becomes smaller.

Figure 4.

A cross-cleft interaction between Y450-G451 in the D1 lobe and D651-S652 in the D2 lobe. Structures corresponding to the peaks with smaller (A) and larger (B) ${\xi }_3$ in the distribution for the unflipped T686A-Glu in Fig. 3C are shown. Yellow dashed lines represent hydrogen bonds. To see this figure in color, go online.

Free-energy landscape of inter-LBD and interlobe distances reveals a hidden stable conformation

To quantify the effect of the hydrogen bonds between D651-S652 in the D2 lobe and Y450-G451 in the D1 lobe on the inter-LBD distance ${\xi }_3$, we use the interlobe distance between the COMs of D651-S652 and Y450-G451 as a reaction coordinate, ${\xi }_4$ (Fig. 5 A). This reaction coordinate better represents the open-close motion of the LDB than ${\xi }_1$. S654-T655 and L479-I481 are buried deep in the cleft and directly interact with the ligand, whereas D651-S652 and Y450-G451 are located at the rim of the cleft so that ${\xi }_4$ represents the extent of cleft opening more accurately than ${\xi }_1$ (Fig. 5 A). We calculated the free-energy landscapes of $\left({\xi }_3,{\xi }_4\right)$ from data of the REUS simulations using MBAR. The landscapes are shown in Fig. 5, B and C. $\left({\xi }_3,{\xi }_4\right)$ in the crystal structures are also shown.

For both flipped and unflipped conformations (Fig. 5, B and C, respectively), the free-energy landscapes of all complexes have a minimum around $\left({\xi }_3,{\xi }_4\right)=$ (63 Å, 7 Å), which corresponds to the closed state of the LBD. ${\xi }_3$ varies in inverse proportion to ${\xi }_4$. This is consistent with the idea that the channel gate opens when the cleft closes. Only unflipped T686A-Glu has a second minimum around $\left({\xi }_3,{\xi }_4\right)=$ (58 Å, 9 Å), which corresponds to the second peak of the distribution of ${\xi }_3$ in Fig. 3 C. Because the LBD is slightly more open than the completely closed state at this minimum, the state is referred to as the “semiclosed state” hereafter. The semiclosed and closed states are separated by a small free-energy barrier, and transition between the two states can occur by thermal fluctuations. The semiclosed state observed here may represent the same state observed in the simulations of Mamonova et al. (45). There, the S652-G451 hydrogen bond was broken, and the cleft slightly opened. For flipped T686A-Glu, unflipped WT-Glu, and unflipped T686A-Quis in Fig. 5, B and C, the region around $\left({\xi }_3,{\xi }_4\right)=$ (58 Å, 9 Å) is also stable, but the semiclosed state is not separated by a free-energy barrier from the more stable closed state.

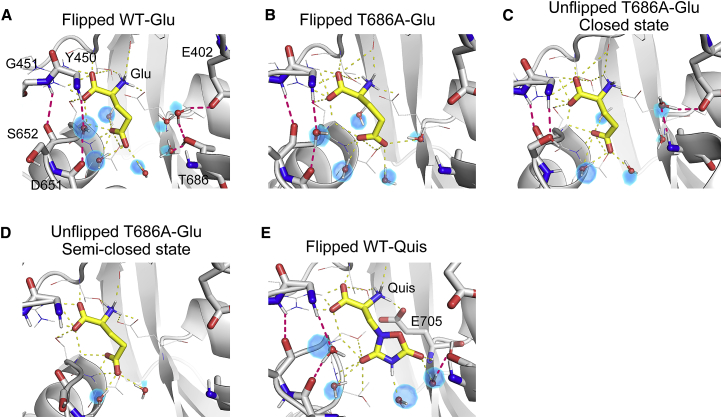
The protein-ligand and interlobe interactions within the cleft provide the physical basis of the free-energy landscapes. By performing conventional 500-ns MD simulations without any restraints and analyzing the hydrogen-bonding network around the bound ligand, we characterized the differences between the closed and semiclosed states. A map of water occupancy within the cleft was constructed by averaging over the MD simulation snapshots. Regions of high occupancy (above 80%) are shown in Fig. 6. In the closed state of the flipped WT-Glu (Fig. 6 A), Glu interacts with the residues of the D1 and D2 lobes as well as with the localized water molecules. D651-S652 and Y450-G451 form direct and water-mediated hydrogen bonds. It is generally believed that E402 and T686 form a direct hydrogen bond, but this was not observed in our simulation. Rather, there is a water-mediated hydrogen bond between E402 and T686, stabilizing the E402-T686 distance (corresponding to ${\xi }_2$), which is slightly larger than that in the crystal as shown in Fig. 2 B. Side-chain atoms of T686 also form hydrogen bonds with water molecules, creating a hydrogen-bonding network with localized waters around the ligand. These localized waters would play a key role in stabilizing the closed cleft.

Figure 6.

Hydrogen bonds within the GluA2 LBD cleft from MD snapshots. (A) Flipped WT-Glu, (B) flipped T686A-Glu, (C) a closed state for unflipped T686A-Glu, (D) a semiclosed state for unflipped T686A-Glu, and (E) flipped WT-Quis. Ligands (in yellow) and E402, Y450, G451, D651, S652, T686, and E705 (in gray) are shown in licorice representation. Hydrogen bonds between a ligand and other molecules are indicated by yellow dashed lines, whereas the interlobe interactions and water-mediated interactions are indicated by magenta dashed lines. The map of water molecules occupying more than 80% of each MD trajectory is shown by blue surfaces, and representative water molecules (ball and stick) from the MD snapshot are superposed on the map. To see this figure in color, go online.

Fig. 6 B shows the interactions in the closed state of the flipped T686A-Glu. The water molecules normally mediating the interactions with T686 are missing, leading to the loss of the D1-D2 interaction and the hydrogen-bonding network around the ligand. The loss of these hydrogen bonds would destabilize the closed state of the LBD as shown in Fig. 5 B. This is also consistent with the free-energy landscape in which the conformation with large ${\xi }_2$ is stabilized in the T686A mutant (Fig. 2 B).

In the conventional MD simulation for the unflipped conformation of the T686A-Glu, we observed both the closed and semiclosed states (Fig. 6, C and D, respectively). Although the interactions involving the ligand are similar to those in the flipped conformation, interlobe interactions differ. In the closed state (Fig. 6 C), the oxygen atoms of the side and main chains of S652 form two hydrogen bonds with the main chains of Y450 and G451, and E402 forms a water-mediated hydrogen bond with the nitrogen of A686. These hydrogen bonds contribute to the stability of the closed state. However, during the simulation, those hydrogen bonds are broken by thermal fluctuations so that Y450, G451, E402, and A686 residues become hydrated by surrounding water molecules, resulting in partial opening of the cleft (Fig. 6 D). We speculate that the T686A mutation and unflipping of the D651-S652 peptide bond break the delicate balance of intracleft interactions, inducing a population shift from the closed state to the semiclosed state.

For the Quis-bound LBD, the T686A mutation and unflipping of the D651-S652 peptide bond would also weaken the interlobe interactions. However, because Quis has more interaction sites than Glu and can interact with the main chain of E705 (Fig. 6 E), the interlobe interaction may be stronger when mediated by Quis than by Glu. As a result, the semiclosed state is less likely to appear in the Quis-bound LBD.

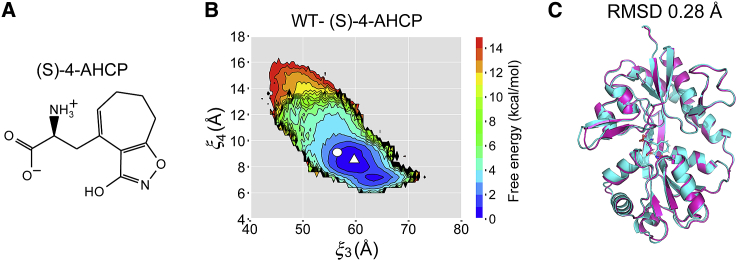
Comparison with a partial agonist

Earlier studies have shown that the extent to which the LBD closes is a major determinant of agonist efficacy and that partial agonists cause less closure of the LBD cleft than full agonists (6, 13). Our results and those of Zhang et al. (19) indicate that Glu behaves as a partial agonist for T686A GluA2. To compare the semiclosed state of the T686A-Glu with that of a partial agonist, we calculated the free-energy landscape for the WT bound with (S)-4-AHCP (WT-(S)-4-AHCP) (Fig. 7 A). The crystal structure of the (S)-4-AHCP-bound LBD has an unflipped conformation, and the LBD cleft is partially open (31). The free-energy landscape of $\left({\xi }_3,{\xi }_4\right)$ obtained by the REUS simulations is shown in Fig. 7 B.

The minimum of the free energy for WT-(S)-4-AHCP is located around $\left({\xi }_3,{\xi }_4\right)=$ (58 Å, 9 Å), which corresponds to the semiclosed state of the unflipped T686A-Glu. We superposed the averaged structure of the semiclosed state of unflipped T686A-Glu onto that of the WT-(S)-4-AHCP (Fig. 7 C). The RMSD between the two averaged structures is 0.28 Å, suggesting that the cleft of the T686A-Glu opens to the same extent as that of the WT-(S)-4-AHCP. Interestingly, the WT-(S)-4-AHCP landscape also has a basin corresponding to the closed state around $\left({\xi }_3,{\xi }_4\right)=$(63 Å, 7 Å), which has not been observed by X-ray crystallography. Evidently, the LBD cleft is able to close perfectly even though the ligand is a partial agonist. The size of the basin is smaller than that for Glu probably because cleft closure would result in steric clashes between (S)-4-AHCP and residues within the binding site because of the increase in ligand size. Although crystal structures with partial agonists point to a mechanism of graded LBD cleft closure (6, 13), our results suggest that a population shift from the closed state to semiclosed state in the LBD occurs upon partial-agonist binding or T686A mutation.

In Fig. 7 B, we observe an energetic step around ${\xi }_4=$ 13 Å. (S)-4-AHCP forms a hydrogen bond with the backbone nitrogen atom of S652 through its 3-hydroxy anion as well as water-mediated hydrogen bonds between its isoxazole ring and surrounding residues in the D2 lobe around ${\xi }_4=$13 Å. These hydrogen bonds break for ${\xi }_4>$13 Å, and (S)-4-AHCP no longer interacts with the D2 lobe, leading to the large energetic change.

Discussion

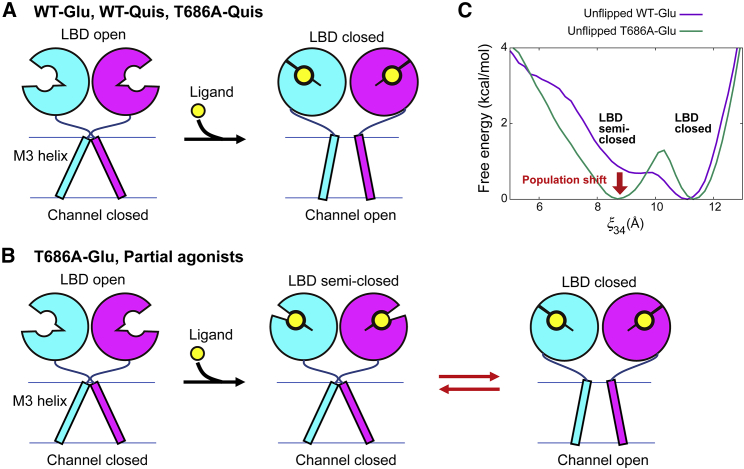
We found a semiclosed state for the unflipped Glu-bound T686A receptor using REUS simulations. The linker residues connect the LBD with helix M3 in the TMD, and the ligand-binding-induced conformational change of the LBD is transmitted through the linkers to the channel, resulting in gate opening. The linker-linker distance between different LBDs becomes shorter in the semiclosed state compared to the closed state (Fig. 3), suggesting that the force acting on the LBD-TMD linkers would become weaker, preventing the channel gate from opening. In fact, the LBD conformation in the unflipped T686A-Glu is almost the same as that in the WT bound with a partial agonist (S)-4-AHCP. Our results imply that Glu behaves as a partial agonist for the T686A mutant, which is consistent with an earlier experimental observation (19).

By combining long, unbiased MD simulations, Yu et al. (46) recently proposed that charged residues on the LBD surface form a ligand-binding pathway, which funnels a ligand into the binding site via a series of metastable interactions. Their model of ligand binding and cleft closing is as follows: 1) the ligand binds to R661 on D2; 2) the ligand’s α-carboxylate interacts with R485 on D1, allowing a metastable interaction to form between D1 and D2; 3) the ligand shifts into the binding pocket while adjusting its interactions with D2; and 4) the ligand’s amine interacts with E705 on D2, resulting in the cleft closure. In the model proposed by Fenwick and Oswald (47), the rotation of the peptide bond between D651 and S652 from unflipped to flipped occurs during the last step of LBD closure. The cleft conformation is locked by hydrogen bonds in the flipped conformation so that the LBD closed state becomes further stabilized. Fenwick and Oswald (47) considered the possibility that this locked state is related to the desensitized state. Our NMR measurements of hydrogen-deuterium exchange (M.S., Y. Ohkubo, H.O., S.R., M. Ito, Y.S., and H.T., unpublished data) have also suggested that the flipped conformation is not associated with channel opening. Salient features of the conventional model for channel activation are presented in Fig. 8 A. This mechanism, which involves distinct and complete conformational changes, would hold true for both an agonist binding to WT GluA2 as well as for Quis binding to the T686A mutant. By contrast, for Glu binding to the T686A mutant, the LBD closed state in the unflipped conformation is less stable and in equilibrium with the semiclosed state so that a significant population shift from the closed state to the semiclosed state is observed (Fig. 8, B and C). The same mechanism seems applicable for partial agonists, such as WT-(S)-4-AHCP binding promoted a landscape with both closed and semiclosed states. This model is supported by earlier electrophysiological or crystallographic studies (13, 14, 48). The measurements of single-channel current revealed the existence of several subconductance states with different conductance levels. Partial agonists preferentially occupy the lower subconductance states relative to full agonists, though they can also populate the higher subconductance state (13, 14). Armstrong et al. (48) showed that the L650T mutation reduces AMPA efficacy, and the crystal structure of AMPA-bound LBD dimer has both partially and fully closed conformations. From these biochemical and structural data, they proposed a mechanism similar to the model shown in Fig. 8 B. The population shift to the LBD semiclosed state would reduce the probability that transmembrane gates of multiple subunits open simultaneously. This would induce a population shift from high-to-low subconductance states of a single channel and reduce the maximal peak current in patches containing GluA2 channels. By calculating the free-energy landscapes, we confirm the population shift mechanism in terms of thermodynamics. To the best of our knowledge, this is the first time that the population shift for partial agonism of AMPA receptors has been unambiguously characterized based on a free-energy landscape.

Figure 8.

Mechanisms of the cleft closure in the ligand-binding domain (LBD) upon ligand binding. (A) A suggested mechanism for WT-Glu, WT-Quis, and T686A-Quis. (B) A suggested mechanism for T686A-Glu or partial agonist binding. (C) The free-energy curves of unflipped WT-Glu and T686A-Glu along the reduced coordinate ${\xi }_{34}$ defined in Fig. 5C. To see this figure in color, go online.

Our study is limited to the cleft closure of the GluA2 LBD monomer. From the free-energy landscapes of the cleft closing, we speculate the effect of displacement of linker residues on the channel opening and the molecular mechanism of the full-length receptor. The LBDs form dimer of dimers, and it is believed that the dimer interface matters for the change in state from active to desensitized. However, a recent work including simulations shows that the ligand-binding process and LBD closure in the dimer are very similar to those in the monomer (46). In addition, cryo-EM structures suggest that the displacement of LBD-TMD linkers would be a main driving force for opening the ion channel (10, 12). From these, we believe that the simulation of monomer performed here is reasonable. The rearrangement of helices in the TMD or the movement of the amino-terminal domain might also affect the LBD conformation, causing a change in the free-energy landscape of the cleft closing. We note, however, that the conformational change of the LBD is the most important in controlling the function of GluA2 channel. We believe that our results on LBD can be at least qualitatively applied to the full-length receptor. Recently, structures of the full-length GluA2 receptor have been determined by both X-ray crystallography (7, 8) and cryo-EM (9, 10, 11), which reveals that a pre-active state exists between the channel-closed and channel-opened states (12). The pre-active state is characterized by intermediate cleft closure of the LBD. We infer that the pre-active state of the full-length receptor with intermediate LBD cleft closure may correspond to the semiclosed state found in this study. Extending simulations to the full-length receptor could possibly verify this.

Conclusion

In this study, we calculated the free-energy landscapes of GluA2 LBD opening/closing to elucidate the partial agonism in the T686A mutant of the AMPA receptor. We performed REUS simulations for both WT and T686A mutant GluA2 LBDs bound with Glu or Quis. Even though crystal structures for almost all complexes exhibit only the closed state, we found a semiclosed state in the free-energy landscape of the Glu-bound T686A LBD. The flipped/unflipped conformational change in the peptide bond of D651-S652 is a major determinant of the semiclosed state: the flipped conformation stabilizes the closed state by interlobe interactions between D651-S652 and Y450-D451, including a water-mediated hydrogen bond, whereas these interactions are weakened in the unflipped conformation, inducing partial opening of the LBD cleft. Our results suggest that the partial agonism in AMPA receptors is driven by a population shift from the closed state to the semiclosed state.

Author Contributions

H.O., S.R., M.S., H.T., and Y.S. designed the research and wrote the manuscript. H.O. conducted the MD simulations and trajectory analyses.

Editor: Chris Chipot.