Accurate Prediction of Amide Exchange in the Fast Limit Reveals Thrombin Allostery

Abstract

Amide hydrogen/deuterium exchange mass spectrometry (HDXMS) of proteins has become extremely popular for identifying ligand-binding sites, protein-protein interactions, intrinsic disorder, and allosteric changes upon protein modification. Such phenomena are revealed when amide exchange is measured in the fast limit, that is, within a few minutes of exchange in deuterated buffer. The HDXMS data have a resolution of the length of peptides and are difficult to interpret because many different phenomena lead to changes in hydrogen/deuterium exchange. We present a quantitative analysis of accelerated molecular dynamics simulations that provides impressive agreement with peptide-length HDXMS data. Comparative analysis of thrombin and a single-point mutant reveals that the simulation analysis can distinguish the subtle differences in exchange due to mutation. In addition, the results provide a deeper understanding of the underlying changes in dynamics revealed by the HDXMS that extend far from the site of mutation.

Introduction

Equilibrium hydrogen/deuterium exchange (HDX) measurements report on the rate of substitution of protein amide hydrogen atoms in a deuterium oxide solution. These measurements represent a powerful tool for investigating the structures, stabilities, and dynamics of native and non-native states of proteins. Specifically, in cases in which exchange occurs via collective conformational transitions or local unfolding, the exchange rate provides valuable information concerning local structural fluctuations occurring on timescales of milliseconds or even longer (1). Pioneering work using NMR-HX in the 1980s provided information on amide exchange in the form of protection factors (2), which represent the ratio of the intrinsic rate for amide hydrogen exchange observed in an unstructured protein to the observed exchange rate in the native state. When the exchange is local, the associated free-energy difference between the hypothetical “closed” (exchange-inactive) and an “open” (exchange-active) state is considered to be related to the extent of amide burial and the number of contacts, particularly H-bonding interactions. Although residue-specific protection factors provide detailed dynamic information concerning local protein folding-unfolding mechanisms in the “slow limit,” occurring on timescales of minutes to days, such measurements provide no information about dynamic events occurring in the fast-exchanging disordered regions of the protein. The advent of HDX measured by mass spectrometry (HDXMS) allowed for the study of amide exchange in the “fast limit,” providing valuable information about conformational fluctuations, including amide exchange in disordered regions, local unfolding and refolding events, and important biological processes, such as dynamic allostery (3, 4, 5, 6, 7, 8). Unlike residue-specific protection factors obtained from NMR-HX, the HDXMS method is not limited by the size of the protein, but HDXMS data typically only provide exchange data at the resolution of peptides. HDXMS analysis of amide exchange in the fast limit can provide a comprehensive view of physiologically relevant protein dynamics such as disorder-to-order transitions occurring upon ligand binding and conformational fluctuations (4).

Theoretical analysis of HDX faces two considerable challenges. First, the HDX phenomenon is a statistically rare event requiring long simulation times and comprehensive sampling beyond the scope of conventional all-atom classical molecular dynamics (CMD) approaches. Secondly, a complete analytical description of the protection factor (in NMR-HX) or deuteron-uptake propensity in HDXMS and the associated free-energy statistics have yet to be developed.

Several groups have attempted to develop computational approaches for predicting NMR-HX results. Hilser and Freire developed a semi-analytical structure-based modeling strategy, COREX, to predict HDX behavior (9). In this molecular modeling approach, a large ensemble of conformational states is generated from a single native structure, and an empirical free-energy parameterization protocol is employed to evaluate the HDX probability of each microstate. Vendruscolo et al. (10) developed phenomenological expressions for the protection factor based on the number of contacts of each residue with all other residues in the system and the number of hydrogen bonds formed by the amide hydrogen; the associated pseudo-energy functions (restraints) were employed in ensemble-averaged Monte-Carlo (10) and molecular dynamics (MD) simulations (11). However, the success of such ensemble-averaged restrained simulations is strongly dependent on the empirical optimization of the pseudo-energy functions for the system at hand. More recently, Wolynes and colleagues (12) used course-grained structure-based model simulations to sample entire folding trajectories from fully unfolded configurations to the native state for a variety of protein systems, allowing for the direct assessment of free-energy statistics associated with local unfolding events spanning a multitude of conformational fluctuations. Protection factors, calculated by a probabilistic analysis of the exchange-competent and exchange-incompetent states of each residue were found to be in good agreement with experimental data. This was a remarkable result, particularly considering the simplicity of the course-grained model.

Here, we attempt to model HDXMS data in the “fast exchange limit.” Our a priori approach to model and hence predict HDXMS data is based on the application of accelerated molecular dynamics (AMD) (13, 14), an enhanced conformational space-sampling MD approach that allows for the efficient study of biomolecular systems up to timescales several orders of magnitude greater than those accessible using standard CMD methods while still maintaining a fully atomistic representation of the system. Analysis of the free-energy reweighted molecular ensembles for the presence of local contacts and solvent accessibility affords an exchange propensity map. The method is stringently validated by comparing the results to HDXMS data on wild-type (WT) human thrombin and a functionally important mutant, W215A (W263A in sequential numbering), which shows subtly different HDX behavior as compared to the WT protein. Researchers use several different numbering schemes for thrombin. In this work, we have numbered the protein sequentially from N-terminus through the cleaved peptide bond between the “light chain” and the “heavy chain.” We have also given the commonly used chymotrypsin numbers in parentheses for each region of the protein that is discussed. When referred to in the text, the chymotrypsin numbers are denoted with a subscripted CT. Mutation of W215A results in apparent changes in thrombin dynamics both near and far from the site of mutation. Others have also demonstrated remarkable allosteric effects mediated by Trp in the Btk kinase (5). The HDXMS data showed that the W215A mutant had increased dynamics in the 170s_CT loop, the 220s_CT loop, and the N-terminus of the heavy chain (Fig. 1) (15). The AMD simulations predicted increases in dynamics in the same regions of the protein as were observed to exchange more in the HDXMS experiments. Because the AMD can predict the HDX results, it allows a deeper understanding of the dynamics changes resulting in the experimentally observed HDXMS results.

Figure 1.

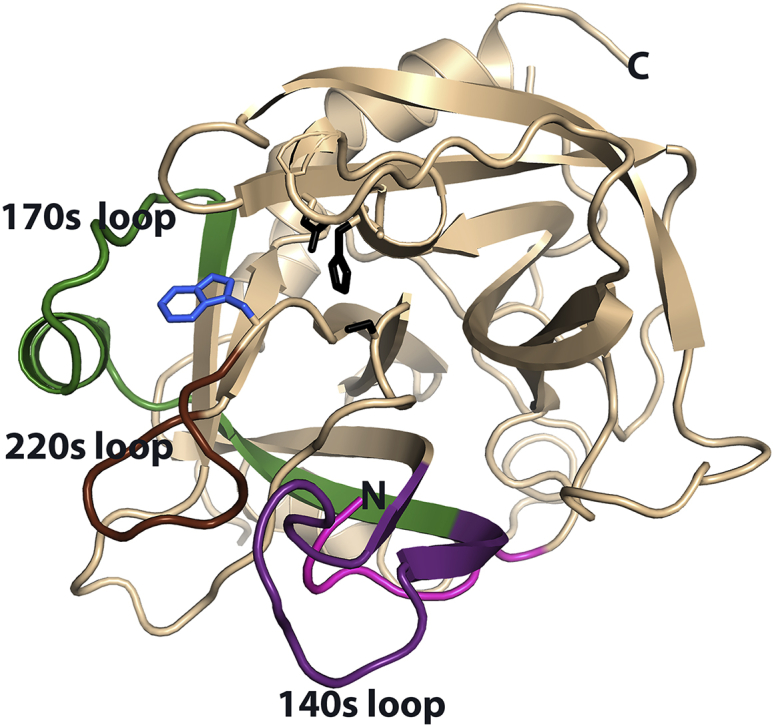
The structure of WT thrombin showing the 170s_CT loop (green), the 220s_CT loop (brown), the 140s_CT loop (purple), and the N-terminus of the heavy chain (magenta) as well as the catalytic triad residues His57_CT, Asp102_CT, and Ser195_CT (black) and the TRP215_CT side chain (blue) that is the site of mutation. To see this figure in color, go online.

Methods

Theoretical approach

The extent of HDX depends on three factors: the presence of “local contacts” (H-bonds), solvent accessibility, both of which should be assessed as free-energy weighted ensemble averages over the different conformational states of the system, and intrinsic residue-specific exchange rates, which have been shown to vary from approximately 0.05 to 5 s⁻¹ (16). The general protocol we implemented involves performing long, extended AMD simulations for both WT thrombin and the W215A mutant systems to assess conformational fluctuations and rare events occurring on timescales of milliseconds to tens of milliseconds. A robust free-energy reweighting protocol is then applied to estimate the free-energy (population) statistics for each molecular conformer in the AMD ensemble. The resulting free-energy weighted molecular ensembles are then analyzed to determine the presence of local contacts and solvent accessibility about the amide proton, affording a free-energy weighted exchange propensity map, which describes the likelihood of exchange for each amide proton. Finally, an empirically optimized exchange-propensity threshold identifies whether each amide proton is exchange active or exchange inactive in the fast limit.

Extended AMD simulations of WT thrombin and W215A thrombin

AMD is an ideal tool for the theoretical study of HDXMS data because it provides a free-energy weighted ensemble of all-atom conformers, which may be analyzed for the presence of local contacts and solvent accessibility about each amide proton. The details of the AMD method have been discussed, and only a brief summary is provided here (13, 14). AMD is an extended biased potential MD approach that allows for the efficient study of biomolecular systems up to timescales several orders of magnitude greater than those accessible using standard CMD methods while still maintaining a fully atomistic representation of the system. Compared to many other approaches, AMD affords efficient enhanced conformation space sampling without any a priori understanding of the underlying free-energy surface nor does it require the specific prior definition of a reaction coordinate or a set of collective variables.

In AMD, a reference, or “boost energy,” Eb, is defined, which lies above the minimum of the potential energy surface. At each step in the simulation, if the potential energy V(r), lies below this boost energy, a continuous, nonnegative bias potential, ΔV(r), is added to the actual potential. If the potential energy is greater than the boost energy, it remains unaltered. The extent to which the potential energy surface is modified depends on the energy difference between the boost energy and the actual potential. Explicitly, the modified potential, V^∗(r) on which the system evolves during an AMD simulation is given by the following (13):

$$V^{\ast }\left(r\right)=V\left(r\right);V\left(r\right)\ge E_b,$$

$$V^{\ast }\left(r\right)=V\left(r\right)+\mathit{\Delta }V\left(r\right);V\left(r\right)<E_b,$$

and the bias potential is defined as

$$\mathit{\Delta }V\left(r\right)=\frac{{\left(E_b-V\left(r\right)\right)}^2}{E_b-V\left(r\right)+\alpha }.$$

In this work, we implemented a “dual boost” AMD approach (17) in which two acceleration potentials are simultaneously applied to the system: a stronger acceleration potential is applied to the torsion terms only, and a second, weaker acceleration is applied across the entire potential. The specific torsional acceleration parameters were defined as [Eb(dih) − <V0(dih)>] = [4 kcal/mol × (number of residues)], and the acceleration parameter, α(dih), was set to one-fifth of this value. The total background acceleration parameters were fixed at [Eb(tot) − <V0(tot)>] = α(tot) = [0.16 kcal/mol × (number of atoms in simulation cell)]. The acceleration parameters defined above are considered to be “optimal parameters,” and they are broadly used by the AMD community. Recently, two independent groups have compared AMD simulations of a variety of proteins to long, brute-force CMD simulations (18, 19). Both studies found that AMD simulations performed over the number of MD steps equivalent to a CMD simulation of hundreds of nanoseconds, provided configurational space sampling and torsional entropy values (a thermodynamic measure of the extent of torsional fluctuation) equal to that observed in a 1-ms brute-force CMD simulation for the same system. These same parameters were also benchmarked against residual dipolar coupling experimental data and were shown to be optimal for thrombin (20).

All CMD/AMD simulations were performed using the AMBER14 simulation suite (21). Atomic coordinates for WT thrombin were obtained from the Protein Data Bank 1.9-Å X-ray crystal structure (PDB: 1PPB) (22), and the active site inhibitor was removed. For the W215A mutant thrombin, the tryptophan at position 215 was manually converted to an alanine. Each system was placed at the center of a periodically repeating box, and the simulation cell was defined such that the distance between the edge of the simulation box and the surface of the solute was at least 12 Å. All simulations were performed in explicit solvent, and three Cl⁻ counter ions were introduced to obtain cell neutrality. After standard energy minimization and equilibration procedures, a 20-ns production-run CMD simulation was performed under periodic boundary conditions with a time step of 2 fs. Bonds involving protons were constrained using the SHAKE algorithm, and electrostatic interactions were treated using the particle mesh Ewald method (23) with a direct space sum limit of 10 Å. The AMBER ff14SB force field (24) was used for the solute residues, and the TIP3P water force field (25) was used for the solvent molecules. The average minimal energy potentials, <V0(dih)> and <V0(tot)>, were obtained from the initial 20-ns CMD simulations.

In this work, two AMD simulations were performed for 750,000,000 steps with a (real time) time step of 2 fs for each protein (equivalent to a 1.5-μs CMD simulation). The effective speedup of three to four orders of magnitude in rate of conformational space sampling allows exploration of dynamics occurring on timescales of milliseconds to tens of milliseconds. Molecular structures were saved every 250 steps along the trajectories. As the average bias potential across the two AMD trajectories for each system was found to differ by less than 2%, the resulting molecular ensembles from each of the two AMD simulations for each system (WT thrombin and W215A thrombin) were concatenated.

Obtaining accurate population statistics from the AMD trajectories. The application of the bias potential destabilizes low-energy regions of the conformational space on the potential energy landscape resulting in incorrect population statistics, and statistical noise error prohibits the practical acquisition of accurate free-energy statistics using simple reweighting procedures. To circumvent this problem, a bias potential block averaging method was performed (14): the concatenated AMD trajectories were consecutively divided into “bins” or “blocks” containing 500 conformers. The correct (free-energy weighted) population, pj, for each block, j, is then given by the following:

$$p_j=p_j^{\ast }\frac{<e^{\beta \Delta V}>}{{\sum }_{j=1}^M<e^{\beta \Delta V}>};j=1,M,$$

and the exponential averages, <exp[βΔV]> were approximated using a cumulant expansion to the second order resulting in a free-energy accuracy on the order of k_BT (26):

$$<e^{\beta \mathit{\Delta }V}>=exp\left\{\sum _{k=1}^2\frac{{\beta }^k}{k!}{C}_k\right\},$$

where

$$C_1=\langle \mathit{\Delta }V\rangle \mathrm{and}$$

$$C_2={\langle \mathit{\Delta }V\rangle }^2-{\langle \mathit{\Delta }V\rangle }^2.$$

In this approach, each conformer in the same block acquires the same population weighting. The ratio of the population of a block to the total of all blocks gives the population fraction of that block. When a rare conformation was identified according to structural analysis, all blocks were analyzed to discover which contained that rare conformation. The sum of all blocks containing a rare conformation then yielded the fractional population of the rare conformation.

Results and Discussion

Slow timescale dynamics in AMD simulations of WT and W215A thrombin

Comparative analysis of the conformational dynamics observed in the AMD simulations of WT and W215A thrombin revealed few differences in backbone root mean-square deviation across different segments of the protein and residue-specific Ramachandran plots except in a few isolated regions. In the first several million AMD steps (molecular motions on microsecond timescales), ostensibly no differences were observed between WT and mutant thrombin. However, on slower timescales extending into the millisecond range, transient, rare conformational transitions indicative of enhanced destabilization of W215A thrombin were observed. The most significant of these was the observation of transient destabilization of residues 202–222 (the 170s_CT loop), including the unfolding-folding of α-helical residues 206–212 within this loop (Fig. 1). Remarkably, the 170s_CT loop showed the largest increase in HDX experimentally (15). Residues 256–275 (the 220s_CT loop and the β-strand that precedes it); residues 37–44, corresponding to the N-terminus of the heavy chain (residues 16_CT-23_CT); and residues 175–185 (the 140s_CT loop) also showed enhanced conformational space sampling in the W215A mutant. Free-energy statistics obtained from the AMD simulations suggest that the population of the transient locally unfolded structures is less than 10%.

Definition of H-bond contacts

We assumed that an amide proton in a given conformational state would not be capable of undergoing HDX if it formed an H-bond with any other protein oxygen or nitrogen atom. The H-bond was considered formed if it had a length less than 2.5 Å and an N-H—X angle between 150 and 180°. The length of the H-bond was calculated as the length of the bond vector from the amide proton to the N or O atom, and the H-bond angle was determined from the dot product of the normalized N-H and H—X bond vectors.

Definition of solvent accessibility criteria

For those amides not participating in an H-bond, a second protocol was implemented to assess if the solvent (D₂O)-accessible volume around the amide proton would be sufficient to allow for HDX. Employing standard geometric values and van der Waals radii, we assumed that a tumbling D₂O molecule could be represented by a sphere, with a diameter of 2.75 Å. For each contact-free amide proton, in each free-energy weighted composite AMD conformer, an imaginary sphere of diameter of 2.75 Å was placed such that the center of the sphere lay 1.7 Å away from the amide proton, projected along the N-H bond. The coordinates of the center of the sphere, X, were calculated by scaling the x, y and z components of the N-H bond vector to obtain a vector length equal to the length of the N-H bond plus 1.7 Å. If any protein atom (with its associated van der Waals radius) was found to lie within the boundary of the imaginary sphere, we assumed that steric interaction would not allow a D₂O molecule to access the NH group. To account for possible nonlinear H-bonds between the amide proton and the D₂O solvent, the center of a second imaginary sphere was placed 1.7 Å away from the amide proton, lying parallel to the N-Cα bond, forming an angle to the N-H bond vector of 150°. The position of the center of this sphere, X, was calculated by first translating the N-Cα-bond vector to sit at the amide proton position and then rescaling the length of this vector to 1.7 Å. The cross product of the N-H and H—X vectors provided a rotation axis vector, n, which lies perpendicular to the plane formed by the N-H and H—X vectors. The correct 150° angle between the N-H and H—X vectors was then obtained by performing a suitable rotation about the rotation axis vector, n, given by R ⋅ n(θ). This sphere was then systematically rotated 120° about the N-H bond vector. In this way, four D₂O exclusion zones (spheres) were generated about each contact-free amide proton. If solute atoms were found to encroach on all four spheres, the respective amide proton for the free-energy weighted composite structure was considered exchange incompetent. The specific contact/solvent accessibility parameters were obtained by comparison to MD simulations performed in explicit solvent.

Development of the HDXMS fast-limit model and comparison to experimental HDXMS data

Because the free-energy weighted AMD ensemble consists of a series of conformers, each of which has an associated fractional population, the exchange propensity represents the relative population of exchange-competent states for each amide proton in the system over the entire configurational space sampled in the AMD simulations. To quantitatively compare to the peptide-length experimental data, the exchange competence calculated from the AMD simulations was summed over each peptide segment for all free-energy weighted conformers sampled in the AMD simulations (three million structures each) to generate a global exchange propensity (ranging from 0 to 100%) for every amide proton in the system.

We first assessed the agreement between the exchange propensity for each amide calculated from the AMD data and summed over each peptide fragment from the experimental HDXMS data (15). This approach did not result in satisfactory agreement. We realized, however, that application of a threshold of 6%, above which the amide was deemed to be “exchange active” and below which the amide was deemed “exchange inactive,” resulted in remarkable agreement. The threshold approach accounts for the fact that the timescale of the AMD simulation (∼20 ms) still does not allow for complete sampling of exchange processes that occur on longer timescales (16). A lower threshold over predicted the experimental HDX, whereas a larger threshold prohibited the accurate modeling of the subtle differences between WT thrombin and W215A thrombin. This approach can be thought of as defining which amides could exchange during the HDXMS experiment. This empirically derived threshold of 6% makes physiological sense because HDX identifies rare conformational transitions between the native state and low-populated excited states. NMR-based relaxation dispersion experiments (27) applied to many protein systems have shown that the population statistics of these “invisible” excited states on physiological timescales are generally on the order of only a few percent. The exchange-competent state is visited rarely and for short periods of time, but within minutes in the HDXMS experiment, exchange is observed. Importantly, it is these rarely visited invisible excited states that are observed in experiments that detect HDX in the fast limit, and it is these states that arguably define important protein functions such as allostery (28).

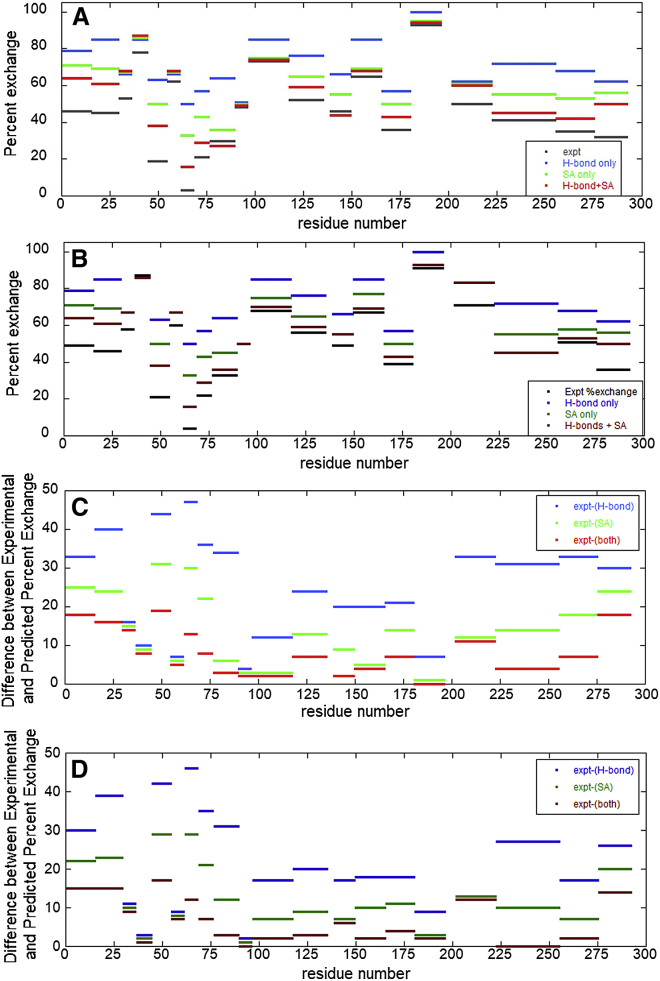
A comparison of the experimental and theoretically predicted HDXMS data for WT thrombin, and the differences between them are shown in Fig. 2, A and C, respectively. The same results for the W215A mutant system are presented in Fig. 2, B and D. It is strikingly apparent that H-bond contacts (blue) alone did not predict HDX behavior (black) well. The reason for this is that within the strict criteria that is defined for a strong H-bond contact, only 65 of the total 280 amide residues in WT thrombin (the more stable of the two systems studied) possess a permanent hydrogen bond across the AMD trajectories. The solvent accessibility criteria (green) were clearly more predictive. Previous course-grained MD simulation studies used to model protection factors in the absence of explicit H-bond geometries also found that “... exchange propensity depends much more on the stability of the local environment than it does on the detailed energetic and microscopic fluctuations of the H-bonded interactions per se...” (9). The theoretical results that best matched experimental HDX (black), however, were obtained when both H-bond and solvent accessibility statistics were considered (red).

Figure 2.

A comparison of experimental and theoretically predicted HDX results. (A) WT thrombin experimental (expt) data (gray), theoretical predictions based solely on H-bond contacts (blue), theoretical prediction based solely on solvent accessibility (green), and theoretical predictions based on H-bonds and solvent accessibility (SA) (red). (B) The W215A mutant thrombin with the same color scheme as in (A), except with muted colors. (C) The difference between the experimental data and the theoretical predictions is plotted for WT thrombin. (D) The difference plot for W215A thrombin. To see this figure in color, go online.

The theoretical peptide HDX propensities were found to be within 12% of their experimental counterparts (Fig. 2, C and D). The theoretical model tends to predict slightly elevated levels of exchange in highly flexible and solvent-exposed regions, particularly in the light chain, residues 1–36, and the C-terminal residues 285–295.

The AMD results reveal specific local dynamics that explain the HDXMS data

One of the most remarkable results of the theoretical approach presented here is its ability to reproduce subtle differences in HDXMS data between WT thrombin and a single-point mutant to provide detailed information about the associated structural and dynamic effects of the mutation. For the vast majority of peptide fragments, experimental HDX was not different in W215A thrombin compared to WT thrombin (15). Mutation of Trp263 (215_CT) to Ala removes the strong aromatic ring interaction with Phe275 (227_CT), causing enhanced mobility on slow timescales of this residue and its neighbor, Tyr276 (228_CT). The two peptides from the HDXMS data that showed the greatest increase in exchange in the W215A mutant spanned residues 202–222 (the 170s_CT loop) and residues 256–275 (the 220s_CT loop).

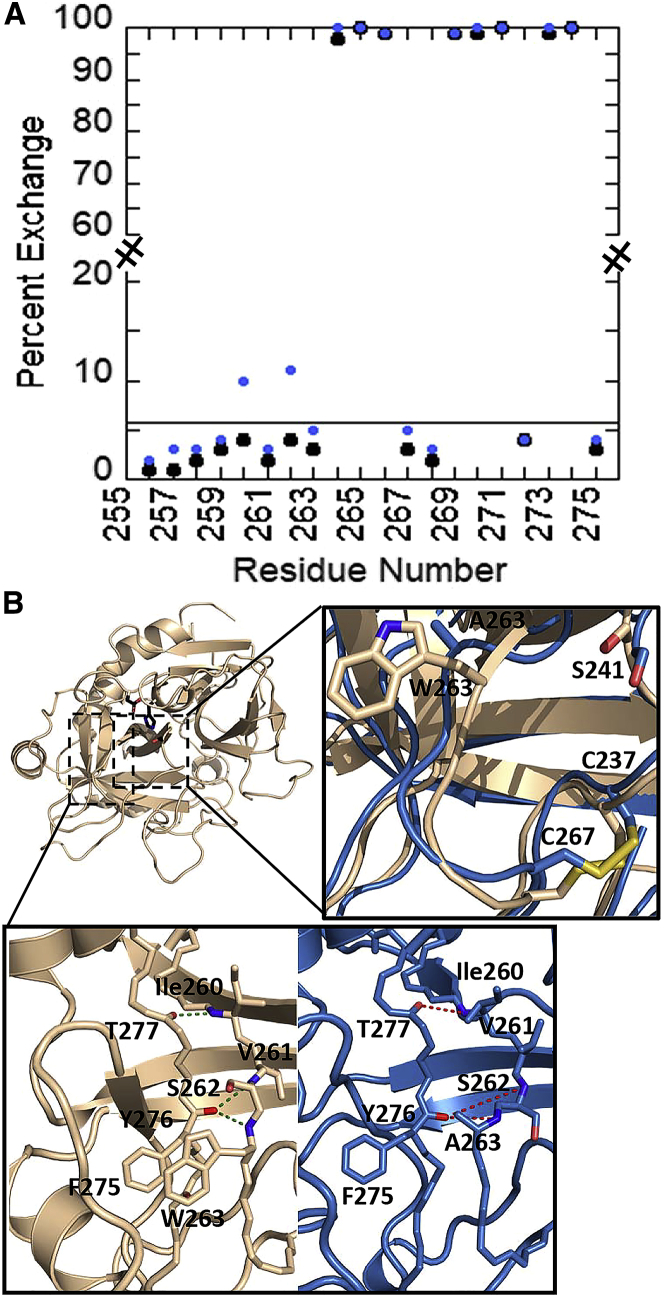
Within residues 202–222 (the 170s_CT loop), the AMD revealed a transient breaking of the backbone H-bond between Phe222NH-Tyr276CO and increased dynamics of the disulfide bridge between Cys209 and Cys223 (residues 168_CT and 182_CT), resulting in rare unfolding/refolding of the α-helical residues 205–212 (residues 164–171_CT). HDXMS experiments in the fast limit revealed 50% of the amides in this region exchanged by 5 min in WT thrombin and 71% in the W215A mutant thrombin. The corresponding theoretically predicted values were 61 and 83% respectively. The AMD simulations revealed four positions, Val208, Lys210, Ser212, and Phe222 that were above the 6% threshold and therefore were predicted to exchange in the W215A mutant but not in the WT thrombin (Fig. 3 A). The HDXMS data for overlapping peptides in this region (Fig. 3 B) were consistent with the predictions revealing that only 1.6 additional amides exchanged within the 202–211 segment, whereas four additional amides exchanged in the other longer peptides (15). An attempt was made to identify a small subset of structures from the ensemble of three million structures of the W215A mutant that represented the “excited state”; however, no small number of structures represented the entire enhanced conformational sampling observed. A representative single structure of the excited state shows the 170s_CT loop has partially rearranged (Fig. 3 C). Examination of specific H-bonds that may have been broken in this and a few other mutant structures could not account for the difference in exchange because new H-bonds are also formed. Instead it appears that the transient unfolding of this region allows partial exposure of the four amides that probably all exchange at different rates and for which the rate of transient exposure also varies.

Figure 3.

(A) A plot of the calculated HDX propensity for the 170s_CT loop (residues 201–223) for WT thrombin (black) as compared to the W215A mutant thrombin (blue). The cutoff line at 6% is shown. (B) A table of the HDXMS results showing the difference in exchange for peptides covering the 170s_CT loop at 0.5 and 5 min. (C) An overlay of the structure of WT thrombin (wheat) with a representative structure of the excited state (blue) in which the 170s_CT loop helix has rearranged. Hydrogen bonds (H-bonds) are shown as dashed lines, and the rearranged region is shown in expanded view. To see this figure in color, go online.

Enhanced slow conformational sampling of residues 256–275 (the 220s_CT loop) was also observed in the AMD simulations because of the mobility of Phe275 (227_CT) and Tyr276 (228_CT) as well as a rearrangement of side-chain packing interactions between the 170s_CT loop and the 220s_CT loop. Here also, the disulfide bond between Cys237 and Cys267 (191_CT and 220_CT) adopted alternative rotameric forms. HDXMS in the fast limit resulted in 35% of the amides exchanging by 5 min in WT thrombin and 51% in the W215A mutant (15). The corresponding theoretically predicted values were 41 and 53%, respectively. The AMD simulations revealed two positions, residues Ile260 and Ser262 that were above the 6% threshold and therefore were predicted to exchange in the W215A mutant but not in the WT thrombin (Fig. 4 A). Three peptides corresponding to residues 256–275, 259–275, and 260–275 all showed an increase in exchange of two to three amides in the W215A mutant; however, because this region contains the site of mutation, it is not possible to quantitatively interpret the HDXMS data. A representative structure of the excited state shows a rearrangement of side chains that likely accounts for the solvent accessibility difference (Fig. 4 B).

Figure 4.

(A) Plot of the calculated HDX propensity for the 220s_CT loop (residues 255–276) for WT thrombin (black) as compared to the W215A mutant thrombin (blue). The site of mutation, W215A, is TRP263 in sequential numbering. The cutoff line at 6% is shown. (B) An overlay of the structure of WT thrombin (wheat) with a representative structure of the excited state (blue) in which the 170s_CT loop helix has rearranged, resulting in changes in side-chain packing of the 220s_CT loop. Hydrogen bonds (H-bonds) are shown as dashed lines, and the rearranged region is shown in expanded view. To see this figure in color, go online.

A slight increase in the conformational dynamics of residues 175–185 (139_CT-149_CT, the 140s_CT loop) was observed in the AMD simulations. This loop contacts the N-terminus of the heavy-chain residues 37–44 (16-23_CT), which showed a subtle increase in exchange (0.5 deuteron) in the W215A mutant by HDXMS. Both the 140s_CT loop and residues 37–44 exchanged completely in both the WT and W215A mutant thrombin and therefore were not predicted to be different.

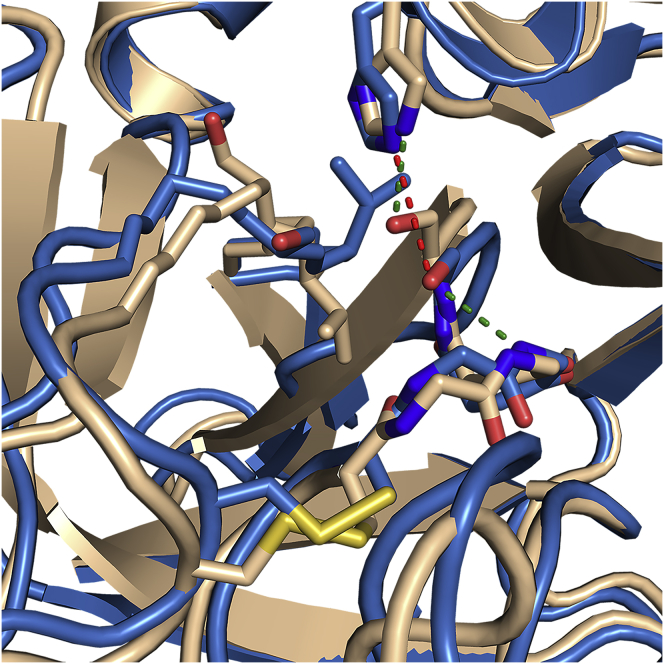
The AMD simulations revealed that in the W215A mutant, Val261 (213_CT), at the base of the 220s_CT loop, partially occludes the active site, and the side chain is in very close proximity to the catalytic Ser241 (Ser195_CT). The serine side chain rotates, and the H-bond distance between Ser241(Ser195_CT) and His79 (HIS57_CT), which is 2.9 Å in WT thrombin, is too long (3.9 Å on average) in the W215A mutant. Instead, Ser241 appears to H-bond to the backbone NH of Gly239, which ordinarily forms part of the oxyanion hole (Fig. 5). This observed distortion of the catalytic triad, which occurs far from the site of mutation but seemed to be present in the transiently visited excited state structure of the W215A mutant, probably accounts for the experimentally observed decrease in the catalytic activity of the W215A mutant compared to WT thrombin (15, 29).

Figure 5.

An overlay of the structure of WT thrombin (wheat) with a representative structure of the excited state (blue) showing rearrangement of the catalytic triad residues His57 (His79) and Ser195 (Ser241). The H-bond distance between the His and the Ser has increased from 2.9 to 3.9 Å, and Ser195 is now apparently occupying the oxyanion hole. To see this figure in color, go online.

Conclusions

Even though AMD is a highly efficient conformational space sampling method, estimating exchange rates between different conformational states sampled across the trajectory is notoriously difficult. The exchange rate between two states depends on both the magnitude of the energy barrier on the free-energy surface and the transmission coefficient. According to the well-known Kramers’ theory, the transmission coefficient is a function of the curvature of the free-energy surface on approaching the transition state and the internal friction coefficient. The application of the bias potential in AMD perturbs both these parameters, and, therefore, although the free-energy statistics (populations) of the native and non-native states may be obtained using a suitable canonical Boltzmann reweighting protocol, the associated transmission coefficient remains ill defined (14). Nevertheless, as demonstrated by the success of the method presented here, population statistics and protein topology clearly have a dominant effect on HDX behavior.

Taken together, the results lead to a profound understanding of what is actually being measured in typical HDXMS experiments, which primarily sample exchange times of minutes. We had previously measured relaxation dispersion experiments on apo thrombin and discovered an invisible state with a global exchange rate of 1770 s⁻¹ (30). If our HDXMS experiments were sampling the same transition to the invisible state, we could write the following:

$$\begin{array}{c}\mathrm{Ground}\\ \mathrm{state}\end{array}\underset{k_{\mathrm{cl}}}{\overset{k_{\mathrm{op}}}{\rightleftarrows }}\begin{array}{c}\mathrm{Excited}\\ \mathrm{state}\end{array}\stackrel{k_{\mathrm{ch}}}{\to }\begin{array}{c}\mathrm{Deuterated}\\ \mathrm{amide}\end{array},$$

where k_op = 170 s⁻¹ and k_cl = 1770 s⁻¹ (30). Remarkably, if we use the chemical exchange rate (also called the intrinsic exchange rate) of an unprotected amide in thrombin, which ranges from 0.2 to 10 s⁻¹ (16, 31), this equation results in an estimated time of complete exchange of 0.5–30 min. Notably, the exchange rates used in this calculation are those for a completely unfolded amide. This calculation helps to demonstrate that HDX in the fast limit measures exchange of amides that are not in stable H-bonds and that may only be occluded from exchange by nearby side chains. It is important to note then that the amides being detected in HDX in the fast limit are mainly in the traditionally defined EX1 limit. This term, however, is used differently in HDXMS in that it refers to bimodal distributions that are indicative of correlated exchange of more than two amides in a protein region covered by a single peptide. The AMD revealed that there is an ensemble of states in which H-bonds are transiently made and broken, and, therefore, the peptide envelope will have the expected shape for uncorrelated motions even though the amides may, in fact, be in the EX1 limit.

The use of AMD simulations to model and hence predict experimental HDXMS data in the fast limit afforded excellent agreement between experiment and theory. In fact, the subtle differences between WT thrombin and the single-point mutant, W215A thrombin, were accurately predicted. The AMD simulations further allowed for a detailed study of the conformational dynamics underlying observed HDXMS in the fast limit, which reflect important functional dynamics such as local unfolding/refolding events and allosteric communication. Importantly, they reveal the deeper mechanisms of exchange that may not be apparent from the mass spectrometry data alone.

Author Contributions

P.R.L.M. performed all the simulations, analyzed them, and helped write the manuscript. R.B.P. provided the HDXMS data and helped with data interpretation. E.A.K. helped with data interpretation and wrote the manuscript.

Editor: Nathan Baker.