Abstract
A red blood cell (RBC) performs its function of adequately carrying respiratory gases in blood by its volume being ∼60% of that of a sphere with the same membrane area. For this purpose, human and most other vertebrate RBCs regulate their content of potassium (K+) and sodium (Na+) ions. The focus considered here is on K+ efflux through calcium-ion (Ca2+)-activated Gárdos channels. These channels open under conditions that allow Ca2+ to enter RBCs through Piezo1 mechanosensitive cation-permeable channels. It is postulated that the fraction of open Piezo1 channels depends on the RBC shape as a result of the curvature-dependent Piezo1-bilayer membrane interaction. The consequences of this postulate are studied by introducing a simple model of RBC osmotic behavior supplemented by the dependence of RBC membrane K+ permeability on the reduced volume (i.e., the ratio of cell volume to its maximal possible volume) of RBC discoid shapes. It is assumed that because of its intrinsic curvature and strong interaction with the surrounding membrane, Piezo1 tends to concentrate in the dimple regions of these shapes, and the fraction of open Piezo1 channels depends on the membrane curvature in that region. It is shown that the properties of the described model can provide the basis for the formation of the negative feedback loop that interrelates cell volume and its content of potassium ions. The model predicts the relation, valid for each cell in an RBC population, between RBC volume and membrane area, thus explaining the large value of the measured membrane area versus the volume correlation coefficient. The mechanism proposed here for RBC volume regulation is in accord with the loss of this correlation in RBCs of Piezo1 knockout mice.
Introduction
Red blood cells (RBCs) are major blood constituents serving primarily to transport oxygen and carbon dioxide. Nonnucleated mammalian RBCs in particular are much simpler than most other eukaryotic cells because they consist essentially of a dense hemoglobin solution enclosed by a smooth and laterally incompressible membrane. In the course of blood circulation, RBCs are exposed to various external forces that change their shape. In capillaries, they resemble a parachute, whereas in the absence of constraints or other external forces, they resemble an axially compressed disc (1). An RBC can change its shape because of the flexibility of its membrane and because of its small (≈0.6) reduced volume (i.e., volume divided by the volume of a sphere with the same surface area) (2). Water moves through the membrane of an RBC sufficiently fast for its volume to be established as the result of the osmotic equilibrium between its internal and external solutions (3). Hemoglobin cannot cross the RBC membrane so that the cell has a tendency to swell. However, because of the control of its cytoplasmic content of potassium, sodium, and chloride ions, its volume remains steady (4). RBC anions exchange much faster than RBC cations and can be considered to be in thermodynamic equilibrium with their outer counterparts. The content of RBC potassium and sodium is established by a pump-leak mechanism (5) based on a sodium-potassium pump that uses cell ATP to expel sodium and take in potassium, together with several channels through which potassium and sodium ions leak through the membrane in the direction of their concentration gradients (6).
Piezo channels (Piezo1 and Piezo2) are large, transmembrane proteins, whose subunits have more than 2500 amino acids. They are involved in processes like touch and sound reception acting to transform mechanical stimulation into a transmembrane flow of cations (7, 8). RBC membranes contain only Piezo1, which plays the role in the establishment of the cell volume, as indicated by the fact that its mutants cause the hereditary disease, xerocytosis (dehydrated stomatocytosis) (9). Cryoelectron microscopy structural studies have shown that the Piezo1 channel operates in the form of a homotrimer (10, 11, 12, 13). The mode of action of Piezo1 in RBCs was revealed by Cahalan et al. (14) who showed, by comparing the behavior of normal mouse RBCs and RBCs of the corresponding Piezo1 knockout mice, that openings of Piezo1 channels lead to a transient increase of cytoplasmic Ca2+ concentration thus triggering increased K+ efflux by activating Ca2+ activated K+ (Gárdos) channels (15).
The mechanism by which Piezo1 acts in the regulation of RBC volume is not firmly established. Its curved structure implies that it is activated by an increase in membrane tension (11), a mechanism indicated by electrophysiological measurements (16). However, the RBC membrane mechanics at its physiological reduced volume of around 0.6 are governed by the bending of its bilayer part and by the shear elasticity of its spectrin network, exhibiting a relatively small stretching constant of its bonds (17). Lateral membrane tension is thus much smaller than that under the conditions of the electrophysiological experiment (16). RBCs exhibit a flickering phenomenon (18), which is further evidence for the membrane not being under high tension. Assuming that mechanosensitive channels can change membrane permeability in response to any kind of mechanical stimulus, it is of interest to search for other possible mechanisms of Piezo1 action. The curved structure of the Piezo1 homotrimer (10, 11, 12, 13) supports the possibility that it could also act through its sensitivity to membrane curvature. This idea is supported by the large size of Piezo1, which is an important factor in determining the strength of the curvature-dependent interaction of membrane inclusions with the surrounding phospholipid membrane moiety (19). The curvature-dependent permeability of Piezo1 is implied by recent observations on RBCs embedded in a gel, which was then compressed, causing them to deform (20). This led to an increased metabolic rate and increased cation (using cesium ions as a replacement for potassium ions) efflux. Further indirect evidence for the curvature-based mechanism of Piezo1 action is its inhibition by the spider venom peptide GsMTx4, which acts by intercalating into the lipid layers of the RBC membrane, thus affecting its nonspecific curvature status (21).
In this work, we have developed a model of RBC volume regulation by the Piezo1-Gárdos channel system based on the thesis that Piezo1 channel permeability depends on membrane curvature and thus on RBC shape. The central idea is that Piezo1 senses the shape of the RBC discocyte, and because it is different at different cell volumes, the fraction of open Piezo1 channels depends on RBC volume. Our main purpose here is to reveal the principle of the corresponding Piezo1 operation. We therefore restrict the model to that part of the RBC pump-leak system that involves the homeostasis of K+ ions. The corresponding simplified picture of the real RBC system is described in RBC Properties Essential for Establishing its Volume. In particular, it is shown how the fraction of open channels relates to the RBC volume. In A Possible Mechanism for the Effect of RBC Shape on Piezo1 Channel Permeability (i.e., the core section of this work), it is shown that the fraction of open Piezo1 channels depends on the RBC reduced volume by assuming that Piezo1 possesses open and closed conformations whose interactions with the surrounding membrane are curvature dependent in different ways. This dependence will be applied to discocyte shapes at different RBC reduced volumes. A Possible Mechanism for the Effect of RBC Shape on Piezo1 Channel Permeability will therefore include a description of the membrane curvature characteristics of these shapes. The proposed model will be in Model Predictions and their Support by Existing Experimental Evidence, applied to describe some observations that support the proposed mechanism of RBC volume regulation. Its implications will be shown to be consistent with the differences in the behavior of normal RBCs and of those of Piezo1 knockout mice (14). It will also be shown that the described mechanism explains why RBCs with larger membrane areas (A) also have, on average, larger volumes (V) (22, 23, 24). The Discussion includes a description of some possible generalizations of the described mechanism.
Methods
In the model, the RBC equilibrium state is described in terms of its macroscopic parameters (i.e., RBC volume, RBC membrane area, osmotic pressure, contents of cell ingredients, and membrane permeability coefficients). The interrelationships between these parameters, which are based on the physicochemical properties of the RBC system, are sought with the emphasis laid on the dependence of the interaction between Piezo1 protein and the surrounding membrane on membrane curvature. The resulting equations are transcendental and are solved by the standard Newton’s method of iteration. In the development of the model, we use some results of previous studies. The corresponding methods will be referred to and commented on where applicable.
Results
RBC properties essential for establishing its volume
Here, we introduce a model for establishing RBC volume by focusing on the effect of Piezo1 on the opening of the calcium-induced potassium (Gárdos) channel and on the resulting RBC K+ ion and water content. The aim is to reveal just the principle of how this process contributes to the RBC volume regulation, so the model developed will be minimal and will represent only a subsystem of the much more complex real system, which has been for some other purposes already described by correspondingly much more complex mathematical models (25, 26, 27).
The RBC interior is a highly concentrated solution of hemoglobin, and cells are situated in the environment of blood plasma that can be treated in practice as a solution of monovalent ions. RBC membrane is permeable to water but not to hemoglobin so that it attains a stationary state only when it is in osmotic (quasi-) equilibrium with the surrounding solution. The physiological volume of the RBC is established through regulation of the content of its cations K+ and Na+. The anions exchange much faster than these cations and can be considered in the model to be in equilibrium with anions of the outside solution (3, 28). The content of monovalent cations is maintained in human and many other RBCs by employing the pump-leak system in which the Na+/K+- ATPase pump actively expels three sodium ions from the cell and takes in two potassium ions in exchange (4). The thus obtained higher cell concentration of K+ and lower concentration of Na+, both relative to those in the environment, causes fluxes of these two cations in the direction of their concentration gradients. The pumping and leaking of K+ and Na+ eventually lead to the stationary state of the system. In parallel, the amount of RBC water is established by the osmotic equilibrium between the inside and outside solutions.
Here, we supplement the basic pump-leak model by taking into consideration the fact that part of the leakage of K+ out of the RBC takes place through the Gárdos channels, whose open state is under the control of Piezo1. The model thus involves, as an additional parameter, the fraction of Gárdos channels that are open (fG). Analysis of this system will be restricted to homeostasis of the potassium ions so that except for their counter ions, it does not include transmembrane movement of sodium or of any other ions or molecules. The rate of potassium entry is taken to be equal to the rate of potassium leak-out. The rate of the former is assumed to be proportional to 2RATPaseA, where A is the area of the RBC membrane, and RATPase measures how many times per second the Na+-K+ ATPases contained on a square meter of RBC membrane extrude three sodium ions and take in two potassium ions. Here, the contents of Na+-K+ ATPases and of other RBC constituents are measured by their number. Because of the small external potassium ion concentration, the potassium leak-out is taken to be proportional to the product of the membrane permeability for potassium PK (in m/s) and cell potassium ion concentration [K+], the latter defined as the cell content of K+ per cell water content (in m−3). Specifically, the potassium permeability is taken to involve the potassium permeability of the Gárdos channels (PK,G), multiplied by the fraction fG, in addition to the potassium efflux with constant permeability (PK,0). The stationary state is reached when the equation that equates potassium influx and efflux is satisfied as follows:
| (1) |
The RBC water content is established by the osmotic equilibrium that causes the cell volume to depend on the cell potassium content. For the osmotic equilibrium, which defines the cell water content, the RBC cytoplasm is taken to contain some molecules and ions that cannot penetrate the membrane (e.g., hemoglobin and 2,3-diphosphoglycerate). The total content of these molecules will be denoted by S. The requirement for the osmotic equilibrium is written as follows:
| (2) |
where V is the volume of cell water, which, to simplify the equations, we equate to the cell volume, thus neglecting the volume of hemoglobin molecules. πout is the external osmotic pressure measured in pascals. T is temperature, and kB is the Boltzmann constant. Potassium content is multiplied by a factor of 2 because for the sake of electrical neutrality of the cytoplasm, the change of the content of K+ ions requires the corresponding change of the content of its penetrable anionic counterions.
The system of Eqs. 1 and 2 can then be solved for its unknowns, RBC volume and potassium concentration. The primary interest here concerns the effects of the fraction of open Gárdos channels fG. We therefore define as the system’s reference state the case in which the Gárdos channels are closed (fG = 0). For this case, it is possible to obtain from Eqs. 1 and 2 the corresponding reference volume V0 and reference potassium concentration [K+]0, both depending on the parameters RATPase and πout/kBT. In the procedure that follows, we choose V0 and [K+]0 as the model parameters and solve Eqs. 1 and 2 by taking in Eq. 1 2RATPase = PK,0[K+]0 and in Eq. 2 πout/kBT = (S+2)/V0, where = [K+]0V0 is the content of potassium ions in the reference state. For the unknowns of Eqs. 1 and 2, it is then possible to define the ratios V/V0 and [K+]/[K+]0. For the sake of further analysis, it is convenient to express both volumes (V and V0) in terms of the corresponding reduced volumes. Reduced volume is defined as the quotient between the volume and the maximal possible volume at a given membrane area A as follows:
| (3) |
It is clear that V/V0 = v/v0. By eliminating the ratio [K+]/[K+]0 from the thus redefined Eqs. 1 and 2, the reduced volume at a given fraction fG reads as follows:
| (4) |
with the parameters η and s being defined as follows:
| (5) |
and
| (6) |
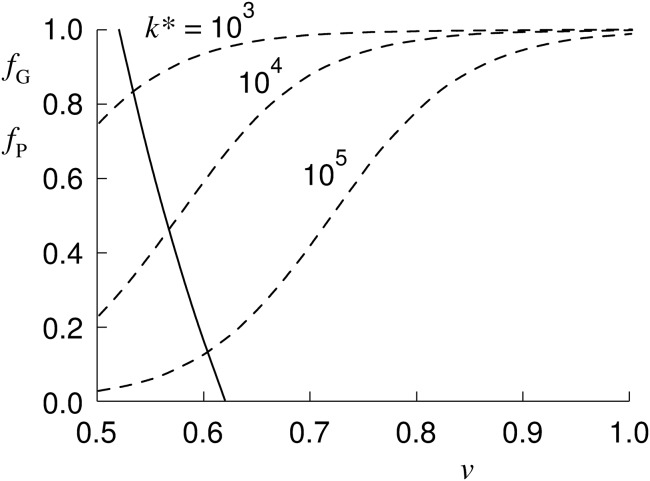
The smallest RBC volume is reached when all the Gárdos channels are fully opened. The corresponding reduced volume (denoted as vG) is obtained from Eq. 4 by taking the fraction fG to be 1. An example of the dependence of fraction fG on the reduced volume v in the interval vG ≤ v ≤ v0, obtained from Eq. 4, is depicted in Fig. 1 (full line). It is assumed that the reference reduced volume v0 is, for a normal RBC, a little greater than the expected reduced volume, 0.6. For vG, the value taken is that which is in the range of the reduced volumes obtained when human (29) or mouse (14) RBCs are dehydrated by applying the Ca2+ ionophore A23187.
Figure 1.
The dependence of the fraction of opened Gárdos channels (fG) on RBC reduced volume (v). The full line represents fG(v) (obtained from Eq. 4) by taking v0 = 0.62, vG = 0.52, and s = 0.5 (which corresponds to [K+]0 = 100 mmol/L); the corresponding value of parameter η is η = 0.106. The three dashed curves represent fP(v) (defined by Eq. 16), the dependences obtained from Eqs. 20 and 21 for the values of model parameters a = 1, α = 4, βpole = 4.0, and the indicated values of k∗.
At each reduced volume in the interval vG ≤ v ≤ v0, the potassium concentration is expressed in terms of the model parameters as follows:
| (7) |
Thus, at a given fraction of open Gárdos channels fG, the osmotic state of the treated model RBC is characterized through Eqs. 4 and 7 by the reduced volume v and potassium concentration [K+].
A possible mechanism for the effect of RBC shape on Piezo1 channel permeability
Here, the basic properties of the RBC discocyte shape relevant for the functioning of the proposed curvature-dependent mechanosensitivity of the Piezo1 channel are briefly recapitulated. A possible mechanism for the dependence of the average permeability of this channel on the RBC reduced volume, v, will then be described.
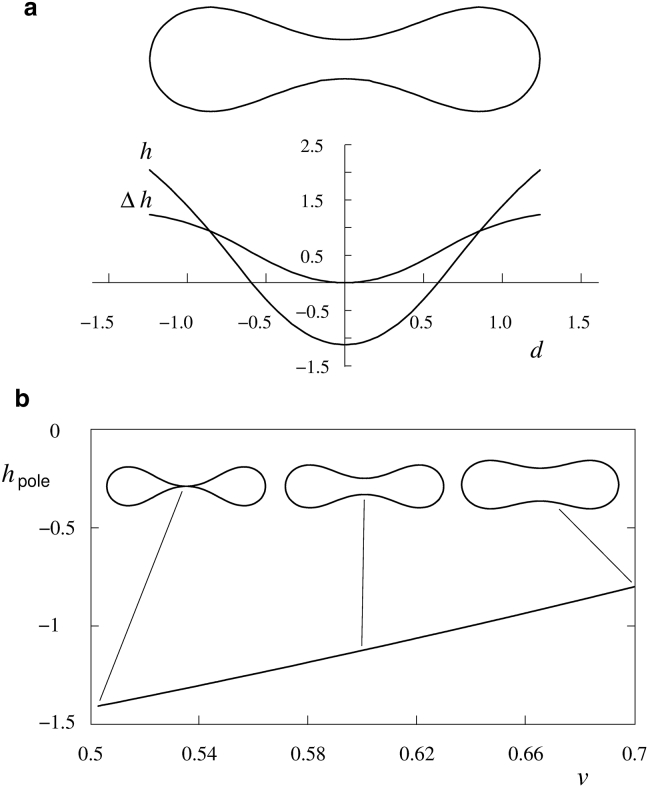
For any nonspherical RBC shape, the possible principal membrane curvatures (Ci, i = 1 and 2; the reciprocals of the membrane principal radii, Ri) lie in the finite interval between their largest and smallest values. The principal curvatures of discoid RBC shapes can be obtained by assuming that the shape is a result of the minimization of the bending energy of the membrane of the vesicular object (30, 31, 32). As an example, in Fig. 2 a is shown the discoid shape obtained at a reduced volume, v = 0.6, together with the corresponding reduced mean membrane curvature, defined as h = (c1 + c2)/2 and one-half of the difference between reduced principal curvatures Δh = (c1 − c2)/2. Here, c1 = C1Rs, c2 = C2Rs (with , the radius of the sphere with area A) and, correspondingly, h = HRs and Δh = ΔHRs (with H = (C1 + C2)/2 and ΔH = (C1 − C2)/2). Reduced variables were introduced because the bending energy of similar shapes does not depend on the system’s size and because all shapes with different areas A but the same reduced volume v are similar and characterized by the same reduced principal curvatures. The reduced mean curvature h is largest at the cell rim and smallest at the cell poles (Fig. 2 a). Principal curvatures are defined as being positive for the convex parts of the membrane and negative for its concave parts. In the axisymmetric RBC discocyte, the principal curvature along the meridians (cm) is greater than that along its parallels (cp) over its whole surface. The positive sign of Δh (Fig. 2 a) thus corresponds to the assignment of principal curvatures, c1, as the principal curvature along the meridians (cm), and c2, that along the parallels (cp). The dependence on v of the reduced mean principal curvature at the cell poles (hpole) is given in Fig. 2 b. Also shown are examples of the discoid RBC shapes at the indicated reduced volumes.
Figure 2.
RBC discocyte shape. (a) Contour of the cross section of the RBC discoid shape at the reduced volume v = 0.6 obtained exactly by minimization of the membrane bending energy, as described in (32), the corresponding dependences of the reduced mean membrane curvature (h), and the difference between reduced principal curvatures (Δh) (see text for the definitions) on the reduced distance from the axis d = D/Rs (where D is the distance from the axis). (b) The dependence of the reduced mean principal curvature at cell poles (hpole) on the reduced volume (v). Also shown are three examples of the corresponding discoid RBC shapes.
The dependence of the reduced mean curvature, hpole (Fig. 2 b), on the reduced volume v in the range of relevant RBC reduced volumes is practically linear so that it is possible to express it as follows:
| (8) |
where hpole,r is the reduced mean curvature at an arbitrarily chosen reference reduced volume vr. The value of the coefficient βpole is 4.0.
The basis for the mechanosensitivity of the Piezo1 channel is assumed to be the mismatch between the principal intrinsic curvatures of the channel and the principal curvatures of the surrounding lipid membrane. Membrane curvature may affect the permeability effectiveness of an ionic channel if it involves conformational states of different energies that exhibit different permeabilities (33). Such a situation is described here by considering the Piezo1 channel to have open and closed conformations exhibiting different energies Wj (index j extending over all conformations, either “open” or “closed”). These energies in general comprise intrinsic energy because of interactions between different parts of molecule and between molecule and the surrounding membrane. It is assumed that part of the latter is curvature dependent and is denoted as Wcurv,j. The curvature-independent energy is denoted as Wint,j. For Wcurv,j, we use a phenomenological expression based on the difference between the intrinsic principal curvatures, C1,P,j and C2,P,j, of the transmembrane part of the channel and the membrane principal curvatures, C1 and C2, at its membrane position. The general expression for the corresponding energy term in the limit of a rigid protein surface has been derived in (34) as follows:
| (9) |
where HP,j = (C1,P,j + C2,P,j)/2 is the mean principal intrinsic curvature of the Piezo1 transmembrane part, and ΔHP,j = (C1,P,j − C2,P,j)/2 is a measure of the difference between the two intrinsic principal curvatures of the channel. κj and κj∗ are independent interaction constants. The angle ωj defines the mutual orientation of the coordinate systems of the intrinsic principal curvatures of the protein and the principal curvatures of the membrane.
The dependence on the curvature of interaction between the channel and surrounding membrane can cause the channels at sufficiently large values of the interaction constants to concentrate in membrane regions in which their intrinsic curvatures are best matched with the membrane curvature. The lateral distribution thus obtained is the result of two tendencies: 1) to decrease the system’s energy by moving channels into regions with the lowest channel-membrane energy and 2) to increase the entropy by making the distribution as homogeneous as possible (35). The resulting normalized areal number density of open and closed channels (channel density in the following) as a function of the membrane position (defined with respect to an arbitrarily chosen reference point) can be approximated by the Boltzmann factor for sufficiently small channel densities (36) as follows:
| (10) |
where NP is the number of RBC’s Piezo1 molecules. The total channel density is then as follows:
| (11) |
Piezo1 is a homotrimer. Because of the size of each subunit, it is plausible to assume that they can, independently of one another, exist in conformations corresponding to either an open or a closed channel. In such a case, Piezo1 could take up four different structures, two axisymmetric, with all subunits being in either a closed or an open conformation, and two nonaxisymmetric, with either one or two of them in an open conformation, for example. In the case of an axisymmetric conformation, it is possible to use a simplified version of Eq. 9 by taking ΔHP,j = 0. In the following, to avoid nonessential complexity, we will take the option that we are dealing with only two axisymmetric conformational states that correspond to an open and a closed channel (j = open or closed), respectively. Because we shall also keep to model constants that represent different structural elements of the system only qualitatively, it will be taken that . The strength of the channel-membrane interaction can then be represented by just a single nondimensional constant (γ), defined here in a nondimensional form as follows:
| (12) |
with the unit of length being defined as the radius of a sphere corresponding to the average area of the membranes in an RBC population . The lateral distribution of channels (Eq. 11) can then be written as follows:
| (13) |
where the effect of the curvature-independent energies is condensed to the constant k, defined as follows:
| (14) |
and
| (15) |
where hP,j = HP,j and a = A/.
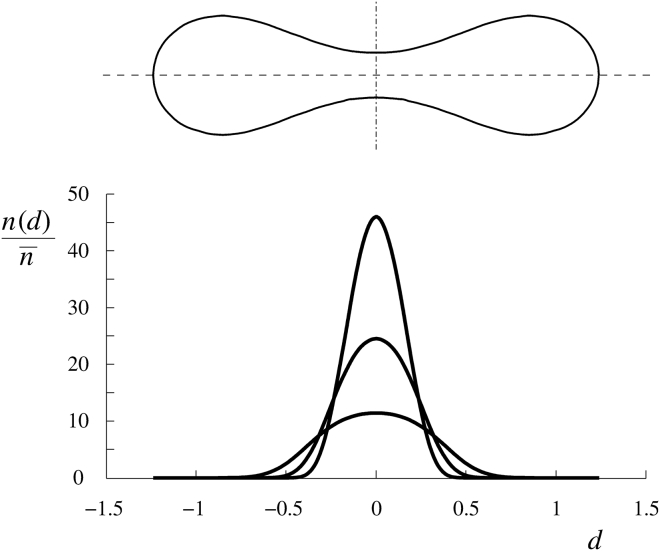
The intrinsic curvature of Piezo1 is strongly negative (10, 11, 12, 13) and, presumably, its interaction with the membrane is very strong. As a consequence, the corresponding constant HP,j would cause them to accumulate in the regions of the RBC discocyte poles (dimples). Examples of the lateral distribution of the channel on the RBC membrane at v = 0.6 are given in Fig. 3 for some values of the constants hP,open, hP,closed, k, and γ.
Figure 3.
RBC membrane areal number density of Piezo1 relative to the mean areal number density at a reduced distance d from the axis for an RBC shape at v = 0.6, calculated as described in Božič et al. (35) for hP,open = −1.2, hP,closed = −1.6, k = 10 and γ = 1, 3 or 10 (from a wide to a narrow distribution).
The permeability of the channel under discussion is proportional to the fraction of all the Piezo1 channels that are open (fP) (i.e., to the integral of the lateral density of just open channels) and is as follows:
| (16) |
This fraction is expected to differ at different reduced volumes. To avoid integration over the lateral distribution of the channel (see Eqs. 10 and 13), we assume that Piezo1 channels accumulate so closely to the pole regions of a discocyte that their interaction with the membrane can be approximated by taking its value at the poles. Recalling that Piezo1 is rotationally symmetric, Eq. 16 can be expressed as follows:
| (17) |
with the newly introduced constants
| (18) |
representing both the strength of the Piezo1-membrane interaction and the way its intrinsic curvatures differ in the open and closed conformations, and
| (19) |
representing the average of the intrinsic curvatures of the open and closed conformations of Piezo1.
The reduced mean curvature hpole, which is the variable in Eq. 17, depends on the RBC reduced volume (Eq. 8), which means that the fraction of open Piezo1 channels changes as this volume changes. By inserting in Eq. 17 the right side of Eq. 8 for hpole, and taking, for the reference reduced volume, its hypothetical value, for which hpole,r = (i.e., vr = ), we obtain the equation for the dependence of the fraction of open channels (fP) on the RBC reduced volume (v) as follows:
| (20) |
where
| (21) |
It is seen that the function fP(v) depends on just two independent parameters, α and k∗. Some examples of the corresponding dependencies fP(v) are given for a = 1 and α = 4 and the indicated values of k∗ in Fig. 1. On increasing the value of the parameter α, the dependences fP(v) become steeper (data not shown).
Model predictions and their support by existing experimental evidence
The essence of the described regulation of RBC volume is that Piezo1 senses mechanically the cell shape that is characterized by the cell’s reduced volume. The regulated variables are thus the latter property and the fraction of open Gárdos channels. They affect each other by the requirements of RBC osmotic equilibrium and by the stationary establishment of the cell content of potassium ions. At a higher fraction of open Piezo1 channels (fP), it is reasonable to expect that more Ca2+ ions are entering the cells which, on average, must also cause an increase of the fraction of open Gárdos channels (fG). By assuming fG = fP, it is possible to solve Eq. 4 by inserting for fG the right side of Eq. 20. The obtained solution is represented in Fig. 1 by the crossing of the two respective f(v) dependences. The system’s behavior depends on numerous parameters: the reduced volume v0 and the concentration [K+]0 that define the reference state of the RBC, the ratio s (Eq. 6), the ratio η (Eq. 5) (or, alternatively, vG), and the parameters of Piezo1, α and k∗, the latter representing constants k and (the latter represented in Eqs. 20 and 21 by vP). An attempt is made to assign to these parameters values at which the model behaves well in accord with the real RBC. However, the model is a gross simplification of the real system, and the main focus will therefore be on testing its predictions, which are more general than parameter-based fitting of the corresponding experimental data.
The crucial model prediction is the relation between RBC membrane area and volume, which is the result of the regulation of the cell’s reduced volume (v). The latter is obtained by solving Eq. 4. For a given membrane area, the corresponding cell volume can be obtained from the value of the reduced volume (Eq. 3). The cell volume, multiplied by potassium concentration and obtained by Eq. 7, then yields also the cell potassium content. Because of the described regulation, the relations between RBC membrane area, volume, and potassium content must be equally valid in each cell of the RBC population. The validity of the model can thus be tested by studying the consequences of these relations and comparing them with the experimental evidence based on measuring different RBC variables on single cells of large, presumably homogeneous cell populations. It will be assumed that all RBCs of a given subject have the same values of the model parameters.
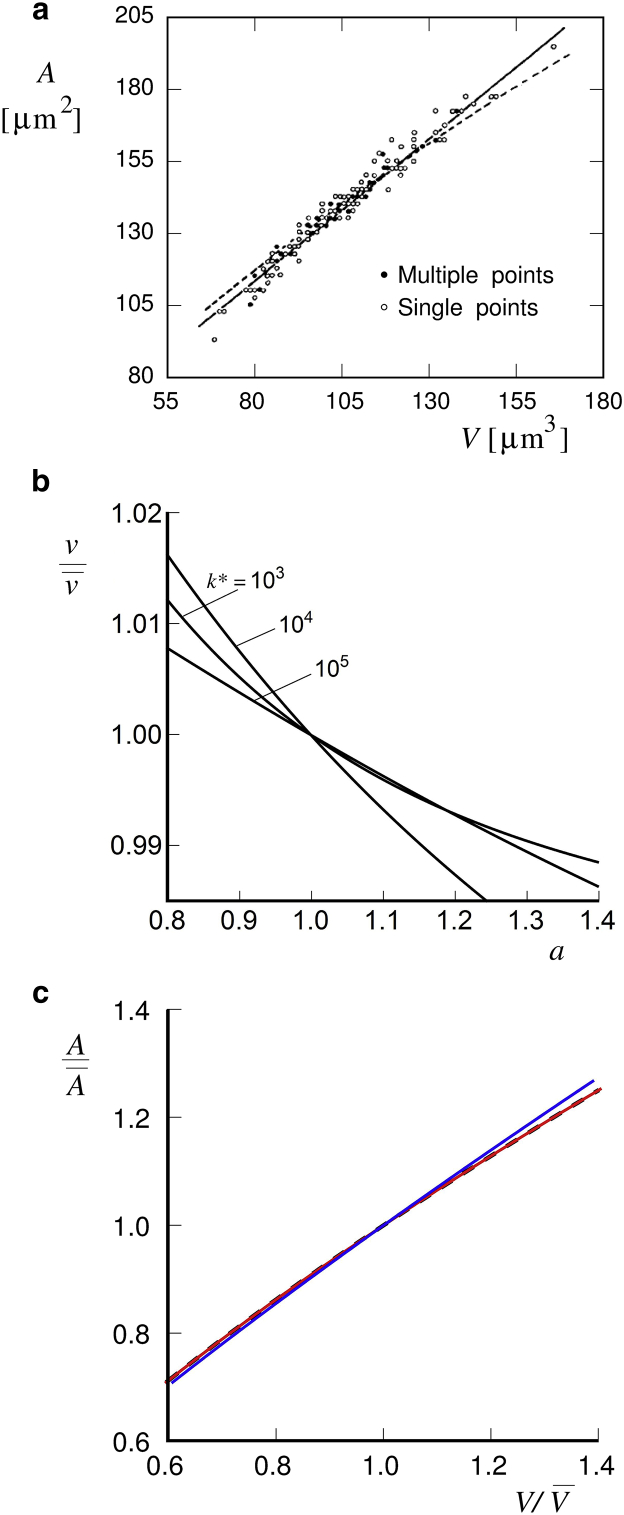
Single-cell simultaneous determinations of RBC surface area and volume in an RBC population showed that there is a strong correlation between its volume and membrane area with a correlation coefficient ρA,V ∼0.97 (22) or ∼0.96 (24). Similarly, Waugh et al. (23) showed that there was little change in surface/volume ratio with RBC age. The fact that the value of ρA,V is so close to unity by itself suggests that there is a relation between A and V that is the same in all cells in a population. For testing the model, the data of Canham and Burton (22), who measured RBC volumes and areas simultaneously, are particularly instructive. In the corresponding scatter plot (Fig. 4 a), they showed quite a close match between the regression line through the measured points and the line of constant sphericity index, which defines the deviation of the shape from that of the sphere and is equivalent to the line of a constant reduced volume (shown by the dashed curve). These observations can be considered as the direct result of the described Piezo1-based mechanism of RBC volume regulation. By solving Eq. 4 with fG equal to fP (Eq. 20), the dependence of the reduced volume (v) relative to its average on the relative area a can be obtained. In Fig. 4 b, this dependence for the parameter values defined in Fig. 1 is shown. In general, the slopes of these dependences are negative. Their steepness depends on the parameter α and is larger at larger values of the latter (data not shown). The relative volume can then be calculated as follows:
| (22) |
Figure 4.
The correlation between RBC membrane area and cell volume. (a) Results of simultaneous determinations of RBC membrane area and cell volume extracted from Fig. 5 of (22) are shown. This figure also contains the regression line (full line) and the line of constant sphericity index (dashed line). The latter is equivalent to the line of constant reduced volume. (b) The dependence of the reduced volume v divided by its average (, defined by taking in Eq. 3 and ) on the relative membrane area a, obtained by solving Eq. 4 with fG defined by Eq. 20. Calculations are presented for the model parameters used for Fig. 1. (c) The dependence of the relative membrane area on relative volume , obtained by Eq. 22. The dashed line is the line with constant reduced volume. The full line that matches it (red) is obtained for the parameters of Fig. 1 with k∗ = 105. The deviating full line (blue) is obtained for α = 20 and k∗ = 1022.
Fig. 4 c represents the theoretical counterpart of Fig. 4 a thus obtained. It can be seen that at α = 4 (red curve), the dependence of the relative membrane area a on the relative volume obtained from Eq. 22 practically does not deviate from the curve of constant reduced volume (dashed curve). With a much larger value of α (α = 20; blue curve), there is such a deviation, and it corresponds to the observed deviation of the regression line in Fig. 4 a from the curve of constant reduced volume (22). The large value of the parameter α supports the idea that the system works on the basis of the accumulation of Piezo1 at the discocyte poles (see Fig. 3).
The strong correlation between A and V is reflected in the fact that the variation of the cell’s reduced volume in the RBC population is much narrower than the variations of their membrane area and cell volume (Appendix A). This is, for example, evidenced by the characteristic dependence of the fraction of hemolyzed RBCs on the external osmotic pressure (osmotic fragility curve). Hemolysis occurs because there is a corresponding increase of cell water at lowering external osmotic pressure; this is due to the requirement of osmotic equilibrium between a cell’s interior and its exterior. Eventually, the cell becomes spherical, and its membrane becomes strained, leading to the formation of a pore and consequent release of cell hemoglobin. The osmotic pressure at which a given RBC lyses is proportional to the ratio between its volume and the volume of a sphere with the same membrane area and, thus directly to the cell’s reduced volume (Eq. 3). In model presented here, the hemolyzing osmotic pressure (πout,h) is proportional to the product of the reduced volume and the osmotic pressure of the normal outside solution (πout), that is,
| (23) |
In the light of Eq. 23, the coefficient of variation of the hemolyzing osmotic pressure (CVh) is the same as that of the RBC reduced volume (CVv) (Appendix A).
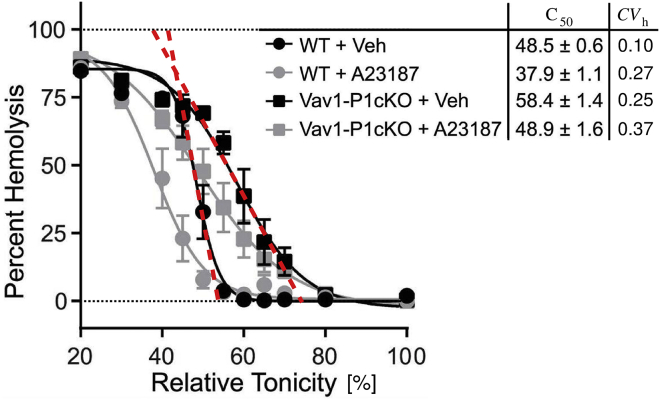
From measured osmotic fragility curves, it is possible to estimate CVh by determining its maximal slope, which, by assuming that the distribution is normal (Gaussian), is proportional to , where is the corresponding SD (expressed here in units of relative tonicity). In the last column of the adjoined table in Fig. 5 are given the thus obtained coefficients of variation for wild-type mouse RBCs and for RBCs of Piezo1 knockout mice in the absence and presence of the Ca2+ ionophore A23187 reported in Fig. 3 D of (14). In Fig. 5, the maximal slopes of the osmotic fragility curves of wild-type mouse RBCs and of RBCs of Piezo1 knockout mice are also added to the copied version of Fig. 3 D of (14). It is seen clearly that Piezo1 knockout RBCs hemolyze over a relatively much wider range of external osmotic pressure. From the analogy between this behavior and the dependence of CVv on of human RBCs presented in Fig. 7 (Appendix A), it can be concluded that there is a correlation between RBC volume and its membrane area in the wild-type mouse RBC, whereas the correlation coefficient is much smaller in the case of RBCs of Piezo1 knockout mice in which CVh is about three times larger. Wider intervals of hemolyzing osmotic pressure can also be observed in both treated RBC populations that have been exposed to the Ca2+ ionophore A23187 for 30 min. From the results of Cueff et al. (37), who have shown that after 30 min of exposure to the Ca2+ ionophore, the osmotic fragility curve does not differ appreciably from that observed 10 min after it was added, it can be deduced that this behavior is due to the K+ loss through the Piezo1-induced opening of Gárdos channels. It can be seen that the shift of the medium lytic osmotic pressure on the addition of Ca2+ ionophore A23187 is closely similar for both normal cells and cells of the Piezo1 knockout mice (Fig. 5). This is consistent with our assumption made about the closeness of the reduced volumes v and v0 in Fig. 1 but also indicates that the observed shift of the osmotic fragility curve of the Piezo1 knockout mice to higher osmotic pressures is the result of processes not included in the treated model.
Figure 5.
The width of the distribution of hemolyzing osmotic pressure of the wild-type (WT) mouse RBCs and of RBCs of Piezo1 knockout mice (Vav1-P1cKO) in the absence and in the presence of the Ca2+ ionophore A23187. In this figure, we reproduce the corresponding osmotic fragility curves and the adjoined table of relative medium tonicities, that is, the tonicities when 50% of cells are lysed (C50) as presented in Fig. 3 D of Cahalan et al. (14). In the newly added column in the adjoining table are given the coefficients of variation of the RBC distribution with respect to the hemolyzing osmotic pressure, defined as . The SD is obtained from the indicated slopes of the osmotic fragility curves (dashed lines) that are equal to for the normal (Gaussian) distributions (shown only for cases without A23187).
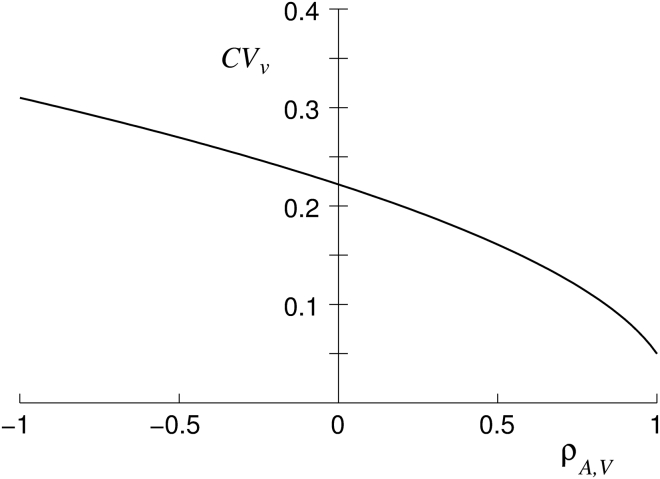
Figure 7.
The dependence of the coefficient of variation for the reduced volume on the correlation coefficient between RBC volume and membrane area obtained from Eq. A2 by taking = 0.13 and = 0.12 (42).
In this section, it is seen that the model introduced to interpret the role of Piezo1 in the regulation of RBC volume provides a possible mechanism for the strong correlation between RBC volume and its membrane area. According to Eq. 23, comparison of the coefficient of variation of reduced volumes of human RBCs, = 0.06 (Appendix A), with those from the experiment extracted value, = 0.054 (38), is clear indication that it is this correlation that is responsible for the observed large steepness of the osmotic fragility curves in normal RBCs. The observed smaller steepness of the osmotic fragility curve in the case of an absent Piezo1 channel (Fig. 5) is therefore consistent with the proposed action of the Piezo1-Gárdos channel system. Further confirmation of the relevance of the model predictions is provided by the fact that the decrease of membrane area/volume correlation in the case of the application of the ionophore A23187 is approximately the same as in the absence of the Piezo1 channel (adjoined table in Fig. 5). With open Gárdos channels, the fraction fG is unity in all cells of the RBC population, which means that the correlation between RBC volume and its membrane area is significantly reduced.
Discussion
RBCs possess a much simpler composition and structure than other eukaryotic cells and can therefore serve as a convenient system on which to study how cell functioning relates to the molecular and supramolecular properties of its constituents. The model developed in this work is aimed at explaining the contribution of the mechanosensitive protein Piezo1 to the regulation of RBC volume. It brings together several previous studies on RBC osmotic properties (3, 39), the shape behavior of vesicles and RBCs (32), the curvature dependence of the lateral distribution of membrane inclusions (34, 35, 36, 40) and consequent curvature-dependent mechanosensitivity (33), and on the relationships between the variability parameters of RBC properties (41, 42, 43). We first comment on the model’s principal constituents, then discuss its outcomes and limitations, finally suggesting its possible extensions and proposing some experimental verifications.
The model content
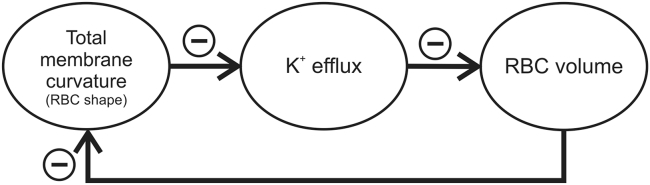
The treated model of RBC volume regulation supplements the otherwise well-established pump-leak mechanism of balancing the influx and efflux of potassium and sodium ions (5) by incorporating the mechanosensitivity aspects of the cationic channel Piezo1 in it. RBC potassium efflux takes place via several separate pathways (6) for which it may be assumed to have different physiological roles. Given this premise, it is shown in this work that at least one of these leaks, specifically of the Gárdos channel whose K+ permeability is under the control of the mechanosensitive ion channel Piezo1, takes part in a negative feedback loop involving RBC volume and shape. In this loop, the increase of total membrane curvature (integral of mean membrane curvature over the membrane area) would cause a diminution of K+ efflux, the increased K+ efflux would cause a decrease in RBC volume, and the increased RBC volume would cause a decrease in total membrane curvature (Fig. 6). In general, the Piezo1-Gárdos channel system can be considered as a complement to the mechanism for the cell volume regulation that operates at the level of passive cation membrane permeability. The involvement of Piezo1 in RBC regulatory circuits was recently also recognized by Kuchel et al. (20).
Figure 6.
A schematic presentation of the negative feedback loop through which RBC volume is regulated by its shape.
At the center of this analysis are the membrane curvatures of the disk shape that is also the resting shape of a normal RBC when placed in a motionless physiological solution. When in the interval of reduced volumes between v = 0.58 and v = 0.63, the discoid shape is also the minimal bending energy shape of simple closed objects such as phospholipid vesicles (32). In RBC, discocyte-stomatocyte or discocyte-dumbbell shape transformations would require an increase of the energy of its membrane skeleton (17). Therefore, it is expected that the corresponding interval of stable discoid shapes is even wider. In the different stages of blood circulation, RBCs are forced to attain shapes other than discoid. Reduced volumes of the resting cell (i.e., around 0.6) are advantageous in this respect because the bending energies of many other types of shapes are not very much larger than that of the discocyte at this reduced volume (44). Our study points to the possibility that the RBC discoid shape can also play a physiological role of being involved in the fine regulation of the RBC volume. For this role to be played, it is an important fact that RBCs spend more than 50% of their time in veins, where the hydrodynamic conditions favor the establishment of their resting discocyte shape. For the proposed mechanism of RBC volume regulation to be efficient, it is important that during the time when an RBC is deformed, there is no significant diffusion of Piezo1 molecules so that their equilibrium lateral distribution would not change significantly. For a typical laterally free mobile membrane protein, the diffusion coefficient in a lipid membrane is ∼5 μm2/s (45). Piezo1 molecules localized around the discocyte poles, would thus, in the absence of their curvature-dependent interaction, attain a uniform lateral distribution estimated from the ratio between the spreading area (one-half of the area of the RBC membrane) and their diffusion constant in approximately 10 s, which is less than about a minute that RBC is deformed. However, in the crowded surroundings of the RBC membrane with more than 104 proteins per 1 μm2, the diffusion coefficient could be about five times smaller (Fig. 4 of (45)) and therefore five times larger this time. The treated curvature-dependent Piezo1-lipid membrane interaction suggests that a piece of membrane containing a Piezo1 molecule could be depressed into the spectrin network, causing the Piezo1 diffusion coefficient in the RBC membrane to be even much smaller and thus allowing Piezo1 lateral distribution to remain practically undisturbed during the period of RBC deformation.
The crucial ingredient of the model is the membrane-curvature-based mechanism by which the RBC discoid shape affects Piezo1 permeability. Mechanosensitive channels are, in general, membrane-embedded proteins that respond to changes of the mechanical state of the membrane (46). Piezo1 has been shown to respond to changes of membrane lateral tension (16). In principle, the feedback system shown in Fig. 6 could also be based on the dependence of the RBC membrane tension on the reduced volume. However, in RBC discoid shapes, the relevant lateral tensions are small. At changing the reduced volume from v = 0.7 to 0.5, the lateral tension due to membrane bending energy would, with the bending constant of the RBC membrane kc = 2 × 10−19 J (47), increase by ∼0.02 μJ/m2, while the contribution due to the accompanying deformation of the membrane skeleton can be neglected (17). In this work, it was inferred that the conformation of Piezo1 may depend on membrane curvature due to its interaction with the surrounding bilayer membrane, thus responding mainly to applied torques exerted by the surrounding membrane. Effects of membrane curvature have now been firmly established to be a ubiquitous biological mechanism (48) by the discovery of many curvature-sensing and curvature-forming proteins. A nonuniform lateral distribution of mobile membrane-embedded proteins as the consequence of curvature-dependent-protein-membrane interaction has been demonstrated experimentally (49). It was shown that a general phenomenological expression for such an interaction, represented by Eq. 9, can be employed as an appropriate basis for a corresponding theoretical analysis (36).
The model outcomes
The scope of this work was to define the least complex system needed to describe the mechanism of Piezo1-based regulation of RBC volume. Thus for example, the Piezo1-based feedback system for the regulation of RBC volume was treated as not being coupled to the rest of the related RBC processes. The model presented therefore cannot provide detailed simulation of the RBC behavior but is rather intended to reveal the principle of Piezo1 operation. In view of this, we will emphasize primarily model outcomes that describe correctly the qualitative features of RBC behavior in the following discussion.
The model elucidates the existence of fine regulation of the RBC volume and defines its location within the complex RBC biochemical circuitry to be at the level of the passive leak of its potassium ions. The gross feature of this regulation is that the Na+-K+ pump drags into the cell more potassium than is finally needed, and then, by way of the feedback loop presented in Fig. 6, a cell attains the physiologically optimal value of its volume by regulating the fraction of Piezo1 channels that are open (fraction fP, Eq. 20). Structural modifications of the normal RBC Piezo1 may lead to a changed value of the fraction fG and to consequent xerocytosis. In known examples of the latter, RBCs are dehydrated (50), which is consistent with the fact that in the normal RBC, the fraction fP has a low value and that in Piezo1 mutations, there is, for example, a lowering of the constant k∗ (Eq. 21) with consequent increase of fraction fP (see Fig. 1). The model also offers a possible interpretation of RBC dehydration in the case of sickle cell disease (51). When cells in their deoxygenated state sickle, they lose their ability to maintain their inhomogeneous Piezo1 lateral distribution, and the loop presented in Fig. 6 is thus broken. On average, Piezo1 channels are in this way opened for longer and consequently leak more potassium so that cells achieve smaller stationary volumes.
A significant result of the model is that it provides an explanation for the strong correlation between RBC membrane area and volume. Membrane area and RBC volume are related because the effect of RBC shape on potassium efflux through the Piezo1-controlled Gárdos channel involves the reduced volume that itself depends on both these cell variables. The values of both these RBC variables have been shown to be widely distributed around their average values (with their variation coefficients ∼0.12–0.13) but to be strongly correlated, in that cells with larger membrane areas have larger volumes on average (22, 23, 24). The general consequence of such strict (i.e., valid for each cell of an RBC population) relations between cell variables are the relations between the parameters that define their population variability (variation coefficients and correlation coefficients) as demonstrated here by Eq. A2 (Appendix A). That there is a strict relation between RBC properties involving the content of its cations and membrane area was previously implied from the analysis of relations between the corresponding variability parameters (38, 41, 42, 43). However, its background was not clear.
By regulating the reduced cell volume, RBCs measure their volume and membrane area simultaneously and, in this sense, differ from many other eukaryotic cells, which regulate independently both their volume and the area of the plasma membrane exposed to the environment (52). The reason for RBCs having their reduced volume as a regulated variable appears to be of physiological significance. It can be anticipated that for an optimal response to the requirements of hydrodynamic stresses, there is also an optimal reduced volume. More specifically, during their lifetime, the amounts of an RBC’s membrane and hemoglobin decrease because of the release of microvesicles (53). On releasing a spherical vesicle, a cell loses relatively less volume than membrane area thus becoming more and more swollen and thus less suited for its rheological function throughout its lifetime of ∼120 days. Because of the Piezo1-Gárdos channel system of regulating RBC monovalent cation content, this does not happen. This system can thus be considered as a self-repairing mechanism for keeping RBCs fit for their function throughout their life.
Model limitations
Electrophysiological experiments have revealed the process of inactivation, indicating that Piezo1 exhibits at least one more conformational state in addition to closed and open conformations (54). This suggests that the two-state model is an oversimplification. However, it has since been shown that the inactivation can be removed (55), meaning that the inactivation process is an amendment to the basic two-state system, serving to regulate the Gárdos potassium efflux in a more subtle manner. But the two-state model of the action of Piezo1 channel is also a simplification because it is an oligomeric homotrimer and has therefore four different structures in assuming that each subunit has two different conformations. Two of these structures in which all three subunits are in the same conformation are rotationally symmetric with the order of three, whereas the other two structures in which the conformation of one of the subunits is different from that of the other two have no rotational symmetry. In the model presented here, it has been assumed for the sake of simplicity that the relevant structures are those exhibiting rotational symmetry, one corresponding to the closed and the other to the open Piezo1 conformation. This may not be the best representation of the system because it has been shown in a recent study using the Piezo1 agonist Yoda1 (56) that the channel assumes an open conformation when Yoda1 binds to only one subunit. It appears that a more complete model of Piezo1 activity will have to involve Piezo1 conformations with no rotational symmetry as well. In the context of this work, it has to be indicated that when the Piezo1 structure is not rotationally symmetric, the Piezo1-bilayer membrane interaction must be described by using the complete Eq. 9. However, it is not expected that the corresponding, more accurate treatment would lead to a qualitatively different prediction concerning the behavior of the Piezo1 action.
The prediction concerning the strict relation between RBC membrane area and volume, obtained by the described model, is correct only approximately because as simultaneous measurement of RBC volume and membrane area show (Fig. 4 a), there is a considerable scatter around the regression line giving rise to a correlation coefficient ρA,V = 0.97 (i.e., not exactly unity). This scatter can be ascribed to RBC variability with respect to the cell’s hemoglobin content as was earlier deduced from the analysis of relations between variations of RBC properties (41). In this respect, the simple model described here is a simplification in which it was taken that the parameter s (Eq. 6), which also involves the cell content of hemoglobin, is the same for all cells. The individual RBCs in a population may actually differ in the amount of any of the parameters involved in (4), (7). For example, the parameter η, which is the ratio between the permeability of the Gárdos channel and the permeability of other potassium channels (Eq. 5), is proportional to the ratio between their areal densities, which may not be the same in all cells of the RBC population. However, a study of the origin of these residual variabilities is outside the scope of this work.
Possible model extensions
Besides defining the limits between known and unknown properties of the studied system, the intention of the treated model is to guide further experimental and theoretical research. Several straightforward generalizations of the simple model are possible to include, for example, in the modeling of RBC osmotic behavior, the volume of hemoglobin molecules, and their buffering capacity (3). Another matter is that the coupling between potassium and sodium fluxes should certainly be included to obtain, for example, the observed shift of the osmotic fragility curve in the case of Piezo1 knockdown mice (14). A subject of interest is whether the measured A-V correlation coefficient can be related in a quantitative manner to the variability of hemoglobin content in a population of RBCs and to the density changes during cell aging (57).
Extensions of the model presented here may also lead to qualitatively new consequences of the action of Piezo1, and we conclude this subsection by indicating two such possibilities. In the model, it was taken that the inclusions redistribute because of their interaction with the surrounding membrane for a given fixed membrane shape. However, in general, the effect is mutual. Because of the curvature-dependent interaction of Piezo1 molecules with the surrounding membrane, the RBC shape may also change. The consequent interplay between cell shape and the lateral distribution of membrane inclusions can be analyzed by minimizing the sum of the membrane bending energy and the free energy of the inclusions (35). Preliminary estimates of this effect have shown that when the intrinsic curvature of Piezo1 (Hm) is more negative than the membrane curvature at the RBC poles (Hpole), the Piezo1-induced shape change decreases the pole-to-pole distance, whereas when it is less negative, it increases it. Within the applied two-state model, the transition from the state of the system in which all Piezo1 channels are in a closed conformation to the state in which they are all open may thus involve a considerable RBC shape transformation.
In the model, it was assumed that Piezo1 channel conformations are in thermodynamic equilibrium. This assumption can be valid when there is sufficient time for the system to equilibrate, as is certainly the case in experiments that last for hours (20). Over short times, the behavior of Piezo1 and Gárdos channels of the RBC system could be different. A possible scenario for the nonstationary behavior of the treated system is that when Piezo1 channels are closed and RBC volume is below its basic stationary value, more potassium ions enter the cell than leak out, causing the volume to increase. Above a certain volume, the energy of opened Piezo1 channels would become lower than the energy of the closed Piezo1 channels, causing them to switch into their open conformation in a collective manner. The subsequent increase of opened Gárdos channels would enhance the potassium leak and cause RBC volume to decrease until the system’s energy corresponding to closed channels became smaller again. The cycle would then repeat.
Conclusions
It can be concluded that there are several possible ways as to how RBC volume can be regulated on the basis of the dependence of Piezo1 cation permeability on membrane curvature. Their common feature is the dependence of the Piezo1 cationic permeability on the RBC discocyte shape for which a novel physiological function has been established. Here, we have elaborated the idea with its general consequences by analyzing the behavior of a hypothetical simplified RBC. Further work will thus be needed to reveal the corresponding behavior of real RBCs. At this stage, verification of the developed concepts would benefit most from experimental determination of the distribution of Piezo1 channels over the RBC membrane but also by determination of the Piezo1 RBC membrane lateral diffusion coefficient and cell population distributions of membrane areal density of different RBC membrane proteins, in particular its pumps and channels.
Author Contributions
The research was carried out by all three authors. S.S. designed the research and wrote the manuscript. T.Š.K. and B.B. contributed to the improvement of its draft.
Acknowledgments
The authors thank Professor Roger H. Pain for critical reading of the manuscript.
The study was supported by the Slovenian Research Agency through grant P1-0055.
Editor: Sean Sun.
Appendix A: Variability of RBC Reduced Volume Expressed in Terms of the Variability Parameters of RBC Volume and Membrane Area
Any strict relation between the parameters that define the state of an individual RBC, such as the dependence of the reduced RBC volume on its membrane area and volume (Eq. 3), is reflected in the relationship between the corresponding variations of these parameters in cell populations (41, 42, 43). RBCs are distributed with respect to both their areas and their volume. Individually, these distributions are well characterized by the corresponding coefficients of variations, which are the ratio between the corresponding SD and the variable’s average value (i.e., and ). The coefficient of variation of the reduced RBC volume, which depends on both variables A and V, is then defined by the joint distribution function with respect to the involved variables, which takes into account the fact that they may be correlated. The relations between the parameters of different distributions are particularly simple when the joint distribution function is Gaussian and the dependence of a given variable (v in our case) on the other ones (A and V in our case) is linear (41). By expressing the reduced volume in terms of the linear expansion around its average value as
| (A1) |
the coefficient of variation for the reduced volume then reads as follows:
| (A2) |
where is the correlation coefficient between RBC volume and its membrane area. Fig. 7 shows that depends strongly on how RBC volume and membrane area are correlated. The negative sign of the middle term in the right-hand side of Eq. A2 results in the fact that the coefficient of variation for the reduced volume may be smaller than each of the coefficients of variation of the RBC volume and membrane area. By taking = 0.13, = 0.12, and = 0.97 (42), we get = 0.06 from Eq. A2.
References
- 1.Skalak R., Branemark P.I. Deformation of red blood cells in capillaries. Science. 1969;164:717–719. doi: 10.1126/science.164.3880.717. [DOI] [PubMed] [Google Scholar]
- 2.Mohandas N., Clark M.R., Shohet S.B. Analysis of factors regulating erythrocyte deformability. J. Clin. Invest. 1980;66:563–573. doi: 10.1172/JCI109888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brumen M., Glaser R., Svetina S. Osmotic states of red blood cells. Bioelectrochem. Bioenerg. 1979;6:227–241. [Google Scholar]
- 4.Hoffmann E.K., Lambert I.H., Pedersen S.F. Physiology of cell volume regulation in vertebrates. Physiol. Rev. 2009;89:193–277. doi: 10.1152/physrev.00037.2007. [DOI] [PubMed] [Google Scholar]
- 5.Tosteson D.C., Hoffman J.F. Regulation of cell volume by active cation transport in high and low potassium sheep red cells. J. Gen. Physiol. 1960;44:169–194. doi: 10.1085/jgp.44.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cossins A.R., Gibson J.S. Volume-sensitive transport systems and volume homeostasis in vertebrate red blood cells. J. Exp. Biol. 1997;200:343–352. doi: 10.1242/jeb.200.2.343. [DOI] [PubMed] [Google Scholar]
- 7.Coste B., Mathur J., Patapoutian A. Piezo1 and Piezo2 are essential components of distinct mechanically activated cation channels. Science. 2010;330:55–60. doi: 10.1126/science.1193270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murthy S.E., Dubin A.E., Patapoutian A. Piezos thrive under pressure: mechanically activated ion channels in health and disease. Nat. Rev. Mol. Cell Biol. 2017;18:771–783. doi: 10.1038/nrm.2017.92. [DOI] [PubMed] [Google Scholar]
- 9.Zarychanski R., Schulz V.P., Gallagher P.G. Mutations in the mechanotransduction protein PIEZO1 are associated with hereditary xerocytosis. Blood. 2012;120:1908–1915. doi: 10.1182/blood-2012-04-422253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ge J., Li W., Yang M. Architecture of the mammalian mechanosensitive Piezo1 channel. Nature. 2015;527:64–69. doi: 10.1038/nature15247. [DOI] [PubMed] [Google Scholar]
- 11.Guo Y.R., MacKinnon R. Structure-based membrane dome mechanism for Piezo mechanosensitivity. eLife. 2017;6:e33660. doi: 10.7554/eLife.33660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Saotome K., Murthy S.E., Ward A.B. Structure of the mechanically activated ion channel Piezo1. Nature. 2018;554:481–486. doi: 10.1038/nature25453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhao Q., Zhou H., Xiao B. Structure and mechanogating mechanism of the Piezo1 channel. Nature. 2018;554:487–492. doi: 10.1038/nature25743. [DOI] [PubMed] [Google Scholar]
- 14.Cahalan S.M., Lukacs V., Patapoutian A. Piezo1 links mechanical forces to red blood cell volume. eLife. 2015;4:e07370. doi: 10.7554/eLife.07370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maher A.D., Kuchel P.W. The Gárdos channel: a review of the Ca2+-activated K+ channel in human erythrocytes. Int. J. Biochem. Cell Biol. 2003;35:1182–1197. doi: 10.1016/s1357-2725(02)00310-2. [DOI] [PubMed] [Google Scholar]
- 16.Lewis A.H., Grandl J. Mechanical sensitivity of Piezo1 ion channels can be tuned by cellular membrane tension. eLife. 2015;4:e12088. doi: 10.7554/eLife.12088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Svetina S., Kokot G., Waugh R.E. A novel strain energy relationship for red blood cell membrane skeleton based on spectrin stiffness and its application to micropipette deformation. Biomech. Model. Mechanobiol. 2016;15:745–758. doi: 10.1007/s10237-015-0721-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Evans J., Gratzer W., Sleep J. Fluctuations of the red blood cell membrane: relation to mechanical properties and lack of ATP dependence. Biophys. J. 2008;94:4134–4144. doi: 10.1529/biophysj.107.117952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wiggins P., Phillips R. Analytic models for mechanotransduction: gating a mechanosensitive channel. Proc. Natl. Acad. Sci. USA. 2004;101:4071–4076. doi: 10.1073/pnas.0307804101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuchel P.W., Shishmarev D. Accelerating metabolism and transmembrane cation flux by distorting red blood cells. Sci. Adv. 2017;3:eaao1016. doi: 10.1126/sciadv.aao1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gnanasambandam R., Ghatak C., Suchyna T.M. GsMTx4: mechanism of inhibiting mechanosensitive ion channels. Biophys. J. 2017;112:31–45. doi: 10.1016/j.bpj.2016.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Canham P.B., Burton A.C. Distribution of size and shape in populations of normal human red cells. Circ. Res. 1968;22:405–422. doi: 10.1161/01.res.22.3.405. [DOI] [PubMed] [Google Scholar]
- 23.Waugh R.E., Narla M., Dale G.L. Rheologic properties of senescent erythrocytes: loss of surface area and volume with red blood cell age. Blood. 1992;79:1351–1358. [PubMed] [Google Scholar]
- 24.Gifford S.C., Frank M.G., Bitensky M.W. Parallel microchannel-based measurements of individual erythrocyte areas and volumes. Biophys. J. 2003;84:623–633. doi: 10.1016/S0006-3495(03)74882-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lew V.L., Bookchin R.M. Volume, pH, and ion-content regulation in human red cells: analysis of transient behavior with an integrated model. J. Membr. Biol. 1986;92:57–74. doi: 10.1007/BF01869016. [DOI] [PubMed] [Google Scholar]
- 26.Armstrong C.M. The Na/K pump, Cl ion, and osmotic stabilization of cells. Proc. Natl. Acad. Sci. USA. 2003;100:6257–6262. doi: 10.1073/pnas.0931278100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ataullakhanov F.I., Korunova N.O., Martinov M.V. How erythrocyte volume is regulated, or what mathematical models can and cannot do for biology. Biochemistry (Moscow). Supplement Series A: Membrane and Cell Biology. 2009;3:101–115. [Google Scholar]
- 28.Freedman J.C., Hoffman J.F. Ionic and osmotic equilibria of human red blood cells treated with nystatin. J. Gen. Physiol. 1979;74:157–185. doi: 10.1085/jgp.74.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lew V.L., Tiffert T., Bookchin R.M. Distribution of dehydration rates generated by maximal Gardos-channel activation in normal and sickle red blood cells. Blood. 2005;105:361–367. doi: 10.1182/blood-2004-01-0125. [DOI] [PubMed] [Google Scholar]
- 30.Canham P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 31.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 32.Svetina S., Zeks B. Membrane bending energy and shape determination of phospholipid vesicles and red blood cells. Eur. Biophys. J. 1989;17:101–111. [Google Scholar]
- 33.Svetina S. Curvature-dependent protein-lipid bilayer interaction and cell mechanosensitivity. Eur. Biophys. J. 2015;44:513–519. doi: 10.1007/s00249-015-1046-5. [DOI] [PubMed] [Google Scholar]
- 34.Kralj-Iglič V., Heinrich V., Žekš B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B. 1999;10:5–8. [Google Scholar]
- 35.Božič B., Kralj-Iglič V., Svetina S. Coupling between vesicle shape and lateral distribution of mobile membrane inclusions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:041915. doi: 10.1103/PhysRevE.73.041915. [DOI] [PubMed] [Google Scholar]
- 36.Božič B., Das S.L., Svetina S. Sorting of integral membrane proteins mediated by curvature-dependent protein-lipid bilayer interaction. Soft Matter. 2015;11:2479–2487. doi: 10.1039/c4sm02289k. [DOI] [PubMed] [Google Scholar]
- 37.Cueff A., Seear R., Thomas S.L. Effects of elevated intracellular calcium on the osmotic fragility of human red blood cells. Cell Calcium. 2010;47:29–36. doi: 10.1016/j.ceca.2009.11.002. [DOI] [PubMed] [Google Scholar]
- 38.Lew V.L., Raftos J.E., Mohandas N. Generation of normal human red cell volume, hemoglobin content, and membrane area distributions by “birth” or regulation? Blood. 1995;86:334–341. [PubMed] [Google Scholar]
- 39.Brumen M., Glaser R., Svetina S. Study of the red blood cell osmotic behaviour in the “pump-leak” model. Period. Biol. 1981;83:151–153. [Google Scholar]
- 40.Kralj-Iglič V., Svetina S., Žekš B. Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 1996;24:311–321. doi: 10.1007/BF00180372. [DOI] [PubMed] [Google Scholar]
- 41.Svetina S. Relations among variations in human red cell volume, density, membrane area, hemoglobin content and cation content. J. Theor. Biol. 1982;95:123–134. doi: 10.1016/0022-5193(82)90291-0. [DOI] [PubMed] [Google Scholar]
- 42.Svetina S., Brumen M., Žnidarčič T. On the variation of parameters that characterize the state of a physiological system. Red blood cells as an example. In: Arnež V.Z.M., Brebbia C.A., Solina F., Stankovski V., editors. Simulations in Biomedicine. WITT Press; 2003. pp. 3–14. [Google Scholar]
- 43.Svetina S. Investigating cell functioning by theoretical analysis of cell-to-cell variability. Eur. Biophys. J. 2017;46:739–748. doi: 10.1007/s00249-017-1258-y. [DOI] [PubMed] [Google Scholar]
- 44.Svetina S. Red blood cell shape and deformability in the context of the functional evolution of its membrane structure. Cell. Mol. Biol. Lett. 2012;17:171–181. doi: 10.2478/s11658-012-0001-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ramadurai S., Holt A., Poolman B. Lateral diffusion of membrane proteins. J. Am. Chem. Soc. 2009;131:12650–12656. doi: 10.1021/ja902853g. [DOI] [PubMed] [Google Scholar]
- 46.Perozo E., Kloda A., Martinac B. Physical principles underlying the transduction of bilayer deformation forces during mechanosensitive channel gating. Nat. Struct. Biol. 2002;9:696–703. doi: 10.1038/nsb827. [DOI] [PubMed] [Google Scholar]
- 47.Hwang W.C., Waugh R.E. Energy of dissociation of lipid bilayer from the membrane skeleton of red blood cells. Biophys. J. 1997;72:2669–2678. doi: 10.1016/S0006-3495(97)78910-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.McMahon H.T., Gallop J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 49.Aimon S., Callan-Jones A., Bassereau P. Membrane shape modulates transmembrane protein distribution. Dev. Cell. 2014;28:212–218. doi: 10.1016/j.devcel.2013.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gallagher P.G. Disorders of erythrocyte hydration. Blood. 2017;130:2699–2708. doi: 10.1182/blood-2017-04-590810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lew V.L., Bookchin R.M. Ion transport pathology in the mechanism of sickle cell dehydration. Physiol. Rev. 2005;85:179–200. doi: 10.1152/physrev.00052.2003. [DOI] [PubMed] [Google Scholar]
- 52.Morris C.E., Homann U. Cell surface area regulation and membrane tension. J. Membr. Biol. 2001;179:79–102. doi: 10.1007/s002320010040. [DOI] [PubMed] [Google Scholar]
- 53.Willekens F.L., Werre J.M., Bosman G.J. Erythrocyte vesiculation: a self-protective mechanism? Br. J. Haematol. 2008;141:549–556. doi: 10.1111/j.1365-2141.2008.07055.x. [DOI] [PubMed] [Google Scholar]
- 54.Bae C., Gnanasambandam R., Gottlieb P.A. Xerocytosis is caused by mutations that alter the kinetics of the mechanosensitive channel PIEZO1. Proc. Natl. Acad. Sci. USA. 2013;110:E1162–E1168. doi: 10.1073/pnas.1219777110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bae C., Gottlieb P.A., Sachs F. Human PIEZO1: removing inactivation. Biophys. J. 2013;105:880–886. doi: 10.1016/j.bpj.2013.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lacroix J.J., Botello-Smith W.M., Luo Y. Probing the gating mechanism of the mechanosensitive channel Piezo1 with the small molecule Yoda1. Nat. Commun. 2018;9:2029. doi: 10.1038/s41467-018-04405-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Franco R.S., Puchulu-Campanella M.E., Cohen R.M. Changes in the properties of normal human red blood cells during in vivo aging. Am. J. Hematol. 2013;88:44–51. doi: 10.1002/ajh.23344. [DOI] [PMC free article] [PubMed] [Google Scholar]