Information-Theoretic Bounds and Approximations in Neural Population Coding

Abstract

While Shannon’s mutual information has widespread applications in many disciplines, for practical applications it is often difficult to calculate its value accurately for high-dimensional variables because of the curse of dimensionality. This article focuses on effective approximation methods for evaluating mutual information in the context of neural population coding. For large but finite neural populations, we derive several information-theoretic asymptotic bounds and approximation formulas that remain valid in high-dimensional spaces. We prove that optimizing the population density distribution based on these approximation formulas is a convex optimization problem that allows efficient numerical solutions. Numerical simulation results confirmed that our asymptotic formulas were highly accurate for approximating mutual information for large neural populations. In special cases, the approximation formulas are exactly equal to the true mutual information. We also discuss techniques of variable transformation and dimensionality reduction to facilitate computation of the approximations.

1. Introduction

Shannon’s mutual information (MI) provides a quantitative characterization of the association between two random variables by measuring how much knowing one of the variables reduces uncertainty about the other (Shannon, 1948). Information theory has become a useful tool for neuroscience research (Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997; Borst & Theunissen, 1999; Pouget, Dayan, & Zemel, 2000; Laughlin & Sejnowski, 2003; Brown, Kass, & Mitra, 2004; Quiroga & Panzeri, 2009), with applications to various problems such as sensory coding problems in the visual systems (Eckhorn & Pöpel, 1975; Optican & Richmond, 1987; Atick & Redlich, 1990; McClurkin, Gawne, Optican, & Richmond, 1991; Atick, Li, & Redlich, 1992; Becker & Hinton, 1992; Van Hateren, 1992; Gawne & Richmond, 1993; Tovee, Rolls, Treves, & Bellis, 1993; Bell & Sejnowski, 1997; Lewis & Zhaoping, 2006) and the auditory systems (Chechik et al., 2006; Gourévitch and Eggermont, 2007; Chase & Young, 2005).

One major problem encountered in practical applications of information theory is that the exact value of mutual information is often hard to compute in high-dimensional spaces. For example, suppose we want to calculate the mutual information between a random stimulus variable that requires many parameters to specify and the elicited noisy responses of a large population of neurons. In order to accurately evaluate the mutual information between the stimuli and the responses, one has to average over all possible stimulus patterns and over all possible response patterns of the whole population. This averaging quickly leads to a combinatorial explosion as either the stimulus dimension or the population size increases. This problem occurs not only when one computes MI numerically for a given theoretical model but also when one estimates MI empirically from experimental data.

Even when the input and output dimensions are not that high, an MI estimate from experimental data tends to have a positive bias due to limited sample size (Miller, 1955; Treves & Panzeri, 1995). For example, a perfectly flat joint probability distribution implies zero MI, but an empirical joint distribution with fluctuations due to finite data size appears to suggest a positive MI. The error may get much worse as the input and output dimensions increase because a reliable estimate of MI may require exponentially more data points to fill the space of the joint distribution. Various asymptotic expansion methods have been proposed to reduce the bias in an MI estimate (Miller, 1955; Carlton, 1969; Treves & Panzeri, 1995; Victor, 2000; Paninski, 2003). Other estimators of MI have also been studied, such as those based on k-nearest neighbor (Kraskov, Stögbauer, & Grassberger, 2004) and minimal spanning trees (Khan et al., 2007). However, it is not easy for these methods to handle the general situation with high-dimensional inputs and high-dimensional outputs.

For numerical computation of MI for a given theoretical model, one useful approach is Monte Carlo sampling, a convergent method that may potentially reach arbitrary accuracy (Yarrow, Challis, & Series, 2012). However, its stochastic and inefficient computational scheme makes it unsuitable for many applications. For instance, to optimize the distribution of a neural population for a given set of stimuli, one may want to slightly alter the population parameters and see how the perturbation affects the MI, but a tiny change of MI can be easily drowned out by the inherent noise in the Monte Carlo method.

An alternative approach is to use information-theoretic bounds and approximations to simplify calculations. For example, the Cramér-Rao lower bound (Rao, 1945) tells us that the inverse of Fisher information (FI) is a lower bound to the mean square decoding error of any unbiased decoder. Fisher information is useful for many applications partly because it is often much easier to calculate than MI (see e.g., Zhang, Ginzburg, McNaughton, & Sejnowski, 1998; Zhang & Sejnowski, 1999; Abbott & Dayan, 1999; Bethge, Rotermund, & Pawelzik, 2002; Harper & McAlpine, 2004; Toyoizumi, Aihara, & Amari, 2006).

A link between MI and FI has been studied by several researchers (Clarke & Barron, 1990; Rissanen, 1996; Brunel & Nadal, 1998; Sompolinsky, Yoon, Kang, & Shamir, 2001). Clarke and Barron (1990) first derived an asymptotic formula between the relative entropy and FI for parameter estimation from independent and identically distributed (i.i.d.) observations with suitable smoothness conditions. Rissanen (1996) generalized it in the framework of stochastic complexity for model selection. Brunel and Nadal (1998) presented an asymptotic relationship between the MI and FI in the limit of a large number of neurons. The method was extended to discrete inputs by Kang and Sompolinsky (2001). More general discussions about this also appeared in other papers (e.g., Ganguli & Simoncelli, 2014; Wei & Stocker, 2015). However, for finite population size, the asymptotic formula may lead to large errors, especially for high-dimensional inputs, as detailed in sections 2.2 and 4.1.

In this article, our main goal is to improve FI approximations to MI for finite neural populations especially for high-dimensional inputs. Another goal is to discuss how to use these approximations to optimize neural population coding. We will present several information-theoretic bounds and approximation formulas and discuss the conditions under which they are established in section 2, with detailed proofs given in the appendix. We also discuss how our approximation formulas are related to other statistical estimators and information-theoretic bounds, such as Cramér-Rao bound and van Trees’ Bayesian Cramér-Rao bound (see section 3). In order to better apply the approximation formulas in high-dimensional input space, we propose some useful techniques in section 4, including variable transformation and dimensionality reduction, which may greatly reduce the computational complexity for practical applications. Finally, in section 5, we discuss how to use the approximation formulas for optimizing information transfer for neural population coding.

2. Bounds and Approximations for Mutual Information in Neural Population Coding

2.1. Mutual Information and Notations.

Suppose the input x is a K-dimensional vector, x = (x₁, x₂, …, x_K)^T, and the outputs of N neurons are denoted by a vector, r = (r₁, r₂, …, r_N)^T. In this article, we denote random variables by uppercase letters (e.g., random variables X and R) in contrast to their vector values x and r. The MI I(X; R) (denoted as I below) between X and R is defined by Cover and Thomas (2006):

$$I={\int }_{\mathcal{X}}{\int }_{\mathcal{R}}p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})\text{ln}\frac{p(\mathbf{r}\mid \mathbf{x})}{p(\mathbf{r})}d\mathbf{r}d\mathbf{x},$$ (2.1)

where $\mathbf{x}\in \mathcal{X}\subseteq {\mathbb{R}}^K$, $\mathbf{r}\in \mathcal{R}\subseteq {\mathbb{R}}^N$, $d\mathbf{x}={\prod }_{k=1}^{K}d{x}_k$, $d\mathbf{r}={\prod }_{n=1}^{N}d{r}_n$, and the integration symbol ∫ is for the continuous variables and can be replaced by the summation symbol ∑ for discrete variables. The probability density function (p.d.f.) of r, p(r), satisfies

$$p(\mathbf{r})={\int }_{\mathcal{X}}p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})d\mathbf{x}.$$ (2.2)

The MI I in equation 2.1 may also be expressed equivalently as

$$I=H(X)-{\langle \text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r},\mathbf{x}}=H(X)-H(X\mid R),$$ (2.3)

where H(X) is the entropy of random variable X,

$$H(X)=-\langle \text{ln}p(\mathbf{x}){\rangle }_{\mathbf{x}},H(X\mid R)=-\langle \text{ln}p(\mathbf{x}\mid \mathbf{r}){\rangle }_{\mathbf{r},\mathbf{x}},$$ (2.4)

and ⟨·⟩ denotes expectation:

$$\langle \cdot {\rangle }_{\mathbf{x}}={\int }_{\mathcal{X}}p(\mathbf{x})(\cdot )d\mathbf{x},$$ (2.5)

$$\langle \cdot {\rangle }_{\mathbf{r}\mid \mathbf{x}}={\int }_{\mathcal{R}}p(\mathbf{r}\mid \mathbf{x})(\cdot )d\mathbf{r},$$ (2.6)

$$\langle \cdot {\rangle }_{\mathbf{r},\mathbf{x}}={\int }_{\mathcal{X}}{\int }_{\mathcal{R}}p(\mathbf{r},\mathbf{x})(\cdot )d\mathbf{r}d\mathbf{x}.$$ (2.7)

Next, we introduce the following notations,

$$l(\mathbf{r}\mid \mathbf{x})=\text{ln}p(\mathbf{r}\mid \mathbf{x}),$$ (2.8)

$$L(\mathbf{r}\mid \mathbf{x})=\text{ln}(p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})),$$ (2.9)

$$q(\mathbf{x})=\text{ln}p(\mathbf{x}),$$ (2.10)

and

$$I_F=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{J}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X),$$ (2.11)

$$I_G=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X),$$ (2.12)

where det (·) denotes the matrix determinant, and

$$\mathbf{J}(\mathbf{x})=\langle l^{\prime }(\mathbf{r}\mid \mathbf{x})l^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{\rangle }_{\mathbf{r}\mid \mathbf{x}},$$ (2.13)

$$\mathbf{G}(\mathbf{x})=\mathbf{J}(\mathbf{x})+\mathbf{P}(\mathbf{x}),$$ (2.14)

$$\mathbf{P}(\mathbf{x})=-q^{″}(\mathbf{x}).$$ (2.15)

Here J(x) is the FI matrix, which is symmetric and positive-semidefinite, and ′ and ″ denote the first and second derivative for x, respectively; that is, l′(r∣x) = ∂l (r∣x) /∂x and q″(r∣x) = ∂² ln p (x)/∂x∂x^T. If p(r∣x) is twice differentiable for x, then

$$\mathbf{J}(\mathbf{x})=\langle l^{\prime }(\mathbf{r}\mid \mathbf{x})l^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{\rangle }_{\mathbf{r}\mid \mathbf{x}}=-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\cdot$$ (2.16)

We denote the Kullback-Leibler (KL) divergence as

$$D(\mathbf{x}\Vert \widehat{\mathbf{x}})={\int }_{\mathcal{R}}p(\mathbf{r}\mid \mathbf{x})\text{ln}\frac{p(\mathbf{r}\mid \mathbf{x})}{p(\mathbf{r}\mid \widehat{\mathbf{x}})}d\mathbf{r},$$ (2.17)

and define

$${\mathcal{X}}_{\omega }(\mathbf{x})=\left\{\breve{\mathbf{x}}\in {\mathbb{R}}^K:(\breve{\mathbf{x}}-\mathbf{x}{)}^T\mathbf{G}(\mathbf{x})(\breve{\mathbf{x}}-\mathbf{x})<N{\omega }^2\right\},$$ (2.18)

as the ω neighborhoods of x and its complementary set as

$${\bar{\mathcal{X}}}_{\omega }(\mathbf{x})=\mathcal{X}-{\mathcal{X}}_{\omega }(\mathbf{x}),$$ (2.19)

where ω is a positive number.

2.2. Information-Theoretic Asymptotic Bounds and Approximations.

In a large N limit, Brunei and Nadal (1998) proposed an asymptotic relationship I ~ I_F between MI and FI and gave a proof in the case of one-dimensional input. Another proof is given by Sompolinsky et al. (2001), although there appears to be an error in their proof when a replica trick is used (see equation B1 in their paper; their equation B5 does not follow directly from the replica trick). For large but finite N, I ≃ I_F is usually a good approximation as long as the inputs are low dimensional. For the high-dimensional inputs, the approximation may no longer be valid. For example, suppose p(r∣x) is a normal distribution with mean A^Tx and covariance matrix I_N and p(x) is a normal distribution with mean μ and covariance matrix ∑,

$$p(\mathbf{r}\mid \mathbf{x})=\mathcal{N}({\mathbf{A}}^T\mathbf{x},{\mathbf{I}}_N),p(\mathbf{x})=\mathcal{N}(\mu ,\Sigma ),$$ (2.20)

where A = [a₁, a₂, …, a_N] is a deterministic K × N matrix and I_N is the N × N identity matrix. The MI I is given by (see Verdu, 1986; Guo, Shamai, & Verdu, 2005, for details)

$$I=\frac{1}{2}\text{ln}\left(\text{det}\left({\Sigma }^{1∕2}\mathbf{A}{\mathbf{A}}^T{\Sigma }^{1∕2}+{\mathbf{I}}_K\right)\right).$$ (2.21)

If rank (J(x)) < K, then I_F = −∞. Notice that here, J(x) = AA^T. When a = a₁ = … = a_N and ∑ = I_k, then by equation 2.21 and a matrix determinant lemma, we have

$$I=\frac{1}{2}\text{ln}\left(\text{det}\left(N\mathbf{a}{\mathbf{a}}^T+{\mathbf{I}}_K\right)\right)=\frac{1}{2}\text{ln}\left(N{\mathbf{a}}^T\mathbf{a}+1\right)\ge 0,$$ (2.22)

and by equation 2.11,

$$I_F=\frac{1}{2}\text{ln}\left(\text{det}\left(N\mathbf{a}{\mathbf{a}}^T\right)\right)=-\infty ,$$ (2.23)

which is obviously incorrect as an approximation to I. For high-dimensional inputs, the determinant det (J(x)) may become close to zero in practical applications. When the FI matrix J(x) becomes degenerate, the regularity condition ensuring the Cramér-Rao paradigm of statistics is violated (Amari & Nakahara, 2005), in which case using I_F as a proxy for I incurs large errors.

In the following, we will show that I_G is a better approximation of I for high-dimensional inputs. For instance, for the above example, we can verify that

$$\begin{array}{cc}\hfill I_G& =\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{1}{2\pi e}(\mathbf{A}{\mathbf{A}}^T+{\Sigma }^{-1})\right)\right)+\frac{1}{2}\text{ln}(\text{det}(2\pi e\Sigma ))\hfill \\ \hfill & =\frac{1}{2}\text{ln}(\text{det}({\Sigma }^{1∕2}\mathbf{A}{\mathbf{A}}^T{\Sigma }^{1∕2}+{\mathbf{I}}_K))=I,\hfill \end{array}$$ (2.24)

which is exactly equal to the MI I given in equation 2.21.

2.2.1. Regularity Conditions.

First, we consider the following regularity conditions for p(x) and p(r∣x):

C1: p(x) and p(r∣x) are twice continuously differentiable for almost every $\mathbf{x}\in \mathcal{X}$, where $\mathcal{X}$ is a convex set; G(x) is positive definite, and ∥ G⁻¹ (x)∥ = O(N⁻¹), where ∥·∥ denotes the Frobenius norm of a matrix. The following conditions hold:

$$\Vert q^{\prime }(\mathbf{x})\Vert <\infty ,$$ (2.25a)

$$\Vert q^{″}(\mathbf{x})\Vert <\infty ,$$ (2.25b)

$${\langle {\left(N^{-1}{l}^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{l}^{\prime }(\mathbf{r}\mid \mathbf{x})\right)}^2\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(1),$$ (2.25c)

$${\langle {\Vert N^{-1}\left(l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\right)\Vert }^2\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}),$$ (2.25d)

and there exists an ω = ω (x) > 0 for $\forall \breve{\mathbf{x}}\in {\mathcal{X}}_{\omega }(\mathbf{x})$ such that

$$N^{-1}\Vert l^{″}(\mathbf{r}\mid \breve{\mathbf{x}})-l^{″}(\mathbf{r}\mid \mathbf{x})\Vert =O(1),$$ (2.25e)

where O indicates the big-O notation.

C2: The following condition is satisfied,

$${\langle {\Vert N^{-1}\left(l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\right)\Vert }^{2(m+1)}\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}),$$ (2.26a)

for $m\in \mathbb{N}$, and there exists η > 1 such that

$${\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{\text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}p(\widehat{\mathbf{x}}\mid \mathbf{r})d\widehat{\mathbf{x}}>ϵp(\mathbf{x}\mid \mathbf{r})\right\}=O(N^{-\eta })$$ (2.26b)

for all ϵ ∈ (0,1/2), $\widehat{\omega }\in (0,\omega )$ and $\mathbf{x}\in \mathcal{X}$ with p(x) > 0, where ${\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\{\cdot \}$ denotes the probability of r given x.

The regularity conditions C1 and C2 are needed to prove theorems in later sections. They are expressed in mathematical forms that are convenient for our proofs, although their meanings may seem opaque at first glance. In the following, we will examine these conditions more closely. We will use specific examples to make interpretations of these conditions more transparent.

Remark 1. In this article, we assume that the probability distributions p(x) and p(r∣x) are piecewise twice continuously differentiable. This is because we need to use Fisher information to approximate mutual information, and Fisher information requires derivatives that make sense only for continuous variables. Therefore, the methods developed in this article apply only to continuous input variables or stimulus variables. For discrete input variables, we need alternative methods for approximating MI, which we will address in a separate publication.

Conditions 2.25a and 2.25b state that the first and the second derivatives of q(x) = ln p(x) have finite values for any given $\mathbf{x}ϵ\mathcal{X}$. These two conditions are easily satisfied by commonly encountered probability distributions because they only require finite derivatives within $\mathcal{X}$, the set of allowable inputs, and derivatives do not need to be finitely bounded.

Remark 2. Conditions 2.25c to 2.26a constrain how the first and the second derivatives of l(r∣x) = ln p(r∣x) scale with N, the number of neurons. These conditions are easily met when p(r∣x) is conditionally independent or when the noises of different neurons are independent, that is, $p(\mathbf{r}\mid \mathbf{x})={\prod }_{n=1}^{N}p(r_n\mid \mathbf{x})$.

We emphasize that it is possible to satisfy these conditions even when p(r∣x) is not independent or when the noises are correlated, as we show later. Here we first examine these conditions closely, assuming independence. For simplicity, our demonstration that follows is based on a one-dimensional input variable (K = 1). The conclusions are readily generalizable to higher-dimensional inputs (K > 1) because K is fixed and does not affect the scaling with N.

Assuming independence, we have $l(\mathbf{r}\mid x)={\sum }_{n=1}^{N}l(r_n\mid x)$ with l(r_n∣x) = ln p(r_n∣x), and the left-hand side of equation 2.25c becomes

$$\begin{array}{cc}\hfill & N^{-2}\langle l^{\prime }(\mathbf{r}\mid x{)}^4{\rangle }_{\mathbf{r}\mid x}\hfill \\ \hfill & =N^{-2}\sum _{n_1,\dots ,n_4=1}^N\langle l^{\prime }(r_{n_1}\mid x)l^{\prime }(r_{n_2}\mid x)l^{\prime }(r_{n_3}\mid x)l^{\prime }(r_{n_4}\mid x){\rangle }_{r_{n_1},r_{n_2},r_{n_3},r_{n_4}\mid x}\hfill \\ \hfill & =N^{-2}\left(\sum _{n\ne m}\langle l^{\prime }(r_n\mid x{)}^2{\rangle }_{r_n\mid x}\langle l^{\prime }(r_m\mid x{)}^2{\rangle }_{r_m\mid x}+\sum _{n=1}^N\langle l^{\prime }(r_n\mid x{)}^4{\rangle }_{r_n\mid x}\right),\hfill \end{array}$$ (2.27)

where the final result contains only two terms with even numbers of duplicated indices, while all other terms in the expansion vanish because any unmatched or lone index k (from n₁, n₂, n₃, n₄) should yield a vanishing average:

$${\langle l^{\prime }(r_k\mid x)\rangle }_{r_k\mid x}={\int }_{\mathcal{R}}p(r_k\mid x)l^{\prime }(r_k\mid x)d{r}_k=\frac{\partial }{\partial x}\left({\int }_{\mathcal{R}}p(r_k\mid x)d{r}_k\right)=0.$$ (2.28)

Thus, condition 2.25c is satisfied as long as ⟨l′(r_n∣x)²⟩_rn∣x and ⟨l′(r_n∣x)⁴⟩_rn∣x are bounded by some finite numbers, say, a and b, respectively, because now equation 2.27 should scale as N⁻² (aN(N – 1) + bN) = O(1). For instance, a gaussian distribution always meets this requirement because the averages of the second and fourth powers are proportional to the second and fourth moments, which are both finite. Note that the argument above works even if ⟨l′(r_n∣x)⁴⟩_rn∣x is not finitely bounded but scales as O(N).

Similarly, under the assumption of independence, the left-hand side of equation 2.25d becomes

$$\begin{array}{c}{N}^{-2}{\langle {\left(l^{″}(\mathbf{r}\mid x)-\langle l^{″}(\mathbf{r}\mid x){\rangle }_{\mathbf{r}\mid x}\right)}^2\rangle }_{\mathbf{r}\mid x}\hfill \\ =N^{-2}\sum _{n,m=1}^N{\langle \left(l^{″}(r_n\mid x)-\langle l^{″}(r_n\mid x){\rangle }_{r_n\mid x}\right)\left(l^{″}(r_m\mid x)-\langle l^{″}(r_m\mid x){\rangle }_{r_m\mid x)}\right)\rangle }_{r_n,r_m\mid x}\hfill \\ =N^{-2}\sum _{n=1}^N{\langle {\left(l^{″}(r_n\mid x)-\langle l^{″}(r_n\mid x){\rangle }_{r_n\mid x}\right)}^2\rangle }_{r_n\mid x}\hfill \\ =N^{-2}\sum _{n=1}^N\left(\langle l^{″}(r_n\mid x{)}^2{\rangle }_{r_n\mid x}-\langle l^{″}(r_n\mid x){\rangle }_{r_n\mid x}^2\right),\hfill \end{array}$$ (2.29)

where, in the second step, the only remaining terms are the squares, while all other terms in the expansion with n ≠ m have vanished because ⟨l″(r_n∣x) – ⟨l″(r_n∣x)⟩_rn∣x⟩_rn∣x = 0. Thus, condition 2.25d is satisfied as long as ⟨l″(r_n∣x)⟩_rn∣x and ⟨l″(r_n∣x)²⟩_rn∣x are bounded so that equation 2.29 scales as N⁻²N = N⁻¹.

Condition 2.25e is easily satisfied under the assumption of independence. It is easy to show that this condition holds when l″(r_n∣x) is bounded.

Condition 2.26a can be examined with similar arguments used for equations 2.27 and 2.29. Assuming independence, we rewrite the left-hand side of equation 2.26a as

$$\begin{array}{cc}\hfill & N^{-z}{\langle {\left(l^{″}(\mathbf{r}\mid x)-\langle l^{″}(\mathbf{r}\mid x){\rangle }_{\mathbf{r}\mid x}\right)}^z\rangle }_{\mathbf{r}\mid x}\hfill \\ \hfill & =N^{-z}\sum _{n_1,\dots ,n_z=1}^N\langle \left(l^{″}(r_{n_1}\mid x)-\langle l^{″}(r_{n_1}\mid x){\rangle }_{r_{n_1}\mid x}\right)\phantom{\rangle }\hfill \\ \hfill & \cdots {\phantom{\langle }\left(l^{″}(r_1\mid x)-\langle l^{″}(r_{n_z}\mid x){\rangle }_{r_{n_z}\mid x}\right)\rangle }_{r_{n_z}\mid x}\hfill \\ \hfill & =N^{-z}\sum _{n_1,\dots ,n_{m+1}=1}^N{\langle \prod _{i=1}^{m+1}{\left(l^{″}(r_{n_i}\mid x)-\langle l^{″}(r_{n_i}\mid x){\rangle }_{r_{n_i}\mid x}\right)}^2\rangle }_{r_{n_i}\mid x}+\cdots \hfill \end{array}$$ (2.30)

where z = 2(m + 1) ≥ 4 is an even number. Any term in the expansion with an unmatched index n_k should vanish, as in the cases of equations 2.27 and 2.29. When ⟨l″ (r_n∣x)⟩_rn∣x and ⟨l″(r_n∣x)²⟩_rn∣x are bounded, the leading term with respect to scaling with N is the product of squares, as shown at the end of equation 2.30, because all the other nonvanishing terms increase more slowly with N. Thus equation 2.30 should scale as N^−zN^m+1 = N^−m−1, which trivially satisfies condition 2.26a.

In summary, conditions 2.25c to 2.26a are easy to meet when p(r∣x) is independent. It is sufficient to satisfy these conditions when the averages of the first and second derivatives of l(r∣x) = ln p(r∣x), as well as the averages of their powers, are bounded by finite numbers for all the neurons.

Remark 3. For neurons with correlated noises, if there exists an invertible transformation that maps r to $\tilde{\mathbf{r}}$ such that $p(\tilde{\mathbf{r}}\mid \mathbf{x})$ becomes conditionally independent, then conditions C1 and C2 are easily met in the space of the new variables by the discussion in remark 2. This situation is best illustrated by the familiar example of a population of neurons with correlated noises that obey a multivariate gaussian distribution:

$$p(\mathbf{r}\mid x)=\frac{1}{\sqrt{\text{det}(2\pi \Sigma )}}\text{exp}\left(-\frac{1}{2}(\mathbf{r}-\mathbf{g}{)}^T{\Sigma }^{-1}(\mathbf{r}-\mathbf{g})\right),$$ (2.31)

where ∑ is an N × N invertible covariance matrix, and g = (g₁(x; θ₁),…, g_N(x; θ_N)) describes the mean resp onses with θ_n being the parameter vector. Using the following transformation,

$$\tilde{\mathbf{r}}={\Sigma }^{-1∕2}\mathbf{r}=({\tilde{r}}_1,{\tilde{r}}_2,\dots ,{\tilde{r}}_N{)}^T,$$ (2.32)

$$\tilde{\mathbf{g}}={\Sigma }^{-1∕2}\mathbf{g}=({\tilde{g}}_1,{\tilde{g}}_2,\dots ,{\tilde{g}}_N{)}^T,$$ (2.33)

we obtain the independent distribution:

$$p(\tilde{\mathbf{r}}\mid x)=\prod _{n=1}^N\frac{1}{\sqrt{2\pi }}\text{exp}\left(-\frac{1}{2}({\tilde{r}}_n-{\tilde{g}}_n{)}^2\right).$$ (2.34)

In the special case when the correlation coefficient between any pair of neurons is a constant c, −1 < c < 1, the noise covariance can be written as

$$\Sigma =a\left((1-c){\mathbf{I}}_N+c\mathbf{u}{\mathbf{u}}^T\right),$$ (2.35)

where a > 0 is a constant, I_N is the N × N identity matrix, and $\mathbf{u}=(1,1,\dots ,1{)}^T\in {\mathbb{R}}^{N\times 1}$. The desired transformation in equations 2.32 and 2.33 is given explicitly by

$${\Sigma }^{-1∕2}=b_0\left({\mathbf{I}}_N-b_1\mathbf{u}{\mathbf{u}}^T\right),$$ (2.36)

where

$$b_0=\frac{1}{\sqrt{a(1-c)}},b_1=\frac{1}{N}\left(1\pm \sqrt{\frac{1-c}{(N-1)c+1}}\right).$$ (2.37)

The new response variables defined in equations 2.32 and 2.33 now read:

$${\tilde{r}}_n=b_0\left(r_n-b_1\sum _{m=1}^N{r}_m\right),$$ (2.38)

$${\tilde{g}}_n=b_0\left(g_n-b_1\sum _{m=1}^N{g}_m\right).$$ (2.39)

Now we have the derivatives:

$$l^{\prime }({\tilde{r}}_n\mid x)=({\tilde{r}}_n-{\tilde{g}}_n)\frac{\partial {\tilde{g}}_n}{\partial x},$$ (2.40)

$$l^{″}({\tilde{r}}_n\mid x)=\langle l^{″}({\tilde{r}}_n\mid x){\rangle }_{r_n\mid x}=({\tilde{r}}_n-{\tilde{g}}_n)\frac{{\partial }^2{\tilde{g}}_n}{\partial x^2},$$ (2.41)

where $\partial {\tilde{g}}_n∕\partial x$ and ${\partial }^2{\tilde{g}}_n∕\partial x^2$ are finite as long as ∂g_n/∂x and ∂²g_n/∂x² are finite. Conditions C1 and C2 are satisfied when the derivatives and their powers are finitely bounded as shown before.

The example above shows explicitly that it is possible to meet conditions C1 and C2 even when the noises of different neurons are correlated. More generally, if a nonlinear transformation exists that maps correlated random variables into independent variables, then by similar argument, conditions C1 and C2 are satisfied when the derivatives of the log likelihood functions and their powers in the new variables are finitely bounded. Even when the desired transformation does not exist or is unknown, it does not necessarily imply that conditions C1 and C2 must be violated.

While the exact mathematical conditions for the existence of the desired transformation are unclear, let us consider a specific example. If a joint probability density function can be morphed smoothly and reversibly into a flat or constant density in a cube (hypercube), which is a special case of an independent distribution, then this morphing is the desired transformation. Here we may replace the flat distribution by any known independent distribution and the argument above should still work. So the desired transformation may exist under rather general conditions.

For correlated random variables, one may use algorithms such as independent component analysis to find an invertible linear mapping that makes the new random variables as independent as possible (Bell & Sejnowski, 1997) or use neural networks to find related nonlinear mappings (Huang & Zhang, 2017). These methods do not directly apply to the problem of testing conditions C1 and C2 because they work for a given network size N and further development is needed to address the scaling behavior in the large network limit N → ∞.

Finally, we note that the value of the MI of the transformed independent variables is the same as the MI of the original correlated variables because of the invariance of MI under invertible transformation of marginal variables. A related discussion is in theorem 3, which involves a transformation of the input variables rather than a transformation of the output variables as needed here.

Remark 4. Condition 2.26b is satisfied if a positive number δ and a positive integer m exist such that

$$\text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\bar{\mathcal{X}}}_{\hat{\omega }}(\mathbf{x})}{\int }_{{\mathcal{B}}_{m,\delta }(\mathbf{x})}p(\mathbf{r}\mid \widehat{\mathbf{x}})p(\widehat{\mathbf{x}})d\mathbf{r}d\widehat{\mathbf{x}}=O(N^{-\eta })$$ (2.42)

for all $\widehat{\mathbf{x}}\in {\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})$, where

$${\mathcal{B}}_{m,\delta }(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:-\delta N^{\frac{\eta -1}{2m}}\mathbf{G}(\mathbf{x})<l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}<\delta N^{\frac{\eta -1}{2m}}\mathbf{G}(\mathbf{x})\right\},$$ (2.43)

and A < B means that the matrix A – B is negative definite. A proof is as follows.

First note that in equation 2.43, if η → 1 or m → ∞, then $N^{\frac{\eta -1}{2m}}\to 1$. Following Markov’s inequality, condition C2 and equation A.19 in the appendix, for the complementary set of ${\mathcal{B}}_{m,\delta }(\mathbf{x})$, ${\bar{\mathcal{B}}}_{m,\delta }(\mathbf{x})$, we have

$$\begin{array}{cc}\hfill {\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\bar{\mathcal{B}}}_{m,\delta }(\mathbf{x})\right\}& \le {\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{\Vert {\mathbf{B}}_0{\Vert }^2\ge {\delta }^2{N}^{\frac{\eta -1}{m}}\right\}\hfill \\ \hfill & \le {\delta }^{-2m}{N}^{-(\eta -1)}\langle \Vert {\mathbf{B}}_0{\Vert }^{2m}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & =O(N^{-\eta }),\hfill \end{array}$$ (2.44)

where

$${\mathbf{B}}_0={\mathbf{G}}^{-1∕2}(\mathbf{x})\left(l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\right){\mathbf{G}}^{-1∕2}(\mathbf{x}).$$ (2.45)

Define the set

$${\mathcal{A}}_{\widehat{\omega }}(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}\frac{p(\widehat{\mathbf{x}}\mid \mathbf{r})}{p(\mathbf{x}\mid \mathbf{r})}d\widehat{\mathbf{x}}>\text{det}(\mathbf{G}(\mathbf{x}){)}^{-1∕2}ϵ\right\}.$$ (2.46)

Then it follows from Markov’s inequality and equation 2.42 that

$$\begin{array}{cc}\hfill & {\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\mathcal{A}}_{\widehat{\omega }}(\mathbf{x})\cap {\mathcal{B}}_{m,\delta }(\mathbf{x})\right\}\hfill \\ \hfill & \le {ϵ}^{-1}\text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\mathcal{B}}_{m,\delta }(\mathbf{x})}{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}\frac{p(\mathbf{r}\mid \widehat{\mathbf{x}})p(\widehat{\mathbf{x}})}{p(\mathbf{x})}d\widehat{\mathbf{x}}d\mathbf{r}\hfill \\ \hfill & =O(N^{-\eta }).\hfill \end{array}$$ (2.47)

Hence, we get

$${\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\mathcal{A}}_{\widehat{\omega }}(\mathbf{x})\right\}\le {\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\mathcal{A}}_{\widehat{\omega }}(\mathbf{x})\cap {\mathcal{B}}_{m,\delta }(\mathbf{x})\right\}+{\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\bar{\mathcal{B}}}_{m,\delta }(\mathbf{x})\right\}=O(N^{-\eta }),$$

which yields condition 2.26b.

Condition 2.42 is satisfied if there exists a positive number ς such that

$$\text{ln}\frac{p(\mathbf{r}\mid \mathbf{x})}{p(\mathbf{r}\mid \widehat{\mathbf{x}})}\ge N_{\varsigma }$$ (2.48)

for all $\widehat{\mathbf{x}}\in {\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})$ and $\mathbf{r}\in {\mathcal{B}}_{m,\delta }(\mathbf{x})$. This is because

$$\begin{array}{cc}\hfill & \text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}{\int }_{{\mathcal{B}}_{m,\delta }(\mathbf{x})}p(\mathbf{r}\mid \widehat{\mathbf{x}})p(\widehat{\mathbf{x}})d\mathbf{r}d\widehat{\mathbf{x}}\hfill \\ \hfill & =\text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}p(\widehat{\mathbf{x}}){\int }_{{\mathcal{B}}_{m,\delta }(\mathbf{x})}p(\mathbf{r}\mid \mathbf{x})\text{exp}\left(-\text{ln}\frac{p(\mathbf{r}\mid \mathbf{x})}{p(\mathbf{r}\mid \widehat{\mathbf{x}})}\right)d\mathbf{r}d\widehat{\mathbf{x}}\hfill \\ \hfill & \le \text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}\text{exp}(-N_{\varsigma })=O(N^{K∕2}{e}^{-N_{\varsigma }}).\hfill \end{array}$$ (2.49)

Here notice that det (G (x))^1/2 = O (N^K/2) (see equation A.23).

Inequality 2.48 holds if p(r∣x) is conditionally independent, namely, $p(\mathbf{r}\mid \mathbf{x})={\prod }_{n=1}^{N}p(r_n\mid \mathbf{x})$, with

$$\text{ln}\frac{p(r_n\mid \mathbf{x})}{p(r_n\mid \widehat{\mathbf{x}})}\ge \varsigma ,\forall n=1,2,\dots ,N,$$ (2.50)

for all $\widehat{\mathbf{x}}\in {\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})$ and $\mathbf{r}\in {\mathcal{B}}_{m,\delta }(\mathbf{x})$. Consider the inequality $\langle \text{ln}p(r_n\mid \mathbf{x})∕p(r_n\mid \widehat{\mathbf{x}}){\rangle }_{r_n\mid \mathbf{x}}\ge 0$ where the equality holds when $\mathbf{x}=\widehat{\mathbf{x}}$. If there is only one extreme point at $\widehat{\mathbf{x}}=\mathbf{x}$ for $\widehat{\mathbf{x}}\in {\mathcal{X}}_{\omega }(\mathbf{x})$, then generally it is easy to find a set ${\mathcal{B}}_{m,\delta }(\mathbf{x})$ that satisfies equation 2.50, so that equation 2.26b holds.

2.2.2. Asymptotic Bounds and Approximations for Mutual Information.

Let

$$\xi =N^{-1}{\langle {\Vert \left(l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\right){\mathbf{G}}^{-1}(\mathbf{x})l^{\prime }(\mathbf{r}\mid \mathbf{x})\Vert }^2\rangle }_{\mathbf{r}\mid \mathbf{x}},$$ (2.51)

and it follows from conditions C1 and C2 that

$$\begin{array}{cc}\hfill \xi & \le {\Vert N{\mathbf{G}}^{-1}(\mathbf{x})\Vert }^2{\langle {\Vert N^{-1}\left(l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\right)\Vert }^4\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\hfill \\ \hfill & \times {\langle {\left(N^{-1}{l}^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{l}^{\prime }(\mathbf{r}\mid \mathbf{x})\right)}^2\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\hfill \\ \hfill & =O(N^{-1∕2}).\hfill \end{array}$$ (2.52)

Moreover, if p(r∣x) is conditionally independent, then by an argument similar to the discussion in remark 2, we can verify that the condition ξ = O (N⁻¹) is easily met.

In the following we state several conclusions about the MI; their proofs are given in the appendix.

Lemma 1. If condition C1 holds, then the MI I has an asymptotic upper bound for integer N,

$$I\le I_G+O(N^{-1}).$$ (2.53)

Moreover, if equations 2.25c and 2.25d are replaced by

$${\langle {\mid N^{-1}{l}^{\prime }(\mathit{r}\mid \mathit{x}{)}^T{l}^{\prime }(\mathit{r}\mid \mathit{x})\mid }^{1+\tau }\rangle }_{\mathit{r}\mid \mathit{x}}=O(1),$$ (2.54a)

$${\langle {\Vert N^{-1}\left(l^{″}(\mathit{r}\mid \mathit{x})-\langle l^{″}(\mathit{r}\mid \mathit{x}){\rangle }_{\mathit{r}\mid \mathit{x}}\right)\Vert }^2\rangle }_{\mathit{r}\mid \mathit{x}}=o(1),$$ (2.54b)

for some τ ∈ (0,1), where o indicates the Little-O notation, then the MI has the following asymptotic upper bound for integer N:

$$I\le I_G+o(1).$$ (2.55)

Lemma 2. If conditions C1 and C2 hold, ξ = O (N⁻¹), then the MI has an asymptotic lower bound for integer N,

$$I\ge I_G+O(N^{-1}).$$ (2.56)

Moreover, if condition C1 holds but equations 2.25c and 2.25d are replaced by 2.54a and 2.54b, and inequality 2.26b in C2 also holds for η > 0, then the MI has the following asymptotic lower bound for integer N:

$$I\ge I_G+o(1).$$ (2.57)

Theorem 1. If conditions C1 and C2 hold, ξ = O (N⁻¹), then the MI has the following asymptotic equality for integer N:

$$I=I_G+O(N^{-1}).$$ (2.58)

For more relaxed conditions, suppose condition C1 holds but equations 2.25c and 2.25d are replaced by 2.54a and 2.54b, and inequality 2.26b in C2 also holds for η > 0, then the MI has an asymptotic equality for integer N:

$$I=I_G+o(1).$$ (2.59)

Theorem 2. Suppose J(x) and G(x) are symmetric and positive-definite. Let

$$\varsigma =\langle Tr(\Psi (x)){\rangle }_x,$$ (2.60)

$$\Psi (\mathit{x})={\mathit{J}}^{-1∕2}(\mathit{x})\mathit{P}(\mathit{x}){\mathit{J}}^{-1∕2}(\mathit{x}).$$ (2.61)

Then

$$I_G\le I_F+\frac{\varsigma }{2},$$ (2.62)

where Tr (·) indicating matrix trace; moreover, if P(x) is positive-semidefinite, then

$$0\le I_G-I_F\le \frac{\varsigma }{2}.$$ (2.63)

But if

$${\varsigma }_1={\langle \Vert \Psi (\mathit{x})\Vert \rangle }_x=O(N^{-\beta })$$ (2.64)

for some β > 0, then

$$I_G=I_F+O(N^{-\beta }).$$ (2.65)

Remark 5. In general, we need only to assume that p(x) and p(r∣x) are piecewise twice continuously differentiable for $\mathbf{x}ϵ\mathcal{X}$. In this case, lemmas 1 and 2 and theorem 1 can still be established. For more general cases, such as discrete or continuous inputs, we have also derived a general approximation formula for MI from which we can easily derive formula for I_G (this will be discussed in separate paper).

2.3. Approximations of Mutual Information in Neural Populations with Finite Size.

In the preceding section, we provided several bounds, including both lower and upper bounds, and asymptotic relationships for the true MI in the large N (network size) limit. Now, we discuss effective approximations to the true MI in the case of finite N. Here we consider only the case of continuous inputs (we will discuss the case of discrete inputs in another paper).

Theorem 1 tells us that under suitable conditions, we can use I_G to approximate I for a large but finite N (e.g., N ⪢ K), that is,

$$I\simeq I_G.$$ (2.66)

Moreover, by theorem 2, we know that if ς ≈ 0 with positive-semidefinite P(x) or ς₁ ≈ 0 holds (see equations 2.60 and 2.64), then by equations 2.63, 2.65, and 2.66, we have

$$I\simeq I_G\simeq I_F.$$ (2.67)

Define

$$\tilde{\mathbf{G}}(\mathbf{x})=\mathbf{J}(\mathbf{x})+\mathbf{P}(\mathbf{x})+\mathbf{Q}(\mathbf{x}),$$ (2.68)

$${\tilde{I}}_G=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\tilde{\mathbf{G}}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X),$$ (2.69)

where $\tilde{\mathbf{G}}(\mathbf{x})$ is positive-definite and Q (x) is a symmetric matrix depending on x and ∥Q (x) ∥ = O(1). Suppose $\Vert {\tilde{\mathbf{G}}}^{-1}(\mathbf{x})\Vert =O(N^{-1})$. If we replace I_G by ${\tilde{I}}_G$ in theorem 1, then we can prove equations 2.58 and 2.59 in a manner similar to the proof of that theorem. Considering a special case where ∥P(x)∥ → 0, det (J(x)) = O(1) (e.g., rank (J(x)) < K) and ∥G⁻¹ (x) ∥ ≠ O(N⁻¹), then we can no longer use the asymptotic formulas in theorem 1. However, if we substitute $\tilde{\mathbf{G}}(\mathbf{x})$ for G(x) by choosing an appropriate Q (x) such that $\tilde{\mathbf{G}}(\mathbf{x})$ is positive-definite and $\Vert {\tilde{\mathbf{G}}}^{-1}(\mathbf{x})\Vert =O(N^{-1})$, then we can use equation 2.58 and 2.59 as the asymptotic formula.

If we assume G(x) and $\tilde{\mathbf{G}}(\mathbf{x})$ are positive-definite and

$$\zeta ={\langle \Vert \mathbf{Q}(\mathbf{x}){\tilde{\mathbf{G}}}^{-1}(\mathbf{x})\Vert \rangle }_{\mathbf{x}}=O(N^{-\beta }),\beta >0,$$ (2.70)

then similar to the proof of theorem 2, we have

$$\begin{array}{cc}\hfill & \langle \text{ln}(\text{det}(\mathbf{G}(\mathbf{x}))){\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle \text{ln}\left(\text{det}\left(\tilde{\mathbf{G}}(\mathbf{x})\right)\right)\rangle }_{\mathbf{x}}+{\langle \text{ln}\left(\text{det}\left({\mathbf{I}}_K-\mathbf{Q}(\mathbf{x}){\tilde{\mathbf{G}}}^{-1}(\mathbf{x})\right)\right)\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle \text{ln}\left(\text{det}\left(\tilde{\mathbf{G}}(\mathbf{x})\right)\right)\rangle }_{\mathbf{x}}+O(N^{-\beta })\hfill \end{array}$$ (2.71)

and

$${\tilde{I}}_G=I_G+O(N^{-\beta }).$$

For large N, we usually have ${\tilde{I}}_G\simeq I_G$.

It is more convenient to redefine the following quantities:

$$\mathbf{Q}(\mathbf{x})={\mathbf{P}}_{+}-\mathbf{P}(\mathbf{x}),$$ (2.72)

$${\mathbf{P}}_{+}={\langle \frac{\partial \text{ln}p(\mathbf{x})}{\partial \mathbf{x}}\frac{\partial \text{ln}p(\mathbf{x})}{\partial {\mathbf{x}}^T}\rangle }_{\mathbf{x}},$$ (2.73)

$${\mathbf{G}}_{+}(\mathbf{x})=\tilde{\mathbf{G}}(\mathbf{x})=\mathbf{J}(\mathbf{x})+{\mathbf{P}}_{+},$$ (2.74)

and

$$I_{G_{+}}={\tilde{I}}_G=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{{\mathbf{G}}_{+}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X).$$ (2.75)

Notice that if p(x) is twice differentiable for x and

$${\int }_{\mathcal{X}}\frac{{\partial }^{2}p(\mathbf{x})}{\partial \mathbf{x}\partial {\mathbf{x}}^T}d\mathbf{x}=\mathbf{0},$$ (2.76)

then

$${\mathbf{P}}_{+}=\langle \mathbf{P}(\mathbf{x}){\rangle }_{\mathbf{x}}={\langle \frac{1}{p(\mathbf{x})}\frac{{\partial }^{2}p(\mathbf{x})}{\partial \mathbf{x}\partial {\mathbf{x}}^T}\rangle }_{\mathbf{x}}-{\langle \frac{{\partial }^2\text{ln}p(\mathbf{x})}{\partial \mathbf{x}\partial {\mathbf{x}}^T}\rangle }_{\mathbf{x}}.$$ (2.77)

For example, if p(x) is a normal distribution, $p(\mathbf{x})=\mathcal{N}(\mu ,\Sigma )$, then

$$\mathbf{P}(\mathbf{x})={\mathbf{P}}_{+}={\Sigma }^{-1}.$$ (2.78)

Similar to the proof of theorem 2, we can prove that

$$0\le I_{G_{+}}-I_F\le \frac{{\varsigma }_{+}}{2},$$ (2.79)

where

$${\varsigma }_{+}={\langle \text{Tr}\left({\mathbf{P}}_{+}{\mathbf{J}}^{-1}(\mathbf{x})\right)\rangle }_{\mathbf{x}}.$$ (2.80)

We find that I_G is often a good approximation of MI I even for relatively small N. However, we cannot guarantee that P(x) is always positive-semidefinite in equation 2.14, and as a consequence, it may happen that det (G(x)) is very small for small N, G(x) is not positive-definite, and ln (det (G(x))) is not a real number. In this case, I_G is not a good approximation to I but I_G+ is still a good approximation. Generally, if P(x) is always positive-semidefinite, then I_G or I_G+ is a better approximation than I_F, especially when p(x) is close to a normal distribution.

In the following, we give an example of 1D inputs. High-dimensional inputs are discussed in section 4.1.

2.3.1. A Numerical Comparison for 1D Stimuli.

Considering the Poisson neuron model (see equation 5.7 in section 5.1 for details), the tuning curve of the nth neuron, f (x; θ_n), takes the form of circular normal or von Mises distribution

$$f(x;{\theta }_n)=A\text{exp}\left(-{\left(\frac{T}{2\pi {\sigma }_f}\right)}^2\left(1-\cos \left(\frac{2\pi }{T}(x-{\theta }_n)\right)\right)\right),$$ (2.81)

where x ∈ [−T/2, T/2), θ_n ∈ [−T_θ/2, T_θ/2], n ϵ {1,2, …, N}, with T = π, T_θ = 1, σ_f = 0.5, and A = 20, and the centers θ₁, θ₂, …, θ_N of the N neurons are uniformly distributed on interval [−T_θ/2, T_θ/2], that is, θ_n = (n – 1) d_θ – T_θ/2, with d_θ = T_θ/(N – 1) and N ≥ 2. Suppose the distribution of 1D continuous input x (K = 1) p(x) has the form

$$p(x)={\mathrm{Z}}^{-1}\text{exp}\left(-{\left(\frac{T}{2\pi {\sigma }_p}\right)}^2\left(1-\cos \left(\frac{2\pi }{T}x\right)\right)\right),$$ (2.82)

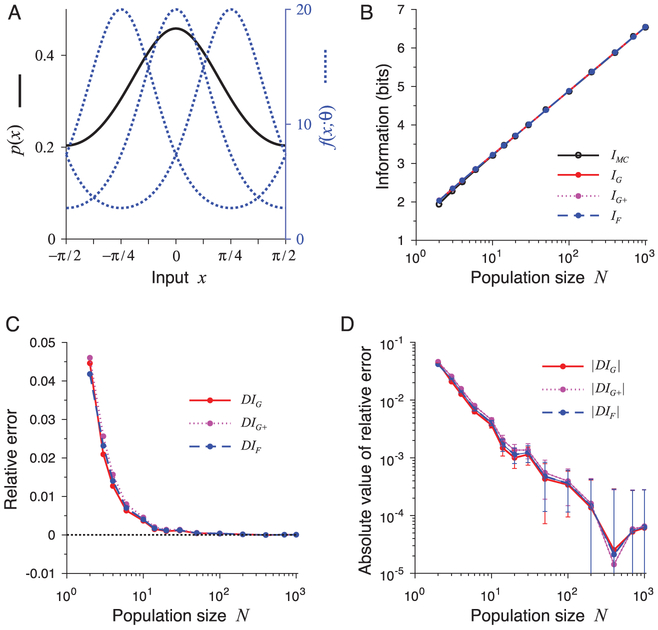
where σ_p is a constant set to π/4 and Z is the normalization constant. Figure 1A shows graphs of the input distribution p(x) and the tuning curves f (x; θ) with different centers θ = −π/4, 0, π/4.

Figure 1:

A comparison of approximations I_MC, I_G, I_G+, and I_F for one-dimensional input stimuli. All of them were almost equally good, even for small population size N. (A) The stimulus distribution p(x) and tuning curves f (x; θ) with different centers θ = −π/4, 0, π/4. (B) The values of I_MC, I_G, I_G+, and I_F all increase with neuron number N. (C) The relative errors DI_G, DI_G+, and DI_F for the results in panel B. (D) The absolute values of the relative errors ∣DI_G∣, ∣DI_G+∣, and ∣DI_F∣, with error bars showing standard deviations of repeated trials.

To evaluate the precision of the approximation formulas, we use Monte Carlo (MC) simulation to approximate MI I. For MC simulation, we first sample an input x_j by the distribution p(x), then generate the neural response r_j by the conditional distribution p(r_j∣x_j), where j = 1, 2, …, j_max. The value of MI by MC simulation is calculated by

$$I_{MC}^{\ast }=\frac{1}{j_{\max }}\sum _{j=1}^{j_{\max }}\text{ln}\left(\frac{p({\mathbf{r}}_j\mid x_j)}{p({\mathbf{r}}_j)}\right),$$ (2.83)

where p(r_j) is given by

$$p({\mathbf{r}}_j)=\sum _{m=1}^{M}p({\mathbf{r}}_j\mid x_m)p(x_m)$$ (2.84)

and x_m = (m – 1) T/M – T/2 for m ϵ {1,2, …, M}.

To evaluate the accuracy of MC simulation, we compute the standard deviation,

$$I_{std}=\sqrt{\frac{1}{i_{\max }}\sum _{i=1}^{i_{\max }}{\left(I_{MC}^i-I_{MC}\right)}^2},$$ (2.85)

where

$$I_{MC}^i=\frac{1}{j_{\max }}\sum _{j=1}^{j_{\max }}\text{ln}\left(\frac{p({\mathbf{r}}_{{\Gamma }_{j,i}}\mid x_{{\Gamma }_{j,i}})}{p({\mathbf{r}}_{{\Gamma }_{j,i}})}\right),$$ (2.86)

$$I_{MC}=\frac{1}{i_{\max }}\sum _{i=1}^{i_{\max }}{I}_{MC}^i,$$ (2.87)

and Γ_j,i ϵ {1,2, …, j_max} is the (j, i)th entry of the matrix $\Gamma \in {\mathbb{N}}^{j_{\max }\times i_{\max }}$ with samples taken randomly from the integer set {1, 2, …, j_max} by a uniform distribution. Here we set j_max = 5 × 10⁵, i_max = 100 and M = 10³.

For different N ∈ {2, 3, 4, 6, 10, 14, 20, 30, 50, 100, 200,400, 700, 1000}, we compare I_MC with I_G, I_G+, and I_F, which are illustrated in Figures 1B to 1D. Here we define the relative error of approximation, for example, for I_G, as

$$D{I}_G=\frac{I_G-I_{MC}}{I_{MC}},$$ (2.88)

and the relative standard deviation

$$D{I}_{std}=\frac{I_{std}}{I_{MC}}.$$ (2.89)

Figure 1B shows how the values of I_MC, I_G, I_G+, and I_F change with neuron number N, and Figures 1C and 1D show their relative errors and the absolute values of the relative errors with respect to I_MC. From Figures 1B to 1D, we can see that the values of I_G, I_G+, and I_F are all very close to one another and the absolute values of their relative errors are all very small. The absolute values are less than 1% when N ≥ 10 and less than 0.1% when N ≥ 100. However, for the high-dimensional inputs, there will be a big difference between I_G, I_G+, and I_F in many cases (see section 4.1 for more details).

3. Statistical Estimators and Neural Population Decoding

Given the neural response r elicited by the input x, we may infer or estimate the input x from the response. This procedure is sometimes referred to as decoding from the response. We need to choose an efficient estimator or a function $\widehat{\mathbf{x}}=\widehat{\mathbf{x}}(\mathbf{r})$ that maps the response r to an estimate $\widehat{\mathbf{x}}$ of the true stimulus x. The maximum likelihood (ML) estimator defined by

$$\widehat{x}(\mathbf{r})=\arg \underset{\mathbf{x}}{\max }p(\mathbf{r}\mid \mathbf{x})=\arg \underset{\mathbf{x}}{\max }l(\mathbf{r}\mid \mathbf{x})$$ (3.1)

is known to be efficient in large N limit. According to the Cramér-Rao lower bound (Rao, 1945), we have the following relationship between the covariance matrix of any unbiased estimator ${\Sigma }_{\widehat{\mathbf{x}}}$ and the FI matrix J (x),

$${\Sigma }_{\widehat{\mathbf{x}}}={\langle (\widehat{x}(\mathbf{r})-\mathbf{x}){(\widehat{x}(\mathbf{r})-\mathbf{x})}^T\rangle }_{\mathbf{r}\mid \mathbf{x}}\ge {\mathbf{J}}^{-1}(\mathbf{x}),$$ (3.2)

where $\widehat{\mathbf{x}}(\mathbf{r})$ is an unbiased estimation of x from the response r, and A ≥ B means that matrix A – B is positive-semidefinite. Thus,

$$\begin{array}{cc}\hfill I_F=& \frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{J}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X)\hfill \\ \hfill \ge & \frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{{\Sigma }_{\widehat{\mathbf{x}}}^{-1}}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X)=I_{\text{var}}.\hfill \end{array}$$ (3.3)

The MI between X and $\widehat{X}$ is given by

$$\widehat{I}=H(\widehat{X})-{\langle H(\widehat{X}\mid X)\rangle }_{\widehat{\mathbf{x}},\mathbf{x}},$$ (3.4)

where $H(\widehat{X})$ is the entropy of random variable $\widehat{X}$ and $H(\widehat{X}\mid X)$ is its conditional entropy of random variable $\widehat{X}$ given X. Since the maximum entropy probability distribution is gaussian, $H(\widehat{X}\mid X)$ satisfies

$$H(\widehat{X}\mid X)\le \frac{1}{2}\text{ln}(\text{det}(2\pi e{\Sigma }_{\widehat{\mathbf{x}}})).$$ (3.5)

Therefore, from equations 3.4 and 3.5, we get

$$\widehat{I}\ge \frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{{\Sigma }_{\widehat{\mathbf{x}}}^{-1}}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(\widehat{X})={\widehat{I}}_{\text{var}}.$$ (3.6)

The data processing inequality (Cover & Thomas, 2006) states that postprocessing cannot increase information, so that we have

$$I\ge \widehat{I}\ge {\widehat{I}}_{\text{var}}.$$ (3.7)

Here we can not directly obtain I ≥ I_F as in Brunel and Nadal (1998) when $H(\widehat{X})=H(X)$ and $I_{\text{var}}={\widehat{I}}_{\text{var}}$. The simulation results in Figure 1 also show that I_F is not a lower bound of I.

For biased estimators, the van Trees’ Bayesian Cramér-Rao bound (Van Trees & Bell, 2007) provides a lower bound:

$${\langle {\Sigma }_{\widehat{\mathbf{x}}}\rangle }_{\mathbf{x}}={\langle {\langle (\widehat{x}(\mathbf{r})-\mathbf{x}){(\widehat{x}(\mathbf{r})-\mathbf{x})}^T\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ge {({\langle \mathbf{J}(\mathbf{x})\rangle }_{\mathbf{x}}+{\mathbf{P}}_{+})}^{-1}={\langle {\mathbf{G}}_{+}(\mathbf{x})\rangle }_{\mathbf{x}}^{-1}.$$ (3.8)

It follows from equations 2.75, 3.6, and 3.8 that

$$I_{G_{+}}\le \frac{1}{2}\text{ln}\left(\text{det}\left(\frac{{\langle {\mathbf{G}}_{+}(\mathbf{x})\rangle }_{\mathbf{x}}}{2\pi e}\right)\right)+H(X)=I_{VT},$$ (3.9)

$$I_{VT}\ge \frac{1}{2}\text{ln}\left(\text{det}\left(\frac{{\langle {\Sigma }_{\widehat{x}}\rangle }_{\mathbf{x}}^{-1}}{2\pi e}\right)\right)+H(X)={\tilde{I}}_{\text{var}},$$ (3.10)

$$I_{\text{var}}\ge {\tilde{I}}_{\text{var}}.$$ (3.11)

We may also regard decoding as Bayesian inference. By Bayes’ rule,

$$p(\mathbf{x}\mid \mathbf{r})=\frac{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}{p(\mathbf{r})}.$$ (3.12)

According to the Bayesian decision theory, if we know the response r, from the prior p(x) and the likelihood p(r∣x), we can infer an estimation of the true stimulus x, $\widehat{\mathbf{x}}(\mathbf{r})$—for example,

$$\widehat{x}(\mathbf{r})=\arg \underset{\mathbf{x}}{\max }p(\mathbf{x}\mid \mathbf{r})=\arg \underset{\mathbf{x}}{\max }L(\mathbf{r}\mid \mathbf{x}),$$ (3.13)

which is also called maximum a posteriori (MAP) estimation.

Consider a loss function $\phi (\widehat{\mathbf{x}}(\mathbf{r})\mid \mathbf{x})$ for estimation,

$$\phi (\widehat{x}(\mathbf{r})\mid \mathbf{x})=-\text{ln}p(\mathbf{x}\mid \mathbf{r}),$$ (3.14)

which is minimized when p(x∣r) reaches its maximum. Now the conditional risk is

$$R(\widehat{x}(\mathbf{r})\mid \mathbf{r})={\langle \phi (\widehat{x}(\mathbf{r})\mid \mathbf{x})\rangle }_{\mathbf{x}\mid \mathbf{r}},$$ (3.15)

and the overall risk is

$$R_o={\langle R(\widehat{x}(\mathbf{r})\mid \mathbf{r})\rangle }_{\mathbf{r}}={\langle {\langle \phi (\widehat{x}(\mathbf{r})\mid \mathbf{x})\rangle }_{\mathbf{x}\mid \mathbf{r}}\rangle }_{\mathbf{r}}=-{\langle \text{ln}p(\mathbf{x}\mid \mathbf{r})\rangle }_{\mathbf{x},\mathbf{r}}.$$ (3.16)

Then it follows from equations 2.3 and 3.16 that

$$I={\langle \text{ln}p(\mathbf{x}\mid \mathbf{r})\rangle }_{\mathbf{r},\mathbf{x}}+H(X)=-R_o+H(X).$$ (3.17)

Comparing equations 2.12, 2.66, and 3.17, we find

$$R_o\simeq -\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}.$$ (3.18)

Hence, maximizing MI I (or I_G) means minimizing the overall risk R_o for a determinate H(X). Therefore, we can get the optimal Bayesian inference via optimizing MI I (or I_G).

By the Cramér-Rao lower bound, we know that the inverse of FI matrix J⁻¹(x) reflects the accuracy of decoding (see equation 3.2). P(x) provides some knowledge about the prior distribution p(x); for example, P⁻¹ (x) is the covariance matrix of input x when p(x) is a normal distribution. ∥P(x)∥ is small for a flat prior (poor prior) and large for a sharp prior (good prior). Hence, if the prior p(x) is flat or poor and the knowledge about model is rich, then the MI I is governed by the knowledge of model, which results in a small ς₁ (see equation 2.64) and I ≃ I_G ≃ I_F. Otherwise, the prior knowledge has a great influence on MI I, which results in a large ς₁ and I ≃ I_G ≄ I_F.

4. Variable Transformation and Dimensionality Reduction in Neural Population Coding

For low-dimensional input x and large N, both I_G are I_F are good approximations of MI I, but for high-dimensional input x, a large value of ς₁ may lead to a large error of I_F, in which case I_G (or I_G+ ) is a better approximation. It is difficult to directly apply the approximation formula I ≃ I_G when we do not have an explicit expression of p (x) or P (x). For many applications, we do not need to know the exact value of I_G and care only about the value of ⟨ln (det (G(x)))⟩_x (see section 5). From equations 2.12, 2.22, and 2.78, we know that if p (x) is close to a normal distribution, we can easily approximate P (x) and H(X) to obtain ⟨ln (det (G(x)))⟩_x and I_G. When p (x) is not a normal distribution, we can employ a technique of variable transformation to make it closer to a normal distribution, as discussed below.

4.1. Variable Transformation.

Suppose $\mathbf{T}:\mathcal{X}\to \tilde{\mathcal{X}}$ is an invertible and differentiable mapping:

$$\tilde{x}=\mathbf{T}(\mathbf{x})={(T_1(\mathbf{x}),T_2(\mathbf{x}),\dots ,T_K(\mathbf{x}))}^T,$$ (4.1)

$\mathbf{x}={\mathbf{T}}^{-1}(\tilde{\mathbf{x}})$, and $\tilde{\mathbf{x}}\in \tilde{\mathcal{X}}\subseteq {\mathbb{R}}^K$. Let $p(\tilde{\mathbf{x}})$ denote the p.d.f. of random variable $\tilde{X}$ and

$$p(\mathbf{r}\mid \tilde{x})={\phantom{\mid }p(\mathbf{r}\mid \mathbf{x})\mid }_{\mathbf{x}={\mathbf{T}}^{-1}(\tilde{x})}.$$ (4.2)

Then we have the following conclusions, the proofs of which are given in the appendix.

Theorem 3. The MI is equivariant under the invertible transformations. More specifically, for the above invertible transformation T, the MI I(X; R) in equation 2.1 is equal to

$$I(\tilde{X};R)={\langle \mathit{ln}\frac{p(\mathit{r}\mid \tilde{x})}{p(\mathit{r})}\rangle }_{\mathit{r},\tilde{x}}.$$ (4.3)

Furthermore, suppose $p(\tilde{x})$ and $p(r\mid \tilde{x})$ fulfill the conditions C1, C2 and ξ = O (N⁻¹). Then we have

$$I(\tilde{X};R)={\tilde{I}}_G+O(N^{-1}),$$ (4.4)

$$\begin{array}{cc}\hfill {\tilde{I}}_G& =\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{\mathit{G}(\tilde{x})}{2\pi e}\right)\right)\rangle }_{\tilde{x}}+H(\tilde{X})\hfill \\ \hfill & =\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{\mathit{G}(\mathit{x})}{2\pi e}\right)\right)\rangle }_x+H(X)\hfill \\ \hfill & =I_G,\hfill \end{array}$$ (4.5)

where $H(\tilde{X})$ is the entropy of random variable $\tilde{X}$ and satisfies

$$H(\tilde{X})=-{\langle \mathit{ln}p(\tilde{x})\rangle }_{\tilde{x}}=H(X)+{\langle \mathit{ln}\mid \mathit{det}(D\mathit{T}(\mathit{x}))\mid \rangle }_{\mathit{x}},$$ (4.6)

and DT (x) denotes the Jacobian matrix of T (x),

$${(D\mathit{T}(\mathit{x}))}_{i,j}=\frac{\partial T_i(\mathit{x})}{\partial x_j},\forall i,j=1,2,\dots ,K.$$ (4.7)

Corollary 1. Suppose p(r∣x) is a normal distribution,

$$p(\mathit{r}\mid \mathit{x})=\mathcal{N}({\mathit{A}}^T\mathit{y},{\mathit{I}}_N),$$ (4.8)

where y = f (B^T x) = (y₁, y₂, …, y_K)^T, $y_k=f_k({\mathit{b}}_k^T\mathit{x})$ for k = 1, 2, …, K, A is a deterministic K × N matrix, B = [b₁, b₂, …, b_K] is a deterministic invertible matrix, and f_k is an invertible and differentiable function. If Y has also a normal distribution, $p(\mathit{y})=\mathcal{N}({\mu }_f,{\Sigma }_f)$, then

$$\begin{array}{cc}\hfill I_G& =I_{G_{+}}=I(X;R)=I({\rm Y};R)\hfill \\ \hfill & =\frac{1}{2}\mathit{ln}\left(\mathit{det}\left(\frac{1}{2\pi e}\left({\mathit{AA}}^T+{\Sigma }_f^{-1}\right)\right)\right)+H({\rm Y})\hfill \\ \hfill & =\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{1}{2\pi e}(\mathit{J}(\mathit{x})+\mathit{P}(\mathit{x}))\right)\right)\rangle }_{\mathit{x}}+H(X),\hfill \end{array}$$ (4.9)

where

$$H({\rm Y})=\frac{1}{2}\mathit{ln}(\mathit{det}(2\pi e{\Sigma }_f))=H(X)+{\langle \mathit{ln}\mid \mathit{det}(\mathit{D}(\mathit{x}))\mid \rangle }_{\mathit{x}},$$ (4.10)

$$\mathit{D}(\mathit{x})={(f_1^{\prime }({\mathit{b}}_1^T\mathit{x}){\mathit{b}}_1,f_2^{\prime }({\mathit{b}}_2^T\mathit{x}){\mathit{b}}_2,\dots ,f_K^{\prime }({\mathit{b}}_K^T\mathit{x}){\mathit{b}}_K)}^T,$$ (4.11)

$$f_k^{\prime }({\mathit{b}}_k^T\mathit{x})={\phantom{\mid }\frac{\partial f_k(y_k)}{\partial y_k}\mid }_{y_k=b_k^{T}x},\forall k=1,2,\dots ,K.$$ (4.12)

Remark 6. From corollary 1 and equation 2.78, we know that the approximation accuracy for I_G ≃ I(X; R) is improved when we employ an invertible transformation on the input random variable X to make the new random variable Y closer to a normal distribution (see section 4.3).

Consider the eigendecompositions of AA^T and ∑_f as given by

$${\mathbf{AA}}^T={\mathbf{U}}_{\mathbf{A}}\widehat{\Sigma }{\mathbf{U}}_{\mathbf{A}}^T,$$ (4.13)

$${\Sigma }_{\mathbf{f}}={\mathbf{U}}_{\mathbf{f}}\tilde{\Sigma }{\mathbf{U}}_{\mathbf{f}}^T,$$ (4.14)

where U_A and U_f are K × K orthogonal matrices; $\widehat{\Sigma }=\text{diag}({\widehat{\sigma }}_1^2,{\widehat{\sigma }}_2^2,\dots ,{\widehat{\sigma }}_K^2)$ and $\tilde{\Sigma }=\text{diag}({\tilde{\sigma }}_1^2,{\tilde{\sigma }}_2^2,\dots ,{\tilde{\sigma }}_K^2)$ are K × K eigenvalue matrices; and ${\widehat{\sigma }}_1\ge {\widehat{\sigma }}_2\ge \cdots \ge {\widehat{\sigma }}_K>0$ and ${\tilde{\sigma }}_1\ge {\tilde{\sigma }}_2\ge \cdots \ge {\tilde{\sigma }}_K>0$. Then by equations 2.11 and 4.9, we have

$$\begin{array}{cc}\hfill I_G& =I_{G_{+}}=I(X;R)=I({\rm Y};R)\hfill \\ \hfill & =\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{1}{2\pi e}({\mathbf{U}}_{\mathbf{A}}\widehat{\Sigma }{\mathbf{U}}_{\mathbf{A}}^T+{\mathbf{U}}_{\mathbf{f}}{\tilde{\Sigma }}^{-1}{\mathbf{U}}_{\mathbf{f}}^T)\right)\right)+H({\rm Y}),\hfill \end{array}$$ (4.15)

$$I_F=\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{\widehat{\Sigma }}{2\pi e}\right)\right)+H({\rm Y}),$$ (4.16)

and

$$I_F-I_G=-\frac{1}{2}\text{ln}(\text{det}({\mathbf{I}}_K+{\widehat{\Sigma }}^{-1∕2}{\mathbf{U}}_{\mathbf{A}}^T{\mathbf{U}}_{\mathbf{f}}{\tilde{\Sigma }}^{-1}{\mathbf{U}}_{\mathbf{f}}^T{\mathbf{U}}_{\mathbf{A}}{\widehat{\Sigma }}^{-1∕2})).$$ (4.17)

Now consider two special cases. If $\tilde{\Sigma }={\mathbf{I}}_K$, then by equation 4.17, we get

$$I_F-I_G=-\frac{1}{2}\sum _{k=1}^K\text{ln}(1+{\widehat{\sigma }}_k^{-2}).$$ (4.18)

If U_A = U_f, then

$$I_F-I_G=-\frac{1}{2}\sum _{k=1}^K\text{ln}(1+{\widehat{\sigma }}_k^{-2}{\tilde{\sigma }}_k^{-2}).$$ (4.19)

Here $\mathbf{J}(\mathbf{x})={\mathbf{U}}_{\mathbf{A}}\widehat{\Sigma }{\mathbf{U}}_{\mathbf{A}}^T$, ${\mathbf{P}}^{-1}(\mathbf{x})={\mathbf{U}}_{\mathbf{f}}\tilde{\Sigma }{\mathbf{U}}_{\mathbf{f}}^T$. The FI matrices J(x) and P⁻¹(x) become degenerate when ${\widehat{\sigma }}_K^2\to 0$ and ${\tilde{\sigma }}_K^2\to 0$.

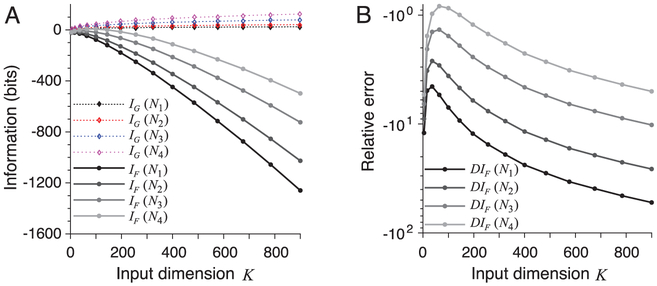
From equations 4.18 and 4.19, we see that if either J(x)or P⁻¹ (x) becomes degenerate, then (I_F – I_G) → −∞. This may happen for high-dimensional stimuli. For a specific example, consider a random matrix A defined as follows. Here we first generate K × N elements A_k,n, (k = 1, 2, …, K; n = 1, 2, …, N) from a normal distribution $\mathcal{N}$ (0,1). Then each column of matrix A is normalized by $A_{k,n}\leftarrow A_{k,n}∕\sqrt{{\sum }_{k=1}^K{A}_{k,n}^2}$. We randomly sample M (set to 2 × 10⁴) image patches with size ω × ω from Olshausen’s nature image data set (Olshausen & Field, 1996) as the inputs. Each input image patch was centered by subtracting its mean: ${\mathbf{x}}_m\leftarrow {\mathbf{x}}_m-\frac{1}{K}{\sum }_{k=1}^K{x}_{k,m}$. Then let ${\mathbf{x}}_m\leftarrow {\mathbf{x}}_m-\frac{1}{M}{\sum }_{m^{\prime }=1}^M{\mathbf{x}}_{m^{\prime }}$ for ∀m ϵ {1, 2, …, M}. Define matrix X = [x₁, x₂, …, x_M] and compute eigendecomposition

$$\frac{1}{M}{\mathbf{XX}}^T={\mathbf{U}}_{\mathbf{x}}\check{\Sigma }{\mathbf{U}}_{\mathbf{x}}^T,$$ (4.20)

where U_x is a K × K orthogonal matrix and $\check{\Sigma }=\text{diag}\left({\check{\sigma }}_1^2,{\check{\sigma }}_2^2,\dots ,{\check{\sigma }}_K^2\right)$ is a K × K eigenvalue matrix with ${\check{\sigma }}_1\ge {\check{\sigma }}_2\ge \cdots \ge {\check{\sigma }}_K>0$. Define

$$\mathbf{y}={\mathbf{U}}_{\mathbf{x}}^T\mathbf{x}.$$ (4.21)

Then

$$\frac{1}{M}\sum _{m=1}^M{\mathbf{y}}_m{\mathbf{y}}_m^T=\check{\Sigma }.$$ (4.22)

The distribution of random variable Y can be approximated by a normal distribution (see section 4.3 for more details). When $p(\mathbf{y})=\mathcal{N}(\check{\mu },\check{\Sigma })$, we have

$$I_G=I_{G_{+}}=I(X;R)=I({\rm Y};R),$$ (4.23)

$$\begin{array}{cc}\hfill I_G& =\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{1}{2\pi e}({\mathbf{AA}}^T+{\check{\Sigma }}^{-1})\right)\right)+H({\rm Y})\hfill \\ \hfill & =\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{1}{2\pi e}({\check{\Sigma }}^{1∕2}{\mathbf{AA}}^T{\check{\Sigma }}^{1∕2}+{\mathbf{I}}_K)\right)\right),\hfill \end{array}$$ (4.24)

$$I_F=\frac{1}{2}\text{ln}\left(\text{det}\left(\frac{{\mathbf{AA}}^T}{2\pi e}\right)\right)+H({\rm Y}).$$ (4.25)

The error of approximation I_F is given by

$$\begin{array}{cc}\hfill d{I}_F& =I_F-I(X;R)=I_F-I_G\hfill \\ \hfill & =-\frac{1}{2}\text{ln}(\text{det}({\mathbf{I}}_K+{({\mathbf{AA}}^T)}^{-1}{\check{\Sigma }}^{-1})),\hfill \end{array}$$ (4.26)

and the relative error for I_F is

$$D{I}_F=\frac{d{I}_F}{I_G}.$$ (4.27)

Figure 2A shows how the values of I_G and I_F vary with the input dimension K = ω × ω and the number of neurons N (with ω = 2, 4, 6, …, 30 and N = 10⁴, 2 × 10⁴, 5 × 10⁴, 10⁵). The relative error DI_F is shown in Figure 2B. The absolute value of the relative error tends to decrease with N but may grow quite large as K increases. In Figure 2B, the largest absolute value of relative error ∣DI_F∣ is greater than 5000%, which occurs when K = 900 and N = 10⁴. Even the smallest ∣DI_F∣ is still greater than 80%, which occurs when K = 100 and N = 10⁵. In this example, I_F is a bad approximation of MI I, whereas I_G and I_G+ are strictly equal to the true MI I across all parameters.

Figure 2:

A comparison of approximations I_G and I_F for different input dimensions. Here I_G is always equal to the true MI with I_G = I_G+ = I(X; R), whereas I_F always has nonzero errors. (A) The values I_G and I_F vary with input dimension K = ω² with ω = 2, 4, 6, …, 30, and the number of neurons N = N_i with N₁ = 10⁴, N₂ = 2 × 10⁴, N₃ = 5 × 10⁴, N₄ = 10⁵. (B) The relative error DI_F changes with input dimension K for different N.

4.2. Dimensionality Reduction for Asymptotic Approximations.

Suppose x = (x₁, … x_K)^T is partitioned into two sets of components, $\mathbf{x}=({\mathbf{x}}_1^T,{\mathbf{x}}_2^T{)}^T$ with

$${\mathbf{x}}_1={(x_1,x_2,\dots ,x_{K_1})}^T,$$ (4.28)

$${\mathbf{x}}_2={(x_{K_1+1},x_{K_1+2},\dots ,x_K)}^T,$$ (4.29)

where ${\mathbf{x}}_1\in {\mathcal{X}}_1\subseteq {\mathbb{R}}^{K_1}$, ${\mathbf{x}}_2\in {\mathcal{X}}_2\subseteq {\mathbb{R}}^{K_2}$, K₁ + K₂ = K, K ≥ 2, K₁ ≥ 1 and K₂ ≥ 1.

Then by Fubini’s theorem, the MI I in equation 2.1 can be written as

$$I={\int }_{{\mathcal{X}}_2}{\int }_{{\mathcal{X}}_1}{\int }_{\mathcal{R}}p(\mathbf{r}\mid {\mathbf{x}}_1,{\mathbf{x}}_2)p({\mathbf{x}}_1,{\mathbf{x}}_2)\text{ln}\frac{p(\mathbf{r}\mid {\mathbf{x}}_1,{\mathbf{x}}_2)}{p(\mathbf{r})}d\mathbf{r}d{\mathbf{x}}_{1}d{\mathbf{x}}_2,$$ (4.30)

where p(x₁, x₂) = p(x) and p(r∣x₁, x₂) = p(r∣x).

First define

$$\mathbf{G}(\mathbf{x})=\left(\begin{array}{cc}\hfill {\mathbf{G}}_{1,1}(\mathbf{x})\hfill & \hfill {\mathbf{G}}_{1,2}(\mathbf{X})\hfill \\ \hfill {\mathbf{G}}_{2,1}(\mathbf{x})\hfill & \hfill {\mathbf{G}}_{2,2}(\mathbf{x})\hfill \end{array}\right),$$ (4.31a)

$${\mathbf{G}}_{i,j}(\mathbf{x})={\mathbf{J}}_{i,j}(\mathbf{x})+{\mathbf{P}}_{i,j}(\mathbf{x}),$$ (4.31b)

where i, j ϵ {1, 2}, and

$${\mathbf{J}}_{i,j}(\mathbf{x})={\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{x})}{\partial {\mathbf{x}}_i}\frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{x})}{\partial {\mathbf{x}}_j^T}\rangle }_{\mathbf{r}\mid \mathbf{x}},$$ (4.32a)

$${\mathbf{P}}_{i,j}(\mathbf{x})=-\frac{{\partial }^2\text{ln}p(\mathbf{x})}{\partial {\mathbf{x}}_i\partial {\mathbf{x}}_j^T}.$$ (4.32b)

Then we have the following results, their proofs are given in the appendix.

Theorem 4. Suppose matrices G (x), G_{1, 1} (x), and G_2,2 (x) are positive-definite. If the matrix ${\mathit{A}}_{\mathit{x}}\in {\mathbb{R}}^{K\times K}$ satisfies

$$\mid Tr({\langle {\mathit{A}}_{\mathit{x}}\rangle }_{\mathit{x}})\mid ⪡1$$ (4.33)

with

$$A_x={\mathit{G}}_{2,2}^{-1∕2}(\mathit{x}){\mathit{G}}_{2,1}(\mathit{x})G_{1,1}^{-1}(\mathit{x}){\mathit{G}}_{1,2}(\mathit{x}){\mathit{G}}_{2,2}^{-1∕2},$$ (4.34)

then we have

$$I_G\simeq I_{G_1}$$ (4.35)

with strict equality if and only if

$${\mathit{G}}_{2,1}(\mathit{x}){\mathit{G}}_{1,1}^{-1}(\mathit{x}){\mathit{G}}_{1,2}(\mathit{x})=0,$$ (4.36)

where

$$I_{G_1}=\frac{1}{2}{\langle \mathit{ln}\left(\text{det}\left(\frac{{\mathit{G}}_{1,1}(\mathit{x})}{2\pi e}\right)\right)\rangle }_x+\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{{\mathit{G}}_{2,2}(\mathit{x})}{2\pi e}\right)\right)\rangle }_x+H(X).$$ (4.37)

Theorem 5. Suppose matrices G (x), G_1,1 (x) and P_2,2 (x) are positive-definite. If the matrix ${\mathit{B}}_{\mathit{x}}\in {\mathbb{R}}^{K_2\times K_2}$ is positive-semidefinite and satisfies

$$0\le Tr({\langle {\mathit{B}}_x\rangle }_x)⪡1$$ (4.38)

with

$${\mathit{B}}_{\mathit{x}}={\mathit{P}}_{2,2}^{-1∕2}(\mathit{x}){\mathit{C}}_{\mathit{x}}{\mathit{P}}_{2,2}^{-1∕2}(\mathit{x}),$$ (4.39)

$${\mathit{C}}_{\mathit{x}}={\mathit{J}}_{2,2}(\mathit{x})-{\mathit{G}}_{2,1}(\mathit{x}){\mathit{G}}_{1,1}^{-1}(\mathit{x}){\mathit{G}}_{1,2}(\mathit{x}),$$ (4.40)

then we have

$$I_G\simeq I_{G_2},$$ (4.41)

with strict equality if and only if

$${\mathit{C}}_{\mathit{x}}=0,$$ (4.42)

where

$$I_{G_2}=\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{{\mathit{G}}_{1,1}(\mathit{x})}{2\pi e}\right)\right)\rangle }_{\mathit{x}}+\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{{\mathit{P}}_{2,2}(\mathit{x})}{2\pi e}\right)\right)\rangle }_{\mathit{x}}+H(X).$$ (4.43)

Corollary 2. If the random variables X₁ and X₂ are independent so that $p(\mathit{x})=p({\mathit{x}}_1)p({\mathit{x}}_2),p({\mathit{x}}_2)=\mathcal{N}({\mu }_2,{\Sigma }_{{\mathit{x}}_2})$ is a normal distribution, and G (x), G_1,1 (x), P_1,1 (x) and P_2,2 (x) are all positive-definite and satisfy equation 4.38, then we have

$$I_G\simeq I_{G_1^{\prime }},$$ (4.44)

$$I_{G_1^{\prime }}=\frac{1}{2}{\langle \mathit{ln}\left(\mathit{det}\left(\frac{{\mathit{G}}_{1,1}(\mathit{x})}{2\pi e}\right)\right)\rangle }_{\mathit{x}}+H(X_1),$$ (4.45)

with strict equality if and only if

$${\mathit{C}}_{\mathit{x}}={\mathit{J}}_{2,2}(\mathit{x})-{\mathit{J}}_{2,1}(\mathit{x}){\mathit{G}}_{1,1}^{-1}(\mathit{x}){\mathit{J}}_{1,2}(\mathit{x})=0,$$ (4.46)

where

$$H(X_1)=-{\langle \mathit{ln}p({\mathit{x}}_1)\rangle }_{{\mathit{x}}_1},$$ (4.47a)

$${\mathit{G}}_{1,1}(\mathit{x})={\mathit{J}}_{1,1}(\mathit{x})+{\mathit{P}}_{1,1}(\mathit{x}),$$ (4.47b)

$${\mathit{P}}_{1,1}(\mathit{x})=-\frac{{\partial }^2\mathit{ln}p({\mathit{x}}_1)}{\partial {\mathit{x}}_1\partial {\mathit{x}}_1^T}.$$ (4.47c)

Remark 7. Sometimes we are concerned only with calculating the determinant of matrix G(x) with a given p(x). Theorems 3 and 4 provide a dimensionality reduction method for computing G (x) or det (G (x)), by which we need only to compute G_1,1 (x) and G_2,2 (x) separately. To apply the approximation 4.35, we do not need to strictly require ∣Tr (⟨A_x⟩_x)∣ ⪡ 1. Instead we need to require only

$$\mid \text{Tr}({\langle {\mathbf{A}}_{\mathbf{x}}\rangle }_{\mathbf{x}})\mid ⪡\mid {\langle \text{ln}(\text{det}({\mathbf{G}}_{1,1}(\mathbf{x}))\text{det}({\mathbf{G}}_{2,2}(\mathbf{x})))\rangle }_{\mathbf{x}}\mid .$$ (4.48)

Similarly, the inequality ∣Tr (⟨B_x⟩_x)∣ ⪡ 1 can be substituted by

$$\mid \text{Tr}({\langle {\mathbf{B}}_{\mathbf{x}}\rangle }_{\mathbf{x}})\mid ⪡\mid {\langle \text{ln}(\text{det}({\mathbf{G}}_{1,1}(\mathbf{x}))\text{det}({\mathbf{P}}_{2,2}(\mathbf{x})))\rangle }_{\mathbf{x}}\mid .$$ (4.49)

By equation 4.44 and the second mean value theorem for integrals, we get

$$I_{G_1^{\prime }}=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{{\mathbf{G}}_{1,1}({\mathbf{x}}_1,{\ddot{x}}_2)}{2\pi e}\right)\right)\rangle }_{{\mathbf{x}}_1}+H(X_1)$$ (4.50)

for some fixed ${\ddot{\mathbf{x}}}_2\in {\mathcal{X}}_2$. When ∥∑_x2∥ is small, ${\ddot{\mathbf{x}}}_2$ should be close to the mean: ${\ddot{\mathbf{x}}}_2\approx {\mu }_2$. It follows from theorem 1 and corollary 2 that the approximate relationship $I\simeq {I_G}_1^{\prime }$ holds. However, equation 4.50 implies that ${I_G}_1^{\prime }$ is determined only by the first component x₁. Hence, there is little impact on information transfer by the minor component (i.e., x₂) for the high-dimensional input x. In other words, the information transfer is mainly determined by the first component x₁, and we can omit the minor component x₂.

4.3. Further Discussion.

Suppose x is a zero-mean vector; if it is not, then let x ← x – ⟨x⟩_x. The covariance matrix of x is given by

$${\Sigma }_{\mathbf{x}}={\langle {\mathbf{xx}}^T\rangle }_{\mathbf{x}}=\mathbf{U}\Sigma {\mathbf{U}}^T,$$ (4.51)

where U is a K × K orthogonal matrix whose kth column is the eigenvector u_k of ∑_x and ∑ is a diagonal matrix whose diagonal elements are the corresponding eigenvalues—$\Sigma =\text{diag}\left({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_K^2\right)$ with σ₁ ≥ σ₂ ≥ … ≥ σ_K > 0. With the whitening transformation,

$$\tilde{x}={\Sigma }^{-1∕2}{\mathbf{U}}^T\mathbf{x},$$ (4.52)

the covariance matrix of $\tilde{\mathbf{x}}$ becomes an identity matrix:

$${\Sigma }_{\tilde{x}}={\langle \tilde{x}{\tilde{x}}^T\rangle }_{\tilde{x}}={\Sigma }^{-1∕2}{\mathbf{U}}^T{\langle {\mathbf{xx}}^T\rangle }_{\mathbf{x}}\mathbf{U}{\Sigma }^{-1∕2}={\mathbf{I}}_K.$$ (4.53)

By the central limit theorem, the distribution of random variable $\tilde{X}$ should be closer to a normal distribution than the distribution of the original random variable X; that is, $p(\tilde{\mathbf{x}})\simeq \mathcal{N}(0,{\mathbf{I}}_K)$. Using Laplace’s method asymptotic expansion (MacKay, 2003), we get

$$\mathbf{P}(\tilde{x})=-\frac{{\partial }^2\text{ln}p(\tilde{x})}{\partial \tilde{x}\partial {\tilde{x}}^T}\simeq {\Sigma }_{\tilde{x}}^{-1}={\mathbf{I}}_K,$$ (4.54)

$${\mathbf{P}}_{+}={\langle \mathbf{P}(\tilde{x})\rangle }_{\tilde{x}}\simeq {\Sigma }_{\tilde{x}}^{-1}={\mathbf{I}}_K.$$ (4.55)

In principal component analysis (PCA), the data set is modeled by a multivariate gaussian. By a PCA-like whitening transformation equation 4.52, we can use the approximation 4.55 with Laplace’s method, which requires only that the peak be close to the mean and the random variable $\tilde{X}$ does not need to be an exact gaussian distribution.

By theorem 3, we have

$$I(\tilde{X};R)\simeq I_G=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{G}(\tilde{x})}{2\pi e}\right)\right)\rangle }_{\tilde{x}}+H(\tilde{X}),$$ (4.56)

where

$$\mathbf{G}(\tilde{x})=\mathbf{J}(\tilde{x})+{\mathbf{I}}_K,$$ (4.57)

$$\mathbf{J}(\tilde{x})={\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \tilde{x})}{\partial \tilde{x}}\frac{\partial \text{ln}p(\mathbf{r}\mid \tilde{x})}{\partial {\tilde{x}}^T}\rangle }_{\mathbf{r}\mid \tilde{x}}$$ (4.58)

$$={\Sigma }^{1∕2}{\mathbf{U}}^T{\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{x})}{\partial \mathbf{x}}\frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{x})}{\partial {\mathbf{x}}^T}\rangle }_{\mathbf{r}\mid \mathbf{x}}\mathbf{U}{\Sigma }^{1∕2}$$ (4.59)

$$={\Sigma }^{1∕2}{\mathbf{U}}^T\mathbf{J}(\mathbf{x})\mathbf{U}{\Sigma }^{1∕2},$$ (4.60)

$$H(\tilde{X})=-{\langle \text{ln}p(\tilde{x})\rangle }_{\tilde{x}}=H(X)-\frac{1}{2}\text{ln}(\text{det}(\Sigma )).$$ (4.61)

Given a K × K orthogonal matrix $\mathbf{B}\in {\mathbb{R}}^{K\times K}$, we define

$$\mathbf{y}={\mathbf{B}}^T\tilde{x}.$$ (4.62)

Then it follows from equations 4.56 to 4.62 that

$$I({\rm Y};R)\simeq I_G=\frac{1}{2}{\langle \text{ln}\left(\text{det}\left(\frac{\mathbf{G}(\mathbf{y})}{2\pi e}\right)\right)\rangle }_{\mathbf{y}}+H({\rm Y}),$$ (4.63)

where

$$\mathbf{G}(\mathbf{y})=\mathbf{J}(\mathbf{y})+{\mathbf{I}}_K,$$ (4.64)

$$\mathbf{J}(\mathbf{y})={\mathbf{B}}^T\mathbf{J}(\tilde{x})\mathbf{B},$$ (4.65)

$$H({\rm Y})=H(\tilde{X}).$$ (4.66)

Suppose y is partitioned into two sets of components, $\mathbf{y}=({\mathbf{y}}_1^T,{\mathbf{y}}_2^T{)}^T$ and

$${\mathbf{y}}_1={(y_1,y_2,\dots ,y_{K_1})}^T,$$ (4.67)

$${\mathbf{y}}_2={(y_{K_1+1},y_{K_1+2},\dots ,y_K)}^T,$$ (4.68)

where K₁ + K₂ = K, K ≥ 2, K₁ ≥ 1 and K₂ ≥ 1. Let

$$\mathbf{G}(\mathbf{y})=\left(\begin{array}{cc}\hfill {\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1}\hfill & \hfill {\mathbf{J}}_{1,2}(\mathbf{y})\hfill \\ \hfill {\mathbf{J}}_{2,1}(\mathbf{y})\hfill & \hfill {\mathbf{J}}_{2,2}(\mathbf{y})+{\mathbf{I}}_{K_2}\hfill \end{array}\right),$$ (4.69)

where

$${\mathbf{J}}_{i,j}(\mathbf{y})={\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_i}\frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_j^T}\rangle }_{\mathbf{r}\mid \mathbf{y}},\forall i,j=1,2.$$ (4.70)

When K ⪢ 1, suppose we can find an orthogonal matrix B and K₁ that satisfy condition 4.38 in theorem 5 or condition 4.49—that is,

$$0\le {\langle \text{Tr}({\mathbf{B}}_{\mathbf{y}})\rangle }_{\mathbf{y}}⪡\gamma ,$$ (4.71)

$${\mathbf{B}}_{\mathbf{y}}={\mathbf{J}}_{2,2}(\mathbf{y})-{\mathbf{J}}_{2,1}(\mathbf{y}){({\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1})}^{-1}{\mathbf{J}}_{1,2}(\mathbf{y}),$$ (4.72)

$$\gamma ={\langle \text{ln}(\text{det}({\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1}))\rangle }_{\mathbf{y}}.$$ (4.73)

Here matrix B_y is positive-semidefinite because

$${\mathbf{J}}_{2,2}(\mathbf{y})-{\mathbf{J}}_{2,1}(\mathbf{y}){({\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1})}^{-1}{\mathbf{J}}_{1,2}(\mathbf{y})={\langle \rho (\mathbf{r}\mid \mathbf{y})\rho {(\mathbf{r}\mid \mathbf{y})}^T\rangle }_{\mathbf{r}\mid \mathbf{y}},$$ (4.74)

where

$$\rho (\mathbf{r}\mid \mathbf{y})=\frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_2}-{\mathbf{J}}_{2,1}(\mathbf{y}){({\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1})}^{-1}\left(\frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_1}+\mathbf{a}(\mathbf{r})\right)$$ (4.75)

and a (r) is a K₁-dimensional random vector that satisfies

$${\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_2}\mathbf{a}{(\mathbf{r})}^T\rangle }_{\mathbf{r}\mid \mathbf{y}}={\langle \frac{\partial \text{ln}p(\mathbf{r}\mid \mathbf{y})}{\partial {\mathbf{y}}_2}\rangle }_{\mathbf{r}\mid \mathbf{y}}{\langle \mathbf{a}{(\mathbf{r})}^T\rangle }_{\mathbf{r}\mid \mathbf{y}}=0,$$ (4.76)

$${\langle \mathbf{a}(\mathbf{r})\mathbf{a}{(\mathbf{r})}^T\rangle }_{\mathbf{r}\mid \mathbf{y}}={\mathbf{I}}_{K_1}.$$ (4.77)

Assuming that J_1,1 (y) is positive-definite, $\Vert {\mathbf{J}}_{1,1}^{-1}(\mathbf{y})\Vert =O(N^{-1})$ and ∥J_1,2(y)∥ = ∥J_2,1(y)∥ = O (N), we have

$${({\mathbf{J}}_{1,1}(\mathbf{y})+{\mathbf{I}}_{K_1})}^{-1}={\mathbf{J}}_{1,1}^{-1}(\mathbf{y})-{\mathbf{J}}_{1,1}^{-2}(\mathbf{y})+O\left({\mathbf{J}}_{1,1}^{-3}(\mathbf{y})\right)$$ (4.78)

and

$$\begin{array}{c}\text{Tr}({\mathbf{C}}_{\mathbf{x}})=\mathrm{Tr}\left({\mathbf{J}}_{2,2}(\mathbf{y})-{\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-1}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y})\right)\hfill \\ +\mathrm{Tr}\left({\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-2}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y})\right)+O(N^{-1}).\hfill \end{array}$$ (4.79)

Hence, if

$$\mid \text{Tr}\left({\mathbf{J}}_{2,2}(\mathbf{y})-{\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-1}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y})\right)\mid ⪡\gamma ,$$ (4.80)

$$\mid \mathrm{Tr}\left({\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-2}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y})\right)\mid \ll \gamma ,$$ (4.81)

then equation 4.71 holds. Notice that the matrix $({\mathbf{J}}_{2,2}(\mathbf{y})-{\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-1}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y}))$ is positive-semidefinite, which is similar to equation 4.74 and $0\le \text{Tr}({\mathbf{J}}_{2,1}(\mathbf{y}){\mathbf{J}}_{1,1}^{-1}(\mathbf{y}){\mathbf{J}}_{1,2}(\mathbf{y}))\le \text{Tr}({\mathbf{J}}_{2,2}(\mathbf{y}))$. Hence, if

$$\mathrm{Tr}({\mathbf{J}}_{2,2}(\mathbf{y}))\ll \gamma ,$$ (4.82)

then equations 4.80 and 4.81 hold so does equation 4.71.

5. Optimization of Information Transfer in Neural Population Coding –

5.1. Population Density Distribution of Parameters in Neural Populations.

If p(r∣x) is conditional independent, we can write

$$p(\mathbf{r}\mid \mathbf{x})=\prod _{n=1}^{N}p(r_n\mid \mathbf{x};{\theta }_n),$$ (5.1)

where ${\theta }_n\in {\mathbb{R}}^{\tilde{K}}$ denotes a $\tilde{K}$-dimensional vector for parameters of the nth neuron, and p(r_n∣x; θ_n) is the conditional p.d.f. of the output r_n given x. With the definition in equation 2.13, we have following proposition.

Proposition 1. If p(r∣x) is conditional independent as in equation 5.1, we have

$$\mathit{J}(\mathit{x})=N{\int }_{\mathrm{\Theta }}p(\theta )\mathit{S}(\mathit{x};\theta )d\theta ,$$ (5.2)

where

$$\mathit{S}(\mathit{x};\theta )={\int }_{\Re }p(r\mid \mathit{x};\theta )\frac{\partial \mathit{ln}p(r\mid \mathit{x};\theta )}{\partial \mathit{x}}\frac{\partial \mathit{ln}p(r\mid \mathit{x};\theta )}{\partial {\mathit{x}}^T}dr,$$ (5.3)

$r\in \Re \subseteq \mathbb{R}$, $\theta \in \mathrm{\Theta }\subseteq {\mathbb{R}}^{\tilde{K}}$, and p(θ) is the population density function of parameter vector θ:

$$p(\theta )=\frac{1}{N}\sum _{n=1}^N\delta (\theta -{\theta }_n),$$ (5.4)

with δ (·) being the Dirac delta function.

Proof.

$$\begin{array}{cc}\hfill \mathbf{J}(\mathbf{x})& ={\int }_{\mathcal{R}}p(\mathbf{r}\mid \mathbf{x})\frac{\partial \ln p(\mathbf{r}\mid \mathbf{x})}{\partial \mathbf{x}}\frac{\partial \ln p(\mathbf{r}\mid \mathbf{x})}{\partial {\mathbf{x}}^T}d\mathbf{r}\hfill \\ \hfill & =\sum _{n=1}^N{\int }_{\Re }p(r_n\mid \mathbf{x};{\theta }_n)\frac{\partial \ln p(r_n\mid \mathbf{x};{\theta }_n)}{\partial \mathbf{x}}\frac{\partial \ln p(r_n\mid \mathbf{x};{\theta }_n)}{\partial {\mathbf{x}}^T}d{r}_n\hfill \\ \hfill & ={\int }_{\mathrm{\Theta }}\sum _{n=1}^N\delta (\theta -{\theta }_n)\left({\int }_{\Re }p(r\mid \mathbf{x};\theta )\frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial {\mathbf{x}}^T}dr\right)d\theta \hfill \\ \hfill & =N{\int }_{\mathrm{\Theta }}p(\theta )\mathbf{S}(\mathbf{x};\theta )d\theta .\hfill \end{array}$$ (5.5)

□

Remark 8. Proposition 1 shows that J(x) can be regarded as a function of the population density of parameters, p(θ). If the p.d.f. of the input p(x) is given, we can find an appropriate p(θ) to maximize MI I.

For neuron model with Poisson spikes, we have

$$p(\mathbf{r}\mid \mathbf{x})=\prod _{n=1}^{N}p(r_n\mid \mathbf{x};{\theta }_n),$$ (5.6)

$$p(r_n\mid \mathbf{x};{\theta }_n)=\frac{f{(\mathbf{x};{\theta }_n)}^{r_n}}{r_n!}\exp (-f(\mathbf{x};{\theta }_n)),$$ (5.7)

where f (x; θ_n) is the tuning curve of the nth neuron, n = 1, 2, …, N. Now we have

$$\begin{array}{cc}\hfill \mathbf{S}(\mathbf{x};\theta )& ={\int }_{\Re }p(r\mid \mathbf{x};\theta )\frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial {\mathbf{x}}^T}dr\hfill \\ \hfill & =\frac{1}{f(\mathbf{x};\theta )}\frac{\partial f(\mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial f(\mathbf{x};\theta )}{\partial {\mathbf{x}}^T}\hfill \\ \hfill & =\frac{\partial g(\mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial g(\mathbf{x};\theta )}{\partial {\mathbf{x}}^T},\hfill \end{array}$$ (5.8)

$$g(\mathbf{x};\theta )=2\sqrt{f(\mathbf{x};\theta )}.$$ (5.9)

Similarly, for a neuron response model with gaussian noise, we have

$$p(\mathbf{r}\mid \mathbf{x})=\prod _{n=1}^{N}p(r_n\mid \mathbf{x};{\theta }_n),$$ (5.10)

$$p(r_n\mid \mathbf{x};{\theta }_n)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{(r_n-f(\mathbf{x};{\theta }_n))}^2}{2{\sigma }^2}\right),$$ (5.11)

where σ is a constant standard deviation. Now we get

$$\mathbf{S}(\mathbf{x};\theta )=\frac{1}{{\sigma }^2}\frac{\partial f(\mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial f(\mathbf{x};\theta )}{\partial {\mathbf{x}}^T}.$$ (5.12)

5.2. Optimal Population Distribution for Neural Population Coding.

Suppose p(x) and p(r∣x) fulfill conditions C1 and C2 and equation 5.1. Following the discussion in section 2.2, we define the following objective for maximizing MI I,

$$\mathrm{maximize}{I}_G[p(\theta )]=\frac{1}{2}{\langle \ln \left(\det \left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X),$$ (5.13)

or, equivalently,

$$\mathrm{minimize}{Q}_G[p(\theta )]=-\frac{1}{2}{\langle \ln (\det (\mathbf{G}(\mathbf{x})))\rangle }_{\mathbf{x}},$$ (5.14)

where

$$\mathbf{G}(\mathbf{x})=\mathbf{J}(\mathbf{x})+\mathbf{P}(\mathbf{x}),$$ (5.15)

$$\mathbf{J}(\mathbf{x})=N{\int }_{\mathrm{\Theta }}p(\theta )\mathbf{S}(\mathbf{x};\theta )d\theta ,$$ (5.16)

$$\mathbf{S}(\mathbf{x};\theta )={\langle \frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial \mathbf{x}}\frac{\partial \ln p(r\mid \mathbf{x};\theta )}{\partial {\mathbf{x}}^T}\rangle }_{r\mid \mathbf{x};\theta }.$$ (5.17)

Here P (x) is given in equation 2.15, and it generally can be substituted by P₊ (see equation 2.78).

When ς₁ ≈ 0 (see equation 2.64), the object function, equation 5.13, can be reduced to

$$\mathrm{maximize}{I}_F[p(\theta )]=\frac{1}{2}{\langle \ln \left(\det \left(\frac{\mathbf{J}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X),$$ (5.18)

or, equivalently,

$$\mathrm{minimize}{Q}_F[p(\theta )]=-\frac{1}{2}{\langle \ln (\det (\mathbf{J}(\mathbf{x})))\rangle }_{\mathbf{x}}.$$ (5.19)

The constraint condition for p(θ) is given by

$$\text{subject to}{\int }_{\mathrm{\Theta }}p(\theta )d\theta =1,p(\theta )\ge 0.$$ (5.20)

However, without further constraints on the neural populations, especially a limit on the peak firing rate, the capacity of the system may grow indefinitely: I(X; R) → ∞. The most common limitation on neural populations is the energy or power constraint. For neuron models with Poisson noise or gaussian noise, a useful constraint is a limitation on the peak power,

$$\mid f(\mathbf{x};{\theta }_n)\mid \le E_{\max },\forall \mathbf{x}\in \mathcal{X}\text{and}\forall n=1,2,\dots ,N,$$ (5.21)

where E_max > 0 is the peak power. Under this constraint, maximizing I_G[p(θ)] or I_F[p(θ)] for independent neurons will result in max_x ∣ f (x; θ_n)∣ = E_max for ∀n = 1,2, …, N.

Another constraint is a limitation on average power. For Poisson neurons given in equation 5.7,

$$\frac{1}{N}\sum _{n=1}^N{\langle {\langle r_{n}p(r_n\mid \mathbf{x};{\theta }_n)\rangle }_{r_n\mid \mathbf{x}}\rangle }_{\mathbf{x}}\le E_{\mathrm{avg}},$$ (5.22)

which can also be written as

$${\langle {\langle f(\mathbf{x};\theta )\rangle }_{\mathbf{x}}\rangle }_{\theta }\le E_{\mathrm{avg}},$$ (5.23)

and for gaussian noise neurons given in equation 5.11,

$${\langle {\langle f{(\mathbf{x};\theta )}^2\rangle }_{\mathbf{x}}\rangle }_{\theta }\le E_{\mathrm{avg}},$$ (5.24)

where E_avg > 0 is the maximum average energy cost.

In equation 5.15, we can approximate the continuous integral by a discrete summation for numerical computation,

$$\mathbf{J}(\mathbf{x})=N\sum _{k=1}^{K_1}{\alpha }_k\mathbf{S}(\mathbf{x};{\theta }_k),$$ (5.25)

where the positive integer K₁ ≤ N denotes the number of subclasses in the neural population and

$$\sum _{k=1}^{K_1}{\alpha }_k=1,{\alpha }_k>0,\forall k=1,2,\dots ,K_1.$$ (5.26)

If we do not know the specific form of p(x) but have M samples, x₁, x₂, …, x_M, which are i.i.d. samples drawn from the distribution p(x), then we can approximate the integral in equation 5.13 by the sample average:

$${\langle \ln (\det (\mathbf{G}(\mathbf{x})))\rangle }_{\mathbf{x}}\simeq \frac{1}{M}\sum _{m=1}^M\ln (\det (\mathbf{G}({\mathbf{x}}_m))).$$ (5.27)

Optimizing the objective 5.13 or 5.18 is a convex optimization problem (see the appendix for a proof).

Proposition 2. The functions I_G[p(θ)] and I_F [p(θ)] are concave about p(θ).

Remark 9. For a low-dimensional input x, we may use equation 5.18 or 5.19 as the objective. Since I_G[p(θ)] and I_F[p(θ)] are concave functions of p(θ), we can directly use efficient numerical methods to get the optimal solution for small K. However, for high-dimensional input x, we need to use other methods (e.g., Huang & Zhang, 2017).

5.3. Necessary and Sufficient Conditions for Optimal Population Distribution.

Applying the method of Lagrange multipliers for the optimization problems 5.13 and 5.20 yields

$$L[p(\theta )]=I_G[p(\theta )]-{\lambda }_1\left({\int }_{\mathrm{\Theta }}p(\theta )d\theta -1\right)+{\int }_{\mathrm{\Theta }}{\lambda }_2(\theta )p(\theta )d\theta ,$$ (5.28)

where λ₁ is a constant and λ₂(θ) is a function of θ. According to Karush-Kuhn-Tucker (KKT) conditions (Boyd & Vandenberghe, 2004), we have

$${\lambda }_2(\theta )p(\theta )=0,{\lambda }_2(\theta )\ge 0,$$ (5.29)

and the necessary condition for optimal population density,

$$\frac{\partial L[p(\theta )]}{\partial p(\theta )}=\frac{1}{2}{\langle \mathrm{Tr}\left(N\mathbf{G}{(\mathbf{x})}^{-1}\mathbf{S}(\mathbf{x};\theta )\right)\rangle }_{\mathbf{x}}-{\lambda }_1+{\lambda }_2(\theta )=0.$$ (5.30)

It follows from equations 5.29 and 5.30 that

$$\frac{1}{2}{\langle \mathrm{Tr}\left(N\mathbf{G}{(\mathbf{x})}^{-1}\mathbf{S}(\mathbf{x};\theta )\right)\rangle }_{\mathbf{x}}={\lambda }_1,p(\theta )\ne 0,$$ (5.31)

$$\frac{1}{2}{\langle \mathrm{Tr}\left(N\mathbf{G}{(\mathbf{x})}^{-1}\mathbf{S}(\mathbf{x};\theta )\right)\rangle }_{\mathbf{x}}={\lambda }_1-{\lambda }_2(\theta ),p(\theta )=0.$$ (5.32)

Since I_G[p(θ)] is a concave function of p(θ), equations 5.31 and 5.32 are the necessary and sufficient conditions for the optimization problems 5.13 and 5.20.

5.4. Channel Capacity for Neural Population Coding.

If p(x) is unknown, then by Jensen’s inequality, we have

$$\begin{array}{cc}\hfill I\simeq I_G[p(\mathbf{x})]& ={\int }_{\mathcal{X}}p(\mathbf{x})\ln \left(p{(\mathbf{x})}^{-1}\det {\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)}^{1∕2}\right)d\mathbf{x}\hfill \\ \hfill & \le \ln {\int }_{\mathcal{X}}\det {\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)}^{1∕2}d\mathbf{x},\hfill \end{array}$$ (5.33)

and the equality holds if and only if p(x)⁻¹ det (G(x))^1/2 is a constant. Thus,

$$I_G[p^{\ast }(\mathbf{x})]=\underset{p(\mathbf{x})}{\max }(I_G[p(\mathbf{x})])=\ln {\int }_{\mathcal{X}}\det {\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)}^{1∕2}d\mathbf{x},$$ (5.34)

$$p^{\ast }(\mathbf{x})=\frac{\det {(\mathbf{G}(\mathbf{x}))}^{1∕2}}{{\int }_X\det {(\mathbf{G}(\widehat{\mathbf{x}}))}^{1∕2}d\widehat{\mathbf{x}}},$$ (5.35)

assuming ${\int }_{\mathcal{X}}\text{det}(\mathbf{G}(\widehat{\mathbf{x}}){)}^{1∕2}d\widehat{\mathbf{x}}<\infty$.

Let us consider a specific example. Suppose J(x) = J₀ is a constant matrix; then it follows from equation 2.12 that

$$I_G=\frac{1}{2}{\langle \ln \left(\det \left(\frac{{\mathbf{J}}_0+\mathbf{P}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+H(X).$$ (5.36)

According to the maximum entropy probability distribution, we know that maximizing H(X) results in a uniformly distributed p(x). Hence we have G(x) = J₀, and p*(x) coincides with the uniform distribution (see equation 5.35). In this case, the maximum I_G[p*(x)] can be regarded as the channel capacity for this neural population.

If we consider a constraint on random variables X and assume that the covariance matrix of X is ∑₀ and satisfies

$${\Sigma }_0^{-1}=\mathbf{P}(\mathbf{x}),$$ (5.37)

then it follows from the maximum entropy probability distribution that

$$H(X)\le \frac{1}{2}(\det (2\pi e{\Sigma }_0)),$$ (5.38)

and the equality holds if and only if the p.d.f. of the input is a normal distribution: $p(\mathbf{x})=\mathcal{N}(\mu ,{\Sigma }_0)$. Hence,

$$\begin{array}{cc}\hfill I_G& =\frac{1}{2}\ln \left(\det \left(\frac{{\mathbf{J}}_0+{\Sigma }_0^{-1}}{2\pi e}\right)\right)+H(X)\hfill \\ \hfill & \le \frac{1}{2}\ln (\det ({\Sigma }_0{\mathbf{J}}_0+{\mathbf{I}}_K))=I_G[p^{\ast }(\mathbf{x})],\hfill \end{array}$$ (5.39)

where I_G[p*(x)] is the channel capacity of neural population. Here the equality holds if and only if $p^{\ast }(\mathbf{x})=\mathcal{N}(\mu ,{\Sigma }_0)$, which is consistent with equation 5.37.

Furthermore, if ς₁ ≈ 0 (see equation 2.64), we have

$$I\simeq I_G[p(\mathbf{x})]\simeq I_F[p(\mathbf{x})]={\int }_{\mathcal{X}}p(\mathbf{x})\ln \left(p{(\mathbf{x})}^{-1}\det {\left(\frac{\mathbf{J}(\mathbf{x})}{2\pi e}\right)}^{1∕2}\right)d\mathbf{x}.$$ (5.40)

Similarly, we also get

$$I_F[p^{\ast }(\mathbf{x})]=\underset{p(\mathbf{x})}{\max }(I_F[p(\mathbf{x})])=\ln {\int }_{\mathcal{X}}\det {\left(\frac{\mathbf{J}(\mathbf{x})}{2\pi e}\right)}^{1∕2}d\mathbf{x},$$ (5.41)

$$p^{\ast }(\mathbf{x})=\frac{\det {(\mathbf{J}(\mathbf{x}))}^{1∕2}}{{\int }_{\mathcal{X}}\det {(\mathbf{J}(\widehat{\mathbf{x}}))}^{1∕2}d\widehat{\mathbf{x}}},$$ (5.42)

assuming ${\int }_{\mathcal{X}}\text{det}(\mathbf{J}(\widehat{\mathbf{x}}){)}^{1∕2}d\widehat{\mathbf{x}}<\infty$. Here I_F[p*(x)] is the channel capacity of the neural population. The distribution p*(x) coincides with the Jeffrey’s prior in Bayesian probability (Jeffreys, 1961). In this case, if we suppose the covariance matrix of X is ∑₀, then similar to equations 5.38 and 5.39, we can get the channel capacity

$$I_F[p^{\ast }(\mathbf{x})]=\frac{1}{2}\ln (\det ({\Sigma }_0{\mathbf{J}}_0))$$ (5.43)

with $p^{\ast }(\mathbf{x})=\mathcal{N}(\mu ,{\Sigma }_0)$.

For another example, consider the Poisson neuron model given in equation 5.7 and suppose the input x is one dimension, K = 1. It follows from equations 5.8 and 5.42 that

$$p^{\ast }(x)=\frac{{\left({\int }_{\mathrm{\Theta }}p(\theta ){\left(\frac{\partial g(x;\theta )}{\partial x}\right)}^{2}d\theta \right)}^{1∕2}}{{\int }_{\mathcal{X}}{\left({\int }_{\mathrm{\Theta }}p(\theta ){\left(\frac{\partial g(\widehat{x};\theta )}{\partial \widehat{x}}\right)}^{2}d\theta \right)}^{1∕2}d\widehat{x}}.$$ (5.44)

If p(θ) = δ(θ – θ₀), equation 5.44 becomes

$$p^{\ast }(x)=\frac{\mid \frac{\partial g(x;{\theta }_0)}{\partial x}\mid }{{\int }_{\mathcal{X}}\mid \frac{\partial g(\widehat{x};{\theta }_0)}{\partial \widehat{x}}\mid d\widehat{x}}.$$ (5.45)

Atick and Redlich (1990) presented a redundancy measure to approximate Barlow’s optimality principle:

$$\mathcal{R}=1-\frac{I(X;R)}{C(R)},$$ (5.46)

where C(R) is the channel capacity. Here for neural population coding, we have C(R) ≃ I_G[p*(x)] and I(X; R) ≃ I_G (or C(R) – I_F[p*(x)] and I(X; R) ≃ I_F). Hence, we can minimize $\mathcal{R}$ by choosing an appropriate J(x) to maximize I_G (or I_F) and simultaneously satisfy equation 5.35 (or 5.42) (see Huang & Zhang, 2017, for further details).

6. Discussion

In this article, we have derived several information-theoretic bounds and approximations for effective approximation of MI in the context of neural population coding for large but finite population size. We have found some regularity conditions under which the asymptotic bounds and approximations hold. Generally these regularity conditions are easy to meet. Special examples that satisfy these conditions include the cases when the likelihood function p(r∣x) for the neural population responses is conditionally independent or has correlated noises with a multivariate gaussian distribution. Under the general regularity conditions, we have derived several asymptotic bounds and approximations of MI for a neural population and found some relationships among different approximations.

How to choose among these different asymptotic approximations of MI in a neural population with finite size N? For a flat prior distribution p(x), we have I_G ≃ I_F; that is, the two approximations I_G and I_F are about equally valid. For a sharply peaked prior distribution p(x), I_G is generally a better approximation to MI I than I_F. Under suitable conditions (e.g., cases C1 and C2) for low-dimensional inputs, I_G and I_F are good approximations of MI I not only for large N but also for small N. For high-dimensional inputs, the FI matrix J(x) (see equation 2.11) or matrix P⁻¹(x) (see equation 2.15) often becomes degenerate, which causes a large error between I_F and MI I. Hence, in this situation, I_G is a better approximation to MI I than I_F. For more convenient computation of the approximation, we have also introduced the approximation formula I_G+ which may substitute for I_G as a proxy of MI I. For some special cases (see corollary 1), I_G and I_G+ are strictly equal to the true MI I. Our simulation results for the one-dimensional case show that the approximations I_G, I_G+, and I_F are all highly precise compared with the true MI I, even for small N (see Figure 1).

These approximation formulas satisfy additional constraints. By the Cramér-Rao lower bound, we know that I_F is related to the covariance matrix of an unbiased estimator (see equation 3.3). By van Trees’ Bayesian Cramér-Rao bound, we get a link between I_G+ and the covariance matrix of a biased estimator (see equation 3.9). From the point of view of neural population decoding and Bayesian inference, there is a connection between MI (or I_G) and MAP (see equation 3.17).

For more efficient calculation of the approximation I_G (or I_G+ ) for high-dimensional inputs, we propose to apply an invertible transformation on the input variable so as to make the new variable closer to a normal distribution (see section 4.1). Another useful technique is dimensionality reduction, which effectively approximates MI by further reducing the computational complexity for high-dimensional inputs. We found that I_F could lead to huge errors as a proxy of the true MI I for high-dimensional inputs even when I_G and I_G+ are strictly equal to the true MI I.

These approximation formulas are potentially useful for optimization problems of information transfer in neural population coding. We have proven that optimizing the population density distribution of parameters p(θ) is a convex optimization problem and have found a set of necessary and sufficient conditions. The approximation formulas are also useful for discussion of the channel capacity of neural population coding (see section 5.4).

Information theory is a powerful tool for neuroscience and other disciplines, including diverse fields such as physics, information and communication technology, machine learning, computer vision, and bioinformatics. Finding effective approximation methods for computing MI is a key for many practical applications of information theory. Generally the FI matrix is easier to evaluate or approximate than MI. This is because calculation of MI involves averaging over both the input variable x and the output variable r (see equation 2.1), and typically p(r) also needs to be calculated from p(r∣x) by another average over x (see equation 2.2). By contrast, the FI matrix J(x) involves averaging over r only (see equation 2.13). Furthermore, it is often easier to find analytical forms of FI for specific models such as a population of tuning curves with Poisson spike statistics. Taking into account the computational efficiency, for practical applications we suggest using I_G or I_G+ as a proxy of the true MI I for most cases. These approximations could be very useful even when we do not need to know the exact value of MI. For example, for some optimization and learning problems, we only need to know how MI is affected by the conditional p.d.f. or likelihood function p(r∣x). In such situations, we may easily solve for the optimal parameters using the approximation formulas (Huang & Zhang, 2017; Huang, Huang, & Zhang, 2017). Further discussions of the applications will be given in separate publications.

Appendix: The Proofs

We consider a Taylor expanding of $L(\mathbf{r}\mid \widehat{\mathbf{x}})$ around x. If $L(\mathbf{r}\mid \widehat{\mathbf{x}})$ is twice differentiable for $\forall \widehat{\mathbf{x}}\in {\mathcal{X}}_{\omega }(\mathbf{x})$, then by condition C1 we get

$$\begin{array}{cc}\hfill & L(\mathbf{r}\mid \widehat{\mathbf{x}})-L(\mathbf{r}\mid \mathbf{x})\hfill \\ \hfill & =(\widehat{\mathbf{x}}-\mathbf{x}{)}^T{L}^{\prime }(\mathbf{r}\mid \mathbf{x})+\frac{1}{2}(\widehat{\mathbf{x}}-\mathbf{x}{)}^T{L}^{″}(\mathbf{r}\mid \breve{\mathbf{x}})(\widehat{\mathbf{x}}-\mathbf{x})\hfill \\ \hfill & ={\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}{\mathbf{y}}^T\mathbf{y}+\frac{1}{2}{\mathbf{y}}^T\mathbf{B}\mathbf{y},\hfill \end{array}$$ (A.1)

where

$$\mathbf{y}={\mathbf{G}}^{1∕2}(\mathbf{x})(\widehat{\mathbf{x}}-\mathbf{x}),$$ (A.2)

$$\tilde{\mathbf{v}}=\mathbf{v}+{\mathbf{v}}_1,\mathbf{v}={\mathbf{G}}^{-1∕2}(\mathbf{x})l^{\prime }(\mathbf{r}\mid \mathbf{x}),{\mathbf{v}}_1={\mathbf{G}}^{-1∕2}(\mathbf{x})q^{\prime }(\mathbf{x}),$$ (A.3)

$$\breve{\mathbf{x}}=\mathbf{x}+t(\widehat{\mathbf{x}}-\mathbf{x})\in {\mathcal{X}}_{\omega }(\mathbf{x}),t\in (0,1),$$ (A.4)

$$\{\begin{array}{cc}\mathbf{B}\hfill & ={\mathbf{G}}^{-1∕2}(\mathbf{x}){\mathbf{CG}}^{-1∕2}(\mathbf{x})={\mathbf{B}}_0+{\mathbf{B}}_1+{\mathbf{B}}_2,\hfill \\ \mathbf{C}\hfill & ={\mathbf{C}}_0+{\mathbf{C}}_1+{\mathbf{C}}_2,\hfill \end{array}\phantom{\}}$$ (A.5)

and

$$\{\begin{array}{cc}{\mathbf{B}}_0\hfill & ={\mathbf{G}}^{-1∕2}(\mathbf{x}){\mathbf{C}}_0{\mathbf{G}}^{-1∕2}(\mathbf{x}),\hfill \\ {\mathbf{B}}_1\hfill & ={\mathbf{G}}^{-1∕2}(\mathbf{x}){\mathbf{C}}_1{\mathbf{G}}^{-1∕2}(\mathbf{x}),\hfill \\ {\mathbf{B}}_2\hfill & ={\mathbf{G}}^{-1∕2}(\mathbf{x}){\mathbf{C}}_2{\mathbf{G}}^{-1∕2}(\mathbf{x}),\hfill \\ {\mathbf{C}}_0\hfill & =l^{″}(\mathbf{r}\mid \mathbf{x})-\langle l^{″}(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}},\hfill \\ {\mathbf{C}}_1\hfill & =l^{″}(\mathbf{r}\mid \breve{\mathbf{x}})-l^{″}(\mathbf{r}\mid \mathbf{x}),\hfill \\ {\mathbf{C}}_2\hfill & =q^{″}(\breve{\mathbf{x}})-q^{″}(\mathbf{x}).\hfill \end{array}\phantom{\}}$$ (A.6)

By condition C1, we know that the matrix B₁ + B₂ is continuous and symmetric for $\check{\mathbf{x}}\in {\mathcal{X}}_{\omega }$ and ∥B₁ + B₂∥ = O(1). By the definition of continuous functions, we can prove the following: for any ϵ ∈ (0, 1), there is an ε ∈ (0, ω) such that for all $\mathcal{Y}\in {\mathcal{Y}}_{\epsilon }$,

$$-ϵ{\mathbf{I}}_K\le {\mathbf{B}}_1+{\mathbf{B}}_2\le ϵ{\mathbf{I}}_K,$$ (A.7)

where

$${\mathcal{Y}}_{\epsilon }=\left\{\mathbf{y}\in {\mathbb{R}}^K:\Vert \mathbf{y}\Vert <\epsilon \sqrt{N}\right\}.$$ (A.8)

Hence,

$$\mid {\mathbf{y}}^T({\mathbf{B}}_1+{\mathbf{B}}_2)\mathbf{y}\mid <ϵ{\Vert \mathbf{y}\Vert }^2.$$ (A.9)

Here $\check{\mathbf{x}}=\mathbf{x}+t{\mathbf{G}}^{-1∕2}(\mathbf{x})\mathbf{y}$, ε is a function of r, ε = ε (r) = O (1), and

$${\mathcal{Y}}_{\epsilon }\subseteq {\mathcal{Y}}_{\omega }=\left\{\mathbf{y}\in {\mathbb{R}}^K:\Vert \mathbf{y}\Vert <\omega \sqrt{N}\right\}.$$ (A.10)

We define the sets

$$\{\begin{array}{cc}{\bar{\mathcal{Y}}}_{\epsilon }\hfill & =\left\{\mathbf{y}\in {\mathbb{R}}^K:\Vert \mathbf{y}\Vert \ge \epsilon \sqrt{N}\right\},\hfill \\ {\mathcal{Z}}_{\widehat{\epsilon }}\hfill & =\left\{\mathbf{z}\in {\mathbb{R}}^K:\mid z_k\mid <\widehat{\epsilon }\sqrt{N∕K},\forall k=1,2,\dots ,K\right\},\hfill \\ {\bar{\mathcal{Z}}}_{\widehat{\epsilon }}\hfill & =\left\{\mathbf{z}\in {\mathbb{R}}^K:\mid z_k\mid \ge \widehat{\epsilon }\sqrt{N∕K},\forall k=1,2,\dots ,K\right\},\hfill \\ {\tilde{\mathcal{Z}}}_{\epsilon }\hfill & =\left\{\mathbf{z}\in {\mathbb{R}}^K:\Vert \mathbf{z}+\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}\Vert <\epsilon \sqrt{N}\right\},\hfill \end{array}\phantom{\}}$$ (A.11)

where

$$\widehat{\epsilon }=\epsilon ∕2,$$ (A.12)

1_(·) denotes an indicator random variable,

$$1_{{\mathcal{R}}_{\widehat{\epsilon }}}=\{\begin{array}{cc}\hfill & 1,\mathbf{r}\in {\mathcal{R}}_{\widehat{\epsilon }}(\mathbf{x})\hfill \\ \hfill & 0,\mathbf{r}\notin {\mathcal{R}}_{\widehat{\epsilon }}(\mathbf{x})\hfill \end{array}\phantom{\}},1_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}=\{\begin{array}{cc}\hfill & 1,\mathbf{r}\in {\bar{\mathcal{R}}}_{\widehat{\epsilon }}(\mathbf{x})\hfill \\ \hfill & 0,\mathbf{r}\notin {\bar{\mathcal{R}}}_{\widehat{\epsilon }}(\mathbf{x})\hfill \end{array}\phantom{\}},$$ (A.13)

and

$$\{\begin{array}{cc}\hfill & {\mathcal{R}}_{\widehat{\epsilon }}(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:\Vert \tilde{\mathbf{v}}\Vert <\widehat{\epsilon }\sqrt{N}\right\},\hfill \\ \hfill & {\bar{\mathcal{R}}}_{\widehat{\epsilon }}(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:\Vert \tilde{\mathbf{v}}\Vert \ge \widehat{\epsilon }\sqrt{N}\right\}.\hfill \end{array}\phantom{\}}$$ (A.14)

For all $\mathbf{z}\in {\mathcal{Z}}_{\widehat{\epsilon }}$, we have ${\Vert \mathbf{z}+\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}\Vert }_2\le \Vert \mathbf{z}{\Vert }_2+{\Vert \mathbf{v}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}\Vert }_2<\epsilon \sqrt{N};$; then

$${\mathcal{Z}}_{\widehat{\epsilon }}\subseteq {\tilde{\mathcal{Z}}}_{\epsilon }.$$ (A.15)

It follows from equations A.3 and A.6 that

$$\langle \mathbf{v}{\rangle }_{\mathbf{r}\mid \mathbf{x}}=0,\langle {\mathbf{B}}_0{\rangle }_{\mathbf{r}\mid \mathbf{x}}=0$$ (A.16)

and

$$\begin{array}{cc}\hfill {\langle \langle {\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}& ={\langle \langle L^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{\mathbf{G}}^{-1}(\mathbf{x})L^{\prime }(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle \text{Tr}\left(\langle L^{\prime }(\mathbf{r}\mid \mathbf{x})L^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{\rangle }_{\mathbf{r}\mid \mathbf{x}}{\mathbf{G}}^{-1}(\mathbf{x})\right)\rangle }_{\mathbf{x}}\hfill \\ \hfill & =K+\zeta \hfill \\ \hfill & =K+O(N^{-1}),\hfill \end{array}$$ (A.17)

and it follows from condition C1 that

$$\begin{array}{cc}\hfill \zeta & ={\langle \text{Tr}\left(\frac{1}{p(\mathbf{x})}\frac{{\partial }^{2}p(\mathbf{x})}{\partial \mathbf{x}\partial {\mathbf{x}}^T}{\mathbf{G}}^{-1}(\mathbf{x})\right)\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle \text{Tr}\left(\left(q^{\prime }(\mathbf{x}{)}^T{q}^{\prime }(\mathbf{x})+q^{″}(\mathbf{x})\right){\mathbf{G}}^{-1}(\mathbf{x})\right)\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle N^{-1}\left(\Vert q^{\prime }(\mathbf{x}{)}^T{q}^{\prime }(\mathbf{x})\Vert +\Vert q^{″}(\mathbf{x})\Vert \right)\Vert N{\mathbf{G}}^{-1}(\mathbf{x})\Vert \rangle }_{\mathbf{x}}\hfill \\ \hfill & =O(N^{-1}).\hfill \end{array}$$ (A.18)

Combining conditions C1 and C2 and equations A.3, A.4, and A.6, we find

$$\{\begin{array}{cc}\hfill & \langle \Vert {\mathbf{B}}_0{\Vert }^{2m}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle \langle \Vert N^{-1}{\mathbf{C}}_0{\Vert }^{2m}\Vert N{\mathbf{G}}^{-1}(\mathbf{x}){\Vert }^{2m}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}=O(N^{-1}),\hfill \\ \hfill & \langle \Vert {\mathbf{B}}_0{\Vert }^{2m+1}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle \Vert N{\mathbf{G}}^{-1}(\mathbf{x}){\Vert }^{2m+1}\langle \Vert N^{-1}{\mathbf{C}}_0{\Vert }^2{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\langle \Vert N^{-1}{\mathbf{C}}_0{\Vert }^{4m}{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\rangle }_{\mathbf{x}}\hfill \\ \hfill & =O(N^{-1}),\hfill \\ \hfill & \langle \Vert \mathbf{v}{\Vert }^{2m_0}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle \mid N^{-1}{l}^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{l}^{\prime }(\mathbf{r}\mid \mathbf{x}){\mid }^{m_0}\rangle }_{\mathbf{r}\mid \mathbf{x}}\Vert N{\mathbf{G}}^{-1}(\mathbf{x}){\Vert }^{m_0}=O(1),\hfill \\ \hfill & \Vert {\mathbf{v}}_1{\Vert }^{2m_0}\le {\mid N^{-1}{q}^{\prime }(\mathbf{x}{)}^T{q}^{\prime }(\mathbf{x})\mid }^{m_0}\Vert N{\mathbf{G}}^{-1}(\mathbf{x}){\Vert }^{m_0}=O(N^{-m_0}),\hfill \end{array}\phantom{\}}$$ (A.19)

together with the power mean inequality,

$$\begin{array}{cc}\hfill {\langle {\left({\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}\right)}^{m_0}\rangle }_{\mathbf{r}\mid \mathbf{x}}& \le {\langle (\Vert \mathbf{v}\Vert +\Vert {\mathbf{v}}_1\Vert {)}^{2m_0}\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le 2^{2m_0-1}\langle \Vert \mathbf{v}{\Vert }^{2m_0}+\Vert {\mathbf{v}}_1{\Vert }^{2m_0}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & =O(1),\hfill \end{array}$$ (A.20)

where $m\in \mathbb{N}$, m₀ ∈ {1, 2}. Notice that ∣G⁻¹ (x)∥ = O (N⁻¹). Here we note that for all conformable matrices A and B,

$$\{\begin{array}{cc}\hfill & \mid \text{Tr}(\mathbf{A}\mathbf{B})\mid \le \Vert \mathbf{A}\Vert \Vert \mathbf{B}\Vert ,\hfill \\ \hfill & \Vert \mathbf{A}\mathbf{B}\Vert \le \Vert \mathbf{A}\Vert \Vert \mathbf{B}\Vert .\hfill \end{array}\phantom{\}}$$ (A.21)

By equation 2.25c, we have

$$\begin{array}{cc}\hfill \text{Tr}{\left(N^{-1}\mathbf{J}(\mathbf{x})\right)}^2& =\langle N^{-1}{l}^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{l}^{\prime }(\mathbf{r}\mid \mathbf{x}){\rangle }_{\mathbf{r}\mid \mathbf{x}}^2\hfill \\ \hfill & \le {\langle {\left(N^{-1}{l}^{\prime }(\mathbf{r}\mid \mathbf{x}{)}^T{l}^{\prime }(\mathbf{r}\mid \mathbf{x})\right)}^2\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(1).\hfill \end{array}$$ (A.22)

Then it follows from equations 2.25b and A.22 that

$$\text{det}(\mathbf{G}(\mathbf{x}))=O(N^K).$$ (A.23)

A.1 Proof of Lemma 1. It follows from equation A.1 that

$$\begin{array}{cc}\hfill {\Gamma }_{\omega }& ={\langle {\langle \text{ln}{\int }_{{\mathcal{X}}_{\omega }(\mathbf{x})}\text{exp}(L(\mathbf{r}\mid \widehat{\mathbf{x}})-L(\mathbf{r}\mid \mathbf{x}))d\widehat{\mathbf{x}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & =-{\langle \frac{1}{2}\text{ln}(\text{det}(\mathbf{G}(\mathbf{x})))\rangle }_{\mathbf{x}}\hfill \\ \hfill & +\underset{{\widehat{\Gamma }}_{\omega }}{\underbrace{{\langle {\langle \text{ln}\left({\int }_{{\mathcal{Y}}_{\omega }}\text{exp}\left({\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}{\mathbf{y}}^T\mathbf{y}+\frac{1}{2}{\mathbf{y}}^T\mathbf{B}\mathbf{y}\right)d\mathbf{y}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}}}.\hfill \end{array}$$ (A.24)

For $\mathbf{y}\in {\mathcal{Y}}_{\epsilon }$, according to the definitions in equations A.13 and A.14, we have

$$\begin{array}{cc}\hfill \mid {\mathbf{y}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}\mid & \le \Vert \mathbf{y}\Vert \Vert \tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}\Vert \hfill \\ \hfill & \le (N{\epsilon }^2{)}^{1∕2}\Vert \tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}\Vert \hfill \\ \hfill & \le 2{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}.\hfill \end{array}$$ (A.25)

Then by condition C1, we get

$$\begin{array}{cc}\hfill {\langle {\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}\rangle }_{\mathbf{r}\mid \mathbf{x}}& \le {\langle \frac{\Vert \tilde{\mathbf{v}}{\Vert }^4}{{\left(\widehat{\epsilon }\sqrt{N}\right)}^2}\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le N^{-1}({\widehat{\epsilon }}_0{)}^{-2}\langle \Vert \tilde{\mathbf{v}}{\Vert }^4{\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}),\hfill \end{array}$$ (A.26)

where ${\widehat{\epsilon }}_0$ is a positive constant and ${\widehat{\epsilon }}_0\in [\text{min}\widehat{\epsilon }(\mathbf{r}),\max \widehat{\epsilon }(\mathbf{r})]$. By equations A.9, A.17, and A.24, we get

$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Gamma }}}_{\omega }& \ge {\langle {\langle \text{ln}\left({\int }_{{\mathcal{Y}}_{\epsilon }}\text{exp}\left({\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}(1+ϵ){\mathbf{y}}^T\mathbf{y}+\frac{1}{2}{\mathbf{y}}^T{\mathbf{B}}_0\mathbf{y}\right)d\mathbf{y}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & \ge {\langle {\langle \text{ln}\left({\int }_{{\mathcal{Z}}_{\widehat{\epsilon }}}\text{exp}\left(\frac{1}{2}{\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right)}^T{\mathbf{B}}_0\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right)\right){\varphi }_{\widehat{\epsilon }}(\mathbf{z})d\mathbf{z}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & +{\langle {\langle \text{ln}({\Psi }_{\widehat{\epsilon }})+\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1+ϵ{)}^2}-\frac{5{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}}{2(1+ϵ{)}^2}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & \le \frac{1}{2}{\langle {\langle \left({\int }_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right)}^T{\mathbf{B}}_0\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right){\varphi }_{\widehat{\epsilon }}(\mathbf{z})d\mathbf{z}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & +{\langle \langle \text{ln}({\Psi }_{\widehat{\epsilon }}){\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}+\frac{K+\zeta }{2(1+ϵ{)}^2}+O(N^{-1}),\hfill \end{array}$$ (A.27)

where $\mathbf{z}=\mathbf{y}-\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}(\mathbf{x})}$, the last step in equation A.27 follows from Jensen’s inequality, and

$$\{\begin{array}{cc}\hfill & {\varphi }_{\widehat{\epsilon }}(\mathbf{z})={\Psi }_{\widehat{\epsilon }}^{-1}\text{exp}\left(-\frac{1+ϵ}{2}{\mathbf{z}}^T\mathbf{z}\right),\hfill \\ \hfill & {\Psi }_{\widehat{\epsilon }}={\int }_{{\mathcal{Z}}_{\widehat{\epsilon }}}\text{exp}\left(-\frac{1+ϵ}{2}{\mathbf{z}}^T\mathbf{z}\right)d\mathbf{z}.\hfill \end{array}\phantom{\}}$$ (A.28)

Integrating by parts yields

$$\langle 1_{{\bar{\mathcal{Z}}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\int }_{{\bar{\mathcal{Z}}}_{\widehat{\epsilon }}}{\left(\frac{1+ϵ}{2\pi }\right)}^{K∕2}\text{exp}\left(-\frac{1+ϵ}{2}{\mathbf{z}}^T\mathbf{z}\right)d\mathbf{z}=O(N^{-K∕2}{e}^{-N\delta })$$ (A.29)

and

$${\left(\frac{2\pi }{1+ϵ}\right)}^{K∕2}\ge {\Psi }_{\widehat{\epsilon }}\ge {\left(\frac{2\pi }{1+ϵ}\right)}^{K∕2}(1-O(N^{-K∕2}{e}^{-N\delta }))$$ (A.30)

for some δ > 0.

Then from equation A.27, we get

$$\begin{array}{c}{\langle {\langle \left({\int }_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right)}^T{\mathbf{B}}_0\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{1+ϵ}\right){\varphi }_{\widehat{\epsilon }}(\mathbf{z})d\mathbf{z}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ ={\left(\frac{2\pi }{1+ϵ}\right)}^{K∕2}{\Psi }_{\widehat{\epsilon }}^{-1}{\langle {\langle \langle {\mathbf{z}}^T{\mathbf{B}}_0{\mathbf{z}1}_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}+\frac{{\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}{1}_{{\mathcal{Z}}_{\widehat{\epsilon }}}{1}_{{\mathcal{R}}_{\widehat{\epsilon }}}}{(1+ϵ{)}^2}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \ge {\left(\frac{2\pi }{1+ϵ}\right)}^{K∕2}{\Psi }_{\widehat{\epsilon }}^{-1}{\langle \langle \langle {\mathbf{z}}^T{\mathbf{B}}_0{\mathbf{z}1}_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ge O(N^{-1}),\hfill \end{array}$$ (A.31)

where

$$\{\begin{array}{cc}\hfill & \langle \cdot {\rangle }_{\mathbf{z}}={\int }_{{\mathbb{R}}^K}(\cdot ){\varphi }_0(\mathbf{z})d\mathbf{z},\hfill \\ \hfill & {\varphi }_0(\mathbf{z})={\left(\frac{1+ϵ}{2\pi }\right)}^{K∕2}\text{exp}\left(-\frac{1+ϵ}{2}{\mathbf{z}}^T\mathbf{z}\right).\hfill \end{array}\phantom{\}}$$ (A.32)

Here, notice that

$${\left(\frac{2\pi }{1+ϵ}\right)}^{K∕2}{\Psi }_{\widehat{\epsilon }}^{-1}=1+O(N^{-K∕2}{e}^{-N\alpha })$$ (A.33)

and

$$\begin{array}{cc}\hfill {\langle \langle \langle {\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z}{1}_{{\bar{\mathcal{Z}}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}& =-{\langle \langle \langle {\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z}{1}_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & \ge -{\langle \langle \Vert {\mathbf{B}}_0{\Vert }^2{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\langle \langle \Vert \mathbf{z}{\Vert }^4{1}_{{\bar{\mathcal{Z}}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\rangle }_{\mathbf{x}}\hfill \\ \hfill & =O(N^{-1}).\hfill \end{array}$$ (A.34)

Hence, from the consideration above, we find

$${\widehat{\Gamma }}_{\omega }\ge \frac{K}{2}\text{ln}\left(\frac{2\pi }{1+ϵ}\right)+\frac{K}{2(1+ϵ{)}^2}+O(N^{-1}).$$ (A.35)

Since ϵ is arbitrary, let it go to zero. Thus, combining equations A.24 and A.35 yields

$${\mathrm{\Gamma }}_{\omega }=-{\langle \frac{1}{2}\text{ln}\left(\text{det}\left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+O(N^{-1}).$$ (A.36)

Considering

$${\langle {\langle \text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ge {\Gamma }_{\omega },$$ (A.37)

and combining equations 2.3 and A.36, we immediately get equation 2.53.

On the other hand, by conditions 2.54a and 2.54b, we have

$$\{\begin{array}{cc}\hfill & {\langle {\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathcal{R}}}_{\widehat{\epsilon }}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le \langle \frac{\Vert \tilde{\mathbf{v}}{\Vert }_2^{2+2\tau }}{{\left(\widehat{\epsilon }\sqrt{N}\right)}^{2\tau }}\rangle \le N^{-\tau }({\widehat{\epsilon }}_0{)}^{-2\tau }{\langle \Vert \tilde{\mathbf{v}}{\Vert }^{2+2\tau }\rangle }_{\mathbf{r}\mid \mathbf{x}}=o(1),\hfill \\ \hfill & {\langle \langle \langle {\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z}{1}_{{\mathcal{Z}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ge -{\langle \langle \Vert {\mathbf{B}}_0{\Vert }^2{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\langle \langle \Vert \mathbf{z}{\Vert }^4{1}_{{\bar{\mathcal{Z}}}_{\widehat{\epsilon }}}{\rangle }_{\mathbf{z}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}\rangle }_{\mathbf{x}}=o(1).\hfill \end{array}\phantom{\}}$$ (A.38)

Similarly we can get equation 2.55. This completes the proof of lemma 1. □

A.2 Proof of Lemma 2. Define the sets

$${\mathrm{\Omega }}_{ϵ}(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:{\mathbf{y}}^T{\mathbf{B}}_0\mathbf{y}<ϵ\Vert \mathbf{y}{\Vert }^2,\forall \mathbf{y}\in {\mathbb{R}}^K\right\}$$ (A.39)

and

$${\mathrm{\Theta }}_{ϵ}(\mathbf{x})=\left\{\mathbf{r}\in \mathcal{R}:{\int }_{{\bar{\mathcal{X}}}_{\epsilon }(\mathbf{x})}\frac{p(\mathbf{r}\mid \widehat{\mathbf{x}})p(\widehat{\mathbf{x}})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}d{x}^{\prime }<ϵ\text{det}(\mathbf{G}(\mathbf{x}){)}^{-1∕2}\right\},$$ (A.40)

where ${\bar{\mathcal{X}}}_{\epsilon }(\mathbf{x})=\mathcal{X}-{\mathcal{X}}_{\epsilon }(\mathbf{x})$, assuming ϵ ∈ (0, 1/2) and p(x) > 0.

Then by Markov’s inequality, we have

$${\langle 1_{{\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{\Vert {\mathbf{B}}_0{\Vert }^2\ge {ϵ}^2\right\}\le {ϵ}^2{\langle \Vert {\mathbf{B}}_0{\Vert }^2\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}),$$ (A.41)

and by equation 2.26b,

$$\begin{array}{cc}\hfill {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}& ={\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{{\int }_{{\bar{\mathcal{X}}}_{\epsilon }(\mathbf{x})}\frac{p(\mathbf{r}\mid \widehat{\mathbf{x}})p(\widehat{\mathbf{x}})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}d\widehat{\mathbf{x}}\ge ϵ\text{det}(\mathbf{G}(\mathbf{x}){)}^{-1∕2}\right\}\hfill \\ \hfill & ={\mathbb{P}}_{\mathbf{r}\mid \mathbf{x}}\left\{\text{det}(\mathbf{G}(\mathbf{x}){)}^{1∕2}{\int }_{{\bar{\mathcal{X}}}_{\widehat{\omega }}(\mathbf{x})}p(\widehat{\mathbf{x}}\mid \mathbf{r})d\widehat{\mathbf{x}}>ϵp(\mathbf{r}\mid \mathbf{x})\right\}\hfill \\ \hfill & =O(N^{-\eta }).\hfill \end{array}$$ (A.42)

Consider the following equality:

$${\langle \text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}={\langle 1_{{\mathrm{\Theta }}_{ϵ}}\text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}+{\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}.$$ (A.43)

For the last term in equation A.43, Jensen’s inequality implies that

$${\langle {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\text{ln}\frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\le {\langle \langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\text{ln}\frac{1}{{\langle \langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}{\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}}=o(N^{-1}).$$ (A.44)

For the first term in equation A.43, it follows from equations A.40 and A.9 that

$$\begin{array}{cc}\hfill & {\langle 1_{{\mathrm{\Theta }}_{ϵ}}\text{ln}\frac{p(\mathbf{r}}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le {\langle 1_{{\mathrm{\Theta }}_{ϵ}}\text{ln}\left({\int }_{{\mathcal{X}}_{\epsilon }(\mathbf{x})}\text{exp}(L(\mathbf{r}\mid \widehat{\mathbf{x}})-L(\mathbf{r}\mid \mathbf{x}))d\widehat{\mathbf{x}}+ϵ\text{det}(\mathbf{G}(\mathbf{x}){)}^{-1∕2}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le -\frac{K}{2}\text{ln}(\text{det}(\mathbf{G}(\mathbf{x})))\hfill \\ \hfill & +{\langle 1_{{\mathrm{\Theta }}_{ϵ}}\text{ln}\left({\int }_{{\mathcal{Y}}_{\epsilon }}\text{exp}\left({\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}(1+ϵ){\mathbf{y}}^T\mathbf{y}+\frac{1}{2}{\mathbf{y}}^T{\mathbf{B}}_0\mathbf{y}\right)d\mathbf{y}+ϵ\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}.\hfill \end{array}$$ (A.45)

The last term, equation A.45, is upper-bounded by

$${\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\mathrm{\Omega }}_{ϵ}}\text{ln}\left({\int }_{{\mathbb{R}}^K}\text{exp}\left({\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}(1-2ϵ){\mathbf{y}}^T\mathbf{y}\right)d\mathbf{y}+ϵ\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}$$ (A.46)

$$+{\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\text{ln}\left({\int }_{{\mathbb{R}}^K}\text{exp}\left({\mathbf{y}}^T\tilde{\mathbf{v}}-\frac{1}{2}(1-ϵ){\mathbf{y}}^T\mathbf{y}+\frac{1}{2}{\mathbf{y}}^T{\mathbf{B}}_0\mathbf{y}\right)d\mathbf{y}+ϵ\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}.$$ (A.47)

Equation A.46 is equal to

$$\begin{array}{cc}\hfill & {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\mathrm{\Omega }}_{ϵ}}\text{ln}\left({\left(\frac{2\pi }{1-2ϵ}\right)}^{K∕2}\text{exp}\left(\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1-2ϵ)}\right)+ϵ\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\mathrm{\Omega }}_{ϵ}}\left(\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1-2ϵ)}+\text{ln}\left({\left(\frac{2\pi }{1-2ϵ}\right)}^{K∕2}+ϵ\right)\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}.\hfill \end{array}$$ (A.48)

Equation A.47 is equal to

$$\begin{array}{cc}\hfill & \langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\text{ln}(\langle {\left(\frac{2\pi }{1-ϵ}\right)}^{K∕2}\text{exp}(\frac{1}{2}{\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}}{1-ϵ}\right)}^T\phantom{)}\phantom{\rangle }\phantom{)}\phantom{\rangle }\hfill \\ \hfill & {\phantom{\langle }\phantom{(}{\phantom{\langle }\phantom{(}{\mathbf{B}}_0\left(\mathbf{z}+\frac{\tilde{\mathbf{v}}}{1-ϵ}\right)+\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1-ϵ)})\rangle }_{\mathbf{z}}+ϵ)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\left(\frac{K}{2}\ln \left(\frac{2\pi }{1-ϵ}\right)+\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1-ϵ)}+\frac{{\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}}{2{(1-ϵ)}^2}+\frac{{\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}}{{(1-ϵ)}^3}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \end{array}$$ (A.49a)

$$+\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\text{ln}({\langle \exp \left(\frac{1}{2}{\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z}+\frac{{\mathbf{z}}^T{\mathbf{B}}_0\tilde{\mathbf{v}}}{1-ϵ}-\frac{{\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}}{{(1-ϵ)}^3}\right)\rangle }_{\mathbf{z}}\phantom{)}\phantom{\rangle }{\phantom{\langle }\phantom{(}+ϵ{\left(\frac{1-ϵ}{2\pi }\right)}^{K∕2})\rangle }_{\mathbf{r}\mid \mathbf{x}},$$ (A.49b)

where

$$\{\begin{array}{c}{\langle \cdot \rangle }_{\mathbf{z}}={\int }_{{\mathbb{R}}^K}(\cdot ){\varphi }_1(\mathbf{z})d\mathbf{z}\hfill \\ {\varphi }_1(\mathbf{z})={\left(\frac{1-ϵ}{2\pi }\right)}^{K∕2}\exp \left(-\frac{1-ϵ}{2}{\mathbf{z}}^T\mathbf{z}\right)\hfill \end{array}\phantom{\}}.$$ (A.50)

Notice that

$${\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle 1_{{\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1})$$ (A.51)

and

$${\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\mathrm{\Omega }}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}=1-{\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}\cup {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}=1+O(N^{-1}).$$ (A.52)

Then by equation A.19, we get

$$\begin{array}{cc}\hfill & {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\left({\langle \exp ({\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z})\rangle }_{\mathbf{z}}^{1∕2}-1\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\sum _{m=0}^{\infty }\frac{1}{m!}{\langle {({\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z})}^m\rangle }_{\mathbf{z}}\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}-{\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}),\hfill \end{array}$$ (A.53)

$${\langle {\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}{1}_{{\bar{\mathrm{\Theta }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle {\Vert \tilde{\mathbf{v}}\Vert }^4\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}{\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}^{1∕2}=O(N^{-1}),$$ (A.54)

and by equation 2.51,

$$\begin{array}{cc}\hfill 0& \le {\langle {\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}{1}_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{\mathrm{\Omega }}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle {\mathbf{v}}^T{\mathbf{B}}_0^2\mathbf{v}\rangle }_{\mathbf{r}\mid \mathbf{x}}+O(N^{-1})\hfill \\ \hfill & \le \xi \Vert N{\mathbf{G}}^{-1}(\mathbf{x})\Vert +O(N^{-1})=O(N^{-1}).\hfill \end{array}$$ (A.55)

Hence, we have

$$\begin{array}{cc}\hfill & {\langle 1_{{\mathrm{\Theta }}_{ϵ}}\left(\frac{K}{2}\ln \left(\frac{2\pi }{1-ϵ}\right)+\frac{{\tilde{\mathbf{v}}}^T\tilde{\mathbf{v}}}{2(1-ϵ)}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & =\left(\frac{K}{2}\ln \left(\frac{2\pi }{1-ϵ}\right)+\frac{K+\zeta }{2(1-ϵ)}\right)+O(N^{-1}),\hfill \end{array}$$ (A.56)

and by Cauchy-Schwarz inequality and equation A.53, the term A.49b is upper-bounded by

$$\begin{array}{cc}\hfill & \langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\text{ln}({\langle \exp ({\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z})\rangle }_{\mathbf{z}}^{1∕2}{\langle \text{exp}\left(\frac{2{\mathbf{z}}^T{\mathbf{B}}_0\tilde{\mathbf{v}}}{1-ϵ}-\frac{2{\tilde{\mathbf{v}}}^T{\mathbf{B}}_0^2\tilde{\mathbf{v}}}{{(1-ϵ)}^3}\right)\rangle }_{\mathbf{z}}^{1∕2}\phantom{)}\phantom{\rangle }\hfill \\ \hfill & {\phantom{\langle }\phantom{(}+ϵ{\left(\frac{1-ϵ}{2\pi }\right)}^{K∕2})\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & ={\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\ln \left({\langle \exp ({\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z})\rangle }_{\mathbf{z}}^{1∕2}+ϵ{\left(\frac{1-ϵ}{2\pi }\right)}^{K∕2}\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & \le {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\left({\langle \exp ({\mathbf{z}}^T{\mathbf{B}}_0\mathbf{z})\rangle }_{\mathbf{z}}^{1∕2}+ϵ{\left(\frac{1-ϵ}{2\pi }\right)}^{K∕2}-1\right)\rangle }_{\mathbf{r}\mid \mathbf{x}}=O(N^{-1}).\hfill \end{array}$$ (A.57)

Since ϵ is arbitrary, we can let it go to zero. Then, taking everything together, we get

$${\langle {\langle \ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{r})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\le -{\langle \frac{1}{2}\ln \left(\det \left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}+O(N^{-1}).$$ (A.58)

Putting equation A.58 into 2.3 yields 2.56.

On the other hand, we have

$$\begin{array}{cc}\hfill & {\langle {\langle \ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\langle {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\mathrm{\Omega }}_{ϵ}}\ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\hfill \end{array}$$ (A.59)

$$+{\langle {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}+{\langle {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}.$$ (A.60)

For equation A.60, it fo11ows from Jensen’s inequa1ity that

$${\langle {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\le {\langle {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ln \frac{1}{{\langle {\langle 1_{{\bar{\mathrm{\Theta }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}}=o(1)$$ (A.61)

and

$${\langle {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\ln \frac{p(\mathbf{r})}{p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\le {\langle {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}\ln \frac{1}{{\langle {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\rangle }_{\mathbf{x}}}=o(1),$$ (A.62)

where

$$\{\begin{array}{c}{\langle 1_{{\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le P({\Vert {\mathbf{B}}_0\Vert }^2\ge {ϵ}^2)\le {ϵ}^{-2}{\langle {\Vert {\mathbf{B}}_0\Vert }^2\rangle }_{\mathbf{r}\mid \mathbf{x}}=o(1),\hfill \\ {\langle 1_{{\mathrm{\Theta }}_{ϵ}\cap {\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}\le {\langle 1_{{\bar{\mathrm{\Omega }}}_{ϵ}}\rangle }_{\mathbf{r}\mid \mathbf{x}}=o(1).\hfill \end{array}\phantom{\}}$$ (A.63)

Similarly we can get equation 2.57. □

A.3 Proof of Theorem 1. By lemmas 1 and 2, we immediately get equation 2.58. The proof of equation 2.59 is similar. □

A.4 Proof of Theorem 2. First, we have

$$\mathbf{G}(\mathbf{x})={\mathbf{J}}^{1∕2}(\mathbf{x})({\mathbf{I}}_K+\Psi (\mathbf{x})){\mathbf{J}}^{1∕2}(\mathbf{x}).$$ (A.64)

Since J(x) and G(x) are symmetric and positive-definite, I_K + Ψ(x) is also symmetric and positive-definite. The eigendecompositon of Ψ(x) is given by

$$\Psi (\mathbf{x})={\mathbf{U}}_{\mathbf{x}}{\Lambda }_{\mathbf{x}}{\mathbf{U}}_{\mathbf{x}}^T,$$ (A.65)

where ${\mathbf{U}}_{\mathbf{x}}\in {\mathbb{R}}^{K\times K}$ is an orthogonal matrix and the matrix ${\Lambda }_{\mathbf{x}}\in {\mathbb{R}}^{K\times K}$ is a K × K diagonal matrix with K nonnegative real numbers on the diagonal, λ₁ ≥ λ₂ ≥, …, ≥ λ_K > −1. Then we have

$${\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}})\rangle }_{\mathbf{x}}={\langle \mathrm{Tr}(\Psi (\mathbf{x}))\rangle }_{\mathbf{x}}={\langle \mathrm{Tr}(\mathbf{P}(\mathbf{x}){\mathbf{J}}^{-1}(\mathbf{x}))\rangle }_{\mathbf{x}}=\varsigma$$ (A.66)

and

$${\langle \ln (\det ({\mathbf{I}}_K+\Psi (\mathbf{x})))\rangle }_{\mathbf{x}}={\langle \mathrm{Tr}(\ln ({\mathbf{I}}_K+{\Lambda }_{\mathbf{x}}))\rangle }_{\mathbf{x}}\le {\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}})\rangle }_{\mathbf{x}}=\varsigma .$$ (A.67)

Notice that ln(1 + x) ≤ x for ∀_x ∈ (−1, ∞). It follows from equations A.64 and A.67 that

$${\langle \ln (\det (\mathbf{G}(\mathbf{x})))\rangle }_{\mathbf{x}}={\langle \ln (\det (\mathbf{J}(\mathbf{x})))\rangle }_{\mathbf{x}}={\langle \ln (\det ({\mathbf{I}}_K+\Psi (\mathbf{x})))\rangle }_{\mathbf{x}}\le \varsigma .$$ (A.68)

From equations 2.12, 2.11, and A.68, we obtain equation 2.62.

If P(x) is positive-semidefinite, then λ₁ ≥ λ₂ ≥, …, ≥ λ_K ≥ 0, ς ≥ 0 and (ln (det ⟨I_K + Ψ(x)))⟩_x ≥ 0. Hence we can get equation 2.63.

On the other hand, it follows from equations 2.64 and A.67 and the power mean inequality that

$$\begin{array}{cc}\hfill \mid \varsigma \mid & \le {\langle {\sum }_{k=1}^K\mid {\lambda }_k\mid \rangle }_{\mathbf{x}}\le \sqrt{K}{\langle {\left({\sum }_{k=1}^K{\lambda }_k^2\right)}^{1∕2}\rangle }_{\mathbf{x}}\hfill \\ \hfill & =\sqrt{K}{\langle \Vert \Psi (\mathbf{x})\Vert \rangle }_{\mathbf{x}}=\sqrt{K}{\varsigma }_1=O(N^{-\beta }).\hfill \end{array}$$ (A.69)

Let ${\mathit{\lambda }}_k^{-}=\text{min}(0,{\mathit{\lambda }}_k)$ for ∀k ∈ {1, 2, …, K}. Then

$${\langle {\sum }_{k=1}^K\ln (1+{\mathit{\lambda }}_k^{-})\rangle }_{\mathbf{x}}\le {\langle \ln (\det ({\mathbf{I}}_K+\Psi (\mathbf{x})))\rangle }_{\mathbf{x}}.$$ (A.70)

Notice that $-1<{\mathit{\lambda }}_k^{-}\le 0$. Then by equation A.69, we have

$${\langle {\sum }_{k=1}^K\ln (1+{\mathit{\lambda }}_k^{-})\rangle }_{\mathbf{x}}={\langle {\sum }_{m=1}^{\infty }\frac{-1}{m}{\sum }_{k=1}^K{(-{\mathit{\lambda }}_k^{-})}^m\rangle }_{\mathbf{x}}=O(N^{-\beta }).$$ (A.71)

From equations 2.12, 2.11, A.68, A.70, and A.71, we immediately get equation 2.65. □

A.5 Proof of Theorem 3. Considering the change of variables theorem, for any real-valued function f and invertible transformation T, we have

$${\int }_{\tilde{\mathcal{X}}}f(\tilde{\mathbf{x}})d\tilde{\mathbf{x}}={\int }_{\mathcal{X}}f(\mathbf{T}(\mathbf{x}))\mid \det (D\mathbf{T}(\mathbf{x}))\mid d\mathbf{x},$$ (A.72)

and for p(x) and $p(\tilde{\mathbf{x}})$,

$$p(\tilde{\mathbf{x}}){\mid }_{\tilde{\mathbf{x}}=T(\mathbf{x})}={\mid \det (D\mathbf{T}(\mathbf{x}))\mid }^{-1}p(\mathbf{x}).$$ (A.73)

Then it follows from equations 4.2, A.72, and A.73 that

$$\{\begin{array}{cc}p(\mathbf{r})\hfill & ={\int }_{\mathcal{X}}p(\mathbf{r}\mid \mathbf{x})p(\mathbf{x})d\mathbf{x}={\int }_{\tilde{\mathcal{X}}}p(\mathbf{r}\mid \tilde{\mathbf{x}})p(\tilde{\mathbf{x}})d\tilde{\mathbf{x}},\hfill \\ H(\tilde{X})\hfill & =-{\int }_{\tilde{\mathcal{X}}}p(\tilde{\mathbf{x}})\ln p(\tilde{\mathbf{x}})d\mathbf{x}\hfill \\ \hfill & =-{\int }_{\mathcal{X}}p(\mathbf{x})\ln \left(p(\mathbf{x}){\mid \det (D\mathbf{T}(\mathbf{x}))\mid }^{-1}\right)d\mathbf{x}\hfill \\ \hfill & =H(X)+{\int }_{\mathcal{X}}p(\mathbf{x})\ln \mid \det (D\mathbf{T}(\mathbf{x}))\mid d\mathbf{x},\hfill \\ \mathbf{G}(\mathbf{x})\hfill & =D\mathbf{T}{(\mathbf{x})}^T\mathbf{G}(\tilde{\mathbf{x}})D\mathbf{T}(\mathbf{x}).\hfill \end{array}\phantom{\}}$$ (A.74)

Substituting equations A.73 and A.74 into 2.1, we can directly obtain equation 4.3. Moreover, if $p(\tilde{\mathbf{x}})$ and $p(\mathbf{r}\mid \tilde{\mathbf{x}})$ fulfill conditions C1, C2 and ξ = O (N⁻¹), then by theorem 1, we immediately obtain equation 4.4. □

A.6 Proof of Corollary 1. It follows from equation 2.21 and theorem 3 that

$$\begin{array}{cc}\hfill I_G& =I_{G+}=I(X;R)=I(Y;R)\hfill \\ \hfill & =\frac{1}{2}\ln \left(\det \left(\frac{1}{2\pi e}(\mathbf{A}{\mathbf{A}}^T+{\Sigma }_{\mathbf{f}}^{-1})\right)\right)+H(Y)\hfill \end{array}$$ (A.75)

and

$$H(Y)=\frac{1}{2}\ln (\det (2\pi e{\Sigma }_{\mathbf{f}}))=H(X)+{\langle \ln \mid \det (\mathbf{D}(\mathbf{x}))\mid \rangle }_{\mathbf{x}}.$$ (A.76)

Here notice that

$$\begin{array}{cc}\hfill \mathbf{J}(\mathbf{x})& ={\langle \frac{\mathrm{\partial }\ln p(\mathbf{r}\mid \mathbf{x})}{\mathrm{\partial }\mathbf{x}}\frac{\mathrm{\partial }\ln p(\mathbf{r}\mid \mathbf{x})}{\mathrm{\partial }{\mathbf{x}}^T}\rangle }_{\mathbf{r}\mid \mathbf{x}}\hfill \\ \hfill & ={\langle \frac{\mathrm{\partial }{\mathbf{y}}^T}{\mathrm{\partial }\mathbf{x}}\frac{\mathrm{\partial }\ln p(\mathbf{r}\mid \mathbf{y})}{\mathrm{\partial }\mathbf{y}}\frac{\mathrm{\partial }\ln p(\mathbf{r}\mid \mathbf{y})}{\mathrm{\partial }{\mathbf{y}}^T}\frac{\mathrm{\partial }\mathbf{y}}{\mathrm{\partial }{\mathbf{x}}^T}\rangle }_{\mathbf{r}\mid \mathbf{y}}\hfill \\ \hfill & =\mathbf{D}{(\mathbf{x})}^T\mathbf{A}{\mathbf{A}}^T\mathbf{D}(\mathbf{x})\hfill \end{array}$$ (A.77)

and

$$\mathbf{P}(\mathbf{x})=-\frac{{\partial }^2\ln p(\mathbf{x})}{\partial \mathbf{x}\partial {\mathbf{x}}^T}=-\frac{\partial {\mathbf{y}}^T}{\partial \mathbf{x}}\frac{{\partial }^2\ln p(\mathbf{y})}{\partial \mathbf{y}\partial {\mathbf{y}}^T}\frac{\partial \mathbf{y}}{\partial {\mathbf{x}}^T}=\mathbf{D}{(\mathbf{x})}^T{\Sigma }_{\mathbf{f}}^{-1}\mathbf{D}(\mathbf{x}).$$ (A.78)

Hence, combining equations A.75 to A.78, we can immediately obtain equation 4.9. □

A.7 Proof of Theorem 4. First, we have

$${\langle \ln \left(\det \left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}=\langle \ln (\det \left(\frac{{\mathbf{G}}_{1,1}(\mathbf{x})}{2\pi e}\right)\phantom{)}\phantom{\rangle }{\phantom{\langle }\phantom{(}\det \left(\frac{1}{2\pi e}({\mathbf{G}}_{2,2}(\mathbf{x})-{\mathbf{G}}_{2,1}(\mathbf{x}){\mathbf{G}}_{1,1}^{-1}(\mathbf{x}){\mathbf{G}}_{1,2}(\mathbf{x}))\right))\rangle }_{\mathbf{x}}=\langle \ln \left(\det \left(\frac{{\mathbf{G}}_{1,1}(\mathbf{x})}{2\pi e}\right)\right)+\ln \left(\det \left(\frac{{\mathbf{G}}_{2,2}(\mathbf{x})}{2\pi e}\right)\right)\phantom{\rangle }+{\phantom{\langle }\ln (\det ({\mathbf{I}}_{K_2}-{\mathbf{A}}_{\mathbf{x}}))\rangle }_{\mathbf{x}}.$$ (A.79)

Then by the eigendecompositon of A_x, we have

$${\mathbf{A}}_{\mathbf{x}}={\mathbf{U}}_{\mathbf{x}}{\Lambda }_{\mathbf{x}}{\mathbf{U}}_{\mathbf{x}}^T,$$ (A.80)

where U_x and Λ_x are K₂ × K₂ eigenvector matrix and eigenvalue matrix, respectively. Since G (x), G_1,1 (x), and G_2,2 (x) are positive-definite, then I_K – A_x is also positive-definite and A_x is positive-semidefinite, with 0 ≤ (Λ_x)_k,k = λ_k < 1 for ∀k ∈ {1, 2, …, K₂}. Moreover, it follows from equation 4.33 that

$$\{\begin{array}{c}0\le {\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}})\rangle }_{\mathbf{x}}={\langle \mathrm{Tr}({\mathbf{A}}_{\mathbf{x}})\rangle }_{\mathbf{x}}\ll 1,\hfill \\ 0\le {\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}}^m)\rangle }_{\mathbf{x}}={\langle {\sum }_{k=1}^{K_2}{\lambda }_k^m\rangle }_{\mathbf{x}}\le {\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}})\rangle }_{\mathbf{x}}\ll 1.\hfill \end{array}\phantom{\}}$$ (A.81)

Then by equation A.81, we have

$$\begin{array}{cc}\hfill {\langle \ln (\det ({\mathbf{I}}_{K_2}-{\mathbf{A}}_{\mathbf{x}}))\rangle }_{\mathbf{x}}& ={\langle \mathrm{Tr}(\ln ({\mathbf{I}}_{K_2}-{\Lambda }_{\mathbf{x}}))\rangle }_{\mathbf{x}}\hfill \\ \hfill & ={\sum }_{m=1}^{\infty }\frac{-1}{m}{\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}}^m)\rangle }_{\mathbf{x}}\simeq 0.\hfill \end{array}$$ (A.82)

Substituting equation A.82 into A.79 and then combining with equation 2.12, we get equation 4.35.

If equation 4.36 holds, then A_x = 0 and I_G = I_G1. Conversely, if I_G = I_G1, then

$$0={\langle \ln (\det ({\mathbf{I}}_{K_2}-{\mathbf{A}}_{\mathbf{x}}))\rangle }_{\mathbf{x}}\le -{\langle \mathrm{Tr}({\mathbf{A}}_{\mathbf{x}})\rangle }_{\mathbf{x}}\le 0,$$ (A.83)

A_x = 0, and equation 4.36 holds. □

A.8 Proof of Theorem 5. Similar to equation A.79, we have

$${\langle \ln \left(\det \left(\frac{\mathbf{G}(\mathbf{x})}{2\pi e}\right)\right)\rangle }_{\mathbf{x}}=\langle \ln \left(\det \left(\frac{{\mathbf{G}}_{1,1}(\mathbf{x})}{2\pi e}\right)\right)+\ln \left(\det \left(\frac{{\mathbf{P}}_{2,2}(\mathbf{x})}{2\pi e}\right)\right)\phantom{\rangle }+{\phantom{\langle }\ln (\det ({\mathbf{I}}_{K_2}-{\mathbf{B}}_{\mathbf{x}}))\rangle }_{\mathbf{x}}.$$ (A.84)

Similar to equation A.65, the eigendecompositon of B_x is given by

$${\mathbf{B}}_{\mathbf{x}}={\mathbf{U}}_{\mathbf{x}}{\Lambda }_{\mathbf{x}}{\mathbf{U}}_{\mathbf{x}}^T,$$ (A.85)

where U_x and Λ_x are K₂ × K₂ eigenvector matrix and eigenvalue matrix, respectively. If the matrix B_x is positive-semidefinite and satisfies equation 4.38, then (Λ_x)_k,k = λ_k ≥ 0 for ∀k ∈ {1, 2, …, K₂} and

$$0\le {\langle \ln (\det ({\mathbf{I}}_{K_2}+{\mathbf{B}}_{\mathbf{x}}))\rangle }_{\mathbf{x}}={\langle {\sum }_{k=1}^{K_2}\ln (1+{\lambda }_k)\rangle }_{\mathbf{x}}\le {\langle \mathrm{Tr}({\Lambda }_{\mathbf{x}})\rangle }_{\mathbf{x}}=\mathrm{Tr}({\langle {\mathbf{B}}_{\mathbf{x}}\rangle }_{\mathbf{x}})\ll 1.$$ (A.86)

Substituting equation A.86 into A.84, we immediately get equation 4.41. If C_x = 0, then ln (det(l_K2 + B_x)) = 0 and I_G = I_G2. And if I_G = I_G2, then ln (det(I_K2 + B_x)) = 0, B_x = 0 and C_x = 0. □

A.9 Proof of Corollary 2. Notice that

$$\{H(X)=H(X_1)+H(X_2),H(X_2)=\frac{1}{2}\ln (\det (2\pi e{\Sigma }_{{\mathbf{x}}_2})),{\mathbf{P}}_{2,1}(\mathbf{x})={\mathbf{P}}_{1,2}(\mathbf{x})=\mathbf{0},{\mathbf{P}}_{2,2}(\mathbf{x})={\Sigma }_{{\mathbf{x}}_2}^{-1},\phantom{\}}$$ (A.87)

and the matrices

$${\mathbf{C}}_{\mathbf{x}}={\mathbf{J}}_{2,2}(\mathbf{x})-{\mathbf{J}}_{2,1}(\mathbf{x}){\mathbf{G}}_{1,1}^{-1}(\mathbf{x}){\mathbf{J}}_{1,2}(\mathbf{x}),$$ (A.88)

$${\mathbf{B}}_{\mathbf{x}}={\mathbf{P}}_{2,2}^{-1∕2}(\mathbf{x}){\mathbf{C}}_{\mathbf{x}}{\mathbf{P}}_{2,2}^{-1∕2}(\mathbf{x})$$ (A.89)

are positive-semidefinite, and the proof is similar to equation 4.74. Then by theorem 5, we immediately get equation 4.41. Substituting equation A.87 into 4.41 yields equation 4.44 with strict equality if and only if C_x = 0. □

A.10 Proof of Proposition 2. By writing p(θ) as a sum of two density functions p₁(θ) and p₂(θ),

$$p(\theta )=\alpha p_1(\theta )+(1-\alpha )p_2(\theta ),$$ (A.90)

we have

$$\mathbf{G}(\mathbf{x})=N{\int }_{\mathrm{\Theta }}p(\theta )\mathbf{S}(\mathbf{x};\theta )d\theta +\mathbf{P}(\mathbf{x})=\alpha {\mathbf{G}}_1(\mathbf{x})+(1-\alpha ){\mathbf{G}}_2(\mathbf{x}),$$ (A.91)

where 0 ≤ α ≤ 1 and

$${\mathbf{G}}_1(\mathbf{x})=N{\int }_{\mathrm{\Theta }}{p}_1(\theta )\mathbf{S}(\mathbf{x};\theta )d\theta +\mathbf{P}(\mathbf{x}),$$ (A.92)

$${\mathbf{G}}_2(\mathbf{x})=N{\int }_{\mathrm{\Theta }}{p}_2(\theta )\mathbf{S}(\mathbf{x};\theta )d\theta +\mathbf{P}(\mathbf{x}).$$ (A.93)

Using the Minkowski determinant inequality and the inequality of weighted arithmetic and geometric means, we find

$$\det {(\mathbf{G}(\mathbf{x}))}^{1∕K}=\det {(\alpha {\mathbf{G}}_1(\mathbf{x})+(1-\alpha ){\mathbf{G}}_2(\mathbf{x}))}^{1∕K}\ge \alpha \det {({\mathbf{G}}_1(\mathbf{x}))}^{1∕K}+(1-\alpha )\det {({\mathbf{G}}_2(\mathbf{x}))}^{1∕K}\ge {\left(\det {({\mathbf{G}}_1(\mathbf{x}))}^{\alpha }\det {({\mathbf{G}}_2(\mathbf{x}))}^{(1-\alpha )}\right)}^{1∕K}.$$ (A.94)

It follows from equations A.91 and A.94 that

$$\ln (\det (\alpha {\mathbf{G}}_1(\mathbf{x})+(1-\alpha ){\mathbf{G}}_2(\mathbf{x})))\ge \alpha \ln (\det ({\mathbf{G}}_1(\mathbf{x})))+(1-\alpha )\ln (\det ({\mathbf{G}}_2(\mathbf{x}))),$$ (A.95)

where the equality holds if and only if G₁(x) = G₂(x). Thus ln (det (G(x))) is concave about p(θ). Therefore I_G[p(θ)] is a concave function about p(θ). Similarly, we can prove that I_F[p(θ)] is also a concave function about p(θ). □