Enhanced Thermoelectric Power Factor of Tensile Drawn Poly(3-hexylthiophene)

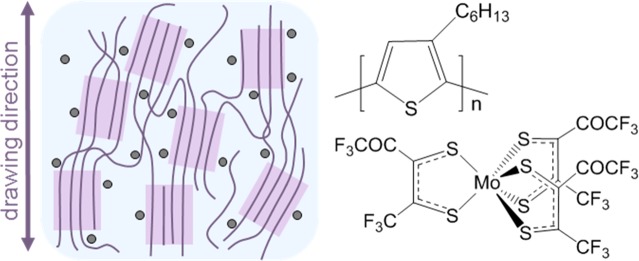
Abstract

The thermoelectric power factor of a broad range of organic semiconductors scales with their electrical conductivity according to a widely obeyed power law, and therefore, strategies that permit this empirical trend to be surpassed are highly sought after. Here, tensile drawing of the conjugated polymer poly(3-hexylthiophene) (P3HT) is employed to create free-standing films with a high degree of uniaxial alignment. Along the direction of orientation, sequential doping with a molybdenum tris(dithiolene) complex leads to a 5-fold enhancement of the power factor beyond the predicted value, reaching up to 16 μW m^–1 K^–2 for a conductivity of about 13 S cm^–1. Neither stretching nor doping affect the glass transition temperature of P3HT, giving rise to robust free-standing materials that are of interest for the design of flexible thermoelectric devices.

Conjugated polymers are heralded as materials that combine excellent electronic and mechanical properties. However, most current progress has focused on printed architectures where the polymer is typically deposited as a thin layer on a carrier substrate. Instead, mechanically robust and free-standing bulk materials are needed for a number of emerging applications such as textile electronics¹ and organic thermoelectrics,^2,3 where up to a millimeter-thick structures must be used to maintain heat gradients. When doping is required, a necessary compromise between the electrical and the mechanical properties arises. With regard to thermoelectrics, doping introduces charge carriers, which increases the conductivity σ and decreases the Seebeck coefficient α, resulting in a power factor α²σ that typically scales with σ according to an empirical power law:⁴

1

An important factor to consider that may not be fully appreciated is that the introduction of dopant molecules (or ions) can reduce the mechanical coupling between polymer chains.¹ Accordingly, at high dopant concentrations, the electronic coupling suffers, which is typically referred to as “perturbations of the morphology”.⁵ Further, it is feasible that a stiffening of polymer chains due to the presence of (dopant-induced) polarons could increase the glass transition temperature T_g, leading to a more brittle material.

One powerful tool to enhance both the mechanical and the electrical properties is solid-state drawing, which can be carried out on films and is an essential step in many fiber spinning processes.¹ Early studies of stretch-aligned conjugated polymers, including polyacetylene,⁶ polyaniline,⁷ polyphenylenevinylenes (PPVs),⁸⁻¹⁰ and polythiophenes¹¹⁻¹³ have found that chain orientation results in a considerable increase in electrical conductivity along the drawing direction. The influence of solid-state drawing on the Seebeck coefficient is less clear; upon stretching, α has been reported to decrease in the case of I₂-doped and FeCl₃-doped polyacetylene¹⁴ and to not change along the drawing direction in the case of I₂-doped PPVs⁸ and polyaniline doped with oxalic acid,¹⁵ but to increase in the case of polyaniline doped with camphorsulfonic acid.¹⁶ Hence, it is currently not evident how tensile deformation will influence the thermoelectric properties of bulk materials. In contrast, for thin films of polythiophenes, a number of recent reports have indicated that in-plane anisotropy can enhance the power factor beyond the trend predicted by eq 1,^5,17 which most (less oriented) organic semiconductors appear to obey.⁴ For instance, Hamidi-Sakr et al. have studied 40 nm thin films of poly(3-hexylthiophene), aligned by rubbing and subsequently doped with 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ).¹⁷ An up to 2-fold increase in the Seebeck coefficient and up to 4-fold increase in electrically conductivity along the rubbing direction gave rise to a power factor of 8.5 μW m^–1 K^–2. Hence, we set out to investigate if structural anisotropy is a suitable strategy to enhance the power factor of bulk materials beyond values predicted by the empirical power law and how this relates to the mechanical properties of the materials.

In this study, we carry out a systematic comparison of free-standing P3HT films, which we orient through solid-state tensile drawing. We correlate the mechanical and electrical properties of isotropic and stretch-aligned samples, both parallel and perpendicular to the drawing direction. We primarily use the molybdenum tris(dithiolene) complex Mo(tfd-COCF₃)₃ (see Figure 1 for chemical structure), which is able to diffuse into P3HT thin films,¹⁸ and also include F4TCNQ in our study for comparison. We find that along the alignment direction the power factor can be increased by up to five times beyond the value predicted by eq 1, whereas T_g is unaffected, which opens up the possibility to use free-standing materials for the design of flexible thermoelectric devices.

Figure 1.

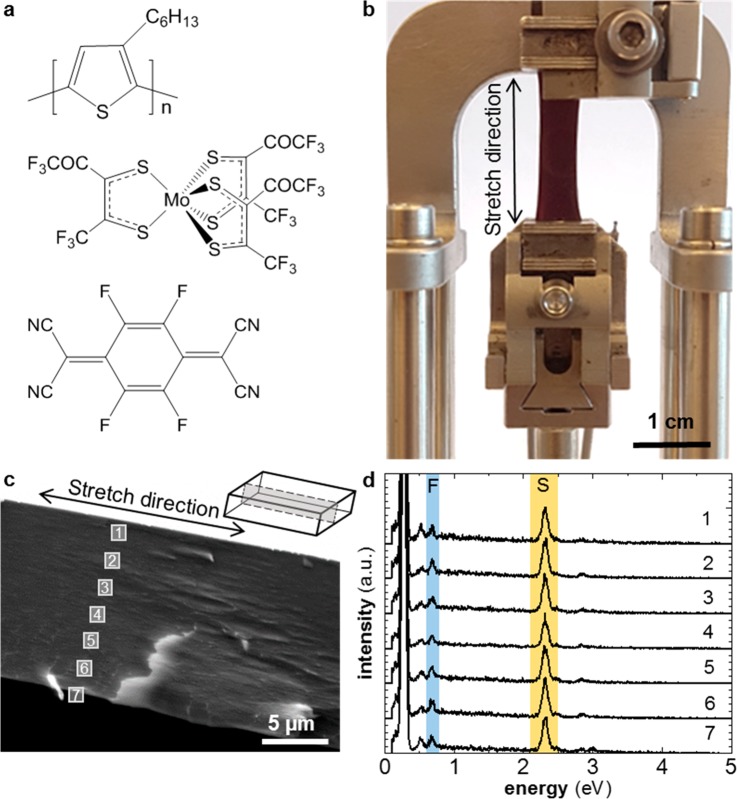
(a) Chemical structures of P3HT, Mo(tfd-COCF₃)₃, and F4TCNQ. (b) Stretched film of P3HT, clamped in a DMA instrument. (c) Scanning electron microscopy (SEM) image of the freeze-fractured surface used for energy dispersive X-ray spectroscopy (EDX); inset: sketch of EDX sample, the freeze fractured surface is shown by the dashed line. (d) EDX spectrogram of stretched P3HT sequentially doped with Mo(tfd-COCF₃)₃ for 72 h; fluorine and sulfur peaks are colored blue and yellow, respectively (note that the molybdenum and sulfur peaks overlap).

We chose to work with a high molecular weight batch of P3HT (number-average molecular weight of M_n ∼ 91 kg mol^–1; polydispersity index ∼ 1.8, regioregularity ∼ 93%) that is able to form tie chains,¹⁹ which we expect to ease solid-state drawing. Films with a thickness of 10–40 μm were cast from 80 °C hot concentrated (20 g L^–1) p-xylene solutions onto 90 °C hot glass substrates to produce smooth films. Dried films were then peeled from the substrate and tensile drawn at 60 °C and a rate of 0.5 mm min^–1 using a dynamic mechanical analysis (DMA) instrument to prepare samples for further analysis (cf. Figure 1b). The stretching was terminated when a draw ratio of λ ∼ 4 had been reached. The maximum draw ratio beyond which fracture occurred was λ_max ∼ 5.

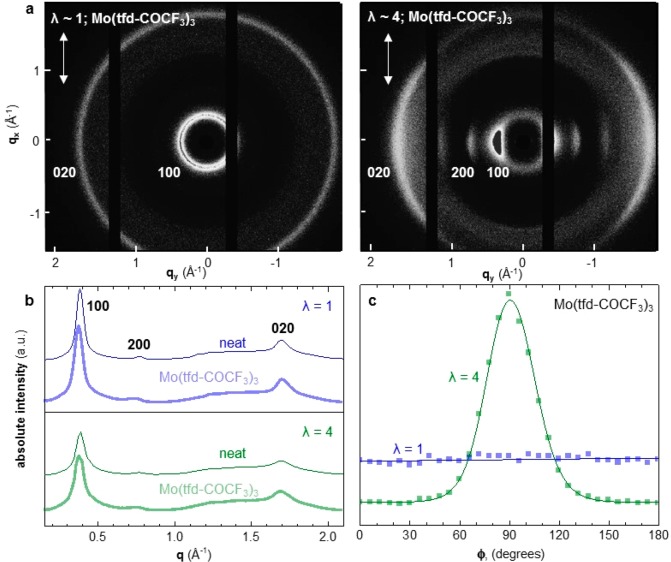
We used wide-angle X-ray scattering (WAXS) to compare the degree of anisotropy of as-cast and stretched samples (Figure 2). X-ray diffractograms of as-cast P3HT indicate an isotropic distribution of crystallites. For the stretched films we deduce considerable orientation of ordered domains, with alignment of the polymer backbone along the fiber axis, as evidenced by the strong equatorial 100 and 020 diffraction peaks. Angular integration of the 100 diffraction peak was used to calculate Herman’s orientation factor, f:

2

where ϕ is the angle of orientation with respect to the direction of tensile drawing (ϕ = 0, π is parallel to drawing direction) and I(ϕ) is the radially integrated intensity of the 100 diffraction peak. The Herman’s orientation factor changed from f ∼ 0 to −0.3 upon stretching, which is indicative of a substantial degree of alignment. First heating differential scanning calorimetry (DSC) thermograms of as-cast and tensile-drawn material show the same melting temperature T_m ∼ 239 °C, but a slight increase of the enthalpy of fusion from ΔH_f ∼ 17 J g^–1 to 21 J g^–1 (Supporting Information, Figure S1), which suggests the same crystal size but somewhat higher crystallinity of drawn P3HT.

Figure 2.

(a) Wide angle X-ray scattering (WAXS) patterns of as-cast (λ = 1) and tensile drawn P3HT (λ ∼ 4; arrows indicate drawing direction) sequentially doped with Mo(tfd-COCF₃)₃. (b) Diffractograms showing the radial intensity distribution for λ = 1 (blue) and λ ∼ 4 (green). (c) Angular distribution of the prominent 100 diffraction (azimuthal angle ϕ = 0, π is parallel to drawing direction).

Sequential doping allowed us to introduce the dopant subsequent to film casting and solid-state drawing. Films of P3HT were immersed for 48 to 72 h in solutions of the dopant Mo(tfd-COCF₃)₃ or F4TCNQ in acetonitrile (AcN; 5 g L^–1), an orthogonal solvent in which P3HT is insoluble. Both as-cast and stretched films show an increase in weight by ∼30 wt % upon doping with Mo(tfd-COCF₃)₃, and by ∼6 wt % in case of F4TCNQ, indicating a dopant concentration of ∼9 and ∼4 mol %, respectively (note that an increase in dopant concentration to 15 g L^–1 resulted in similar concentrations of ∼9 and ∼5 mol %). We carried out energy dispersive X-ray spectroscopy (EDX) on doped films to investigate to which extent the larger dopant Mo(tfd-COCF₃)₃ had diffused into the sample (Figure 1 and Supporting Information, Figure S2). EDX of cross sections of both as-cast and stretched films indicates that both dopants are evenly distributed throughout the bulk of the sample, as evidenced by a constant ratio of the intensity of the sulfur and fluorine signals, and a similar strength of the latter (cf. EDX of P3HT doped with F4TCNQ, Supporting Information, Figure S3). We conclude that sequential doping for the period of time chosen here, that is, 72 h, is sufficient to saturate the P3HT films with dopant.

To investigate the position of the dopant within the solid-state nanostructure, we compared WAXS diffractograms of as-cast and doped films. Mo(tfd-COCF₃)₃ doped films only show a marginal change in the q-spacing of crystalline peaks in comparison to the neat film of P3HT (Figure 2), which suggests that the bulky Mo(tfd-COCF₃)₃ does not penetrate the crystallites but resides in the amorphous domains. In contrast, WAXS diffractograms of F4TCNQ doped films (as-cast and stretched) confirm that the dopant ingresses into crystalline domains and sits between the side chains, as evidenced by the previously reported shift in the 100 and 020 diffraction peaks (Supporting Information, Figure S4).²⁰⁻²³ Further, we confirm that doping with Mo(tfd-COCF₃)₃ does not change the degree of anisotropy obtained through solid state drawing (cf. Supporting Information, Table S1).

Doping can have a pronounced effect on the mechanical properties of a conjugated polymer.¹ We therefore recorded the storage modulus E′ and loss modulus E′′ from −100 to +40 °C using variable-temperature DMA (Figure 3 and Supporting Information, Figures S5 and S6). We observe a T_g ∼ 20 °C that does not change upon tensile drawing or doping with Mo(tfd-COCF₃)₃ (Table 1), which implies that this type of dopant does not result in a more brittle material. Instead, doping with F4TCNQ appears to slightly increase the T_g to 40 °C (Supporting Information, Figure S6). Further, both neat and Mo(tfd-COCF₃)₃-doped P3HT feature a pronounced T_β ∼ −90 °C, below which side chain relaxation becomes arrested,²⁴ meaning that the polymer should be characterized by a high impact toughness. As-cast P3HT features a storage modulus of E′ ∼ 0.6 GPa at 0 °C, which increases to E_∥′ ∼ 1.1 GPa upon tensile drawing when measured parallel to the direction of orientation (Table 1). Instead, the perpendicular storage modulus E_⊥′ decreases to 0.2 GPa, giving rise to a high anisotropy of E_∥′/E_⊥′ ∼ 6. Upon doping the storage modulus of as-cast samples only slightly decreases to E′ ∼ 0.5 GPa. For stretched samples we measure the same E_⊥′ before and after doping, but observe a 3-fold decrease in storage modulus parallel to the direction of orientation to E_∥′ ∼ 0.4 GPa, leading to a lower anisotropy of about E_∥′/E_⊥′ ∼ 4. We explain the change in storage modulus upon doping with a reduced cohesion between adjacent polymer chains in amorphous domains where the Mo(tfd-COCF₃)₃ dopant is located, that is, the dopant acts as a plasticizer (note that deformation was carried out in the elastic region where only amorphous domains deform). Nevertheless, an appreciable storage modulus is maintained, for example, the value E_∥′ ∼ 0.2 GPa at room temperature is similar to the modulus of unoriented low-density polyethylene (LDPE).²⁵

Figure 3.

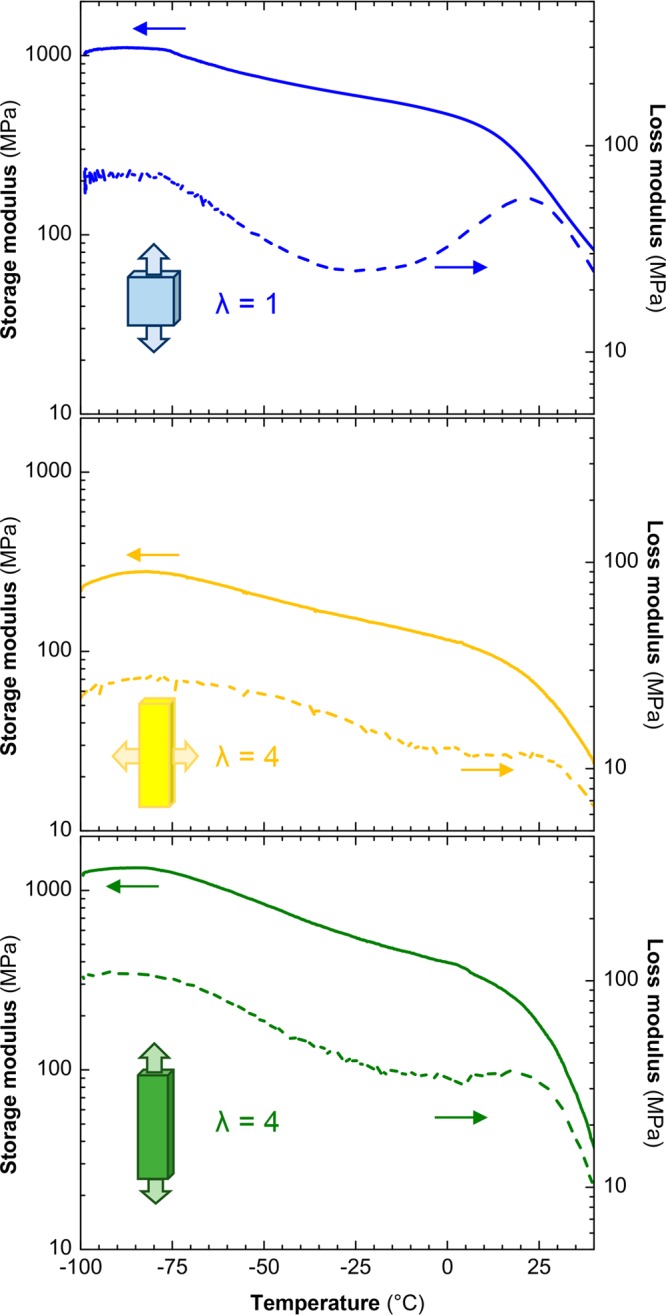
Dynamic mechanical analysis (DMA) thermograms of Mo(tfd-COCF₃)₃ doped P3HT: λ = 1 (blue), λ ∼ 4 perpendicular to the stretching direction (yellow), and λ ∼ 4 parallel to the stretching direction (green); Storage and loss modulus, E′ and E′′ (solid and dashed lines).

Table 1. Draw Ratio λ, Storage and Loss Modulus, E′ and E′′, at 0 °C, Glass Transition Temperature T_g, and β-Relaxation Temperature T_β from DMA (T_g and T_β from Peaks of E′′); Electrical Conductivity σ and Seebeck Coefficient α at Room Temperature.

dopant	λ (−)	Tg (°C)	Tβ (°C)	direction of measurement	E′ (GPa)	σ (S cm–1)	α (μV K–1)
none	1	23	–87	isotropic	0.6
	4	29	–93	⊥	0.2
	4	21	–90	II	1.1
Mo(tfd-COCF3)3	1	21	–91	isotropic	0.5	0.3 ± 0.1	138 ± 1
	4	20	–82	⊥	0.1	1.6 ± 0.4	113 ± 1
	4	17	–90	II	0.4	12.7 ± 3.3	112 ± 1

In a further set of experiments, we explored the thermoelectric properties of Mo(tfd-COCF₃)₃-doped P3HT. For as-cast films we measure a conductivity of σ₀ ∼ 0.3 ± 0.1 S cm^–1 and a Seebeck coefficient of α₀ ∼ 138 ± 1 μV K^–1, which differ considerably from the corresponding values of 34.1 ± 0.2 S cm^–1 and 64 ± 1 μV K^–1, respectively, found for 70 nm thin films. It appears that the bulk samples studied here are less heavily doped than thin spin-coated films. Since we do not observe a gradient in dopant concentration (cf. EDX; Figure 1), we argue that our bulk samples are saturated with the Mo(tfd-COCF₃)₃ dopant, and therefore, thin films cannot merely contain a higher concentration of the dopant. We tentatively propose that the higher conductivity of thin films is due to a more strongly doped surface layer where additional dopant does not need to fully diffuse into the polymer to still dope a significant fraction of the active layer. Further, we would like to point out that Mo(tfd-COCF₃)₃ (electron affinity EA ∼ 5.6 eV;^26,27 reduction potential E_red ∼ +0.39 V vs ferrocene²⁸) is a stronger oxidant than F4TCNQ (EA ∼ 5.2 eV²⁹), which allows the former, but not the latter, to dope disordered P3HT (cf. doping of regiorandom P3HT; Supporting Information, Figure S7). This explains why we observe a high electrical conductivity despite the dopant being located only in amorphous domains.

For stretched samples we find increased conductivity both parallel and perpendicular to the drawing direction, with values of σ_∥ ∼ 12.7 ± 3.3 S cm^–1 and σ_⊥ ∼ 1.6 ± 0.4 S cm^–1, respectively, leading to an anisotropy of σ_∥/σ_⊥ ∼ 8. In contrast, the Seebeck coefficient only slightly changes from α₀ ∼ 138 μV K^–1 to 112 μV K^–1 upon drawing, but does not display any anisotropy. As a result, the power factor of 16 μW m^–1 K^–2 that we measure along the drawing direction deviates from the empirical trend given by eq 1, leading to a significant gain upon stretching, that is, the power factor is about 5× larger than predicted (Figure 4). We also compared our results with F4TCNQ doped films, and find that the conductivity of as-cast P3HT σ₀ ∼ 0.4 S cm^–1 only increases to σ_∥ ∼ 5 S cm^–1 for stretched samples, accompanied by a lower Seebeck coefficient of ∼80 μV K^–1. As a result, the power factor of 3 μW m^–1 K^–2 that we measure along the drawing direction does not deviate significantly from the empirical trend given by eq 1.

Figure 4.

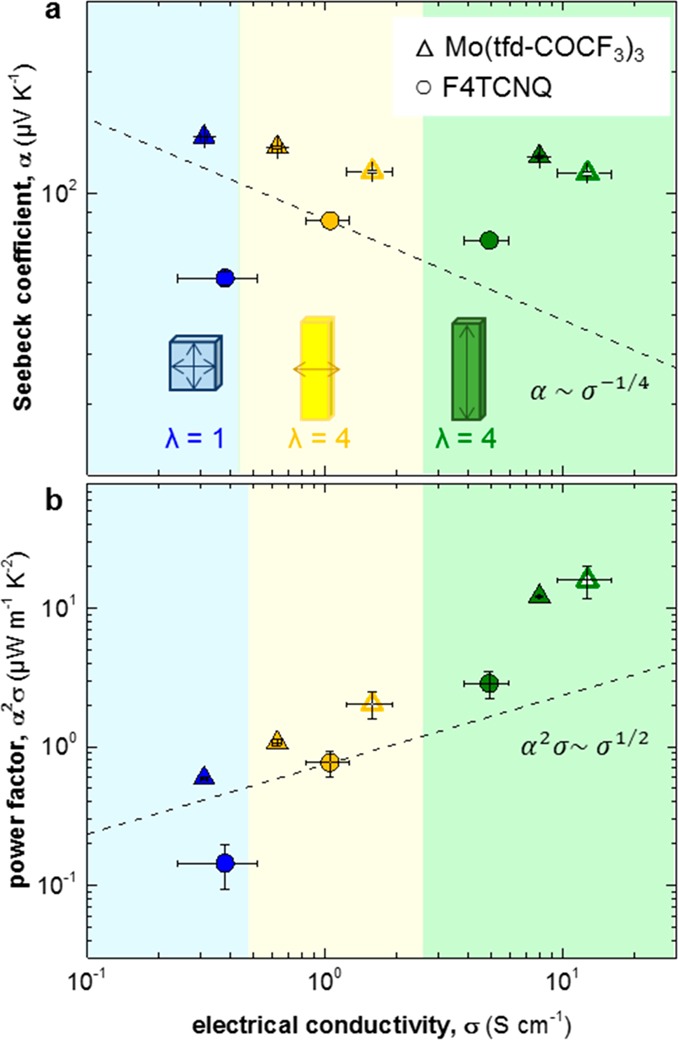
(a) Seebeck coefficient α and (b) power factor α²σ as a function of electrical conductivity σ for P3HT doped with Mo(tfd-COCF₃)₃ (triangles) and F4TCNQ (circles); closed symbols indicate 48 h doping; open symbols indicate 72 h doping; dashed lines show the empirical trends α ∼ σ^–1/4 and α²σ ∼ σ^1/2.

We constructed a simple model to rationalize the impact of anisotropy on the thermoelectric properties of the doped polymer. The model consists of a two-dimensional resistor network forming a rectangular grid (Figure 5b), where the resistance between sites i and j with energies E_i and E_j, randomly sampled from an exponential density of states (DOS; disorder = 60 meV),^30,31 is given by

3

where E_F is the Fermi level. Using the Einstein relation, the prefactor R₀ can be approximated by

4

where n is the total charge concentration, ν is the attempt frequency of hopping, which includes the tunneling probability, and ξ is a characteristic length scale in the direction of the current. Both ν and ξ can differ parallel and perpendicular to the drawing direction, giving rise to two prefactors R₀^∥ and R₀. We define an anisotropy ratio as R₀^⊥/R₀ that we vary from R₀^⊥/R₀ = 1 for an as-cast and, therefore, isotropic sample, to R₀^⊥/R₀ ≫ 1 for a highly oriented sample, in which the resistance is lower along the drawing direction due to a higher ν and/or ξ, that is, a higher charge carrier mobility along the drawing direction. Hence, the model assumes that, to a first approximation, stretching the sample affects the relative positions of the hopping sites (i.e., the nanostructure) rather than the site energies.

Figure 5.

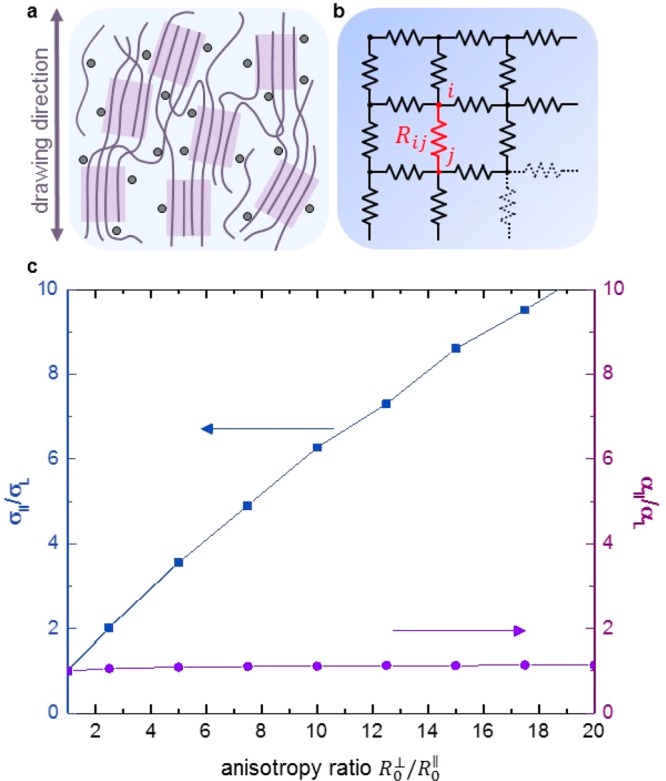
(a) Schematic of the nanostructure of tensile drawn P3HT illustrating crystals (purple) within an amorphous matrix (light blue); the dopant Mo(tfd-COCF₃)₃ (gray circles) is only located in amorphous domains. (b) Two-dimensional resistor network used to simulate the electrical properties of tensile drawn P3HT. Dots indicate hopping sites connected by resistive links. The resistance R_ij depends on the (random) energies E_i and E_j of sites i and j, as well as the temperature according to the (inverse) hopping rate, as calculated from the Miller-Abrahams expression, as outlined in the Supporting Information. (c) Anisotropy in electrical conductivity σ_∥/σ_⊥ and Seebeck coefficient α_∥/α_⊥ parallel and perpendicular to the drawing direction (charge carrier concentration c = 0.1).

The anisotropy in conductivity and thermopower are calculated by solving Kirchhoff’s laws for the resistor network as detailed in the Supporting Information. We find that the anisotropy in conductivity increases roughly linearly with the anisotropy ratio, reaching a value of σ_∥/σ_⊥ ∼ 8 for R₀^⊥/R₀ ∼ 10 (Figure 5c), while the Seebeck coefficient, in contrast, is only slightly enhanced with increasing anisotropy. Both findings agree with our experimental results (cf. Figure 4a), indicating that the tensile drawing mainly affected the material’s nanostructure while preserving the energetics.

We conclude that tensile drawing of the conjugated polymer P3HT creates the opportunity to enhance the thermoelectric power factor when doped with large acceptors such as Mo(tfd-COCF₃)₃. The conductivity strongly increases along the drawing direction, whereas the Seebeck coefficient is largely unaffected, leading to a power factor of up to 16 μW m^–1 K^–2. Doping of oriented samples does not affect the T_g ∼ 20 °C and an adequate storage modulus of, for example, E_∥′ ∼ 0.2 GPa is maintained at room temperature, which suggests that tensile drawing is a promising tool for the fabrication of flexible thermoelectric materials.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsmacrolett.8b00820.

• Experimental details, additional characterization, calculation of anisotropy, and supplemental figures (PDF).

The authors declare no competing financial interest.