Mesh convergence behavior and the effect of element integration of a head injury model

Abstract

Numerous head injury models exist that vary in mesh density by orders of magnitude. A careful study of the mesh convergence behavior is necessary, especially in terms of strain most relevant to brain injury. To this end, as well as to investigate the effect of element integration on simulated strains, we re-meshed the Worcester Head Injury Model (WHIM) at five mesh densities (~7.2–1000 k hexahedral elements of the brain). Results from explicit dynamic simulations of three cadaveric impacts and an in vivo head rotation were compared. First, scalar metrics of the whole brain only considering magnitude were used, including peak maximum principal strain and population-based median strain. They were further extended to deep white matter regions and the entire brain elements, respectively, to form two “response vectors” to account for both magnitude and distribution. Using benchmark enhanced full-integration elements (C3D8I), a minimum of 202.8 k brain elements was necessary to converge for response vectors of the deep white matter. This model was further used to simulate with reduced integration (C3D8R). We found that hourglass energy higher than the rule of thumb (e.g., up to 44.38% vs. <10% of internal energy) was necessary to maintain comparable strain relative to C3D8I. Based on these results, it is recommended that a head injury model should have an average element size of no larger than 1.8 mm for the brain. C3D8R formulation with relax stiffness hourglass control using a high scaling factor (e.g., 15) is also recommended to achieve sufficient accuracy without substantial computational cost.

Introduction

Finite element (FE) models of the human head serve as an important bridge to translate head impact kinematics into brain tissue responses. As tissue responses such as strain and strain rate are thought to cause injury ¹⁶, these models have been increasingly used to study the mechanisms of traumatic brain injury (TBI) and to predict its occurrence ³⁹. To date, numerous head FE models have been developed. However, even “validated” head injury models produce significantly discordant brain mechanical responses under identical impact conditions ¹³. The substantial model inconsistency precludes effective comparisons among simulation results and significantly hampers the collective efforts in the investigation of TBI biomechanical mechanisms.

One important contributor to such inconsistency is the substantially varied mesh resolution over several orders of magnitude ¹³. Early 3D models of the human head only consisted of hundreds of elements for the brain, with an estimated mesh size of ~ 19 mm ³⁷. Recent models have increased the numbers to thousands (1760 ³¹, 5320 for SUFEHM ³³, 7128 for the KTH model ¹¹; mesh sizes of ~9 mm, up to 7.73 mm, and 5.8 mm, respectively) and tens (~30k for SIMon ³⁶, ~55k for WHIM ¹⁵) and hundreds of thousands (~164k for GHBMC ²⁴; mesh sizes of 3.0 mm, 3.3 mm, and 2 mm respectively). Converting MRI voxels directly into brain elements could even reach the level of 1–2 millions of elements ^8,27; mesh size of ~1 mm). As FE model simulation accuracy depends on mesh size, a mesh convergence study is typically required to ensure that an accurate solution is achieved and independent of mesh size. However, only a few studies reported mesh convergence behaviors of a head injury model, which were especially lacking in terms of strain most relevant to brain injury.

Kleiven and von Host studied mesh size dependency with pressure but not strain ²⁰. Mao et al. extended a simplified 2D mesh of a rat brain to 3D to study mesh convergence using peak maximum principal strain in two representative regions. However, they did not use an actual 3D model due to challenges in creating a 3D brain mesh ²⁵. Their more recent study on a human brain model was similarly limited to pressure and relative brain-skull displacements, with no report on strain ²⁴. Another study reported mesh convergence behavior in strain, but it was averaged across the whole brain, without considering strain distribution ¹⁰.

Investigating strain distribution is likely important to the study of mild TBI, given the observed widespread neuroimaging alterations ⁴ and a diverse spectrum of clinical signs and symptoms ⁹. Therefore, there is a need for a more systematic mesh convergence study of a head injury model that considers both strain magnitude and distribution. This would allow identifying the appropriate mesh resolutions suitable for impact simulation to reduce inconsistencies among different head injury models.

In parallel, element integration schemes must also be considered, as they similarly amount to significant model inconsistency. Selectively reduced integration (reduced integration in volumetric terms, but full integration in deviatoric terms) was used in some head injury models ^6,17,18 to reduce volumetric locking. However, this integration scheme is susceptible to shear locking. It was observed that large element distortion could lead to unstable results as well as a high computational cost ³⁵.

Most head injury models adopt a “reduced integration” scheme (in both volumetric and deviatoric terms; with one integration point per element, vs. eight in “full integration” for hexahedral element). The drawback with this type of element is that it introduces mesh “hourglass” instability, which is especially severe with coarse meshes ¹. Typically, this is mitigated by introducing an artificial hourglass stiffness, with a rule of thumb to control its energy within a certain percentage relative to either internal (e.g. <10% ^11,26,27,40) or total energy of the system (which includes internal, kinetic, and hourglass energy components; e.g. <3%–10% ^7,36,38). However, this empirical rule was questioned for applicability in head injury models, where reasonable displacements were achieved when hourglass energy was much higher (200–300% of internal energy), but nonphysical nodal displacements occurred when the energy ratio was within the recommended level ³⁵. In addition, the different options for hourglass energy control (e.g., enhanced hourglass control ³⁴, relax stiffness control ²⁹, or no control ²⁸) further amounted to significant confusion among research groups that led to substantial model inconsistencies.

The aims of this study are two-fold. First, we investigate the mesh convergence behavior of a head injury model using impacts at both ends of the impact severity spectrum. We use enhanced full-integration for the brain (C3D8I element formulation), which is widely used as a benchmark element type immune to hourglass or shear locking issues together with reduced volumetric locking ¹. Second, by adopting the appropriate mesh density, we further examine the rule of thumb in controlling the hourglass energy using reduced integration scheme (C3D8R) by comparing strains against the baseline counterparts obtained from C3D8I. Based on these investigations, we provide recommendations for continual model development with an intention to minimize inconsistencies among head injury models. In turn, these efforts may help better facilitate the collective investigations of TBI biomechanical mechanisms in the future.

Materials and Methods

Re-meshed Worcester Head Injury Models (WHIMs)

We used the same high-resolution MRI used to develop the WHIM ¹⁵ for re-meshing. The WHIM has been extensively utilized to incorporate modeling with neuroimaging ^41,43 and to develop a real-time brain response atlas ^14,44,46. An improved multi-block structure was created (Truegrid; XYZ Scientific Application, Inc., Livermore, CA) to generate hexahedral elements of the brain at five distinct mesh resolutions (Fig. 1). The first three resolutions (number of brain elements ranging ~7.2–202.8 k) approximately corresponded to that of the KTH model ¹⁷/SUFEHM ³³, previous WHIM ¹⁵, and GHBMC ²⁴/THUMS ² (Table 1). Two additional mesh densities were created (number of brain elements of ~500 k and ~1000 k, respectively). The finest mesh was comparable to voxel-based models ^8,27, and it served as the baseline in this study.

Fig. 1.

Re-meshed Worcester Head Injury Models (WHIMs) at five distinct mesh densities, with hexahedral elements of the brain ranging from ~7.2 k to ~1000 k (left to right).

Table 1.

The numbers of nodes and elements of the brain (excluding those of other head components), and the corresponding element sizes for the five re-meshed models. Existing head injury models with comparable mesh densities are also shown for comparison.

	Model I	Model II	Model III	Model IV	Model V
Number of brain elements	7.2k	55.9k	202.8k	482.9k	954.4k
Number of brain nodes	9.9k	66.2k	227.4k	524.2k	1000k
Avg. element size (mm)	5.5±1.4	2.9±0.6	1.8±0.4	1.4±0.3	1.1±0.2
Models with similar mesh resolution	KTH 17/SUFEHM 33	Isotropic WHIM 15	GHBMC 24/THUMS v4.02 2	N/A	Voxel-based models 8,27

All meshes satisfied a variety of quality criteria ²⁴ (Table 2; histograms of the element quality measures are reported in Supplementary, Figs. A1–A5). For all models, the brain shared common nodes with elements of the surrounding cerebrospinal fluid (CSF), whose material was assigned with a low shear modulus to enable relative brain-skull tangential motion ²⁶. The brain was modeled by an isotropic first-order Ogden hyper-viscoelastic material determined from porcine brain (Table 3; tension test at a strain rate of 30/s; ³⁰). This material property was selected because it provided a reasonable response at both ends of the impact severity spectrum using the previous WHIM ⁴². Material properties of all other head components were identical to those of the previous WHIM ¹⁵. It should be noted that the re-meshed models here should not be considered as “validated” yet.

Table 2.

Summary of mesh quality measures for the five WHIMs based on a variety of quality criteria ²⁴. From left to right in brackets are models I–V, respectively. Detailed histograms of the element quality measures are reported in Supplementary.

Parameter	Criterion	Failure percentage	Max/min value
Warpage	<20º	[3, ~0, ~0, ~0,~0] %	[50.81, 56.48, 65.10, 60.35, 55.49]
Aspect	<3	[8, 1, 1, 1, 1] %	[6.61, 6.11, 5.62, 8.52, 10.18]
Skew	<50º	[1, 1, 1, 1, 1] %	[62.11, 64.35, 71.14, 72.78, 78.11]
Jacobian	>0.8	[38, 6, 1, 1, ~0] %	[0.33, 0.34, 0.41, 0.42, 0.40]
Min angle	>40º	[3, 2, 2, 1, 1] %	[26.88, 24.24, 17.17, 16.88, 11.79]
Max angle	<140º	[4, 2, 2, 1, 2] %	[162.99, 169.43, 168.13, 171.66, 176.28]

Table 3.

Material properties of the brain adopted for the re-meshed models, drawn from a porcine test ³⁰.ρ: density; µ₀: initial shear modulus; α: stiffening parameter; g₁, g₂, τ₁, and τ₂: Prony series parameters. k: bulk modulus.

ρ (kg/m3)	µ0 (Pa)	α	g1	g2	τ1 (s)	τ2 (s)	K (MPa)
1040	2780	6	0.5663	0.3246	0.0350	0.0351	219

Mesh convergence

The five re-meshed WHIMs were used to perform explicit dynamic simulations using three representative cadaveric head impacts (impact cases C288-T3, C380-T4, and C380-T6 ¹²) as well as a volunteer head rotation ³² as input. The two extreme impact conditions (peak magnitudes of resultant angular acceleration of 15.1–26.3 krad/s² vs. 299 rad/s²) served as the upper and lower severity bounds for the majority of real-world head impacts ⁴². They offered insight into the model behaviors for a range of concussive and sub-concussive head impacts on the field.

For nearly incompressible material such as the brain, it was important to use reduced integration on volumetric terms (e.g., C3D8, C3D8R, and C3D8I) to reduce volumetric locking ¹. Hexahedra with C3D8 formulation adopt full-integration in deviatoric terms but are susceptible to shear locking. This behavior was observed with the first-generation SIMon, where shear locking due to large distortion led to unstable results ³⁵. Nevertheless, the same element formulation was also employed in an earlier version of the KTH model ^17,19, which was recently revised to fully reduced integration, C3D8R ¹¹. C3D8R uses reduced integration in both volumetric and deviatoric terms. However, this element type is notorious for its nonphysical hourglass deformation, which must be controlled.

Given these considerations, we chose C3D8I elements to benchmark the mesh convergence behavior. This type of element enhances over C3D8 by introducing additional incompatible deformation modes into the element shape functions to further eliminate shear locking without inducing hourglass deformation (vs. C3D8R). C3D8I elements are widely used for model simulation benchmark tests in Abaqus ¹ (e.g., static analysis of a double cantilever beam ²¹; springback phenomenon in a split-ring test ²³). A recent study also identified C3D8I as the most accurate linear element in eigenfrequecy analysis of a real structure ²². Similarly, full integration S4 elements were also used for all 2D structures of the head injury models so that to avoid the need for hourglass control.

Response sampling

Simulation comparisons and mesh convergence depended on the response metrics of interest. For each simulation, maximum principal strains (ɛ) were first obtained in each brain element at every temporal time frame (at a resolution of 0.2 ms, as needed for the finest mesh). Element-wise peak values (ɛ_elm), regardless of the time of occurrence, were then calculated. They were further resampled onto an evenly distributed set of 3D sampling points via interpolation within the brain (at a spatial resolution of 1 mm³). Resampling the brain responses onto the same set of grid points was necessary to facilitate subsequent response comparison across various mesh resolutions.

To sample the brain response, the whole-brain peak maximum principal strain (ɛ_brain) was determined at the 95^th percentile level of ɛ_elm, regardless of the location of occurrence. In addition, a population-based pop50 measure was also obtained based on the resampled grid points (vs. FE model nodes ³⁴, which implied a uniform nodal distribution). Effectively, it represented the median strain of the entire brain (p_brain). The choice of this metric over the more common CSDM ³ was to avoid determining a strain threshold, which may not be valid here as the re-meshed models were not yet “validated” for injury studies. Regardless, both ɛ_brain and p_brain have been used as injury metrics for injury prediction ^17,34,41.

The two resulting scalar metrics effectively treated the whole-brain as a single unit but did not account for response distribution. To rectify, the two response metrics were further calculated for each of the 50 deep white matter (WM) regions of interest (ROIs) via a co-registered neuroimage atlas ⁴¹. The resulting group-wise response vectors, ɛ_ROIs and p_ROIs, characterized the brain response distribution in the deep WM regions. Essentially, they were a series of maximum peak principal strains and median strains of the ROIs, respectively. Analogously, element-wise response, ɛ_elm, served as a vector metric to characterize the response distribution of the entire brain. It was identical to the population-based median value when considering each element individually (thus, the latter was not included).

Response comparison

To investigate how mesh resolution affected simulation responses, the two scalar metrics (ɛ_brain and p_brain) from models I–IV were compared against those from the baseline (Model V) in terms of magnitude. For the three vector response metrics characterizing magnitude and distribution for either the deep WM regions or the whole-brain, linear regression (with zero intercept) and Pearson correlation were conducted using ɛ_ROIS, p_ROIS and ɛ_elm against their respective baseline counterparts. Response similarities in magnitude and distribution were measured using regression slope (k) and correlation coefficient (r), respectively.

For scalar metrics, a given mesh resolution was said to have converged when its difference relative to the baseline response was within 10%. For response vectors, mesh convergence was said to have reached when k was within 0.9–1.1 and r was above 0.9.

All simulations were conducted using Abaqus/Explicit (Version 2016; Dassault Systèmes, France). The computational costs (double precision with 45 CPUs (Intel Xeon E5–2698 with 256 GB memory) and GPU acceleration (6 NVidia Tesla K20 GPUs with 12 GB memory)) as well as the minimum time increments for all the models are reported in Fig. 2a.

Fig. 2.

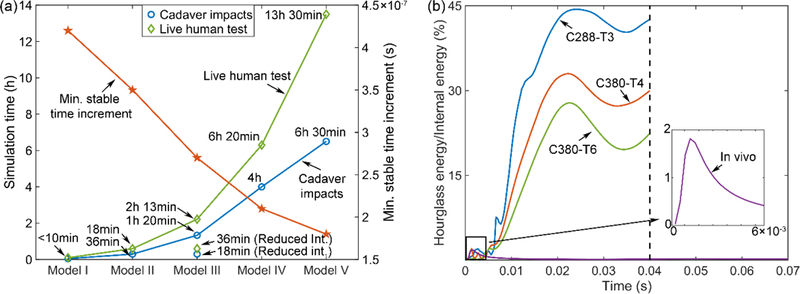
(a) Simulation runtime for the cadaver head impacts (averaged from the three impacts; duration of 40 ms) and live human head rotation (duration of 70 ms), together with the corresponding minimum stable time increment. (b) The ratio of the hourglass energy to internal energy for each head impact.

Element integration

Most head injury models employ reduced integration (C3D8R) to improve simulation efficiency (one integration point in each element vs. eight in a C3D8I element). A well-known drawback with this element formulation is its zero-energy “hourglass” mode, which was recommended to be minimized in order to preserve simulation fidelity. The empirical rule of thumb is to control the hourglass artificial energy to be within 3%–10% of the internal ^11,26,27,40 or total energy ^7,36,38. To investigate how effective this rule applies to a head injury model, we selected Model III to simulate the same head impacts using C3D8R elements for the whole brain. This model was selected because both of its ROI-wise response metrics were considered converged at this mesh resolution (see Results).

For hyerelastic materials, Abaqus recommends enhanced hourglass control ¹. This method uses stiffness coefficients based on the enhanced assumed strain method. However, it does not allow a user to adjust the energy control. Therefore, we chose to use relax stiffness hourglass control for investigation ²⁹. Specifically, the hourglass stiffness scaling factor was iteratively adjusted so that the linear regression, k, between ɛ_ROIS from C3D8R and those from the benchmark C3D8I elements was within 1.00±0.10 for all simulations. This led to a scaling factor of 15. The simulation runtimes and the energy ratios are reported in Fig. 2b.

Finally, additional simulations were conducted by controlling the hourglass energy within 10% of the internal energy (obtained with a scaling factor of 0.02), as recommended in previous studies ^11,26,27,40. The resulting responses were similarly compared with those from C3D8I using linear regression and Pearson correlation.

Results

Mesh convergence

Fig. 3 compares accumulated peak strains regardless of the time of occurrence (resampled ɛ_elm) for the five models. In general, ɛ_elm increased with the increase in mesh density. The coarsest mesh (Model I) produced substantially lower response magnitudes for all simulations.

Fig. 3.

Accumulated peak maximum principal strain, ɛ_elm, regardless of the time of occurrence, for the five models when simulating three cadaveric impacts and a live human head rotation. Higher mesh resolutions provide finer details in strain distribution, as expected.

The underestimation of scalar response metrics is quantified in Fig. 4. For ɛ_brain, at least 55.9 k elements for the brain were required to reach responses within 10% of the baseline. For p_brain, at least 202.8 k elements were needed.

Fig. 4.

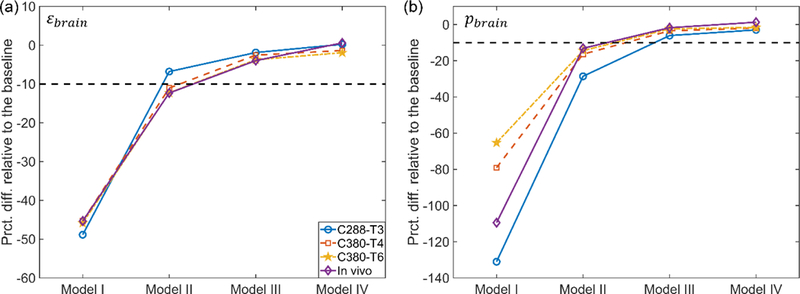
Percentage differences in whole-brain peak maximum principal strain (ɛ_brain; a) and a population-based median strain (p_brain; b) relative to the baseline for the five models. The magnitudes of both response metrics asymptotically increase with the increase in mesh density.

For vector response metrics, ɛ_ROIS and p_ROIs, k and r increased with the increase in mesh density (Fig. 5). Larger differences existed in ɛ_ROIS and p_ROIs for cadaveric impacts than in the in vivo head rotation. At least 55.9 k brain elements were needed to achieve convergence for the in vivo head rotation, whereas at least 202.8 k brain elements were necessary for cadaveric impacts.

Fig. 5.

Linear regression slopes (k; left, with zero intercept) and Pearson correlation coefficients (r; right) for ROI-wise peak magnitudes of maximum principal strain (ɛ_ROIS; top) and median strain (p_ROIs; bottom) relative to their respective baselines. It is clear that both ɛ_ROIS and p_ROIs asymptotically increase with the increase in mesh density. They are considered converged when the number of brain elements reached 202.8 k (Model III) and 55.9 k (Model II) for cadaveric and live human head impacts, respectively.

Similarly, for the whole-brain response, ɛ_elm, at least 202.8 k elements were required to reach convergence in terms of magnitude, k, while at least 482.9k elements were required to converge when considering the distribution in terms of r(Fig. 6).

Fig. 6.

Linear regression slopes (k; left, with zero intercept) and Pearson correlation coefficients (r; right) for element-wise peak magnitudes of maximum principal strain (ɛ_elm) relative to the baseline. While ɛ_elm starts to converge when the number of brain elements reached 202.8 k (Model III), the distribution requires at least 482.9 k brain elements (Model IV) to reach convergence.

Element formulation

When adjusting the scaling factor of hourglass stiffness so that ɛ_ROIs from C3D8R was nearly identical to the baseline in terms of magnitude (k of 1.02–1.03; Fig. 7a), both scalar metrics from C3D8R, ɛ_brain and p_brain, were within 10% and 5% difference relative to their baselines from C3D8I, respectively, regardless of the impact (not shown). The similarity in strain distribution in terms of r somewhat varied, with a range from 0.85 (C288-T3) to 0.99 (in vivo rotation; Fig. 7b). These observations were similar to the response vector, p_ROIs: while their magnitudes were similar on a group-wise basis (k of 0.98–1.02; Fig. 7c), the similarity in distribution somewhat varied, with r ranging from 0.86 (C380-T4) to 0.99 (in vivo rotation; Fig. 7d).

Fig. 7.

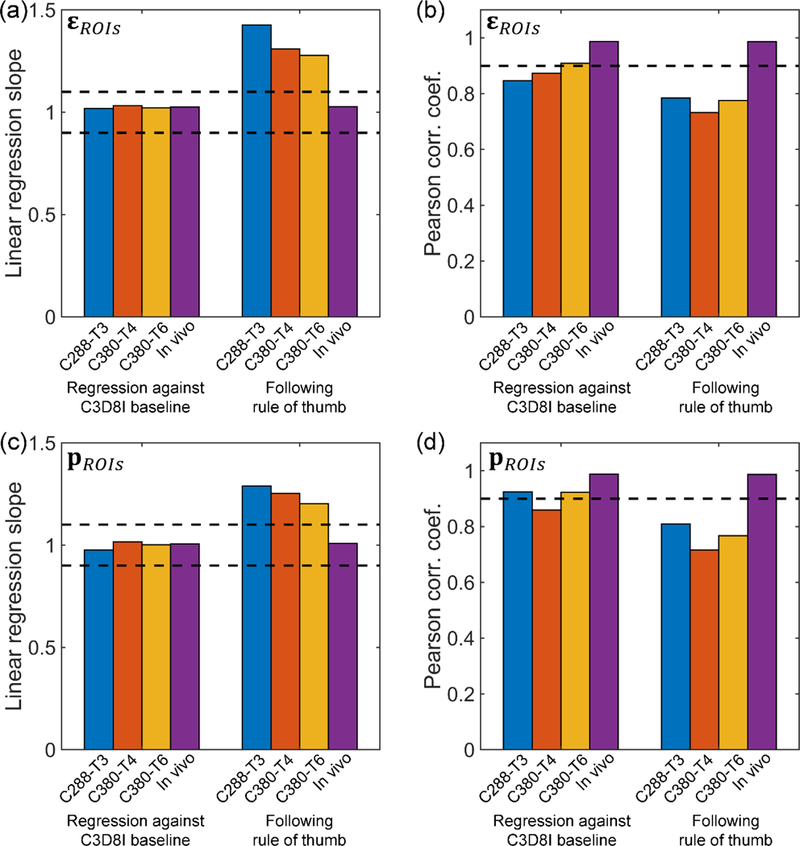
Linear regression slopes (left) and Pearson correlation coefficients (right) for ɛ_ROIs (top) and p_ROIs (bottom) relative to their respective baselines for each impact, using two competing strategies to control the hourglass energy. When maintaining the relative magnitude by regressing against the C3D8I baselines (i.e., linear regression slopes close to 1.0), the Pearson correlation coefficients somewhat decreased, especially for the cadaveric impacts. However, when following the rule of thumb, much large differences in magnitude and distribution existed relative to the baselines.

When instead following the rule of thumb to control the hourglass energy to be within 10% of the internal energy, both ɛ_brain and p_brain remained largely comparable to the baseline (relative difference of 4.7%–13.0% and −0.7% – −4.4%, respectively; not shown). However, both vector metrics from C3D8R, ɛ_ROIs and p_ROIs, were largely overestimated (k> 1.2) with significantly degraded similarity in distribution (r<0.81) relative to the baseline for cadaveric impacts, but not for the in vivo head rotation (k within 1.00±0.10 and r>0.98).

Discussion

Mesh convergence and element integration scheme are important issues in FE modeling. To date, however, they have been largely under-appreciated in brain injury studies. Here, we systematically investigated the two issues using a family of re-meshed WHIMs and head impacts at both ends of the impact severity spectrum relevant to real-world concussion and sub-concussion. Both scalar and vector strain metrics were used to quantify the significance of mesh resolution and element integration, as they have been used in injury predictions.

Mesh convergence

Mesh convergence was investigated using a benchmark element type, C3D8I. The mesh convergence behavior depended on the response metric and impact severity. For the scalar metrics of the whole brain only considering strain magnitude, convergence was approached when mesh density reached 55.9 k and 202.8 k elements for ɛ_brain and p_brain, respectively. They corresponded to average brain element size of 2.9 mm and 1.8 mm, respectively. For the vector metrics in the deep WM ROIs (ɛ_ROIs and p_ROIs), at least 202.8 k elements were necessary to converge in both magnitude and distribution. As expected, convergence became more challenging when using element-wise ɛ_elm to characterize response distribution of the entire brain, as it required at least 482.9 k elements (average brain element size of 1.4 mm) to converge in distribution (Model IV; Fig. 6b).

For the in vivo head impact, a lower mesh resolution (i.e. Model II with 55.9 k elements) may be considered sufficient to converge, regardless of the strain response metric. However, this was insufficient for cadaveric impacts, where significant underestimation in magnitude and disparity in distribution were observed (e.g., k of 0.71–0.81 and 0.72–0.81 for ɛ_ROIs and p_ROIs, respectively; Fig. 5a and Fig. 5c). The strain distribution appeared especially sensitive to mesh resolution, as r degraded further when considering element-wise strains of the whole brain (r of 0.72–0.83 for ɛ_ROIs in Fig. 5b vs. 0.60–0.77 for ɛ_elm in Fig. 6).

The lowest mesh density evaluated here (with 7.2 k brain elements; Model I) led to substantial underestimation in magnitude and poor distribution similarity, for all impacts simulated and strain response metrics used. For example, the differences in ɛ_brain and p_brain relative to their baseline counterparts ranged from −48.8% to −45.3% and from −131% to −65.3%, respectively (Fig. 4), and the linear regression slope, k was lower than 0.6 for both ɛ_ROIs and p_ROIs(Fig. 5a and Fig. 5c).

It may be tempting to suggest that models with very low mesh densities (e.g., < 10 k; SUFEHM ³³ and KTH model ¹¹) should be avoided because of the substantial strain underestimation. However, it should be recognized that the brain material properties of a given head injury model were often adjusted to satisfy model validation. Therefore, it was possible for a coarse model to use more compliant material properties for the brain in order to compensate for the under-estimation in strain magnitude. However, it remains to be explored whether the degradation in strain distribution can also be compensated for. Nevertheless, these findings do suggest that it may not be appropriate to adopt material properties of the brain obtained from a coarse mesh for use in a model with a much finer mesh, and vice versa.

Element integration scheme

Reduced integration improves computational efficiency relative to full integration but introduces a serious hourglass issue that requires an artificial stiffness to resist this nonphysical deformation. In general, head injury models have controlled the hourglass energy to be within 3–10% relative to either internal or total energy. However, the rationale behind the empirical rule was unclear in brain injury studies and was further questioned after an extensive literature review ³⁵.

We found that a much higher hourglass energy ratio (27.8% of internal energy for C380-T6 and 44.38% for C288-T3; Fig. 2b) was necessary to maintain a comparable group-wise strain magnitude in the deep WM ROIs for cadaveric head impacts. This was consistent with the previous finding, where reasonable displacements were obtained when hourglass energy was as much as 200–300% that of internal energy ³⁵. With much lower hourglass energy (<10%), significant overestimation in strain was observed, apparently because of the effectively more compliant material property of the brain (Fig. 7). In terms of strain distribution, using reduced integration led to some degradation in distribution similarity. This was more severe with lower hourglass energy (r of 0.85–0.91 and 0.86–0.92 for ɛ_ROIs and p_ROIs, respectively, for high hourglass energy; vs. r below 0.91 for both strain metrics; Fig. 7). For the in vivo head rotation, however, virtually identical strain responses in magnitude and distribution were obtained, regardless of how hourglass energy was controlled (Fig. 7).

By default, Abaqus utilizes enhanced hourglass control for hyperelastic material models ¹, which was employed in some studies ³⁴. This method uses stiffness coefficients based on assumed strain method without the need to scale hourglass stiffness. When this hourglass control was selected, brain behaved overly stiff with a substantial underestimation in strain, especially for cadaveric impacts (k ranged from 0.51 to 0.70 and from 0.49 to 0.67 for ɛ_ROIs and p_ROIs respectively). This observation agreed with the notion that enhanced hourglass control provides increased resistance for nonlinear materials ¹. Therefore, it is advised that enhanced hourglass control be avoided in head injury models.

Conclusion

Selecting an appropriate mesh resolution and element integration scheme for a given head injury model is a trade-off between model complexity, simulation runtime, and the actual use of the model for injury studies. When using a scalar metric such as peak maximum principal strain of the whole brain, coarser meshes at a resolution as low as 55.9 k for brain elements (average element size <2.9 mm; similar to the previous WHIM ^15,45) and a reduced integration scheme using relax stiffness control (but not the Abaqus recommended enhanced hourglass control) may be sufficient. When considering response distribution, at least 202.8 k brain elements (average element size <1.8 mm) were necessary to converge for response vectors of the deep WM ROIs, or even higher (482.9 k; average element size <1.4 mm) for the whole-brain response distribution. The latter two mesh resolutions were on the order of typical neuroimage resolutions of 1–2 mm³.

However, finer mehes also led to significantly increased computational runtime. Using the benchmark C3D8I elements, these three mesh resolutions (55.9 k, 202.8 k, and 482.9 k) required ~18 min, ~80 min, and ~4 h, respectively, to simulate a typical 40 ms impact (Fig. 2a). With reduced integration (relax stiffness control) using the 202.8 k model, the runtime was decreased to ~18 min, a 77.5% reduction. With a higher-than-recommended hourglass energy ratio (Fig. 2b), a reduced integration scheme was sufficient to maintain comparable response magnitude and distribution (Fig. 7). This would likely to be true for the majority of real-world concussive/sub-concussive head impacts, as their severities lie in-between the two extremes of impact severity spectrum ⁴².

The advantage of a response vector over scalar metrics in injury prediction was supported by a recent study, where feature-based machine learning/deep learning utilizing all of the voxel-wise WM fiber strains (vs. element-wise maximum principal strain evaluated here) significantly outperformed all scalar injury metrics via conventional logistic regression for concussion prediction. Comparable performances were also retained when using a subset of the response vector via feature-selection ⁵.

Given these considerations, therefore, we recommend that a head injury model with at least 202.8 k elements for the brain (average element size of no larger than 1.8 mm) is necessary to generate reliable response features of the deep WM ROIs for future TBI investigations. Further increasing the mesh resolution may require justification for any added benefit in accuracy or injury prediction performance. In addition, a reduced integration scheme using relax stiffness hourglass control (with a high scaling factor, e.g., 15) may also be preferred for improved computational efficiency without significant compromise in accuracy (magnitude and distribution) for the deep WM ROIs. These general guidelines based on results from the family of WHIMs are likely applicable to other head injury models as well, as they model the same organ and have adopted material properties of the brain to satisfy model validations against the same set of cadaveric impact cases.

Limitations

An important limitation of this work was the use of an isotropic material property of the whole brain, without considering white/gray matter heterogeneity or WM anisotropy ⁴⁵. In addition, we considered the response vectors on a group-wise basis, rather than focusing on a particular region ²⁵. From the accumulated fringe plot (Fig. 3), it was clear that higher mesh resolution did provide a more detailed response distribution, as expected. However, it merits further investigation how these finer response details contribute in practical applications such as injury prediction or correlation with neuroimaging or cognitive impairment.

A closer scrutiny in a specific “injured” region (vs. the group-wise ROIs here) may be important in a given injury case. However, this was not feasible in the current study, as the impact cases we simulated were either from cadaveric tests or an in vivo head rotation where no specific injury locations were available. For localized injury investigations, incorporating additional anatomical features such as the sulci may seem important, even though challenges may occur because of the lack of experimental data for validation at this scale of modeling.

Finally, we assumed results from C3D8I elements using the finest mesh were the most accurate baseline. However, this type of elements could still be subjected to potential errors due to poor element shape (trapezoidal vs. rectangular), skew angle, etc. ¹. While all of our models reasonably satisfied the various element quality criteria ²⁴ (Table 2 and Figs. A1–A5), such a concern cannot be eliminated. Unfortunately, no absolute “ground-truth” existed.