Ankle rotation and muscle loading effects on the calcaneal tendon moment arm: an in vivo imaging and modeling study

Abstract

In this combined in vivo and computational modeling study, we tested the central hypothesis that ankle joint rotation and triceps surae muscle loading have independent and combinatory effects on the calcaneal (i.e., Achilles) tendon moment arm (CTma) that are not fully captured in contemporary musculoskeletal models of human movement. We used motion capture guided ultrasound imaging to estimate instantaneous variations in the CTma during a series of isometric and isotonic contractions compared to predictions from scaled, lower extremity computational models. As hypothesized, we found that muscle loading: (i) independently increased the CTma by up to 8% and (ii) attenuated the effects of ankle joint rotation, the latter likely through changes in tendon slack and tendon curvature. Neglecting the effects of triceps surae muscle loading in lower extremity models led to an underestimation of the CTma, on average, particularly in plantarflexion when those effects were most prominent. We also found little agreement between in vivo estimates and model predictions on an individual subject by subject basis, alluding to unaccounted for variation in anatomical morphology and thus fundamental limitations in model scaling. Together, these findings contribute to improving our understanding of the physiology of ankle moment and power generation and novel opportunities for model development.

Introduction

The calcaneal (i.e., Achilles) tendon moment arm (CTma), the distance from the tendon’s line of action to the ankle joint center, is a critical component of the human musculoskeletal system, transforming triceps surae muscle forces into a moment about the ankle. The CTma can also exhibit highly complex and sometimes unanticipated changes during activities spanning isolated contractions to more dynamic activities such as walking. In vivo evidence from isolated ankle exercises almost universally supports that the CTma changes as a function of ankle joint rotation^{7, 9, 15, 17}, an intuitive outcome given the distal insertion of the tendon onto the calcaneus. Although magnetic resonance imaging (MRI) remains the gold standard for such measurements, more recent advances in the use of ultrasound imaging provide the opportunity to estimate the CTma during functional activity^{17, 23} Indeed, instantaneous changes in the CTma during the stance phase of walking allude to sizeable and potentially interdependent effects of ankle joint rotation and triceps surae muscle loading²³. Using MRI during isometric contractions, Maganaris (2004) found similar evidence for an increase in the CTma due to triceps surae muscle loading, arising primarily from bulging during force generation rather than from changes in the ankle’s center of rotation¹⁵. However, those results remain equivocal, as more recent measurements from isolated contractions have failed to capture such load-dependent effects. For example, Manal et al. (2013) found no significant effect of muscle contraction on the CTma¹⁸, and Fath et al. (2010) concluded that the relation between the CTma and ankle joint angle is independent of contraction level¹⁰ (note that we exclude here estimates derived from tendon excursions, given recent evidence⁴ that these are prone to significant errors). Perhaps accordingly, only the anatomical effects of ankle joint rotation on the CTma is currently considered in contemporary musculoskeletal models and simulations of the lower limb².

Physiological variations in the CTma, both those between and within individuals, are functionally meaningful. For example, Lee and Piazza (2009) and Baxter et al. (2012) found that sprinters, on average, have a smaller CTma than non-sprinters, which they suggest conveys a performance benefit in the form of greater plantarflexor mechanical work during acceleration^{3, 13} Lee and Piazza (2009) also reported that smaller calcaneal tendon moment arms estimated during isolated ankle rotation correlated with slower walking speeds in some older adults¹⁴. As a biomechanical explanation, we more recently added that, during walking, a smaller CTma in older versus young adults correlated with age-related reductions in peak ankle moment during push-off²². Equally striking, advanced age in that study also significantly attenuated changes in the CTma during the stance phase of walking; only in young adults did the CTma increase with stance phase muscle loading, by an average of 10% between heel-strike and push-off at the same ankle angle. Nevertheless, due to the complex neuromechanics of muscle-tendon and ankle joint function during walking, our mechanistic understanding of those CTma variations in young subjects remains incomplete.

Methodological approaches to estimate the CTma in vivo vary significantly, and the most rigorous (i.e., MRI) tend to have practical limitations for translation to functional activity. With its ability to overcome those limitations, ultrasound imaging is an attractive alternative that has been applied to acquire in vivo estimates of the CTma during walking. We posit that a similar ultrasound imaging approach may be leveraged during isolated contractions to better understand the factors governing physiological variations in the CTma, for example those during walking. To our knowledge, only one study has used motion capture-guided ultrasound imaging during isolated contractions to estimate the CTma in a protocol designed to identify the presence of changes due to triceps surae muscle loading¹⁸. Although the CTma was larger at peak ankle moment than at rest, those values did not differ significantly across the range of motion tested (20° dorsiflexion to 20° plantarflexion). However, there are several opportunities that motivate the need for additional study. First, upon closer inspection, this difference was larger at 20° plantarflexion than other ankle joint angles, alluding to a potentially greater effect of muscle loading at more plantarflexed postures. Indeed, tendon slack (due to operating lengths longer than required to develop passive tension) and tendon curvature (dorsoventral changes in the tendon’s line of action), both more prominent in ankle plantarflexion⁷, could influence the effect of muscle loading on the CTma. Second, isotonic contractions, in which load through the calcaneal tendon can be somewhat preserved across the ankle’s range of motion, provide a promising complement to isometric contractions that have yet to be systematically explored. Finally, motion capture-guided ultrasound allows instantaneous measurements, thereby providing a time history of changes in the CTma during isolated contractions that are not yet available in the literature.

Contemporary musculoskeletal models use triceps surae muscle-tendon geometry descriptions, and thus moment arms, that are derived from cadaveric data, scale in proportion to subject anthropometries, and vary based solely on ankle joint kinematics². These assumptions likely fail to fully capture the complex, potentially subject-specific variations in the CTma with wide-ranging implications for our use and interpretation of model predictions; models provide a foundation for interpreting motor control¹⁹, developing rehabilitation strategies⁶, and planning surgical intervention¹. In addition, despite sharing a common tendon, the three heads of the triceps surae (i.e., lateral gastrocnemius, medial gastrocnemius, and soleus) are treated as independent actuators, each having their own moment arm relative to the ankle joint center. This latter design decision may not be physiologically implausible; the calcaneal tendon is comprised of subtendons arising from each of those three muscles that may convey some mechanical independence²⁶. However, the moment arms attributed to those three muscles in our musculoskeletal models do have physiological bounds - those governed by the thickness of any subject’s calcaneal tendon. Thus, there is a growing need to integrate in vivo measurements with musculoskeletal models and simulations to inform our understanding of the physiology of ankle moment generation.

Our first goal was to determine the kinematic (i.e., ankle joint rotation) and kinetic (i.e., triceps surae muscle loading) determinants of physiological variations in the CTma during a series of isometric and isotonic plantarflexor contractions. We co-registered motion capture measurements with cine ultrasound images of the instantaneous calcaneal tendon line of action. Using in vivo estimates, we tested the hypothesis that variations in the CTma reflect independent and combinatory effects of ankle joint rotation and triceps surae muscle loading. Regarding those combinatory effects, we also hypothesized that the effects of muscle loading would be larger when in ankle plantarflexion than in dorsiflexion. Our second goal was to benchmark these in vivo estimates against predictions of the moment arms for each the three heads of the triceps surae derived from a widely used contemporary musculoskeletal model (i.e., Gait2392, OpenSim⁸). Here, we hypothesized that we would find little agreement between in vivo estimates and scaled musculoskeletal model predictions, but that correlations would be stronger at rest than under muscle contraction.

Materials and Methods

Subjects and protocol

An a priori power analysis determined that n=11 subjects would have 80% power to detect (p<0.05) a difference in the CTma due to muscle loading as small as one-half of that found previously during walking (i.e., 3.3±1.7 mm)23. Thus, we recruited eleven young adults (age: 25.0±5.4 years, height: 1.76±0.06 m, mass: 70.6±10.4, 4F/7M) participated. Subjects provided written informed consent according to a protocol approved by the UNC Biomedical Sciences Institutional Review Board. We excluded subjects based on the following: lower extremity injury or fracture in the preceding 6 months, taking medication which causes dizziness, having a leg prosthesis, and need of assistive device for walking.

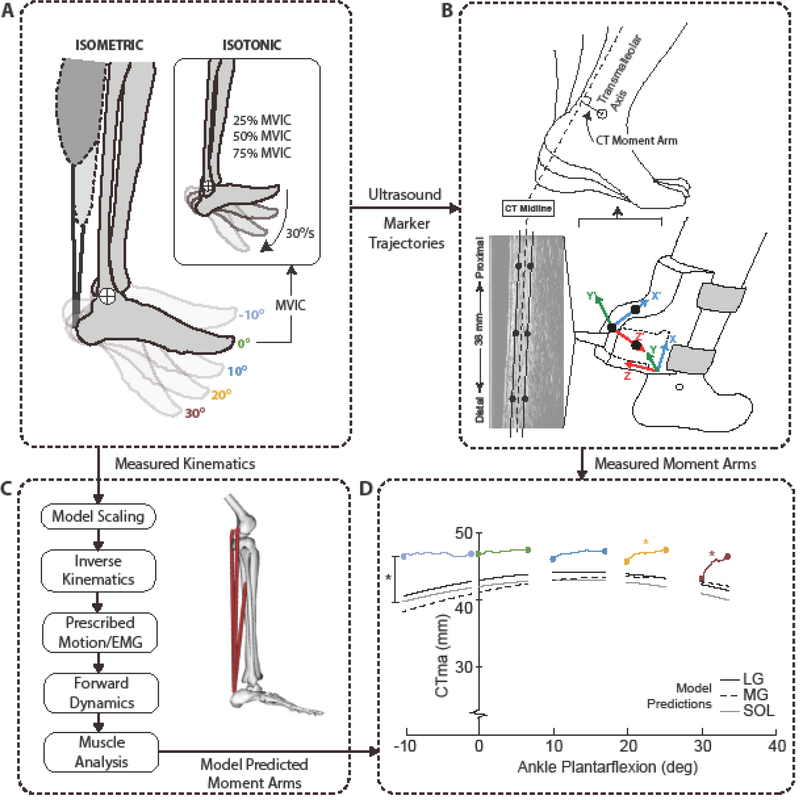
Subjects first completed a 6 min treadmill walking trial at 1.25 m/s to precondition their calcaneal tendon¹². All testing was subsequently performed on subjects’ right leg while the subject was seated in a computer-controlled dynamometer (Biodex Medical Systems, Inc., Shirly, NY). For all testing, we positioned the knee at ~20° flexion to replicate knee angle during the push-off phase of walking. Specifically, subjects performed a series of plantarflexor muscle contractions organized in two phases (Fig. 1A), completed in the same order as we explain below. Phase 1 tested the effects of muscle loading independent of ankle joint rotation. Here, subjects performed three ramped maximum voluntary isometric contractions (MVIC) at five ankle joint angles (10° dorsiflexion to 30° plantarflexion in 10° increments) performed in randomized order and each separated by at least one minute. We instructed subjects to follow a linear ramp increase over 2 seconds to reach their peak ankle moment before deceasing back to rest over another 2 seconds, following a verbal count by the investigator. Subjects were provided two opportunities to practice this MVIC at their first ankle angle, and we monitored the torque time series to ensure successful, symmetric ramped profiles. After completing Phase 1 testing, we immediately extracted each subject’s maximum ankle moment from the 0° isometric test for use in Phase 2. Specifically, Phase 2 tested the effects of ankle joint rotation independent of muscle loading. Here, subjects performed three isotonic contractions at 30°/s spanning 10° dorsiflexion to 30° plantarflexion, the same range used for isometric testing, at each of three plantarflexor moment generation levels (25%, 50%, and 75% of the maximum isometric value extracted from Phase 1).

Figure 1.

Summary of our experimental and modeling approach and analytics. (A) Subjects performed a series of isometric and isotonic plantarflexor contractions while seated in a dynamometer. (B) We manually tracked the edges of the calcaneal (i.e. Achilles) tendon in B-mode ultrasound images and co-registered those coordinates with the transmalleolar axis acquired via motion capture to estimate the instantaneous calcaneal tendon moment arm. (C) We also used scaled, subject-specific musculoskeletal models to estimate the moment arm of the three muscles that share the calcaneal tendon (LG: lateral gastrocnemius, MG: medial gastrocnemius, SOL: soleus). (D) A summary of in vivo estimates versus model predictions extracted from isometric contractions across the range of motion tested. The angle ankle variation evident in each contraction represents that associated with unavoidable heel rise during the isometric testing. Black asterisk (*) indicates significant (p<0.05) pairwise comparison between in vivo estimate and model prediction, and colored asterisks indicate significant effects of muscle loading for the associated ankle angle.

Equipment and measurements

For all testing, we recorded the net ankle moment and the foot attachment angle and angular velocity from the dynamometer at 1000 Hz using an analog-to-digital converter in synchrony with the ultrasound and motion capture measurements that follow. Simultaneously, a 38-mm transducer (L14–5W/38, Ultrasonix Corporation, Richmond, BC) operating at 70 frames/s recorded 128 lines of ultrasound radiofrequency (RF) data from a 20 mm deep longitudinal cross section of each subject’s right calcaneal tendon. A custom orthotic positioned the transducer distal to the soleus muscle-tendon junction and approximately 6 cm superior to the calcaneal insertion. Finally, eight cameras from a 14-camera motion capture system (Motion Analysis, Corp., Santa Rosa, CA) operating at 100 Hz recorded the three-dimensional positions of 14 retroreflective markers, including anatomical markers placed on each subject’s right medial and lateral malleoli, first and fifth metatarsal heads, calcaneus, and lateral knee joint center, 7 tracking markers placed on their lateral right thigh and lower leg, and 3 markers placed on the ultrasound orthotic. These orthotic markers remained fixed for the duration of the study and tracked the position and orientation of the ultrasound image plane. In a pre-calibration session prior to commencing the study, we used an instrumented wand to digitize the coordinates of three points on the face of the transducer and used those points to establish: (i) a “probe-centered” coordinate system defining the imaging plane and (ii) the transformation between the imaging plane and a coordinate system defined by those markers placed on the custom orthotic, consistent with previously published work²³.

Data reduction and analysis

We low-pass filtered the analog data from the dynamometer and motion capture data using 4^th order Butterworth filters with cutoff frequencies of 100 Hz and 6 Hz, respectively. We used custom MATLAB scripts to process the ultrasound imaging data, co-register those data with motion capture measurements, and thereby estimate the CTma (Fig. 1B). We first created cine B-mode images of the calcaneal tendon from the recorded RF data across time regions of interest from each trial. For isometric trials, assuming a symmetric loading and loading cycle, this time region started with the rise in ankle moment using a 5% threshold of the peak value and ended at the instant of peak ankle moment. For isotonic trials, this time region started at the onset of ankle rotation and ended at the instant of peak plantarflexion. Using those B-mode images, we manually tracked²³ the coordinates of the superficial and deep edges of the calcaneal tendon at three locations (proximal, median, and distal) within the image window, each longitudinally separated by 10 mm along the length of the imaged tendon.

We then defined lines of action associated with the superficial and deep tendon edges as lines of best fit through points corresponding to the respective edge, and the tendon midline as the line of best fit through points corresponding to average of the superficial and deep edges at each location. Finally, leveraging data from the pre­calibration session, we co-registered each tendon line of action with the instantaneous transmalleolar axis by transforming the local coordinates from the image plane and motion capture marker locations into a common reference frame. We then estimated three values of the CTma at each time point as the perpendicular distance between each tendon line of action and the transmalleolar axis. Based on the recommendations of Siston et al. (2005), we used the transmalleolar axis as a surrogate for locating the ankle’s sagittal plane center of rotation²⁴. In that study, direct comparisons to MRI show agreement to within 2–4 mm between the transmalleolar axis and more sophisticated estimates of the ankle’s center of rotation²⁴. Finally, we computed group average moment arm time series by time-normalizing and averaging the three trials for each condition and then computing the average and standard deviation across subjects.

Musculoskeletal modeling

For each subject, we scaled a seven-segment, 18 degree-of-freedom musculoskeletal model of the pelvis and lower limbs (Gait2392, OpenSim⁸) to a standing calibration trial that included additional markers on each subject’s pelvis and left leg². We then performed inverse kinematics using marker trajectories recorded from one representative trial for each experimental condition (5 isometric trials and 3 isotonic trials) per subject (Fig. 1C). We used the inverse kinematics results and an available MATLAB routine (prescribeMotionInModel, simtk.org) to prescribe each subject’s ankle and knee joint kinematics in subsequent forward dynamic simulations of each trial. We also prescribed excitations for the medial gastrocnemius, lateral gastrocnemius, and soleus muscles in a manner that would correspond to those elicited during the experimental trials. Specifically, we focused here on our isometric trials, in which we prescribed linear ramped excitations that started from rest (0) and linearly increased to maximum (1) at the instant of measured peak ankle moment. We then performed forward dynamic simulations using the prescribed kinematics and muscle excitations for each trial per subject, and extracted the resulting moment arm of the medial gastrocnemius, lateral gastrocnemius, and soleus.

Statistical analysis

Our in vivo outcome measures focused on the CTma estimated from the tendon’s midline. First, for the isometric measurements, a two-way repeated measures (rm) ANOVA tested for significant main effects of and interactions between ankle joint angle and triceps surae muscle loading (rest, peak ankle moment) on the CTma using an alpha level of 0.05. When a significant interaction was found, post-hoc least significant difference (LSD) pairwise comparisons were focused on identifying the ankle joint angles at which muscle loading affected the CTma. Second, for isotonic contractions, a similar two-way rmANOVA tested for significant main effects of and interactions between ankle joint angle and triceps surae muscle loading (25%, 50%, 75% MVIC) using the CTma extracted at the five ankle joint angles corresponding to those from the isometric trials (i.e., −10°, 0°, 10°, 20°, and 30° plantarflexion).

We then evaluated model predictions versus in vivo measurements. First, to test our hypothesis, we calculated correlations between in vivo measurements and computational model predictions of the CTma, the latter estimated as the average of the lateral gastrocnemius, medial gastrocnemius, and soleus, both: (i) at rest and (ii) at peak ankle moment. We repeated those analyses at 10° dorsiflexion and 30° plantarflexion, representing the range of motion tested in this study. Second, a 3-way rmANOVA tested for a significant interaction between method (measurement vs. prediction) and load (rest vs. peak moment) and joint angle (10° dorsiflexion vs. 30° plantarflexion) effects on the CTma. Finally, for in vivo measurements and model predictions, we calculated correlations between the CTma at 10° dorsiflexion and at 30° plantarflexion both: (i) at rest and (ii) at peak ankle moment. Here, although the conventional modeling framework may neglect muscle loading effects, we anticipated agreement both: (i) within the in vivo measurements and (ii) within model predictions across the ankle’s range of motion.

Results

In vivo effects of ankle joint rotation and triceps surae muscle loading

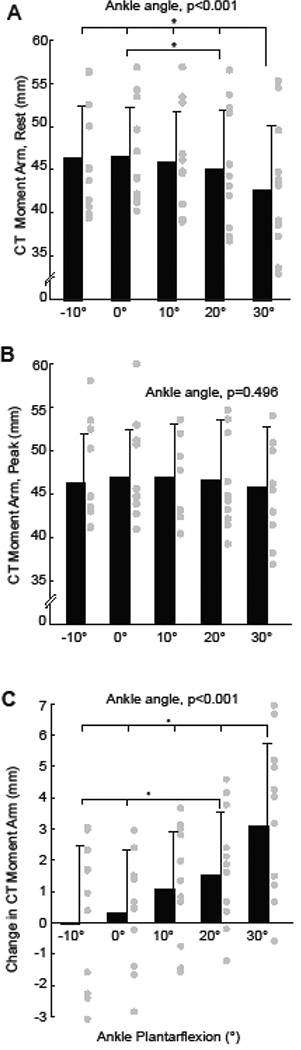
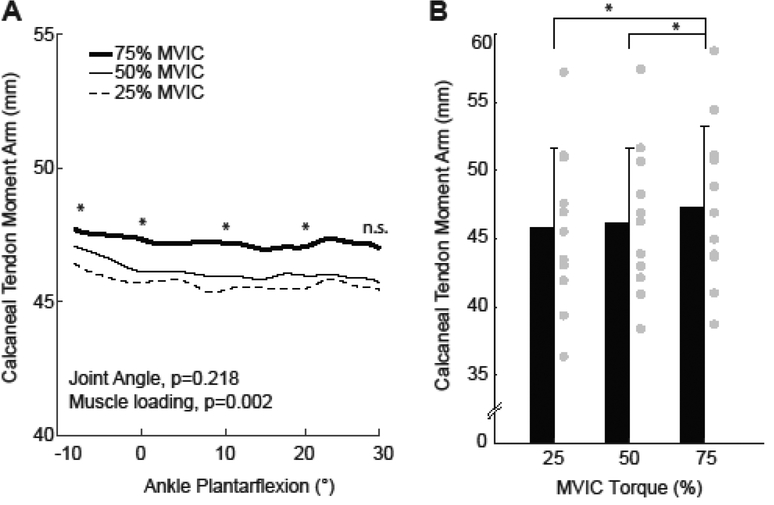
We found a significant interaction between joint angle and triceps surae muscle loading on the CTma during maximum isometric voluntary contractions (p<0.001) (Fig. 1D, Fig. 2). In the absence of muscle loading during the isometric tasks, we found that the CTma became systematically smaller with increasing ankle plantarflexion (p<0.001, Fig. 2A). For example, at rest, the CTma was 7% smaller on average at 30° plantarflexion than at 10° dorsiflexion. In contrast, at maximum isometric activation, we found no significant effect of ankle joint angle on the CTma (p=0.496, Fig. 2B). We similarly found no significant main effect of ankle joint rotation across the range of motion tested during isotonic contractions performed at ≥25% maximum isometric ankle moment (p=0.218, Fig. 3). Triceps surae muscle loading also independently increased the CTma. During ramped isometric contractions, the CTma increased by as much as 8% compared to resting values (Fig. 2C). However, this effect reached significance only for the two most plantarflexed ankle positions (i.e., 20°: p=0.001; 30°: p=0.008). We also found a significant main effect of muscle loading on the CTma during concentric isotonic contractions (p=0.002, Fig. 3). Post-hoc comparisons revealed this result was driven by modest but progressive increases in the CTma from 25% maximum isometric ankle moment to 50% (p=0.032) and again to 75% (p=0.017) - effects that held across much of the range of motion tested.

Figure 2.

Group mean (standard deviation) calcaneal (i.e., Achilles) tendon moment arms from isometric contractions across the range of ankle angles tested. From each contraction, we extracted (A) the resting value, (B) the value at peak ankle moment, and (C) the change from rest to peak ankle moment. Repeated measures ANOVA main effects of ankle angle shown, with significant (p<0.05) pairwise comparisons designated by asterisks (*). Gray circles indicate individual subject data for each condition and outcome measure.

Figure 3.

(A) Group mean calcaneal (i.e., Achilles) tendon moment arms from isotonic contractions performed at three levels of ankle moment generation across the range of motion tested. (B) Group mean (standard deviation) calcaneal tendon moment arm from (A) averaged across the range of motion, thereby illustrating the main effect of muscle loading. Repeated measures ANOVA main effects of joint and angle and muscle loading shown, with significant pairwise comparisons designated by asterisks (*). p<0.05 significant. n.s.: not significant. Gray circles indicate individual subject data for each condition.

Computational model predictions

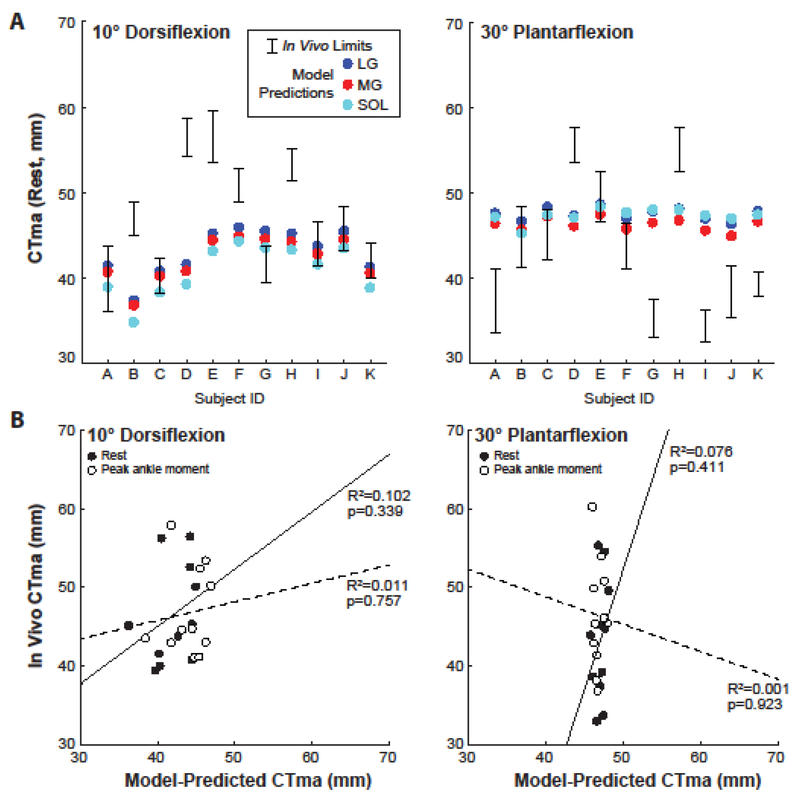
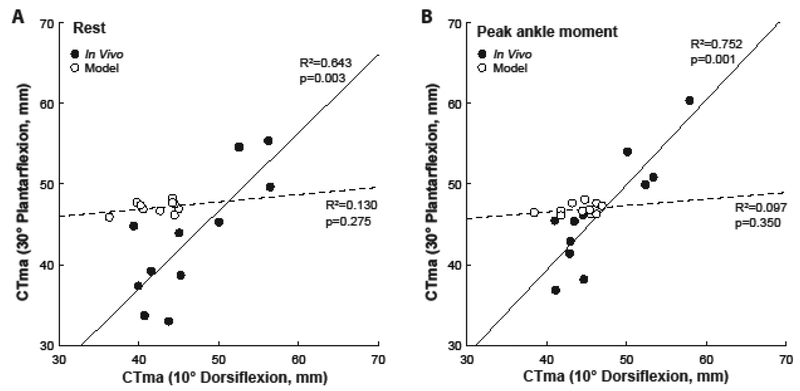
A significant interaction revealed that, compared to in vivo measurements, model predictions underestimated the CTma by an average of 10%, but this reached significance only for resting values at 10° dorsiflexion (method×load×angle, p<0.001; pairwise: p=0.037) (Fig. 1D). In addition, the range of moment arms predicted for individual triceps surae muscles was smaller than the physiological limits imposed by the tendon’s dorsal-ventral thickness for all subjects (Fig. 4A). However, despite some similarities in average values, we found no measurable agreement between in vivo measurements and computational model predictions (Fig. 4B). Finally, only the in vivo measurements were significantly and positively correlated between 10° dorsiflexion and 30° plantarflexion (Fig. 5). Indeed, in contrast to in vivo measurements, model predictions failed to correlate with themselves across the ankle’s range of motion.

Figure 4.

(A) Individual subject comparisons between in vivo estimates and model predictions for each of the muscles that share the calcaneal tendon (LG: lateral gastrocnemius, MG: medial gastrocnemius, SOL: soleus) at angles representing the range of motion tested. In vivo estimates show the range of physiologically plausible values for each subject as defined by the superficial and deep edges of the calcaneal tendon. (B) Correlations between in vivo estimates and model predictions at 10° dorsiflexion and 30° plantarflexion for values extracted at rest (solid line) and at peak ankle moment (dashed line) from isometric testing. Model predicted values here represent the average moment arm of the three muscles that shared the calcaneal tendon.

Figure 5.

Correlations between the calcaneal (i.e., Achilles) tendon moment arm at 10° dorsiflexion and 30° plantarflexion for in vivo estimates (solid lines) and model predictions (dashed lines) at (A) rest and at (B) peak ankle moment extracted from isometric testing.

Discussion

This study had two overarching goals, accomplished through the complementary use of in vivo imaging and musculoskeletal simulation. First, we sought to quantify the effects of ankle joint rotation and triceps surae muscle loading on physiological variations in the CTma during isolated contractions. As hypothesized, and consistent with earlier measurements made using the same experimental approach during walking²³, we found here that the CTma exhibits independent and combinatory effects of ankle joint rotation and triceps surae muscle loading. Second, we sought to benchmark in vivo estimates of the calcaneal tendon moment arm against contemporary model predictions of those for each the three heads of the triceps surae. Model predictions, when averaged across our study cohort, were closer to in vivo estimates than anticipated. However, as hypothesized, we found lesser agreement and little to no correlation between in vivo estimates and model predictions on an individual subject by subject basis. In addition, while we found distinct effects of muscle loading that clearly differentiated in vivo estimates from model predictions as anticipated, our results also point to fundamental limitations in model scaling that we expand upon below. Briefly, unaccounted for variation in anatomical morphology may compromise our ability to reliably estimate subject-specific calcaneal tendon moment arms from conventional musculoskeletal models - another major takeaway from this study that should inform the design of future work.

Ankle joint rotation independently affected resting values of the CTma during isolated isometric contractions. Although ankle rotation effects on the CTma are regularly reported, the directionality of these effects varies across the availabile literature^{7, 9,15, 17, 18} Here, we found that the CTma decreased with increasing plantarflexion, an observation consistent with some^{9, 15, 20} but not all^{7, 18} prior reports, and also consistent with musculoskeletal geometry descriptions in the modeling framework used in this study (Fig. 1D)². However, a novel contribution of this study is that we found no effect of ankle joint rotation when the calcaneal tendon was under load, whether during isometric contractions at peak ankle moment or during isotonic contractions performed at ≥25% maximum isometric ankle moment. We interpret these findings to suggest that while ankle joint rotation systematically influences the CTma, a result fully consistent with prior reports and model predictions, muscle loading substantially attenuates those effects. One possible explanation is that the effects of ankle joint rotation on the CTma, at least those with increasing plantarflexion, are governed primarily by tendon slack and tendon curvature - factors that are themselves both attenuated by triceps surae muscle loading. For example, Csapo et al. (2013) reported a significant dorsoventral curvature of the calcaneal tendon in plantarflexion, an effect that those authors estimated would decrease the CTma by ~5% and posited could be offset by rigorous triceps surae muscle loading. Although our specific ankle rotation effects contradict those in Csapo et al. (2013), who found larger values with increasing plantarflexion, the influence of tendon curvature suggested in that paper is highly consistent with the 7% reduction we observed across the range of motion tested.

Our results fully support the conceptual premise that the transmission of muscle force alters the tendon’s line of action and thereby increases the CTma. This premise also has support from muscles in the upper extremity²⁵. As hypothesized, isometric contractions revealed that muscle loading effects on the CTma were most prominent in plantarflexed joint positions, explaining up to an 8% increase from resting values at 30° plantarflexion. Moreover, isotonic contractions performed in a dynamometer, while not perfect in achieving constant tendon tension, do provide a valuable means to regulate muscle loading during ankle joint rotation, which we found to support and bolster findings from isometric contractions. Specifically, we found that the CTma increased by ~3–4% during isotonic contractions, on average, when exerting ankle moments prescribed as 75% MVIC versus 25% MVIC values. Together, this would suggest that approximately half of the variation in the CTma due to muscle loading occurs over 50% of the range of ankle moment generating capacity, and thus that these effects may scale in proportion to muscle loading. More curiously, we found more uniform increases in the CTma due to muscle loading during isotonic contractions than during isometric contractions spanning the same range of ankle rotation. One likely explanation is that inadvertent heel rise, a well-documented occurrence for isometric plantarflexor tasks¹⁶ and which was largest in this study at more neutral and dorsiflexed postures, led to joint rotation effects at those ankle angles that offset any increase due to muscle loading.

The potential implications of muscle loading effects on the CTma, or any moment arm across the musculoskeletal system, include their relevance to the development and use of contemporary musculoskeletal models. Indeed, muscle-tendon geometry descriptions in these models vary according to ankle joint kinematics alone. In this study, we show that neglecting the effects of triceps surae muscle loading in these models leads to an underestimation of the CTma, on average, particularly in plantarflexion when those effects are most prominent. This may be especially relevant when simulating locomotor tasks, in which peak ankle moment and power generation occur as the ankle moves into plantarflexion and the need for mechanical advantage at the ankle is most critical. By benchmarking the independent and combinatory effects of joint rotation and muscle loading, we hope to improve understanding of the physiology of ankle moment generation that can be leveraged by the musculoskeletal modeling community. As one example, future work may assess the efficacy of muscle force multipliers that vary as a function of ankle angle and muscle excitation in forward dynamic simulations of human movement.

Despite some similarities in average values across the range of ankle motion tested (Fig. 1D), and as hypothesized, we found no measurable agreement between in vivo estimates of the CTma and model-predicted values among individual subjects (Fig. 4). Although not strongly in support of our third hypothesis, as neither correlation proved statistically significant, we did find modestly better agreement between these values at rest than at peak ankle moment, at least for more dorsiflexed ankle positions. Poor correlations at 30° plantarflexion were at least in part affected by the almost complete loss of inter-subject variation, and thus lack of sufficient distribution, in model-predicted values for more plantarflexed joint positions. This outcome was interesting considering a wide range of AT moment arms and anthropometric measurements across our study cohort (see supplementary material). The compression of values across our study cohort at 30° plantarflexion may also explain why, unlike in vivo estimates, model-predicted values of the CTma failed to correlate with themselves across the range of motion tested - an unanticipated outcome. Although inter-subject variation in model-predicted values evident at 10° dorsiflexion failed to improve correlations with in vivo estimates, it does illustrate the influence of model scaling on CTma predictions. However, our results suggest that conventional model scaling procedures likely fail to account for variation in anatomical morphology critical to reliably estimate subject-specific moment arms. Although, knowing if and how to perform such scaling remains a challenge; previous work has revealed little evidence that calcaneal tendon moment arms predictably scale to anthropometric measurements²⁷ or correlate to body height¹¹. Our results support those earlier studies; a post-hoc exploratory analysis found that in vivo estimates of the CTma at rest at 10° dorsiflexion failed to significantly correlate with subject mass (p=0.42), height (p=0.17), foot length (p=0.78), or shank length (p=0.50). In addition, none of these anthropometric measurements, and thus presumably the amount of conventional scaling required, correlated with the difference between those in vivo estimates and model predictions (p-values≥0.16). The required complexity of model development and interrogation procedures should be most informed by the scientific question at hand. For example, in this study we avoided assumptions regarding the complex anatomical organization and twisted nature of sub-tendons comprising the calcaneal tendon, which could influence force transmission from the individual triceps surae muscles^{21, 26} However, in the event that those questions regard the physiology of net ankle moment or power generation, more sophisticated scaling procedures may be necessary, particularly with regard to individual subject estimates. In those cases, additional studies that combine musculoskeletal models with subject-specific MRI are needed to inform precise recommendations to improve model scaling.

There are several assumptions and limitations in this study relevant to the interpretation of our in vivo estimates and musculoskeletal modeling approach. First, we used the instantaneous transmalleolar axis as a surrogate for locating the ankle’s sagittal plane center of rotation. This methodological decision is consistent with the recommendations of Siston et al. (2005), who quantitatively compared five anatomically-based methods (including the transmalleolar axis) and two kinematically-derived model fits to estimate the functional ankle joint axis compared to ground truth measurements from subject-specific MRI²⁴. Moreover, this approach is identical to earlier measurements made during walking²³, during which more sophisticated approaches to track the ankle joint center, such as computing the finite helical axis, may be impractical. Nevertheless, we acknowledge that our in vivo estimates are themselves based on a model of the ankle joint. Based on our individual subject data, we can exclude the possibility that these decisions introduced systematic bias in our computational model comparisons. However, their contribution to differences we report as load-dependent effects will require additional. We also opted not to correct for an anatomical offset between the transmalleolar axis and the talus, as recommended by Bruening et al. (2008), based on the level of uncertainty in the specific correction factor due to inter-subject variation⁵. 2D ultrasound can also only resolve moment arms from the imaging plane, which we carefully selected to closely approximate the sagittal plane. We can thus not comment on any variation across the mediolateral width of the tendon. Moreover, while the ankle joint may undergo complex 3D rotation during functional activity, our protocol largely confined ankle rotation to the sagittal plane. Based on recent evidence²⁸, unanticipated inversion/eversion of the foot is unlikely to have affected our CTma estimates. Second, the accuracy of our coordinate transformations, and thus the conversion of the tendon’s line of action to 3D coordinates, rests on the resolution of our motion capture system to accurately estimate the positions of the probe tracking markers. An earlier Monte Carlo simulation determined that tracking errors encompassing standard deviations of ±1 mm at any one location would introduce only small (1.6%) variations in the estimated CTma23, adding confidence to our results. Regarding our modeling approach, we opted to benchmark our in vivo estimates against predictions from OpenSim’s Gait2392, given its widespread use in the biomechanics community. It is unclear how well our results would generalize beyond this model. Indeed, variations on lower extremity musculoskeletal models, even within the OpenSim modeling framework, continue to become available. We also used conventional model scaling practices with default uniform settings for marker weightings based on a standing calibration due to their widespread use and thus relevance to the community. Although not routinely performed in simulations of human movement, we acknowledge that different marker weightings are possible. This represents an added opportunity for future work focused on improving best practices in model scaling, at least for those interested in more accurate predictions of muscle-tendon moment arms such as those of the triceps surae.

To summarize, in this combined in vivo and computational modeling study, we provide evidence that ankle joint rotation and triceps surae muscle loading have independent and combinatory effects on the CTma that are not fully captured in contemporary models used to simulate human movement. This outcome is fully consistent with our earlier interpretations of the mechanisms governing physiological variations in the CTma observed during walking. Despite being treated as independent muscle-tendon actuators, model-predicted moment arms for the individual triceps surae muscles are at least consistent with the physiological limits imposed by the tendon’s dorsal-ventral thickness for all subjects. However, we also conclude that variation in anatomical morphology, something that is not well accounted for in these musculoskeletal models, may limit our ability to reliably estimate subject-specific calcaneal tendon moment arms.