Abstract
We investigated the volumetric and kinetic profile of the conformational landscape of a poly dA loop DNA hairpin (Hp) in the presence of salts, osmolytes and crowding media, mimicking the intracellular milieu, using single-molecule FRET methodology. Pressure modulation was applied to explore the volumetric and hydrational characteristics of the free-energy landscape of the DNA Hp, but also because pressure is a stress factor many organisms have to cope with, e.g. in the deep sea where pressures even up to the kbar level are encountered. Urea and pressure synergistically destabilize the closed conformation of the DNA Hp due to a lower molar partial volume in the unfolded state. Conversely, multivalent salts, trimethylamine-N-oxide and Ficoll strongly populate the closed state and counteract deteriorating effects of pressure. Complementary smFRET measurements under immobilized conditions at ambient pressure allowed us to dissect the equilibrium data in terms of folding and unfolding rate constants of the conformational transitions, leading to a deeper understanding of the stabilization mechanisms of the cosolutes. Our results show that the free-energy landscape of the DNA Hp is a rugged one, which is markedly affected by the ionic strength of the solution, by preferential interaction and exclusion of cosolvents as well as by pressure.
INTRODUCTION
A significant portion of the global biosphere (∼62%) exists at a depth in excess of 1000 m and is therefore subject to high hydrostatic pressure (HHP) of 100 bar or more, and can reach up to 1 kbar in the Mariana Trench of the Pacific Ocean (1,2). A plethora of organisms are thriving under such extreme conditions, such as in the deep sea floor, marine hydrothermal vents and volcanic environments, which are also discussed to be the potential birthplace of life on Earth (3). Adaptation mechanisms must exist to stabilize biomolecular systems and ensure life under such harsh environmental conditions. Yancey et al. have found that extremophiles acquire a particular set of osmolytes to combat the extreme conditions and the amount of particular osmolytes such as trimethylamine-N-oxide (TMAO), increases with increasing depth of capture (4,5). To reveal the underlying mechanisms of adaptation, the combined effects of pressure and cosolutes mimicking intracellular conditions on the stability and conformational dynamics of biomolecular systems, such as membranes, proteins and nucleic acids, have to be explored (3). Apart from the biological relevance, high-pressure studies on biomolecular systems are also fundamental from the physical-chemical point of view (1,6–8). Whereas temperature dependent studies provide the change of enthalpy (ΔH) and entropy (ΔS) upon conformational transitions or reactions of biomolecules, complementary pressure studies provide volumetric information (ΔV), which are generally linked to changes in structure (packing) and hydration. According to Le Châtelier’s principle, pressure shifts the conformational equilibrium of the system towards states with smaller partial molar volume. The driving forces dictating pressure-induced conformational shifts are the release of packing defects or voids and changes in hydration (e.g. upon exposure of charged residues), resulting in an overall smaller volume of the system (1,8,9–17).
Even though HHP studies have become a common biophysical technique in studying the thermodynamics and kinetics of biomolecular systems, pressure studies on nucleic acids are still relatively scarce (9,12,14–21). In particular, the effect of cosolutes, such as salts, osmolytes and crowding agents mimicking intracellular conditions, on the folding landscape and structural dynamics of nucleic acids are still largely under research (17,18,21–24). Canonical DNA duplex structures such as B-DNA are generally found to be pressure resistant (14,15). Application of pressure decreases the Watson-Crick H-bond distance, favors base stacking interactions and hence stabilizes the double-stranded DNA structure (14,15). Conversely, only recently it has been found, pioneered by the Sugimoto, Chalikian and Macgegor labs, that noncanonical DNA structures, such as G-quadruplex DNA and polydA loop DNA hairpins, are rather sensitive to pressure (16,17,19–21).
Herein, we have used a DNA hairpin (DNA Hp) that contains 32 adenine residues in the loop (Figure 1) (25), which has recently been found to be pressure sensitive (9,17). Hairpins regulate gene expression, act as target sites for protein recognition and nucleation sites for higher order RNA structures, and they play an important role in DNA recombination and transposition (26–28). Hairpins are also found in applications as biosensors and in DNA nanotechnology (29,30). The stem-loop hairpin structures are also very attractive systems from a biophysical point of view to investigate the base pairing and unpairing kinetics (25,31). The stability of these structures depends on a complex interplay of base stacking interactions, H-bonding and hydration (32). The solution environment plays an important role in modulating these interactions and controlling the structure, dynamics and function of these biomolecules (17,24,33).
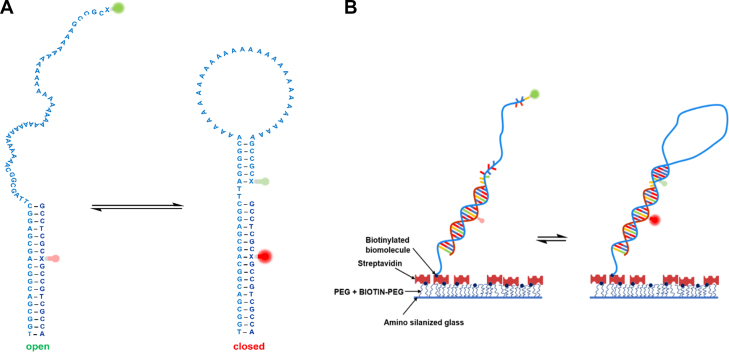
Figure 1.
(A) Chemical structure of the open and closed conformational state of the Atto 550 (donor) and Atto 647N (acceptor) labeled DNA Hp. The positions of the donor (green) and acceptor (red) fluorophore are shown as fluorescent bulbs. The open state has a large donor-to-acceptor separation and therefore displays a low FRET. Loop formation in the closed state leads to a smaller donor-to-acceptor separation and therefore to a high FRET signal. Monitoring the FRET intensity versus time traces allows also to determine the dynamics (rate constants) of the conformational changes involved. (B) Schematic diagram of the surface preparation for the immobilization of the DNA Hp. First, the cover slip is coated with aminosilane and then PEGylated to avoid nonspecific binding of the biomolecule. In the next step, avidin is attached to the biotinylated surface. In the final step, biotin-labeled DNA Hp along with its fluorescent markers are attached to the avidinylated surface. The DNA Hp is labeled with biotin using a C6 spacer, which eliminates any detrimental effects of surface attachment and allows the molecule to undergo spontaneous conformational changes.
Knowledge of the energy and conformational landscape of DNA hairpins is of fundamental biological interest. Despite a number of recent studies on DNA Hps, a deep understanding of the folding energy landscape of this class of biomolecules is still lacking and a subject of debate (17,31,34–37). The poly dA loop DNA hairpin was chosen owing to the significant pressure sensitivity compared to the double-stranded DNA and smaller loop DNA or RNA hairpins. Further, it is a well-characterized system under ambient buffer conditions. Initial studies, which also include fluorescence correlation spectroscopy (FCS), have revealed a two-state system with a distinct free energy barrier between them (31,34,35,38). Later studies based on single-molecule Förster resonance energy transfer (smFRET), diffusion decelerated FCS, dual-beam fluorescence cross correlation spectroscopy and laser temperature-jump studies have indicated a rather rugged energy landscape with possible involvement of stable and metastable intermediates, and recent smFRET studies on such hairpin systems again indicate a two-state behavior (17,36,39,40). In addition to the sketchiness of these data, the scenario of how different types of cosolutes affect the conformational landscape of such hairpin systems and the rate constants of conformational transitions remains still largely unexplored. Herein, we put a spotlight on the effect of various salts, osmolytes and crowding agents on the structural transitions of a DNA Hp (Figure 1A) by using smFRET, which has several advantages over ensemble techniques (41–44). FRET measures distance on the nanometer length scale (typically 2–10 nm) and therefore on the single-molecule level, which allows to distinguish different conformational states that are often masked in an ensemble experiment upon averaging. Further, the dynamics of the conformational transitions can be studied under equilibrium conditions, so synchronization is not necessary. On the other hand, pressure studies are carried out, which are perfectly suited in mapping volumetric (packing and hydrational) properties of the folding energy landscapes of the DNA Hp. Such smFRET measurements under high pressure have only recently been realized by utilizing a square-shaped silica microcapillary system, which provides minimum optical aberration and at the same time withstands pressures as high as 2 kbar (17).
We have chosen monovalent (K+), divalent (Mg2+) and trivalent (Co3+) cationic salts to investigate the effect of charge density on the folding energy landscapes of the DNA hairpin under pressure. Osmolytes are small, neutrally charged organic cosolutes accumulated by organisms to combat osmotic stress, such as high salinity, HHP and the presence of denaturants. We used two commonly used osmolytes, TMAO as a stabilizing and urea as a destabilizing osmolyte. Ficoll has been used to study the effect of macromolecular crowding on the folding energy landscapes of the DNA Hp. Ficoll is a copolymer of sucrose and epichlorohydrin and forms a network structure at higher concentrations (45). All pressure dependent smFRET measurements were carried out under freely diffusing condition. The volume changes (ΔV) obtained for the conformational transitions of the DNA hairpin in the absence and presence of the cosolutes from the high-pressure smFRET measurements provide a novel mechanistic understanding of packing and hydration effects in dictating the conformational preferences. Additional smFRET experiments carried out under immobilized conditions at ambient pressure revealed the underlying dynamic information (rate constants) of the conformational transitions, which is inaccessible from diffusion-based measurements as the observation time is limited by diffusion. Moreover, smFRET under immobilized measurements allowed us to unambiguously identify the presence of low-populated and intermediate states in the course of conformational transitions, which are difficult to assign from diffusion-based measurements, only. Overall, the present study provides crucial volumetric and kinetic information on the DNA Hp in the presence of biologically relevant cosolutes. Moreover, the results obtained are also immensely helpful in understanding the adaptation mechanisms of extremophiles used to combat environmental stresses.
MATERIALS AND METHODS
DNA sequence and sample preparation
The nucleotide sequence for the hairpin strands used in the smFRET measurements under freely diffusing and immobilized conditions are H1: 5′-biotin-TGG CGA CGG CAG CGA GGC TTA GCG GCA AAA AAA AAA AAA AAA AAA AAA AAA AAA AAA AGC CGC X-3′ (X is T-Atto 550) and H2: 5′-TGG CGA CGG CAG CGA GGC TTA GCG GCA AAA AAA AAA AAA AAA AAA AAA AAA AAA AAA AGC CGC X-3′ (X is T-Atto 550), respectively. The sequence of the complementary strand is A2: 5′-GCC TCG CXG CCG TCG CCA-3′ (X is T-Atto 647 N). The oligonucleotide strands were synthesized and fluorescently labeled by IBA Life Solutions GmbH (Göttingen, Germany). The complementary oligonucleotide strands (H1 and A2, H2 and A2) were annealed according to a reported protocol to prepare the double-stranded DNA hairpin. Both the hairpin strand (H1 or H2) and the complementary strand (A2) were mixed in a 1:1 ratio in buffer containing 20 mM Tris–HCl, 50 mM NaCl (pH 8.0) to a final concentration of 1 pmol μL−1. The annealing was performed by first heating the sample at 95°C for 5 min, followed by a gradual cooling to room temperature at a rate of −0.5°C min−1 using a thermocycler.
TMAO, urea, Ficoll PM 70, tris(hydroxymethyl)aminomethane hydrochloride (Tris–HCl), molecular biology grade potassium chloride (KCl) ≥ 99.0%, magnesium chloride (MgCl2) anhydrous (≥ 98.0%) and hexammine Co(III) chloride ([Co(NH3)6]Cl3) were procured from Sigma-Aldrich (Germany) and used as received. D-glucose, glucose oxidase from Aspergillus niger, catalase from bovine liver were purchased from Sigma-Aldrich (Germany), 6-hydroxy-2,5,7,8-tetramethylchromane-2-carboxylic acid (Trolox) from Fisher Scientific GmbH (Germany). Sodium chloride (NaCl), DNase, Ribonuclease free tips were purchased from VWR International GmbH (Germany). The high-pressure smFRET measurements were carried out in a square-shaped flexible fused silica capillary (WWP 050375, Polymicro Technologies), which was procured from CM Scientific (UK). Bottom-less flow channels (sticky slide VI0.4) and glass coverslips with geometry 25 mm × 75 mm and thickness 175 μm were purchased from Ibidi GmbH (Martinsried, Germany) to prepare the sample chamber with 6 channels for the smFRET measurement under immobilized conditions. N-[3-(trimethoxysilyl)propyl]ethylenediamine for the aminosilanization of the coverslip in immobilized smFRET measurements was purchased from abcr GmbH (Karlsruhe, Germany). Methoxy polyethylene glycol-succinimidyl carbonate (mPEG-SC) and biotinylated polyethylene glycol-succinimidyl carbonate (Biotin-PEG-SC) for the PEGylation of the aminosilanized coverslip were obtained from Laysan Bio Inc. (USA). Streptavidin from Streptomyces Avidini was procured from Sigma-Aldrich (Germany). Sodium bicarbonate (NaHCO3) was purchased from Biochrom GmbH (Berlin, Germany). All the measurements were performed in a buffer containing 20 mM Tris–HCl, 15 mM NaCl (pH 7.5). The buffer also contains 3 wt% D-glucose, 0.02 mg mL−1 catalase, 0.1 mg mL−1 glucose oxidase and 1 mM trolox to reduce photobleaching and photoblinking of the fluorophores. The buffer solutions were filtered using Whatman puradisc 30 syringe filters (GE Healthcare Life Sciences) of pore size 0.2 μm to remove any large particles from the solution.
High-pressure methodology and smFRET measurements
High-pressure smFRET measurements under freely diffusing conditions were carried out in a square shaped flexible fused silica capillary with outer diameter 360 μm and inner diameter 50 μm (17,46). The capillary serves both as an optical window and mechanical body of the high-pressure cell. The optical window thickness of the capillary is ∼150 μm resembling the standard coverslip used in smFRET measurements. Details of this set up are fully described in a recent report (9). The smFRET measurements were carried out in a commercial time resolved confocal fluorescence microscope (MicroTime 200, PicoQuant). Details of the setup are described elsewhere (47). The pulsed interleaved excitation (PIE) FRET technique was used to filter the signal of the dually labeled species from the singly labeled species. In PIE-FRET, alternating laser excitation is used such that the fluorescence due to donor excitation appears in the early time window and fluorescence due to direct excitation of the acceptor appears in the late time window (48–50). Such information is used to determine the photon stoichiometry, which allows one to separate the dually labeled species from either donor only labeled or acceptor only labeled species. The fluorescence coming from dually labeled species only are used to calculate the FRET efficiency (E). Donor and acceptor fluorophores are excited by using pulsed diode lasers (LDH series, PicoQuant) with pulsed repetition rate of 20 MHz of wavelength 560 and 635 nm, respectively. The excitation power in the diffusion-based smFRET mode was 12 μW, while for the immobilized-based smFRET measurements, an excitation power of 0.7 μW was used. The excitation light of the green and red laser is reflected to the entrance port of the microscope with the help of a quad band dichroic mirror (ZT 405/488/560/640, Chroma). The fluorescence was collected in the same optical path guided through a dichroic mirror, a 575 nm long pass filter (HQ 575 LP, Chroma), and spatially filtered by using a 50 μm pinhole, which only allowed the light to pass which comes from the focal spot, and thus defined the observation volume. The fluorescence light coming from the donor and acceptor fluorophore were then spectrally separated into two detection channels by using a dichroic mirror (FF 650 Di 01, Semrock). In addition to that, two band pass filters FF01–593/40 and FF01–676/29 were used in front of the donor and acceptor fluorescence detection channel, respectively, to further suppress spectra leakage and background signals. Two SPCM-AQR (Perkin Elmer Inc.) series single photon avalanche diodes (SPAD) were used to detect the donor and acceptor fluorescence. A time correlated single photon counting unit with the TimeHarp 200 PCI (Peripheral Component Interconnect) board in a Time-Tagged-Time Resolved mode was used to store each photon with individual timing and channel information to generate the donor and acceptor fluorescence traces with time.
Analysis of smFRET data under freely diffusing conditions
All the high-pressure smFRET measurements were carried out in solution under freely diffusing conditions. Each transit of the donor and acceptor fluorophore labeled DNA hairpin through the observation volume gives rise to characteristic fluorescence signals, also known as fluorescence bursts, due to multiple excitation and emission cycles. These fluorescence bursts were recorded photon by photon in the donor and acceptor fluorescence detection channels and were binned into a 1 ms time window, which is close to the diffusion time of the DNA hairpin, to generate the characteristic fluorescence intensity versus time traces in the donor and acceptor channel. The concentration of the DNA hairpin was kept at ∼200–300 pM to ensure that on average only one molecule is present in the confocal volume at a given time. A threshold criterion was used to separate the single-molecule fluorescence bursts from background noise. Only when the sum of the fluorescence photons in a time bin (1 ms) is larger than a threshold value, it is regarded as a single-molecule event (51,52). The photons above the threshold value in each burst were used to calculate the FRET efficiency, defined by E = nA/(nA+γ nD), where nA and nD are the number of photons in the acceptor and donor channel, respectively; γ is a correction factor that accounts for the differences in the fluorescence quantum yield (ϕA and ϕD) and detection efficiency (ηA and ηD) of the donor and acceptor fluorophore, respectively, defined as γ = (ϕAηA)/(ϕDηD); γ = 0.88 for the donor-acceptor pair Atto 550 and Atto 647N and the SPCM AQR series SPAD detectors.
Measurement of smFRET and data analysis under immobilized conditions
To study the conformational dynamics over an extended period of time, the molecule needs to be localized in space. This is achieved by immobilizing the molecule on the glass coverslip via biotin–streptavidin interaction using reported procedures (44,53). The important point in the surface immobilization of biomolecules is to avoid nonspecific binding of the molecule on the glass surface. In the very first step, the glass coverslip is cleaned using a plasma cleaner to remove any organic impurities, which is followed by washing with MilliQ water and drying in a nitrogen stream. Surface passivation is initiated with aminosilanization of the glass coverslip. To this end, the glass coverslip is dipped into a solution of 1% (v/v) 3-aminopropyltriethoxysilane in slightly acidic methanol (5% v/v acetic acid) for 10 min. Excess silane is washed away with MilliQ water and blow drying. The silane coated coverslips are then fixed to the sticky slide to prepare the flow channel. Next, the flow channels are incubated with a solution of 98% (w/v) mPEG-SC and 2% (w/v) BIOTIN-PEG-SC in 100 mM NaHCO3 buffer (pH 8.25) for 3–4 h to prepare the biotinylated glass surface. The flow channels are then repeatedly rinsed with MilliQ water to remove any excess unattached PEG, which is followed by drying in a nitrogen gas stream. In the next step, the glass surface is avidinylated by incubating the flow channel with a 1 mg mL−1 solution of streptavidin in a buffer containing 20 mM Tris–HCl, 15 mM NaCl, pH 7.5, for 15 min, and the excess unattached streptavidin is washed away by rinsing with buffer multiple times. Finally, the biotin-labeled DNA hairpin with fluorescent markers is attached to the avidinylated glass surface by incubating the flow channel with a 20 pM solution of the DNA hairpin in buffer for 20 min. The unattached DNA hairpins are removed by repeated rinsing with buffer solution. A scheme of the immobilization setup is depicted in Figure 1B. Before starting the measurements, the flow channel is filled with imaging buffer containing 3 wt% D-glucose, 0.02 mg mL−1 catalase, 0.1 mg mL−1 glucose oxidase and 1 mM trolox to reduce the photoblinking and photobleaching of the fluorophores (54,55). The corresponding cosolvents and crowding agent were added to the imaging buffer prior to the measurements.
At a 20 pM concentration, around 50 single molecules are immobilized in an area of 12 × 12 μm2. The bright spots indicating single molecules remain well separated. Point measurements were taken on these bright spots. Single-step photobleaching of the donor and acceptor fluorescence recorded indicate that the FRET is due to a single molecule. The donor and acceptor fluorescence intensity versus time trajectories from about 30 single molecules were exported as a .dat file for further analysis in ebFRET, which is a freely available programme run in Matlab to obtain the kinetic information of the transitions between different conformational states (56,57). FRET efficiency (E) versus time trajectories were obtained from the donor (Atto 550) and acceptor (Atto 647N) intensity versus time series. E is calculated by dividing the donor intensity by the sum of the donor and acceptor intensity at each point in the trajectories (see the ESI). Each FRET state (E-value) represents a distinct conformational state. By determining the time, the molecule stays in one particular FRET state (denoted as dwell time) before making a transition to another state, provides the kinetics for that conformational transition. The dwell time for each transition in the E versus time trajectories are determined using the Hidden Markov Model (HMM) in the ebFRET software package. HMM allows to identify the states and the probability of transitions between different states in an otherwise noisy time series using a variational Bayesian approach (58). The raw dwell time distribution histograms obtained are then integrated to generate a cumulative plot where each point indicates the number of counted events that have a dwell time less than or equal to the specified time (59,60). These cumulative distribution plots are then fitted with single exponential functions to obtain the dwell time of that particular FRET state, which in turn provides the rate constant (k) for that transition.
Ensemble FRET measurements
Ensemble FRET measurements were carried out in a K2 multifrequency phase and modulation fluorimeter (ISS Inc. USA). The concentration of the donor (Atto 550) and acceptor (Atto 647N) fluorophore labeled DNA Hp was 0.17 μM. The same Tris buffer (20 mM Tris–HCl, 15 mM NaCl, pH 7.5) was used also in the ensemble FRET measurements. The excitation wavelength (λex) was 550 nm, which corresponds to the absorption maximum of the Atto 550 fluorophore.
RESULTS
Volumetric profile of the unfolding process of the DNA Hp in the presence of salts
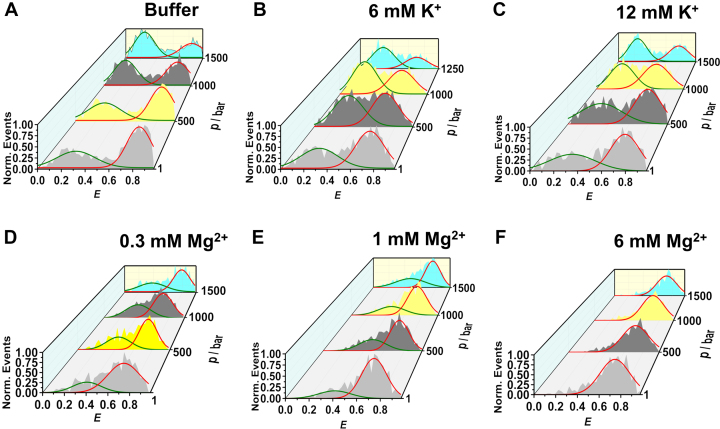
High-pressure smFRET measurements under freely diffusing conditions were carried out in the presence of monovalent (K+), divalent (Mg2+) and trivalent cationic (Co3+) salts to quantify the effect of charge density on the volumetric profile of the conformational transitions of the DNA Hp. This is of particular importance as the ionic strength affects the hydration and packing arrangement of the DNA Hp, which dictate its conformational stability in the intracellular environment. Figure 2 exhibits the FRET efficiency (E) histograms of the DNA Hp in the presence of different concentrations of K+ and Mg2+. The E-histograms corresponding to 0.3, 1 and 6 mM Co3+ are shown in Supplementary Figure S1 (see the ESI). The two peaks seen in the E-histograms clearly reveal two conformations. The low-FRET peak at E ≈ 0.3 represents the open (unfolded) conformation where the donor-to-acceptor distance is large. The high-FRET peak at E ≈ 0.80 represents the closed (folded) conformation where the donor-to-acceptor distance is short. Pressure application in neat buffer solution gradually populates the low-FRET species (E ≈ 0.3), i.e. leads to unfolding of the DNA Hp (Figure 2A). Addition of 6 and 12 mM K+ does not have any significant effect on the conformational stability of the DNA Hp against pressure. Conversely, the addition of Mg2+ and Co3+ strongly stabilizes the high-FRET species (closed state) and counteracts the destabilization effect of pressure such that in 6 mM Mg2+ or Co3+ the closed state prevails (Figure 2 and Supplementary Figure S1).
Figure 2.
Normalized 3D plots of the FRET efficiency (E) histograms of the DNA Hp in (A) neat buffer (20 mM Tris–HCl, 15 mM NaCl, pH 7.5), in the presence of (B) 6 mM K+, (C) 12 mM K+, (D) 0.3 mM Mg2+, (E) 1 mM Mg2+ and (F) 6 mM Mg2+ at different pressures, p. The green and red curves represent Gaussian fits to the E-histograms representing open and closed conformations, respectively.
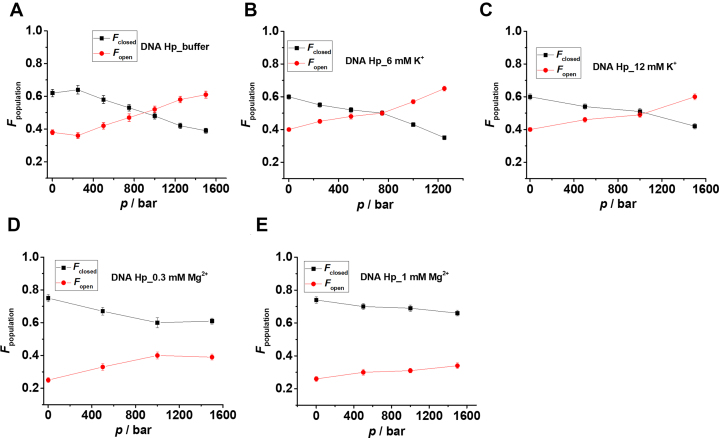
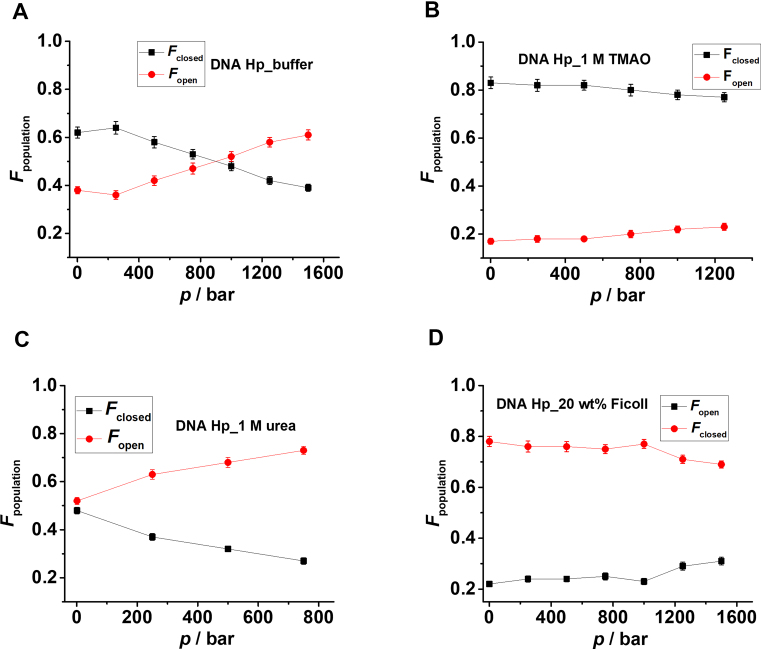
The population of different conformational states is determined from the peak areas of the Gaussian fits representing the different conformations. Fopen = (area of the low-FRET peak)/total area, represents the fraction of the open state, and Fclosed = 1 - Fopen the fraction of closed (high-FRET peak) state. Figure 3 and Supplementary Figure S1 show Fopen and Fclosed as a function of pressure in the absence and presence of the salts. From the plots it is quite evident that the addition of Mg2+ and Co3+ strongly stabilizes the high-FRET species (closed) with E ≈ 0.8 and also counteracts the destabilization effect of pressure, while the effect of Na+ is negligible on the stability of the DNA Hp. The equilibrium constant (Keq) for the closed-to-open transition, i.e. for unfolding of the DNA Hp, is determined from the Fclosed and Fopen data at different pressures, both in absence and presence of salts (Supplementary Figures S1 and S2). From the slope of the plot lnKeq versus p, the transition volume ΔVo = Voopen - Voclosed for unfolding is determined. The data are listed in Table 1. The ΔVo-value in neat buffer is found to be about −18 cm3mol−1, in good agreement with literature data (9). A negative volume change associated with unfolding means that the open conformation has a smaller partial molar volume than the closed state. Upon increasing the salt concentrations, particularly in the presence of Mg2+ and Co3+, ΔVo changes from −17.7 cm3mol−1 in neat buffer to −5.9 and −5.2 cm3mol−1 in the presence of 1 mM Mg2+ and 1 mM Co3+, respectively (Table 1). The smaller volume differences account for the strong counteracting effects of the salts on the pressure-induced destabilization of the closed state. The stability of the DNA Hp follows the order Co3+ > Mg2+ > K+, i.e. increases with increasing charge density of the salt. Complementary ensemble fluorescence measurements carried out in the presence of various salt concentrations support these observations found in single-molecule measurements (Supplementary Figures S3 and S4).
Figure 3.
Fraction (F) of closed (black square, E ≈ 0.7–0.8) and open (red circle, E ≈ 0.3–0.4) conformational states as determined from the peak areas of the Gaussian fits in Figure 2 at different pressures for (A) neat buffer, (B) 6 mM K+, (C) 12 mM K+, (D) 0.3 mM Mg2+and (E) 1 mM Mg2+. The equilibrium constant (Keq) for the closed to open state transition is determined from Keq = Fopen/Fclosed at different pressures (T = 25°C) in neat buffer, 6 mM K+, 12 mM K+, 0.3 mM Mg2+ and 1 mM Mg2+. From the slope of the lnKeq versus p plot, the transition volume (ΔVo) for the closed to open state conformational transition is determined as (dlnKeq/dp)T = −ΔVo/(RT) (see Supplementary Figure S2).
Table 1.
Transition volume (ΔVo) for unfolding of the DNA Hp obtained from the slope of lnKeq versus p plot (Supplementary Figures S1, S2 and S5) in neat buffer and in the presence of different concentrations of cosolutes (T = 25°C)
| [Salt] | ΔVo / cm3mol−1 |
|---|---|
| Neat buffer | −17.7 ± 1.7 |
| 6 mM K+ | −18.8 ± 2.2 |
| 12 mM K+ | −12.7 ± 2.2 |
| 0.3 mM Mg2+ | −11.1 ± 3.5 |
| 1 mM Mg2+ | −5.9 ± 1.0 |
| 0.3 mM Co3+ | −7.9 ± 1.9 |
| 1 mM Co3+ | −5.2 ± 2.9 |
| 1 M TMAO | −7.8 ± 0.9 |
| 1 M urea | −29.5 ± 3.8 |
| 20 wt% Ficoll | −6.6 ± 1.9 |
Volumetric profile of the unfolding process of the DNA Hp in the presence of osmolytes and crowders
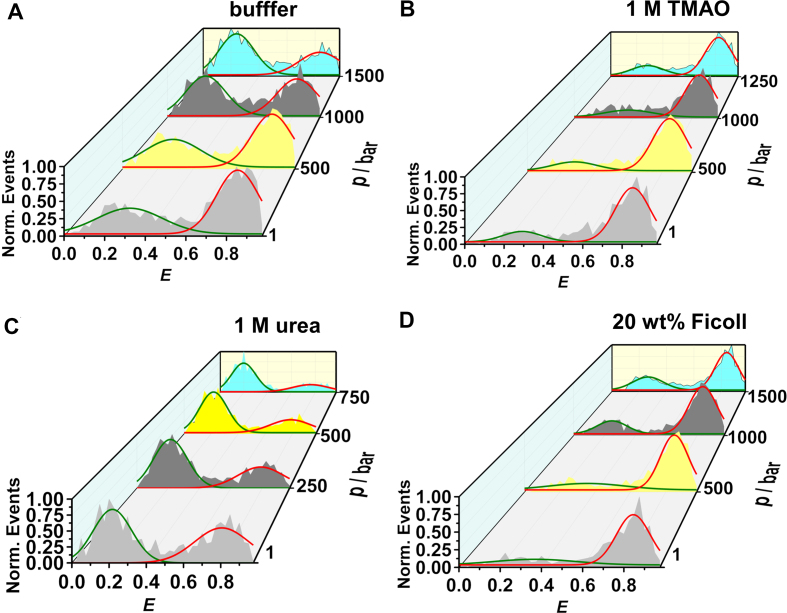
High-pressure smFRET measurements were also carried out in the presence of osmolytes and crowders. This is of particular physiological relevance as the cell takes up osmolytes to cope with environmental stresses and the cellular interior is also crowded with macromolecules (61–64). Herein, we have used examples of most common stabilizing and destabilizing osmolytes, TMAO and urea, respectively, and the polysaccharide Ficoll to mimic intracellular crowding conditions. The E-histograms obtained in neat buffer and in the presence of 1 M TMAO, 1 M urea and 20 wt% Ficoll are shown in Figure 4. It is clearly seen that TMAO and 20 wt% Ficoll stabilize the closed state (E ≈ 0.8). On the other hand, 1 M urea destabilizes the native fold of the DNA Hp, and, along with pressure synergistically populates the open conformation of the DNA Hp.
Figure 4.
Normalized FRET efficiency (E) histograms of the DNA Hp in (A) neat buffer, in the presence of (B) 1 M TMAO, (C) 1 M urea and (D) 20 wt% Ficoll, respectively. TMAO and Ficoll stabilize the high FRET species (closed state), thereby counteracting the destabilization effect of pressure.
The population of the different conformational states is determined from the peak areas of the Gaussian fits shown in Figure 5. 1 M TMAO and 20 wt% Ficoll stabilize the closed state and fully compensate the deteriorating effect of pressure up to the whole pressure range covered and found in the biotic window (∼1000 bar). Keq is plotted as a function of pressure both in neat buffer and in the presence of osmolytes and crowders in Supplementary Figure S5, the ΔVo data are also presented in Table 1. The ΔVo decreases from −17.7 cm3mol−1 in neat buffer to −7.8 and −6.6 cm3mol−1 in the presence of 1 M TMAO and 20 wt % Ficoll, respectively, thereby rendering the unfolded state less favorable upon compression. Ensemble fluorescence measurements carried out in the presence of 20 wt% Ficoll support these findings (Supplementary Figure S6). On the other hand, in the presence of 1 M urea, ΔVo amounts to −29.5 cm3mol−1, which is considerably larger than the ΔVo obtained for neat buffer. As a result, urea assists in pressure-induced destabilization of the folded state.
Figure 5.
Plot of fraction of the open and closed conformations Fopen, Fclosed of the DNA Hp as a function of pressure in (A) neat buffer without any cosolvent, in the presence of (B) 1 M TMAO, (C) 1 M urea and (D) 20 wt% Ficoll. Fopen and Fclosed are determined from the peak areas of the Gaussian fits in Figure 4. Equilibrium constants (Keq) for unfolding, defined as Keq = Fopen/Fclosed, are determined and plotted as lnKeq versus p in neat buffer, 1 M TMAO, 1 M urea and 20 wt% Ficoll in Supplementary Figure S5. From the slope of the plots, the transition volumes for unfolding are determined (see Supplementary Figure S5).
smFRET measurements under immobilized conditions
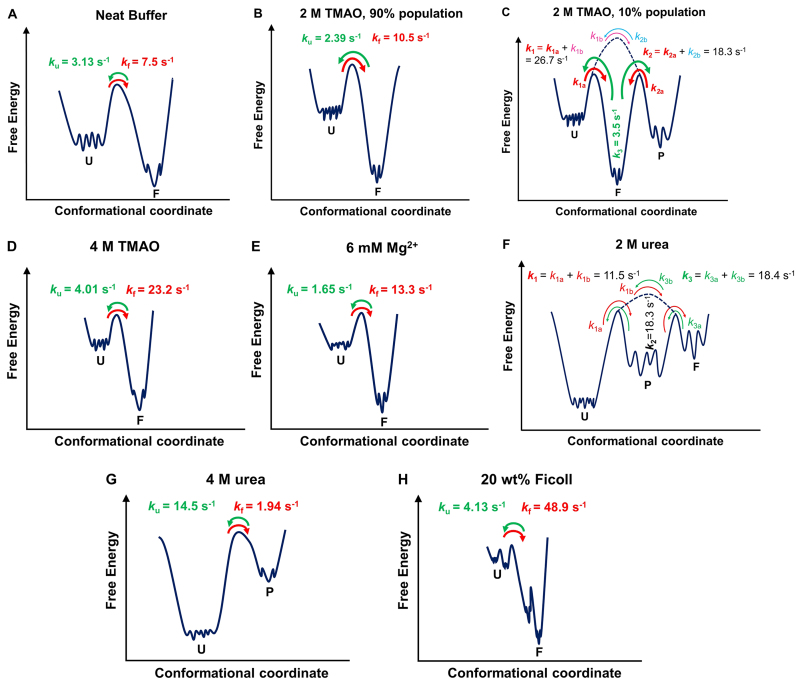
The smFRET measurements were also carried on surface-attached DNA Hp to observe the opening and closing dynamics directly over longer times scales and to determine the underlying kinetic constants. Owing to the design and dimensions of the high-pressure capillary, such measurements can be carried out under ambient conditions, only. Representative fluorescence intensity traces of a single Atto 550 and Atto 647N labeled DNA Hp in neat buffer and in the presence of additives are shown in Figure 6. The E-histograms are obtained from at least 30 of such single-molecule fluorescence traces. The opening and closing dynamics of the DNA Hp produces anticorrelated donor and acceptor fluorescence, a typical FRET signature. In neat buffer, the DNA Hp spends roughly equal time in the open and closed state as can be seen from the fluorescence trace and the E-histogram (Figure 6A). With increasing TMAO concentration, the DNA Hp resides increasingly longer in the closed state as indicated by the predominant acceptor (red) fluorescence in the time trace and the increasing events with high E-value (∼0.85) in the E-histograms (Figure 6B). A similar behavior is observed in case of Mg2+ (Figure 6C). The E-histograms reveal a two-state transitional behavior for the DNA Hp in neat buffer, in the presence of Mg2+ as well as in TMAO solution (in 90% of the cases for 2 M TMAO).
Figure 6.
Donor (green) and acceptor (red) intensity versus time traces obtained for a typical single Atto 550 and Atto 647N labeled DNA Hp in (A) neat buffer and in the presence of (B) TMAO, (C) Mg2+, (D) urea and (E) 20 wt% Ficoll. The FRET efficiency (E) is calculated at each point of these traces using E = nA/(nA+γ nD), where nA and nD are the counts in the donor and acceptor channel, respectively, and γ is the correction factor for detector efficiency, to obtain the FRET time series as shown in Supplementary Figure S7. The FRET efficiency (E) histograms are obtained from the HMM fits to the FRET time series of about 30 single molecules. E-histograms are fitted to a bimodal Gaussian distribution in case of neat buffer, TMAO, Mg2+ and 4 M urea, where each Gaussian curve represents a distinct conformational state. In case of 2 M urea, three conformational states were identified from the FRET time series (see Supplementary Figure S11), where state 1 has a FRET distribution (green curve) centered at E = 0.17 ± 0.01, state 2 (purple color) at E = 0.38 ± 0.01 and state 3 displays a bimodal FRET distribution (blue color overall fit) at E = 0.51 ± 0.01 (pink color) and E = 0.86 ± 0.01 (red color). In case of 20 wt% Ficoll, the FRET-time series (see Supplementary Figure S14) display a two-state transition with folded and unfolded conformations, each state displaying a bimodal FRET distribution (blue and pink overall fit) centered at E = 0.60 ± 0.01/E = 0.85 ± 0.01 and E = 0.13 ± 0.01/E = 0.31 ± 0.01, respectively. The folding and unfolding kinetic constants are determined from the exponential fits to the cumulative dwell time distribution analysis, which is derived by integrating the raw dwell time distribution histograms as shown in Supplementary Figure S7. The raw dwell time distribution is directly obtained from the HMM fits to the FRET time series (see Supplementary Figure S7). Characteristic cumulative dwell time distribution plots for folding and unfolding are shown for the case of 20 wt% Ficoll (e).
The dynamic constants between the open and closed states are obtained from the Hidden Markov Model (HMM) fit to the FRET time series (E versus time) as shown exemplarily in Supplementary Figure S7, which yields the dwell time, i.e. the time the molecule spent in one FRET state before transitioning to another one. The opening (unfolding) and closing (folding) rate constants are determined from single exponential fits to the cumulative dwell time histograms of the closed and open state, respectively (Supplementary Figure S8) and are summarized in Table 2.
Table 2.
Folding and unfolding rate constants of the DNA Hp in neat buffer and in the presence of TMAO, Mg2+, 4 M urea and Ficoll, determined from single exponential fits to the dwell time distribution histograms of the open and closed state as shown in Supplementary Figures S8, S13, 6
| Solvent |
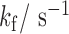
|
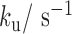
|
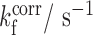
|
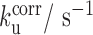
|
|---|---|---|---|---|
| Neat buffer | 7.5 ± 0.2 | 3.13 ± 0.05 | ||
| 2 M TMAO | 5.7 ± 0.2 | 1.29 ± 0.04 | 10.5 ± 0.4 | 2.39 ± 0.07 |
| 4 M TMAO | 5.9 ± 0.1 | 1.25 ± 0.05 | 23.2 ± 0.4 | 4.01 ± 0.16 |
| 1 mM Mg2+ | 11.9 ± 0.3 | 1.25 ± 0.02 | ||
| 6 mM Mg2+ | 13.3 ± 0.2 | 1.65 ± 0.04 | ||
| 4 M urea | 1.94 ± 0.03 | 14.5 ± 0.5 | ||
| 20 wt % Ficoll | 11.7 ± 0.4 | 1.00 ± 0.02 | 48.9 ± 0.1 | 4.13 ± 0.08 |
In case of TMAO and 20 wt% Ficoll, the rate constants had to be corrected (index corr) for changes in viscosity (1.65 and 3.50 mPa⋅s of 2 M and 4 M TMAO, respectively (17), 3.73 mPa⋅s of 20 wt% Ficoll (47)).
The addition of Mg2+ stabilizes the closed state by enhancing the folding rate, kf, and by decreasing the unfolding rate, ku: kf increases from 7.5 ± 0.2 s−1 in neat buffer to 11.9 ± 0.3 s−1 and 13.3 ± 0.2 s−1 in the presence of 1 and 6 mM Mg2+, while ku decreases from 3.13 ± 0.05 s−1 in neat buffer to 1.25 ± 0.02 s−1 and 1.65 ± 0.04 s−1 for 1 and 6 mM Mg2+, respectively.
On the contrary, TMAO exhibits a decrease in both kf and ku. However, addition of high TMAO concentrations also leads to a significant enhancement in the solution viscosity, η. To obtain viscosity-corrected folding and unfolding rate constants, the folding and unfolding times obtained from the exponential fit to the dwell time histograms have to be corrected for the viscosity change, using 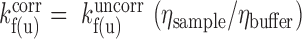 and published microviscosity data of 2 and 4 M TMAO (17,47,65);
and published microviscosity data of 2 and 4 M TMAO (17,47,65); 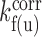 and
and 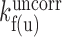 are the corrected and uncorrected folding (unfolding) rate constants, respectively. The viscosity-corrected folding rates,
are the corrected and uncorrected folding (unfolding) rate constants, respectively. The viscosity-corrected folding rates, 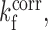 for 2 and 4 M TMAO are found to be 10.5 ± 0.4 s−1 and 23.2 ± 0.4 s−1, respectively. The corrected unfolding rate constant,
for 2 and 4 M TMAO are found to be 10.5 ± 0.4 s−1 and 23.2 ± 0.4 s−1, respectively. The corrected unfolding rate constant, 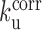 , for 2 and 4 M TMAO are quite similar to the neat buffer data and amount to 2.39 ± 0.07 s−1 and 4.01 ± 0.16 s−1, respectively. Hence, TMAO strongly affects the folding rate constant, while the unfolding rate remains more or less the same with respect to that in neat buffer solution. This kinetic stabilizing mechanism found for TMAO is quite different from that of Mg2+, where both rate constants are affected.
, for 2 and 4 M TMAO are quite similar to the neat buffer data and amount to 2.39 ± 0.07 s−1 and 4.01 ± 0.16 s−1, respectively. Hence, TMAO strongly affects the folding rate constant, while the unfolding rate remains more or less the same with respect to that in neat buffer solution. This kinetic stabilizing mechanism found for TMAO is quite different from that of Mg2+, where both rate constants are affected.
Interestingly, apart from the fully open and closed state, different conformational states have been observed by the immobilized smFRET measurements. Almost 10% of the population in the presence of 2 M TMAO displays a three-state behavior as shown in Supplementary Figure S9. E-histograms corresponding to those states have E-values of 0.14 ± 0.01, 0.51 ± 0.01 and 0.78 ± 0.01. State 1 with E = 0.14 represents the fully open conformation, state 3 with E = 0.78 the fully closed state, in agreement with literature data (17,25). State 2 with E = 0.51 might represent a partially folded conformer where the stem is incompletely formed. All these states interconvert among themselves. However, according to the FRET time series shown in Supplementary Figure S9, we recognize that the most probable transitions are between state 3 and state 1 or state 3 and state 2. Only occasionally, transitions occur between state 2 and state 1. The dwell time distribution plots obtained from the HMM fits to the FRET time series (Supplementary Figure S7) for each of these states are shown in Supplementary Figure S10. The dwell times were corrected for the viscosity contribution and are used to obtain the corresponding rate constants (Table 3): k1 represents the transition rate mostly from the fully open state 1 to the fully closed state 3 conformer, and also to some extent to the partially folded conformer (state 2); k2 indicates mostly the transition rate from the partially folded conformer (state 2) to the fully closed state 3, and to a lesser extent to the fully open state 1; k3 provides the rate constant for the transition from the fully closed state 3 to the fully open or partially folded conformers (states 1, 2). Hence, k1 and k2 represent essentially folding and k3 unfolding rates. The values of k1 and k2 are much higher than k3, indicating that even though TMAO populates to some extent the partially folded state, it still favors complete folding and it strongly stabilizes the closed conformation of the DNA Hp.
Table 3.
The dwell times obtained from the single exponential fits to the respective dwell time distribution plots in case of 2 M TMAO (Supplementary Figure S10) and 2 M urea (Supplementary Figure S12)
| Parameters | 2 M TMAO | 2 M urea |
|---|---|---|
 / ms / ms |
69.8 ± 7.4 | 87.1 ± 3.0 |
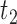 / ms / ms |
101.0 ± 10.6 | 54.7 ± 3.0 |
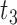 / ms / ms |
527.2 ± 28.0 | 54.3 ± 2.6 |
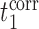 / ms / ms |
37.6 ± 1.8 | |
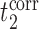 / ms / ms |
54.5 ± 5.7 | |
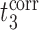 / ms / ms |
284.3 ± 15.1 | |
| k 1 / s−1 | 26.7 ± 1.3 | 11.5 ± 0.4 |
| k 2 / s−1 | 18.3 ± 2.0 | 18.3 ± 1.0 |
| k 3 / s−1 | 3.5 ± 0.2 | 18.4 ± 0.9 |
The rate constants in case of 2 M TMAO belong to the 10% population of the DNA Hp that displays a three-state behavior. In case of 2 M TMAO, the t and k values are corrected for the viscosity contribution.
Conversely and as expected, the addition of urea to the buffer solution destabilizes the closed state and favors the open state of the DNA Hp. This is already visible from the increasing amount of donor signal (green) in the fluorescence traces with increasing urea concentration (Figure 6D). Additional peaks in the E-histograms are observed for 2 M urea, apart from the two peaks due to the fully open (E = 0.14) and fully closed state (E = 0.85), indicating a more complex conformational landscape in the presence of urea. In case of urea, all the single-molecule traces display a three-state transition as shown in Supplementary Figure S11. The FRET efficiency distribution of state 1 is centered at E = 0.17 ± 0.01, of state 2 at E = 0.38 ± 0.01 and the state 3 has a bimodal FRET efficiency distribution with peak maxima centered at E = 0.51 ± 0.01 and E = 0.86 ± 0.01, respectively. This is because some molecules of the DNA Hp in the presence of 2 M urea do not exhibit the state with E ≈ 0.85 but rather show a three-state dynamics corresponding to the states with E ≈ 0.5, 0.3 and 0.2. Hence, for the state 3 a bimodal FRET distribution has been assigned. The kinetic constants between these states are obtained from the dwell time distribution plots (Supplementary Figure S12) and are displayed in Table 3. The rate constant k1 represents the dynamics for the transition from the fully open state 1 to the partially unfolded state 2 and folded state 3; k2 indicates the dynamics from the partially unfolded state to either the fully open or the fully closed state and k3 dictates the rate at which the fully closed state transforms to the partially folded and fully open states, i.e. represents the unfolding dynamics in the presence of 2 M urea. The k3 value of 18.4 s−1 is much higher than the unfolding rate of ku = 3.13 s−1 found in neat buffer. Hence, 2 M urea populates partially unfolded and fully open states by increasing the unfolding rate constant, while interfering little with the folding rate k1 in comparison to the scenario in neat buffer solution. In case of 4 M urea, ∼92% of the population has shifted to the fully open state (E = 0.17) already, only a tiny fraction of the molecules remains in a state with E = 0.51, which represents a partially folded conformer. The folding rate constant kf determined in case of 4 M urea from the dwell time of the state with E = 0.17 amounts to 1.94 ± 0.03 s−1, which is much lower than the value of 7.5 s−1 observed in neat buffer (Supplementary Figure S13, Table 2). On the other hand, the value of ku for 4 M urea determined from the dwell time of the state with E = 0.51 is found to be 14.5 ± 0.5 s−1, which is again faster than the value of ku = 3.13 s−1 found in neat buffer. Hence, 4 M urea stabilizes the fully open conformation of the DNA Hp by increasing the ku and decreasing the kf value concomitantly.
The introduction of the crowding agent 20 wt% Ficoll leads also to the formation of additional peaks in the E-histograms for the DNA Hp (Figure 6E). Peak maxima are recorded at E = 0.13 ± 0.01, 0.31 ± 0.01, 0.60 ± 0.01 and 0.85 ± 0.01, pointing to an even more rugged conformational landscape of the DNA Hp. In case of 20 wt% Ficoll, the single-molecule fluorescence traces display mostly two-state dynamics as shown in Supplementary Figure S14. We may consider the two-state dynamics in terms of folded and unfolded states with a bimodal FRET distribution each. The FRET distribution in case of the folded state is centered at E = 0.60 ± 0.01 and 0.85 ± 0.01, and that of the unfolded state at E = 0.13 ± 0.01, 0.31 ± 0.01, respectively. The dwell times were corrected for the increased viscosity in 20 wt% Ficoll solution and used to determine the folding ( ) and unfolding (
) and unfolding (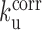 ) rate constants. The
) rate constants. The 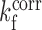 value is found to be 48.9 ± 0.1 s−1, which is drastically faster than the value of 7.5 ± 0.2 s−1 observed for neat buffer (Table 3). The
value is found to be 48.9 ± 0.1 s−1, which is drastically faster than the value of 7.5 ± 0.2 s−1 observed for neat buffer (Table 3). The 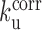 value of 4.13 ± 0.08 s−1 observed in the presence of 20 wt% Ficoll does not differ much from the neat buffer value of 3.13 ± 0.05 s−1, however (Table 2). Hence, Ficoll stabilizes the folded state ensemble kinetically by markedly enhancing the folding rate.
value of 4.13 ± 0.08 s−1 observed in the presence of 20 wt% Ficoll does not differ much from the neat buffer value of 3.13 ± 0.05 s−1, however (Table 2). Hence, Ficoll stabilizes the folded state ensemble kinetically by markedly enhancing the folding rate.
DISCUSSION
The volumetric profile for a conformational transition depends strongly on the packing arrangement of the structural units in their respective conformational state and is very sensitive to hydration changes. The partial molar volume, Vo, of a solute in solution can be decomposed into a sum of following contributions (11,16,66):
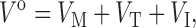 |
(1) |
where VM is the molecular volume, i.e. the geometric volume impenetrable to water molecules, VT is the thermal volume indicating the void space surrounding the solvent accessible surface area (SASA) resulting from mutual vibrations and librations of the solute and solvent molecules and VI represents the interaction volume indicating interfacial hydration changes. For an unfolding transition of the DNA Hp, the volume change, ΔVo, is given by the sum of the molecular, thermal and interaction volume changes (12,16,18,19,67,68):
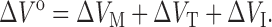 |
(2) |
Generally, ΔVM < 0 arises only from a release of void volume (originating in an imperfect packing) upon unfolding. For a perfectly matched DNA duplex structure, the change in molecular volume ΔVM is typically assumed negligible due to the absence of any internal voids (14). However, Son et al. have found a negative volume change for ΔVM upon unfolding of a DNA duplex (12). Nevertheless, in the case of DNA duplex unfolding, all the volume contributions cancel each other largely, leading to a very small positive volume change, which is similar to the volume of one H2O molecule, only (12). ΔVT is proportional to the SASA and is always positive for unfolding transitions. The change of interaction volume, ΔVI, represents the hydration volume change resulting from the difference between water molecules in the denser hydration layer around the biomolecule and the bulk phase. The partial molar volume of water in the hydration shell is ∼10% smaller than the volume of water in the bulk water phase (12,16,69), which is due to the contraction of water around polar and charged groups of the biomolecule (electrostriction effect). For an unfolding transition, the change in interaction volume can be represented by ΔVI = Δnh(Vh–Vo), where Δnh is the number of water molecules taken up or released during the unfolding transition, Vh and Vo are the partial molar volumes of water in the hydration shell and the bulk phase, respectively (12,16). Consequently, an increase in hydration upon unfolding leads always to an overall negative volume change.
In neat buffer, pressurization shifts the conformational equilibrium of the DNA Hp towards the unfolded state (Figures 2A and 4B). The volume change upon unfolding amounts to −17.7 ± 1.7 cm3mol−1, indicating a lower molar volume of the unfolded state than the folded state for the polydA loop DNA Hp (Figure 7). Generally, such negative volume change is attributed to the hydration volume change upon unfolding as the unfolded state has a larger SASA than the folded state (12,16,19). For a smaller loop DNA Hp, the ΔVo has been found to be in the range of −2.35 to +6.74 cm3mol−1, depending on the salt concentration and on temperature (67). A simulation study on a small loop RNA hairpin estimated the ΔVo upon pressure-induced unfolding to be about −4 cm3mol−1 (70). This suggests that packing defects of the bases in the folded structure of our DNA Hp (i.e. void volume which is filled with water upon unfolding) contributes to ΔVo as well.
Figure 7.
Schematic representation of the volumetric profile of the DNA Hp at 25°C for the unfolding transition in neat buffer and in the presence of salts (K+, Mg2+ and Co3+), osmolytes (TMAO, urea) and the crowding agent Ficoll, based on the results listed in Table 1. U and F represent the unfolded and folded states, respectively, and ΔVo = Vou - Vof the partial molar volume change upon unfolding. In the presence of salts, TMAO and Ficoll, the unfolded states are more collapsed, leading to a lower SASA, to a smaller hydration contribution, and hence an overall larger volume compared to Vou in neat buffer. Conversely, in the presence of 1 M urea, the unfolded state becomes more extended. The larger SASA leads to a strong hydration contribution and hence an overall smaller volume in comparison to the unfolded state in neat buffer. Please note that the volume changes are very small (for comparison, one H2O molecule has a molar volume of 18 cm3mol−1). The diagram is not to scale. Relative positions of ΔVo should be viewed as qualitative, only.
Upon addition of salt, in particular the divalent Mg2+ and trivalent Co3+, ΔVo decreases and strongly counteracts the destabilization effect of pressure on the folded state (Figure 7). The addition of salt reduces the repulsive interaction between the backbone’s phosphate groups of the DNA Hp by charge screening, resulting in more compact packing and smaller void volume in the folded state and, probably more significantly, a more compact state with smaller SASA for the unfolded state in comparison to the neat buffer scenario (Figure 7). This effect increases with increasing charge density (Co3+ > Mg2+ > K+). Hence, the unfolded state in the presence of salt will have a lower SASA and lower hydration contribution, resulting in an overall larger volume compared to the unfolded state in neat buffer (Figure 7).
The addition of TMAO and Ficoll also populates the high-FRET state and counteracts the pressure effect by rendering the unfolding process volumetrically less favorable (Table 1). The interaction of TMAO with the phosphate groups and also with the nucleobases of nucleic acids has been found to be strongly unfavorable (9,23,71,72). This results in an exclusion of TMAO from the surface of the DNA Hp and a compaction of the DNA Hp structure with minimal SASA. The preferential exclusion effect is particularly strong in case of the unfolded state, which leads to a compact unfolded state (ensemble) with overall larger volume owing to a smaller hydration contribution (Figure 7). In addition, the folded state in the presence of TMAO might have a somewhat smaller volume with lower void volume due to the strong excluded volume effect as well. On the other hand, the crowding agent Ficoll (radius ∼5.5 nm), due to its larger size, reduces the available space in the solvent for the biomolecules to occupy (61,62). As a result of this strong steric excluded volume effect, the most compact conformation of the DNA Hp is favored. Hence, the effect on the unfolded state structure is significantly larger than on the folded state. Overall, the presence of Ficoll leads to a smaller volume change upon unfolding as presented schematically in Figure 7.
On the contrary, addition of urea renders the pressure-induced unfolding process of the DNA Hp volumetrically more favorable, i.e. it synergistically destabilizes the folded state of the DNA Hp at high pressures (Figures 4C and 5C). The ΔV° changes from −17.7 cm3mol−1 in neat buffer to −29.5 cm3mol−1 in 1 M urea. Urea interacts favorably with the nucleobases and therefore favors extended conformations with large SASA (17,23,73,74). As a result, the unfolded state is strongly hydrated, leading to a smaller volume in comparison to the unfolded state in neat buffer (Figure 7). Urea also weakens base stacking interactions, which may result in breaking of a few base pairs between the two complementary strands, which leads to a stronger hydration and a more negative hydration volume change.
The kinetic profile of the conformational dynamics of the DNA Hp in neat buffer and in the presence of cosolvents and crowding media obtained from the smFRET measurements under immobilized conditions provide deeper insights into cosolute effects on the folding energy landscapes (Figure 8). In neat buffer, a two-state conformational dynamics is obtained (Figure 6A) with folding (kf) and unfolding (ku) rates of 7.5 and 3.13 s−1, respectively which are similar to the ambient-pressure literature data (25,75). Two-state dynamics is also observed in the case of 2 M TMAO (90% population), 4 M TMAO, Mg2+ and 4 M urea (Figures 6 and 8). Increasing concentrations of TMAO and Mg2+ strongly stabilize the folded state, however, the mechanism of this stabilization seems to be different. In case of TMAO, kf is strongly enhanced, while ku does not differ much from the value observed in neat buffer (Table 2). Addition of Mg2+ affects both, kf and ku. Mg2+ leads to an effective charge screening of the phosphate backbone, thereby enhancing kf and reducing ku. Mg2+ is also strongly hydrated and this might decrease the number of water molecules surrounding the DNA Hp, favoring a structure with lowest possible SASA, i.e. the folded state. On the other hand, TMAO stabilizes the folded structure due to a pronounced excluded volume effect, owing to its unfavorable interaction with both the phosphate and nucleobase backbone (23,68,71). Conversely, urea leads to a significant enhancement of ku and a drop of kf due to its favorable interaction with the nucleobases, and therefore stabilizes structures with larger nucleobase SASA, i.e. the unfolded state (73,74,76).
Figure 8.
Schematic of the free energy landscape of the DNA Hp in (A) neat buffer, (B and C) 2 M TMAO, (D) 4 M TMAO, (E) 6 mM Mg2+, (F) 2 M urea, (G) 4 M urea and (H) 20 wt% Ficoll. U, F and P denote unfolded, folded and partially folded conformations. In the case of 2 M TMAO, the two schematics describe the two-state dynamics observed for 90% of the population of states observed, and three-state dynamics displayed by the remaining 10% of the population. In (a) neat buffer, (b) 90% population in 2 M TMAO, (d) 4 M TMAO, (e) 6 mM Mg2+ and (g) 4 M urea, a two-state dynamics is observed where the states are separated by a distinct free energy barrier. Green and red curved arrows display the unfolding and folding dynamics, respectively, ku and kf denote the corresponding unfolding and folding rate constants. A more complex conformational landscape is observed in the case of (c)10% population of 2 M TMAO, (f) 2 M urea and (h) 20 wt% Ficoll. In the case of 2 M TMAO, 10% of the population exhibits a three-state behavior, indicating the presence of a relatively stable partially folded state (P) along with U and F. As can be seen in Figure S9 (SI), most of the transitions in 2 M TMAO occur between U and F or F and P (indicated by thick red and green curved arrows), only occasionally transitions occur between U and P (indicated by thin purple and blue curved arrows). Hence, in 2 M TMAO k1 signifies the dynamics from U to mostly F (red curved arrow) and occasionally to P (thin purple curved arrow), k2 represents the transition rate from P to mostly F (red curves arrow) and occasionally to U (thin blue curved arrow) and k3 indicates the transition from F to either P or U. Hence, for the 10% population in 2 M TMAO, k1 and k2 essentially represent folding and k3 unfolding rates. A three-state behavior is also observed in case of 2 M urea (e). Here, k1 represents the transition rate from U to either F or P, k2 from P to either U or F and k3 the transition from F to U or P. Thus, k3 indicates the rate of unfolding, which is much larger compared to neat buffer. For 20 wt% Ficoll (g), two kinds of unfolded and folded states have been identified, which may still be described by an overall two-state dynamics where each of the unfolded states converts to a folded state and vice versa.
Interestingly, we found that cosolvents and crowding can populate different conformational substates to some extent that are not encountered in the case of neat buffer solution. Indications for a more rugged free energy landscapes for the DNA Hp with stable or metastable intermediates can be found in the literature as well (17,36,37,39,40). We showed that in the presence of 2 M TMAO, almost 10% of the population visits a third substate (P) with a different E-value (E = 0.51) next to the fully open (U) and closed state (F). Such partially folded state is most likely a conformer where the stem is incompletely formed, but which displays an excluded-volume-induced low-SASA structure, already. Figure 8 depicts a schematic of the free energy landscape of the DNA Hp and how it is modulated by the cosolutes. In case of 2 M TMAO, the most probable transitions occur between U (E ≈ 0.2) and F (E ≈ 0.8) or P (E ≈ 0.5) and F. Only occasionally, a transition is observed between U and P (Supplementary Figure S9). Hence, for the 10% population in 2 M TMAO, k1 and k2 represent essentially the folding dynamics from the unfolded (U) and partially folded ensembles (P), which are found to be 26.7 and 18.3 s−1, respectively, and which are much larger than the value of kf = 7.5 s−1 found in neat buffer, while k3 specifies the unfolding dynamics and amounts to 3.5 s−1, a value very similar to the value of ku = 3.13 s−1 in neat buffer. Thus, both the unfolded and partially folded states tend to give way to the folded state, which is the most stable conformation in the presence of TMAO as it has the lowest SASA (Figure 8). Two different unfolded ensembles with distinct refolding times have also been observed using temperature- and ion-jump perturbation techniques (37). According to literature reports for this class of DNA Hp, the unfolded basin is very broad and flat with many local minima while the folded state occupies minima of a narrow funnel (37). Configuration diffusion on this rather flat energy surface characterizes the dynamics within the unfolded states, which fold with distinct folding times from different regions of the conformational landscape. In the presence of TMAO, compact conformations are favored and might be trapped in an intermediate state denoted P, which could be a partially folded state where the stem of the hairpin is incompletely formed. This might be the reason why 10% of the population displays a three-state dynamics in the presence of 2 M TMAO.
A rugged energy landscape with a multitude of partially folded conformational states is also observed in the presence of 2 M urea (Figure 6D). Urea interacts strongly with nucleobases, thereby weakening base stacking interactions and H-bonding, leading to the formation of partially folded conformers. The rate constant k3 in the presence of 2 M urea indicates unfolding of the closed state to partially folded (P) and unfolded (U) conformations, and amounts to 18.4 s−1, which is much higher compared to ku = 3.13 s−1 in neat buffer. The formation of partially folded states is also observed in case of 4 M urea. The high-FRET state (with E value of 0.51) indicates a partially folded conformation, only (Figure 6D).
Also in the presence of Ficoll, formation of additional conformational substates is observed (Figure 6E). Although we found a two-state dynamics in the presence of Ficoll (Supplementary Figure S14), both the folded and unfolded states exhibit a bimodal FRET distribution (Figure 6E), indicating two different kinds of unfolded and folded conformers (Figure 8). The unfolded state in 20 wt% Ficoll with E = 0.13 and E = 0.31 represents the fully open state and, most likely, a conformation where only one or two base pairs in the stem are formed (Figure 8). The folded conformer with E = 0.60 suggests a partially folded structure where a stable but yet incomplete stem is formed (Figure 8). Due to a strong excluded volume effect, eventually in concert with soft ‘quinary’ enthalpic interactions between the crowder and DNA HP, such additional compact structures may have formed. The underlying kinetic stabilization mechanism is very similar to the TMAO case. The strong excluded volume effect drastically enhances the kf value (kf = 48.9 s−1), while ku = 4.13 s−1 does not change much in comparison to neat buffer (Table 2).
CONCLUSIONS
To conclude, we have performed smFRET measurements in the presence of different biologically relevant salts, cosolvents and crowding media, mimicking intracellular conditions, to deduce their impact on the volumetric and kinetic profile of the conformational dynamics of a DNA Hp. The results provide novel mechanistic insights into the conformational landscape of this class of biomolecule and how it is affected by stressors, including pressure. Using pressure modulation, the volumetric properties of the various conformational states of the DNA Hp could be exploited. We found pressurization to shift the conformational equilibrium towards the unfolded state, which occupies a smaller partial molar volume. Addition of salt, TMAO and Ficoll counteracts the pressure-induced destabilization of the folded conformation by rendering the unfolding process volumetrically less favorable. The salt effect is particularly strong at high charge density of the cation (Co3+ > Mg2+ > K+). Conversely, urea synergistically destabilizes the folded state with pressure, as the unfolding process becomes volumetrically more favorable. The results can be rationalized by invoking changes in hydration and intrinsic void volume of the conformers involved. The smFRET measurements under immobilized conditions provided the underlying rate constants for the various conformational transitions, providing also detailed insights into the mechanism dictating the conformational preference of the biomolecule at the different solution conditions. Furthermore, these data provide compelling evidence of a more rugged energy and conformational landscape in the presence of osmolytes and crowders. The dissection into volumetric and kinetic parameters at different solution conditions advances our understanding of the impact of the complex cellular milieu on the conformational dynamics of biomolecules such as the DNA Hp studied here. We believe that the stabilizing or destabilizing effect of the cosolutes in terms of volumetric and kinetic properties will be similar to other hairpin systems. Our data also demonstrate the important role of compatible osmolytes and cellular crowding in rescuing biological function under harsh environmental conditions, such as at HHP even of the 1000 bar-level. Equilibrium and kinetic parameters at high-pressure conditions are controlled by the cosolute’s impact on the volumetric properties of the dissolved biomolecule.
Supplementary Material
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Cluster of Excellence RESOLV (EXC 1069) (by DFG). Funding for open access charge: German Research Foundation DFG (Cluster of Excellence EXC 1069, RESOLV).
Conflict of interest statement. None declared.
REFERENCES
- 1. Akasaka K., Matsuki H.. High Pressure Bioscience: Basic Concepts, Applications and Frontiers. 2015; Dordrecht: Springer. [Google Scholar]
- 2. Meersman F., Daniel I., Bartlett D.H., Winter R., Hazael R., McMillan P.F.. High-pressure biochemistry and biophysics. Rev. Mineral. Geochem. 2013; 75:607–648. [Google Scholar]
- 3. Daniel I., Oger P., Winter R.. Origins of life and biochemistry under high-pressure conditions. Chem. Soc. Rev. 2006; 35:858–875. [DOI] [PubMed] [Google Scholar]
- 4. Yancey P.H., Blake W.R., Conley J.. Unusual organic osmolyres in deep-sea animals: adaptations to hydrostatic pressure and other perturbants. Compar. Biochem. Physiol. A. 2002; 133:667–676. [DOI] [PubMed] [Google Scholar]
- 5. Yancey P.H. Organic osmolytes as compatible, metabolic and counteracting cytoprotectants in high osmolarity and other stresses. J. Exp. Biol. 2005; 208:2819–2830. [DOI] [PubMed] [Google Scholar]
- 6. Roche J., Caro J.A., Norberto D.R., Barthe P., Roumestand C., Schlessman J.L., Garcia A.E., Garcia-Moreno E.B., Royer C.A.. Cavities determine the pressure unfolding of proteins. Proc. Natl. Acad. Sci. U.S.A. 2012; 109:6945–6950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Fu Y., Kasinath V., Moorman V.R., Nucci N.V., Hilser V.J., Wand A.J.. Coupled motion in proteins revealed by pressure perturbation. J. Am. Chem. Soc. 2012; 134:8543–8550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Silva J.L., Oliveira A.C., Vieira T.C.R.G., De Oliveira G.A.P., Suarez M.C., Foguel D.. High-pressure chemical biology and biotechnology. Chem. Rev. 2014; 114:7239–7267. [DOI] [PubMed] [Google Scholar]
- 9. Patra S., Anders C., Schummel P.H., Winter R.. Antagonistic effects of natural osmolyte mixtures and hydrostatic pressure on the conformational dynamics of a DNA hairpin probed at the single-molecule level. Phys. Chem. Chem. Phys. 2018; 20:13159–13170. [DOI] [PubMed] [Google Scholar]
- 10. Mitra L., Rouget J.B., Garcia-Moreno B., Royer C.A., Winter R.. Towards a quantitative understanding of protein hydration and volumetric properties. ChemPhysChem. 2008; 9:2715–2721. [DOI] [PubMed] [Google Scholar]
- 11. Chalikian T.V., Breslauer K.J.. Volumetric properties of nucleic acids. Biopolymers. 1998; 48:264–280. [DOI] [PubMed] [Google Scholar]
- 12. Son I., Shek Y.L., Dubins D.N., Chalikian T.V.. Hydration changes accompanying helix-to-coil DNA transitions. J. Am. Chem. Soc. 2014; 136:4040–4047. [DOI] [PubMed] [Google Scholar]
- 13. Voloshin V.P., Medvedev N.N., Smolin N., Geiger A., Winter R.. Exploring volume, compressibility and hydration changes of folded proteins upon compression. Phys. Chem. Chem. Phys. 2015; 17:8499–8508. [DOI] [PubMed] [Google Scholar]
- 14. Wilton D.J., Ghosh M., Chary K.V.A., Akasaka K., Williamson M.P.. Structural change in a B-DNA helix with hydrostatic pressure. Nucleic Acids Res. 2008; 36:4032–4037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Girard E., Prangé T., Dhaussy A.C., Migianu-Griffoni E., Lecouvey M., Chervin J.C., Mezouar M., Kahn R., Fourme R.. Adaptation of the base-paired double-helix molecular architecture to extreme pressure. Nucleic Acids Res. 2007; 35:4800–4808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Fan H.Y., Shek Y.L., Amiri A., Dubins D.N., Heerklotz H., MacGregor R.B., Chalikian T.V.. Volumetric characterization of sodium-induced G-quadruplex formation. J. Am. Chem. Soc. 2011; 133:4518–4526. [DOI] [PubMed] [Google Scholar]
- 17. Patra S., Anders C., Erwin N., Winter R.. Osmolyte effects on the conformational dynamics of a DNA hairpin at ambient and extreme environmental conditions. Angew. Chemie. Int. Ed. 2017; 56:5045–5049. [DOI] [PubMed] [Google Scholar]
- 18. Takahashi S., Sugimoto N.. Effect of pressure on thermal stability of G-Quadruplex DNA and double-stranded DNA structures. Molecules. 2013; 18:13297–13319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Takahashi S., Sugimoto N.. Effect of pressure on the stability of G-quadruplex DNA: thermodynamics under crowding conditions. Angew. Chemie. Int. Ed. 2013; 52:13774–13778. [DOI] [PubMed] [Google Scholar]
- 20. Takahashi S., Sugimoto N.. Pressure-dependent formation of i-motif and G-quadruplex DNA structures. Phys. Chem. Chem. Phys. 2015; 17:31004–31010. [DOI] [PubMed] [Google Scholar]
- 21. Knop J.-M., Patra S., Balasubramanian H., Royer C., Winter R.. The deep sea osmolyte TMAO and macromolecular crowders rescue the antiparallel conformation of the human telomeric G-Quadruplex from urea and pressure stress. Chem. Eur. J. 2018; 24:14346–14351. [DOI] [PubMed] [Google Scholar]
- 22. Aslanyan L., Ko J., Kim B.G., Vardanyan I., Dalyan Y.B., Chalikian T.V.. Effect of urea on G-Quadruplex stability. J. Phys. Chem. B. 2017; 121:6511–6519. [DOI] [PubMed] [Google Scholar]
- 23. Holmstrom E.D., Dupuis N.F., Nesbitt D.J.. Kinetic and thermodynamic origins of osmolyte-influenced nucleic acid folding. J. Phys. Chem. B. 2015; 119:3687–3696. [DOI] [PubMed] [Google Scholar]
- 24. Gao M., Held C., Patra S., Arns L., Sadowski G., Winter R.. Crowders and Cosolvents—Major contributors to the cellular milieu and efficient means to counteract environmental stresses. ChemPhysChem. 2017; 18:2951–2972. [DOI] [PubMed] [Google Scholar]
- 25. Baltierra-Jasso L.E., Morten M.J., Laflör L., Quinn S.D., Magennis S.W.. Crowding-Induced hybridization of single DNA hairpins. J. Am. Chem. Soc. 2015; 137:16020–16023. [DOI] [PubMed] [Google Scholar]
- 26. Roth D.B., Menetski J.P., Nakajima P.B., Bosma M.J., Gellert M.. V(D)J recombination: broken DNA molecules with covalently sealed (hairpin) coding ends in scid mouse thymocytes. Cell. 1992; 70:983–991. [DOI] [PubMed] [Google Scholar]
- 27. Varani G. Exceptionally Stable Nucleic Acid Hairpins. Annu. Rev. Biophys. Biomol. Struct. 1995; 24:379–404. [DOI] [PubMed] [Google Scholar]
- 28. Bikard D., Loot C., Baharoglu Z., Mazel D.. Folded DNA in action: hairpin formation and biological functions in prokaryotes. Microbiol. Mol. Biol. Rev. 2010; 74:570–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Tomov T.E., Tsukanov R., Liber M., Masoud R., Plavner N., Nir E.. Rational design of DNA motors: fuel optimization through single-molecule fluorescence. J. Am. Chem. Soc. 2013; 135:11935–11941. [DOI] [PubMed] [Google Scholar]
- 30. Omabegho T., Sha R., Seeman N.C.. A bipedal DNA Brownian motor with coordinated legs. Science (80-.). 2009; 324:67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Bonnet G., Krichevsky O., Libchaber A.. Kinetics of conformational fluctuations in DNA hairpin-loops. Proc. Natl. Acad. Sci. U.S.A. 1998; 95:8602–8606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Bloomfield V.A., Crothers D.M., Tinoco I. Jr. Nucleic Acids: Structures, Properties and Functions. 2000; Sausalito: University Science Books. [Google Scholar]
- 33. Oprzeska-zingrebe E.A., Smiatek J.. Preferential binding of urea to Single-Stranded DNA structures: a molecular dynamics study. Biophys. J. 2018; 114:1551–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wallace M.I., Ying L., Balasubramanian S., Klenerman D.. FRET fluctuation Spectroscopy: exploring the conformational dynamics of a DNA hairpin loop. J. Phys. Chem. B. 2000; 104:11551–11555. [Google Scholar]
- 35. Gralla J., Crothers D.M.. Free energy of imperfect Nucleic Acid Helices II. Small hairpin loops. J. Mol. Biol. 1973; 73:497–511. [DOI] [PubMed] [Google Scholar]
- 36. Jung J., Van Orden A.. A three-state mechanism for DNA hairpin folding characterized by multiparameter fluorescence fluctuation spectroscopy. J. Am. Chem. Soc. 2006; 128:1240–1249. [DOI] [PubMed] [Google Scholar]
- 37. Narayanan R., Zhu L., Velmurugu Y., Roca J., Kuznetsov S.V., Prehna G., Lapidus L.J., Ansari A.. Exploring the energy landscape of nucleic acid hairpins using laser temperature-jump and microfluidic mixing. J. Am. Chem. Soc. 2012; 134:18952–18963. [DOI] [PubMed] [Google Scholar]
- 38. Goddard N.L., Bonnet G., Krichevsky O., Libchaber A.. Sequence dependent rigidity of single stranded DNA. Phys. Rev. Lett. 2000; 85:2400–2403. [DOI] [PubMed] [Google Scholar]
- 39. Jung J., Ihiy R., Scott E., Yu M., Van Orden A.. Probing the complete folding trajectory of a DNA hairpin using dual beam fluorescence fluctuation spectroscopy. J. Phys. Chem. B. 2008; 112:127–133. [DOI] [PubMed] [Google Scholar]
- 40. Yin Y., Wang P., Yang X.X., Li X., He C., Zhao X.S.. Panorama of DNA hairpin folding observed via diffusion-decelerated fluorescence correlation spectroscopy. Chem. Commun. 2012; 48:7413. [DOI] [PubMed] [Google Scholar]
- 41. Ha T. Single-molecule fluorescence methods for the study of nucleic acids. Curr. Opin. Struct. Biol. 2001; 11:287–292. [DOI] [PubMed] [Google Scholar]
- 42. Schuler B., Lipman E.A., Eaton W.A.. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002; 419:743–748. [DOI] [PubMed] [Google Scholar]
- 43. Deniz A.A., Dahan M., Grunwell J.R., Ha T., Faulhaber A.E., Chemla D.S., Weiss S., Schultz P.G.. Single-pair fluorescence resonance energy transfer on freely diffusing molecules: observation of Förster distance dependence and subpopulations. Proc. Natl. Acad. Sci. U.S.A. 1999; 96:3670–3675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Ha T., Selvin P.R.. Selvin PR, Ha T. Single Molecule Techniques. The New Era of Biology In Singulo. 2008; Cold Spring Harbor Laboratory Press; 1–36. [Google Scholar]
- 45. Seeliger J., Werkmüler A., Winter R.. Macromolecular crowding as a suppressor of human IAPP fibril formation and cytotoxicity. PLoS One. 2013; 8:e69652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Müller J.D., Gratton E.. High-pressure fluorescence correlation spectroscopy. Biophys. J. 2003; 85:2711–2719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Patra S., Erwin N., Winter R.. Translational dynamics of lipidated ras proteins in the presence of crowding agents and compatible osmolytes. ChemPhysChem. 2016; 17:2164–2169. [DOI] [PubMed] [Google Scholar]
- 48. Müller B.K., Zaychikov E., Bräuchle C., Lamb D.C.. Pulsed interleaved excitation. Biophys. J. 2005; 89:3508–3522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Hendrix J., Lamb D.C.. Pulsed interleaved Excitation: Principles and applications. Methods Enzymol. 2013; 518:205–243. [DOI] [PubMed] [Google Scholar]
- 50. Ruettinger S., Buschmann V., Kraemer B., Orthaus S., Koberling F.. FRET analysis with Pulsed Interleaved Excitation (PIE) using the MicroTime 200. Appl. note, PicoQuant GmbH. 2013; https://www.picoquant.com/images/uploads/page/files/7266/appnote_pie-fret.pdf. [Google Scholar]
- 51. Sisamakis E., Valeri A., Kalinin S., Rothwell P.J., Seidel C.A.M.. Accurate Single-Molecule FRET studies using multiparameter fluorescence detection. Methods Enzymol. 2010; 475:455–514. [DOI] [PubMed] [Google Scholar]
- 52. Kudryavtsev V., Sikor M., Kalinin S., Mokranjac D.. Combining MFD and PIE for accurate Single-Pair Fçrster resonance energy transfer measurements. ChemPhysChem. 2012; 13:1060–1078. [DOI] [PubMed] [Google Scholar]
- 53. Roy R., Hohng S., Ha T.. A practical guide to single-molecule FRET. Nat. Methods. 2008; 5:507–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Cordes T., Vogelsang J., Tinnefeld P.. On the mechanism of trolox as antiblinking and antibleaching reagent. J. Am. Chem. Soc. 2009; 131:5018–5019. [DOI] [PubMed] [Google Scholar]
- 55. Holzmeister P., Gietl A., Tinnefeld P.. Geminate recombination as a photoprotection mechanism for fluorescent dyes. Angew. Chemie. Int. Ed. 2014; 53:5685–5688. [DOI] [PubMed] [Google Scholar]
- 56. Kinz-Thompson C.D., Bailey N.A., Gonzalez R.L.. Precisely and accurately inferring Single-Molecule rate constants. Methods Enzymol. 2016; 581:187–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Van De Meent J.W., Bronson J.E., Wiggins C.H., Gonzalez R.L.. Empirical bayes methods enable advanced population-level analyses of single-molecule FRET experiments. Biophys. J. 2014; 106:1327–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. McKinney S.A., Joo C., Ha T.. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006; 91:1941–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Blanco M., Walter N.. Analysis of complex single molecule FRET time trajectories. Methods Enzymol. 2010; 472:153–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Rueda D., Bokinsky G., Rhodes M.M., Rust M.J., Zhuang X., Walter N.G.. Single-molecule enzymology of RNA: essential functional groups impact catalysis from a distance. Proc. Natl. Acad. Sci. U.S. A. 2004; 101:10066–10071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Minton A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media *. J. Biol. Chem. 2001; 276:10577–10581. [DOI] [PubMed] [Google Scholar]
- 62. Minton A.P. Models for excluded volume interaction between an unfolded protein and rigid macromolecular cosolutes: macromolecular crowding and protein stability revisited. Biophys. J. 2005; 88:971–985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Trajkovski M., Endoh T., Tateishi-Karimata H., Ohyama T., Tanaka S., Plavec J., Sugimoto N.. Pursuing origins of (poly)ethylene glycol-induced G-quadruplex structural modulations. Nucleic Acids Res. 2018; 46:4301–4315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Zimmerman S.B., Minton A.P.. Macromolecular crowding: biochemical, biophysical and physiological consequences. Annu. Rev. Biophys. Biomol. 1993; 22:27–65. [DOI] [PubMed] [Google Scholar]
- 65. Sherman E., Itkin A., Kuttner Y.Y., Rhoades E., Amir D., Haas E., Haran G.. Using fluorescence correlation spectroscopy to study conformational changes in denatured proteins. Biophys. J. 2008; 94:4819–4827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Chalikian T.V., Breslauer K.J.. On volume changes accompanying conformational transitions of biopolymers. Biopolymers. 1996; 39:619–626. [DOI] [PubMed] [Google Scholar]
- 67. Amiri A.R., Macgregor R.B.. The effect of hydrostatic pressure on the thermal stability of DNA hairpins. Biophys. Chem. 2011; 156:88–95. [DOI] [PubMed] [Google Scholar]
- 68. Gao M., Arns L., Winter R.. Modulation of the thermodynamic signatures of an RNA thermometer by osmolytes and salts. Angew. Chemie Int. Ed. 2017; 56:2302–2306. [DOI] [PubMed] [Google Scholar]
- 69. Dubins D.N., Lee A., Macgregor R.B., Chalikian T.V.. On the stability of double stranded nucleic acids. J. Am. Chem. Soc. 2001; 123:9254–9259. [DOI] [PubMed] [Google Scholar]
- 70. Garcia A.E., Paschek D.. Simulation of the pressure and temperature folding/unfolding equilibrium of a small RNA hairpin. J. Am. Chem. Soc. 2008; 130:815–817. [DOI] [PubMed] [Google Scholar]
- 71. Lambert D., Leipply D., Draper D.E.. The osmolyte TMAO stabilizes native RNA tertiary structures in the absence of Mg2+: evidence for a large barrier to folding from phosphate dehydration. J. Mol. Biol. 2010; 404:138–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Lambert D., Draper D.E.. Effects of Osmolytes on RNA secondary and tertiary structure stabilities and RNA-Mg2+ interactions. J. Mol. Biol. 2007; 370:993–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Miner J.C., García A.E.. Equilibrium denaturation and preferential interactions of an RNA tetraloop with urea. J. Phys. Chem. B. 2017; 121:3734–3746. [DOI] [PubMed] [Google Scholar]
- 74. Lambert D., Draper D.E.. Denaturation of RNA secondary and tertiary structure by urea: simple unfolded state models and free energy parameters account for measured m -values. Biochemistry. 2012; 51:9014–9026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Tsukanov R., Tomov T.E., Masoud R., Drory H., Plavner N., Liber M., Nir E., Sheva B.. Detailed study of DNA hairpin dynamics using Single-Molecule fluorescence assisted by DNA origami. J. Phys. Chem. B. 2013; 117:11932–11942. [DOI] [PubMed] [Google Scholar]
- 76. Holmstrom E.D., Nesbitt D.J.. Biophysical insights from temperature-dependent single-molecule förster resonance energy transfer. Annu. Rev. Phys. Chem. 2016; 67:441–465. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.