Label-Free Optical Detection of DNA Translocations through Plasmonic Nanopores

Abstract

Solid-state nanopores are single-molecule sensors that hold great potential for rapid protein and nucleic-acid analysis. Despite their many opportunities, the conventional ionic current detection scheme that is at the heart of the sensor suffers inherent limitations. This scheme intrinsically couples signal strength to the driving voltage, requires the use of high-concentration electrolytes, suffers from capacitive noise, and impairs high-density sensor integration. Here, we propose a fundamentally different detection scheme based on the enhanced light transmission through a plasmonic nanopore. We demonstrate that translocations of single DNA molecules can be optically detected, without the need of any labeling, in the transmitted light intensity through an inverted-bowtie plasmonic nanopore. Characterization and the cross-correlation of the optical signals with their electrical counterparts verify the plasmonic basis of the optical signal. We demonstrate DNA translocation event detection in a regime of driving voltages and buffer conditions where traditional ionic current sensing fails. This label-free optical detection scheme offers opportunities to probe native DNA–protein interactions at physiological conditions.

Nanopores are an emergent class of label-free single-molecule biosensors that are projected to significantly impact the multibillion dollar markets of diagnostics and medicine^1,2 by providing a starting point on the roadmap to personalized medicine.³ The simple concept of shrinking the sensor down to the size of the molecule that it is probing has already brought a commercial DNA sequencing device,⁴ and applications in diagnostics and biophysics are currently being explored. Example applications include the analysis of blood serum,⁵ the classification of proteins in solution,⁶⁻⁸ and characterization of DNA–protein binding.^9,10 To date, nanopore-based detection schemes rely almost exclusively on the modulation of an ionic current to report on the small changes in physical size of the analyte during its passage through the nanopore.¹¹ However, the ionic current is set up by a transmembrane driving voltage that controls the translocation speed of the molecules, thus inextricably linking the signal strength and the translocation time. Furthermore, the ionic current strongly depends on the electrolyte concentration, characteristically high-molar (∼1 M) salt solutions, rendering sensing at physiological conditions impractical. Finally, the requirement for individual current amplifiers for read-out of each nanopore limits the sensors density in scalable integration on chip.¹² Alternative read-out strategies based on silicon nanowire FETs,¹³ calcium fluorescence,^14,15 tunneling junctions,¹⁶ and even graphene nanoribbons¹⁷⁻¹⁹ have been developed to address these issues. While some of these approaches are more permissive for sensor parallelization, these schemes have not demonstrated full independence of ion flow or electrolyte composition to mediate and amplify the signal of interest. Completely decoupling the biomolecular signal from the driving voltage and buffer conditions will increase the versatility and scalability of nanopore sensing.

To overcome these challenges, we propose a radically different, purely optical, nanopore read-out mechanism based on single-molecule plasmonic resonance sensing through enhanced light transmission.^11,20 In this scheme, changes in light intensity transmitted through a resonant nanoscale aperture report on the presence and conformation of biomolecules. The plasmonic excitations of the metal’s electron gas can mediate the propagation of light through subdiffraction-limit apertures, enhancing the light transmission.^21,22 The magnitude of this light transmission is strongly dependent on the wavelength and polarization of the excitation light, the geometry of the nanostructure, and its dielectric environment.²³ The latter strong sensitivity of the resonance of nanoaperture to the local environment allows for the optical sensing of molecules²⁰ that reside in the optical near-field of the aperture. The near-fields can be highly concentrated in the aperture by using small nanogaps²⁴ that focus the plasmon oscillation into this gap, creating intense optical hotspots. These hotspots have been used to study nonlinear optical effects,²⁵ perform molecular spectroscopy,²⁶ and trap single-molecules through nanotweezing.^27,28 The resonance that excites the gap is extremely sensitive to the local refractive index in the hotspot, and the presence of biomolecules in the gap is thus communicated to the far field by variations in the light transmission intensity.

By integrating a nanopore right at the feed gap of the plasmonic nanoantenna, biomolecules can be directly delivered to the nanogap, ensuring interaction of the analyte with the hotspot,²⁹ overcoming electrostatic surface repulsion and bypassing the otherwise diffusion-limited arrival times of biomolecules to the sensor.³⁰ Several experimental accounts have been published on plasmonic nanopores for single-molecule biosensing, but so far these focused on nanoplasmonic heating,^31,32 Raman scattering,³³ and fluorescence detection,³⁴ while plasmon resonance sensing has remained unexplored. Because plasmon resonance sensing is purely optical, the signal from a translocating biomolecule is without any fluorescent labels and entirely independent of the buffer conditions and driving voltage used, creating a versatile and more powerful nanopore sensor that naturally allows for high-density integration on a device.³⁵

Here, we experimentally show simultaneous ionic-current and optical-transmission-based detection of single-molecule DNA translocations through a nanopore integrated in the gap of a bowtie-shaped gold plasmonic nanoaperture. By characterizing the optical signal, we verify the plasmonic origin of the effect and show that the amplitude of the optical transients is driving-voltage and buffer independent. We demonstrate that the optical detection scheme outperforms the ionic-current detection at high measurement bandwidth and can detect translocations of DNA molecules in e.g. physiological buffer conditions where the traditional ionic-current detection loses its sensitivity.

Results and Discussion

Fabrication and Characterization of the Inverted-Bowtie Plasmonic Nanopore

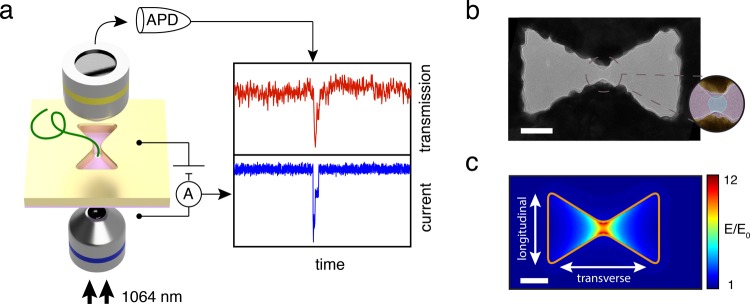
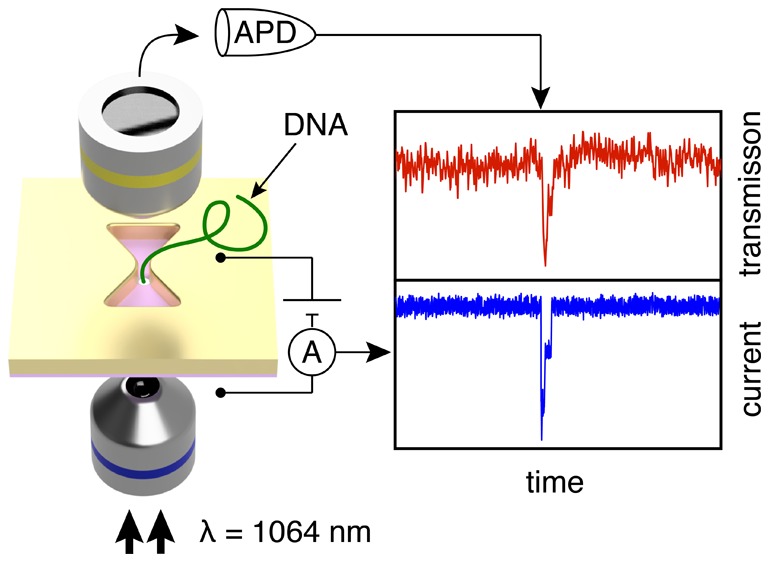
Figure 1a shows a schematic of the experimental setup. Light transmission is monitored by sandwiching a plasmonic nanopore device in between two objectives, one for excitation and one for collection of the transmitted light (Figure 1a). The plasmonic antenna is a bowtie-shaped nanoaperture in a 100 nm thick gold film. The apertures, fabricated using electron-beam lithography on a thick PMMA/MMA-MAA/PMGI resist layer, are placed on a 20 nm thin freestanding silicon-nitride (SiN) membrane by wedging transfer (for fabrication details, see Methods section). Figure 1b shows a transmission electron microscopy (TEM) image of a typical nanoantenna with a feed gap of 20 nm, a width of 160 nm across, and a side length of 100 nm. More images can be found in Supporting Information (SI) Section S1. The nanopore is drilled right in the center of the feed gap of the antenna using TEM drilling, as shown in the false-colored zoom in Figure 1b.

Figure 1.

Inverted-bowtie plasmonic nanopore. (a) Schematic of the plasmonic nanopore experimental setup. (b) Transmission electron microscope (TEM) image of a plasmonic inverted-bowtie with a nanopore drilled in its gap. The zoom shows a false-colored TEM image of the nanopore in the gap. (c) Normalized electric-field density distribution simulated for the idealized geometry (outlined in orange) of the nanoantenna in (b), clearly revealing optical-field localization and field enhancement up to 12 times in the gap region of the antenna. Scale bars are 50 nm.

We illuminate the inverted bowtie with an infrared 1064 nm laser, while an electrical bias is applied across the supporting SiN membrane. The DC electrical bias serves to drive biomolecules through the nanopore sensor by electrophoresis. The light transmitted through the nanoantenna is monitored using an avalanche photodetector (APD), and the ionic current is simultaneously observed using a conventional current amplifier (see Methods section). When illuminated with light that is polarized across the feed gap direction of the antenna (longitudinal polarization, see Figure 1c), a plasmon resonance is excited that enhances and concentrates the electromagnetic field to the hotspot in the gap of the antenna. Figure 1c shows the spatial distribution of the normalized electric-field strength in the antenna at 1064 nm wavelength excitation resulting from a finite-difference time-domain (FDTD) simulation. The light is clearly concentrated in the gap, and an electric field enhancement up to a factor 12 compared to the incident light can be achieved (see Methods section for simulation details). The simulations are validated through a comparison of experimental transmission spectra with simulated ones, see SI Section S2. Importantly, the gap resonance is not excited when illuminating the antenna with light polarized in the orthogonal orientation (transverse polarization), and hence the field localization is absent and light transmission through the nanoaperture is minimal in that case (see SI Section S3). The approach presented here aims to optically sense single DNA molecules as they traverse through a plasmonic nanopore, where the presence of the DNA in the hotspot may affect the resonance of the nanoantenna, hence modulating the optical transmission intensity (Figure 1a).

Before adding DNA, we first test and characterize the plasmonic nanopore. After mounting the sample in a custom-made flow cell, electrolyte is flushed in, a bias voltage of 100 mV is applied using a pair of Ag/AgCl electrodes to induce an ionic current flow, and the membrane is scanned with a 1064 nm wavelength laser focused to a diffraction-limited spot (∼0.8 μm in size). Excitation of the plasmonic nanopore by the laser focus will lead to localized plasmonic heating. This, in turn, creates a small temperature increase at the nanopore that can be observed by monitoring the temperature-sensitive ionic current through the pore³⁶ and allows for accurately aligning the nanopore with the laser focus. 7.5 milliwatts of excitation power, for example, resulted in a measured temperature increase of 3.6 °C at the nanopore, in good agreement with predictions from simulations (see SI Section S4). Please note that the temperature increase observed in the inverted antenna is very significantly lower than that observed for a typical freestanding dimer antenna,³¹ due to a much more efficient heat dissipation by the 100 nm thick surrounding gold film and the slight off-resonant excitation of the plasmonic gap mode.

Optical Light Transmission Exhibits Transient Signals Caused by DNA Translocations

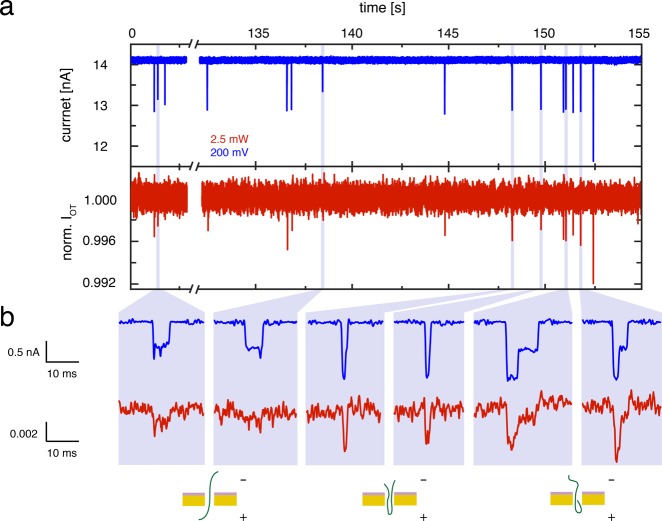
Next, we test the use of these plasmonic nanopores as optical single-molecule sensors. After adding λ-DNA to the SiN side of the chip and applying a 200 mV bias, transient decreases characteristic for DNA translocations can be clearly observed in the time traces of the ionic current, as shown in blue in Figure 2a. Gratifyingly, concurrent spikes are also observed in the time traces of the normalized optical transmission intensity (I_OT), as shown in red in Figure 2a. This demonstrates that the nanoantenna can be used to optically detect DNA translocations through a nanopore in a label-free manner. Inspection of the two traces shows that the transient signals are very closely correlated, i.e., each time that an optical spike is observed, there is a concurrent spike in the ionic current signal, which demonstrates that the signals in the optical transmission are induced by translocating DNA molecules.

Figure 2.

Simultaneous detection of DNA translocations in the ionic current and transmitted light. (a) Time traces of both the ionic current (blue) and normalized optical light transmission (norm. I_OT, red) in 2 M LiCl after the addition of λ-DNA, at a bias voltage of 200 mV and 2.5 mW laser power. Clear transients due to DNA translocation can be observed concurrently in both traces. (b) Zooms and schematic interpretation of the events observed in (a), for two linear DNA translocations (left), two fully folded DNA translocations (middle), and two partially folded DNA translocations (right). Whereas 5 out of 19 linear events are detected optically, 86 out of 92 folded events are optically detected. For display purposes, electrical traces are low-pass filtered with a 1 kHz Gaussian filter, and optical traces are band-pass filtered using 2-pole Butterworth filter with a 4 Hz to 1 kHz window.

Closer examination of the spikes in the ionic current (blue, Figure 2b) reveals current blockade signatures that are typical of DNA translocations: for large nanopores (>5 nm) DNA molecules can either enter in a linear fashion (blue, left two examples Figure 2b), with one double strand of DNA in the nanopore, or they can traverse the pore in a folded fashion (blue, remaining examples Figure 2b) with two double strands of DNA temporarily residing in the nanopore.^37,38 The use of 2 M LiCl electrolyte produces excellent signal-to-noise characteristics in the electrical trace (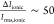) and allows these folds to be easily identified. Interestingly, inspection of the optical traces reveals very similar characteristics, where the folds detected in the ionic current are also discernible in the optical channel (red, right two examples Figure 2b), albeit at a clearly lower signal-to-noise level (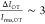). Whereas with the current signal-to-noise ratio, linear translocations may occasionally escape our optical detection (red, second example from the left in Figure 2b), folded events are systematically detected (red, remaining examples on the right of Figure 2b). Notably, the excellent correlation of electrical and optical signals as well as the observation of folded events in the optical signal immediately leads to the conclusion that the optical signal arises from the nanoscale localized region of the nanoaperture. Moreover, the optical signatures from DNA molecules that are translocated from the gold side of the chip are identical to translocations from the SiN side, and thus the observed signals are not due to modulation of the light by the large (∼1 μm) DNA polymer blob that resides above or below the pore before or after the molecule translocates through the pore.

DNA Signals in Optical Light Transmission Arise from a Plasmonic Resonance Shift

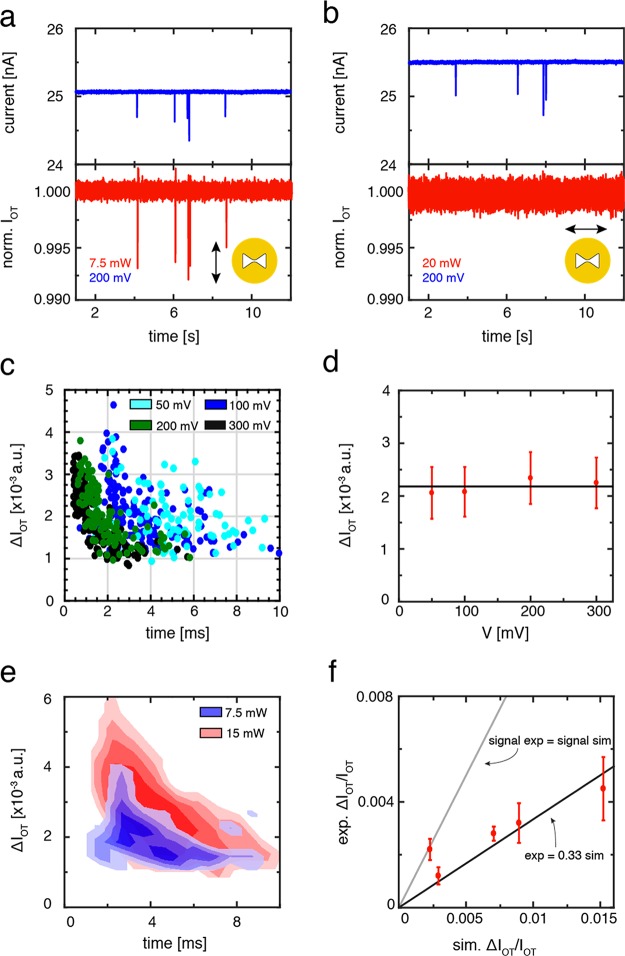
Next, we verify that our optical transmission signals originate from the plasmonic gap resonance of the nanoantenna. First, we confirm that the signal from translocating DNA molecules is mediated by the excitation of the plasmonic gap resonance. For this, we perform DNA translocations under different illumination conditions. When the incident laser light is polarized in the longitudinal direction (cf. inset to Figure 3a), it excites the gap resonance and concurrent transient signals from translocating DNA molecules are observed in both the electrical and optical channels (Figure 3a). For the transverse polarization (inset Figure 3b), on the contrary, no optical transients are observed whatsoever, whereas DNA translocations are clearly discerned in the ionic current (Figure 3b). This confirms expectations since changing the polarization of the incident light to the transverse orientation should remove the field localization in the gap of the antenna, and hence the light transmission should no longer be sensitive to changes in dielectric environment of the gap region. Typically, the light transmission through the antenna under the transverse illumination is significantly lower than under longitudinal excitation. To make a fair comparison, we increase the detector gain and the incident laser power from 7.5 mW to 20 mW such that the absolute transmission baseline during transverse illumination is matched to the transmission baseline during longitudinal excitation. Still, no optical transients can be detected. The absence of signatures from translocating DNA molecules in the transverse illumination condition clearly shows that the signals in the optical channel indeed originate from the excitation of the plasmonic gap mode.

Figure 3.

Characterization of the optical signals for DNA translocations. (a) λ-DNA translocations in 2 M LiCl under longitudinal polarization. Translocations produce clear transients in both the electrical trace (top, blue) and in the transmitted light trace when longitudinal excitation is used (bottom, red). (b) λ-DNA translocations in 2 M LiCl under transverse polarization. No transients are produced in the optical trace, whereas they are clearly discerned in the ionic current trace. (c) Scatter plot of optical event amplitudes versus the signal durations for 20 kbp DNA at 7.5 mW laser power and different driving voltages. A clear shift is observed toward short event durations at different driving voltages, but the average event amplitude remains unchanged. (d) Histogram peak of all optical events for 20 kbp DNA translocations as a function of driving voltage. The signal amplitude seems to be independent of applied voltage. The peak signal indicates the signal strength from a folded translocation. Error bars are the standard deviation in the normalized transmission baseline. (e) Heat map from the scatter plot of average optical event amplitudes versus the signal durations for 20 kbp DNA for two different excitation powers. (f) Normalized average experimental signal amplitude from all optical events versus the normalized simulated transmission change upon the insertion of two double strands of DNA in the gap of each individual nanoantenna (see SI Section S8). The experimental signal follows a linear trend through the origin as predicted by the simulations, albeit with a factor three lower signal amplitude (linear fit, blackline, ).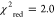

To assess whether or not the amplitude of the optical transients is independent from the electrical bias, we characterize the dependence of the optical signal on the driving voltage. Figure 3c shows a scatter plot of the optical event amplitudes ΔI_OTversus the event durations for translocations of 20 kbp DNA molecules at different voltages (for details on the event detection and analysis, see Methods). The scatters show a characteristic L-shape clustering of events (see SI Section S5) that is typically observed for ionic current events in nanopores that are wide enough to permit folded translocations.³⁸ Clearly, the clusters shift to shorter event duration times for higher driving voltages. Notably, however, the optical signal amplitude remains unchanged. This sharply contrasts the amplitude of the electrical signals which originates from the ionic current blockade and scales linearly with voltage (see SI Section S5). Figure 3d quantifies this independence of the transmission signal amplitude for folded events versus voltage (see SI Section S6 for details).

The fact that we observe a well-defined amplitude level of the optical signal from a dsDNA strand present in the gap is actually striking in light of extensive previous work that reported a strong heterogeneity of the signal strengths. Generally, molecules that approach a plasmonic nanostructure encounter a spatially inhomogeneous hotspot, producing varying signal strengths as a result.³⁹ In our case, the nanopore delivers the biomolecule directly into the hotspot by design, reducing uncertainties in the exact location for the interaction of the molecule with the hotspot of the nanoantenna, and furthermore the hotspot region is approximately homogeneous due to off-resonant excitation of the antenna (see Figure 1c and SI Section S7).

Because the optical signals from translocating DNA molecules are only observed in longitudinal excitation and are voltage independent, we conclude that these signals originate from a shift of the plasmonic gap resonance that is temporarily induced by the translocating molecule. First, this explains the observed transient decreases in transmitted light as the presence of a molecule in the hotspot will induce a redshift of the antenna resonance, which results in a reduction in transmitted light intensity as the antenna is excited at a wavelength shorter than the peak of the resonance of the nanoantenna. Second, this predicts that the signal strength should depend linearly on the excitation power, since the transmitted light intensity through the nanoaperture I_OT will scale linearly with the excitation power of the 1064 nm wavelength laser. Figure 3e shows a heat map of the absolute event amplitudes ΔI_OTversus the event durations for 7.5 mW and 15 mW of laser power. An increase in signal strength is indeed observed, indicated by a shift of the event population toward higher signal amplitude. The average signal amplitude for two double strands of DNA increased from ΔI_OT = 2.0 ± 0.7 · 10^–3 au to ΔI_OT = 3.4 ± 1.0 · 10^–3 au (mean values and standard deviations of the distribution). Increasing the laser power leaves the signal-to-noise level unchanged, as the increased baseline transmission is accompanied by a similar increase in baseline variance. We note that the larger incident power produces a slightly higher temperature increase at the nanopore (7.0 °C increase at 15 mW, compared to 3.6 °C at 7.5 mW), but we do not expect this to have an impact on the optical signal strength, contrary to what is observed for the ionic current signal.³¹

Finally, we compare the signal amplitude from DNA translocations with predictions from FDTD simulations. Here, we examine the resonance of the fabricated nanoantennas with and without two double strands of DNA present in the center of the nanopore, and we extract the DNA signal amplitude by subtracting the two simulated transmission values at λ = 1064 nm (details in SI Section S8 and Methods). Figure 3f shows the normalized average experimental signal amplitude for two double strands of DNA versus the normalized simulated signal amplitude. The simulated and experimental signal intensities correlate very well and follow a linear trend through the origin, though quantitatively the simulations overestimate the signal strength by a factor of 3. The good correlation between the experimental and simulated results is quite striking, considering the crudeness of the simplified DNA modeling,^40,41 and it further corroborates that the optical transients arise from a shift of the plasmonic gap resonance.

The Optical Sensing Volume Is Located in the Gap of the Nanoantenna

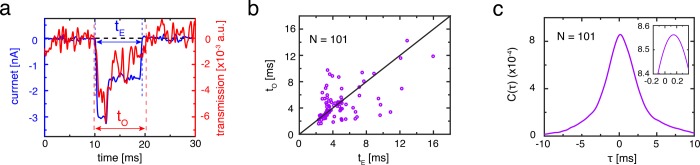
The transit times for moving the DNA through the plasmonic nanopore are very similar for the optical and electrical signals. Figure 4a displays an example of the electrical signal and the optical signal for the same DNA-translocation event. Using simple thresholding, the duration of an event is defined as the time in between the baseline crossings prior and posterior to the spike. Figure 4b shows the scatter of the signal durations for the electrical (t_E) and optical channels (t_O), for events that are simultaneously well resolved in both channels (63% of all events) for λ-DNA translocations at 200 mV. The data show a clear linear correlation (r = 0.58) but display an appreciable scatter as the low signal-to-noise levels for one double strand of DNA in the optical channel troubled the correlation. The observed passage times are similar to the passage times observed in a normal solid-state SiN nanopore under these conditions, indicating that plasmonic trapping forces⁴² and DNA gold-surface interactions⁴³ do not play a major role here. However, appropriate excitation of the nanoantenna closer to the plasmon resonance can strengthen optical forces⁴⁴ that could slow down and even stall the DNA translocation process.²⁹

Figure 4.

Electrical and optical signal time correlation analysis. (a) Overlay of the optical (red) and electrical signal (blue) for one DNA translocation event; t_E and t_O indicate the event duration for an electrical and optical signal, respectively. Signal duration is defined as the time taken between two consecutive baseline crossings before and after the spike that is detected by thresholding (see Methods section). (b) Correlation plot of the electrical and optical signal durations of all simultaneously detected events (63% (33 out of 74 linear events and 68 out of 86 folded events) from all ionic current events, conducted in 2 M LiCl and 200 mV, 2.5 mW) showing a correlation between both signal durations (r = 0.58). The deviations from t_E = t_O (black line) arise from inaccurate determination of the optical signal duration due to its lower signal-to-noise ratio. (c) Cross-correlation between all events in (b). A broad peak emerges around τ = 0. The zoom shows a closer inspection of the peak, which reveals a small delay in the optical signal of around 140 ± 190 μs.

Even though the optical and electrical signals both probe the DNA molecule at the nanopore during the translocation, the sensing regions of both signals are not exactly identical. For the ionic current, the sensing region largely comprises of the nanopore volume⁴⁵ that spans the 20 nm thickness of the SiN membrane. For the optical signal, however, the sensing region is confined to the hotspot region with the increased optical field, which is localized within the gap of the inverted-bowtie antenna and which spans roughly uniformly across the total thickness of the 100 nm gold film on top of the nanopore (SI Section S7). Modifying the nanostructure design will allow for the engineering of the field localization to create even more focused sensing regions, for example by using tapering of the sidewall of the gold structure.⁴⁶ From a detailed analysis of the signals, we can deduce a subtle timing difference between these sensing regions. Due to the design of the plasmonic nanopore, the electrical and optical sensing regions are stacked vertically. Since the analyte is added to the SiN side of the chip, the translocating molecules are first inserted in the nanopore, passing its electrical sensing region, before they subsequently enter the optical sensing region in the gold nanoaperture. Figure 4c shows the lumped cross-correlation of all simultaneously detected signals from Figure 4b. A broad peak (full-width half-maximum 4.3 ms) is observed around a time delay of zero, as is expected for signals that originate from the same translocation events. However, a closer inspection (see inset Figure 4c) reveals that the correlation function C(τ) peaks at τ = 140 ± 190 μs (mean and standard error of the mean), i.e., the onset of the optical signal is measured slightly later than the electrical signal. This delay time corresponds to roughly 560 ± 760 nm distance traveled for a translocating DNA molecule, using an average translocation time of ∼4 ms for a linear 16 μm long λ-DNA molecule (Figure 3c). The very large error bar prevents an accurate comparison to the expected offset of ∼100 nm, viz., the vertical distance between the electrical and optical sensing volumes.

Advantages of Optical Transmission Sensing over Conventional Ionic Current Sensing

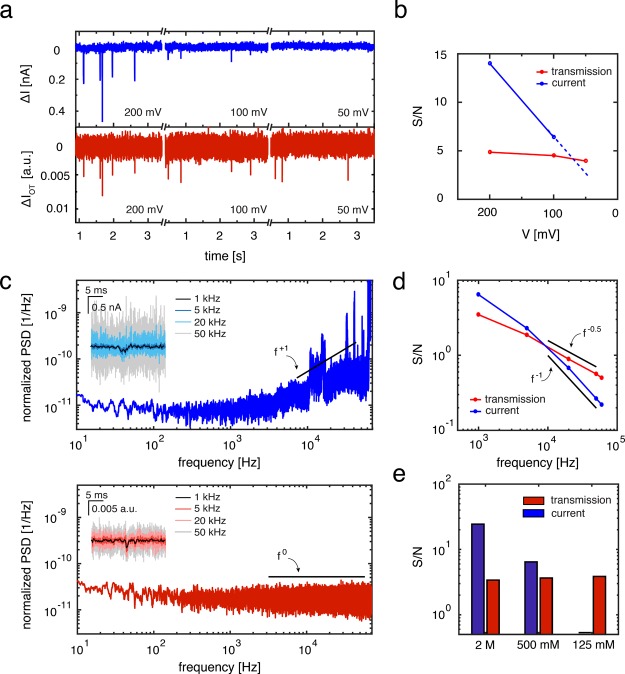
After validating the reliability of the optical sensing method, we demonstrate some of the advantages that the method offers over traditional ionic current sensing. The first and foremost benefit is the decoupling of the driving voltage from the signal strength. Signals in ionic current sensing rely on the physical obstruction of an ion flow by the volume of the biomolecule, and better signals are obtained if larger currents are present, which intrinsically requires the application of a larger driving voltage. In sharp contrast, the optical signals rely on a change in plasmon resonance that is independent of the bias voltage. The decoupling of the signal from the driving allows the translocation process to be studied at any driving voltage, even in the absence of any bias. Figure 5a demonstrates this by showing time traces of 20 kbp DNA molecules translocating a 20 nm nanopore at 500 mM LiCl at different driving voltages. DNA translocation events can clearly be observed in both the electrical and optical channels at 200 mV bias voltage (left, Figure 5a). At 100 mV bias, the signal strength from the events in the current channel is decreased significantly (center, Figure 5a), and at 50 mV it completely disappears in the noise floor (right, Figure 5a). On the contrary, the signal in the optical channel remains the same at each bias voltage, and translocations can still be well resolved at 50 mV bias. This is also demonstrated in Figure 5b, where the optical signal-to-noise ratio stays constant versus applied bias voltage, whereas the electrical signal-to-noise ratio decreases steeply.

Figure 5.

Advantages of optical light transmission over traditional ionic current sensing. (a) Electrical (blue) and optical (red) time traces during a 20 kbp DNA translocation experiment at 500 mM LiCl at different driving voltages. Whereas the ionic current signal decreases with driving voltage and disappears at 50 mV bias, the optical signal remains unchanged, and translocations can still be detected. (b) The signal-to-noise level as a function of decreasing voltage for both electrical and optical signals displayed in (a). (c) Normalized power spectral density (PSD, divided by the square of the average baseline signal) of the ionic current (top, blue) and optical transmission (bottom, red). For the ionic current a clear f¹ scaling is present at high frequencies due to dielectric noise, and interference peaks are present. Contrary to the electrical channel, the power spectrum of the optical channel is flat (f⁰) and free of interference. The insets show a typical event (taken from a measurement conducted at 500 mM, 100 mV, and 7.5 mW using 20 kbp DNA) filtered using various low-pass cutoff filter frequencies. (d) Log–log plot of the signal-to-noise ratio (S/N) versus low-pass cutoff filtering frequency, assuming a fixed signal strength for each. A f^–0.5 scaling can be observed for the optical S/N versus a f^–1 scaling for the electrical S/N. (e) S/N for both the optical and electrical signal of 20 kbp DNA translocations at 100 mV and 7.5 mW in different LiCl concentrations. A clear decrease can be observed for the electrical signal, preventing DNA translocations to be detected electrically at 125 mM LiCl. The optical signal-to-noise ratio remains unchanged with different LiCl concentrations, and DNA translocations can still be discerned at 125 mM.

As a second advantage, optical detection schemes offer, in principle, much higher-bandwidth data acquisition, as was also pointed out by others.¹⁴Figure 5b shows the normalized power spectral density (PSD) versus frequency plot of the electrical (top, blue) and optical channels (bottom, red). The ionic current channel displays 1/f type noise in the low-frequency region as well as dielectric noise⁴⁷ in the high-frequency region, manifested as a linear dependence of the PSD on f (see Figure 5c). Moreover, the channel suffers from electrical interference pick-up in the high frequency part of the spectrum, indicated by the strong peaks in this region. By contrast, the PSD from the optical transmission channel is flat at high frequencies (indicated by the horizontal line in Figure 5c) and is free of any electric interference. It implies that the signal-to-noise ratio will decrease more rapidly for the electrical signals than for the optical signals if the larger acquisition bandwidth is used. This is illustrated by the insets in Figure 5c, where the same translocation event (500 mM LiCl, 100 mV) is shown at full bandwidth in the electrical (inset in top panel) and optical channel (inset in bottom panel), but subsequently filtered at different low-pass cutoff frequencies. It is clear that the noise levels increase much more strongly with higher cutoff frequencies for the electrical compared to the optical channel, resulting more quickly in the onset of signal loss. Figure 5d quantifies this assertion by plotting the signal-to-noise ratio as a function of frequency. The signal-to-noise levels for the ionic current scale as f^–1 for high frequencies (blue, Figure 5d). On the other hand, the spectrally flat frequency dependence of the background fluctuations in the optical channel leads to a f^–0.5 dependence in the signal-to-noise ratio (red in Figure 5d), meaning that the optical signal will be more tolerant to increasing measurement bandwidth than the electrical signal.

Finally, the signal strength from plasmon resonance changes is independent of buffer conditions, contrary to the ionic current sensing which requires high concentrations of ions, thus allowing experiments to be conducted at any buffer composition and electrolyte concentration. Figure 5e shows the signal-to-noise level for translocation experiments at different electrolyte concentrations for the electrical signal (blue) and optical signal (red). A clear decrease in the electrical signal-to-noise ratio can be observed for lower salt concentrations. Importantly, at a physiological salt concentration of 125 mM LiCl the electrical signal completely disappears in the noise floor. This decrease can be attributed to a decrease in signal strength, as the current noise does not lower significantly upon lowering the electrolyte concentrations.⁴⁸ By contrast, the optical signal-to-noise ratio remains unchanged, as expected, and translocations can still be observed even at 125 mM LiCl. This demonstrates that, importantly, the optical sensing technique alleviates the restriction to high-salt concentrations which often limits nanopore sensing if physiological conditions are required.

Conclusion

In conclusion, we have demonstrated a label-free optical sensing technique using plasmonic nanopores that allows for probing translocating biomolecules independently from the applied driving voltage and electrolyte concentrations used. The detection is based on the enhanced light transmission through an inverted bowtie nanoantenna with a nanopore drilled in its feed gap and relies on a plasmon resonance shift induced by the presence of the molecule in the gap of the nanoantenna. We have shown that the transmitted light through the nanoantenna produces an optical signal that can report on the conformation of translocating DNA molecules. Our observations indicate that the optical sensing region lies within the gap of the plasmonic nanoantenna and that the noise for this optical sensing scheme increases with measurement bandwidth more favorably than for ionic current detection. In future work, it will be advantageous to improve the signal in our detection scheme, for example by bringing the resonance of the plasmonic nanoantennas closer to the excitation laser or by modifying the antenna layout.

The here reported label-free optical detection scheme may be used in various biosensing applications. The optical observation of DNA in such wide (20 nm) plasmonic nanopores naturally allows for an extension to the detection of protein–DNA complexes and large proteins in native salt conditions. Moreover, optical detection schemes are well suited for high-density nanopore device integration, which is challenging to be achieved when ionic current sensing is employed. Finally, the decoupling of the signal and driving voltage allows for alternative measurement modes. For instance, polymers that are electrophoretically inserted in the nanopore can be studied under the application of only a very weak bias, and their escape can be studied in the absence of any bias, all without any loss of signal. Alternatively, this sensing technique can be used to study thermophoretically or pressure driven polymer translocations, omitting an electrical bias all together. Finally, this detection scheme will aid the development of plasmonic nanopores as a platform for label-free nanotweezing and single-molecule Raman spectroscopy.

Methods

Sample Fabrication

Inverted-bowtie nanoapertures are fabricated using electron-beam lithography. First, a trilayer stack of (from substrate to top) PMGI/MMA-MAA copolymer/PMMA is spin-coated at 400 nm/1000 nm/100 nm thickness on a piece of a silicon wafer. The multilayer stack is essential to allow the gold layer on top of the stack to be stripped and the resulting gold flake to be handled. The resist is patterned with an array of bowties at a dose of 2500 μC/cm² using a 100 keV electron bundle from an electron-beam pattern generator (EBPG5200, Raith) and developed in MIBK:IPA 1:3 for 1 min followed by a 15 s dip into MF321 to transfer the pattern also to the PMGI layer. Next, 100 nm of gold is evaporated onto the layers using an electron-beam evaporator (Temescal 2000) at a rate of 3 Å/s, without the use of any adhesion layers. The MMA-MAA/PMMA/gold flake is then stripped from the substrate by submerging the sample in a 3% KOH solution for 15 min to dissolve the PMGI. Subsequently, the MMA-MAA/PMMA is removed using acetone, and the flake is transferred into an isopropyl alcohol solution. Using a wedging technique,⁴⁹ the flake is picked up from the solution and placed onto a freestanding SiN membrane. After drying, the flake is sealed onto the sample by covering the edge of the gold flake with PDMS. The sample is then cleaned in O₂ plasma (50 W) for 1 h to prevent carbon contamination in the TEM chamber. Finally, a TEM is used to select a suitable nanostructure, and a nanopore is drilled in the feed gap of the nanoaperture.

Experimental Setup

Prior to the experiment, the sample is rinsed in ethanol and ddH₂O and cleaned in O₂ plasma for 30 s (50 W). The sample is mounted in a custom-made PEEK flow cell that allows the plasmonic nanopore to be illuminated and the transmission light to be collected. Next, electrolyte, 2 M LiCl buffered to pH 8 with 20 mM Tris and 2 mM EDTA, unless otherwise stated, is flushed in. Current through the plasmonic nanopore is measured using a pair of Ag/AgCl electrodes and acquired using a Axopatch 200B (Molecular Devices) and analog filtered at 100 kHz using a low-pass 4-pole Bessel filter. The laser (M9-A64-0200 laser-diode, Thorlabs) is operated in constant injection-current mode and focused to a diffraction-limited spot on the sample using a 60× 1.2 NA water-immersion objective (Olympus) in an inverted microscope setup. The transmission light is collected using a 10× 0.3 NA objective (Nikon) and projected onto an Avalanche Photo Diode (APD410C/M, Thorlabs). Subsequently, the position of the laser focus is aligned to the plasmonic nanopore by scanning the membrane through the focus of the laser using a piezoelectric positioning stage (MadCity Laboratories, Inc.) and maximizing the current increase that is induced by plasmonic heating. Data acquisition is performed using custom-made Labview software through a NI DAQ (NI USB-6251, National Instruments) at a sampling rate of 200 kHz, where both the current amplifier and photodiode are read-out simultaneously to ensure synchronized signal acquisition.

Event Detection and Analysis

Event detection and analysis is performed using Tranzalyser,⁵⁰ a custom-made MATLAB-based software package developed in our lab. All traces, both electrical and optical, are low-pass filtered using a Gaussian filter with a cutoff at 1 kHz for analysis. Event detection is done in both channels by using a 5-sigma-threshold spike detection, using a baseline and sigma value calculated from a moving average window of 30000 data points for the electrical traces and 5000 data points for the optical traces. For display purposes, electrical traces are low-pass filtered using 1 kHz cutoff, and optical traces are band-pass filtered using a 2-pole Butterworth filter between 4 Hz and 1 kHz.

FDTD Simulations

We use FDTD Solutions (Lumerical Solutions, Inc., Canada) to model the optical properties of the inverted-bowtie plasmonic nanoantennas. The inverted bowtie is modeled as a bowtie-shaped aperture in a 100 nm thick gold film with a width of 160 nm, a side length of 100 nm, a 20 nm gap, and a 30 nm-in-radius in-plane tip rounding to resemble the fabricated structures. The antenna is positioned on a 20 nm thin silicon-nitride membrane with a refractive index (RI) of 2. The surrounding medium is modeled as water with a RI of 1.33. Symmetry is used to reduce the computational time. The plasmonic aperture is excited by a pulse from a total-field scattered-field source incident normal to the gold surface and with the polarization in either the longitudinal or the transverse mode. The fractional light transmission through the nanostructure is calculated by integrating the far-field power flux through a screen placed 350 nm below the membrane and normalized to the total incident power at each frequency.

The optical response of fabricated nanostructures is simulated by extracting the planar geometry from a TEM image, using the image import function of the FDTD Solutions program. The planar geometry is extruded 100 nm  to model an aperture in the gold film. The optical response with and without DNA inserted into the gap is calculated using the far-field power flux, where the DNA molecule is simulated as a 200 nm long rod of 2.2 nm in diameter and a refractive index of 2.5.⁴¹

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b06758.

• Additional TEM images of inverted-bowtie plasmonic nanopores, experimental and simulated spectrum of plasmonic nanopore, simulation of idealized inverted-bowtie nanoantenna in transverse polarization, experimental and simulated temperature increase in a plasmonic nanopore, blockade current versus dwell time scatter plots, all-point histograms of optically detected events at different bias voltages, simulation of normalized electric field across gold nanoantenna gap, details on determination of relative simulated signal amplitude (PDF)

The authors declare no competing financial interest.