We focus comments on data transformations. The Box-Cox transformation is a common data-driven transformation and the one in Eq. (8) is a generalized version with a shift parameter ‘c’ that allows for non-positive data. However, the range of the transformed outcome is restricted to a left truncated domain with a bounded support not covering the entire range [1]. Thus, the choice of ‘c’ could influence parameter estimation. Two variants of the Box-Cox transformation that cover the entire range (−∞, ∞) are available. One variant that covers the entire range is proposed by Manly [2]. The other is Bickel and Doksum’s modification [3] that transforms the original data yik to |yik + c|λ if λ ≠ 0 and log(yik + c) if λ = 0 and the transformed response is multiplied by the sign of (yik + c). However, none of them is reliable when there is substantial proportion of zeros in the data. Such zero-inflated data sets may require different approaches other than data-driven transformations [4, 5].
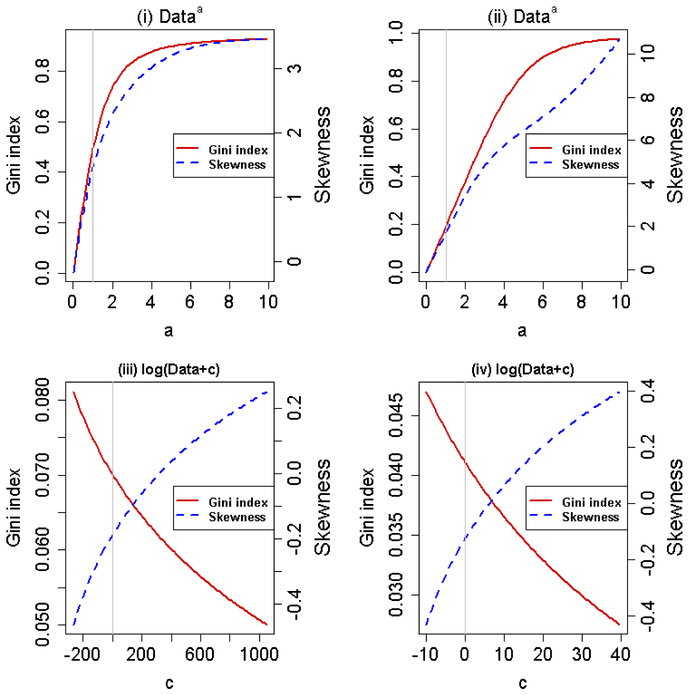
During implementations of the data-driven transformations to EDOMEX, it was observed that the estimates of Gini index are much more sensitive to the transformations than those for Mean and HCR, but no discussion was given for the underestimated Gini indices. We performed small simulation studies to investigate the effect of transformations on the estimate of the Gini index using the two datasets. One concerns simulated annual incomes and the other is the wage data in the R package ISLR called Wage. Fig. 1 (i)–(ii) plot the Gini index estimate and the skewness of the transformed data by the power transformation versus the power parameter ‘a’ in the form of Dataa for the simulated data and the wage data, respectively. Fig. 1 (iii)–(iv) display the same plots with the log transformation log(Data + c). For the power transformation, the estimate of the Gini index is proportional to the skewness of the distribution of the transformed data. It is interesting to note that this relationship is opposite for the log transformation, and the estimates from the log transformed data are always under-estimated compared to that from the untransformed data. The implication is that extra caution is required to transform the data for estimating the Gini index.
Figure 1.
The relationship between the power transformation (Dataa) and the Gini index estimate/skewness in subfigures (i) and (ii), and between the log transformation (log(Data + c)) and the Gini index estimate/skewness in subfigures (iii) and (iv). The grey vertical lines represent the cases when a = 1 or c = 0. The simulated income data, (531, 786, 1363, 2011, 2321, 2435, 3138, 4310, 5137, 5301, 6382, 8204, 10904, 15901, 21261), are used for subfigures (i) and (iii) and the subfigures (ii) and (iv) are based on the wage data for a group of 3000 male workers in the Mid-Atlantic region available in the R package ISLR called Wage.
Literature Cited
- 1.Sakia RM, The Box-Cox Transformation Technique - a Review. Journal of the Royal Statistical Society Series D-the Statistician, 1992. 41(2): p. 169–178. [Google Scholar]
- 2.Manly BFJ, Exponential Data Transformations. Statistician, 1976. 25(1): p. 37–42. [Google Scholar]
- 3.Bickel PJ and Doksum KA, An Analysis of Transformations Revisited. Journal of the American Statistical Association, 1981. 76(374): p. 296–311. [Google Scholar]
- 4.Pfeffermann D, Terryn B, and Moura FAS, Small area estimation under a two-part random effects model with application to estimation of literacy in developing countries. Survey Methodology, 2008. 34(2): p. 235–249. [Google Scholar]
- 5.Chandra H and Sud UC, Small Area Estimation for Zero-Inflated Data. Communications in Statistics-Simulation and Computation, 2012. 41(5): p. 632–643. [Google Scholar]