Summary
The control of cell position and division act in concert to dictate multicellular organization in tissues and organs. How these processes shape global order and molecular movement across organs is an outstanding problem in biology. Using live 3D imaging and computational analyses, we extracted networks capturing cellular connectivity dynamics across the Arabidopsis shoot apical meristem (SAM) and topologically analyzed the local and global properties of cellular architecture. Locally generated cell division rules lead to the emergence of global tissue-scale organization of the SAM, facilitating robust global communication. Cells that lie upon more shorter paths have an increased propensity to divide, with division plane placement acting to limit the number of shortest paths their daughter cells lie upon. Cell shape heterogeneity and global cellular organization requires KATANIN, providing a multiscale link between cell geometry, mechanical cell-cell interactions, and global tissue order.
Keywords: network, 3D imaging, plant, tissue, dynamics, cell division, organ design, connectome, tissue topology, emergence
Graphical Abstract

Highlights
-
•
Examination of global cellular order using 3D imaging and network science
-
•
Cells in the Arabidopsis SAM lie upon many shortest paths
-
•
Shortest wall divisions in native tissue generates emergent global order
-
•
Native cell shape, geometry, and microtubule structure are required for this emergence
The control of cell division plane orientation is becoming increasingly well characterized. How these local rules scale to generate global emergent properties in tissues is less well understood. Combining 3D imaging and network science in the shoot apical meristem of Arabidopsis revealed the presence of global topological order, whereby cells are prevented from lying on large numbers of short paths. This property emerges from local geometric divisions minimizing wall length and is dependent upon native cell geometry and microtubule reorganization.
Introduction
Pattern formation in complex multicellular organs is driven by a combination of control of the cell cycle and the placement of cells within organs (Meyerowitz, 1997). Local interactions between cells are proposed to underlie the emergence of complex ordered structures through the iterative repetition of simple rules (Gibson et al., 2011). Such bottom-up self-organizing principles have been described in a wide variety of biological systems at the cellular level (Sasai, 2013).
Organogenesis in plants is no exception and is thought to be mediated by communication through cell-to-cell interactions (Di Laurenzio et al., 1996, Lucas et al., 1995). Unlike in animal systems, where cells are capable of migrating across organs, plant cells physically adhere to one another through shared cell walls such that their positions relative to one another do not change (Coen et al., 2004). In light of these spatial constraints, the orientation of cell division planes plays an integral role in pattern formation (Besson and Dumais, 2011, Shapiro et al., 2015, Errera, 1886).
Models that predict the placement of cell division planes have been proposed previously in both plant and animal systems (Hofmeister, 1863, Thompson, 1942, Besson and Dumais, 2014). These cell division rules rely upon heterogeneity in cell shape in order to break symmetry in cell division plane choice. A rule proposed by Errera in 1886 states that a plant cell will divide in half through its center using the shortest wall possible (Errera, 1886). Adding a stochastic element (Besson and Dumais, 2011) or integrating multiple geometric factors simultaneously (Shapiro et al., 2015) to the placement of the division plane further increases the accuracy with which the placement of the division plane can be predicted. These local geometric principles are capable of predicting many, but not all, symmetric cell divisions in plants (Kwiatkowska, 2004).
Mechanical forces between adjacent plant cells exert influence over their neighbors (Hamant et al., 2008), and these interactions can alter the orientation of cell division planes (Louveaux et al., 2016, Lintilhac and Vesecky, 1984). Further work examining the organization of animal and plant epidermis has shown that the topology of a neighboring cell can influence division plane placement (Gibson et al., 2011). A limited number of local cell interactions can therefore impact cell division plane placement.
The regulatory mechanisms underlying the cell cycle in plants has been the subject of intensive investigation (Inzé and De Veylder, 2006, Dewitte and Murray, 2003, Sablowski, 2016). In unicellular systems, models can use both cell size (sizer) and length of time since their last cell division (adder) to predict when cells will undergo mitosis (Turner et al., 2012, Robert et al., 2014, Wallden et al., 2016). The exploration of the sizer versus adder principles underlying the control of cell division in a complex plant organ suggests that each partially contribute toward the control of cell size (Willis et al., 2016, Jones et al., 2017).
Studies examining the control of the cell cycle have largely focused on individual cells. Likewise, the prediction of cell division planes has been based on local cell geometry (Besson and Dumais, 2011) or the local neighbourhood of cells in 2D epithelia (Gibson et al., 2011, Gibson and Gibson, 2009). Previous work has also explored the impact of complex tissue shape and differential growth on cell division (Louveaux et al., 2016), yet the effectiveness and consequences of these rules in the global 3D context of cellular organization are not yet understood.
In plants, the shoot apical meristem (SAM) contains the stem cell niche from which all above ground organs are formed. Control of the cell cycle and orientation of cell divisions in the SAM therefore plays a key role in the generation of cellular patterns that comprise future organs and form the template upon which molecular events take place (Besson and Dumais, 2011, Shapiro et al., 2015). The SAM has also provided a useful experimental system to explore cell cycle control (Willis et al., 2016, Jones et al., 2017) and regulation of cell division (Shapiro et al., 2015, Besson and Dumais, 2011, Louveaux et al., 2016, Schaefer et al., 2017).
In this study, we investigate the dynamic organizational properties of the Arabidopsis SAM using 3D imaging and network science in order to uncover the emergent global properties induced in these systems. We show that the emergence of global order within the multicellular consortia emerges from local cell division rules that are rooted in the mechanical interactions between cells.
Results
Extraction of Multicellular Topological Dynamics in the Arabidopsis SAM
Live imaging of four independent wild-type Arabidopsis SAMs carrying a plasma membrane targeted YFP marker (Yang et al., 2016) was performed at 11-h intervals (Figure 1A). Every cell in the first 4 layers of the SAM central and peripheral zones was segmented in 3D and converted into polygonal meshes at each the 0 h (T0), 11 h (T1), and 22 h (T2) time points using the image analysis software MorphoGraphX (de Reuille et al., 2015) (Figure S1). In the instances where cells divided, lineage was established by manually performing registration between the cell meshes.
Figure 1.
Experimental Workflow
(A) Extraction of cellular connectivity networks from segmented cells within an Arabidopsis SAM. On the left are 3D segmented cells and the right depicts their abstraction into a network of nodes (red) and edges (green) that depict their physical associations.
(B) Live time-lapse imaging of the Arabidopsis SAM was performed over 11-h intervals. The flowchart illustrates the procedure used to extract geometric and topological information from these 3D image data. This started with cell segmentation and the registration of cells that had divided in addition to the extraction of connectivity networks. The geometric and topological dynamics of this system was in turn statistically analyzed.
Networks describing cellular connectivity in the SAM at each time point were also extracted as previously described (Jackson et al., 2017b, Montenegro-Johnson et al., 2015) (Data S1; Video S1). Here, cells are represented as nodes and shared cell interfaces between adjacent cells as edges (Figure 1B). In light of the central role of cell-to-cell communication in SAM function (Jönsson et al., 2006, Smith et al., 2006, de Reuille et al., 2006, Heisler et al., 2005, Stoma et al., 2008, Bayer et al., 2009), these structural networks represent the “roadmaps” upon which molecular processes unfold over these multicellular templates (Jackson et al., 2017a). Edges provide the routes of possible “information flow” across the structural template of cells in the SAM (Bassel, 2018) and not necessarily observed functional communication between adjacent cells.
These connectivity networks represent the abstraction and discretization of patterning at a cellular level in the SAM. In this way, the topological dynamics of the processes of multicellular self-organization in the SAM at both local and global scales can be quantitatively analyzed using tools from network science (Jackson et al., 2017a, Barthélemy, 2011, Newman, 2010). The 3D digitization of individual cells simultaneously enables the geometric analysis of the components within these multicellular systems.
Confocal imaging of the SAM is limited in both depth and field of view. These limitations lead to the introduction of boundary artefacts in the intercellular networks used in this study. The impact of these edge effects in our analyses was mitigated in two ways. First, analyses were performed on a cellular network representing a broad region of the SAM, but only data from the central region of these cells were reported in the analyses presented (Figure S2A) and is much greater than that displayed in Figure 2. This focus acted to minimize the influence of missing cells from the periphery of the network. Second, the first 4 layers of cells were segmented and included in topological analyses, but only results from the top 3 layers (L1–L3) are presented (Figure S2B).
Figure 2.
Spatial Distribution of Geometric and Topological Properties in the Central Zone of a Representative Arabidopsis SAM
(A and B) (A) Cell volume and (B) surface area.
(C) Fold increase in cell volume over 11 h.
(D) Location of cell divisions.
(E–G) (E) Cell degree, (F) log10 betweenness centrality (BC), and (G) random walk centrality (RWC). Cells are false colored using the corresponding measure and scale associated with each panel. Meristem cell layers (L1–L3) are separated as indicated in the left-hand column.
Spatial Distributions of Geometric and Topological Features in the Arabidopsis SAM
To examine the spatial relationships between the geometric and topological properties of cells in the SAM, we analyzed cell size and growth using the image analysis software MorphoGraphX (de Reuille et al., 2015). These quantitative data are false colored onto the individual cells of a 3D-segmented SAM sample across each of the top 3 cell layers (L1–L3) (Figure 2). Both cell volume and area are heterogeneous across each of the cell layers, with cells in L1 being smaller than those in the underlying layers (Figures 2A and 2B). The distribution of cell growth, representing the change in cell volume across the 11-h time frame of this experiment, showed a similar broad distribution (Figure 2C) (Kierzkowski et al., 2012, Kwiatkowska, 2006). The locations of cells that divided were also distributed in a moderately uniform pattern across the layers of the Arabidopsis SAM (Figure 2D) (Table S1) (Reddy et al., 2004, Willis et al., 2016, Dumais and Kwiatkowska, 2002, Fernandez et al., 2010, Laufs et al., 1998).
The topological properties of the cellular connectivity network of the SAM were computed and also visualized by false coloring cells with their associated node values. The local property of cell degree describes the number of neighbors a cell has. Cell degree was broadly distributed across the cells of the SAM (Figure 2E).The L2 and L3 layers have higher values owing to the presence of adjacent cells on all faces, as opposed to the L1, which is at the surface of the organ. The majority of cells have between 6 and 18 neighbors (Figure S3D; for a comparison with young flowers, see Fernandez et al., 2010), a larger number than was observed in isolated epithelia (Gibson et al., 2011, Gibson et al., 2006, Willis et al., 2016, Sahlin and Jönsson, 2010).
While degree is an informative topological property, it only provides information related to the local connectivity of a cell. Biologically significant “higher-order” properties of cellular organization—the properties that are relevant to the network at a mesoscale—were also investigated. In light of the spatial constraints of cells embedded within organs and the immobility of plant cells relative to one another, path length represents a biologically pertinent property of these spatial networks (Jackson et al., 2017b, Jackson et al., 2017a, Barthélemy, 2011).
Networks of cellular connecitivity provide structural templates upon which information can be exchanged and not that which is observed (Jackson et al., 2017a, Bullmore and Sporns, 2009). Given these physical associations, communication is therefore possible between all pairs of cells connected in the SAM. The movement of molecules from one cell to the next following a shortest path (number of intermediate cells) represents an optimization in transport efficiency. Cells that lie upon shorter paths between other pairs of cells have a greater capacity to control the movement of information across systems (Barabási, 2016, Newman, 2010). These cells can be identified in at least two ways.
Betweenness centrality (BC) measures the frequency of a particular node (cell) being traversed if the shortest paths between all pairs of cells are traveled (Brandes, 2001). In tangible terms, BC models the direct transport of information given prior knowledge of the fastest route to the destination.
Random walk centrality (RWC) does not make use of the prior knowledge of network topology and measures the frequency nodes are traversed by using random walkers between all pairs of cells. These random paths taken may not necessarily be the shortest and are stochastically determined by the paths followed by the random walkers (Newman, 2005a). In contrast to BC, RWC reflects the potential diffusion of a signal through cells in a tissue, given that the signal has defined source and destination nodes. Each of these global measurements allow us to examine higher-order organization of cells within the SAM. BC in the spatially constrainted networks capturing cellular connectivity is approximately log-normal distributed and is log10 transformed in order to make comparisons with other measures (Jackson et al., 2017b, Seguin et al., 2018).
Both log10 BC and RWC showed a spotty distribution across each layer of the SAM, again owing to their peripheral position in the network (Figures 2F and 2G), with the L1 having lower values than the underlying layers because fewer short paths lie on the external interface of the structure. The distributions of cell size, growth, cell division, and topological properties at local and global scales appear visually to follow no obvious spatial pattern across the Arabidopsis SAM.
Predicting Divisions from Cell Position in the SAM
Given the patchy spatial distribution of cell divisions and cell properties, these features do not appear to be linked to their physical position within the SAM, at least in the simplest scenario. The relationship between cell size and propensity to divide has been examined previously in the Arabidopsis SAM, with larger cells showing a greater predisposition to enter mitosis (Willis et al., 2016). Here, we expand upon this work to understand the relationship between the position of a cell within local and global contexts of the SAM and control of the cell cycle.
Cells were split into three groups: (1) “non-dividing” cells at the initial time point (T0) that do not go on to divide within the time frame of our imaging; (2) “dividing” cells at the initial time point (T0) that go on to divide before the second time point; and (3) “divided” cells at the second time point (T1) that are the daughter cells from the T0 stage. For all analyses, quadruplicate biological replicates were used. Data in Figure 3A were normalized for comparative purposes.
Figure 3.
Geometric and Topological Dynamics during SAM Development
(A) Mean average fold change of geometric and topological cell properties in non-dividing (T0) (n = 582), dividing (T0) (n = 32), and divided (T1) (n = 64) cells in the Arabidopsis SAM. Fold change was calculated from cells in one meristem, and averaged over four biological replicates.
(B) Likelihood ratio (type II ANOVA test statistic) of cell properties when all properties are incorporated into a logistic regression classification model.
(C) Classification of cells as non-dividing or dividing, using logistic regression with varying inclusion of cell properties.
(D) Pairwise comparisons of cell geometry and topology in the Arabidopsis meristem, measured using Pearson correlation coefficient (R2). Error bars in (A) are the standard error (SE) from four biological replicates. Asterisks in (A) indicate a significant difference in the mean measurements (t tests: p ≤ 0.01). Asterisks in (B) indicate significant contributions to a logistic regression classification model (p ≤ 0.01, type II ANOVA).
Cell area, volume, and degree were significantly higher in dividing cells than non-dividing cells (Figure 3A), consistent with previous work (Willis et al., 2016). Following cell division, a significant drop in these values is observed again. These observations reflect intuitive physical consequences of splitting a cell within a 3D spatially embedded system, notably, the reduction of cell size by half following division.
The impact of the cell cycle on the centrality measures of SAM cells (nodes) was also examined. Both log10 BC and RWC were significantly higher in dividing cells than in non-dividing cells (Figure 3A). Moreover, the daughter cells following a division had a comparable average log10 BC and RWC to the non-dividing T0 cells. These observations suggest a cycling “reversion,” where high centrality cells have an increased propensity to divide, reducing their centrality toward the mean when they do so.
Having identified these differences between dividing and non-dividing cells, we asked which cellular properties could be used to distinguish when a cell will divide. We used a logistic regression model to assess the statistical support for models where individual properties or combinations of properties were used for this prediction. In agreement with previous work, we found that features linked to cell size—specifically, volume and area—both statistically supported the predictors of division propensity. Once these features were included in a model, there was little support for the inclusion of other factors (Figure 3B).
We also compared the classification performances of these models on the data (Figure 3C). A low proportion of cells were observed to divide (Table S1), limiting our ability to parameterize the classifier and leading to rather low positive identification rates. However, models including volume (and to a lesser extent, area) substantially outperformed null and random classification models.
Pairwise correlations between measurements were performed to explore relationships between geometric and topological measures (Figure 3D). Intuitively, a very strong correlation between cell area and volume is present because the cells have a very consistent height. Strong relationships between the local topological measure of degree and global measures of log10 BC and RWC are also present. The relationship between cell size and topological measures of degree, log10 BC, and RWC show an intermediate level of correlation. These results combine to form a picture where the strongest predictors of division propensity are measures of cell size, to which topological measures including RWC are quantitatively linked, leading to a resultant relationship between RWC and division propensity.
We can therefore predict to some extent when a cell will divide in the SAM, based on its position within the global multicellular context. However, this is unlikely to reflect a causal linkage, as the extent to which log10 BC and RWC discriminates between cell classes is almost entirely explained by cell size. The link between division and these higher-order properties emerges as a consequence of cell size within the spatial embedding of the multicellular SAM. Larger cells likely have an increased number of neighbors, which raises the probability that they lie upon shorter paths when viewed from a system-level scale. This quantitative analysis has shown the first suggestion of an overlap of links between local and global properties of cells in predicting cell divisions.
Predicting Cell Division Plane Orientation Using Topology: Errera’s Rule Also Minimizes RWC in Daughter Cells
Intrigued by this link between local and global relationships with cell division propensity, we next asked whether local and global properties had a bearing on the placement of cell division planes within the cell and whether this impacted global ordering in the SAM.
A classical symmetric cell division rule uses local cell geometry to predict the placement of a division plane, enforcing that it pass through the geometric center of a cell using the shortest wall (minimal area) possible (Errera, 1886). This local rule is capable of predicting most, but not all divisions, in the Arabidopsis SAM central and peripheral zones (Shapiro et al., 2015). Gibson et al. (2011) proposed a rule that looks at the local neighbourhood of a cell and predicts that the placement of the division plane will intersect with the neighboring cell having the lowest degree (Gibson et al., 2011). This local topological rule has a greater than random chance of predicting the placement of a cell division plane. We examined whether a cell having a low degree neighbor is also effective at predicting when a cell in the Arabidopsis SAM will divide and found this not to be the case (Figure 3B).
We next sought to understand the relationship between the position of the cell division plane, as chosen by a variety of rules (Yoshida et al., 2014), and the topological properties of the resulting daughter cells. To do this, we first compared the cell division planes (Figure 4A) observed in our experiments to those computationally predicted according to four different rules: (1) “shortest wall,” the shortest wall as described by Errera (Besson and Dumais, 2011, Errera, 1886); (2) “minimum degree,” a rule that minimizes the summed degree of the daughter cells; (3) “minimum RWC,” a rule that minimized the summed RWC of the daughter cells (the division plane that minimizes the number of shortest paths the daughter cells lie upon); and (4) “Gibson Rule,” the local topology rule proposed by Gibson et al. (2011) (Figure 4B) (Data S2). Because Errera’s rule matches the tension rule in the meristem center, due to this tissue shape being isotropic and having minimal differential growth (Louveaux et al., 2016), we did not examine division planes in relation to directions of tension.
Figure 4.
Predicting Cell Wall Placement Using Topology
(A) Schematic illustrating how predicted division planes were compared to real division planes by measuring the angle between plane normals.
(B) Computational prediction of cell division planes using different rules.
(C) Distribution of the predicted planes’ deviation from real planes following using different division rules. Dotted lines indicate angle deviation means. Significant differences in mean angles are denoted by different letters above each violin distribution (Tukey’s HSD test, p < 0.05).
(D) Relationship between perturbation to RWC and angular displacement between planes. An asterisk denotes a significant difference between means (t test, p < 0.05).
(E) Distribution of angles from which different cell division planes deviate from the RWC minimizing division plane. Dashed lines indicate the percentage of planes that change RWC if they deviate by less than 10 degrees (left) and 20 degrees (right).
(F) Venn diagram showing which rules predicted the closest plane to the real division, and where different rules predicted the same plane (+/− 1 degree). Error shown is one standard deviation, where the source of the error is altering the order of divisions in each meristem sample.
(G) Number of times each rule predicted the closest plane to the real division.
(H) Illustration of a hypothetical tissue and impact of divisions (dashed line) following the shortest wall rule, or minimum random walk rule, on the RWC of daughter cells. The number within the daughter cells is their RWC following division.
We report the angular “deviation” between two planes as a measure of discrepancy: aligned planes have a 0-degree deviation, and planes at right angles have a 90-degree deviation. We plotted the distribution of deviations between experimentally observed division planes and those computationally predicted using the four different rules over a set of 108 different cells we observed to divide (Figure 4C). The shortest wall and minimum RWC rules showed no significant difference in deviation, suggesting the two rules have similar power to predict division plane placement. The minimum degree and Gibson rules were both significantly different from these former predictions, with a higher mean deviation. Random wall placement, included as a negative control, was significantly worse at predicting division plane than any rule. Thus, in the Arabidopsis SAM, local (shortest wall) and global (minimum RWC) rules largely predicted the same division plane placement.
We next examined the deviation between division planes predicted for a given cell by the shortest wall and minimum RWC rules (Figure 4D). Both the predicted shortest wall and observed plane were significantly better at predicting RWC minimizing division plane placement than a randomly placed division. This agreement demonstrates that the application of simple rules, reflected in biological observations, has a much stronger than random propensity to optimally shape these global patterns.
Observing that the minimum RWC rule predicted planes close to (but not always perfectly aligned with) the observed division planes, we considered the dual question, whether observed division planes minimize the RWC of the resulting daughter cells. We verified the small deviations typically observed between planes predicted by the minimum RWC rule and observed planes have no functional effect on RWC. Topological differences emerging from divisions along planes less than 10 degrees apart are almost always zero (Figure 4E), and only 16.2% of planes less than 20 degrees apart displayed topological differences. Around 80% of experimentally observed planes can thus be assumed to minimize RWC of their daughter cells.
The number of division planes correctly predicted by each rule were examined individually and plotted in a Venn diagram (Figure 4F). Each rule was individually capable of predicting divisions the others were not, while a large number of divisions were predicted by both shortest wall and random walk rules. This trend is also present within each of the individual layers of the SAM (Figures S4 and S5).
In absolute terms, the minimum RWC rule was the most accurate single predictor for the largest number of cell division planes (Figure 4G).
These results show that cell division plane placement according to simple local rules (shortest wall) leads to the consistent emergence of a global property (minimizing RWC of daughter cells). Here, local cell geometry predisposes a cell for a division following the shortest wall, which in turn minimizes the number of shortest paths daughter cells lie upon. Together, these results suggest that Errera’s rule also minimizes RWC in daughter cells.
The boundary region of the SAM has been demonstrated to have division plane orientations that follow directions of tensile stress (Louveaux et al., 2016). We examined whether the RWC property is conserved in this cellular sub-domain of the SAM, wondering if global topology can be used to predict division plane placement here. The distribution of RWC in central zone cells is significantly different from that of boundary region cells, which have a greater RWC (Figure S6). The RWC rule, like cell geometry, can thus be uncoupled from maximal tensile stress direction.
Cell Division Rules Differentially Impact the Homeostasis of RWC
We next sought to understand the consequences of iterated cell division rules on both local and higher-order cellular topology. To do this, we computationally divided Arabidopsis meristem cells (Figure 5A) using local geometric and topological cell division rules and examined their consequences on distributions of (global) minimum RWC and (local) minimum degree (Gibson et al., 2011, Gibson et al., 2006). This was done in order to understand what division rules (generative processes) are sufficient to preserve the RWC distribution of the cells in the SAM.
Figure 5.
Simulation of Topological Dynamics in the Arabidopsis SAM
(A) Cross-section of meristem cells before simulated divisions.
(B–E) (B) Cross-section of meristem cells where each cell has been divided twice in silico following the shortest wall rule, (C) Gibson rule, (D) degree rule, and (E) randomly chosen division plane.
(F) Comparisons between distributions of random walk centrality before and after simulating divisions across the Arabidopsis SAM, using different division rules. Earth mover’s distance is used to compare distributions. Crosses represent individual earth mover’s distances between distributions.
(G) Comparisons between distributions of degree before and after simulating divisions across the Arabidopsis SAM, using different division rules. Error bars in (F) and (G) are one standard deviation, and simulations were carried out on 4 separate meristems. An asterisk over two linked means denotes a significant difference (Mann-Whitney U test, p < 0.05).
Rules examined included the shortest wall rule, Gibson rule, degree rule, and a randomly placed wall rule that acted as a control (Figures 5B–5E). Each cell was computationally divided twice, resulting in a quadrupling of cell number from the initial subset of meristematic cells. We computed the changes in the cell-to-cell distribution of RWC induced by these iterated divisions. Changes in distributions were quantified using the earth mover’s distance (Vallender, 1974), a measure of change integrated over the entire distribution (Figures 5F and S7). Using this measure, both the shortest wall and minimum degree rules preserved RWC distribution of the undivided organ significantly better than a randomly placed division plane (Figure 5F). The change in RWC distribution caused by the Gibson rule better resembles random wall placement, but its difference from the other rules did not pass a significance threshold (Figure 5F). Thus, in agreement with the observations of true division planes, the global RWC property is better preserved by the shortest wall rule than a randomly chosen cell division plane. By contrast, distributions of degree displayed some heterogeneity but did not show strong enough effects to significantly deviate from random plane placement under any alternative rule (Figure 5G) (Sahlin and Jönsson, 2010). Some division rules, therefore, preserve the cell-to-cell RWC distribution more than others.
The Impact of Cell Shape and Topology on Emergence from Cell Division Rules
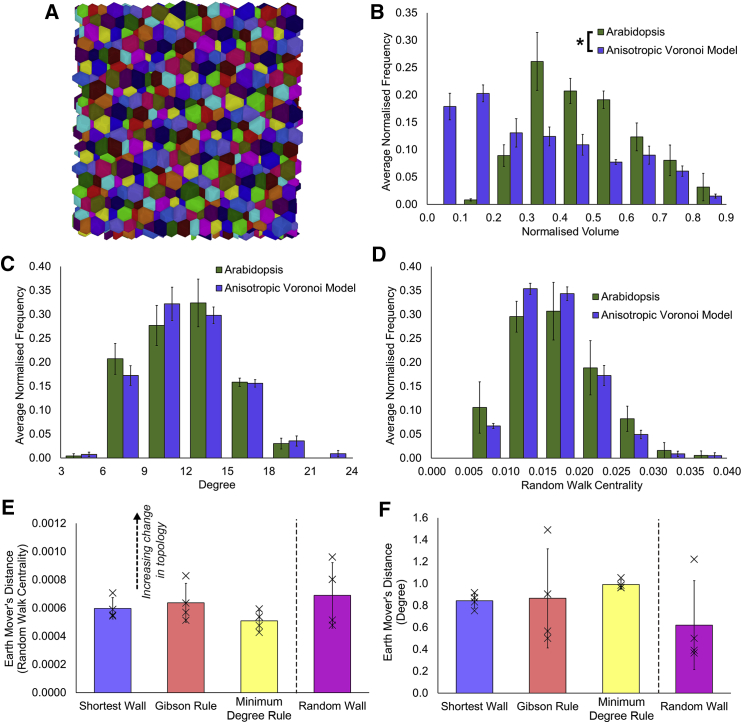
A link between local cell geometry and global topology emerges from our analyses of cell division plane placement and global order of cells in the Arabidopsis SAM. We next examined the extent to which this link is an intrinsic property of all 3D spatially embedded systems, or if it is reliant on specific properties of the organ we consider. In other words, does any given multicellular system having shared topological properties with the Arabidopsis SAM, allow for the emergence of minimized RWC by following a shortest wall cell division rule?
In order to examine this, we generated digital multicellular assemblies using 3D anisotropic Voronoi tesselation (Du and Wang, 2005) (Figures 6A and S8). These models are topologically equivalent to the Arabidopsis SAM in terms of degree (Figure 6C) and RWC centrality (Figure 6D) but not in the distribution of cell sizes (Figure 6B). Using different approaches and changing parameters did not result in models that shared both topological and cell geometric equivalence to the Arabidopsis SAM (Figures S8–S10) (Sánchez-Gutiérrez et al., 2016). Similar cell-to-cell correlations between the geometric and topological features of the selected anisotropic model (Figures S8 and S11) are observed as in the Arabidopsis SAM (Figure 3D).
Figure 6.
Simulation of Topological Dynamics in an Artificially Constructed SAM
(A) Digital reconstruction of a multicellular consortia of cells using a 3D anisotropic Voronoi approach. Colors indicate unique cells.
(B) Distribution of cell sizes in the models.
(C and D) (C) Distribution of degree and (D) RWC in the Voronoi models.
(E) Earth mover’s distance for RWC following the computational division of cells after 2 rounds of cell division following different rules. Crosses represent individual earth mover’s distances between distributions.
(F) Same as (E) for degree. Error bars in (B)–(D) represent the standard deviation within each bin (n = 4), and in (E)–(F) the standard error of the mean earth mover’s distance (n = 4). An asterisk denotes a significant difference in distributions (Kolmogorov-Smirnov test, p ≤ 0.05).
As previously (Figure 5), we performed two rounds of cell divisions on computationally generated models sharing topological equivalence to the Arabidopsis SAM, applying different topology-based division rules. In light of the topological nature of these division rules, the lack of cell size equivalence did not play a factor in these analyses. Strikingly, analysis of the simulation outputs revealed no significantly improved preservation of RWC under any division rule compared to random plane placement (Figure 6E). This result stands in contrast with the above result obtained from the natural system, where the (local) shortest wall rule preserved global RWC to a significantly higher extent than random wall placement (Figure 5F). This result demonstrates that native cell geometry within the Arabidopsis SAM is required for the emergence of global cellular order from local geometric cell division plane placement rules.
Impact of Mechanical Interactions on the Emergence of Global Order in the SAM
Cell shape in multicellular plant organs is strongly influenced by intercellular mechanical interactions (Sampathkumar et al., 2014, Majda et al., 2017, Sapala et al., 2018). In the Arabidopsis SAM, we found native cell shape is likely required for the emergence of preserved RWC from local division rules in constituent cells (Figure 6). We therefore examined the impact of mechanical interactions on cell shape and global cellular organization. The KATANIN1 gene encodes a microtubule severing protein (Bichet et al., 2001), which has been demonstrated to be involved in intercellular mechanical interactions in the Arabidopsis SAM (Uyttewaal et al., 2012). More specifically, reorientation of cortical microtubules is slower in the absence of katanin, and deposition of cellulose does not necessarily follow the maximum of tensile stress, meaning that cell walls are not properly reinforced. Plant cells carrying mutations in this gene are therefore compromised in their ability to mechanically resist the growth of their neighbors, which we call here a defective mechanical interaction. If mechanical interactions are required in order to modify cell shape, this property will be lost in the katanin1 (ktn1) mutant.
We performed imaging and topological analyses using the ktn1 mutant to establish the impact of perturbing mechanical interactions on the emergence of global order in the Arabidopsis SAM (Figures 7A and 7B) (Figure S12; Data S1). The cell-to-cell correlations between geometric and topological features were similar in the ktn1 meristem (Figure S13) as in the wild-type meristem (Figure 3D). Cell size was not significantly impacted in the mutant compared with the wild-type SAM (Figures 7C and S14). However, cell shape was significantly more anisotropic (t test, p = 2.88 × 10−11) (Figure 7D), suggesting a role for mechanical interactions in controlling the extent of heterogeneity in this local geometric property, and conversely demonstrating the role of katanin in maintaining the homogeneity of native meristematic cell shapes in the wild-type.
Figure 7.
Geometric and Topological Analysis of the katanin1 (ktn1) Mutant
(A) Confocal image of the wild-type Arabidopsis SAM.
(B) Same as (A) for the ktn1 SAM.
(C) Distribution of cell size in the wild-type and ktn1 SAM.
(D) Same as (C) for cell anisotropy.
(E) Same as (C) for cell degree.
(F) Same as (C) for cell RWC. Error bars in (C)–(F) represent the standard deviation within each bin (n = 4). Significance tests were performed using a t test, and error bars indicated the standard deviation within each bin. An asterisk indiciates significance at the p ≤ 0.05 level. A total of 614 cells was analyzed in the wild-type and 478 cells in ktn1.
(G) Comparison of the angle at which floral organs are initiated in each wild-type (Ws) and ktn1 SAMs. Kolmogorov-Smirnov test found this to be significant (p ≤ 0.001).
Both the local topological property of degree (Figure 7E) and global property of RWC (Figure 7F) showed significantly different distributions in the ktn1 mutant. Notably, RWC was significantly shifted to higher values (t test, p = 4.20 × 10−3), suggesting a breakdown in the ability to preserve lower RWC values. This observation is in agreement with our expectation that native mechanical interactions are required in order for local geometric division rules to control RWC.
Therefore, compromising mechanical interactions modulating cell shape modify cellular organization at both local and global scales in the Arabidopsis SAM. The ktn1 mutant serves to illustrate the perturbation resulting from a weakened coupling between the local and global scales in the establishment of higher-order cell organization in the SAM.
Altered Topology in ktn1 Mutant Correlates with Minor Phyllotactic Defects
The SAM is the site where new organs are initiated, and the order and sequential position of new organs create a stereotypical pattern termed phyllotaxis (Smith et al., 2006, Jönsson et al., 2006). This can be achieved through polarized localization of auxin transporters to generate local maxima of this hormone, leading to organ initiation. In theory, the topology of the multicellular template upon which this transport occurs may impact the functioning of this developmental program. Given that phyllotaxis is well known for its robustness (Fal et al., 2017), such a defect may not be detectable and/or could be compensated for by other factors in nature.
To test whether altered topological organization in the SAM could be related to phyllotactic defects, we examined floral organ positioning in ktn1 using the LEAFY promoter as a proxy for the next initiation site (Landrein et al., 2013). This revealed a small but significant difference in phyllotactic patterning in ktn1 relative to the wild-type control (Figure 7G). A correlation can then be detected between global cellular organization and correct positioning of organs within the SAM.
Discussion
Complex systems, including multicellular tissues, are often defined according to the emergence of non-trivial large-scale behavior from the local behavior of interacting agents. Here we have shown that control of a global organizational principle of a plant organ (minimizing RWC) emerges naturally from the application of local division rules (dividing using the shortest wall).
The significance of establishing minimal RWC in the SAM may lie in the structure-function relationships between cellular organization and organ function (Ollé-Vila et al., 2016, Thompson, 1942). Cells in organs do not exist in isolation, nor is their influence in a tissue limited to their immediate neighbors. This investigation of the higher-order properties of cellular organization provides a means to understanding how collections of cells function together to create an integrated multicellular system. Revealing how molecules move between all cells in a tissue, in this case via diffusion in the form of random walkers, underpins the co-operative activity of such multicellular assemblies.
Uncovering the explicit absence of optimized routes in the Arabidopsis SAM provides a novel perspective of tissue organization. Having a low RWC means a cell lies on relatively few shortest paths. In any reasonable structure it follows that shortest paths are distributed over many cells; if one cell was involved in a high number of shortest paths, its RWC would be high. Inasmuch as short paths reflect routes of molecular flow between cells, preserving low RWC ensures that flux is not reliant on a privileged subset of cells.
The topological homogeneity of the SAM may provide robustness for the communication of cells. When there are a small number of cells creating reduced path lengths across a network, optimized routes of movement are provided. However, in this scenario system-wide flux is susceptible to failure should any of the short path conduits be compromised. In a network such as the SAM where optimal paths are uniformly distributed (minimized RWC of cells), the perturbation of any single route has a less profound impact on system-level communication. This is due to other routes having similar path length compensating for any failure, for example biotic attacks and failure of individual cells.
The reorganization of microtubules plays a key role in the control of local geometric and global topological properties of the SAM. The KATANIN1 gene limits cell shape heterogeneity, in contrast to its role in promoting cell growth heterogeneity (Uyttewaal et al., 2012). As a result of this, cell RWC has a broader distribution, indicating the introduction of a small number of shorter paths into the system, while diminishing the topological homogeneity observed in the wild-type.
A potential consequence of this increase in global topological heterogeneity may be seen at the level of the processes that unfold with the constraints of this multicellular template. Phyllotactic patterning is one such example, with auxin transport among other factors occurring across the cells of the SAM. Although the defects are small, the ktn1 mutant exhibits significantly perturbed phyllotaxis (Figure 7G), suggesting cellular organization may contribute to this developmental process.
This work has provided a quantitative analysis of the emergent organ-level implications of following long-established division rules. In so doing, we have expanded the scale of features that may influence the selection of these rules, from local biophysical arguments to functional properties at the level of the whole organ.
We note the principles and methods we have developed in the study of the Arabidopsis meristem may have general application. The combination of 3D live imaging and network analysis can be applied to quantitatively explore hypotheses about local cell behavior, global organ structure, and emergent links between the two, in other organisms and taxa. We anticipate that structures allowing the bottom-up control of organ structure and function may be selected for more broadly across biology, potentially constituting a universal principle of multicellular design in complex life and reveal futher simple rules that underpin the self-organizing processes in complex tissues.
STAR★Methods
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Wild-type Col and ktn1 image and connectivity datasets | Open Science Framework | https://osf.io/mxgrh/ |
| Images showing the computational analysis of cell division plane 607 orientation in the Arabidopsis SAM following different rules | Open Science Framework | https://osf.io/ucd76/ |
| Experimental Models: Organisms/Strains | ||
| Arabidopsis Col seeds | NASC | N1093 |
| Arabidopsis bot1-7 (ktn1) seeds | Olivier Hamant | Uyttewaal et al., 2012 |
| Arabidopsis YFP targeted to plasma membrane | Raymond Wightman | Yang et al., 2016 |
| Software and Algorithms | ||
| MorphoGraphX | www.morphographx.org | http://www.mpipz.mpg.de/MorphoGraphX/software |
Contact for Reagent and Resource Sharing
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, George W. Bassel (g.w.bassel@bham.ac.uk).
Experimental Model and Subject Details
Plant Material and Image Acquisition
Z-stacks of biological quadruplicate wild-type Arabidopsis Colombia (Arabidopsis thaliana Colombia) and katanin1 (Bichet et al., 2001) shoot apical meristems (SAM) carrying YFP targeted to the plasma membrane (Yang et al., 2016) were imaged at several timepoints, 0 h (T0), 11 h (T1) and 22 h (T2). Confocal imaging was performed on a Leica SP8 up-right confocal microscope using long working-distance water immersion objectives (AP 40x/0.8). Excitation of YFP was performed using an argon laser at 514 nm. Images were collected at 529–545 nm for YFP using HyD detector. Time-lapse imaging was performed as described previously (Kierzkowski et al., 2012). Data were collected as 12-bit images and prepared and analyzed using MorphoGraphX software (de Reuille et al., 2015).
Method Details
Image Analysis
To prepare the TIFF images for analysis, a Gaussian blur was used (0.3 μm in the x-, y- and z-directions). The blurred images were then segmented at cellular resolution using the ITK automatic segmentation algorithm, converting them into TIFF stacks with labelled voxel regions corresponding to individual cells. The segmented stacks were then manually corrected. These stacks were converted into polygonal meshes using the 3D marching cubes algorithm with cube size 1 μm, as previously described (Jackson et al., 2017b, de Reuille et al., 2015, Bassel et al., 2014). The meshes were subsequently manually edited to ensure that only the cells within the complete uppermost 4 layers of the SAM remained. The peripheral region of the SAM is split into three clear layers, L1, L2 and L3, and cells in different layers were manually identified. Cell lineage tracking and registration was then performed between each timepoint using MorphoGraphX.
Co-segmentation within MorphoGraphX was used to identify cells that divided between timepoints, and was performed manually. The L1, L2 and L3 cell layers of each timepoint previously identified were digitally overlaid respectively, and parent and daughter cells were assigned common labels. This enabled lineage tracking, as well as the visualisation of cell divisions by viewing each cell layer as a proliferation heatmap.
Quantification and Statistical Analysis
Quantitative Analysis of 3D Cell Shapes
MorphoGraphX was used to calculate surface area and volume of each cell in the central region of meristem meshes, using the Heat Map function. Cell anisotropy was calculated using the PCAnalysis process within MorphoGraphX, which abstracts cell shape into three principle directions of shape. The magnitudes of these three directions were each divided by the sum of all three components, and the maximum value of these three was used to define cell anisotropy.
Cellular Connectivity Network Extraction and Edge Filtering
Networks were extracted from meshes as a list of physically interacting pairs of cells, using CellAtlas3D (Montenegro-Johnson et al., 2015). Edges representing a pair of cells that shared less than 0.01 μm2 cell wall area were omitted from topological analyses.
Topological Analyses of Cellular Connectivity Graphs
Topological properites for each cell were calculated using the NetworkX package for Python (Schult and Swart, 2008). In order to make different cell connectivity networks comparable, the centrality measurements were normalised by 2/((n -1)(n -2)) where n is the number of nodes in a network (i.e. the number of cells) (Schult and Swart, 2008). Cellular networks were not normalised by network density, as all networks were subject to physical embedding within Euclidean space, resulting in similar densities.
Degree, betweenness centrality and random walk centrality were calculated for each cell. Whilst degree and random walk centrality in the cell networks were normally distributed, betweenness centrality of cells had an approximately log-normal distribution. In order to perform equivalent statistical analyses with all topological measurements, betweenness centrality was log10 transformed, resulting in a normal distribution.
Statistical Analyses
t-tests, linear regressions to determine correlations (R2), earth mover’s distance calculations (Wasserstein distance) and Kolmogorov-Smirnov tests were performed using the SciPy package for Python (Jones et al., 2014). ANOVA and post-hoc Tukey’s HSD tests were performed using SPSS.
Logistic regression was carried out using the glm2, car and ROCR packages in R (Marschner, 2011, Fox and Weisberg, 2011, Sing et al., 2005). Data were treated as one complete set and fitted to a logistic regression model to classify non-dividing and dividing cells in T0. A large likelihood ratio (LR χ2) indicates a measurement’s usefulness in making the correct prediction, and it’s incorporation into the model.
Cell Division Plane Analysis
Cells were fused in T1 to represent the T0 connectivity network, and in T2 to represent the T1 connectivity network, before division simulation. 112 unique cell divisions were simulated, while the order of dividing cells was varied.
For division planes simulating the minimisation of degree and random walk centrality, or the Gibson rule, division order permutations were carried out for each meristem sample at each timepoint. This was to account for the unknown order of divisions between the T0 and T1, or T1 and T2 timepoints. Division orders were randomised on three separate simulations for each time interval, for a total of 24 permutations
Where multiple planes satisfied the minimisation of random walk centrality, degree, or satisfied the Gibson rule, the wall with the lowest surface area was chosen from this subset. Divisions were restricted to positioning within 0.2 μm of the cell center, satisfying the geometry of most real cell divisions, according to previous observations (Shapiro et al., 2015).
To compare both observed and simulated divisions, division planes were extracted from MorphoGraphX, and the angle between plane normals was calculated using Python and the SymPy package (Meurer et al., 2017).
Computational Generation of SAMs
Three methods were used to generate model meristems, the centroidal Voronoi tessellation (CVT) path (Sánchez-Gutiérrez et al., 2016), Voronoi tessellation with varying centroid positions, and anisotropic Voronoi tessellation (Du and Wang, 2005).
The centroidal Voronoi tessellation path models were generated by starting with the Voronoi tessellation of a random set of 3D coordinates within a confined boundary region (Sánchez-Gutiérrez et al., 2016), in MorphoGraphX (Fabri et al., 2000). This generated step 1 in the CVT path, while additional steps were generated by calculating the centroid of each Voronoi cell in the previous step, and performing another Voronoi tessellation with these centroids.
Voronoi tessellation with varied centroid positions was carried out by starting with a ordered lattice of four layers of equidistant centroids, staggered in a lattice across each layer (the z-direction). These centroids were then randomly moved in the x- and y-directions by a uniform, Gaussian (Simon, 2007) or Pareto distributed random amount (Newman, 2005b) within a given interval. The resulting centroids were then used to perform Voronoi tessellation, within MorphoGraphX, to generate a set of different models.
Anisotropic Voronoi tessellation was performed using the same ordered lattice described above, but instead the extent to which each centroid could extend in any given direction was varied (Du and Wang, 2005). Three directions of expansion were randomly chosen for each cell, while varying magnitudes of expansion were randomly chosen for each direction, before Voronoi tessellation was performed.
Analysis of Phyllotaxis
The analysis of organ positioning in ktn1 (bot1-7 allele (Uyttewaal et al., 2012) and corresponding wild-type Control (Ws-4) was done as previously described, using the pLFY::GFPi marker (Deveaux et al., 2003) as a proxy for the position of successive floral primordia within the SAM (Landrein et al., 2013).
Data and Software Availability
Software used for this study can be downloaded at www.morphographx.org.
Supplemental dataset 1: Wild-type Col and ktn1 image and connectivity datasets. Raw TIFF image datasets for each biological replicate and timepoint in each of these genotypes is provided at the link https://osf.io/mxgrh/. Segmentations in the MorphoGraphX format .MGXS are provided along with cellular connectivity networks and cell lineages in .CSV format. README.TXT contains relevant information.
Supplemental dataset 2: Images showing the computational analysis of cell division plane orientation in the Arabidopsis SAM following different rules. These can be found at the link https://osf.io/ucd76/.
Acknowledgments
M.D.B.J. was supported by BBSRC DTP BB/M01116X/1 MIBTP, G.W.B. by BBSRC grants BB/L010232/1 and BB/J017604/1, H.X. and G.W.B. by BBSRC grant BB/N009754/1, and G.W.B. and S.D.-N. by Leverhulme grant MIBTP RPG-2016-049. I.G.J. was supported by a Birmingham Fellowship. S.S. and R.S.S. were funded by DFG Plant MorphoDymanics Research Unit FOR2581, and D.K. by NSERC Discovery Grant RN000758. We thank Miltos Tsiantis for hosting some experiments by D.K. in his lab with funding from DFG Sonderforschungsbereich 680. We thank Theo Greaney, Hagley Road High School, Birmingham, UK, for assistance annotating 3D datasets.
Author Contributions
M.D.B.J., S.D.-N., I.G.J., and G.W.B. analyzed the data. D.K. collected image datasets. M.D.B.J., and H.X. segmented and annotated 3D datasets. S.S. and R.S.S. provided computational tools. B.L. and O.H. provided phyllotaxis data. G.W.B. designed the project. G.W.B. and I.G.J. wrote the manuscript with input from all other authors.
Declaration of Interests
The authors declare no competing interests.
Published: January 16, 2019
Footnotes
Supplemental Information includes 14 figures, 1 table, and 1 video and can be found with this article online at https://doi.org/10.1016/j.cels.2018.12.009.
Supplemental Information
References
- Barabási A.-L. Cambridge University Press; 2016. Network Science. [Google Scholar]
- Barthélemy M. Spatial networks. Phys. Rep. 2011;499:1–101. [Google Scholar]
- Bassel G.W. Information processing and distributed computation in plant organs. Trends Plant Sci. 2018;23:994–1005. doi: 10.1016/j.tplants.2018.08.006. [DOI] [PubMed] [Google Scholar]
- Bassel G.W., Stamm P., Mosca G., barbier De Reuille P.B., Gibbs D.J., Winter R., Janka A., Holdsworth M.J., Smith R.S. Mechanical constraints imposed by 3D cellular geometry and arrangement modulate growth patterns in the Arabidopsis embryo. Proc. Natl. Acad. Sci. U S A. 2014;111:8685–8690. doi: 10.1073/pnas.1404616111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayer E.M., Smith R.S., Mandel T., Nakayama N., Sauer M., Prusinkiewicz P., Kuhlemeier C. Integration of transport-based models for phyllotaxis and midvein formation. Genes Dev. 2009;23:373–384. doi: 10.1101/gad.497009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besson S., Dumais J. Universal rule for the symmetric division of plant cells. Proc. Natl. Acad. Sci. U S A. 2011;108:6294–6299. doi: 10.1073/pnas.1011866108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besson S., Dumais J. Stochasticity in the symmetric division of plant cells: when the exceptions are the rule. Front. Plant Sci. 2014;5:538. doi: 10.3389/fpls.2014.00538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bichet A., Desnos T., Turner S., Grandjean O., Höfte H. BOTERO1 is required for normal orientation of cortical microtubules and anisotropic cell expansion in Arabidopsis. Plant J. 2001;25:137–148. doi: 10.1046/j.1365-313x.2001.00946.x. [DOI] [PubMed] [Google Scholar]
- Brandes U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001;25:163–177. [Google Scholar]
- Bullmore E., Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Coen E., Rolland-Lagan A.G., Matthews M., Bangham J.A., Prusinkiewicz P. The genetics of geometry. Proc. Natl. Acad. Sci. U S A. 2004;101:4728–4735. doi: 10.1073/pnas.0306308101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Reuille P.B., Bohn-Courseau I., Ljung K., Morin H., Carraro N., Godin C., Traas J. Computer simulations reveal properties of the cell-cell signaling network at the shoot apex in Arabidopsis. Proc. Natl. Acad. Sci. U S A. 2006;103:1627–1632. doi: 10.1073/pnas.0510130103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Reuille P.B., Routier-Kierzkowska A.-L., Kierzkowski D., Bassel G.W., Schüpbach T., Tauriello G., Bajpai N., Strauss S., Weber A., Kiss A. MorphoGraphX: a platform for quantifying morphogenesis in 4D. Elife. 2015;4:e05864. doi: 10.7554/eLife.05864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deveaux Y., Peaucelle A., Roberts G.R., Coen E., Simon R., Mizukami Y., Traas J., Murray J.A., Doonan J.H., Laufs P. The ethanol switch: a tool for tissue-specific gene induction during plant development. Plant J. 2003;36:918–930. doi: 10.1046/j.1365-313x.2003.01922.x. [DOI] [PubMed] [Google Scholar]
- Dewitte W., Murray J.A. The plant cell cycle. Annu. Rev. Plant Biol. 2003;54:235–264. doi: 10.1146/annurev.arplant.54.031902.134836. [DOI] [PubMed] [Google Scholar]
- Di Laurenzio L., Wysocka-Diller J., Malamy J.E., Pysh L., Helariutta Y., Freshour G., Hahn M.G., Feldmann K.A., Benfey P.N. The SCARECROW gene regulates an asymmetric cell division that is essential for generating the radial organization of the Arabidopsis root. Cell. 1996;86:423–433. doi: 10.1016/s0092-8674(00)80115-4. [DOI] [PubMed] [Google Scholar]
- Du Q., Wang D. Anisotropic centroidal Voronoi tessellations and their applications. SIAM J. Sci. Comput. 2005;26:737–761. [Google Scholar]
- Dumais J., Kwiatkowska D. Analysis of surface growth in shoot apices. Plant J. 2002;31:229–241. doi: 10.1046/j.1365-313x.2001.01350.x. [DOI] [PubMed] [Google Scholar]
- Errera, L. (1886) Sur une condition fondamentale d'équilibre des cellules vivantes. Available at: https://www.cabdirect.org/cabdirect/abstract/19431401837.
- Fabri A., Giezeman G.J., Kettner L., Schirra S., Schönherr S. On the design of CGAL a computational geometry algorithms library. Software. Pract. Exper. 2000;30:1167–1202. [Google Scholar]
- Fal K., Liu M., Duisembekova A., Refahi Y., Haswell E.S., Hamant O. Phyllotactic regularity requires the Paf1 complex in Arabidopsis. Development. 2017;144:4428–4436. doi: 10.1242/dev.154369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez R., Das P., Mirabet V., Moscardi E., Traas J., Verdeil J.L., Malandain G., Godin C. Imaging plant growth in 4D: robust tissue reconstruction and lineaging at cell resolution. Nat. Methods. 2010;7:547–553. doi: 10.1038/nmeth.1472. [DOI] [PubMed] [Google Scholar]
- Fox J., Weisberg S. Sage Publications; 2011. An R Companion to Applied Regression. [Google Scholar]
- Gibson M.C., Patel A.B., Nagpal R., Perrimon N. The emergence of geometric order in proliferating metazoan epithelia. Nature. 2006;442:1038–1041. doi: 10.1038/nature05014. [DOI] [PubMed] [Google Scholar]
- Gibson W.T., Gibson M.C. Cell topology, geometry, and morphogenesis in proliferating epithelia. Curr. Top. Dev. Biol. 2009;89:87–114. doi: 10.1016/S0070-2153(09)89004-2. [DOI] [PubMed] [Google Scholar]
- Gibson W.T., Veldhuis J.H., Rubinstein B., Cartwright H.N., Perrimon N., Brodland G.W., Nagpal R., Gibson M.C. Control of the mitotic cleavage plane by local epithelial topology. Cell. 2011;144:427–438. doi: 10.1016/j.cell.2010.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamant O., Heisler M.G., Jönsson H., Krupinski P., Uyttewaal M., Bokov P., Corson F., Sahlin P., Boudaoud A., Meyerowitz E.M. Developmental patterning by mechanical signals in Arabidopsis. Science. 2008;322:1650–1655. doi: 10.1126/science.1165594. [DOI] [PubMed] [Google Scholar]
- Heisler M.G., Ohno C., Das P., Sieber P., Reddy G.V., Long J.A., Meyerowitz E.M. Patterns of auxin transport and gene expression during primordium development revealed by live imaging of the Arabidopsis inflorescence meristem. Curr. Biol. 2005;15:1899–1911. doi: 10.1016/j.cub.2005.09.052. [DOI] [PubMed] [Google Scholar]
- Hofmeister W. Zusatze und Berichtigungen zu den 1851 Veröffentlichen Untersuchungen der Entwicklung höherer kryptogamen. Jahrb. für Wiss. und Bot. 1863;3:259–293. [Google Scholar]
- Inzé D., De Veylder L. Cell cycle regulation in plant development. Annu. Rev. Genet. 2006;40:77–105. doi: 10.1146/annurev.genet.40.110405.090431. [DOI] [PubMed] [Google Scholar]
- Jackson M.D.B., Duran-Nebreda S., Bassel G.W. Network-based approaches to quantify multicellular development. J. R. Soc. Interface. 2017;14 doi: 10.1098/rsif.2017.0484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson M.D., Xu H., Duran-Nebreda S., Stamm P., Bassel G.W. Topological analysis of multicellular complexity in the plant hypocotyl. Elife. 2017;6 doi: 10.7554/eLife.26023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones A.R., Forero-Vargas M., Withers S.P., Smith R.S., Traas J., Dewitte W., Murray J.A. Cell-size dependent progression of the cell cycle creates homeostasis and flexibility of plant cell size. Nat. Commun. 2017;8:15060. doi: 10.1038/ncomms15060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones, E., Oliphant, T., and Peterson, P. (2014) {SciPy}: Open Source Scientific Tools for {Python}.
- Jönsson H., Heisler M.G., Shapiro B.E., Meyerowitz E.M., Mjolsness E. An auxin-driven polarized transport model for phyllotaxis. Proc. Natl. Acad. Sci. U S A. 2006;103:1633–1638. doi: 10.1073/pnas.0509839103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kierzkowski D., Nakayama N., Routier-Kierzkowska A.L., Weber A., Bayer E., Schorderet M., Reinhardt D., Kuhlemeier C., Smith R.S. Elastic domains regulate growth and organogenesis in the plant shoot apical meristem. Science. 2012;335:1096–1099. doi: 10.1126/science.1213100. [DOI] [PubMed] [Google Scholar]
- Kwiatkowska D. Structural integration at the shoot apical meristem: models, measurements, and experiments. Am. J. Bot. 2004;91:1277–1293. doi: 10.3732/ajb.91.9.1277. [DOI] [PubMed] [Google Scholar]
- Kwiatkowska D. Flower primordium formation at the Arabidopsis shoot apex: quantitative analysis of surface geometry and growth. J. Exp. Bot. 2006;57:571–580. doi: 10.1093/jxb/erj042. [DOI] [PubMed] [Google Scholar]
- Landrein B., Lathe R., Bringmann M., Vouillot C., Ivakov A., Boudaoud A., Persson S., Hamant O. Impaired cellulose synthase guidance leads to stem torsion and twists phyllotactic patterns in Arabidopsis. Curr. Biol. 2013;23:895–900. doi: 10.1016/j.cub.2013.04.013. [DOI] [PubMed] [Google Scholar]
- Laufs P., Grandjean O., Jonak C., Kiêu K., Traas J. Cellular parameters of the shoot apical meristem in Arabidopsis. Plant Cell. 1998;10:1375–1390. doi: 10.1105/tpc.10.8.1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lintilhac P.M., Vesecky T.B. Stress-induced alignment of division plane in plant tissues grown in vitro. Nature. 1984;307:363–364. [Google Scholar]
- Louveaux M., Julien J.-D., Mirabet V., Boudaoud A., Hamant O. Cell division plane orientation based on tensile stress in Arabidopsis thaliana. Proc. Natl. Acad. Sci. U S A. 2016;113:E4294–E4303. doi: 10.1073/pnas.1600677113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucas W.J., Bouché-Pillon S., Jackson D.P., Nguyen L., Baker L., Ding B., Hake S. Selective trafficking of KNOTTED1 homeodomain protein and its mRNA through plasmodesmata. Science. 1995;270:1980–1983. doi: 10.1126/science.270.5244.1980. [DOI] [PubMed] [Google Scholar]
- Majda M., Grones P., Sintorn I.M., Vain T., Milani P., Krupinski P., Zagórska-Marek B., Viotti C., Jönsson H., Mellerowicz E.J. Mechanochemical polarization of contiguous cell walls shapes plant pavement cells. Dev. Cell. 2017;43:290–304.e4. doi: 10.1016/j.devcel.2017.10.017. [DOI] [PubMed] [Google Scholar]
- Marschner I.C. glm2: fitting generalized linear models with convergence problems. R J. 2011;3:12–15. [Google Scholar]
- Meurer A., Smith C.P., Paprocki M., Čertík O., Kirpichev S.B., Rocklin M., Kumar A., Ivanov S., Moore J.K., Singh S. SymPy: symbolic computing in Python. PeerJ Comput. Sci. 2017;3:e103. [Google Scholar]
- Meyerowitz E.M. Genetic control of cell division patterns in developing plants. Cell. 1997;88:299–308. doi: 10.1016/s0092-8674(00)81868-1. [DOI] [PubMed] [Google Scholar]
- Montenegro-Johnson T.D., Stamm P., Strauss S., Topham A.T., Tsagris M., Wood A.T., Smith R.S., Bassel G.W. Digital single-cell analysis of plant organ development using 3DCellAtlas. Plant Cell. 2015;27:1018–1033. doi: 10.1105/tpc.15.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman M. Oxford University Press; 2010. Networks: An Introduction. [Google Scholar]
- Newman M.E.J. A measure of betweenness centrality based on random walks. Soc. Netw. 2005;27:39–54. [Google Scholar]
- Newman M.E. Power laws, Pareto distributions and Zipf's law. Contemp. Phys. 2005;46:323–351. [Google Scholar]
- Ollé-Vila A., Duran-Nebreda S., Conde-Pueyo N., Montañez R., Solé R. A morphospace for synthetic organs and organoids: the possible and the actual. Integr. Biol. (Camb.) 2016;8:485–503. doi: 10.1039/c5ib00324e. [DOI] [PubMed] [Google Scholar]
- Reddy G.V., Heisler M.G., Ehrhardt D.W., Meyerowitz E.M. Real-time lineage analysis reveals oriented cell divisions associated with morphogenesis at the shoot apex of Arabidopsis thaliana. Development. 2004;131:4225–4237. doi: 10.1242/dev.01261. [DOI] [PubMed] [Google Scholar]
- Robert L., Hoffmann M., Krell N., Aymerich S., Robert J., Doumic M. Division in Escherichia coliis triggered by a size-sensing rather than a timing mechanism. BMC Biol. 2014;12:17. doi: 10.1186/1741-7007-12-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sablowski R. Coordination of plant cell growth and division: collective control or mutual agreement? Curr. Opin. Plant Biol. 2016;34:54–60. doi: 10.1016/j.pbi.2016.09.004. [DOI] [PubMed] [Google Scholar]
- Sahlin P., Jönsson H. A modeling study on how cell division affects properties of epithelial tissues under isotropic growth. PLoS One. 2010;5:e11750. doi: 10.1371/journal.pone.0011750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampathkumar A., Krupinski P., Wightman R., Milani P., Berquand A., Boudaoud A., Hamant O., Jönsson H., Meyerowitz E.M. Subcellular and supracellular mechanical stress prescribes cytoskeleton behavior in Arabidopsis cotyledon pavement cells. Elife. 2014;3:e01967. doi: 10.7554/eLife.01967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Gutiérrez D., Tozluoglu M., Barry J.D., Pascual A., Mao Y., Escudero L.M. Fundamental physical cellular constraints drive self-organization of tissues. EMBO J. 2016;35:77–88. doi: 10.15252/embj.201592374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sapala A., Runions A., Routier-Kierzkowska A.L., Das Gupta M.D., Hong L., Hofhuis H., Verger S., Mosca G., Li C.B., Hay A. Why plants make puzzle cells, and how their shape emerges. Elife. 2018;7:e32794. doi: 10.7554/eLife.32794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasai Y. Cytosystems dynamics in self-organization of tissue architecture. Nature. 2013;493:318–326. doi: 10.1038/nature11859. [DOI] [PubMed] [Google Scholar]
- Schaefer E., Belcram K., Uyttewaal M., Duroc Y., Goussot M., Legland D., Laruelle E., De Tauzia-Moreau M.L., Pastuglia M., Bouchez D. The preprophase band of microtubules controls the robustness of division orientation in plants. Science. 2017;356:186–189. doi: 10.1126/science.aal3016. [DOI] [PubMed] [Google Scholar]
- Schult, D.A., and Swart, P. (2008). Exploring network structure, dynamics, and function using NetworkX. Proceedings of the 7th Python in Science Conferences (SciPy 2008), pp. 11–16.
- Seguin C., Van Den Heuvel M.P., Zalesky A. Navigation of Brain Networks. Proc. Natl. Acad. Sci. U S A. 2018;115:6297–6302. doi: 10.1073/pnas.1801351115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro B.E., Tobin C., Mjolsness E., Meyerowitz E.M. Analysis of cell division patterns in the Arabidopsis shoot apical meristem. Proc. Natl. Acad. Sci. U S A. 2015;112:4815–4820. doi: 10.1073/pnas.1502588112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon M.K. Springer Science & Business Media; 2007. Probability Distributions Involving Gaussian Random Variables: A Handbook for Engineers and Scientists. [Google Scholar]
- Sing T., Sander O., Beerenwinkel N., Lengauer T. ROCR: visualizing classifier performance in R. Bioinformatics. 2005;21:3940–3941. doi: 10.1093/bioinformatics/bti623. [DOI] [PubMed] [Google Scholar]
- Smith R.S., Guyomarc'h S., Mandel T., Reinhardt D., Kuhlemeier C., Prusinkiewicz P. A plausible model of phyllotaxis. Proc. Natl. Acad. Sci. U S A. 2006;103:1301–1306. doi: 10.1073/pnas.0510457103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoma S., Lucas M., Chopard J., Schaedel M., Traas J., Godin C. Flux-based transport enhancement as a plausible unifying mechanism for auxin transport in meristem development. PLoS Comput. Biol. 2008;4:e1000207. doi: 10.1371/journal.pcbi.1000207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, D.W. (1942) On Growth and Form.
- Turner J.J., Ewald J.C., Skotheim J.M. Cell size control in yeast. Curr. Biol. 2012;22:R350–R359. doi: 10.1016/j.cub.2012.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyttewaal M., Burian A., Alim K., Landrein B.T., Borowska-Wykręt D., Dedieu A., Peaucelle A., Ludynia M., Traas J., Boudaoud A. Mechanical stress acts via katanin to amplify differences in growth rate between adjacent cells in Arabidopsis. Cell. 2012;149:439–451. doi: 10.1016/j.cell.2012.02.048. [DOI] [PubMed] [Google Scholar]
- Vallender S.S. Calculation of the Wasserstein distance between probability distributions on the line. Theory Probab. Appl. 1974;18:784–786. [Google Scholar]
- Wallden M., Fange D., Lundius E.G., Baltekin Ö., Elf J. The synchronization of replication and division cycles in individual E. coli cells. Cell. 2016;166:729–739. doi: 10.1016/j.cell.2016.06.052. [DOI] [PubMed] [Google Scholar]
- Willis L., Refahi Y., Wightman R., Landrein B., Teles J., Huang K.C., Meyerowitz E.M., Jönsson H. Cell size and growth regulation in the Arabidopsis thaliana apical stem cell niche. Proc. Natl. Acad. Sci. U S A. 2016;113:E8238–E8246. doi: 10.1073/pnas.1616768113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., Schuster C., Beahan C.T., Charoensawan V., Peaucelle A., Bacic A., Doblin M.S., Wightman R., Meyerowitz E.M. Regulation of meristem morphogenesis by cell wall synthases in Arabidopsis. Curr. Biol. 2016;26:1404–1415. doi: 10.1016/j.cub.2016.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida S., Barbier De Reuille P.B., Lane B., Bassel G.W., Prusinkiewicz P., Smith R.S., Weijers D. Genetic control of plant development by overriding a geometric division rule. Dev. Cell. 2014;29:75–87. doi: 10.1016/j.devcel.2014.02.002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Software used for this study can be downloaded at www.morphographx.org.
Supplemental dataset 1: Wild-type Col and ktn1 image and connectivity datasets. Raw TIFF image datasets for each biological replicate and timepoint in each of these genotypes is provided at the link https://osf.io/mxgrh/. Segmentations in the MorphoGraphX format .MGXS are provided along with cellular connectivity networks and cell lineages in .CSV format. README.TXT contains relevant information.
Supplemental dataset 2: Images showing the computational analysis of cell division plane orientation in the Arabidopsis SAM following different rules. These can be found at the link https://osf.io/ucd76/.