Prediction of lumbar vertebral body compressive strength of overweight and obese older adults using morphed subject-specific finite element models to evaluate the effects of weight loss

Abstract

Background:

Diet and exercise can promote weight loss in older adults, however there is potential to increase fracture risk due to loss of bone mineral density (BMD) known to accompany weight loss. Weight loss effects on measures of bone quality and strength are currently unknown.

Aims:

The purpose of this study is to develop subject-specific finite element (FE) models of the lumbar spine and study the effect of intentional weight loss on bone strength in a pilot data set.

Methods:

Computed tomography (CT) scans of the lumbar spine of 30 overweight and obese (mean BMI = 29.7±3.9 kg/m²), older adults (mean age = 65.9±4.6 years) undergoing an 18-month intentional weight loss intervention were obtained at baseline and post-intervention. Measures of volumetric BMD (vBMD) and variable cortical thickness were derived from each subject CT scan. Development of the subject-specific FE models of the lumbar spine involved model morphing techniques to accelerate the development of the models. vBMD-derived material properties and cortical thickness measures were directly mapped to baseline and post-intervention models. Bone strength was estimated through simulation of a quasi-static uniaxial compression test.

Results:

From baseline to 18-month post weight loss intervention, there were statistically significant decreases in estimated bone strength (6.5% decrease; p<0.05). Adjusting for baseline bone measures and gender revealed no statistically significant correlations between weight change and change in vBMD, cortical thickness, or bone strength.

Conclusion:

Integration of CT-based measures and FE models with conventional areal BMD can improve the understanding of the effects of intentional weight loss on bone health.

BACKGROUND

Compression fracture of the vertebral body are the most common fractures in patients with osteoporosis and are associated with increased back pain, depression, and reduced quality of life [1-3]. Observational data suggests that weight loss increases the risk of vertebral fracture in older women [4], which is affirmed by recent randomized controlled trial data suggesting intentional caloric restriction reduces dual x-ray absorptiometry (DXA)-derived spine areal bone mineral density (aBMD) in middle-aged and younger adults [5,6]. Although aBMD is the gold standard for assessment of osteoporosis and fracture risk [7-9], it is limited in its prognostic capabilities (as over half of all fractures occur in patients with aBMD values above the defined thresholds for osteoporosis [10,11]), with spinal measurements particularly susceptible to measurement error introduced by obesity and weight loss [12]. Due to these limitations, more robust assessments of bone density and additional information on bone morphometry and strength are required to further understand the effects of weight loss on vertebral fracture risk.

Additional noninvasive measures of osteoporosis and fracture risk can be derived from quantitative clinical tomography (QCT) data which include measures of volumetric BMD (vBMD), cortical thickness, and bone strength estimates using finite element (FE) models. Correlations between vertebral strength and aBMD (r²= 0.51-0.80) and vBMD (r²= 0.37-0.72) reveal that these measures of BMD only account for roughly 40 to 80% of vertebral strength [13-19]. Recent studies have shown that FE models derived from CT scans are a better predictor of vertebral bone strength in comparison to aBMD and vBMD as FE models factor in variations in vertebral geometry, cortical thickness, and material properties which all contribute to bone strength and subsequently fracture risk [20-22]. As a result, the development of subject-specific FE models of the spine provides a powerful tool to measure vertebral bone strength in vivo and the ability to study bone quality in clinical trials [23-26]. However, these methods have not been applied to study the changes in bone strength in a longitudinal study of weight loss in older adults. In addition, previously developed FE models of the vertebrae use simplified techniques including voxel-based meshing which do not model the distinction between cortical and trabecular bone and are known to produce inaccuracies especially for the predicted stresses and strains on the bone surface.

Therefore, the primary purpose of this study is to develop and validate subject-specific lumbar spine vertebrae FE models using morphing techniques to examine the effect of intentional weight loss over 18-months in overweight and obese older adults on vBMD, cortical thickness, and bone strength in a pilot data set. Secondarily, we aimed to describe baseline correlations between participant demographic information and bone measures and correlations between each of the baseline bone measures.

METHODS

Study Design and Participants

This is an ancillary study to a recently completed clinical trial, the Cooperative Lifestyle Intervention Program II (CLIP II; NCT01547182), which included 252 older (60-79 years), overweight and obese (body mass index (BMI)≥28 kg/m²) adults who had cardiovascular disease or metabolic syndrome and self-reported mobility disability, and was designed to evaluate the effects of diet-induced weight loss and exercise on mobility and lower-body strength [27,28]. Weight loss interventions included diet-induced weight loss, diet-induced weight loss and aerobic training, and diet-induced weight loss and resistance training. Full design detail can be found in the published methods paper [27]. Participants in this larger study were recruited in 8 waves of 24 to 30 participants per wave. A subset of participants from the CLIP II parent study (n=55) were recruited from waves 7 and 8. This subset consented to participate in the present study and were administered a CT scan at baseline and 18-month follow-up (n=34) to determine associations between weight change and CT-derived vBMD, cortical thickness, and strength estimated by FE models. A total of 21 participants (38%) did not have an 18-month CT scan (n=6 completed the intervention but did not have a post-intervention CT scan, n=15 dropped out of the study entirely). In terms of baseline descriptive characteristics, the larger study population and the CT cohort were very similar.

CT Imaging

Helical CT scans of the lumbar spine (120 kVp, 250 mA, 2.5 mm helical with a pitch of 1.375:1, standard reconstruction with secondary reconstruction to 0.625 mm slice thickness) covering the region from the superior endplate of L1 vertebra through the inferior endplate of L5 vertebra were obtained using a 64-slice CT scanner (LightSpeed VCT, General Electric Medical Systems, Milwaukee, WI). The bony anatomy of L1-L4 was segmented for each subject using thresholding, region growing, and manual editing to generate binary images and masks which were subsequently converted into 3D triangulated surface models of each lumbar vertebra (Mimics, Materialise, Plymouth, MI). Segmentations were done by a single user and consistent thresholding and region growing techniques were applied.

Volumetric Bone Mineral Density Measurement

Measurements of vBMD of the lumbar spine (L1-L4) were obtained using N-vivo software (Image Analysis, Columbia, KY). The CT Hounsfield units (HU) are calibrated using a 4-port InTable bone mineral phantom to derive equivalent calcium hydroxyapatite density measures or vBMD in mg/cm³. Material properties for each subject vertebra FE model were derived from elasticity-density relationships from the literature. The calibrated vBMD (ρ_CT, mg/cm³) was converted into an elastic modulus (E, MPa) using the empirical relationship for vertebral trabecular bone (Eq. 1) [29]. Elastic modulus was derived and assigned to the trabecular region of the FE model for each vertebra for baseline and 18-month post-intervention follow-up. The elastic modulus of the cortical bone remained constant across all patients with the given baseline FE model parameters as cortical vBMD was not collected [30].

$$E=-34.7+3.23\ast {\rho }_{CT}$$ (1)

Cortical Thickness Assessment

Vertebral cortical thickness changes were quantified from CT scans using a validated cortical density-based algorithm for cortical thickness estimation [31,32]. The algorithm estimates cortical thickness by fitting a mathematical model constrained by a global cortical density and out-of-plane blur to the HU intensity profile along a line normal to the vertebral cortical surface. The software outputs include point clouds of the inner and outer surfaces as well as calculated thickness values across the entire surface of the bone, with approximately 3,000 cortical thickness measurements per vertebra (Stradwin v5.2, Cambridge University, UK). Cortical thickness of each vertebra was collected at baseline and 18-month post-intervention follow-up.

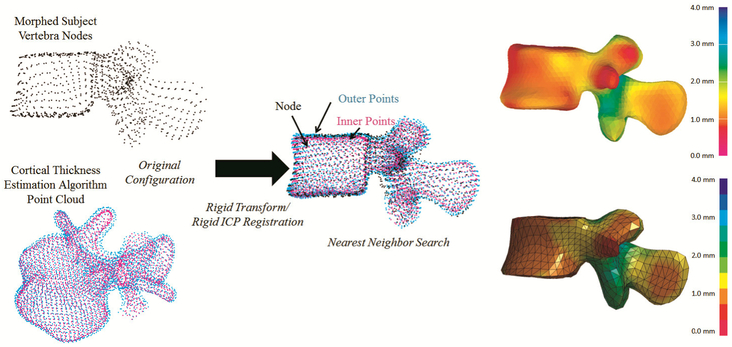
A cortical thickness mapping approach was developed to incorporate the derived cortical thickness surface maps and thickness values into the cortical shell elements of the subject-specific FE models. The cortical thickness point cloud of each vertebrae was transformed into the FE model space using a rigid transformation performed using Geomagic Studio (version 2014, 3D Systems, Inc., Rock Hill, SC) and an iterative closest point (ICP) algorithm applied using custom Matlab code (The MathWorks, Inc., Natick, MA). Following the alignment, custom Matlab code was used to perform a nearest neighbor search for each FE node and assign the thickness value based on the output of the cortical thickness estimation algorithm (Fig 1).

Fig 1.

Cortical thickness mapping workflow. Above, the transformations and nearest neighbor search processes. On the right, the results of the cortical thickness mapping. The output of the cortical thickness estimation algorithm for an example subject is shown on top right with the resulting subject-specific FE model with cortical thickness mapped on the bottom right

Finite Element Model Development

To accelerate the development of the subject-specific FE models of the lumbar spine, morphing techniques using radial basis function interpolation with the basis function thin-plate spline and a relaxation algorithm were used to morph an existing FE model to a subject-specific geometry [33-36]. Thin-plate spline morphing utilizes interpolation functions derived from homologous landmark data in a reference and target configuration to move the nodal coordinates of the reference FE model to that of the target or subject-specific geometry. Homologous landmark data are points on analogous positions on each respective geometry that allow for a one-to-one mapping between the reference and target configurations. The lumbar spine of the Total HUman Model for Safety (THUMS) AM50 v4.01 was used for the reference homologous landmark data and FE model. The THUMS AM50 v4.01 FE model is representative of a 50^th percentile male with a height and weight of 175 cm and 77 kg, respectively [30]. The lumbar spine FE model has been validated against post-mortem human surrogate (PMHS) data in various loading conditions including quasi-static flexion, extension, lateral bending, anterior shearing, torsion, and compression of functional spinal units [37-39]. The validation results showed good agreement with the experimental data for all loading conditions and therefore the model was selected as the reference model for this study due to its biofidelity and robustness. The target homologous landmark data was derived from the subject-specific CT data for each lumbar spine vertebra.

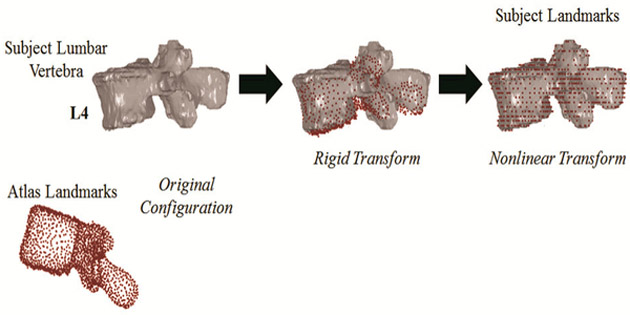
To collect the homologous landmark data for the reference and subject-specific vertebrae, techniques involving image segmentation, atlas development, and image registration were used [40,41]. An image registration algorithm was applied using rigid and nonlinear transformations to register the binary images of the atlas vertebrae to the binary images of the segmented subject-specific vertebrae to map the atlas landmarks of the vertebrae to each subject-specific vertebra (Fig 2a). The image registration is used to control for any differences in scan alignment. The outputs of the image registration process are the homologous landmarks for the subject-specific vertebrae which serve as the inputs to the model morphing procedure in addition to the atlas landmarks and the FE nodal coordinates. The thin-plate spline morphing process for an example vertebra is depicted in Fig 2b. A deviation analysis was performed to measure the point-to-surface distances to evaluate the quality and robustness of the image registration algorithm and thin-plate spline morphing algorithm (see Supplemental Appendix).

Fig 2.

(a) Registration of atlas landmarks (red) to the subject segmentations (grey) using rigid and nonlinear transformations for an L4 vertebra to generate subject landmarks. (b) Model morphing of THUMS AM50 v4.01 FE atlas model to a subject-specific model. Homologous landmarks of the atlas (red) and subject (grey) are used to derive an interpolation function that morphs the atlas FE model to the target or subject-specific model

Finite Element Model Simulation

Bone strength of each vertebra (L1-L4) was estimated through simulation of a quasi-static uniaxial compression simulation [21]. The published experimental data for the uniaxial compression test utilized isolated L1-L4 vertebrae of 13 cadavers (7 F + 6 M) with an average age of 69 ± 14 years old (range: 37-87 years). The atlas THUMS AM50 v4.01 vertebrae were validated against the published experimental data to evaluate the biofidelity (See Supplemental Appendix). Subject-specific FE models were developed for 30 participants who had complete bone measurements at baseline and follow-up. For the 34 participants with baseline and follow-up CT scan data, baseline and 18-month post-intervention vBMD, cortical thickness, and bone strength was obtained for 30 participants. Missing baseline and follow-up bone measurements were due to missing bone mineral phantom ports (n=2) and incomplete measurement of vBMD for each vertebrae (n=2). A total of 240 simulations were performed for the developed subject-specific vertebrae FE models. The simulations included 1 loading configuration (uniaxial compression), 4 isolated vertebra (L1-L4), and 2 models per subject (baseline and 18-month post-intervention) for the 30 participants. All simulations were performed using nonlinear implicit analysis with LS-Dyna (v6.0.0 rev 71482, LSTC, Livermore, CA).

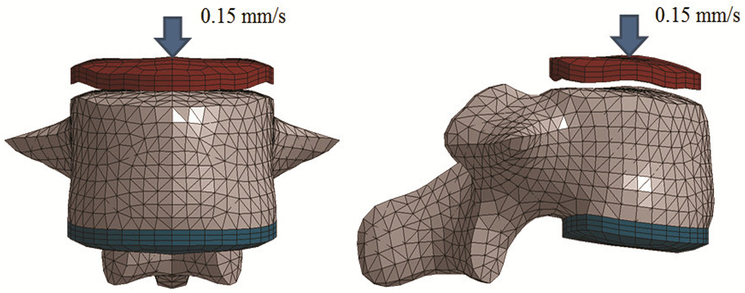
For the uniaxial compression configuration, boundary conditions were selected to match the experimental and FE simulation as performed in the literature [21]. Briefly, the inferior endplate of the vertebral body was fixed to a molded 3 mm layer of polymethylmethacrylate (PMMA) that was meshed node-to-node and fully constrained (Fig 3). A molded PMMA impactor compressed the superior endplate of the vertebral body at a rate of 0.15 mm/s until failure. The molded PMMA impactor for the superior endplate was also meshed node-to-node with the vertebral body. Boundary conditions for each subject-specific model were generated with a custom script to ensure consistent setup across all simulations. The peak fracture force was defined as the peak force achieved during the loading cycle. The lumbar spine was modeled as an isotropic elastic-plastic material with a failure strain. Strain-based criteria have proved effective to model bone fracture [42]. Bone fracture prediction was modeled using the element deletion method which removes elements exceeding a given strain threshold. For the lumbar spine, trabecular bone fracture was modeled with a fracture threshold of 0.0061 effective plastic strain [43]. Previous studies have concluded that the cortical shell only has a minor structural role [21,44,16]. In addition, the majority of published studies on material properties of the vertebrae only contain data for trabecular bone [43,45,46]. Due to the minor structural role and lack of failure criteria specific to vertebral cortical bone, no fracture criterion was set for the cortical bone.

Fig 3.

Simulation setup for the uniaxial compression test

Statistical Analysis

The primary outcome measures of interest included the bone measurements of vBMD, cortical thickness, and estimated bone strength. These measures were characterized at baseline and at 18-months post-intervention. Descriptive statistics were calculated overall and by gender at baseline among all participants with baseline bone measurements, and gender and race group comparisons of baseline bone measures were performed using t-tests. Associations between bone measures and continuous patient characteristics as well as correlations among bone measures were performed using both Pearson correlations and simple linear regression. Changes at 18-months used only participants with both baseline and 18-month data, and comparisons of participants with and without follow-up data were performed using t-tests for continuous variables and chi-square tests for discrete characteristics. One-sample t-tests were used to test the differences in weight and bone measure data across the 18-month change. The associations between changes in bone measures were analyzed using Pearson correlations and simple linear regression. Further associations between changes in bone measures and changes in weight were measured using partial Pearson correlations and multiple linear regression models adjusted for gender and baseline bone measure data. Due to the hypothesis-generating nature of these analyses there were no adjustments for multiple comparisons. All statistical analyses were performed using SAS v9.4 (SAS Institute, Cary, NC) and a p-value less than 0.05 was considered statistically significant.

RESULTS

Baseline Demographic Characteristics

Baseline characteristics of the 55 participants are included in Table 1, including descriptive statistics of age, weight, BMI, race, FRAX score (calculated with DXA BMD), and clinical categorization of bone health. Briefly, participants were 65.8 ± 4.3 years of age, with the majority being female (64%) and Non-Hispanic white (69%). Weight was 96.1 ± 16.9 kg and BMI was 34.0 ± 3.5 kg/m² with 53% of the study sample classified as Type I Obese. T-scores indicated normal bone density in 36% of the participants, osteopenia in 53% of participants, and osteoporosis in 11% of participants. Overall, participants were at a low risk of major osteoporotic fracture in the next 10 years based on the FRAX 10-year probability.

Table 1.

Mean (SD) baseline characteristics of study population.

Variable	Men (n = 20)	Women (n = 35)	Overall (n = 55)
Age (years)	65.6 ± 4.4	66.0 ± 4.3	65.8 ± 4.3
Weight (kg)	109.2 ± 16.8	88.6 ± 11.6	96.1 ± 16.9
BMI (kg/m2)	34.3 ± 3.8	33.8 ± 3.5	34.0 ± 3.5
African American, n (%)	5 (25)	11(31)	16 (29)
FRAX 10 year probability (%)
Major Fracture	3.9 ± 2.9	4.2 ± 2.2	4.1 ± 2.4
Hip Fracture	0.05 ± 0.09	0.04 ± 0.08	0.04 ± 0.08
Clinical Categorization, n (%)
Normal	6 (30)	14 (40)	20 (36)
Osteopenia	10 (50)	19 (54)	29 (53)
Osteoporosis	4 (20)	2 (6)	6 (11)

Baseline Bone Measure Summary

Baseline bone measure descriptive data, where available (n= 53-55), for the full baseline sample (n=55) are summarized in Table 2. Of the 55 participants that were administered baseline CT scans, baseline bone measures were collected for all 55 participants for cortical thickness and for 53 participants for vBMD and bone strength as two participants were missing bone mineral phantom ports. Mean estimated strength was within the range of the published experimental testing. As a sensitivity analysis, descriptive data were stratified by gender and by race. There were no statistically significant differences in vBMD, cortical thickness, or vertebral strength between men and women. In addition, no significant differences were noted in cortical thickness or strength between different races. African Americans had significantly greater vBMD in comparison to Non-Hispanic whites (p<0.001).

Table 2.

Baseline bone measure descriptive data.

	Baseline
	N	Mean ± SD
vBMD (mg/cm3)	53	126.47 ± 40.14
Cortical Thickness (mm)	55	1.16 ± 0.15
Estimated Strength (kN)	53	3.69 ± 1.06

Correlations and parameter estimates between continuous baseline patient characteristics and baseline bone measures are listed in Table 3. For baseline BMI, a significant positive correlation was found with baseline vBMD (r=0.37, p=0.044). For baseline weight, a significant positive correlation was found with baseline estimated strength (r=0.41, p=0.023). Correlations and parameter estimates between each of the baseline bone measures are listed in Table 4. Baseline vBMD (r=0.39, p=0.033) and cortical thickness (r=0.56, p=0.001) were positively correlated with baseline estimated strength.

Table 3.

Correlations and parameter estimates between baseline bone measures and baseline patient characteristics.

	Age (years)		BMI (kg/m2)		Weight (kg)
Bone Measure	r	β (SE)	r	β (SE)	r	β (SE)
vBMD (mg/cm3)	−0.11	−1.116 (1.991)	0.37*	4.587 (2.179)	−0.12	−0.399 (0.639)
Cortical Thickness (mm)	0.28	0.009 (0.006)	0.11	0.004 (0.007)	0.21	0.002 (0.002)
Estimated Strength (kN)	0.25	0.065 (0.047)	0.13	0.039 (0.056)	0.41*	0.034 (0.014)

^*p-value <0.05.

Table 4.

Correlations and parameter estimates between baseline bone measures.

Bone Measure Correlations	r	β (SE)
vBMD (mg/cm3) & Cortical Thickness (mm)	0.12	0.000 (0.001)
vBMD (mg/cm3) & Estimated Strength (kN)	0.39*	0.009 (0.004)
Cortical Thickness (mm) & Estimated Strength (kN)	0.56*	4.716 (1.313)

^*p-value <0.05

18-month Change in Weight and Bone Measure Summary

Descriptive statistics of the 30 participants (65.6 ± 4.6 average age, 70% female, 20% African American, BMI 29.7± 3.9 kg/m²) with baseline and 18-month post-intervention bone measure data are presented in Table 5. There were no significant differences between the baseline population with post-intervention bone measure data (n=30) and the full baseline population (n=55) for age, gender, race, or BMI (all p>0.05). Overall loss of body weight (−9.46 ± 8.65 kg) was statistically significant from baseline to 18-month post-intervention. No statistically significant changes were noted for vBMD or cortical thickness. However, vBMD decreased by 6.6% from baseline to 18-month post-intervention and approached significance (p=0.10). Statistically significant decreases in estimated bone strength were observed with strength decreasing by 6.5% (p=0.03). Correlations and parameter estimates between the change of each of the bone measures are listed in Table 6. For changes in bone measures, the change in vBMD was positively correlated with the change in estimated strength (r=0.75, p<0.001).

Table 5.

Baseline and 18 month post-intervention weight and bone measure descriptive data (n=30). p-values indicate if change from baseline to 18 months is significant

	Baseline Mean ± SD	18 month Mean ± SD	Change (95% CI)	p-value
Weight (kg)	90.87 ± 14.17	81.41 ± 13.29	−9.46 (−12.69, −6.23)	<.0001*
vBMD (mg/cm3)	129.72 ± 48.22	121.22 ± 36.81	−8.50 (−18.81, 1.80)	0.10
Cortical Thickness (mm)	1.124 ± 0.139	1.123 ± 0.140	−0.002 (−0.043, 0.040)	0.93
Estimated Strength (kN)	3.60 ± 1.17	3.36 ± 0.95	−0.23 (−0.44, −0.03)	0.03*

^*(p-value <0.05).

Table 6.

Correlations and parameter estimates between change in bone measures.

Δ Bone Measure Correlations	r	β (SE)
Δ vBMD (mg/cm3) & Δ Cortical Thickness (mm)	0.04	0.000 (0.001)
Δ vBMD (mg/cm3) & Δ Estimated Strength (kN)	0.75*	0.015 (0.002)
Δ Cortical Thickness (mm) & Δ Estimated Strength (kN)	0.22	1.062 (0.907)

^*p-value <0.05

Correlations and parameter estimates between weight change and change in bone measures, both unadjusted and adjusted for baseline bone measures and gender are summarized in Table 7. Correlations were observed between weight change and all bone measures with unadjusted correlations ranging from −0.20 to 0.06 and adjusted correlations ranging from −0.13 to 0.22. No significant correlations between weight change and change in bone measures were observed.

Table 7.

Correlations and parameter estimates between weight change (kg) and change in bone measures, unadjusted and adjusted for baseline bone measures and gender.

Δ Bone Measure	Δ Weight (kg)
	Unadusted		Adjusted
	r	β (SE)	r	β (SE)
Δ vBMD (mg/cm3)	0.02	0.075 (0.602)	0.22	0.548 (0.481)
Δ Cortical Thickness (mm)	−0.20	−0.003 (0.002)	−0.20	−0.002 (0.002)
Δ Estimated Strength (kN)	0.06	0.004 (0.012)	−0.13	−0.007 (0.010)

^*p-value <0.05

DISCUSSION

In this study, subject-specific FE models of the lumbar vertebrae of overweight and obese older adults undergoing intentional weight loss were successfully developed from CT scan data by characterizing subject-specific geometry, vBMD-derived material properties, and variable cortical thickness. The results in this pilot study agree with findings from previous studies regarding weight loss and BMD of the lumbar spine as no statistically significant changes were noted in vBMD measures. In a recent meta-analysis of randomized controlled trials of intentional weight loss, no significant changes in aBMD of the lumbar spine were observed with diet-induced weight loss [47]. Analysis of the 18-month change in bone measure data revealed statistically significant decreases from baseline to 18-months post weight loss intervention in estimated strength. Although changes in vBMD and cortical thickness were not significant, decreases in vBMD were directly correlated with estimated strength and in combination with the geometry of the FE model resulted in significant decreases in estimated strength. In addition, redistribution of cortical thickness due to changes in mechanical loads on the lumbar spine following weight-loss could affect the estimated strength [48]. The probability of vertebral fracture for a given strength has been defined using age-adjusted logistic regression models for both men and women [23]. For the baseline to 18-month post-intervention estimated strength data aggregated by gender, the change in strength for males and females would result in an approximately 2% increase in fracture risk.

Among Caucasian women 65 years and older without a prevalent vertebral fracture, there is a 0.9% increased risk of vertebral fracture each year [49,50]. This annual risk increases to 1.7% among those 80 years and older. While statistically significant decreases in strength were noted from baseline to 18-months, overall these decreases would result in negligible increases in fracture risk which would be on par with increases in fracture risk due to aging. In analyses adjusted for baseline bone measures and gender, no significant correlations between weight change and change in any of the bone measures was observed. While this pilot data set revealed small changes in bone measures in the lumbar spine, it is important to measure such changes to gain a better understanding of the effects of weight loss on bone health in order to aid clinicians in identifying optimal weight loss strategies to minimize bone loss.

No significant changes in vBMD, cortical thickness, or estimated strength were noted for weight change. While the exact mechanisms underlying weight-loss induced bone loss are unknown, one theory is related to the reduction of mechanical stress on the weight-bearing skeleton [51]. Changes in BMD have been found at the hip which is sensitive to changes induced at the impact-bearing skeletal site. Although the lumbar spine is an important weight-bearing structure, it is less sensitive to changes in mechanical stress and therefore results in little to no change in BMD [52]. Similarly, this low sensitivity to weight change also results in little to no change in cortical thickness and bone strength. Additionally, the lumbar spine is known for greater DXA measurement error in the context of aging and obesity [47,53]. Excess fat tissue, spinal osteoarthritis and osteophytes, and vascular calcifications can contribute to measurement error [54,55,53].

The use of model morphing techniques in this study offers various advantages over previously developed models. The most common method for developing subject-specific vertebrae models from CT data is using voxel-based meshing techniques which allows for automatic generation of the models [21,22,56-59]. However, there are limitations associated with voxel-based meshing including lower accuracies in predicted stresses and strains at the bone surface due to the inability to accurately capture the geometry and the inability to model the distinction between cortical and trabecular bone [60,9,61]. In modeling the vertebrae, it is important to capture the variations in geometry, cortical thickness, and material properties as these all contribute to bone strength [62]. These techniques presented allow for characterization of geometry, cortical thickness, and material properties which can ultimately provide FE models that better predict bone strength and fracture risk [63].

The presented study has a number of limitations. For model development and assignment of material properties, the use of homogenous material properties for trabecular components poses a limitation. The use of inhomogeneous material properties in the literature has shown improved results in estimating strength of the vertebrae and it has been shown that the anterior area of the vertebral body is less strong than the posterior region [64]. Therefore, future work includes implementing inhomogeneous material properties for both the cortical and trabecular regions to produce more accurate predictions of bone strength. Another limitation is associated with the cortical bone modeling and lack of failure criteria. Previously developed FE models of the vertebrae typically do not model the cortical shell explicitly [21-23]. Bone strength predictions in this study were in range of experimental testing without the inclusion of cortical bone failure. Future work includes characterization of cortical bone failure criteria to more accurately model vertebral fracture and to determine its effect on bone strength estimates. A limitation also exists for the collection of cortical thickness data using the cortical thickness estimation algorithm. Potential issues exist in detecting the cortical border and partial volumning which could lead to inaccuracies in cortical thickness measurement. These issues are addressed by the mathematical model fit to the underlying HU values in the cortex voxels and surrounding voxels and the assumption of a constant cortical density. The algorithm requires the segmentation of the vertebral body to identify initial locations of the outer bone surface and subsequently optimizes the location by identifying the cortical and soft tissue HU values such that the blurred model best fits the sample data to measure the cortical thickness. Currently, this technique is the best option for measuring vertebral cortical thickness in vivo. Ultimately, no significant changes in cortical thickness were noted. Future work includes determining the level of confidence in detecting changes in cortical thickness and exploration of potential alternative techniques.

Validation of the atlas FE model also poses as a limitation. The model response was compared to peak fracture force data reported in the literature. Future work includes further validation using force-time or force-displacement data when the experimental data becomes available. In order to improve the validation of the atlas model and fully validate the subject-specific models, the techniques developed in this study must be validated against controlled cadaveric experiments to establish a prediction accuracy of the modeling technique. The focus of this study was on the change in bone parameters including estimated strength using the developed FE models. Therefore, while the subject-specific FE strength data falls within the range of published experimental data, the focus should not be on the exact value predicted but rather the change in bone strength in order to estimate effects of weight loss.

Uniaxial compression loading of isolated vertebral bodies is considered the testing paradigm for non-invasive strength evaluation due to its well-defined and repeatable loading conditions [22,21,17,65]. A limitation of this setup involves the simple loading condition which does not fully capture in vivo loading conditions involving multiaxial and non-uniform loads. Future simulation work could include more realistic loading configurations including forward bending. Previous FE models have found poor correlation in predicting bending strength due to the inability predict failure behavior [65,24]. The methods developed in this study were applied to a pilot data set of 30 participants. To draw clinically meaningful conclusions on weight loss and bone health related to the primary clinical endpoint of fracture, additional data is necessary. The primary purpose of this pilot study was to develop the modeling methodology and explore the associations between weight change and the newly generated bone quality measures. The findings in this study are useful in helping to power future trials and to eventually draw definitive conclusions with a properly powered study.

In conclusion, subject-specific FE models of the lumbar spine of overweight and obese older adults were developed to study the effect of intentional weight loss on vBMD, cortical thickness, and strength. The ability to accurately model subject-specific geometry, cortical thickness, and material properties allows for better estimation of bone strength and fracture risk in comparison to density measures alone. Pilot data presented here do not suggest weight loss adversely affects measures of bone in older adults undergoing intentional weight loss, however, replication in a larger, adequately powered sample is warranted before definitive conclusions can be drawn. The methods presented can be used for larger clinical studies to improve the understanding of geometrical, compositional, and material changes of bones with weight loss intervention effects. Subject-specific FE models in combination with DXA can be valuable tools in assessing fracture risk as well as aid in clinical recommendations regarding weight loss in the elderly population.