Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2019 Jan 7;5(1):109–115. doi: 10.1021/acscentsci.8b00728

A Laser Driven Flow Chemistry Platform for Scaling Photochemical Reactions with Visible Light

Kaid C Harper 1,*, Eric G Moschetta 1,*, Shailendra V Bordawekar 1, Steven J Wittenberger 1
PMCID: PMC6346387  PMID: 30693330

Abstract

graphic file with name oc-2018-00728y_0006.jpg

Visible-light-promoted organic reactions can offer increased reactivity and selectivity via unique reaction pathways to address a multitude of practical synthetic problems, yet few practical solutions exist to employ these reactions for multikilogram production. We have developed a simple and versatile continuous stirred tank reactor (CSTR) equipped with a high-intensity laser to drive photochemical reactions at unprecedented rates in continuous flow, achieving kg/day throughput using a 100 mL reactor. Our approach to flow reactor design uses the Beer–Lambert law as a guideline to optimize catalyst concentration and reactor depth for maximum throughput. This laser CSTR platform coupled with the rationale for design can be applied to a breadth of photochemical reactions.

Short abstract

A continuous stirred tank reactor was equipped with a high-intensity laser to drive photochemical reactions at unprecedented rates in continuous flow, achieving kg/day throughput.

The use of visible light as an energy source in organic synthesis has expanded rapidly over the past decade driven by the use of photocatalysts.1−7 Photocatalysts that absorb in the visible spectrum have been applied to a wide variety of synthetically useful chemical transformations, resulting in improvements to existing transformations and identification of transformations that have opened up new possibilities in synthetic route design. These new photochemical methodologies often exhibit enhanced reactivity, enhanced selectivity, and improved tolerance for molecular complexity, and are well-suited to pharmaceutical development at both the discovery and development stages. However, implementation of photochemistry at multikilogram scale has been hindered by several inherent challenges associated with the attenuation of light as dictated by the Beer–Lambert law. Herein, we disclose the design and successful evaluation on scale of a modular continuous flow reactor, a laser driven continuous stirred tank reactor (CSTR) (Figure 1) that was designed using an understanding of the impact of the Beer–Lambert law on the photochemical process.

Figure 1.

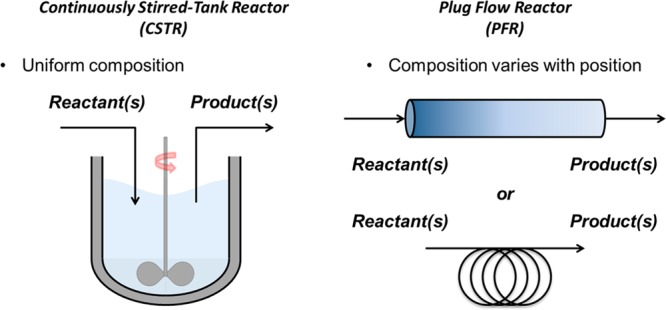
Figure 1

Open in a new tab

Comparison of CSTRs and PFRs.

The primary challenge in scaling photochemical reactions is addressing the Beer–Lambert law, which dictates the depth to which light can penetrate a solution. Rearranging the Beer–Lambert law in terms of path length L (eq 1), transmittance T, concentration of the absorbing species c, and its molar extinction coefficient ε demonstrates a limiting exponential relationship.8

graphic file with name oc-2018-00728y_m001.jpg 1

In photochemical reactor design, flow chemistry has been universally identified as the solution to overcome the attenuation of light by providing reactor geometries with increased surface-area-to-volume ratios, allowing increased illumination of the reaction solution relative to conventional batch reactors.9−12 Among photochemical flow reactors, the plug flow reactor (PFR) (Figure 1) design of Booker-Milburn has been favored, composed of semitransparent tubing in combination with an array of LEDs or UV lamps.13,14 Reactors of this type have been applied across academia and industry with excellent success for gram-scale reactions.15−30 However, extension of these plug flow reactors to kilogram-scale production remains a significant challenge. One approach that has been pursued involves increasing the number of identical reactors operating in parallel, thereby increasing the overall throughput.31,32 While this approach is tenable in some circumstances, it also presents several operational and practical challenges, particularly in the highly regulated manufacture of pharmaceuticals. The other approach is to extend the length of the reactor to increase the volume/throughput, which necessitates a more elaborate lighting array. Efforts by the Stephenson group and others have demonstrated some limited scale-up with this design; however, a key challenge remains the translation of results between bench-scale reactors used for reaction optimization to production-scale reactors.27,33,34 The geometry of the lighting array and the reactor both significantly impact the performance of the reactor, and subtle changes in this geometry can lead to dramatic effects on the reactor throughput. Chemical actinometry, a method for relating the rate of reaction to the rate of photon absorption in a reactor, can correlate reactor performance across scales, but requires time, effort, and equivalent amounts of material to generate accurate calibrations.35−37 LED-based reactors are generally challenging to scale due to the diffusive emission of LEDs, which dictates they must be array arrayed in close proximity to the tubing to illuminate the reactive fluid. As a result, the heat that the LEDs generate may negatively influence the reaction, requiring additional engineering solutions at scale. In general, the engineering challenges inherent to building an LED-based tubular flow reactor capable of multikilogram throughput necessitate construction of a fixed volume reactor and a fixed light source, thereby significantly limiting the modularity and adaptability benefits of flow chemistry. After studying the scalability of plug flow photoreactors, we concluded that these reactors would not meet our adaptability requirements and accordingly directed our efforts to developing a more modular system.

Our studies indicated that higher-intensity light sources would lead to increased rates of reaction, thereby increasing throughput and yield.38 The Beer–Lambert law only dictates the fraction of incident light that is absorbed, not the total amount of light, so we reasoned that using higher-intensity light sources would increase process throughputs if coupled to an appropriately designed reactor. Our efforts to find higher-intensity monochromatic light sources led us to employ laser diodes in photochemical reactions.39 Continuous wave lasers have only been utilized in limited context within photochemistry, particularly in conjunction with microreactors, and only at low power (10–50 mW), which is comparable to the light emitted by a single common LED.40 Comparatively high-power diode lasers (up to 6 W) are readily available in common wavelengths, and we applied these lasers to a number of reactions of interest and immediately observed vastly improved rates of reaction.41 The benefits of such lasers include the ability to directly measure the output power, the relative ease of directing the light into the reaction mixture, coherence of the light, and the ability to shape the beam to fit the reactor.

We compared lasers to other light sources in relevant photochemical reactions and generated several broad observations that informed our efforts to develop a versatile platform for visible light photocatalysis.42 The most impactful observation was the universal dependence of the rate of reaction on the intensity of the light source. Similar results have also been reported by MacMillan and co-workers across a separate set of reactions.43 These combined results suggest a general trend across catalysts and transformations, which directed us to apply even higher-powered lasers.

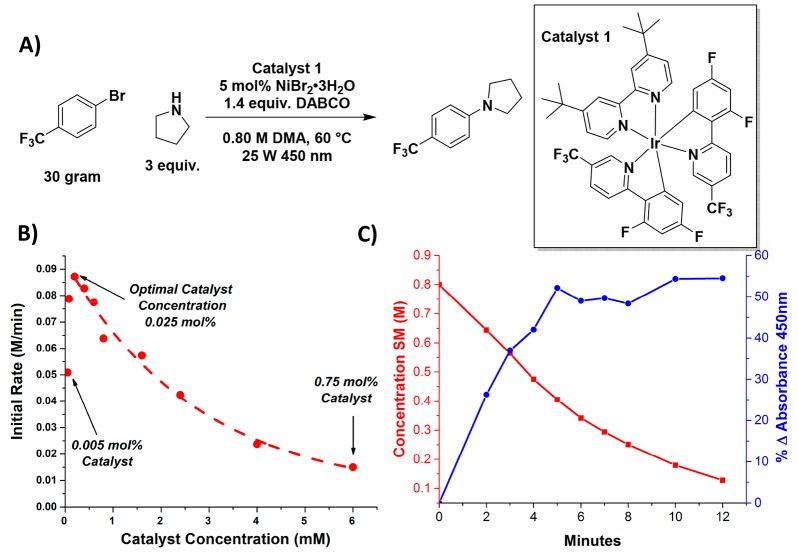
To explore the potential of higher-powered light sources, a 25 W 450 nm fiber coupled laser system was fit with an adjustable beam expander. A recently reported C–N coupling reaction was selected as a model reaction (Figure 2A) as we viewed it as representative of an increasing number of metallaphotoredox cross-coupling reactions, which are of particular interest in the pharmaceutical industry.44−53 Preliminary kinetic investigation in batch revealed apparent zero-order kinetics up to 81% conversion, followed by an apparent shift in the rate-determining step. The rate of reaction was not affected by variations in concentration of DABCO or pyrrolidine, but did depend on photocatalyst, Ni, and aryl bromide concentrations. In preparation for eventual scale-up, the optimal reaction concentration was determined to be 0.8 M in aryl bromide, beyond which DABCO–HBr salt precipitation became a limiting factor.

Figure 2.

Figure 2

Open in a new tab

(A) C–N coupling reaction used with the optimized conditions. (B) Plot of the initial rates of reaction at several different catalyst concentrations with the proposed exponential relationship shown as a dotted line. (C) Time course plot of the C–N coupling reaction showing the conversion of aryl bromide in red and the solution darkening effect in blue.

Under optimized conditions, we first examined the effect of photocatalyst concentration across two orders of magnitude (0.05–6 mM), holding the laser configuration and liquid depth (5 cm) constant while measuring the rate of reaction. Figure 2B shows the optimal catalyst concentration to be 0.2 mM (0.025 mol %) as well as two different rate behaviors around this optimal point. At concentrations lower than the optimal concentration, traditional kinetic behavior is observed, implying that catalyst quenching is the rate-limiting step. At catalyst concentrations higher than the optimal point, the rate of reaction declines exponentially, a relationship which appears to be counterintuitive to the general principles of catalysis where increased catalyst loadings should result in faster rates. However, the Beer–Lambert law states that light attenuates exponentially as the catalyst concentration (the absorbing species) increases. These differences in rates arise from variations in the effective concentration of quenching species relative to that of the excited state catalyst. At the highest catalyst concentrations, 99.9% of the incident light is absorbed at 1 cm of depth. Hence, all of the excited catalyst is contained in 20% of the total volume, but the quenching species is distributed uniformly across the entire volume, creating a lower proximal ratio of activated catalyst to quenching species (presumably the Ni-aryl species). At the optimal catalyst loading, the light penetrates to the bottom of the reactor (5 cm depth), and the optimal ratio of excited state catalyst to quencher is achieved, leading to the interesting observation that while the rate of reaction remains constant through high conversion, increasing the concentration of quencher can impact the rate. This correlation to the Beer–Lambert law can be powerfully applied to design photochemical systems where the solution depth (path length) and catalyst concentration can be adjusted relative to each other and adapted to process constraints, whether those constraints are on catalyst loading or reactor geometry. Beyond the context of the high-intensity laser, we have observed this same trend where decreasing catalyst concentration up to a certain point leads to increased rate of reaction, independent of the light source used.38,54 Indeed, at the beginning of our evaluation, the system was designed based on the Beer–Lambert law calculation for 0.05 mol % of photocatalyst to give maximum absorption at a reaction depth of 5 cm. We attribute the difference in observed catalyst concentration to that determined from the Beer–Lambert law to significant solution darkening which occurs during the reaction which is equivalent to 50% increase in absorbance at 450 nm, Figure 2C.

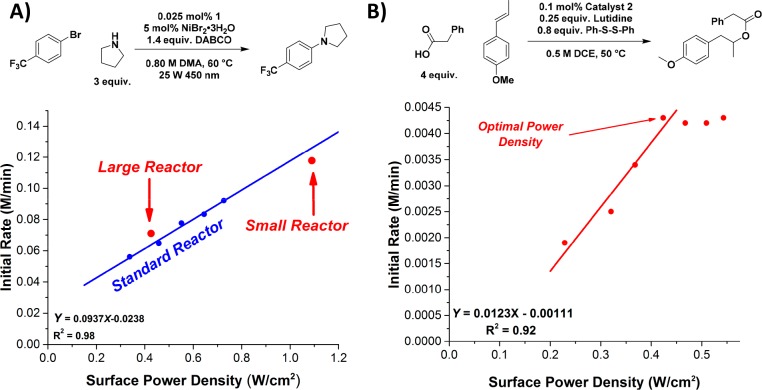
Initially surprised by this counterintuitive trend, we sought to explore the generality of this principle in other reactions. We evaluated the effect of catalyst concentration in two other reactions of interest (Figure 3). We performed these reactions at smaller scale with less powerful diode lasers and observed the same general trend where the fastest rates of these very different reactions could all be directly attributed to the concentration designed to give 99% absorbance of the incident light at the predetermined, fixed reaction depth. These combined results strongly indicate that optimal reaction performance in terms of rate is directly correlated to photocatalyst concentration which can be determined entirely from the Beer–Lambert law based on the vessel used and not the associated chemical transformation.

Figure 3.

Figure 3

Open in a new tab

(A) Initial rates as a function of catalyst concentration demonstrating a Beer–Lambert law relationship in decarboxylative C–C bond formation. (B) Initial rates as a function of catalyst concentration as another demonstration of the Beer–Lambert law in the anti-Markovnikov addition of carboxylic acids to alkenes.

This demonstration of the impact of the Beer–Lambert law on the rate of reaction led us to consider alternate flow reactor designs. The absolute molar concentrations for common photocatalysts result in complete extinction of light within millimeters of liquid depth, especially for catalysts with molar extinction coefficients orders of magnitude higher than Catalyst 1 (567 M–1 cm–1) as used in the C–N coupling.7 The extremely small extinction depth at commonly employed catalyst concentrations has led to the notion that smaller reactors with smaller cross-sections and increased surface areas are the only solution to overcoming the attenuation effect. Perhaps due to its counterintuitive nature, little consideration has been given to optimizing reactors with larger cross-sectional areas and decreased photocatalyst concentrations; however, our results suggested a reactor of this type would be ideal when coupled to a high-intensity light source.

Another key variable we explored was the effect of laser output power on the reaction rate by varying the output from 10 to 26 W. We hypothesized that, by optimizing the catalyst concentration and solution depth using the Beer–Lambert law, the reaction rate should increase as the power emitted by the laser increases as long as quenching of the excited state remains the rate-limiting step. At a depth of 5 cm, a linear relationship was observed between rate and power, which is described in terms of power density (W/cm2) (Figure 4A). This relationship is the most direct evidence that the rate-limiting step is quenching of the excited state and that quenching is limited only by concentration of catalyst in the excited state. Increasing the excited state concentration simply by bombarding the reaction with increasing numbers of photons can drive the reaction to significantly faster rates. Applied to a flow reactor, this relationship is extraordinarily powerful because it implies that the reaction throughput can only be increased by increasing both the reaction volume (as a function of surface area) and the power of the light, if the reactor depth and catalyst concentration are already optimized using the Beer–Lambert law. To test this relationship as a design principle, identical conditions were evaluated in larger and smaller diameter reactors resulting in two different power densities, while maintaining the optimal 5 cm depth. The rates were measured and compared to those predicted based on the relationship in Figure 4A. The results shown in Figure 4A clearly demonstrate the predictive power of such a relationship, with the error between the predicted and measured rates being less than 5%.

Figure 4.

Figure 4

Open in a new tab

(A) Correlation between initial rates in the C–N coupling and power density of the laser source where the standard reactor employed was 6.5 cm diameter (167 mL total volume), the large reactor was 8 cm (250 mL total volume), and the small reactor was 5 cm in diameter (100 mL). (B) Example reaction where the rate/power correlation breaks down providing an optimal power density for scale-up.

While the correlation in Figure 4A was extrapolated well outside the experimental data, theoretically, at some power density, a maximum concentration of excited catalyst must be achieved, and a corresponding shift in the rate-determining step would be indicated by a break in linearity in the power density relationship. Equipment power limitations prohibited further exploration in the C–N coupling; however, such a deviation in linearity was observed in our exploration of the anti-Markovnikov addition to alkenes reported by Nicewicz and co-workers.55−57 Performing a similar variable power experiment under the conditions shown in Figure 4B resulted in a deviation where increasing power density no longer resulted in increased rate. We interpret this deviation in linearity to indicate the maximum photon absorption rate where the rate-limiting step is no longer quenching of the excited state. This type of relationship can also inform reactor design and indicates the optimal power density where increasing the power output from the laser no longer improves throughput. Where this type of behavior is observed, the reactor size can be increased as long as this power density is maintained, providing increased throughput.

With these fundamental studies as guides, the optimal flow reactor was designed to implement the high-powered laser as the light source. However, to incorporate the laser as a light source and to take advantage of the concepts detailed above, a CSTR became an obvious choice. CSTRs are better suited to handling solids as opposed to tubular or plug flow reactors. Most importantly, a simple CSTR design enables the easy adaptation of our laser light source and provides modularity in reaction vessel choice, enabling the use of common laboratory equipment. For the optimized C–N coupling reaction (Figure 5A), the smaller diameter vessel (100 mL reactor) which was employed in the power density studies in Figure 4A was modified into a CSTR. Using a simple CSTR design, the depth of the reactor could be controlled at 5 cm by the reactor outlet, the optimal depth based on the Beer–Lambert law for our desired catalyst concentration.

Figure 5.

Figure 5

Open in a new tab

(A) Optimized reaction conditions determined for 1.85 kg flow reaction. (B) Kinetic time course for the reaction conditions shown in part A in a 100 mL vessel. (C) Levenspiel analysis of the reaction kinetics from part B. (D) Schematic of the CSTR used in the flow reaction.

With the volume of the CSTR set, it was necessary to determine the residence time to achieve the desired conversion. Familiar to chemical engineers, Levenspiel plots are a graphical method for determining the necessary volume or residence time of a chemical reactor based on the kinetics of the reaction. Levenspiel plots are convenient for designing CSTRs and PFRs because they are constructed from laboratory kinetic data, do not require complete rate expression(s), and allow for simple visualization of different combinations of reactors in series. The residence time is the volume of the reactor divided by the flow rate, so setting the volume required determining the residence time using a Levenspiel plot. Under the optimized conditions shown in Figure 5A and in a 100 mL reactor demonstrated in Figure 4A, we collected the kinetic time course data shown in Figure 5B. The residence time then was determined easily from the Levenspiel plot shown in Figure 5C. We desired a conversion of 90%, balancing throughput with ease of workup and isolation of the product, in the CSTR. From the Levenspiel plot shown in Figure 5C (blue dashed box), this conversion corresponded to a residence time of 20 min, giving a flow rate of 5 mL/min.58,59

The CSTR described above was run for a total of 32 h at steady-state (Figure 5D). The system proved remarkably stable with the laser giving precise power output over the entire course of operation. In total, 1.85 kg of aryl bromide was processed, achieving 89% conversion at steady-state, which corresponded nicely with the projected output given by the Levenspiel analysis. Isolation of the product produced 1.54 kg, corresponding to a throughput of 1.2 kg/day and 85% adjusted yield with >99% purity. Remarkably, this excellent throughput was achieved in a 100 mL reactor in a common fumehood and required only 2.22 g of photocatalyst. Inspection of the reactor after run completion revealed a fine precipitation or coating of the reactor walls. This minor fouling did not affect the measurable reactor performance. However, such fouling is commonly observed in tubular flow reactors where it leads to decreased reactor performance by blocking the light.

Overall, the modular design of the laser CSTR lends itself to facile scalability and flexibility. Limitations in our equipment prevented us from applying a multistage CSTR; however, our Levenspiel analysis of the reaction kinetics allows us to project a system of two cascading CSTRs (Figure 5C, red dashed boxes) requiring two 25 W lasers that would be capable of the same 90% conversion end point and 3.9 kg/day throughput, more than three times the throughput of a single CSTR operating at the same end point.60 Similarly, higher-powered lasers could also be applied in the same system to give even greater throughput, providing a clear path forward for commercialization of photochemical processes that use visible light. Use of a fiber coupled laser allows reactor configuration flexibility, enabling gas–liquid flow and subzero reaction temperatures. Perhaps more importantly, through the application of lasers, the key relationship between light source and reaction rate can be determined, providing the foundation for successful scale-up.

Acknowledgments

The authors would like to thank Anuj Verma, Steve Richter, Moiz Diwan, Travis Dunn, Michael Tudesco, Andrew Radosevich, Jeffrey Kallemeyn, Jianguo Ji, Shashank Shekhar, Elizabeth Swift, David Barnes, Dennie Welch, Nathan Ide, Dan Tao, and Patrick Brady for helpful discussions and preparing the manuscript. The authors declare no competing financial interests. The design, study conduct, and financial support for this research were provided by AbbVie. AbbVie participated in the interpretation of data, writing, reviewing, and approving the publication. K.C.H., E.G.M., and S.V.B. are AbbVie employees. All data is available in the main text or the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00728.

  • Information about reactor setups, background experiments, full kinetic data, experimental details, and a tutorial guide for Levenspiel analysis (PDF)

Author Contributions

K.C.H. and E.G.M designed and executed the research and contributed equally to the work. S.V.B. and S.J.W. supervised the research.

The authors declare no competing financial interest.

Notes

Safety statement: the lasers used to generate the data described in this manuscript were Class IV lasers, and appropriate safety precautions were taken. See the Supporting Information for more details regarding their safe use.

Supplementary Material

oc8b00728_si_001.pdf (708.1KB, pdf)

References

  1. Shaw M. H.; Twilton J.; MacMillan D. W. C. Photoredox Catalysis in Organic Chemistry. J. Org. Chem. 2016, 81 (16), 6898–6926. 10.1021/acs.joc.6b01449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Twilton J.; Le C.; Zhang P.; Shaw M. H.; Evans R. W.; MacMillan D. W. C. The merger of transition metal and photocatalysis. Nature Reviews Chemistry 2017, 1, 0052. 10.1038/s41570-017-0052. [DOI] [Google Scholar]
  3. Kärkäs M. D.; Porco J. A.; Stephenson C. R. J. Photochemical Approaches to Complex Chemotypes: Applications in Natural Product Synthesis. Chem. Rev. 2016, 116 (17), 9683–9747. 10.1021/acs.chemrev.5b00760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Romero N. A.; Nicewicz D. A. Organic Photoredox Catalysis. Chem. Rev. 2016, 116 (17), 10075–10166. 10.1021/acs.chemrev.6b00057. [DOI] [PubMed] [Google Scholar]
  5. Prier C. K.; Rankic D. A.; MacMillan D. W. C. Visible Light Photoredox Catalysis with Transition Metal Complexes: Applications in Organic Synthesis. Chem. Rev. 2013, 113 (7), 5322–5363. 10.1021/cr300503r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Skubi K. L.; Blum T. R.; Yoon T. P. Dual Catalysis Strategies in Photochemical Synthesis. Chem. Rev. 2016, 116 (17), 10035–10074. 10.1021/acs.chemrev.6b00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Teegardin K.; Day J. I.; Chan J.; Weaver J. Advances in Photocatalysis: A Microreview of Visible Light Mediated Ruthenium and Iridium Catalyzed Organic Transformations. Org. Process Res. Dev. 2016, 20 (7), 1156–1163. 10.1021/acs.oprd.6b00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. See the Supporting Materials for a detailed derivation.
  9. Garlets Z. J.; Nguyen J. D.; Stephenson C. R. J. The Development of Visible-Light Photoredox Catalysis in Flow. Isr. J. Chem. 2014, 54 (4), 351–360. 10.1002/ijch.201300136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cambié D.; Bottecchia C.; Straathof N. J. W.; Hessel V.; Noël T. Applications of Continuous-Flow Photochemistry in Organic Synthesis, Material Science, and Water Treatment. Chem. Rev. 2016, 116 (17), 10276–10341. 10.1021/acs.chemrev.5b00707. [DOI] [PubMed] [Google Scholar]
  11. Plutschack M. B.; Pieber B.; Gilmore K.; Seeberger P. H. The Hitchhiker’s Guide to Flow Chemistry. Chem. Rev. 2017, 117 (18), 11796–11893. 10.1021/acs.chemrev.7b00183. [DOI] [PubMed] [Google Scholar]
  12. Su Y.; Straathof N. J. W.; Hessel V.; Noël T. Photochemical Transformations Accelerated in Continuous-Flow Reactors: Basic Concepts and Applications. Chem. - Eur. J. 2014, 20 (34), 10562–10589. 10.1002/chem.201400283. [DOI] [PubMed] [Google Scholar]
  13. Hook B. D. A.; Dohle W.; Hirst P. R.; Pickworth M.; Berry M. B.; Booker-Milburn K. I. A Practical Flow Reactor for Continuous Organic Photochemistry. J. Org. Chem. 2005, 70 (19), 7558–7564. 10.1021/jo050705p. [DOI] [PubMed] [Google Scholar]
  14. Bou-Hamdan F. R.; Seeberger P. H. Visible-light-mediated photochemistry: accelerating Ru(bpy)32+-catalyzed reactions in continuous flow. Chemical Science 2012, 3 (5), 1612–1616. 10.1039/c2sc01016j. [DOI] [Google Scholar]
  15. Tucker J. W.; Zhang Y.; Jamison T. F.; Stephenson C. R. J. Visible-Light Photoredox Catalysis in Flow. Angew. Chem., Int. Ed. 2012, 51 (17), 4144–4147. 10.1002/anie.201200961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Beatty J. W.; Stephenson C. R. J. Synthesis of (−)-Pseudotabersonine, (−)-Pseudovincadifformine, and (+)-Coronaridine Enabled by Photoredox Catalysis in Flow. J. Am. Chem. Soc. 2014, 136 (29), 10270–10273. 10.1021/ja506170g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Elliott L. D.; Berry M.; Harji B.; Klauber D.; Leonard J.; Booker-Milburn K. I. A Small-Footprint, High-Capacity Flow Reactor for UV Photochemical Synthesis on the Kilogram Scale. Org. Process Res. Dev. 2016, 20 (10), 1806–1811. 10.1021/acs.oprd.6b00277. [DOI] [Google Scholar]
  18. Baumann M.; Baxendale I. R. Continuous photochemistry: the flow synthesis of ibuprofen via a photo-Favorskii rearrangement. Reaction Chemistry & Engineering 2016, 1 (2), 147–150. 10.1039/C5RE00037H. [DOI] [Google Scholar]
  19. Abdiaj I.; Alcázar J. Improving the throughput of batch photochemical reactions using flow: Dual photoredox and nickel catalysis in flow for C(sp2)C(sp3) cross-coupling. Bioorg. Med. Chem. 2017, 25 (23), 6190–6196. 10.1016/j.bmc.2016.12.041. [DOI] [PubMed] [Google Scholar]
  20. Hughes D. L. Applications of Flow Chemistry in Drug Development: Highlights of Recent Patent Literature. Org. Process Res. Dev. 2018, 22 (1), 13–20. 10.1021/acs.oprd.7b00363. [DOI] [Google Scholar]
  21. Lima F.; Kabeshov M. A.; Tran D. N.; Battilocchio C.; Sedelmeier J.; Sedelmeier G.; Schenkel B.; Ley S. V. Visible Light Activation of Boronic Esters Enables Efficient Photoredox C(sp2)–C(sp3) Cross-Couplings in Flow. Angew. Chem., Int. Ed. 2016, 55 (45), 14085–14089. 10.1002/anie.201605548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Guerra J.; Cantillo D.; Kappe C. O. Visible-light photoredox catalysis using a macromolecular ruthenium complex: reactivity and recovery by size-exclusion nanofiltration in continuous flow. Catal. Sci. Technol. 2016, 6 (13), 4695–4699. 10.1039/C6CY00070C. [DOI] [Google Scholar]
  23. Cantillo D.; de Frutos O.; Rincón J. A.; Mateos C.; Kappe C. O. A Continuous-Flow Protocol for Light-Induced Benzylic Fluorinations. J. Org. Chem. 2014, 79 (17), 8486–8490. 10.1021/jo5016757. [DOI] [PubMed] [Google Scholar]
  24. Rueping M.; Vila C. Visible Light Photoredox-Catalyzed Multicomponent Reactions. Org. Lett. 2013, 15 (9), 2092–2095. 10.1021/ol400317v. [DOI] [PubMed] [Google Scholar]
  25. Palaychuk N.; DeLano T. J.; Boyd M. J.; Green J.; Bandarage U. K. Synthesis of Cycloalkyl Substituted 7-Azaindoles via Photoredox Nickel Dual Catalytic Cross-Coupling in Batch and Continuous Flow. Org. Lett. 2016, 18 (23), 6180–6183. 10.1021/acs.orglett.6b03223. [DOI] [PubMed] [Google Scholar]
  26. DeLano T. J.; Bandarage U. K.; Palaychuk N.; Green J.; Boyd M. J. Application of the Photoredox Coupling of Trifluoroborates and Aryl Bromides to Analog Generation Using Continuous Flow. J. Org. Chem. 2016, 81 (24), 12525–12531. 10.1021/acs.joc.6b02408. [DOI] [PubMed] [Google Scholar]
  27. Yayla H. G.; Peng F.; Mangion I. K.; McLaughlin M.; Campeau L.-C.; Davies I. W.; DiRocco D. A.; Knowles R. R. Discovery and mechanistic study of a photocatalytic indoline dehydrogenation for the synthesis of elbasvir. Chemical Science 2016, 7 (3), 2066–2073. 10.1039/C5SC03350K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Halperin S. D.; Kwon D.; Holmes M.; Regalado E. L.; Campeau L.-C.; DiRocco D. A.; Britton R. Development of a Direct Photocatalytic C–H Fluorination for the Preparative Synthesis of Odanacatib. Org. Lett. 2015, 17 (21), 5200–5203. 10.1021/acs.orglett.5b02532. [DOI] [PubMed] [Google Scholar]
  29. Rackl D.; Kreitmeier P.; Reiser O. Synthesis of a polyisobutylene-tagged fac-Ir(ppy)3 complex and its application as recyclable visible-light photocatalyst in a continuous flow process. Green Chem. 2016, 18 (1), 214–219. 10.1039/C5GC01792K. [DOI] [Google Scholar]
  30. Turconi J.; Griolet F.; Guevel R.; Oddon G.; Villa R.; Geatti A.; Hvala M.; Rossen K.; Göller R.; Burgard A. Semisynthetic Artemisinin, the Chemical Path to Industrial Production. Org. Process Res. Dev. 2014, 18 (3), 417–422. 10.1021/op4003196. [DOI] [Google Scholar]
  31. Su Y.; Kuijpers K.; Hessel V.; Noel T. A convenient numbering-up strategy for the scale-up of gas-liquid photoredox catalysis in flow. Reaction Chemistry & Engineering 2016, 1 (1), 73–81. 10.1039/C5RE00021A. [DOI] [Google Scholar]
  32. Zhao F.; Cambié D.; Janse J.; Wieland E. W.; Kuijpers K. P. L.; Hessel V.; Debije M. G.; Noël T. Scale-up of a Luminescent Solar Concentrator-Based Photomicroreactor via Numbering-up. ACS Sustainable Chem. Eng. 2018, 6 (1), 422–429. 10.1021/acssuschemeng.7b02687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Beatty J. W.; Douglas J. J.; Miller R.; McAtee R. C.; Cole K. P.; Stephenson C. R. J. Photochemical Perfluoroalkylation with Pyridine N-Oxides: Mechanistic Insights and Performance on a Kilogram Scale. Chem. 2016, 1 (3), 456–472. 10.1016/j.chempr.2016.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Elliott L. D.; Knowles J. P.; Stacey C. S.; Klauber D. J.; Booker-Milburn K. I. Using batch reactor results to calculate optimal flow rates for the scale-up of UV photochemical reactions. Reaction Chemistry & Engineering 2018, 3 (1), 86–93. 10.1039/C7RE00193B. [DOI] [Google Scholar]
  35. Hsieh H.-W.; Coley C. W.; Baumgartner L. M.; Jensen K. F.; Robinson R. I. Photoredox Iridium–Nickel Dual-Catalyzed Decarboxylative Arylation Cross-Coupling: From Batch to Continuous Flow via Self-Optimizing Segmented Flow Reactor. Org. Process Res. Dev. 2018, 22 (4), 542–550. 10.1021/acs.oprd.8b00018. [DOI] [Google Scholar]
  36. Noël T. A personal perspective on the future of flow photochemistry. J. Flow Chem. 2017, 7 (3–4), 87–93. 10.1556/1846.2017.00022. [DOI] [Google Scholar]
  37. McCallum T.; Pitre S. P.; Morin M.; Scaiano J. C.; Barriault L. The photochemical alkylation and reduction of heteroarenes. Chemical Science 2017, 8 (11), 7412–7418. 10.1039/C7SC03768F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Moschetta E. G.; Richter S. M.; Wittenberger S. J. Heuristics, Protocol, and Considerations for Flow Chemistry in Photoredox Catalysis. ChemPhotoChem. 2017, 1 (12), 539–543. 10.1002/cptc.201700128. [DOI] [Google Scholar]
  39. Please see the Supporting Information for a discussion about laser safety.
  40. Naumann R.; Kerzig C.; Goez M. Laboratory-scale photoredox catalysis using hydrated electrons sustainably generated with a single green laser. Chemical Science 2017, 8 (11), 7510–7520. 10.1039/C7SC03514D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. The wattages reported in this manuscript refer to output wattages as measured from an appropriate power meter in contrast to the more commonly reported input wattages.
  42. Unpublished results compared rates of various reactions using laser diodes, LEDs, and CFLs and guided the published research.
  43. Le C. C.; Wismer M. K.; Shi Z.-C.; Zhang R.; Conway D. V.; Li G.; Vachal P.; Davies I. W.; MacMillan D. W. C. A General Small-Scale Reactor To Enable Standardization and Acceleration of Photocatalytic Reactions. ACS Cent. Sci. 2017, 3 (6), 647–653. 10.1021/acscentsci.7b00159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Corcoran E. B.; Pirnot M. T.; Lin S.; Dreher S. D.; DiRocco D. A.; Davies I. W.; Buchwald S. L.; MacMillan D. W. C. Aryl amination using ligand-free Ni(II) salts and photoredox catalysis. Science 2016, 353 (6296), 279–283. 10.1126/science.aag0209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tellis J. C.; Primer D. N.; Molander G. A. Single-electron transmetalation in organoboron cross-coupling by photoredox/nickel dual catalysis. Science 2014, 345 (6195), 433–436. 10.1126/science.1253647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Heitz D. R.; Tellis J. C.; Molander G. A. Photochemical Nickel-Catalyzed C–H Arylation: Synthetic Scope and Mechanistic Investigations. J. Am. Chem. Soc. 2016, 138 (39), 12715–12718. 10.1021/jacs.6b04789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tellis J. C.; Kelly C. B.; Primer D. N.; Jouffroy M.; Patel N. R.; Molander G. A. Single-Electron Transmetalation via Photoredox/Nickel Dual Catalysis: Unlocking a New Paradigm for sp3–sp2 Cross-Coupling. Acc. Chem. Res. 2016, 49 (7), 1429–1439. 10.1021/acs.accounts.6b00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Lin K.; Wiles R. J.; Kelly C. B.; Davies G. H. M.; Molander G. A. Haloselective Cross-Coupling via Ni/Photoredox Dual Catalysis. ACS Catal. 2017, 7 (8), 5129–5133. 10.1021/acscatal.7b01773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Primer D. N.; Molander G. A. Enabling the Cross-Coupling of Tertiary Organoboron Nucleophiles through Radical-Mediated Alkyl Transfer. J. Am. Chem. Soc. 2017, 139 (29), 9847–9850. 10.1021/jacs.7b06288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Ahn J. M.; Peters J. C.; Fu G. C. Design of a Photoredox Catalyst that Enables the Direct Synthesis of Carbamate-Protected Primary Amines via Photoinduced, Copper-Catalyzed N-Alkylation Reactions of Unactivated Secondary Halides. J. Am. Chem. Soc. 2017, 139 (49), 18101–18106. 10.1021/jacs.7b10907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zhao W.; Wurz R. P.; Peters J. C.; Fu G. C. Photoinduced, Copper-Catalyzed Decarboxylative C–N Coupling to Generate Protected Amines: An Alternative to the Curtius Rearrangement. J. Am. Chem. Soc. 2017, 139 (35), 12153–12156. 10.1021/jacs.7b07546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zuo Z.; Ahneman D. T.; Chu L.; Terrett J. A.; Doyle A. G.; MacMillan D. W. C. Merging photoredox with nickel catalysis: Coupling of α-carboxyl sp3-carbons with aryl halides. Science 2014, 345 (6195), 437–440. 10.1126/science.1255525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Kalyani D.; McMurtrey K. B.; Neufeldt S. R.; Sanford M. S. Room-Temperature C–H Arylation: Merger of Pd-Catalyzed C–H Functionalization and Visible-Light Photocatalysis. J. Am. Chem. Soc. 2011, 133 (46), 18566–18569. 10.1021/ja208068w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Andrews R. S.; Becker J. J.; Gagné M. R. A Photoflow Reactor for the Continuous Photoredox-Mediated Synthesis of C-Glycoamino Acids and C-Glycolipids. Angew. Chem., Int. Ed. 2012, 51 (17), 4140–4143. 10.1002/anie.201200593. [DOI] [PubMed] [Google Scholar]
  55. Perkowski A. J.; Nicewicz D. A. Direct Catalytic Anti-Markovnikov Addition of Carboxylic Acids to Alkenes. J. Am. Chem. Soc. 2013, 135 (28), 10334–10337. 10.1021/ja4057294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Romero N. A.; Nicewicz D. A. Mechanistic Insight into the Photoredox Catalysis of Anti-Markovnikov Alkene Hydrofunctionalization Reactions. J. Am. Chem. Soc. 2014, 136 (49), 17024–17035. 10.1021/ja506228u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Margrey K. A.; Nicewicz D. A. A General Approach to Catalytic Alkene Anti-Markovnikov Hydrofunctionalization Reactions via Acridinium Photoredox Catalysis. Acc. Chem. Res. 2016, 49 (9), 1997–2006. 10.1021/acs.accounts.6b00304. [DOI] [PubMed] [Google Scholar]
  58. See the Supporting Information for a detailed discussion of how this analysis was performed.
  59. Levenspiel O.Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, 1998; p 688. [Google Scholar]
  60. See the Supporting Information for a full discussion and calculations.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc8b00728_si_001.pdf (708.1KB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES