Abstract
The full configuration interaction (full-CI) method is capable of providing the numerically best wave functions and energies of atoms and molecules within basis sets being used, although it is intractable for classical computers. Quantum computers can perform full-CI calculations in polynomial time against the system size by adopting a quantum phase estimation algorithm (QPEA). In the QPEA, the preparation of initial guess wave functions having sufficiently large overlap with the exact wave function is recommended. The Hartree–Fock (HF) wave function is a good initial guess only for closed shell singlet molecules and high-spin molecules carrying no spin-β unpaired electrons, around their equilibrium geometry, and thus, the construction of multiconfigurational wave functions without performing post-HF calculations on classical computers is highly desired for applying the method to a wide variety of chemistries and physics. In this work, we propose a method to construct multiconfigurational initial guess wave functions suitable for QPEA-based full-CI calculations on quantum computers, by utilizing diradical characters computed from spin-projected UHF wave functions. The proposed approach drastically improves the wave function overlap, particularly in molecules with intermediate diradical characters.
Short abstract
Diradical characters enable us to efficiently construct multiconfigurational wave functions suitable for the initial guess of full configuration interaction calculations on quantum computers.
1. Introduction
Quantum computing and quantum information processing (QC/QIP) is one of the most innovative research fields not only in computer and information sciences, but also in interdisciplinary areas among physics, mathematics, chemistry, materials science, and so on. The appearance of a quantum computer processor consisting of 72 quantum bits (qubits) from Google LLC reminds us that it is close to “quantum supremacy”,1 and intercontinental quantum communications between China and Austria have been demonstrated very recently.2 Among the diverse subjects in QC/QIP, quantum simulation of electronic structure problems of atoms and molecules is one of the most intensively studied realms.3−53 Studies on quantum simulations of quantum chemical objects can date back to the first proposal of quantum computers by Feynman in the early 1980s.54 Feynman suggested that the computer built of quantum mechanical elements obeying quantum mechanical laws has an ability to simulate other quantum systems efficiently. Quantum computers use qubits as the minimum unit of information.55 Qubits provide any arbitrary superposition of their two basis states; c0|0⟩ + c1|1⟩, where |0⟩ and |1⟩ represent the bases of the quantum states in the Dirac’s bra-ket notation, while classical bits can have only one of two values: either 0 or 1. From the viewpoint of practical applications of quantum computing, those to quantum chemistry are of significant importance, and the implementation of quantum algorithms to empower quantum chemistry is the focus of the applications in QC/QIP.
An approach to calculate the full configuration interaction (full-CI) energy of atoms and molecules, which is the variationally best possible energy within a given basis set, was proposed by Aspuru-Guzik and co-workers in 2005,3 and the first experimental demonstrations of the full-CI/STO-3G calculations of the H2 molecule were reported by using photonic and NMR quantum computers in 2010.8,9 Computational time of the full-CI on classical computers scales exponentially against the system size, and it is an intractable problem to deal with even small molecules; however, time scaling becomes polynomial on quantum computers. The approach is based on the quantum phase estimation algorithm (QPEA) proposed by Abrams and Lloyd,56 and it relies on projective measurements with an electronic Hamiltonian H: Measurement projects an initially prepared quantum state onto the eigenstate of a given Hamiltonian, and the probability to obtain a particular outcome is proportional to the square of overlap between the prepared wave function and corresponding eigenfunction. In this context, importance of the preparation of good initial guess wave functions having sufficiently large overlap with the particular eigenstate cannot be overemphasized.
The most important electronic state in chemistry is an electronic ground state. A Hartree–Fock (HF) wave function |ΨHF⟩, which is approximated to the single Slater determinant, is usually a good initial guess for typical closed shell singlet molecules and high-spin open shell systems carrying no unpaired electrons of spin-β, around their equilibrium geometry. However, it is well-known that the restricted Hartree–Fock (RHF) method cannot describe potential energy curve associated with covalent bond cleavage correctly. Single bond dissociation creates a spin-singlet diradical, in which the wave function is represented by a linear combination of two Slater determinants.59 The number of Slater determinants required to represent a low-spin multiradical wave function increases exponentially against the number of unpaired electrons and those of spin-β,60 and the overlap between the Slater determinant and the exact wave function decays exponentially. This means that we have to carry out QPEA experiments an exponential number of times to capture a correct ground state by using a single Slater determinant as the initial guess, which spoils advantages of quantum speedup. The overlap between the initial guess and exact wave functions can be improved systematically by adopting more sophisticated wave functions like complete active space self-consistent field (CASSCF)43 and adaptive sampling CI (ASCI),45 or by using adiabatic state preparation (ASP) techniques3,9,44 starting from HF wave functions. ASP can generate a full-CI wave function starting from a HF wave function based on the adiabatic theorem, by slowly changing the system Hamiltonian from HF to full-CI. However, these approaches require time-consuming calculations on classical and quantum computers, respectively, and therefore, it is preferable to develop theoretical approaches to improve wave functions without performing post-HF calculations.
Recently, we investigated the “overlap catastrophe” in open shell systems based on the spin symmetry.49,50 Origin of the overlap decay in open shell systems is the symmetry requirement from S2 operators. In previous papers, we reported that the wave function consisting of one spin symmetry-adapted configuration state function (CSF) has large overlap with the full-CI wave function of the ground state in open shell molecules, and proposed quantum circuits to prepare CSF on quantum registers in polynomial time.49,50
CSF is a linear combination of Slater determinants to become an eigenfunction of the S2 operator (hereafter denoted as a spin eigenfunction).60 By making use of spin eigenfunctions one issue on the “overlap catastrophe” inherent in open shell systems can be solved. However, the previous study focused on single CSF’s, and it is just a starting point. In fact, as discussed below in detail, the overlap with the exact wave function of the ground state and one CSF as well as RHF becomes small at intermediate bond regions. It is highly desirable to develop a method to construct multiconfigurational wave functions without performing time-consuming computations on both classical and quantum computers. In this work, we propose a method to construct multiconfigurational wave functions having large overlap with the exact ground state on quantum registers, by making use of diradical characters61−64 calculated from spin-unrestricted HF (UHF) wave functions with spin projections. Importantly, a diradical character is a measure of open shell nature, and it can be calculated from the occupation number of natural orbitals. Thus, we utilize diradical characters to estimate weights of open shell electronic configurations. Applications of the proposed method to covalent bond dissociations in H2, ethane (C2H6), ethylene (C2H4), and acetylene (C2H2), and the electronic ground state of phenylene-1,4-dinitrene as an important chemical entity, will be given.
2. Theory
2.1. Diradical Characters
Let us consider a potential energy curve of the H2 molecule as an example of the covalent bond dissociation of closed shell singlet molecules. Interactions between 1s orbitals of two hydrogen atoms generate bonding (1σg) and antibonding (1σu) orbitals. At the geometry close to its equilibrium, an electronic configuration for which two electrons occupy the 1σg orbital dominantly contributes to the full-CI wave function of the ground state, and therefore the RHF wave function has a large overlap with the full-CI wave function. As the H···H distance increases, the orbital energy difference between 1σg and 1σu decreases, and the weight of the two-electron excited configuration (1σg)0(1σu)2 increases. At the dissociation limit, the system is regarded as two hydrogen atoms, and the full-CI wave function is approximated by the following wave function in the canonical orbital basis:
| 1 |
Two numbers in the ket represent the occupation numbers of 1σg and 1σu orbitals, respectively. For example, |20⟩ represents the determinant that the 1σg orbital is doubly occupied while the 1σu orbital is unoccupied, namely, RHF configuration. In the localized orbital basis, the wave function is expressed as in eq 2, which corresponds to one CSF.
| 2 |
Here, eq 2 indicates that the molecular orbital is singly occupied by a spin-α and β electron, respectively. The Slater determinant appearing in eq 2 is not a spin eigenfunction, but a linear combination of spin-triplet and singlet wave functions of MS = 0. Because the determinant |αβ⟩ breaks both spatial and spin symmetries, the single determinant wave function carrying spin-β unpaired electrons in the localized orbital basis is termed a broken-symmetry (BS) wave function.63
At the intermediate H···H distance the wave function is approximated as in eq 3.
| 3 |
Here, C1 > C2 and C12 + C22 = 1. This wave function is expressed by the linear combinations of RHF (|20⟩) and open shell singlet diradical (given in eq 1) configurations. The coefficients C1 and C2 change continuously along the potential energy curve, depending on the open shell characters. In quantum chemistry, the open shell characters can be measured by diradical characters denoted by yi (0 ≤ yi ≤ 1, i = 0, 1, 2, ...). The diradical characters yi can be calculated from the occupation number of the lowest unoccupied natural orbital (LUNO) + i, which is equal to twice the weight of the doubly excited configuration from HOMO – i to LUMO + i in the perfect pairing double excitation CI scheme. In closed shell singlet states, a diradical character y0 = 0, and for pure open shell states like the dissociation limit of H2, y0 becomes unity. At intermediate bond regions y0 is between 0 and 1. Diradical characters have attracted attention in the theoretical design for organic nonlinear optical (NLO) and singlet fission molecular systems.65−69 The diradical characters can be calculated from UHF wave functions, but UHF wave functions suffer from unwilling contributions from higher spin multiplicities, which are known as spin contaminations. Therefore, the spin projection procedure is important. The diradical characters at the spin-projected UHF (PUHF) level (yiPUHF) can be calculated using eq 4.62,63
| 4 |
Here, nLUNO+i represents the occupation number of the LUNO + i natural orbital.
2.2. Quantum Chemical Calculations on Quantum Computers
The approach to perform full-CI calculations on quantum computers developed by Aspuru-Guzik and co-workers3 is based on the quantum phase estimation algorithm (QPEA) proposed by Abrams and Lloyd:56 Time evolution of a wave function |Ψ⟩ is conditionally simulated with a unitary operator U = exp(−iHt) (controlled-U; ctrl-U) as given in eq 5, and the energy eigenvalue E is read out as a phase difference ϕ between |0⟩ and |1⟩ using an inverse quantum Fourier transformation.
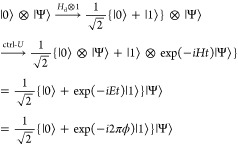 |
5 |
where Hd denotes a Hadamard transformation, and it generates the superposition state {|0⟩ + |1⟩}/√2 from |0⟩. Importantly, the QPEA utilizes projective measurements with an electronic Hamiltonian H to readout the eigenenergy, and therefore, the preparation of good initial guess wave functions having sufficiently large overlap with the particular eigenstate is essential.
The QPEA-based full-CI initially scales O(Norb11) in the upper bound (O(Norb9) in the empirical base),26 where Norb denotes the number of spin orbitals, but currently the gate scaling is reduced to be Õ(η2Norb3t) and Õ(Norb5t) for Gaussian orbitals with first- and second-quantized representations, respectively,29,32 by adopting qubitization57 or truncated Taylor series techniques,58 on-the-fly computations of molecular integrals, and so on. Here, O indicates an asymptotic upper bound and Õ represents an asymptotic upper bound suppressing polylogarithmic factors, and η is a number of electrons.
To perform quantum simulations of atoms and molecules on quantum computers, information on electronic wave functions should be mapped onto quantum registers. Several approaches for wave function mapping were proposed,3,36,37,40 and the most fundamental one is a direct mapping (DM).3 In the DM, each qubit represents the occupation number of a particular spin orbital (|1⟩ if the spin orbital is occupied, otherwise |0⟩), and requires Norb of qubits (Norb is the number of spin orbitals). In this work, we construct a quantum circuit in the DM representation.
It should be noted that the classical–quantum hybrid system known as a variational quantum eigensolver (VQE) has attracted attention as near-future applications of quantum computers for quantum chemical problems.13−22 In VQE, the wave function is generated by applying a unitary operator U(θ) to an initial guess wave function, and the energy expectation value of the prepared wave function is calculated using quantum computers; then, the parameters θ in the unitary operator are variationally optimized on classical computers to minimize the energy expectation value. VQE-based molecular energy calculations were experimentally implemented using photonic systems,13 superconducting circuits,15,20,21 and trapped ion systems,19,22 exemplifying the error-resilient nature of the calculations.
2.3. Preparation of Multiconfigurational Wave Functions on Quantum Registers
As discussed above, the wave function of the molecules having intermediate diradical characters have multiconfigurational characters, and in such cases neither RHF nor CSF has sufficiently large overlap with the full-CI root. The construction of the multiconfigurational wave function by making an appropriate linear combination of closed shell and open shell wave functions is a straightforward solution to improve the overlap. For the construction of multiconfigurational wave functions, a method to estimate expansion coefficients of individual Slater determinants (or CSFs) is required. In this study, we utilized diradical characters for this purpose. From the definitions of diradical characters given in Section 2.1, we can calculate yi from approximated wave functions like UHF and use them to estimate the weights of closed shell and open shell electronic configurations in the CI expansion.
Our strategy is as follows: (I) perform a BS-UHF calculation, (II) diagonalize one-particle density matrix to generate natural orbitals, (III) determine spin-projected diradical characters yi using eq 4, and (IV) construct a multiconfigurational wave function using an assumption given in eq 6:
| 6 |
Here, |φ(CSS)⟩ and |φ(OSS)⟩ represent closed shell singlet and open shell singlet wave functions, respectively. By using natural orbitals as the basis of the wave function expansion and applying eq 1, the following equation can be obtained.
| 7 |
Equation 7 is equivalent to the definition of diradical characters in the perfect pairing double excitation CI scheme. For tetraradical systems, the wave function is approximated as follows:
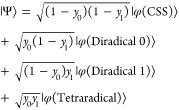 |
8 |
Here, |φ (Diradical 0)⟩ stands for the configuration having an open shell singlet character for HONO–LUNO pair whereas (HONO – 1)–(LUNO + 1) has a closed shell singlet character. In a similar way to eq 8, multiconfigurational wave functions for hexa- and higher-radical characters can be readily constructed.
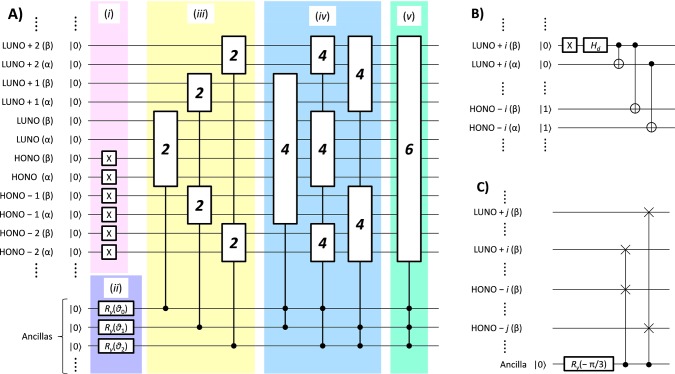
A quantum circuit to prepare the multiconfigurational wave function is illustrated in Figure 1. In Figure 1, each horizontal line corresponds to a qubit, and quantum gates depicted by squares, circles, and vertical lines are applied in left-to-right order. The circuit contains ancilla qubits, which keep information on diradical characters yi, in addition to Norb of qubits used for DM. The number of the ancilla qubits equals that of the diradical characters considered in the wave function preparation.
Figure 1.
A quantum circuit for the construction of multiconfigurational wave functions on quantum registers. (A) The quantum circuit consists of the following steps as indicated by roman numbers and background colors. (i) Generation of the RHF configuration, (ii) ancilla qubit rotation with an angle θi, (iii) diradical configuration generations, (iv) tetraradical configuration generations, (v) hexaradical configuration generations, and so on. Detailed quantum circuits for the di-, and tetraradical configuration generations are given in parts B and C, respectively. We draw the full circles if the controlled operation is applied when the control qubit is |1⟩. Wave functions of more extended spin systems can be constructed systematically expanding the circuit. (B) Quantum circuit for the preparation of diradical configurations specified 2 in part A. (C) Quantum circuit for the preparation of tetraradical configurations specified 4 in part A.
The quantum circuit starts RHF configuration preparation (specified i in Figure 1A). This step consists of NOT operations (denoted by X) to the qubits representing occupied orbitals to change the qubit states from |0⟩ to |1⟩. The second step (ii) is rotations applied to the ancilla qubits with the rotating angle θi depending on diradical characters yi:
| 9 |
| 10 |
The third and following steps, iii–v, and so on, are sequential generations of di-, tetra-, hexa-, and higher-radical configurations conditional to ancilla qubits. These steps generate open shell electronic configurations if the corresponding ancilla qubits are in state |1⟩ and adopt no operations if the ancillas are the |0⟩ state. These conditional operations produce linear combinations of open shell and closed shell electronic configurations as given in eq 6. The diradical wave function given in eq 1 can be generated using a circuit given in Figure 1B, by analogy with Bell state preparations. The diradical wave function preparation in Figure 1B consists of two single-qubit rotations and following three CNOT operations. The first three quantum gates generate the linear combination of states in which LUNO + i is doubly occupied and unoccupied. The subsequent two CNOT gates conditionally change the occupation number of the HONO – i orbital from doubly occupied to unoccupied, if the LUNO + i is doubly occupied. The wave function after diradical configuration generations specified iii in Figure 1A is given in eq 11.
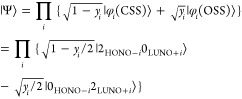 |
11 |
Upon comparison of eqs 8 and 11, the wave function component corresponding to tetraradical configuration at this stage is given in eq 12.
| 12 |
The genuine tetraradical wave function we want to construct is given in eq 13.
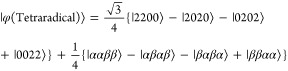 |
13 |
To generate the configuration in eq 13 from that in eq 12, we introduce another ancilla qubit and perform two Fredkin (controlled-SWAP) gates with conditionally interchange occupation of the spin-β electron between HONO – i and LUNO + i as illustrated in Figure 1C. In Figure 1C black circles and crosses represent control and target qubits, respectively, and the SWAP operations between two target qubits are performed if the control qubit is in the |1⟩ state. These operations generate, for example, |ααββ⟩ from |2200⟩. The constructions of the hexaradical configuration specified v in Figure 1A and higher-radical configurations can be also achieved by introducing ancillas and applying Fredkin gates.
3. Results and Discussion
To exemplify the performance of the proposed approach, we carried out quantum chemical calculations of small molecules on classical computers and to evaluate the overlap between the full-CI or CAS-CI wave function of the ground state and the multiconfigurational wave function constructed by utilizing diradical characters. The calculations were carried out using the GAMESS-US program package.70
3.1. Potential Energy Curve of a H2 Molecule
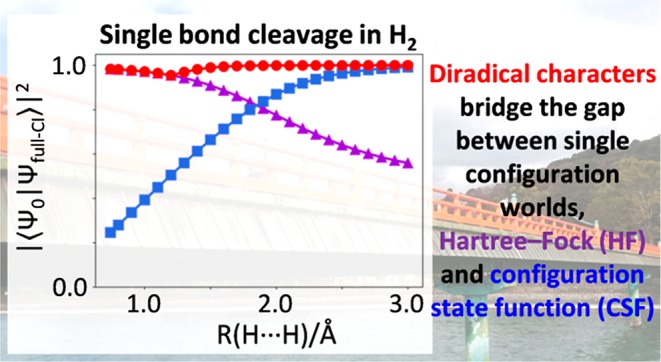
First, we focused on the simplest system; potential energy curve of a H2 molecule. The overlaps between the full-CI/cc-pVDZ wave function and RHF wave function, a wave function consisting of one CSF, and the two-configurational wave function prepared using diradical characters calculated from the UHF wave function were computed by changing the H···H distance from 0.74 (equilibrium geometry) to 3.0 Å. The results are summarized in Figure 2. As expected, the RHF wave function has large overlap with the full-CI root around the equilibrium geometry, but the overlap decreases with increasing H···H distance. CSF has an opposite trend: Large overlap is obtained for the long H···H distance, but overlap becomes small as it approaches the equilibrium geometry. By contrast, the two-configurational wave function gives sufficiently large overlap with the full-CI wave function at any H···H distances. Note that BS-UHF converges to RHF root for the atom–atom distance 1.2 Å and shorter. The calculated diradical character y0 is plotted as an inset of Figure 2. When SCF converged to unrestricted root, a nonzero y0 value is obtained, and the y0 value increases as the H···H distance becomes longer, and approaches to unity for the bond dissociation limit. We also checked overlaps of the two-configurational wave functions prepared using diradical characters obtained from the DFT framework with different HF exchange contributions using BLYP, B3LYP, BHandHLYP, and LC-BLYP functionals71−73 (see Figure S1 in the Supporting Information). The pure exchange–correlation functional (BLYP) tends to converge the spin-restricted root for the longer H···H distance, and the inclusion of HF exchange stabilizes the broken-symmetry state. The overlaps between the full-CI and two-configurational wave functions are similar among BS-UHF and DFT-based calculations. In the following calculations, we utilized diradical characters calculated from the BS-UHF wave functions.
Figure 2.
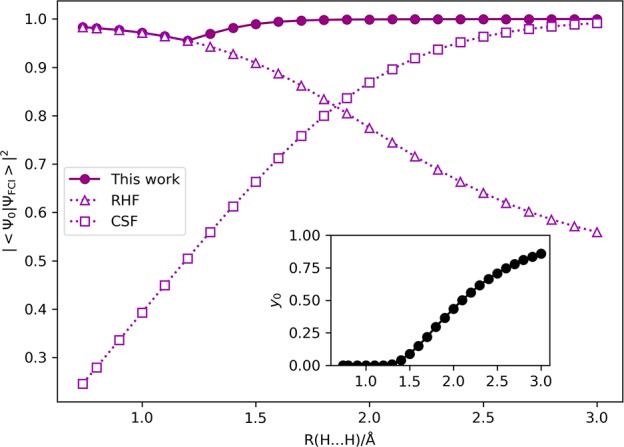
Square of overlap between the full-CI/cc-pVDZ wave function of the ground state and initial guess wave functions in H2. Inset: diradical character y0 obtained from the PUHF calculations.
3.2. C–C Bond Cleavage in Ethane, Ethylene, And Acetylene
Next, we adopted the present method to multiple bond cleavages in ethane (C2H6), ethylene (C2H4), and acetylene (C2H2) with different C···C distances. The full-CI calculations were performed using the STO-3G basis set. Note that we could not perform the full-CI/STO-3G calculations of ethane because of the limitation of our computational resources, and therefore, we excluded 1s orbital of carbon atoms from the CI expansion and adopted full-valence CAS-CI for ethane. The square overlap between the initial guess and reference wave functions is plotted in Figure 3, and the calculated diradical characters are summarized in Figure S2 in the Supporting Information. Note that in acetylene the two π bonds are degenerate, and therefore y0 = y1. In this case, an arbitrary mixing of LUNO and LUNO + 1 (and also HONO and HONO – 1) does not change their eigenvalues (occupation numbers). We discriminated the two π bonds by utilizing spatial symmetry in the generation of natural orbitals.
Figure 3.
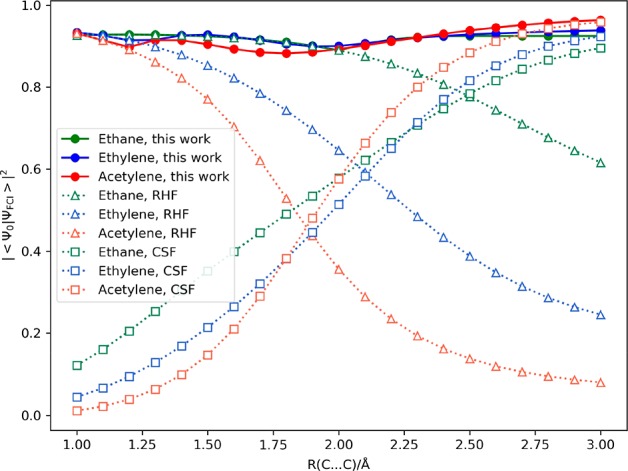
Square of overlap between the reference and initial guess wave functions in ethane, ethylene, and acetylene molecules.
The square overlap between the reference and RHF wave functions strongly depends on the bond order. This is because O(2k) of Slater determinants are required to describe the multiradical configuration of k-ple bond dissociations. In acetylene, the square overlap is less than 0.1 at the dissociation limit. The square overlap between the reference wave function and one CSF is less dependent on the bond order, because CSF consists of O(2k) of Slater determinants. However, the overlap between CSF and the reference wave function approaches zero around the equilibrium geometry. By contrast, the multiconfigurational wave function has larger overlap with reference compared with RHF and CSF, and the square overlap is always larger than 0.882. The numerical calculations of triple bond cleavage in acetylene illustrated that the proposed approach can generate good initial guess wave functions for the molecules containing as many as six unpaired electrons. It should be emphasized that the proposed approach does not need prior knowledge of electronic structures, and open shell characters are automatically determined from the occupation number of natural orbitals. This feature is very important when the number of diradical pairs that should be considered to obtain sufficiently large overlap with the full-CI root is unknown.
3.3. Singlet Ground State of Phenylene-1,4-dinitrene
Usefulness of multiconfigurational wave functions is not limited on intermediate bond regions of potential energy surfaces. Here, we focus on the electronic ground state of phenylene-1,4-dinitrene as an important chemical entity. Phenylene-1,4-dinitrene is a heteroatomic analog of non-Kekulé molecules, and it has two major resonance structures: quinonoidal diradical and phenyl dinitrene as illustrated in Scheme 1. The electronic ground state of phenylene-1,4-dinitrene is a spin-singlet diradical, in which two unpaired electrons occupy in-plane 2p orbitals of nitrogen atoms.74−78 However, because of the existence of the dinitrene resonance structure, the π system is expected to have non-negligible diradical characters.
Scheme 1. Two Major Resonance Structures of Phenylene-1,4-dinitrene.
Natural orbitals and the corresponding occupation numbers calculated from BS-UHF/cc-pVDZ level at the UB3LYP/6-31G* optimized geometry are given in Figure 4. The BS-UHF calculation revealed that the in-plane 2p orbitals of the nitrogen atoms (HONO and LUNO) are in almost pure diradical states with y0 = 0.9892. The HONO – 1 and LUNO + 1 pair has an intermediate diradical character with y1 = 0.1584. The other valence π orbitals also have small diradical characters (y2 = 0.0109, y3 = 0.0071, and y4 = 0.0009). Note that y5 is less than 0.0001, and therefore diradical characters of valence σ/σ* bonded orbitals are negligibly small.
Figure 4.
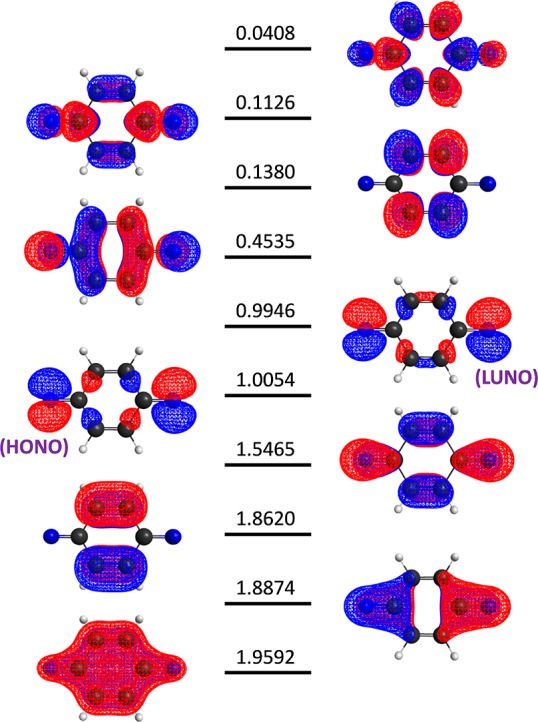
BS-UHF/cc-pVDZ natural orbitals and the occupation numbers of phenylene-1,4-dinitrene.
Needless to say, the full-CI calculation of phenylene-1,4-dinitrene is impossible, and hence, we used the CAS-CI(10e,10o)/cc-pVDZ wave function as a reference. As illustrated in Figure 4, 10 natural orbitals illustrated in are used as active orbitals. The number of Slater determinants of Sz = 0 within the active space is 63 504, and the number of spin-singlet CSFs is 19 404. Upon consideration of five diradical characters (y0–y4) the approximated wave function consisting of 264 determinants can be constructed. However, the contributions from octaradical and decaradical configurations are less than 1%, and therefore, we omitted these configurations and generated the wave function containing 72 important Slater determinants. The square overlap between the multiconfigurational wave function and CAS-CI wave function is calculated to be 0.9286, and we conclude that multiconfigurational wave functions can be safely used as initial guess wave functions for QPEA. Dependence of the square overlap against the number of diradical characters used for the multiconfigurational wave function preparation is summarized in Table S1 in the Supporting Information. If the RHF configuration is used as the initial guess wave function, the square overlap with the CAS-CI wave function is calculated to be 0.3894. The square overlap increases to be 0.8754 if one diradical character y0 is used, and the inclusion of higher-radical characters systematically improves the overlap. Note that spin projection is important if more than one diradical character is used for the wave function preparation. The enhancement of the overlap by using higher-diradical characters such as y3 and y4 is not significant, and therefore, they can be neglected in the case when a sufficient number of qubit resources are not available.
4. Conclusions
In the quantum simulations for molecular energies it has been assumed that the HF wave function is a “good” approximation of the ground state wave function. However, validity of this assumption is rather limited, and construction of multiconfigurational wave functions is crucial to describe a wide variety of chemistries. The proposed approach generates multiconfigurational wave functions utilizing diradical characters computed from the occupation number of BS-UHF natural orbitals. Numerical calculations on the covalent bond dissociation of H2, ethane, ethylene, and acetylene and electronic ground state of phenylene-1,4-dinitrene revealed that the multiconfigurational wave functions prepared using diradical characters have large overlap with the reference (full-CI or CAS-CI) wave functions. The worst case in the systems under study is found in the triple bond dissociation of acetylene, but the square overlap value is still 0.882. In the proposed approach, the number of orbital pairs having non-negligible diradical characters as well as diradical characters is automatically determined from the BS-UHF calculations. Preparation of the multiconfigurational wave functions on quantum registers can be accomplished by introducing ancilla qubits retaining information on diradical characters, and perform Bell state preparations and Fredkin gates, conditional on the ancilla qubits. The proposed approach enables us to efficiently take into account static electron correlation effects via diradical characters. In the case of prominent dynamical electron correlations, the square overlap becomes smaller, and additional computations such as ASP and ASCI may be preferable to ensure sufficiently large overlap with the full-CI root. We can reasonably assume that the multiconfigurational wave functions prepared using diradical characters are good initial guesses for further computations like ASP and ASCI. Note that the prepared wave function is a spin eigenfunction, and it contains 2k-ple excited configurations from the RHF configuration, where k is the number of diradical characters used for the preparation of wave function. The multiconfigurational wave function is inherently suitable as the initial guess wave function for not only the QPEA-based full-CI calculations but also other computational models like VQE.
Acknowledgments
This work was supported by AOARD Scientific Project on “Quantum Properties of Molecular Nanomagnets” (Award FA2386-13-1-4029, 4030, 4031) and AOARD Project on “Molecular Spins for Quantum Technologies” (Grant FA2386-17-1-4040), USA, and by Grants-in-Aid for Scientific Research B (17H03012) and Scientific Research C (18K03465) from the MEXT, Japan. This work has been partially supported by Grants-in-Aid for Scientific Research on Innovative Areas (Quantum Cybernetics), Scientific Research B (23350011), Grants-in-Aid for Challenging Exploratory Research (25620063) from MEXT, Japan, and by FIRST Quantum Information Processing Project, the Cabinet Office, Japan.
Glossary
Abbreviations
- ASCI
adaptive sampling configuration interaction
- ASP
adiabatic state preparation
- BS
broken-symmetry
- CAS
complete active space
- CI
configuration interaction
- CSF
configuration state function
- DM
direct mapping
- HF
Hartree–Fock
- HONO
highest occupied natural orbital
- LUNO
lowest unoccupied natural orbital
- QCC-on-QC
quantum chemical calculation on quantum computers
- QPEA
quantum phase estimation algorithm
- SCF
self-consistent field
- VQE
variational quantum eigensolver
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00788.
Square overlap between the full-CI/cc-pVDZ wave function of the ground state and two-configurational wave functions using diradical characters computed from DFT in H2; diradical characters of ethane, ethylene, and acetylene calculated at UHF; and square overlap of the initial guess and CAS-CI wave functions in phenylene-1,4-dinitrene (PDF)
Author Contributions
K. Sugisaki, K. Sato, and T. Takui planned and conducted the project. K. Sugisaki proposed the theoretical approach and performed quantum chemical calculations. All the other authors discussed the results. K. Sugisaki and T. Takui wrote the paper.
The authors declare no competing financial interest.
Supplementary Material
References
- Kelly J.Engineering superconducting qubit arrays for quantum supremacy; APS March Meeting, 2018.
- Liao S.-K.; Cai W.-Q.; Handsteiner J.; Liu B.; Yin J.; Zhang L.; Rauch D.; Fink M.; Ren J.-G.; Liu W.-Y.; et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 2018, 120, 030501. 10.1103/PhysRevLett.120.030501. [DOI] [PubMed] [Google Scholar]
- Aspuru-Guzik A.; Dutoi A. D.; Love P. J.; Head-Gordon M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. 10.1126/science.1113479. [DOI] [PubMed] [Google Scholar]
- Kassal I.; Jordan S. P.; Love P. J.; Mohseni M.; Aspuru-Guzik A. Polynomial-time quantum algorithm for the simulation of chemical dynamics. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 18681–18686. 10.1073/pnas.0808245105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veis L.; Višňák J.; Fleig T.; Knecht S.; Saue T.; Visscher L.; Pittner J. Relativistic quantum chemistry on quantum computers. Phys. Rev. A: At., Mol., Opt. Phys. 2012, 85, 030304. 10.1103/PhysRevA.85.030304. [DOI] [Google Scholar]
- Whitfield J. D.; Biamonte J.; Aspuru-Guzik A. Simulation of electronic structure Hamiltonians using quantum computers. Mol. Phys. 2011, 109, 735–750. 10.1080/00268976.2011.552441. [DOI] [Google Scholar]
- Jones N. C.; Whitfield J. D.; McMahon P. L.; Yung M.-H.; Van Meter R.; Aspuru-Guzik A.; Yamamoto Y. Faster quantum chemistry simulation on fault-tolerant quantum computers. New J. Phys. 2012, 14, 115023. 10.1088/1367-2630/14/11/115023. [DOI] [Google Scholar]
- Lanyon B. P.; Whitfield J. D.; Gillett G. G.; Goggin M. E.; Almeida M. P.; Kassal I.; Biamonte J. D.; Mohseni M.; Powell B. J.; Barbieri M.; et al. Towards quantum chemistry on a quantum computer. Nat. Chem. 2010, 2, 106–111. 10.1038/nchem.483. [DOI] [PubMed] [Google Scholar]
- Du J.; Xu N.; Peng X.; Wang P.; Wu S.; Lu D. NMR implementation of a molecular hydrogen quantum simulation with adiabatic state preparation. Phys. Rev. Lett. 2010, 104, 030502. 10.1103/PhysRevLett.104.030502. [DOI] [PubMed] [Google Scholar]
- Yung M.-H.; Casanova J.; Mezzacapo A.; McClean J.; Lamata K.; Aspuru-Guzik A.; Solano E. From transistor to trapped-ion computers for quantum chemistry. Sci. Rep. 2015, 4, 3589. 10.1038/srep03589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Dolde F.; Biamonte J.; Babbush R.; Bergholm V.; Yang S.; Jakobi I.; Neumann P.; Aspuru-Guzik A.; Whitfield J. D.; Wrachtrup J. Quantum simulation of helium hydride cation in a solid-state spin register. ACS Nano 2015, 9, 7769–7774. 10.1021/acsnano.5b01651. [DOI] [PubMed] [Google Scholar]
- Zhu G.; Subaşı Y.; Whitfield J. D.; Hafezi M. Hardware-efficient fermionic simulation with a cavity-QED system. npj Quantum Info. 2018, 4, 16. 10.1038/s41534-018-0065-3. [DOI] [Google Scholar]
- Peruzzo A.; McClean J.; Shadbolt P.; Yung M.-H.; Zhou X.-Q.; Love P. J.; Aspuru-Guzik A.; O’Brien J. L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. 10.1038/ncomms5213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClean J. R.; Romero J.; Babbush R.; Aspuru-Guzik A. The theory of variational hybrid quantum–classical algorithms. New J. Phys. 2016, 18, 023023. 10.1088/1367-2630/18/2/023023. [DOI] [Google Scholar]
- O’Malley P. J. J.; Babbush R.; Kivlichan I. D.; Romero J.; McClean J. R.; Barends R.; Kelly J.; Roushan P.; Tranter A.; Ding N.; et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 2016, 6, 031007. 10.1103/PhysRevX.6.031007. [DOI] [Google Scholar]
- Romero J.; Babbush R.; McClean J. R.; Hempel C.; Love P.; Aspuru-Guzik A. Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz. Quantum Sci. Technol. 2019, 4, 014008. 10.1088/2058-9565/aad3e4. [DOI] [Google Scholar]
- Li Y.; Benjamin S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 2017, 7, 021050. 10.1103/PhysRevX.7.021050. [DOI] [Google Scholar]
- McClean J. R.; Kimchi-Schwartz M. E.; Carter J.; de Jong W. A. Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states. Phys. Rev. A: At., Mol., Opt. Phys. 2017, 95, 042308. 10.1103/PhysRevA.95.042308. [DOI] [Google Scholar]
- Shen Y.; Zhang X.; Zhang S.; Zhang J.-N.; Yung M.-H.; Kim K. Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure. Phys. Rev. A: At., Mol., Opt. Phys. 2017, 95, 020501. 10.1103/PhysRevA.95.020501. [DOI] [Google Scholar]
- Kandala A.; Mezzacapo A.; Temme K.; Takita M.; Brink M.; Chow J. M.; Gambetta J. M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. 10.1038/nature23879. [DOI] [PubMed] [Google Scholar]
- Colless J. I.; Ramasesh V. V.; Dahlen D.; Blok M. S.; Kimchi-Schwartz M. E.; McClean J. R.; Carter J.; de Jong W. A.; Siddiqi I. Computation of molecular spectra on a quantum processor with an error-resilient algorithm. Phys. Rev. X 2018, 8, 011021. 10.1103/PhysRevX.8.011021. [DOI] [Google Scholar]
- Hempel C.; Maier C.; Romero J.; McClean J.; Monz T.; Shen H.; Jurcevic P.; Lanyon B.; Love P.; Babbush R.; et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 2018, 8, 031022. 10.1103/PhysRevX.8.031022. [DOI] [Google Scholar]
- Toloui B.; Love P. J.. Quantum algorithms for quantum chemistry based on the sparsity of the CI-matrix. 2013, arXiv:1312.2579. arXiv.org e-Print archive. https://arxiv.org/abs/1312.2579.
- McArdle S.; Endo S.; Li Y.; Benjamin S.; Yuan X.. Variational quantum simulation of imaginary time evolution with applications in chemistry and beyond., 2018. arXiv:1804.03023. arXiv.org e-Print archive. https://arxiv.org/abs/1804.03023.
- Xia R.; Kais S. Quantum machine learning for electronic structure calculations. Nat. Commun. 2018, 9, 4195. 10.1038/s41467-018-06598-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wecker D.; Bauer B.; Clark B. K.; Hastings M. B.; Troyer M. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys. Rev. A: At., Mol., Opt. Phys. 2014, 90, 022305. 10.1103/PhysRevA.90.022305. [DOI] [Google Scholar]
- Hastings M. B.; Wecker D.; Bauer B.; Troyer M. Improving quantum algorithms for quantum chemistry. Quantum Info. Comput. 2015, 15 (1-2), 1–21. [Google Scholar]
- Moll N.; Fuhrer A.; Staar P.; Tavernelli I. Optimizing qubit resources for quantum chemistry simulations in second quantization on a quantum computer. J. Phys. A: Math. Theor. 2016, 49, 295301. 10.1088/1751-8113/49/29/295301. [DOI] [Google Scholar]
- Babbush R.; Berry D. W.; Kivlichan I. D.; Wei A. Y.; Love P. J.; Aspuru-Guzik A. Exponentially more precise quantum simulation of fermions in second quantization. New J. Phys. 2016, 18, 033032. 10.1088/1367-2630/18/3/033032. [DOI] [Google Scholar]
- Kivlichan I. D.; McClean J.; Wiebe N.; Gidney C.; Aspuru-Guzik A.; Chan G. K.-L.; Babbush R. Quantum simulation of electronic structure with linear depth and connectivity. Phys. Rev. Lett. 2018, 120, 110501. 10.1103/PhysRevLett.120.110501. [DOI] [PubMed] [Google Scholar]
- Babbush R.; Wiebe N.; McClean J.; McClain J.; Neven H.; Chan G. K.-L. Low-depth quantum simulation of materials. Phys. Rev. X 2018, 8, 011044. 10.1103/PhysRevX.8.011044. [DOI] [PubMed] [Google Scholar]
- Babbush R.; Berry D. W.; Sanders Y. R.; Kivlichan I. D.; Scherer A.; Wei A. Y.; Love P. J.; Aspuru-Guzik A. Exponentially more precise quantum simulation of fermions in the configuration interaction representation. Quantum Sci. Technol. 2018, 3, 015006. 10.1088/2058-9565/aa9463. [DOI] [Google Scholar]
- McClean J. R.; Babbush R.; Love P. J.; Aspuru-Guzik A. Exploiting locality in quantum computation for quantum chemistry. J. Phys. Chem. Lett. 2014, 5, 4368–4380. 10.1021/jz501649m. [DOI] [PubMed] [Google Scholar]
- Babbush R.; McClean J.; Wecker D.; Aspuru-Guzik A.; Wiebe N. Chemical basis of Trotter–Suzuki errors in quantum chemistry simulation. Phys. Rev. A: At., Mol., Opt. Phys. 2015, 91, 022311. 10.1103/PhysRevA.91.022311. [DOI] [Google Scholar]
- Sawaya N. P. D.; Smelyanskiy M.; McClean J. R.; Aspuru-Guzik A. Error sensitivity to environmental noise in quantum circuits for chemical state preparation. J. Chem. Theory Comput. 2016, 12, 3097–3108. 10.1021/acs.jctc.6b00220. [DOI] [PubMed] [Google Scholar]
- Seeley J. T.; Richard M. J.; Love P. J. The Bravyi–Kitaev transformation for quantum computation of electronic structure. J. Chem. Phys. 2012, 137, 224109. 10.1063/1.4768229. [DOI] [PubMed] [Google Scholar]
- Tranter A.; Sofia S.; Seeley J.; Kaicher M.; McClean J.; Babbush R.; Coveney P. V.; Mintert F.; Wilhelm F.; Love P. J. The Bravyi–Kitaev transformation: Properties and applications. Int. J. Quantum Chem. 2015, 115, 1431–1441. 10.1002/qua.24969. [DOI] [Google Scholar]
- Whitfield J. D. Spin-free quantum computational simulations and symmetry adapted states. J. Chem. Phys. 2013, 139, 021105. 10.1063/1.4812566. [DOI] [PubMed] [Google Scholar]
- Whitfield J. D.; Havlíček V.; Troyer M. Local spin operators for fermion simulations. Phys. Rev. A: At., Mol., Opt. Phys. 2016, 94, 030301. 10.1103/PhysRevA.94.030301. [DOI] [Google Scholar]
- Setia K.; Whitfield J. D. Bravyi–Kitaev superfast simulation of electronic structure on a quantum computer. J. Chem. Phys. 2018, 148, 164104. 10.1063/1.5019371. [DOI] [PubMed] [Google Scholar]
- Daskin A.; Kais S. Decomposition of unitary matrices for finding quantum circuits: Application to molecular Hamiltonians. J. Chem. Phys. 2011, 134, 144112. 10.1063/1.3575402. [DOI] [PubMed] [Google Scholar]
- Trout C. J.; Brown K. R. Magic state distillation and gate compilation in quantum algorithms for quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1296–1304. 10.1002/qua.24856. [DOI] [Google Scholar]
- Veis L.; Pittner J. Quantum computing applied to calculations of molecular energies: CH2 benchmark. J. Chem. Phys. 2010, 133, 194106. 10.1063/1.3503767. [DOI] [PubMed] [Google Scholar]
- Veis L.; Pittner J. Adiabatic state preparation study of methylene. J. Chem. Phys. 2014, 140, 214111. 10.1063/1.4880755. [DOI] [PubMed] [Google Scholar]
- Tubman N. M.; Mejuto-Zaera C.; Epstein J. M.; Hait D.; Levine D. S.; Huggins W.; Jiang Z.; McClean J. R.; Babbush R.; Head-Gordon M.; Whaley K. B.. Postponing the orthogonality catastrophe: efficient state preparation for electronic structure simulations on quantum devices, 2018. arXiv:1809.05523. arXiv.org e-Print archive. https://arxiv.org/abs/1809.05523.
- Babbush R.; Love P. J.; Aspuru-Guzik A. Adiabatic quantum simulation of quantum chemistry. Sci. Rep. 2015, 4, 6603. 10.1038/srep06603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.; Kais S.; Aspuru-Guzik A.; Hoffmann M. R. Quantum algorithm for obtaining the energy spectrum of molecular systems. Phys. Chem. Chem. Phys. 2008, 10, 5388–5393. 10.1039/b804804e. [DOI] [PubMed] [Google Scholar]
- Wang H.; Ashhab S.; Nori F. Efficient quantum algorithm for preparing molecular-system-like states on a quantum computer. Phys. Rev. A: At., Mol., Opt. Phys. 2009, 79, 042335. 10.1103/PhysRevA.79.042335. [DOI] [Google Scholar]
- Sugisaki K.; Yamamoto S.; Nakazawa S.; Toyota K.; Sato K.; Shiomi D.; Takui T. Quantum chemistry on quantum computers: A polynomial-time quantum algorithm for constructing the wave functions of open-shell molecules. J. Phys. Chem. A 2016, 120, 6459–6466. 10.1021/acs.jpca.6b04932. [DOI] [PubMed] [Google Scholar]
- Sugisaki K.; Yamamoto S.; Nakazawa S.; Toyota K.; Sato K.; Shiomi D.; Takui T.. Open shell electronic state calculations on quantum computers: A quantum circuit for the preparation of configuration state functions based on Serber construction. Chem. Phys. Lett.: X 2018, in press. 10.1016/j.cpletx.2018.100002 [DOI] [Google Scholar]
- Berry D. W.; Kieferová M.; Scherer A.; Sanders Y. R.; Low G. H.; Wiebe N.; Gidney C.; Babbush R. Improved techniques for preparing eigenstate of fermionic Hamiltonians. npj Quantum Info. 2018, 4, 22. 10.1038/s41534-018-0071-5. [DOI] [Google Scholar]
- Dallaire-Demers P.-L.; Romero J.; Veis K.; Sim S.; Aspuru-Guzik A.. Low-depth circuit ansatz for preparing correlated fermionic states on a quantum computer, 2018. arXiv:1801.01053. arXiv.org e-Print archive. https://arxiv.org/abs/1801.01053.
- Bian T.; Murphy D.; Xia R.; Daskin A.; Kais S.. Comparison study of quantum computing methods for simulating the Hamiltonian of the water molecule, 2018. arXiv:1804.05453. arXiv.org e-Print archive. https://arxiv.org/abs/1804.05453.
- Feynman R. P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. 10.1007/BF02650179. [DOI] [Google Scholar]
- Nielsen M. A.; Chuang I. L.. Quantum computation and quantum information; Cambridge University Press: Cambridge, U.K., 2000. [Google Scholar]
- Abrams D. S.; Lloyd S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 1999, 83, 5162–5165. 10.1103/PhysRevLett.83.5162. [DOI] [Google Scholar]
- Helgaker T.; Jørgensen P.; Olsen J.. Molecular electronic-structure theory; John Wiley & Sons, Ltd.: Chichester, U.K., 2000. [Google Scholar]
- Pauncz R.The construction of spin eigenfunctions. An exercise book; Kluwer Academic/Plenum Publishers: New York, 2000. [Google Scholar]
- Hayes E. F.; Siu A. K. Q. Electronic structure of the open forms of three-membered rings. J. Am. Chem. Soc. 1971, 93, 2090–2091. 10.1021/ja00737a064. [DOI] [Google Scholar]
- Yamaguchi K. In Self-consistent field: Theory and applications; Carbo R., Klobukowski M., Eds.; Elsevier: Amsterdam, 1990; pp 727–828. [Google Scholar]
- Yamaguchi K. The electronic structures of biradicals in the unrestricted Hartree–Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. 10.1016/0009-2614(75)80169-2. [DOI] [Google Scholar]
- Döhnert D.; Koutecký J. Occupation numbers of natural orbitals as a criterion for biradical character, Different kinds of biradicals. J. Am. Chem. Soc. 1980, 102, 1789–1796. 10.1021/ja00526a005. [DOI] [Google Scholar]
- Nakano M.; Kishi R.; Nitta T.; Kubo T.; Nakasuji K.; Kamada K.; Ohta K.; Champagne B.; Botek E.; Yamaguchi K. Second hyperpolarizability (γ) of singlet diradical system: Dependence of γ on the diradical character. J. Phys. Chem. A 2005, 109, 885–891. 10.1021/jp046322x. [DOI] [PubMed] [Google Scholar]
- Nakano M.; Kishi R.; Ohta S.; Takahashi H.; Kubo T.; Kamada K.; Ohta K.; Botek E.; Champagne B. Relationship between third-order nonlinear optical properties and magnetic interactions in open-shell systems: A new paradigm for nonlinear optics. Phys. Rev. Lett. 2007, 99, 033001. 10.1103/PhysRevLett.99.033001. [DOI] [PubMed] [Google Scholar]
- Nakano M.; Champagne B. Theoretical design of open-shell singlet molecular systems for nonlinear optics. J. Phys. Chem. Lett. 2015, 6, 3236–3256. 10.1021/acs.jpclett.5b00956. [DOI] [Google Scholar]
- Minami T.; Nakano M. Diradical character view of singlet fission. J. Phys. Chem. Lett. 2012, 3, 145–150. 10.1021/jz2015346. [DOI] [PubMed] [Google Scholar]
- Nakano M. Open-shell-character-based molecular design principles: Applications to nonlinear optics and singlet fission. Chem. Rec. 2017, 17, 27–62. 10.1002/tcr.201600094. [DOI] [PubMed] [Google Scholar]
- Low G. H.; Chuang I. L.. Hamiltonian simulation by qubitization, 2016. arXiv:1610.06546. arXiv.org e-Print archive. https://arxiv.org/abs/1610.06546.
- Berry D. W.; Childs A. M.; Cleve R.; Kothari R.; Somma R. D. Simulating Hamiltonian dynamics with a truncated Taylor series. Phys. Rev. Lett. 2015, 114, 090502. 10.1103/PhysRevLett.114.090502. [DOI] [PubMed] [Google Scholar]
- Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S. J.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle–Salvetti correlation energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Iikura H.; Tsuneda T.; Yanai T.; Hirao K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–3544. 10.1063/1.1383587. [DOI] [Google Scholar]
- Singh B.; Brinen J. S. Low-temperature photochemistry of p-diazidobenzene and 4,4’-diazidoazobenzene. J. Am. Chem. Soc. 1971, 93, 540–542. 10.1021/ja00731a051. [DOI] [Google Scholar]
- Nimura S.; Kikuchi O.; Ohara T.; Yabe A.; Kaise M. Singlet–triplet energy gaps of quinonoidal dinitrenes. Chem. Lett. 1996, 25, 125–126. 10.1246/cl.1996.125. [DOI] [Google Scholar]
- Minato M.; Lahti P. M. Characterizing triplet states of quinonoidal dinitrenes as a function of conjugation length. J. Am. Chem. Soc. 1997, 119, 2187–2195. 10.1021/ja963648d. [DOI] [Google Scholar]
- Ichimura A. S.; Lahti P. M. Meta- and para-phenylenedinitrene: An ab initio computational study. Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A 1993, 233, 33–40. 10.1080/10587259308054945. [DOI] [Google Scholar]
- Nicolaides A.; Tomioka H. Direct observation and characterization of p-phenylenebisnitrene. A labile quinoidal diradical. J. Am. Chem. Soc. 1998, 120, 11530–11531. 10.1021/ja982574y. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.