 Interplay between mode specific electronic friction and surface corrugation determines hot electron effects in H2 scattering on Ag(111).
Interplay between mode specific electronic friction and surface corrugation determines hot electron effects in H2 scattering on Ag(111).
Abstract
The breakdown of the Born–Oppenheimer approximation gives rise to nonadiabatic effects in gas-surface reactions at metal surfaces. However, for a given reaction, it remains unclear which factors quantitatively determine whether these effects measurably contribute to surface reactivity in catalysis and photo/electrochemistry. Here, we systematically investigate hot electron effects during H2 scattering from Ag(111) using electronic friction theory. We combine first-principles calculations of tensorial friction by time-dependent perturbation theory based on density functional theory and an analytical neural network representation, to overcome the limitations of existing approximations and explicitly simulate mode-specific nonadiabatic energy loss during molecular dynamics. Despite sizable hot-electron-induced energy loss, no measurable nonadiabatic effects can be found for H2 scattering on Ag(111). This is in stark contrast to previous reports for vibrationally excited H2 scattering on Cu(111). By detailed analysis of the two systems, we attribute this discrepancy to a subtle interplay between the magnitude of electronic friction along intramolecular vibration and the shape of the potential energy landscape that controls the molecular velocity at impact. On the basis of this characterization, we offer guidance for the search of highly nonadiabatic surface reactions.
Introduction
Energy exchange between adsorbate and substrate degrees of freedom (DOFs) has a potentially significant impact on chemical reaction dynamics at solid surfaces.1 At metal surfaces, in particular, energy carried by the adsorbate could dissipate to either surface phonons or electrons.2 Due to the continuous distribution of metallic electronic states across the Fermi level, the excitation of electron–hole pairs (EHPs) can be induced by the interaction between the adsorbate and metal atoms with the electrons in the metal surface.3,4 Indeed, electronic excitations have been found to play a key role in many processes at various transition metal surfaces, such as inelastic scattering of vibrationally excited molecules,5–7 adsorption of atomic and molecular species,8–10 as well as vibrational relaxation of adsorbates.11 They further promise an increased level of reaction control in plasmonic catalysis and photoelectrochemistry.12–14 This non-adiabatic energy dissipation channel arises from the breakdown of the Born–Oppenheimer approximation leading to a coupling of slow nuclear motion of the adsorbate and fast electronic motion of surface electrons. This breakdown is omnipresent in chemical reactions at metal surfaces, yet only a limited number of systems show measurable signatures of these effects, such as chemicurrents8 or particular energy loss profiles during atomic scattering.9 Despite a large body of work in this field, only recently have computational studies15 and experimental efforts16,17 reached a level of detail that enabled the identification of factors that determine the existence of experimental signatures of nonadiabaticity.
Given the large number of DOFs in molecule–surface systems, exact quantum nonadiabatic dynamics calculations are currently infeasible to interrogate these systems, yet a variety of approximate models have been developed in recent years to computationally simulate nonadiabatic dissipation during gas-surface dynamics.18 In the weak coupling limit, molecular dynamics with electronic friction (MDEF) models have been widely applied to account for the excitation of low-energy EHPs by the motion of adsorbate molecules.19–22 The electronic friction approach replaces the explicit account of EHPs by coupling of the molecular dynamics with an electronic bath that exerts frictional forces on the adsorbate dynamics within a generalized Langevin dynamics framework.20 This approach is approximate, yet highly efficient as it reduces the description of the EHP spectrum to a single coordinate-dependent quantity, namely the electronic friction tensor. Combined with the local density friction approximation (LDFA),23 which assumes a single friction coefficient for each non-substrate atom depending on the local electron density of the substrate, MDEF simulations have successfully captured the non-adiabatic energy loss of atomic scattering9,24,25 and hot atom relaxations,26,27 at least qualitatively. Within the independent atom approximation (IAA), the LDFA-based MDEF model has also been extended to describe the reactive and non-reactive scattering of molecules,23,28–32 Eley–Rideal reactions,33–35 and laser-induced desorption processes36 at various metal surfaces. In such cases, the electrons in the metal surface are represented by a homogeneous free electron gas within which each atom of the adsorbate is assumed to be embedded. However, the validity of LDFA-IAA has been continuously questioned due to the lack of intrinsic anisotropy in the friction tensor.15,37–41 The latter issue has been partially addressed via the Hirshfeld partitioning of the overall system density to contributions of relevant atoms, which has recently been applied to the relaxation of hot atoms and molecules on metal surfaces.27,38,42
The approximations in the LDFA-IAA model can be overcome using first-order time-dependent perturbation theory (TDPT) that fully accounts for the electronic structure of the interacting molecule–surface system.19,20,43 Because of the high computational costs of calculating the nonadiabatic matrix elements, however, TDPT calculations of electronic friction have been mostly restricted to low-dimensional problems20,37 until very recently. Maurer and coworkers have recently reported an efficient implementation of TDPT based on the Kohn–Sham (KS) orbitals of Density Functional Theory (DFT).40,41 Applications of TDPT to nonadiabatic vibrational relaxation rates for a number of diatomic molecules on metal surfaces revealed the significance of friction-induced mode-coupling.40,41 Based on MD simulations with an on-the-fly calculated TDPT friction tensor, we recently found that tensorial friction induces more energy loss of rovibrational over translational energy in scattering of H2 on Ag(111), resulting in a significant impact on the fate as well as the final energy distributions of individual H2 scattering trajectories.39 Due to the limited number of trajectories, unfortunately, state-to-state scattering probabilities were not obtained. This prediction was later confirmed by Spiering and Meyer for a similar system,15 namely for H2 on Cu(111). These authors overcame the high cost of the on-the-fly friction tensor calculations by using an analytical representation of the friction tensor and obtained an up to six times higher vibrational deexcitation probability of H2(ν = 2, j = 1 → ν = 1, j = 1) upon inclusion of hot electron effects. Interestingly, mode-dependent friction as described by TDPT provides a deexcitation probability that is three times higher than an isotropic description based on LDFA. The latter finding, if experimentally verified, could serve as an important experimental fingerprint to evidence dynamical signatures of the mode-selectivity and anisotropy of electronic friction effects.35
In this work, we report state-to-state scattering and dissociation probabilities of vibrationally excited H2 and D2 from Ag(111) using MDEF with both the TDPT and LDFA models. To this end, we develop an alternative and more general analytical representation of the friction tensor as a function of Cartesian coordinates using neural networks (NNs). Interestingly, with a larger number of trajectories on an analytical potential energy surface (PES), the MDEF simulations with TDPT and with LDFA both yield scattering-induced vibrational deexcitation probabilities of H2(ν = 2, j = 0 → ν = 1, j = 0) that are not significantly increased compared to the adiabatic case, which is in stark contrast to findings on Cu(111). Deeper analysis reveals large differences in electronic friction between the two methods and between the two substrates (Ag vs. Cu). We find that, for nonadiabatic effects to significantly affect experimental measurements, the velocity profile as controlled by the PES is equally important as the magnitude of electronic friction with respect to the intramolecular stretching motion. The strong interplay between the two quantities is in fact another manifestation of mode-selective electronic friction and the analysis of the two can provide guidance on whether nonadiabatic effects can produce quantum state-resolved measurable differences in experimental attributes.
Theory
Electronic friction based on time-dependent perturbation theory
In MDEF simulations, the nuclear dynamics are defined via a generalized Langevin equation (GLE):20
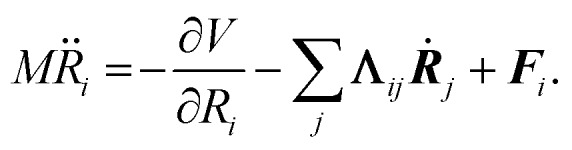 |
1 |
Herein, the three force components on the right side of eqn (1) are the conservative force due to the potential energy V, the electronic friction force given as a product between the electronic friction tensor Λ and the velocity vector of the atoms Ṙ, and a temperature- and friction-dependent random force term that restores detailed balance. To arrive at a GLE, one must assume that the electron-nuclear coupling acts instantaneously, which equates to the Markov approximation. The result is that, within 1st order TDPT, we evaluate the electronic friction tensor using Fermi's golden rule:40,43
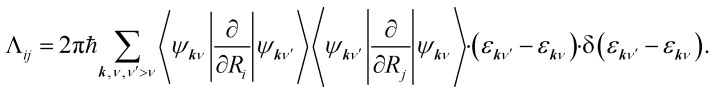 |
2 |
Herein, the factor 2 accounts for spin multiplicity in the case of non-spin-polarised calculations and ψkν and εkν correspond to KS eigenvectors and eigenstates. In eqn (2), we have not explicitly addressed occupation factors that arise from finite temperature state populations. As our DFT calculations generate a finite number of states at discrete points k in momentum space, we need to interpolate between k states to obtain a continuous electronic structure representation giving rise to friction tensor elements, which correspond to relaxation rates due to electron-nuclear coupling along the (mixed) Cartesian directions i and j. We are using local atomic orbital basis functions and evaluate nonadiabatic coupling matrix elements by numerical finite difference in terms of Hamiltonian and overlap matrices in real-space basis representation that are subsequently transformed into k-space. As detailed in our previous work39 and by Spiering and Meyer,15 we do this by replacing the delta function with a normalized Gaussian function of finite width 0.6 eV. It has recently been pointed out that such broadening can introduce contributions that are not rigorously contained in a zero-frequency 1st order approximation within many-body perturbation theory44,45 and leads to relaxation rates that depend on the choice of broadening. This pragmatic choice has been discussed in detail in our previous work39 and further methodological developments to overcome the existing restrictions of Markovian MDEF with TDPT are in progress. All elements of the friction tensor are calculated as a function of adsorbate atom position using the all-electron, local atomic orbital code FHI-aims46 and the PBE functional.47 Our computational settings regarding model set-up, basis set, and Brillouin zone sampling have been detailed in our previous publication.39 In practice, we carry out MDEF calculations with the quasi-classical trajectory (QCT) method as detailed elsewhere48 and briefly described in the ESI.† Adiabatic QCT calculations for reactive and nonreactive scattering of H2 on several metal surfaces have been validated before to reproduce almost quantitatively the quantum results.49,50 We neglect the random force term in eqn (1) considering the short collision time in this process which will simplify the discussion.15
Neural network representation of the potential energy surface, electron density, and friction tensor
To make extensive MDEF simulations affordable, one must rely on efficient representations of both the Born–Oppenheimer PES and electronic friction tensor. The PES used in this work was constructed based on the permutation invariant polynomial neural network (PIP-NN) approach51,52 using more than 4000 DFT data points.53 This approach satisfies surface symmetry and periodicity of the interaction between H2 and a rigid Ag(111) surface. In the LDFA-IAA framework, the friction coefficient is solely related to the embedding electron density for each atom on the Ag surface.23 In the frozen surface approximation, it is straightforward to obtain the electron density of the clean metal surface by a single DFT calculation. We then use the same PIP-NN form to fit the three-dimensional electron density surface,29 which possesses the same symmetry as the PES. This is an established strategy widely applied in previous studies.23,28,29,31
Nevertheless, the TDPT-based friction tensor is directionally-dependent on all coordinates of the molecule. Consequently, a proper transformation matrix must exist to link the correlated friction tensors of two symmetry equivalent molecular geometries due to the intertwined translational, rotational, and permutational symmetries. In this work, we explicitly account for the complicated covariance properties of the friction tensor with respect to the surface symmetry by a simple mapping scheme. We transform the original data of coordinates and friction tensor elements into an irreducible triangle in the surface unit cell, as depicted in Fig. 1b. The molecular geometry and friction tensor thus form a symmetry unique one-to-one mapping in this triangle, which can be represented by NNs. Since NNs are analytical functions of the nuclear coordinates, the calculation of the interpolated friction tensor at any given geometry can be computed efficiently. Our approach and the interpolation procedure are briefly described in the SI and will be more thoroughly discussed in a forthcoming publication.56
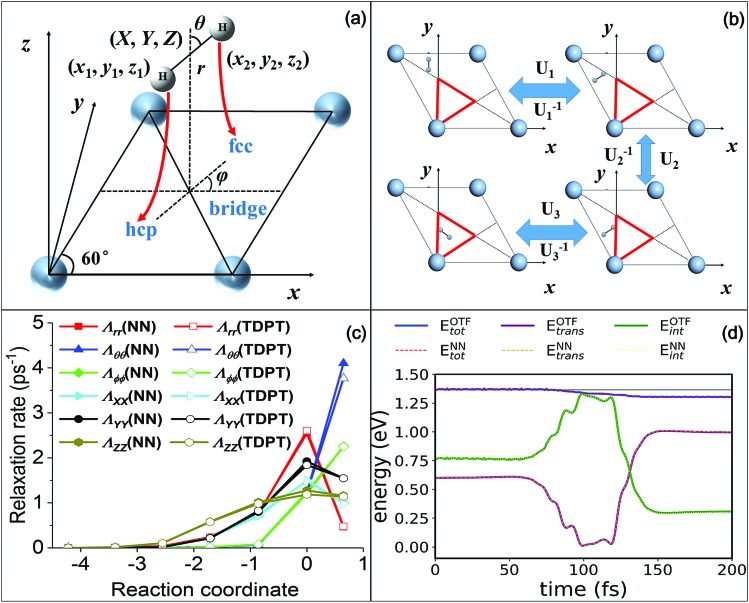
Fig. 1. (a) Internal (X, Y, Z, r, θ, φ) and Cartesian (x1, y1, z1, x2, y2, z2) coordinates used in the H2 + Ag(111) system, and MEP following red arrows along which the molecule dissociates from a bridge site to two hollow sites. (b) Mirror reflections that can move a molecular geometry outside the irreducible triangle (red) into the triangle. U1/U1–1, U2/U2–1, or U3/U3–1 corresponds to the transformation/inverse transformation matrix for each reflection, respectively. (c) Diagonal terms of nonadiabatic relaxation rates (effective friction coefficients) obtained by NNs (solid symbols) and TDPT (open symbols) along the MEP in terms of internal coordinates. (d) Comparison of the total, internal and translational energies as a function of time for an H2(ν = 1) molecule scattering vertically from a hollow site with a translational incidence energy of 0.6 eV (ref. 39) with the on-the-fly MDEF simulation (OTF, solid lines) and those with the simulation based on the interpolated friction tensor (NN, dotted lines).
Results and discussion
Accuracy of the NN representation of friction tensor
Before presenting the simulation results, we demonstrate first the quality of our NN representation of the friction tensor. In Fig. 1c, we compare the TDPT diagonal friction tensor elements with their NN representations along the minimum energy path (MEP) for H2 dissociative chemisorption, as schematically displayed in Fig. 1a. As pointed out previously,39,54 the diagonal elements with respect to the intramolecular stretch (r) and the center of mass distance from the surface (Z) both peak at the dissociation transition state, while the angular diagonal elements increase monotonously along the reaction coordinate and peak in the product channel. It is clearly seen that our NN values agree well with TDPT ones, successfully reproducing the distinct dependences of various tensorial friction elements along the MEP. In addition, we compare in Fig. 1d the friction-induced energy loss and the distribution of internal and translational energies during a non-reactive scattering event as simulated with TDPT and NN interpolated electronic friction for an exemplary MDEF trajectory (Trajectory #14 in ref. 39). With the same initial conditions, we find that the trajectory based on the interpolated tensor correctly reproduces the rate and magnitude of energy loss of the MD with on-the-fly (OTF) calculated electronic friction. More importantly, the time-dependent distribution of the internal (rotational and vibrational) and translational energies of the H2 molecule are virtually indistinguishable between the two calculations. We have actually compared more OTF and NN trajectories and similar results can be found in Fig. S1.† These results validate that our mapping scheme combined with the high fidelity NN-based interpolation provides a faithful representation of the position- and mode-dependence of the electronic friction tensor, which enables us to perform extensive MDEF simulations for state-to-state molecular scattering.
Effects of electron–hole pairs
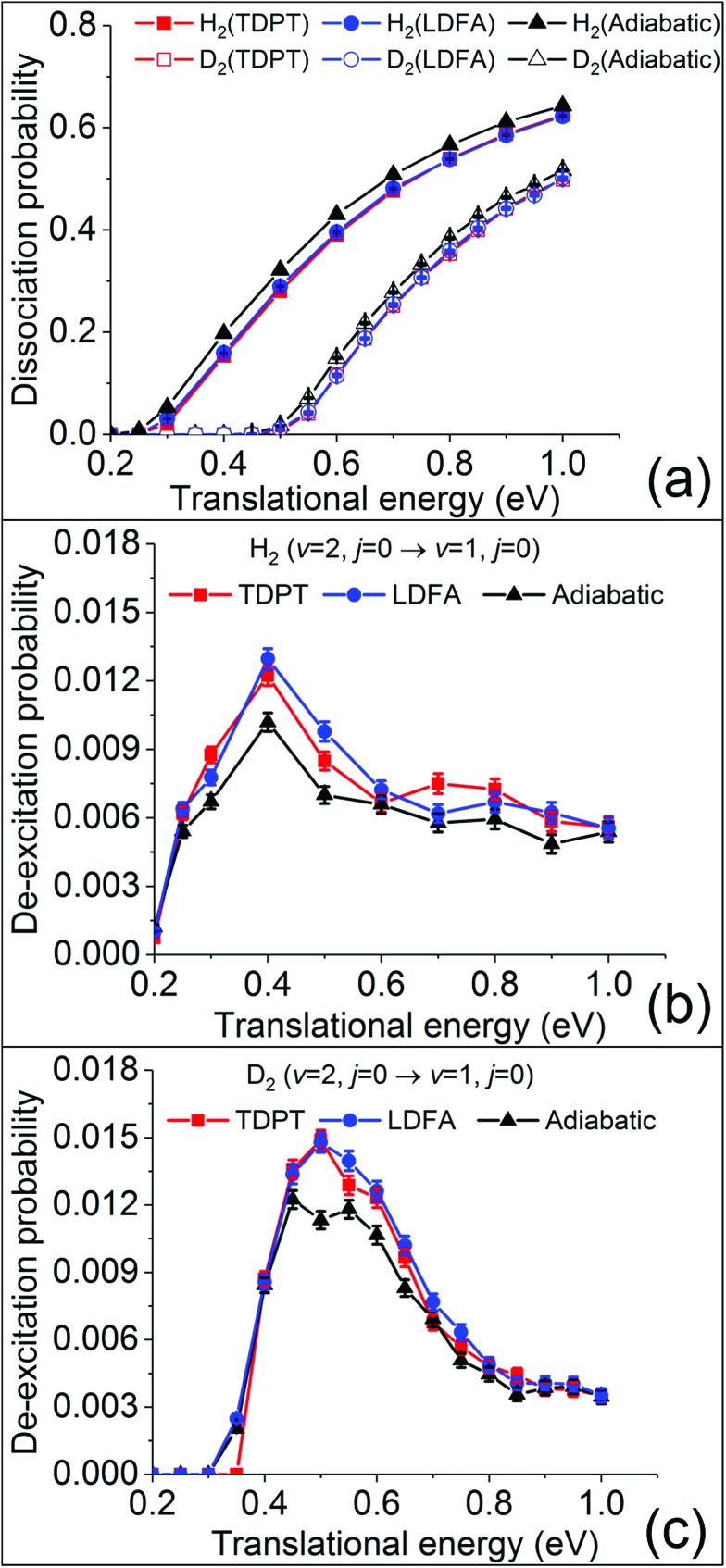
To obtain converged dissociation and state-to-state scattering probabilities, up to 75 000 QCT trajectories were run at each translational energy for H2(ν = 2, j = 0) and D2(ν = 2, j = 0). The initial conditions of the trajectories are specified in the SI. Fig. 2a compares the calculated dissociation probabilities without (adiabatic) and with electronic friction based on LDFA and TDPT. As observed in previous studies,15,28,29 the non-adiabatic energy loss induced by surface electronic excitations leads to a small reduction of the reaction probability. Interestingly, the differences between LDFA and TDPT results are almost invisible. Our results are consistent with the findings in H2 (D2) dissociation on Cu(111).15 We thus find that the observations in ref. 15 for H2 dissociation on Cu(111), namely that the differences in EHP effects described by LDFA and TDPT on dissociative sticking probability are hardly measurable, also hold for H2 dissociation on Ag(111).
Fig. 2. Dissociation probabilities (a) of H2/D2 (ν = 2, j = 0) and vibrational de-excitation probabilities from (ν = 2, j = 0) scattered to (ν = 1, j = 0) of H2 (b) and D2 (c) on Ag(111), as a function of translational energy. Adiabatic MD (black), MDEF with LDFA (blue) and TDPT (red) results are compared.
Despite the lack of EHP effects on the sticking probability, Spiering and Meyer found significant EHP effects for the vibrational de-excitation probabilities. Following their work, we analyse the de-excitation probabilities of scattered molecules H2 (D2) from the (ν = 2, j = 0) state to (ν = 1, j = 0) state (P2→1) as a function of incident energy via the standard histogram binning scheme. As shown in Fig. 2b and c, P2→1 shows an initial increase followed by a gradual decrease with the increasing Ei, peaking at Ei = 0.4 (0.5) eV by ∼1.5%. This dependence and magnitude of P2→1 are similar to what have been observed in H2 (D2) scattering from Cu(111).15 The vibrational deexcitation probability measures how effectively adsorbate vibrational energy is lost during molecular scattering at a given molecular impact velocity. The peak at 0.4 eV indicates that vibrational energy loss is most effective at intermediate kinetic energies. One may notice that the translational energy thresholds for both the dissociation and vibrational deexcitation of H2 and D2 differ by roughly 0.2 eV, which may be attributed to the difference of the vibrationally adiabatic barriers for the two isotopologues. This suggests that the vibrational deexcitation possibly occurs when the molecule has sufficient energy to climb up from the entrance channel to the transition state region but fails to dissociate. H2(ν = 2) carries more vibrational energy than D2(ν = 2) and hence requires less translational energy to access the high density and repulsive region, resulting in a lower threshold for vibrational deexcitation. However, surprisingly, we do not find a noticeable increase of P2→1 when accounting for nonadiabatic energy loss with MDEF compared to the adiabatic results, as reported in the study of Spiering and Meyer.15 This is true for both tensorial TDPT friction and isotropic LDFA friction. In contrast, for H2 (D2) scattering from Cu(111), the vibrational deexcitation probabilities in the presence of tensorial friction were found to increase by a factor of up to 6 (3) for H2 and 3 (1.5) for D2 when compared to the adiabatic (LDFA) ones.15 Surprisingly, the seemingly similar H2 + Cu(111) and H2 + Ag(111) systems behave quite differently with respect to the EHP effects for molecular scattering. We note in passing that this small nonadiabatic effect in our case is independent on the final rotational states and scattering angles (see Fig. S2†).
How can the effects of electronic friction on the vibrational deexcitation probability lead to a significant change of a measurable observable in one case and leave no measurable trace in the other? In the adiabatic case, the possibility of vibrational-to-translational energy transfer largely determines the vibrational deexcitation probability, since the total energy is conserved. When accounting for the nonadiabatic energy loss induced by electronic friction, vibrational energy can be dissipated to surface EHPs in addition to being transferred to translation, which increases the vibrational deexcitation probability. In this regard, the larger the vibrational-to-electronic energy dissipation, the larger the vibrational deexcitation probability is expected to be.
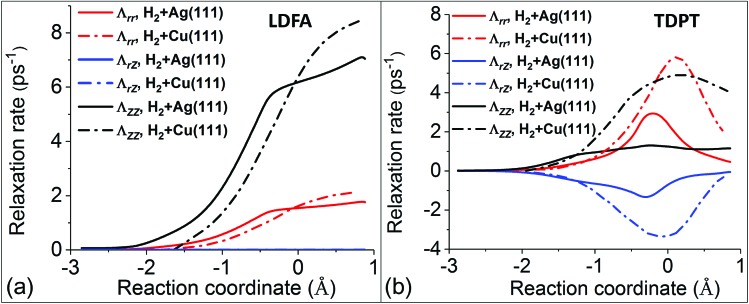
Following this line of thought, we first compare the most important components of the electronic friction tensor computed by the LDFA and TDPT methods, in terms of internal coordinates along the MEPs for H2 dissociative chemisorption on Cu(111) and Ag(111). The LDFA friction coefficients Λrr and ΛZZ shown in Fig. 3a are more or less the same for both metal substrates (note that the LDFA model does contain mode–mode coupling between internal coordinates, and ΛrZ values are close to zero here because of the parallel orientation of H2 along the minimum energy path). On the other hand, Fig. 3b presents TDPT results for Λrr, ΛZZ, and ΛrZ. Remarkably, although these three coefficients exhibit similar trends and peak at transition states for both systems, the absolute values of Λrr, ΛZZ, and ΛrZ for H2 + Cu(111) are more than twice of those for H2 + Ag(111).
Fig. 3. Comparison of several LDFA (a) and TDPT (b) friction coefficients in internal coordinates (Λrr, ΛZZ, and ΛrZ) for the H2 + Cu(111)15 (dashed–dotted curves) and H2 + Ag(111) (solid curves) systems. Note that the data for H2 + Cu(111) are extracted from Fig. 2 in ref. 15, and the reaction coordinates (s) are defined by the arc length in the (Z, r) plane starting from the transition state (s = 0) for both systems.
Upon careful comparison of our computational approach and numerical settings with the calculations in ref. 15, we conclude that this difference is rooted in the differences in the underlying electronic structure of the two metals. In comparison of the two models, for H2 + Ag(111), LDFA gives up to 6 times larger friction coefficients with respect to translation parallel to the surface normal (ΛZZ) than TDPT, while both models predict a similar magnitude of the friction coefficient with respect to H–H vibration (Λrr). Interestingly, for H2 + Cu(111), the overall magnitudes of TDPT friction elements are quite large, with Λrr and ΛZZ being much larger and comparable to the counterparts based on LDFA, respectively. The difference between the TDPT and LDFA based electronic friction models can be largely attributed to their different physical contents. Whereas LDFA only depends on the magnitude of the electron density of the clean substrate – a quantity that is similar along the MEPs for both substrates, TDPT captures the electronic structure differences between the two molecule–surface systems.
The above analysis is based on the comparison of the friction tensor elements of the two systems along the global MEP on which the molecular center is more or less over the bridge site. However, the molecules could be scattered upon the impact at other sites in the unit cell. In Fig. S3a,† we show the distribution of initial lateral positions of the scattered trajectories with H2(ν = 2, j = 0) to H2(ν = 1, j = 0). Given the weak steering effect observed previously,55 it is clear that the vibrational deexcitation process occurs with higher probabilities near the top site than other places, due presumably to the lower reactivity and stronger repulsion there. We therefore include the friction tensor analyses for the reaction paths at fixed top, bridge, and fcc sites for H2 + Ag(111) in Fig. S3b and c.† Interestingly, the results are qualitatively similar for the three paths, along which the absolute values of TDPT-based friction tensor elements gradually increase up to the barrier region then go down. The molecules that follow the top site path could not reach too closely to the surface atoms (high density region) because of the strongly repulsive potential, resulting in the smallest friction tensor values. These additional results further suggest a minor role of EHPs in the H2 + Ag(111) case.
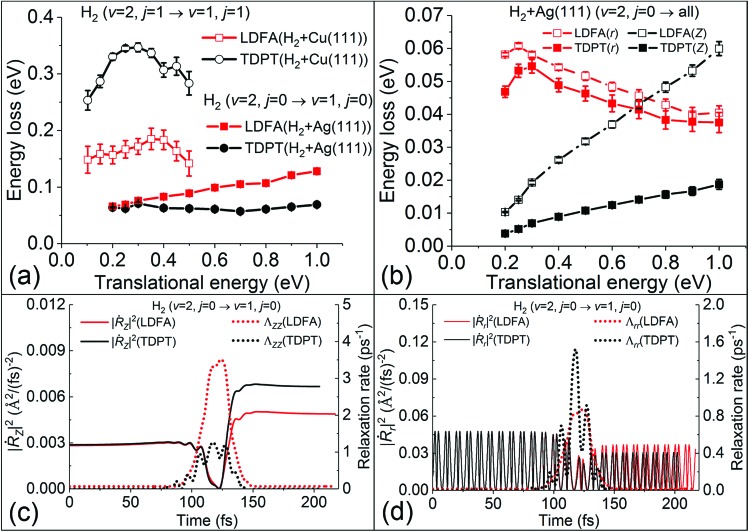
These findings on electronic friction lead us to a better understanding of the mode-specific nonadiabatic energy loss, which naturally explains our observations. In Fig. 4a, the total nonadiabatic energy losses as predicted by TDPT and LDFA for the state-to-state H2(ν = 2, j = 0 → ν = 1, j = 0) scattering on Ag(111) are compared. The LDFA energy loss is on average greater than that with the TPDT model using the same initial conditions. Interestingly, LDFA induces increasingly stronger energy loss with increased translational energy than TDPT, due apparently to the much higher ΛZZ values with LDFA along the MEP seen in Fig. 3 and S3.† This difference can be more clearly seen in Fig. 4b by comparing the mode-dependent energy losses due to EHPs, which can be separately evaluated by the integration of the friction force,27
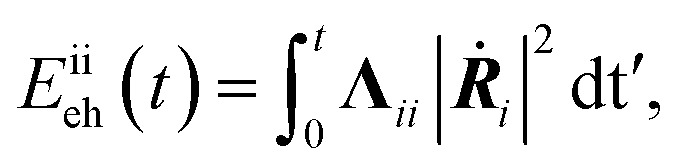 |
3 |
where we only consider the integral contributions with i corresponding to Z and r coordinates and average the quantities over hundreds of scattering trajectories to achieve good statistics. In comparison, the mean energy loss along the translation coordinate Z with LDFA increases sharply with the translational energy, whereas the energy loss with TDPT only shows a slight increase, which is responsible for the translational energy dependence of total energy loss shown in Fig. 4a. More importantly, the vibrational energy losses along r with LDFA and TDPT exhibit similar magnitudes and behaviors and both are small relative to the total energy of the molecule, resulting in the same minute effect on the increase of P2→1.
Fig. 4. (a) Average non-adiabatic energy loss with the TDPT and LDFA models as a function of translational energy for H2 scattering from Ag(111) and Cu(111) (approximately converted from Fig. 4 in ref. 15 by energy conservation). (b) Mean energy losses along translational (Z) and vibrational coordinate (r) as a function of translational energy for H2. The variation of square of velocity (solid lines) in Z (|Ṙz|2, panel c) and r (|Ṙr|2, panel d) direction along with the corresponding friction coefficients (dotted lines), as a function of time for a representative trajectory with the same initial conditions at translational energy of 0.3 eV.
On the contrary, the amount of nonadiabatic energy loss for H2 + Cu(111), which has been extracted from ref. 15 and displayed in Fig. 4a, is much larger and the pattern is quite different. We find in that case that the TDPT induced energy loss is on average about 0.30 eV, which is twice as large than that for LDFA due mainly to the larger value of the Λrr component with TDPT. This large vibrational energy loss due to EHPs certainly affects the vibrational deexcitation probabilities, and as a result, P2→1 of H2 with TDPT is about 2–3 times higher than that with LDFA, both of which prove a significant increase compared to the adiabatic results.
It is important to note that the energy loss in eqn (1) arises from the product of electronic friction and the velocity of the particle. Therefore, the underlying potential energy landscape and the velocity profile along the scattering trajectories also play an important role. One notices that the dissociation barrier locations are different for H2 + Ag(111) and H2 + Cu(111). The transition state of H2 dissociation on Ag(111) is more “product-like”,53 which features a longer H–H distance (r = 1.26 Å) and higher barrier (Ea = 1.16 eV), compared to r = 1.03 Å and Ea = 0.63 eV on Cu(111).50 The large barrier and the late transition state for H2 dissociation on Ag(111) could cause strongly reduced velocities of atoms in a large region around the turning point, as illustrated in Fig. 4c and d for a representative scattering trajectory. In Fig. 4c, the velocity along Z direction shows a sharp dip as the molecule approaches the point of reflection at the surface (∼110 fs) where the corresponding friction coefficients are the largest for both TDPT and LDFA models. A similar reduction of velocity and increase of friction coefficients along the intramolecular stretching DOF can be also seen in the same region in Fig. 4d, although the velocity is highly oscillating as the molecule vibrates. Interestingly, the TDPT based Λrr also oscillates out of phase with the velocity. This is indeed a signature of the mode-specific electronic friction varying with the molecular structure, which is absent in the LDFA-IAA friction. As a result, even when the electronic friction near the transition state region close to the surface is quite large, the H2 molecule has a low velocity, which effectively diminishes the electronic friction effects. The nonadiabatic energy loss, i.e. the integral over the friction force that can be calculated by eqn (3), is therefore very small relative to the total energy of the molecule. The potential energy landscape during scattering, therefore, plays a critical role in enabling or inhibiting large nonadiabatic energy loss by its effect on the average velocity profile during a scattering event. In case of H2 on Ag(111), the velocity profile and friction profile are such that the effect on the dynamic deexcitation probabilities is small. On Cu(111), in contrast, it is expected that the molecule can more easily reach the region of high electron density, due the lower barrier, giving rise to much larger energy loss as seen in Fig. 4a and a more remarkable increase of P2→1. The important role of this interplay between the velocity and friction coefficients has been remarked by Juaristi et al. when using LDFA to understand EHP effects for dissociative chemisorption.23 We further emphasize in the present work that this interplay depends on the mode-specific friction coefficients and corresponding velocity profile, which is the key to understand the role of electronic excitation in state-to-state scattering of molecules from metal surfaces.
Conclusions
To summarize, we systematically investigate the hot-electron effects during non-reactive and reactive scattering of H2 from Ag(111) based on the electronic friction theory using the LDFA and TDPT models. An accurate and analytical NN representation combined with a simple mapping scheme is developed for interpolating the friction tensor calculated within TDPT, enabling us to perform extensive MDEF simulations with low cost. Similar to the H2 + Cu(111) system,15 both LDFA and TDPT models result in a minor reduction of the H2 dissociation probability on Ag(111) because of the nonadiabatic energy loss. Contrary to H2 + Cu(111),15 however, the vibrational deexcitation probability of the H2(ν = 2, j = 0 → ν = 1, j = 0) scattering from Ag(111) calculated using TDPT or LDFA based electronic friction does not show much difference from that obtained in adiabatic dynamics. This difference was previously proposed as a potential “fingerprint” of mode-dependent friction and a benchmark for testing the approximations in MDEF simulations for the case of H2 on Cu(111). Our analysis reveals two important factors that dictate whether nonadiabatic effects contribute significantly to the vibrational deexcitation probability. Firstly, the magnitude of the friction coefficient along the intramolecular vibration DOF needs to be significant over a wide range of geometries far before reaching the transition state in order to significantly affect the vibrational state of a molecule during an unreactive scattering event (due apparently to the diminished velocity at the turning point). Secondly, the molecule-metal potential energy landscape that controls the velocity profile during molecular scattering needs to be such that during the molecule–surface encounter, velocities and surface residence times are large before the turning point. Hence, the measurability of nonadiabatic effects depends sensitively on the choice of system and experimental conditions. For example, the two aforementioned factors could be experimentally studied in more detail by molecular beam scattering experiments with variable incidence angles. Particularly, scattering at very low incidence angles with respect to the surface could maximise the velocity close to the surface and surface residence time and provide a more sensitive measure of EHP-induced energy loss.
Our results emphasize the importance of simultaneously accounting for the mode-dependent magnitude and the tensorial nature of electronic friction and the underlying molecule–surface interaction as described by a realistic ab initio calculated PES. The latter is much more system-dependent, which means that strong intrinsic electronic friction components during a gas-surface reaction do not a priori lead to measurable electronic dissipation effects. For such measurable effects, an interplay between high adsorbate velocities along DOFs and strong electronic friction is required and should be a guiding principle when selecting systems with high propensity for nonadiabatic effects. To arrive at a clearer picture of nonadiabatic dissipation during gas-surface dynamics, and, more importantly, to design systems where nonadiabatic effects can be utilized to selectively control chemical reactions as envisioned in hot-electron chemistry, this interplay needs to be studied systematically in the future.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
YZ and BJ acknowledge support by National Key R&D Program of China (2017YFA0303500), National Natural Science Foundation of China (91645202, 21722306, and 21573203), Anhui Initiative in Quantum Information Technologies, and computational resources offered by the Supercomputing Center of USTC and Advanced Materials High-Performance Company. RJM acknowledges financial support by the US Department of Energy - Basic Energy Science grant DE-FG02-05ER15677 (J. C. Tully, PI) and computational resources provided by the HPC facilities of the Yale Center for Research Computing, the University of Warwick Scientific Computing Research Technology Platform, and the EPSRC-funded HPC Midlands Plus centre (EP/P020232/1). HG is supported by the U.S. National Science Foundation (Grant No. CHE-1462109). BJ thanks Dr S. P. Rittmeyer and Prof. Maite Alducin (during Stereodynamics 2018) for some helpful discussions. The primary research data for this article is available upon request from the authors.
Footnotes
†Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03955k
References
- Wodtke A. M., Matsiev D., Auerbach D. J. Prog. Surf. Sci. 2008;83:167–214. [Google Scholar]
- Rittmeyer S. P., Bukas V. J., Reuter K. Adv. Phys.: X. 2018;3:1381574. [Google Scholar]
- Alducin M., Díez Muiño R., Juaristi J. I. Prog. Surf. Sci. 2017;92:317–340. [Google Scholar]
- Wodtke A. M., Tully J. C., Auerbach D. J. Int. Rev. Phys. Chem. 2004;23:513–539. [Google Scholar]
- Huang Y., Rettner C. T., Auerbach D. J., Wodtke A. M. Science. 2000;290:111–114. doi: 10.1126/science.290.5489.111. [DOI] [PubMed] [Google Scholar]
- Huang Y., Wodtke A. M., Hou H., Rettner C. T., Auerbach D. J. Phys. Rev. Lett. 2000;84:2985–2988. doi: 10.1103/PhysRevLett.84.2985. [DOI] [PubMed] [Google Scholar]
- Shenvi N., Roy S., Tully J. C. Science. 2009;326:829–832. doi: 10.1126/science.1179240. [DOI] [PubMed] [Google Scholar]
- Gergen B., Nienhaus H., Weinberg W. H., McFarland E. W. Science. 2001;294:2521–2523. doi: 10.1126/science.1066134. [DOI] [PubMed] [Google Scholar]
- Bünermann O., Jiang H., Dorenkamp Y., Kandratsenka A., Janke S. M., Auerbach D. J., Wodtke A. M. Science. 2015;350:1346–1349. doi: 10.1126/science.aad4972. [DOI] [PubMed] [Google Scholar]
- Nienhaus H. Surf. Sci. Rep. 2002;45:1–78. [Google Scholar]
- Morin M., Levinos N. J., Harris A. L. J. Chem. Phys. 1992;96:3950–3956. [Google Scholar]
- Christopher P., Xin H., Linic S. Nat. Chem. 2011;3:467–472. doi: 10.1038/nchem.1032. [DOI] [PubMed] [Google Scholar]
- Christopher P., Xin H., Marimuthu A., Linic S. Nat. Mater. 2012;11:1044–1050. doi: 10.1038/nmat3454. [DOI] [PubMed] [Google Scholar]
- Park J. Y., Kim S. M., Lee H., Nedrygailov I. I. Acc. Chem. Res. 2015;48:2475–2483. doi: 10.1021/acs.accounts.5b00170. [DOI] [PubMed] [Google Scholar]
- Spiering P., Meyer J. J. Phys. Chem. Lett. 2018;9:1803–1808. doi: 10.1021/acs.jpclett.7b03182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper R., Bartels C., Kandratsenka A., Rahinov I., Shenvi N., Golibrzuch K., Li Z., Auerbach D. J., Tully J. C., Wodtke A. M. Angew. Chem., Int. Ed. 2012;51:4954–4958. doi: 10.1002/anie.201201168. [DOI] [PubMed] [Google Scholar]
- Kruger B. C., Bartels N., Bartels C., Kandratsenka A., Tully J. C., Wodtke A. M., Schafer T. J. Phys. Chem. C. 2015;119:3268–3272. [Google Scholar]
- Tully J. C. J. Chem. Phys. 2012;137:22A301. doi: 10.1063/1.4757762. [DOI] [PubMed] [Google Scholar]
- Persson M., Hellsing B. Phys. Rev. Lett. 1982;49:662–665. [Google Scholar]
- Head-Gordon M., Tully J. C. J. Chem. Phys. 1995;103:10137–10145. [Google Scholar]
- Dou W. J., Miao G. H., Subotnik J. E. Phys. Rev. Lett. 2017;119:046001. doi: 10.1103/PhysRevLett.119.046001. [DOI] [PubMed] [Google Scholar]
- Dou W., Subotnik J. E. J. Chem. Phys. 2018;148:230901. doi: 10.1063/1.5035412. [DOI] [PubMed] [Google Scholar]
- Juaristi J. I., Alducin M., Muiño R. D., Busnengo H. F., Salin A. Phys. Rev. Lett. 2008;100:116102. doi: 10.1103/PhysRevLett.100.116102. [DOI] [PubMed] [Google Scholar]
- Kandratsenka A., Jiang H., Dorenkamp Y., Janke S. M., Kammler M., Wodtke A. M., Bünermann O. Proc. Natl. Acad. Sci. U. S. A. 2018;115:680–684. doi: 10.1073/pnas.1710587115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroes G.-J., Pavanello M., Blanco-Rey M., Alducin M., Auerbach D. J. J. Chem. Phys. 2014;141:054705. doi: 10.1063/1.4891483. [DOI] [PubMed] [Google Scholar]
- Blanco-Rey M., Juaristi J. I., Díez Muiño R., Busnengo H. F., Kroes G. J., Alducin M. Phys. Rev. Lett. 2014;112:103203. doi: 10.1103/PhysRevLett.112.103203. [DOI] [PubMed] [Google Scholar]
- Novko D., Blanco-Rey M., Juaristi J. I., Alducin M. Phys. Rev. B: Condens. Matter Mater. Phys. 2015;92:201411. [Google Scholar]
- Luo X., Jiang B., Juaristi J. I., Alducin M., Guo H. J. Chem. Phys. 2016;145:044704. doi: 10.1063/1.4959288. [DOI] [PubMed] [Google Scholar]
- Jiang B., Alducin M., Guo H. J. Phys. Chem. Lett. 2016;7:327–331. doi: 10.1021/acs.jpclett.5b02737. [DOI] [PubMed] [Google Scholar]
- Martin-Gondre L., Alducin M., Bocan G. A., Díez Muiño R., Juaristi J. I. Phys. Rev. Lett. 2012;108:096101. doi: 10.1103/PhysRevLett.108.096101. [DOI] [PubMed] [Google Scholar]
- Füchsel G., del Cueto M., Díaz C., Kroes G.-J. J. Phys. Chem. C. 2016;120:25760–25779. [Google Scholar]
- Liu Q., Zhou X., Zhou L., Zhang Y., Luo X., Guo H., Jiang B. J. Phys. Chem. C. 2018;122:1761–1769. [Google Scholar]
- Galparsoro O., Petuya R., Busnengo F., Juaristi J. I., Crespos C., Alducin M., Larregaray P. Phys. Chem. Chem. Phys. 2016;18:31378–31383. doi: 10.1039/c6cp06222a. [DOI] [PubMed] [Google Scholar]
- Galparsoro O., Busnengo H. F., Juaristi J. I., Crespos C., Alducin M., Larregaray P. J. Chem. Phys. 2017;147:121103. doi: 10.1063/1.4997127. [DOI] [PubMed] [Google Scholar]
- Galparsoro O., Juaristi J. I., Crespos C., Alducin M., Larregaray P. J. Phys. Chem. C. 2017;121:19849–19858. doi: 10.1063/1.4997127. [DOI] [PubMed] [Google Scholar]
- Loncaric I., Alducin M., Saalfrank P., Juaristi J. I. Phys. Rev. B. 2016;93:014301. [Google Scholar]
- Luntz A. C., Makkonen I., Persson M., Holloway S., Bird D. M., Mizielinski M. S. Phys. Rev. Lett. 2009;102:109601. doi: 10.1103/PhysRevLett.102.109601. [DOI] [PubMed] [Google Scholar]
- Rittmeyer S. P., Meyer J., Juaristi J. I., Reuter K. Phys. Rev. Lett. 2015;115:046102. doi: 10.1103/PhysRevLett.115.046102. [DOI] [PubMed] [Google Scholar]
- Maurer R. J., Jiang B., Guo H., Tully J. C. Phys. Rev. Lett. 2017;118:256001. doi: 10.1103/PhysRevLett.118.256001. [DOI] [PubMed] [Google Scholar]
- Maurer R. J., Askerka M., Batista V. S., Tully J. C. Phys. Rev. B. 2016;94:115432. doi: 10.1103/PhysRevLett.116.217601. [DOI] [PubMed] [Google Scholar]
- Askerka M., Maurer R. J., Batista V. S., Tully J. C. Phys. Rev. Lett. 2016;116:217601. doi: 10.1103/PhysRevLett.116.217601. [DOI] [PubMed] [Google Scholar]
- Zhou L., Zhou X., Alducin M., Zhang L., Jiang B., Guo H. J. Chem. Phys. 2018;148:014702. doi: 10.1063/1.5016054. [DOI] [PubMed] [Google Scholar]
- Hellsing B., Persson M. Phys. Scr. 1984;29:360–371. [Google Scholar]
- Novko D., Alducin M., Blanco-Rey M., Juaristi J. I. Phys. Rev. B. 2016;94:224306. [Google Scholar]
- Novko D., Alducin M., Juaristi J. I. Phys. Rev. Lett. 2018;120:156804. doi: 10.1103/PhysRevLett.120.156804. [DOI] [PubMed] [Google Scholar]
- Blum V., Gehrke R., Hanke F., Havu P., Havu V., Ren X., Reuter K., Scheffler M. Comput. Phys. Commun. 2009;180:2175–2196. [Google Scholar]
- Perdew J. P., Burke K., Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Kolb B., Luo X., Zhou X., Jiang B., Guo H. J. Phys. Chem. Lett. 2017;8:666–672. doi: 10.1021/acs.jpclett.6b02994. [DOI] [PubMed] [Google Scholar]
- Muzas A. S., Juaristi J. I., Alducin M., Muiño R. D., Kroes G. J., Díaz C. J. Chem. Phys. 2012;137:064707. doi: 10.1063/1.4742907. [DOI] [PubMed] [Google Scholar]
- Díaz C., Pijper E., Olsen R. A., Busnengo H. F., Auerbach D. J., Kroes G.-J. Science. 2009;326:832–834. doi: 10.1126/science.1178722. [DOI] [PubMed] [Google Scholar]
- Jiang B., Guo H. J. Chem. Phys. 2014;141:034109. doi: 10.1063/1.4887363. [DOI] [PubMed] [Google Scholar]
- Jiang B., Guo H. J. Chem. Phys. 2013;139:054112. doi: 10.1063/1.4817187. [DOI] [PubMed] [Google Scholar]
- Jiang B., Guo H. Phys. Chem. Chem. Phys. 2014;16:24704–24715. doi: 10.1039/c4cp03761h. [DOI] [PubMed] [Google Scholar]
- Luntz A. C., Persson M. J. Chem. Phys. 2005;123:074704. doi: 10.1063/1.2000249. [DOI] [PubMed] [Google Scholar]
- Hu X., Jiang B., Xie D., Guo H. J. Chem. Phys. 2015;143:114706. doi: 10.1063/1.4931040. [DOI] [PubMed] [Google Scholar]
- Maurer R. J., Zhang Y., Guo H., Jiang B., Faraday Discuss. , , in press . [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.