Age at menarche and osteoporosis: A Mendelian randomization study

Abstract

Purpose:

Traditional epidemiological studies suggest that there is an association between age at menarche (years) (AAM) and bone mineral density (BMD) at the sites of the femoral neck and lumbar spine (FNK and LS BMD), indicating a potentially important relationship between AAM and the development of osteoporosis (OP). However, these findings may be influenced by unmeasured confounding factors that can obscure the true relationship between the phenotypic traits. Therefore, we performed Mendelian randomization (MR) analyses to determine whether there is a causal relationship between AAM and BMD (FNK and LS BMD), where late AAM may increase the risk of developing OP.

Methods:

Adopting a two-sample MR approach we incorporated genome-wide association (GWAS) summary statistics from the Reproductive Genetics (ReproGen) Consortium (n = 182,416) (females only) and the GEnetic Factors for OSteoporosis (GEFOS) Consortium (n = 53,236) (both males and females).

Results:

Using this MR approach we discovered that each additional year in AAM is associated with a modest reduction in FNK BMD (β = −0.072 se = 0.022, 95% CI (−0.115, −0.030), p = 0.001) and LS BMD ((β = −0.072, se = 0.025, 95% CI (−0.121, −0.023), p = 0.004), and therefore influences OP susceptibility.

Conclusions:

This study demonstrates that AAM in females may play a causal role in OP etiology and provides novel insights into the pathophysiology of bone related diseases like osteoporosis, osteopenia and fracture.

Summary:

Our study demonstrates that AAM in females may play a causal role in OP etiology and provides novel insights into the pathophysiology of bone related diseases like osteoporosis, osteopenia and fracture. By adopting Mendelian Randomization approaches, our study was not susceptible to bias from unmeasured confounders or reverse causation.

1. Introduction

Osteoporosis (OP) is a common metabolic skeletal disease characterized by reduced bone mineral density (BMD) that results in increased bone fragility and higher risk for bone fractures among affected elderly individuals. It is estimated that osteoporosis affects over 200 million people worldwide, including 10% of women aged > 60, 20% of women aged > 70, 40% of women aged > 80, and two-thirds of women aged > 90 [1]. Approximately 9 million osteoporosis patients develop bone fractures every year [2], and by the year 2050 the incidence rate of hip fractures is expected to increase by 240% and 310% in women and men respectively [1]. Although osteoporosis is an important public health concern, the biological mechanisms underlying this complex disease are still poorly understood.

BMD, a highly heritable trait and an important index of bone strength, is frequently used in osteoporosis diagnosis for clinical and epidemiological studies. While there are many environmental factors that may influence the risk of osteoporosis, it is estimated that nearly 75% of the variance in BMD at the site of the femoral neck (FNK) and 83% in the lumbar spine (LS) may be explained by genetic determinants [3,4]. Despite the fact that previous studies have identified dozens of trait-associated genetic loci [5,6], these efforts have only been able to explain approximately 10% of the variability in BMD and very few causal factors have been identified so far [7].

Researchers have shown that age at menarche (AAM) may potentially play a critical role in the etiology of complex diseases developed by women later in life such as osteoporosis [8]. A series of studies have shown that late AAM is associated with elevated risk of reduced BMD and subsequent osteoporosis/osteoporotic fractures [9,10]. It is believed that this may be due to the fact that women who have a late AAM in turn have a shorter duration of exposure to estrogen, a vital hormonal factor for bone formation and growth in women [11]. A recent publication also demonstrated strong association between estrogen 17 β-estradiol (E2, genetic determinants of circulating estrogen levels) and BMD [12]. Another study supported these findings by demonstrating that AAM may influence osteoporosis susceptibility, although the association was diminished in FNK BMD while remaining significant in LS BMD after adjusting for potential confounding factors such as alcohol intake, cigarette smoking, and exercise [13].

In contrast to the findings in Caucasian populations, a cross sectional population-based study conducted in China demonstrated that AAM is not associated with osteoporosis [14]. However, it is believed that the association between AAM and BMD may be mediated by BMI and waist circumference (WC), so it is conceivable these mediators may contribute to an attenuation of the association in this study. Multiple observational studies have reported significant associations between elevated adult BMI and younger AAM [15,16], and therefore the relationship between AAM and OP may be mediated by adult BMI or obesity. To minimize the effects of unmeasured confounding factors in distorting the association between AAM and OP, a more efficient approach is needed to infer a potential causal relationship between these traits.

The Mendelian randomization (MR) [17] approach enables us to investigate potentially causal relationships by using genetic instrumental variables to assess the potential causal effect of a risk factor (AAM) on the outcome (FNK and LS BMD). The instrumental variable analysis requires a variable that is a proxy for the exposure of interest and must satisfy several important requirements. The ideal instrument must have a strong association with the exposure of interest, no direct association with the outcome other than via the exposure, no association with both measured and unmeasured confounders, and it cannot introduce potential confounding into the relationship being tested. Given an appropriate instrument the confounders will be randomly distributed across the conditions of interest, similar to a randomized trial. Thus the MR studies will not be distorted by confounders in contrast to traditional observational studies.

MR has the ability to enable causal inference in several important ways. The direct association between SNPs and the outcome provides evidence for the existence of a causal relationship. Additionally, the magnitude of the associations between SNPs-exposure and SNPs-outcome may be used to estimate the magnitude of the causal effect of the exposure on the outcome. Compared with one-sample MR, which extracts the effect estimates for instrumental variable-exposure association and instrumental variable-outcome association from the same sample, two-sample MR estimates these associations in different samples and the estimates are then combined to infer the potential exposure-outcome causal association. Additionally, the two-sample MR can overcome any weak instrument biases that may confound the one-sample MR as well as avoid the situation of “Winner’s curse” where one-sample MR may tend to underestimate the true causal effect [18].

In order to estimate whether AAM is causally associated with OP susceptibility, we carried out a two-sample MR analysis using GWAS summary statistics. The aim of this study is to clarify the causal relationship between AAM and OP and better understand the biological mechanisms that underlie osteoporosis and how they may influence the risk of bone related diseases.

2. Materials and methods

2.1. Data sources and SNP selection

Summary statistics for AAM-associated SNPs were extracted from a GWAS meta-analysis performed by the ReproGen Consortium, which consists of 182,416 women of European descent from 57 studies [19]. For the implementation of MR, we selected SNPs that achieved genome-wide significance (p < 5 × 10⁻⁸) in this GWAS dataset as instrumental variables. Effect estimates of these AAM-associated SNPs on the risk of OP were assessed using the summary statistics of European individuals for FNK BMD and LS BMD from the GEFOS Consortium [20]. The European samples from the 1000 genomes project were adopted to estimate linkage disequilibrium (LD) between chosen SNPs. When target SNPs were not available in the outcome (FNK and LS BMD) study, we used proxy SNPs that were in high LD (r² > 0.8) with the SNPs of interest.

Since age at menopause is a major potential confounding factor for this study, we also checked the association of AAM associated SNPs with age at natural menopause (ANM) in the GWAS summary statistics. Summary statistics for ANM were extracted from a GWAS meta-analysis performed by the ReproGen Consortium, which consists of 69,360 women of European descent from 33 studies [21]. Calcium concentration were used as negative control for BMD, the summary statistics of it were derived from CHARGE Consortium [22], including 20,611 individuals of European ancestry. Summary statistics from these consortia can be downloaded at the following public websites: REPROGEN, http://www.reprogen.org/data_download.html, GEFOS, http://www.gefos.org/?q=content/data-release-2015.

3. SNP validation

3.1. LD assessment

To ensure the SNPs used as instrumental variables for AAM are not in LD with each other, a vital assumption of MR, we calculated pairwise-LD between all of our selected SNPs in the 1000 Genomes European reference sample using PLINK 1.90 [23]. For all pairs of SNPs determined to violate the independence assumption with r² > 0.01 we retained only the SNP with the smaller AAM association p-value. To ensure the effect of a SNP on the exposure (AAM) and the effect of that SNP on the outcome (FNK and LS BMD) correspond to the same allele, we harmonized the effect of these instrumental SNPs by using a function that ensures all corresponding risk factor (AAM) and outcome (FNK and LS BMD) alleles are on the same strand where possible. If they are not then the function will flip alleles and use allele frequency to infer the strand of palindromic SNPs.

3.2. Pleiotropy assessment

Another important assumption of MR is that the exposure-related SNPs do not exert influence on FNK and LS BMD through other pleiotropic pathways except through the exposure itself (AAM). To assess whether there are horizontal pleiotropic effects where instrumental variables affect BMD via more than one biological pathway [24], we employed MR-Egger regression (25), which is often used in meta-analysis to examine whether there is evidence of publication bias [26].

When applying the MR-Egger method the SNP’s effect estimate for exposure (AAM) is plotted against its effect estimate on the outcome (FNK and LS BMD), and an intercept that deviates from the origin may provide evidence for potential pleiotropic effects across the genetic instrumental variables. Similar to the use of funnel plots in the meta-analysis literature [27], this plot can be adopted to provide a visual inspection of symmetry where any departures may be suggestive of potential pleiotropy across the genetic instrumental variables. Additionally, the estimate for MR-Egger regression slope provides the pleiotropy-corrected causal effect. However, this estimate may be underpowered if the selected SNPs collectively fail to explain a large proportion of the variance in the exposure [25]. An important assumption for the MR-Egger regression, referred to as InSIDE (INstrument Strength is Independent of Direct Effect) [25] states that a SNP’s effect estimate on the exposure must be independent from its direct effect upon the outcome. Nonetheless, the MR-Egger approach tends to provide robust causal effect estimates even if the selected SNPs are weak instruments [25].

Furthermore, the weighted median approach [28] was also utilized to complement the MR-Egger method to provide more robust MR estimates. Using this approach, the MR estimates were ordered from the smallest to largest weighted by their inverse variances. Then the weighted median estimator is the 50% weighted percentile. This method is believed to generate unbiased estimates of the MR causal effect provided that > 50% of the weight comes from valid SNPs. Previous studies have confirmed that the weighted median approach affords some distinct superiorities over MR-Egger for its improved power of causal effect detection, lower type I error and robustness to the In-SIDE assumption [28]. Therefore, we adopted both approaches in this study to better estimate the causal effect and to assess potential bias in the results.

3.3. Population stratification assessment

Population stratification is another potential bias-inducing factor for MR analyses since the minor allele frequency (MAF) differences among different ancestries may result in SNPs that are associated with both ancestry and the outcome [29]. To avoid this situation, we selected SNPs and their corresponding summary statistics (p-value, beta effect, and standard error) from studies that include only individuals of European descent for both AAM and FNK and LS BMD. However, it is plausible that there may still exist residual effects of population stratification among European subgroups [30] although the original studies of the two meta-analyses already assessed and/or corrected for potential stratification [19,20]. For further understanding of residual population stratification, we assessed whether heterogeneity exists for the chosen SNPs by performing the by performing the Cochran’s Q test, the Cochran’s Q statistic is calculated as the weighted sum of squared differences between individual SNP effect and the pooled effect across all SNPs.

3.4. MR estimates

We applied the principles of two-sample MR to assess the role of AAM in the susceptibility of OP. Briefly, we selected SNPs that were strongly associated (p < 5E-8) with AAM in the REPROGEN consortium as our instrumental variables and then obtained the corresponding effect estimates of these variables on AAM. The effect estimates for the selected SNPs on FNK and LS BMD were extracted from the GEFOS release in 2015 [20]. Then a two-sample MR approach was adopted by weighting the effect estimate of each SNP on FNK and LS BMD by its effect on AAM. These estimates were then pooled using a fixed or random effect meta-analysis model [31,32] to provide a comprehensive summary of the effect of genetically late AAM upon BMD risk. All the analyses were implemented by the Two Sample MR package [33] in R software environment.

3.5. MR robust adjusted profile score

Previous GWASs demonstrated that the AAM associated SNPs explain limited variance of AAM, the MR might fail if the selected SNPs are weak instruments. Hence, we carried out a recently proposed method called Robust Adjusted Profile Score (MR.RAPS) [34] which considers the measurement error in SNP-exposure effects and is unbiased when there are many (e.g. hundreds of) weak instruments, and is robust to systematic and idiosyncratic pleiotropy. Detailed information about this method please refer to the original paper [34].

3.6. Sensitivity analyses

In order to guarantee the MR estimates are not influenced by the inclusion of proxy SNPs, we implemented sensitivity analysis after these SNPs were excluded. To ensure the MR estimates are not mediated by BMI and waist ratio (WC), SNPs associated with BMI and WC were also removed to see how they would affect the results. Furthermore, analysis that removed all the proxy SNPs and the SNPs that were associated with BMI and WC was also conducted to further ensure the random error was not introduced into our results.

To determine if there is any single SNP driving the association we also performed a leave-one-out analysis, where the MR is performed removing a different SNP in each iteration. Last, to further identify the causal relationship between AAM and BMD, we performed GO enrichment analysis using the AAM-associated genes and found which genes are enriched in female hormone modulation. Then we used those female hormone modulation associated SNPs to perform MR analysis again.

4. Results

4.1. SNP selection

Overall, we obtained 120 LD-independent SNPs that achieved genome-wide significance for AAM in the ReproGen Consortium after implementing the pruning strategy previously described. However, not all of the SNPs were directly found in the BMD dataset. There were 10 SNPs that were not available in the FNK and LS BMD datasets and therefore we used proxy SNPs that were highly correlated (r² > 0.8) based on the 1000 Genomes European sample data. Four SNPs were removed because they were palindromic with intermediate allele frequencies (where “palindromic SNPs” referred to the SNPs with A/T or G/C alleles and “intermediate allele frequencies” referred to 0.01 < allele frequency < 0.30)). Finally, 116 SNPs remained to perform the MR analysis for each BMD trait, as shown in Table S1 and Table S2. For negative control SNPs please find in Table S3.

4.2. SNP validation

Next we tested whether our selected SNPs were influenced by LD, pleiotropy or population stratification. We determined that all SNPs included in the analysis are independent as they all have pairwise LD with r² < 0.01. Furthermore, SNPs selected in our analysis showed no direct evidence of association with the outcome (FNK and LS BMD) (Table S1 and Table S2). The MR-Egger regression results showed that the estimated value for the intercept term was null for AAM and FNK BMD (β = 0.003, 95% CI (−0.003, 0.008), p = 0.314) as well as for AAM and LS BMD (β = 0.0009, 95% CI (−0.006, 0.008), p = 0.790) (Table 1). This suggests that horizontal pleiotropy does not heavily influence the results.

Table 1.

Results of MR analyses and sensitivity analyses.

Analysis	Number of SNPs	Number of proxies	MR estimates		MR Egger regression	Weighted median
			β (95% CI)	p-Value	Intercept (95% CI)	β (SE)
All SNPs for AAM and FNK BMD	116	8	−0.072 (−0.115, −0.030)	0.001	0.003 (−0.003, 0.008)	−0.0984734(0.0323424)
All proxies excluded	108	0	−0.073 (−0.120, −0.026)	0.002
All SNPs for AAM and LS BMD	116	8	−0.072 (−0.121, −0.023)	0.004	0.0009 (−0.006, 0.008)	−0.0842956(0.0362930)
All proxies excluded	108	0	−0.079 (−0.130, −0.028)	0.003

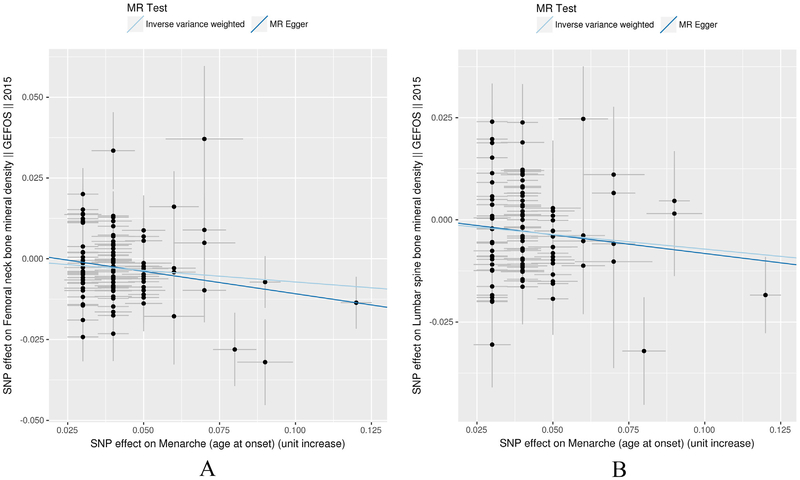
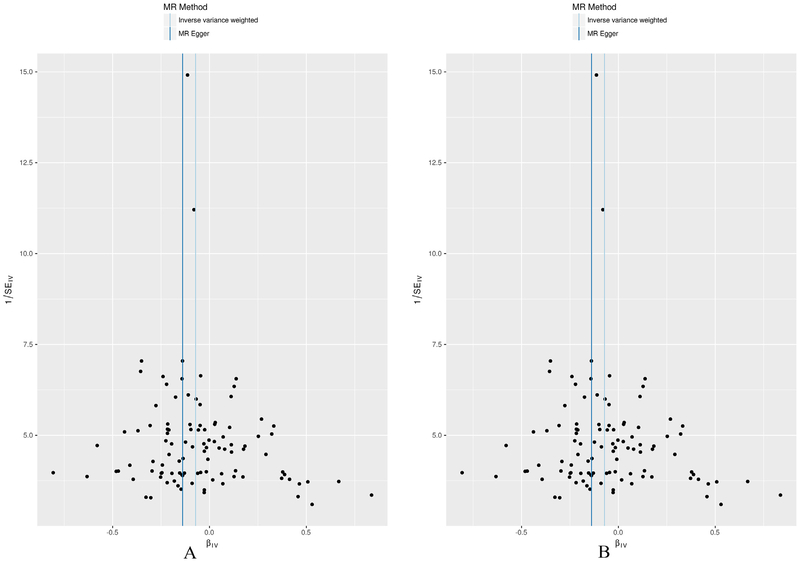
We performed a comparison of the standard inverse-variance weighting (IVW) analysis compared with the MR-Egger analysis that was corrected for potential horizontal pleiotropy. The scatter plot (Fig. 1) which was used to demonstrate the relationship of the SNP effects on the exposure (AAM) against the SNP effects on the outcome (BMD) further confirmed the null-pleiotropy results. These findings are supported by the funnel plot, which appears to be symmetrical (Fig. 2). The Heterogeneity test also demonstrated that there is no evidence of heterogeneity in our chosen SNPs (Table S4).

Fig. 1.

IVW and MR-Egger regression scatterplot for AAM on FNK (A) and LS BMD (B) analysis. The light blue line shows the results of standard MR analysis (inverse-variance weighting [IVW]), and the dark blue line shows the pleiotropy-adjusted MR-Egger regression line. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

MR-Egger regression funnel plot for AAM on FNK (A) and LS BMD (B) analysis. Each SNP’s MR estimate is plotted against its minor allele frequency corrected association with AAM. A minor allele frequency (MAF) correction proportional to the SNP-AAM standard error is used since a low-frequency allele is likely to be measured with low precision. Similar to the use of funnel plots in the meta-analysis literature, this plot can be used for visual inspection of symmetry, where any deviation can be suggestive of pleiotropy. We note that our plot appears generally symmetrical.

4.3. MR estimates

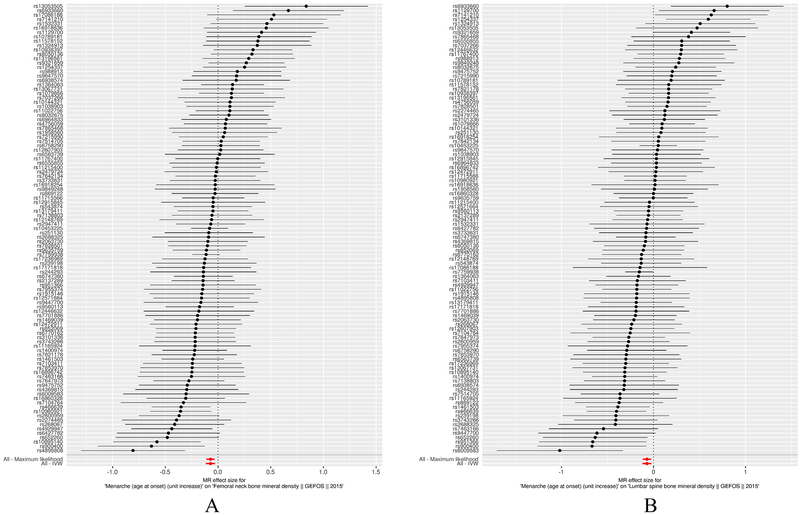
Standard IVW MR results showed that each additional year in AAM is associated with decreasing FNK BMD (β = −0.072 se = 0.022, 95% CI (−0.115, −0.030), p = 0.001) and decreasing LS BMD ((β = −0.072 se = 0.025, 95% CI (−0.121, −0.023), p = 0.004) (Table 1). The slope estimates of other methods including MR-Egger regression, fixed/random effects meta-analysis, and weighted median and maximum likelihood were all consistent with the IVW result (Table 2, Fig. 3, Fig. S1).

Table 2.

Results from different MR methods for FNK BMD and LS BMD.

Method	nSNP	β (FNK (95%CI))	p-Value (FNK BMD)	β (LS BMD(95%CI))	p-Value (LS BMD)
Fixed effects meta analysis (simple SE)	116	−0.072 (−0.111, −0.033)	0.0002	−0.072 (−0.115, −0.029)	0.002
Fixed effects meta analysis (delta method)	116	−0.071 (−0.110, −0.032)	0.0003	−0.070 (−0.115, −0.025)	0.002
Random effects meta analysis (delta method)	116	−0.066 (−0.111, −0.021)	0.004	−0.067 (−0.116, −0.018)	0.008
Maximum likelihood	116	−0.072 (−0.111, −0.033)	0.0003	−0.071 (−0.116, −0.026)	0.002
MR Egger	116	−0.139 (−0.276, −0.002)	0.0497	−0.091 (−0.244, 0.062)	0.245
Weighted median	116	−0.098 (−0.161, −0.035)	0.002	−0.084 (−0.155, −0.013)	0.020
Inverse variance weighted	116	−0.072 (−0.115, −0.030)	0.001	−0.072 (−0.121, −0.023)	0.004

Fig. 3.

Forest plot of MR estimates AAM on FNK (A) and LS BMD (B). Forest plots of all main analyses. The estimated effect size of the IVW, expressed as a β, was (β = −0.072 se = 0.022, 95% CI (−0.115, −0.030), p = 0.001) for FNK BMD and ((β = −0.072 se = 0.025, 95% CI (−0.121, −0.023), p = 0.004) for LS BMD.

4.4. MR robust adjusted profile score

The results turned out to be consistent with the MR results that a late AAM is associated with decreased FNBMD (β = −0.070, se = 0.022, p = 0.001, 95% CI (−0.113, −0.026)) and LSBMD (β = −0.076, se = 0.02526572, p = 0.002, 95% CI (−0.125, −0.026)).

4.5. Sensitivity analyses

We found similar causal effect association between AAM and FNK BMD (β = −0.073, 95% CI (−0.120, −0.026), p = 0.002) and AAM and LS BMD (β = −0.079, se = 0.026, 95% CI (−0.130, −0.028), p = 0.003) after removing all the 8 proxy SNPs. A total of 37 SNPs were found to be associated with BMI, WC and height (p < 1E-4) (Table S5, Table S6, Table S7). After removing these 37 SNPs, there is still modest association between AAM and FNK BMD (β = −0.073, se = 0.023, 95% CI (−0.118, −0.028), p = 0.001) as well as AAM and LS BMD (β = −0.083, se = 0.026, 95% CI (−0.134, −0.032), p = 0.001). Then, we removed all the proxy SNPs and those 37 SNPs that were associated with BMI, WC and height and demonstrated similar results for AAM and FNK BMD (β = −0.071, se = 0.028, 95% CI (−0.126, −0.016), p = 0.011) as well as AAM and LS BMD (β = −0.070, se = 0.030, 95% CI (−0.130, −0.011), p = 0.022). The leave-one-out analysis showed none of the individual genetic markers are driving the majority of the association signal.

Since age at menopause is a major potential confounding factor for this study, we also checked the association of AAM associated SNPs with age at menopause in the GWAS summary statistics and no association signal was detected among all the SNPs we selected. Lastly, GO enrichment found 18 genes were enriched in the pathway related to female hormone modulation and the top ranked pathway in our analysis was “steroid hormone mediated signaling pathway (GO:0043401)”, and then the MR analysis showed that each additional year in AAM is associated with decreasing FNK BMD (β = −0.143, se = 0.007, 95% CI (−0.156, −0.129), p = 0.007) and decreasing LS BMD ((β = −0.139, se = 0.008, 95% CI (−0.155, −0.123), p = 0.009) (Table S8 and Table S9), which further confirmed the causal relationship between AAM and BMD.

5. Discussion

Performing the two sample MR analysis by using summary statistics for FNK and LS BMD and AAM of large European populations, we detected that one year late in AAM was associated with reduced FNK BMD and LS BMD, therefore increasing risk for OP. These findings support the hypothesis that AAM may play a causal role in the pathway of developing OP. Our findings are consistent with some traditional observational studies that suggested late years of AAM is significantly related to higher risk of low FNK and LS BMD or fractures [9,10]. Additionally, these findings may cast doubt on the study that demonstrated age distribution of menarche has no effect on BMD of FNK after adjusted potential confounding factors [13].

Our MR analysis results may provide evidence of the causal role of AAM in the development of OP since the influence of traditional confounding factors in observational studies is minimized/eliminated. By leveraging the summary statistics from the largest available GWAS studies for AAM and BMD we attempted to maximize statistical power.

Our findings may have significant clinical implications since they support the notion that AAM is one of the most important factors that may affect women later in life. Additionally, late years of AAM was reported to be associated with many disorders in elderly women including cardiovascular disease, diabetes [35] and multiple sclerosis [36]. Taken together, this evidence suggests the need to focus on proper prevention and protection strategies for women who may have an increased risk for OP and fracture. These preventive measures may include increasing calcium intake, keeping sufficient protein intake, reduced drinking and smoking, improving physical activity, and maintaining proper daily sun exposure [37]. Study showed that [38] isoflavone intervention significantly attenuates bone loss of the spine in menopausal women and the effects become more significant when > 90 mg/day of isoflavones are consumed. We assume that isoflavone intervention will also attenuate bone loss in late AAM, however, which needs further confirmation in our future studies.

There are several important strengths to note for the MR analysis. First, since the alleles follow the principle of random distribution when forming gametes at meiosis, the causal effect of genotype on disease in MR studies will not be distorted by the confounding factors, a major limitation of traditional observational studies. Second, adopting the summary-level data of two large GWASs genetic consortium of AAM and BMD provides us more convenience to test the hypothesized association between AAM and BMD than by using the individual-level data, which is not readily available. Furthermore, previous studies have shown that performing the MR analysis by using summary statistics data and by using individual-level data have similar efficiency [39].

There may also be some limitations in our study. First, the FNKBMD dataset we used in our study contains both females and males. We would have preferred to use the 2012 FNKBMD dataset (6) which only includes females, however the 2012 FNKBMD dataset did not provide the summary statistics (effect sizes and standard errors) that we needed for the MR analysis. We expected that choosing to use a dataset that includes both males and females would have attenuated the association signal between AAM and OP in this study, thus rendering our results conservative. Therefore, future MR studies may be warranted to verify our results in female only samples (when such samples are available). In addition, although our analysis supported the MR hypothesis that a causal role of late AAM in OP susceptibility, we could not conclude that female hormone actually plays a role in disease modulation. However, MR Egger was employed to ensure the analysis was not biased by the pleiotropy of the instrumental SNPs. In theory [39], the MR main analysis will not be affected by the residual pleiotropy.

In conclusion, our results confirmed that female individuals who bear late years of AAM might have greater risk of lower FNKBMD and LABMD and therefore higher possibility of developing OP and fractures, which strongly supports the MR hypothesis that a causal role of late AAM in OP susceptibility.