Intraspecific scaling laws are preserved in ventricular hypertrophy but not in heart failure

Abstract

It is scientifically and clinically important to understand the structure-function scaling of coronary arterial trees in compensatory (e.g., left and right ventricular hypertrophy, LVH and RVH) and decompensatory vascular remodeling (e.g., congestive heart failure, CHF). This study hypothesizes that intraspecific scaling power laws of vascular trees are preserved in hypertrophic hearts but not in CHF swine hearts. To test the hypothesis, we carried out the scaling analysis based on morphometry and hemodynamics of coronary arterial trees in moderate LVH, severe RVH, and CHF compared with age-matched respective control hearts. The scaling exponents of volume-diameter, length-volume, and flow-diameter power laws in control hearts were consistent with the theoretical predictions (i.e., 3, 7/9, and 7/3, respectively), which remained unchanged in LVH and RVH hearts. The scaling exponents were also preserved with an increase of body weight during normal growth of control animals. In contrast, CHF increased the exponents of volume-diameter and flow-diameter scaling laws to 4.25 ± 1.50 and 3.15 ± 1.49, respectively, in the epicardial arterial trees. This study validates the predictive utility of the scaling laws to diagnose vascular structure and function in CHF hearts to identify the borderline between compensatory and decompensatory remodeling.

NEW & NOTEWORTHY

A scaling law analysis was performed to enhance the understanding of fractal-regulated remodeling of coronary arterial trees in moderate left ventricular hypertrophy, severe right ventricular hypertrophy, and congestive heart failure (CHF) pig hearts. The findings show that the altered scaling exponents reflect the impaired structure-function hierarchy of coronary arterial trees in CHF.

the scaling power laws of dimensional proportions characterize natural form with remarkable simplicity (29, 34, 38, 39). Intraspecific scaling power laws of vascular trees have recently been proposed to explain morphological and hemodynamic scaling and structure-function relation in a vascular tree (16, 18, 19, 26, 43), which were validated using the measured morphometric data of vascular trees in various organs and species. These scaling laws were used to estimate and diagnose diffuse coronary artery disease (21) and Glagov's positive remodeling in early stages of coronary atherosclerosis (12), as well as other clinical applications in epicardial coronary arteries (6, 35). There is, however, a lack of scaling analysis in an entire coronary arterial tree in compensatory (e.g., moderate left ventricular hypertrophy, LVH, and severe right ventricular hypertrophy, RVH) or decompensatory (e.g., congestive heart failure, CHF) vascular remodeling.

The objective of the study was to understand the changes of exponents and coefficients of scaling power laws that dictate the relations between volume-diameter, length-volume, and flow-diameter in various disease conditions. The altered power-law relations are associated with both global and local changes of morphometry and hemodynamics in epicardial, transmural, and perfusion arterial trees, as well as the entire coronary arterial trees of control, LVH, RVH, and CHF hearts in diastolic, vasodilated condition. Here, we hypothesize that compensatory remodeling in moderate LVH and severe RVH maintains the structure-function relationship in coronary arterial trees, whereas decompensatory remodeling in CHF alters the scaling laws of coronary vasculature. To test the hypothesis, the entire left circumflex (LCx) arterial trees were reconstructed from measured morphometric and histological data in control, LVH, and CHF hearts (14, 17), whereas the entire right coronary arterial (RCA) trees were determined in control and RVH hearts (20, 27). A steady-state model was used to compute the flow distribution in the reconstructed trees (14, 17). On the basis of morphometry and hemodynamics in the entire coronary arterial trees, we investigated the effects of LVH, RVH, and CHF on scaling exponents and coefficients. The study is important because it shows that the scaling laws can identify the borderline between compensatory and decompensatory vascular remodeling in LVH, RVH, and CHF hearts.

METHODS

Morphometric data.

Huo and Kassab have reported morphometric data of coronary arterial trees of LVH (14), RVH (27), and CHF (17). Briefly, a 5-wk period of aortic banding was applied to six Yorkshire pigs (2 mo old before surgery) (14), where the constriction was placed supravalvular and hence the increase in LV pressure was transmitted to the coronary arteries given that coronary ostia sat below constriction. Age-matched control animals of the same strain were used compared with LVH. The systolic pressure was 144 ± 21 mmHg compared with the control pressure of 106 ± 7 mmHg (P < 0.05), whereas the diastolic pressures and ejection factions (EF) were similar (∼80 mmHg and ∼73%, respectively). The LV/BW (body wt) had values of 4.04 ± 0.24 and 3.35 ± 0.24 (g/kg) for LVH and control, respectively (P < 0.05). A 5-wk period of pulmonary artery banding was applied to six Yorkshire pigs (3 mo old before surgery) (27). Age-matched control animals of the same strain were used compared with RVH. RVH and control animals had similar diastolic pressures (∼85 mmHg) and EF (∼75%). The RV/LV had values of 0.66 ± 0.03 and 0.29 ± 0.01 for RVH and control, respectively (P < 0.05). A 4-wk period of ventricular pacing (190–220 beats per minute) was used to induce CHF in six Yorkshire pigs (4.5 mo old before surgery) (17). Age-matched control animals were used compared with CHF pigs. CHF resulted in a slight drop of diastolic pressure with no statistical difference from controls and ∼50% drop of EF (P < 0.05) compared with controls (i.e., ∼77 mmHg and <40% in CHF vs. ∼80 mmHg and ∼75% in controls). The LV/BW has values of 3.22 ± 0.61 and 3.14 ± 0.25 (g/kg) for CHF and control, respectively.

Morphometric data on coronary arterioles of diameter <40 μm were measured from histological specimens, whereas coronary arteries of diameter >40 μm were obtained from casts. Briefly, 12 plugs of myocardial tissue were removed from LV (or RV) free wall of three diseased pigs and 12 plugs from LV (or RV) wall of three control pigs (at regions corresponding to those in the diseased hearts). Each plug was ∼4 × 4 mm² in cross section and extended transmurally from epicardium to endocardium. Each plug was completely sectioned transmurally into 60–80-μm thickness. Each section was dehydrated with alcohol and cleared with methyl salicylate to render transparent myocardium and visible microvasculature. After removal of tissue plugs, the same hearts were digested with a 30% KOH solution for several days. The digested tissue was washed away with soap and water. The veins were carefully pruned away, leaving the LCx (or RCA) and its branches intact with clusters of capillaries. The morphometric measurements from histological specimens and casts of swine hearts were identical to those described previously (28).

A computer reconstruction of the entire coronary arterial tree was performed based on the morphometric measurements. Briefly, a two-step approach was employed in reconstruction of the entire coronary arterial tree down to the capillary level. The cast data were reconstructed one bifurcation at a time. The simulated growth of a broken terminal cast vessel >40 μm entailed the search of intact bifurcations (for which mother and the 2 daughter vessels were measured from the cast data) with mother diameter closest (smallest difference) to the terminal vessel. Once such a bifurcation was found, it was “pasted” to the broken vessel. A search was then made for each of the two daughter vessels of the pasted bifurcation and so on. This process was repeated until the tree was reconstructed down to ∼40 μm. On the other hand, the growth of a broken or terminal cast vessel ≤40 μm entailed the search of intact subtrees (for which a subtree was determined from the histological data) with the inlet diameter closest (smallest difference) to the terminal vessel. The selected subtree was then pasted to the cut vessel. The above process was repeated until the entire coronary arterial tree had terminal vessels with diameters ≤8 μm. The diameter-defined Strahler system (28) was assigned to the reconstructed entire coronary arterial tree.

Flow simulation.

After the branching pattern and vascular geometry of the entire coronary arterial tree were generated in diastole in the absence of vessel tone, a steady-state flow analysis was performed similar to a previous study (17). Briefly, the governing equations are that Z(0) = (128μL)/(πD⁴) + Z(L), the conservation of mass at each junction, Q_mother = ∑Q_daughters, and the continuous pressure at each junction, P(L)_mother = P(0)_daughters, where L, D, and Q are the length, diameter, and flow rate of the vessel segment, respectively, Z(0) and Z(L) are the resistance at the entrance and exit of the vessel, respectively, P(0) and P(L) are the pressures at the entrance and exit of the vessels, respectively, and μ is the blood viscosity as a function of vessel diameter (31). The pressure at the inlet of the coronary arterial tree was 80 mmHg to mimic the diastolic pressure for control, LVH, RVH, and CHF pigs. The resistance at each outlet of coronary arterial tree was taken as (128μ_capillaryL_capillary)/(πD_capillary⁴), where D_capillary, L_capillary, and μ_capillary refer to the diameter, length, and viscosity, respectively, in the first capillary segments to mimic the distal resistance. The method of solution was similar to that outlined in a previous study (17).

Scaling laws.

We defined a vessel segment as a stem and the tree distal to the stem as a crown (16). A coronary arterial tree has many stem-crown units. In an integrated system of stem-crown units, the crown volume (V_C; unit: ml) is defined as the sum of the intravascular volume of each vessel segment, and the crown length (L_C; unit: cm) is defined as the sum of the lengths of each vessel segment in the entire crown from the stem to the most distal vessels. D_S is the stem diameter, and Q_S is the flow rate through the stem in a stem-crown unit. On the basis of the fractal nature of coronary trees (16), we derived the volume-diameter scaling power law as:

$$V_c=K_{VD}{D}_s^3$$ (1)

where the scaling coefficient, K_VD, is a constant. On the basis of the volume-diameter scaling law and the minimum energy hypothesis, we derived the length-volume scaling power law as:

$$L_c=K_{LV}{V}_c^{\frac{7}{9}}$$ (2)

where the scaling coefficient, K_LV, is a constant. Furthermore, the flow-diameter scaling power law is given as:

$$Q_s=K_{QD}{D}_s^{\frac{7}{3}}$$ (3)

where the scaling coefficient, K_QD, is a constant. When V_C = (V_C)_max, L_C = (L_C)_max, and D_S = (D_S)_max [where (V_C)_max, (L_C)_max, and (D_S)_max refer to the entire vascular volume, the entire vascular length, and the most proximal stem diameter in a tree structure, respectively], Eqs. 1–3 can be written as: (V_C)_max = K_VD(D_S)_max³, (L_C)_max = K_LV(V_C)_max^7/9, and (Q_S)_max = K_QD(D_S)_max^7/3. Hence, we obtain the following equations:

$$\frac{V_c}{{\left(V_c\right)}_{\max }}={\left[\frac{D_s}{{\left(D_s\right)}_{\max }}\right]}^3$$ (4)

$$\frac{L_c}{{\left(L_c\right)}_{\max }}={\left[\frac{V_c}{{\left(V_c\right)}_{\max }}\right]}^{\frac{7}{9}}$$ (5)

$$\frac{Q_s}{{\left(Q_s\right)}_{\max }}={\left[\frac{D_s}{{\left(D_s\right)}_{\max }}\right]}^{\frac{7}{3}}$$ (6)

Equations 4–6 are the normalized volume-diameter, length-volume, and flow-diameter scaling power laws.

Data analysis.

Scaling laws in the entire coronary arterial trees of control and disease groups are presented as the log-log density plot showing the frequency of data. To obtain these figures, a grid was superimposed on the data of interest, and the number of data points in each square was counted. On the basis of a normalized count (frequency), a shade was assigned proportional to the frequency, i.e., darkest shade reflects highest frequency or density, and the lightest shade reflects the lowest frequency.

The exponent of scaling power laws is a signature of hierarchy to characterize the structure-function self-similarity in a tree structure. Hence, exponents X_VD, X_LV, and X_QD in the three normalized scaling power laws of [V_C/(V_C)_max] = [D_S/(D_S)_max]^X_VD, [L_C/(L_C)_max] = [V_C/(V_C)_max]^X_LV, and [Q_S/(Q_S)_max] = [D_S/(D_S)_max]^X_QD were determined by a least-square fit of epicardial arterial trees (orders 9–11), transmural arterial trees (orders 5–8), perfusion arteriolar trees (orders 1–4), and entire coronary arterial trees (orders 1–11) in control, LVH, RVH, and CHF groups to the corresponding power laws. The scaling exponent in a normalized power law can quantify the hierarchy of a fractal-like tree. To eliminate the potential interaction of exponent and coefficient in a power law, coefficients K_VD, K_LV, and K_QD of the three scaling power laws with exponents equal to the theoretical values (i.e., 3 in Eq. 1, 7/9 in Eq. 2, and 7/3 in Eq. 3) were determined by a least-square fit of epicardial, transmural, and perfusion arterial trees, as well as the entire coronary arterial trees for the corresponding power laws.

The means ± SD values were computed for the parameters. A two-way ANOVA (SigmaStat 3.5) was used to detect the statistical difference of scaling coefficients and exponents between control and disease groups as well as among epicardial, transmural, and perfusion subnetworks. P < 0.05 was indicative of a significant difference between the two populations. Moreover, a linear mixed model (SPSS 20) was used to account for the relation of epicardial arterial trees, transmural arterial trees, and perfusion arteriolar trees in each animal, where animal body weight was set as a covariate.

RESULTS

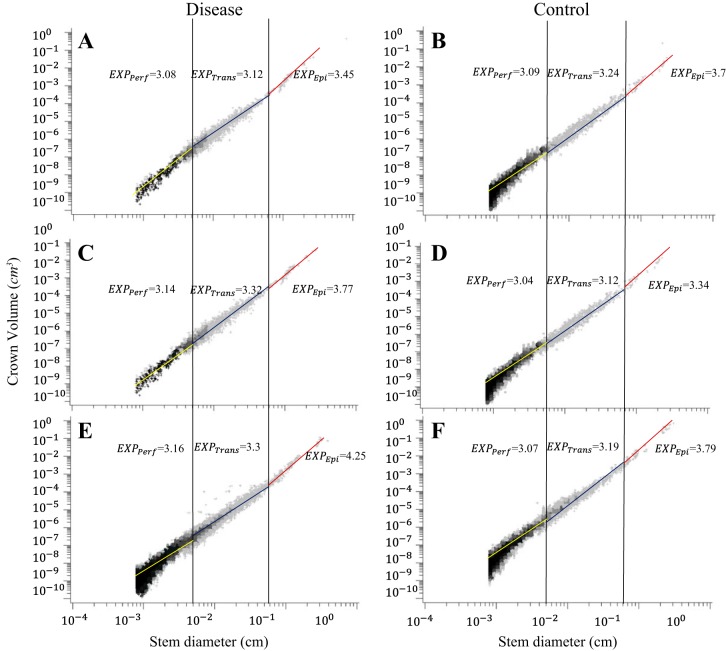
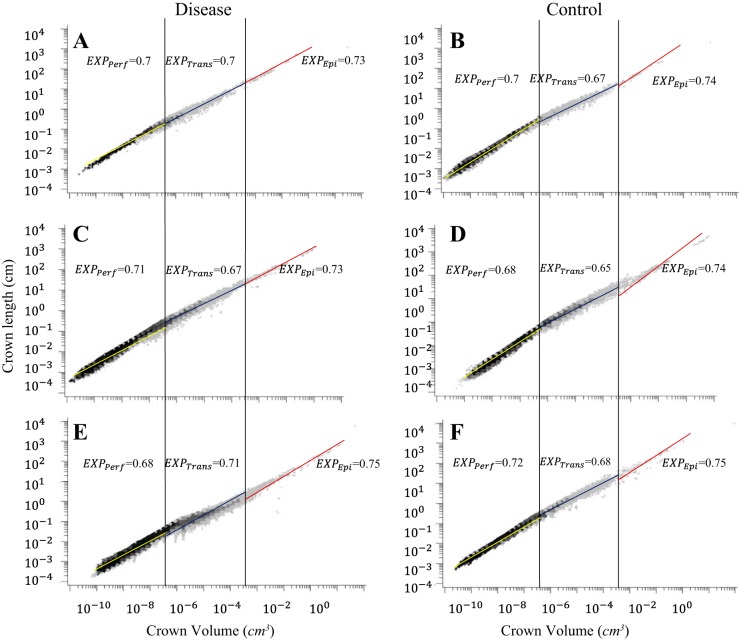
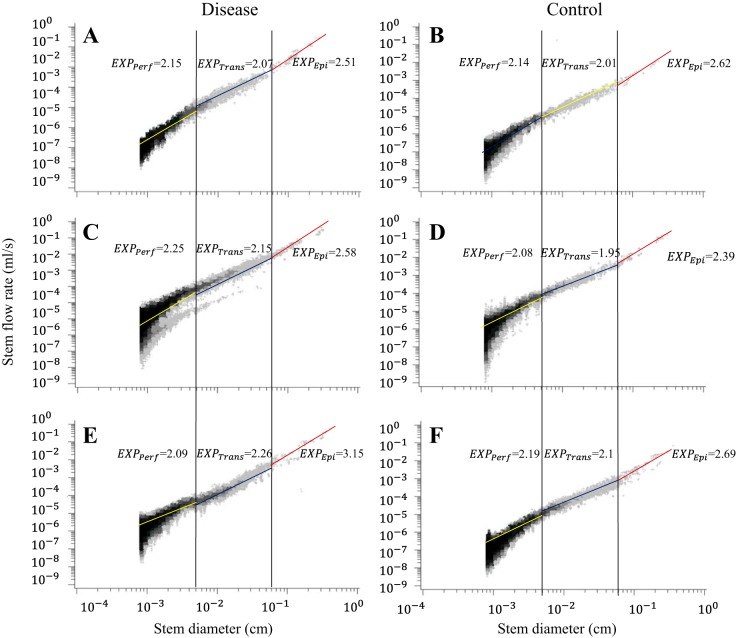
Figure 1, A and B, shows log-log density plots of crown volume as a function of stem diameter in the entire LCx arterial trees of LVH and control pigs. Figure 1, C and D, shows log-log density plots of volume-diameter scaling power law in the entire RCA trees of RVH and control pigs. Figure 1, E and F, shows log-log density plots of volume-diameter scaling power laws in the entire LCx arterial trees of CHF and control pigs. Similarly, Figs. 2 and 3 show log-log density plots of length-volume and flow-diameter scaling power laws in the entire coronary arterial trees, respectively. Correspondingly, Table 1 lists coefficients and exponents of the three scaling power laws in the entire coronary arterial trees of LVH, RVH, CHF, and control groups. There were no statistical differences in the coefficients and exponents between diseased and control groups. Moreover, Table 1 shows a significant increase of vessel number with the increase of BW in controls. The vessel number was also increased significantly by moderate LVH (compensatory) and severe RVH (compensatory) but reduced by CHF (decompensatory).

Fig. 1.

Log-log density plots of volume-diameter scaling power law in the entire coronary arterial trees of left ventricular hypertrophy (LVH) (A) and control (B), right ventricular hypertrophy (RVH) (C) and control (D), and congestive heart failure (CHF) (E) and control (F).

Fig. 2.

Log-log density plots of length-volume scaling power law in the entire coronary arterial trees of LVH (A) and control (B), RVH (C) and control (D), and CHF (E) and control (F).

Fig. 3.

Log-log density plots of flow-diameter scaling power law in the entire coronary arterial trees of LVH (A) and control (B), RVH (C) and control (D), and CHF (E) and control (F).

Table 1.

Coefficients and exponents for three scaling power laws

		LVH	RVH	CHF	Control-LVH	Control-RVH	Control-CHF
Volume-diameter scaling law	XVD	3.08 ± 0.17	3.14 ± 0.15	3.16 ± 0.11	3.09 ± 0.11	3.04 ± 0.10	3.07 ± 0.09
	KVD	12.40 ± 1.70	18.00 ± 1.80	11.40 ± 1.90	16.20 ± 1.80	16.50 ± 1.80	15.40 ± 1.70
	R2	0.87	0.85	0.87	0.86	0.88	0.89
Length-volume scaling law	XLV	0.70 ± 0.01	0.71 ± 0.01	0.67 ± 0.02	0.70 ± 0.01	0.68 ± 0.02	0.72 ± 0.01
	KLV	36732.00 ± 1.20	38516.00 ± 1.20	34881.00 ± 1.30	37385.00 ± 1.20	37520.00 ± 1.20	34579.00 ± 1.20
	R2	0.98	0.98	0.97	0.98	0.98	0.99
Flow-diameter scaling law	XQD	2.15 ± 0.12	2.25 ± 0.17	2.09 ± 0.12	2.14 ± 0.12	2.08 ± 0.15	2.19 ± 0.11
	KQD	15.60 ± 1.70	10.80 ± 2.30	16.50 ± 2.00	15.20 ± 1.80	12.30 ± 2.20	16.80 ± 1.90
	R2	0.82	0.68	0.72	0.77	0.77	0.76
Stem-crown units in entire tree		∼510,000	∼880,000	∼550,000	∼330,000	∼350,000	∼1,030,000
Epicardial stem-crown units		∼150	∼460	∼180	∼70	∼100	∼420
Transmural stem-crown units		∼7,000	∼20,000	∼11,000	∼7,000	∼8,000	∼12,000
Perfusion stem-crown units		∼500,000	∼860,000	∼535,000	∼320,000	∼340,000	∼1,015,000

Applicable values are means ± SD. Coefficients and exponents for length-volume, volume-diameter, and flow-diameter scaling power laws are shown, as well as stem-crown units in the entire coronary arterial trees of left ventricular hypertrophy (LVH), right ventricular hypertrophy (RVH), congestive heart failure (CHF), and control groups and stem-crown units in epicardial arterial trees (orders 9–11), transmural arterial trees (orders 5–8), and perfusion arteriolar trees (orders 1–4).

On the basis of the stem-crown data in Figs. 1–3, Tables 2, 3, and 4 list coefficients and exponents of the volume-diameter, length-volume, and flow-diameter scaling power laws in epicardial arterial trees, transmural arterial trees, and perfusion arteriolar trees of LVH, RVH, and CHF vs. respective control groups. The scaling exponents and coefficients in the entire coronary arterial tree are approximately consistent with those in perfusion arteriolar trees (Table 1 vs. Tables 2–4). The linear mixed model shows higher scaling exponents in epicardial arterial trees (P < 0.05) than those in transmural arterial trees and perfusion arteriolar trees despite no statistical difference between transmural and perfusion trees (Table 5). Scaling coefficient, K_VD, shows no statistical difference in the three subtrees; epicardial K_LV < transmural K_LV < perfusion K_LV (P < 0.05); K_QD values in epicardial arterial trees are significantly smaller (P < 0.05) than those in transmural arterial trees and perfusion arteriolar trees, as shown in Table 5. Furthermore, an increase of body weight (BW, a covariate in the linear mixed model) with aging has negligible effects on the scaling exponents.

Table 3.

Coefficients and exponents for three scaling power laws in epicardial, transmural, and perfusion arterial trees of RVH and control

Scaling power laws		RVH			Control
		Epi	Trans	Perf	Epi	Trans	Perf
Least-squares fit of X values in normalized scaling power laws
Volume-diameter scaling law	XVD	3.77 ± 0.68	3.32 ± 0.15	3.14 ± 0.10	3.34 ± 0.95	3.12 ± 0.16	3.04 ± 0.10
	R2	0.74	0.92	0.81	0.93	0.93	0.85
Length-volume scaling law	XLV	0.71 ± 0.06	0.67 ± 0.02	0.71 ± 0.01	0.74 ± 0.07	0.65 ± 0.02	0.68 ± 0.02
	R2	0.93	0.94	0.98	0.98	0.96	0.98
Flow-diameter scaling law	XQD	2.58 ± 0.65	2.15 ± 0.14	2.25 ± 0.15	2.39 ± 0.73	1.95 ± 0.13	2.08 ± 0.15
	R2	0.79	0.83	0.64	0.90	0.91	0.76
Least-squares fit of K values with X equal to theoretical values
Volume-diameter scaling law	KVD	13.90 ± 2.10	14.80 ± 1.60	18.00 ± 1.80	12.70 ± 1.60	16.70 ± 1.60	16.40 ± 1.80
	R2	0.74	0.92	0.81	0.93	0.93	0.85
Length-volume scaling law	KLV	177.00 ± 1.50*	4365.00 ± 1.40*	38570.00 ± 1.20	81.90 ± 1.10	3487.00 ± 1.40	37698.00 ± 1.20
	R2	0.93	0.94	0.98	0.99	0.96	0.98
Flow-diameter scaling law	KQD	5.40 ± 2.20*	12.80 ± 1.70	10.80 ± 2.30	2.80 ± 1.40	12.00 ± 1.70	12.40 ± 2.20
	R2	0.79	0.83	0.64	0.90	0.91	0.76

Values are means ± SD. Coefficients and exponents are shown for length-volume, volume-diameter, and flow-diameter scaling power laws in epicardial arterial trees (orders 9–11), transmural arterial trees (orders 5–8), and perfusion arteriolar trees (orders 1–4) of RVH and control groups (ages before surgery: ∼3 mo).

^*Statistical difference between CHF and control (2-way ANOVA).

Table 4.

Coefficients and exponents for three scaling power laws in epicardial, transmural, and perfusion arteriolar trees of CHF and control

Scaling power laws		CHF			Control
		Epi	Trans	Perf	Epi	Trans	Perf
Least-squares fit of X values in normalized scaling power laws
Volume-diameter scaling law	XVD	4.25 ± 1.50*	3.30 ± 0.17	3.16 ± 0.11	3.79 ± 0.80	3.19 ± 0.16	3.07 ± 0.09
	R2	0.56	0.91	0.83	0.82	0.92	0.88
Length-volume scaling law	XLV	0.75 ± 0.11	0.71 ± 0.03	0.68 ± 0.01	0.75 ± 0.06	0.68 ± 0.02	0.72 ± 0.01
	R2	0.88	0.95	0.97	0.96	0.95	0.99
Flow-diameter scaling law	XQD	3.15 ± 1.49*	2.26 ± 0.15	2.09 ± 0.12	2.69 ± 0.69	2.10 ± 0.13	2.19 ± 0.11
	R2	0.54	0.85	0.69	0.75	0.88	0.74
Least-squares fit of K values with X equal to theoretical values
Volume-diameter scaling law	KVD	6.50 ± 2.50*	10.10 ± 1.80*	11.40 ± 1.90*	9.80 ± 3.30	12.10 ± 1.60	15.40 ± 1.70
	R2	0.56	0.91	0.83	0.82	0.92	0.88
Length-volume scaling law	KLV	103.00 ± 1.60*	2330.00 ± 1.50*	35263.00 ± 1.20	131.00 ± 1.40	4640.00 ± 1.30	34587.00 ± 1.20
	R2	0.88	0.95	0.97	0.96	0.95	0.99
Flow-diameter scaling law	KQD	2.40 ± 2.80*	5.70 ± 1.70*	16.70 ± 1.90	4.80 ± 1.90	19.60 ± 1.60	16.90 ± 1.90
	R2	0.54	0.85	0.69	0.75	0.88	0.74

Values are means ± SD. Coefficients and exponents are shown for length-volume, volume-diameter, and flow-diameter scaling power laws in epicardial arterial trees (orders 9–11), transmural arterial trees (orders 5–8), and perfusion arteriolar trees (orders 1–4) of CHF and control groups (ages before surgery: ∼4.5 mo).

^*Statistical difference between CHF and control (2-way ANOVA).

Table 2.

Coefficients and exponents for three scaling power laws in epicardial, transmural, and perfusion arterial trees of LVH and control

Scaling Power Laws		LVH			Control
		Epi	Trans	Perf	Epi	Trans	Perf
Least-squares fit of X values in normalized scaling power laws
Volume-diameter scaling law	XVD	3.45 ± 0.59	3.12 ± 0.18	3.08 ± 0.10	3.70 ± 0.78	3.24 ± 0.16	3.09 ± 0.11
	R2	0.76	0.88	0.85	0.89	0.90	0.85
Length-volume scaling law	XLV	0.73 ± 0.09	0.70 ± 0.02	0.70 ± 0.01	0.74 ± 0.06	0.67 ± 0.02	0.70 ± 0.02
	R2	0.99	0.97	0.98	0.97	0.96	0.98
Flow-diameter scaling law	XQD	2.51 ± 0.48	2.07 ± 0.14	2.15 ± 0.10	2.62 ± 0.74	2.01 ± 0.12	2.14 ± 0.12
	R2	0.75	0.85	0.81	0.89	0.88	0.75
Least-squares fit of K values with X equal to theoretical values
Volume-diameter scaling law	KVD	10.10 ± 2.50	12.20 ± 1.90	12.40 ± 1.70*	10.90 ± 1.50	11.50 ± 1.70	16.20 ± 1.80
	R2	0.76	0.88	0.85	0.89	0.90	0.85
Length-volume scaling law	KLV	137.00 ± 1.20	4080.00 ± 1.40	36842.00 ± 1.20	136.00 ± 1.20	4249.00 ± 1.40	37445.00 ± 1.20
	R2	0.99	0.97	0.98	0.97	0.96	0.98
Flow-diameter scaling law	KQD	4.80 ± 1.60	16.20 ± 1.70	15.60 ± 1.70	4.60 ± 1.50	18.50 ± 1.60	15.20 ± 1.80
	R2	0.75	0.85	0.81	0.89	0.88	0.75

Values are means ± SD.

Length-volume, volume-diameter, and flow-diameter scaling power laws are shown in epicardial (Epi) arterial trees (orders 9–11), transmural (Trans) arterial trees (orders 5–8), and perfusion (Perf) arteriolar trees (orders 1–4) of LVH and control groups (ages before surgery: ∼2 mo).

^*Statistical difference between LVH and control (2-way ANOVA).

Table 5.

Estimates of fixed effects (epicardial, transmural, and perfusion arterial tree) in a linear mixed model

				95% Confidence Interval
	Estimate	SE	P Value	Lower bound	Upper bound
	XVD
Intercept	3.170	0.06	<0.050	3.050	3.300
Epi	0.470	0.08	<0.050	0.310	0.630
Perf	−0.050	0.08	0.520	−0.200	0.100
Trans	0.000	0.00
	XLV
Intercept	0.679	0.004	<0.050	0.675	0.684
Epi	0.057	0.006	<0.050	0.056	0.058
Perf	0.009	0.005	0.150	0.004	0.014
Trans	0.000	0.000
	XQD
Intercept	2.070	0.050	<0.050	1.980	2.170
Epi	0.510	0.060	<0.050	0.380	0.640
Perf	0.040	0.060	0.490	−0.080	0.160
Trans	0.000	0.000
	KVD
Intercept	14.700	3.510	<0.050	7.740	21.700
Epi	4.240	4.990	0.390	−5.650	14.100
Perf	2.720	4.960	0.590	−7.130	12.600
Trans	0.000	0.000
	KLV
Intercept	4036.000	127.000	<0.050	3785.000	4287.000
Epi	−3797.000	234.000	<0.050	−4259.000	−3336.000
Perf	33654.000	177.000	<0.050	33303.000	34004.000
Trans	0.000	0.000
	KQD
Intercept	17.500	0.470	<0.050	16.600	18.400
Epi	−12.100	0.730	<0.050	−13.600	−10.700
Perf	−0.170	0.660	0.800	−1.480	1.150
Trans	0.000	0.000

Estimates of fixed effects (i.e., epicardial arterial tree, transmural arterial tree, and perfusion arteriolar tree) in a linear mixed model are shown, where animal body weight was used as a covariate.

A two-way ANOVA shows no statistical difference of the three scaling laws between control and LVH in Table 2 except that K_VD decreases from 16.2 ± 1.8 to 12.4 ± 1.7 in perfusion arteriolar trees. Similarly, there is no statistical difference between control and RVH except that K_LV increases from 81.9 ± 1.1 to 177.0 ± 1.5 in epicardial arterial trees and from 3,487.0 ± 1.4 to 4,365.0 ± 1.4 in transmural arterial trees and K_QD increases from 2.8 ± 1.4 to 5.4 ± 2.2 in epicardial arterial trees. Moreover, X_VD and X_QD increase to 4.25 ± 1.50 and 3.15 ± 1.49, respectively, in epicardial LCx arterial trees of CHF compared with the respective controls (P < 0.05), as shown in Table 4. There is a significant decrease of scaling coefficients in CHF pig hearts compared with the respective controls (P < 0.05) except for the preserved K_LV (35,263.0 ± 1.2 vs. 34,587.0 ± 1.2) and K_QD (16.7 ± 1.9 vs. 16.9 ± 1.9) in perfusion arteriolar trees. On the other hand, a two-way ANOVA shows no statistical difference of scaling exponents among LVH, RVH, and CHF groups except for a significant increase of X_VD and X_QD in epicardial LCx arterial trees of CHF.

DISCUSSION

This study determined the changes of volume-diameter, length-volume, and flow-diameter scaling power laws in epicardial arterial trees (orders 9–11), transmural arterial trees (orders 5–8), perfusion arteriolar trees (orders 1–4), and entire coronary arterial trees (orders 1–11) caused by moderate LVH, severe RVH, and CHF compared with the respective controls in diastole without vessel tone. The major findings are as follows: 1) scaling exponents show no statistical difference in transmural arterial trees and perfusion arteriolar trees of control hearts, whereas scaling exponents are significantly higher in epicardial arterial trees; 2) scaling exponents in epicardial, transmural, and perfusion subnetworks of control hearts remain relatively unchanged with the increase of body weight; 3) scaling exponents and coefficients are preserved in moderate LVH except for the decreased volume-diameter scaling coefficient, K_VD, in perfusion arteriolar trees; 4) scaling exponents and coefficients are preserved in severe RVH except for the increased length-volume coefficient, K_LV, in epicardial and transmural subnetworks and the increased flow-diameter coefficient, K_QD, in epicardial arterial trees; and 5) CHF increases X_VD and X_QD in epicardial arterial trees and decreases scaling coefficients significantly but preserves other exponents as well as K_LV and K_QD in perfusion arteriolar trees.

Scaling power laws in control hearts.

The architecture of the arterial tree has fractal-like features of scale-independent self-similarity (2, 10, 33). In control hearts, the fractal nature of vascular trees determines constant exponents of intraspecific scaling laws in transmural arterial trees and perfusion arteriolar trees despite higher mean and SD values of scaling exponents in epicardial LCx arterial trees. There are higher diameter and length asymmetries (i.e., D_large/D_small and L_large/L_small, where D_large and D_small refer to the diameter of large and small daughter vessels; L_large and L_small are the corresponding length) at an epicardial bifurcation than those at transmural and perfusion bifurcations (24, 25) because of large variability at the level of epicardial vessels in the anatomy of the coronary network. Because of heterogeneous myocardial metabolism (1, 3, 13), some larger epicardial arteries have lower crown volumes and flow rates that result in higher mean and SD values of X_VD, X_LV, and X_QD in epicardial arterial trees given that [D_S/(D_S)_max] ≤ 1 and [V_C/(V_C)_max] ≤ 1. This implies that an increase of morphometric and hemodynamic heterogeneity may significantly affect the scaling features of vascular trees, which requires further investigations.

On the other hand, the fractal nature reflects self-similarity of the millions of vessels in the entire LCx arterial tree down to the smallest arterioles (9, 41, 42). Because most stem-crown units are in the arteriolar bed (14, 17), scaling exponents and coefficients in the entire LCx arterial tree are mainly determined by perfusion arteriolar trees.

Scaling power laws in normal growth.

On the basis of the micro-CT measurements of coronary arterial trees in mice at different ages, we have recently shown a constant exponent in the length-volume scaling power law during normal growth and aging (4). The pig model supports the conclusion (i.e., an age-independent exponent but an age-dependent coefficient in the length-volume scaling law during normal growth) and further shows age-independent exponents of volume-diameter, length-volume, and flow-diameter scaling power laws in epicardial, transmural, and perfusion arterial trees, as well as the entire LCx arterial tree during normal growth. Hence, the self-similar fractal-like branching pattern attributable to diffusion-limited aggregation (8, 23, 30) may be a potential mechanism that guides the normal growth of coronary arterial trees.

Scaling power laws in compensatory LVH and RVH.

Coronary capillary density and perfusion were either relatively unchanged or slightly increased in the young of normal EF under various degrees of LVH (i.e., a 20–70% increase of LV/BW for different animal models) (7, 32, 37). We found a 50% increase of vessel number (particularly transmural arteries and perfusion arterioles) as well as a slight increase of vascular density in young pig hearts of LVH with normal EF (14). The compensatory remodeling in moderate LVH attributable to pressure overload also maintains the exponents of volume-diameter, length-volume, and flow-diameter scaling power laws in epicardial, transmural, and perfusions subnetworks, as shown in Table 2. This confirms the preserved structure-function hierarchy of the fractal-like LCx arterial tree in compensatory LVH. On the other hand, the compensatory LVH results in a significant decrease of K_VD in perfusion arteriolar trees. The decrease of K_VD represents lower crown volumes in perfusion arteriolar trees of LVH than the respective controls at a given stem diameter. Hence, moderate LVH decreases the blood volume in a single perfusion subtree despite an increase of the total blood volume attributable to the increased vessel number in the entire LCx arterial tree. These results may not be generalized to the decompensatory LVH in long-term hypertension (36) in which there is a very different degree of remodeling of coronary vasculature in contrast to moderate LVH (14). The decompensatory LVH may decouple the structure-function hierarchy of the coronary arterial tree and alter the scaling exponents, which requires further investigations.

The degree of hypertrophy in flow overload-induced RVH was substantially higher (i.e., 200% increase of RV/BW and 300% increase of vessel numbers in RVH) than that in pressure overload-induced LVH (i.e., 20% increase of LV/BW and 50% increase of vessel numbers in LVH) (14, 20). As shown in Table 3, the compensatory remodeling in RVH maintains the structure-function hierarchy (preserved scaling exponents) of the fractal-like coronary arterial tree similar to that in LVH despite the different degree of hypertrophy. The flow overload refers to the 100% increase of flow rate in epicardial arteries attributable to the 300% increase of vessel numbers in transmural and perfusion subnetworks of RVH (20, 27), which increases K_QD significantly in epicardial arterial trees. The vascular remodeling leads to a significant decrease of diameter in orders 5–10 (27) and hence increases K_LV in epicardial and transmural arterial trees.

In summary, the unchanged scaling exponents illustrate the preserved fractal-like hierarchy (global feature) in epicardial, transmural, and perfusion arterial trees, as well as the entire coronary arterial trees of moderate LVH and severe RVH, albeit the local vascular remodeling (including vessel number, diameter, length, volume, and flow rate) were characterized by the changes of scaling coefficients.

Scaling power laws in decompensatory CHF.

There is a significant increase of X_VD and X_QD in epicardial arterial trees of CHF despite no statistical difference of other scaling exponents, as shown in Table 4. CHF was induced by rapid ventricular pacing (190–220 beats per minute), which increases the work load of the heart but decreases diastolic time intervals greatly. This may lead to a significant increase in ventricle wall stress (owning to ∼2-fold increase of LV lumen volume without change in LV wall mass) and cause coronary vascular rarefaction and remodeling (17). This increases X_VD and X_QD significantly in epicardial arterial trees, which reflects the altered fractal dimension as well as the decreased self-similarity attributable to a lower coefficient of determination. Furthermore, a comparison of pressure/flow overload-induced ventricular hypertrophy and rapid pacing-induced CHF implies that the changes of scaling exponents can characterize the irreversibly impaired structure-function hierarchy of coronary arterial trees.

On the other hand, CHF significantly decreased the coefficients of the three scaling power laws in epicardial and transmural arterial trees, with a decrease of vessel number, increase of vessel length and diameter, and no change of vascular flow rate in the two subnetworks (17). The decrease of vessel number in CHF also results in the significant decrease of K_VD in perfusion arteriolar trees given the relatively unchanged diameter and length and flow rate in arterioles. Because crown length and volume reflect the integrated properties in a stem-crown unit and the flow-diameter scaling law only focuses on the flow and diameter in a stem (16), the decrease of vessel number in CHF has negligible effects on K_LV and K_QD in perfusion arteriolar trees, as shown in Table 4. Moreover, a comparison of LVH and CHF implies that a significant decrease of scaling coefficients in epicardial and transmural arterial trees can be a potential index for the irreversibly impaired structure and function of vascular trees.

In summary, a significant increase of X_VD and X_QD with a lower coefficient of determination characterizes the irreversibly impaired fractal dimension and self-similarity of epicardial arterial trees in CHF, whereas a significant decrease of K_VD, K_LV, and K_QD represents the local structure-function changes of epicardial and transmural arterial trees.

Critique of study.

The scaling analysis was performed based on the reconstructed LCx arterial trees of LVH and CHF pig hearts (14, 17) and RCA trees of RVH pig hearts (20, 27). When morphometric data are available, the scaling response of left anterior descending trees is needed to understand the structure-function remodeling of the entire coronary arterial trees in response to LVH, RVH, and CHF. Moreover, all vessels were assumed to be vasodilated and in diastole, consistent with the experimental preparation of the cast morphometric data. It is known that myogenic response, flow-dependent dilation, and metabolic control regulate vessel tone of small arteries to affect the coronary circulation (5, 40). A future hemodynamic model that considers vasoactivity (11, 22) is needed to investigate the effects of vessel tone on the scaling changes of coronary arterial trees in LVH, RVH, and CHF. Finally, the scaling analysis of pulsatile flows (15) in the three-dimensional reconstructed arterial trees (13) is needed for understanding the role of myocardium-vessel interaction in LVH, RVH, and CHF.

On the other hand, LVH increases aortic pressures, RVH increases coronary flows, and CHF reduces both aortic pressures and coronary flows. The various hemodynamic perturbations can affect vascular remodeling differentially. The scaling changes should be considered under pathological conditions at various time points in the progression of LVH, RVH, and CHF from compensatory to decompensatory stages in future studies. Because some remodeling can be reversed by interventions such as the renin-angiotensin-aldosterone inhibitors, β-adrenergic antagonists, or assist devices, the scaling parameters can be used to assess the efficacy of the therapy based on the vascular morphometric data.

Conclusions.

On the basis of the measured morphometry and simulated hemodynamics of the entire coronary arterial trees, this study predicts the scaling power laws in LVH, RVH, and CHF pig hearts. The compensatory remodeling in moderate LVH and severe RVH preserves the exponents of the volume-diameter, length-volume, and flow-diameter scaling power laws in epicardial, transmural, and perfusion subnetworks. In contrast, the exponents of volume-diameter and flow-diameter scaling laws in epicardial arterial trees are significantly increased by the decompensatory CHF, which alters the corresponding structure-function hierarchy and implies significant impairment of vascular trees. This is of potential clinical significance as a diagnostic tool given that epicardial trees can be easily imaged with angiography or CT. Moreover, the scaling exponents in controls agreed with the theoretical predictions, which remained unchanged during normal growth. The scaling analysis is of importance to understand the fractal-regulated remodeling of coronary arterial trees in LVH, RVH, and CHF to delineate the borderline between compensatory and decompensatory remodeling.

GRANTS

This research is supported in part by Natural Science Foundation of China Grant 11372010 (Y. Huo), China MOST Grant 2014DFG32740 (Y. Huo), and U01 HL119578 (G. Kassab).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Y.G. performed experiments; Y.G. interpreted results of experiments; Y.F. and X.C. analyzed data; Y.F. and X.C. prepared figures; W.T., Y.H., and G.S.K. edited and revised manuscript; Y.H. conception and design of research; Y.H. drafted manuscript; Y.H. and G.S.K. approved final version of manuscript.