plotROC: A Tool for Plotting ROC Curves

Abstract

Plots of the receiver operating characteristic (ROC) curve are ubiquitous in medical research. Designed to simultaneously display the operating characteristics at every possible value of a continuous diagnostic test, ROC curves are used in oncology to evaluate screening, diagnostic, prognostic and predictive biomarkers. I reviewed a sample of ROC curve plots from the major oncology journals in order to assess current trends in usage and design elements. My review suggests that ROC curve plots are often ineffective as statistical charts and that poor design obscures the relevant information the chart is intended to display. I describe my new R package that was created to address the shortcomings of existing tools. The package has functions to create informative ROC curve plots, with sensible defaults and a simple interface, for use in print or as an interactive web-based plot. A web application was developed to reach a broader audience of scientists who do not use R.

1. Introduction

1.1. About ROC curves

The receiver operating characteristic (ROC) curve is used to assess the accuracy of a continuous measurement for predicting a binary outcome. In medicine, ROC curves have a long history of use for evaluating diagnostic tests in radiology and general diagnostics. ROC curves originated in the field of signal detection theory.

For a continuous measurement that I denote as M, convention dictates that a test positive is defined as M equaling or exceeding some threshold c: M c. The goal of ROC analysis is to evaluate the classification accuracy of M in reference to the binary outcome D, which takes possible values 0 (negative) or 1 (positive). It is implicitly assumed that the subpopulation having D = 1 tends to have larger values of M compared to the subpopulation with D = 0. The classification accuracy of M can be evaluated by considering the confusion matrix (Table 1). The confusion matrix cross-classifies the predicted outcome M ≥ c versus the true outcome D. The four cells of the matrix correspond to the possible classification outcomes: a true positive, a false positive, a true negative, and a false negative. ROC analysis assesses the trade-offs between the test’s fraction of true positives versus the false positives as c varies over the range of M.

Table 1:

Confusion matrix illustrating the possible classification outcomes of a continuous test M with threshold c versus the true outcome D.

	D
	1	0	Total
M ≥ c	true positive	false positive	test positive
M < c	false negative	true negative	test negative
Total	disease positive	disease negative

Formally, for a fixed cutoff c, the true positive fraction is the probability of a test to be positive in the diseased population:

$$TPF(c)=\text{P}\{M\ge c|D=1\}$$

and the false positive fraction is the probability of a test to be positive in the healthy population:

$$FPF(c)=P\{M\ge c|D=0\}.$$

Since the cutoff c is not fixed in advance, one can plot the TPF against the FPF for all possible values of c. This is exactly what the ROC curve is, a plot of FPF (c) on the x axis and TPF (c) along the y axis as c varies. A useless test that is not informative at all in regards to the disease status has TPF (c) = FPF (c) for all c. The ROC plot of a useless test is thus the diagonal line. A perfect test that is completely informative about disease status has TPF (c) = 1 and FPF (c) = 0 for at least one value c. If the assumption that support of M|D = 1 is greater than that of M|D = 0 holds, then the ROC curve will lie in the upper left quadrant above the diagonal line, however this may not be the case in a particular sample.

Given a sample of test and disease status pairs, (M₁, D₁), …, (M_n, D_n), one can estimate the ROC curve by computing proportions in the diseased and healthy subgroups separately. Specifically, given a fixed cutoff c, an estimate of the TPF (c) is the proportion of test positives among the diseased subgroup:

$$T\widehat{PF}(c)=\frac{{\sum }_{i=1}^{n}1\left\{M_i\ge c\right\}\cdot 1\left\{D_i=1\right\}}{{\sum }_{i=1}^{n}1\left\{D_i=1\right\}},$$

where 1{·} is the indicator function that equals 1 when the condition inside the parentheses is true and 0 otherwise. An estimate for FPF (c) is the proportion of test positives among the healthy subgroup and is given by a similar expression with D_i = 1 replaced with D_i = 0. Calculating these proportions for c equal to each unique value of the observed M_i yields what is known as the empirical ROC curve estimate. The empirical estimate is a step function. Other methods exist to estimate the ROC curve, such as the binormal parametric estimate which can be used to get a smooth curve. There are also extensions that allow for estimation with time-to-event outcomes subject to censoring. For a more thorough reference on the methods and theory surrounding ROC curves, interested readers may look into Pepe (2003).

A common way to summarize the value of a test for classifying disease status is to calculate the area under the ROC curve (AUC). The greater the AUC, the more informative the test. The AUC summarizes the complexities of the ROC curve into a single number and therefore is widely used to facilitate comparisons between tests and across populations. It has been criticized for the same reason because it does not fully characterize the trade-offs between false and true positives.

1.2. Design considerations

The main purpose of visually displaying the ROC curve is to show the trade-off between the FPF and TPF as the cutoff c varies. This can be useful for aiding viewers in choosing an optimal cutoff for decision making, for comparing a small number of candidate tests, and for generally illustrating the performance of the test as a classifier. In practice, once the FPF and TPF are computed for each unique observed cutoff value, they can be plotted as a simple line chart or scatter plot using standard plotting tools. This often leads to the unfortunate design choice of obscuring the critical and useful third dimension, the range of cutoff values c.

Another key design element is the use of a diagonal guideline for comparison. They allow observers to roughly estimate the area between the diagonal and the estimated ROC curve, which serves as a proxy for estimating the value of the test for classification above a useless test. Likewise, grid lines inside the plotting region and carefully selected axes allow for accurate assessment of the TPF and FPF at particular points along the ROC curve. Many medical studies use ROC curves to compare a multitude of candidate tests to each other. In those cases, curves need to be distinguished by using different colors or line types combined with a legend, or direct labels inside the plotting region.

In the medical literature, FPF and TPF are usually referred to in terms of the jargon sensitivity and specificity. Sensitivity is equivalent to the true positive fraction. Specificity is 1−FPF, the true negative fraction. Sometimes, the FPF and TPF are incorrectly referred to as rates, using the abbreviations FPR and TPR. These are probabilities and their estimates are proportions, therefore the use of the term fraction as opposed to rate is preferred.

1.3. Existing plotting software

The ROC curve plot is, at the most basic level, a line graph. Therefore, once the appropriate statistics are estimated, existing plotting functions can be used to create a ROC curve plot. Viewers can identify ROC plots through context, by observing the shape of the line, and through the addition of axis labels, titles, legends, and so on. In a review of the oncology literature, I observed plots with the distinctive characteristics of the plotting functions from Microsoft Excel (Microsoft 2015), SAS (SAS Institute Inc. 2014), SPSS (IBM Corporation 2015), and the base R plotting functions (R Core Team 2017).

There are several R packages related to ROC curve estimation that contain dedicated plotting functions. The ROCR package (Sing, Sander, Beerenwinkel, and Lengauer 2005) plots the FPF versus TPF, as usual, and then takes the interesting approach of encoding the cutoff values as a separate color scale along the ROC curve itself. A legend for the color scale is placed along the vertical axis on the right side of the plotting region. The pROC package (Robin, Turck, Hainard, Tiberti, Lisacek, Sanchez, and Müller 2011) provides an option for plotting cutoff labels (print.thres = TRUE) and is mainly focused on estimating confidence intervals and regions for restricted ranges of the ROC curve. The plotting methods therein use the base R plotting functions to create nice displays of the curves along with shaded confidence regions. The plotROC package (Sachs 2017) uses the ggplot2 (Wickham 2009) package to create clear, informative ROC plots, with interactive features for use on the web, and sensible defaults for use in print. plotROC is available from the Comprehensive R Archive Network (CRAN) at https://CRAN.R-project.org/package=plotROC.

1.4. Literature review

Anyone giving a cursory look at any of the major medical journals is likely to find at least one ROC curve plot. I sought to assess the usage of ROC curve plots and to evaluate the design choices made in the current oncology literature by conducting a small literature review. I searched PubMed for clinical trials or observational studies in humans reported in major oncology journals for the past 10 years for the terms “ROC Curve” OR “ROC Analysis” OR “Receiver operating characteristic curve”. I conducted the search on October 8, 2014 and it returned 54 papers. From those papers, I extracted and reviewed 47 images.¹

Each image consisted of a single ROC curve plot or a panel of multiple plots. I inspected each plot manually for the following design features: the number of curves displayed, the type of axis labels (sensitivity/1−specificity or true/false positive fractions), presence or absence of grid lines, presence or absence of a diagonal guide line, whether any cut points were indicated, the type of curve label (legend or direct label), and presence of other textual annotations such as the AUC. The numerical results of the survey are summarized in Table 2.

Table 2:

Results of a literature review of major oncology journals for ROC curve plots. The rows indicate the frequency and count of key design elements of a ROC curve plot. FPR = false positive rate; TPR = true positive rate; sens = sensitivity; spec = specificity; AUC = area under the curve.

	Percent (count)
Number of curves
1	19.6 (9)
2	43.5 (20)
3	10.9 (5)
4+	26.1 (12)
Average (SD)	2.6 (1.5)
Axis labels
FPF/TPF	13.0 (0)
mixed	2.2 (1)
none	2.2 (1)
sens/spec	82.6 (38)
Diagonal guide	43.5 (20)
Grid lines	17.4 (8)
Cutoffs indicated	15.2 (7)
AUC indicated	50.0 (23)
Curve labels
direct	10.9 (5)
legend	63.0 (29)
none	19 6 (9)
title	6.5 (3)

The small minority of the figures make any attempt to indicate the values of the test cutoffs, which is an integral component of the ROC curve. I conjecture that this is mainly due to the use of default plotting procedures in statistical software. The software, by default, treats the ROC curve as a 2-dimensional object, obscuring the cutoff dimension. Grid lines and direct labels are also somewhat out of the ordinary. The absence of these features make accurate determination and comparison of the values more difficult. Many of the plots included large tables containing estimates and inference for AUC values, while the ROC curves themselves, numerous and without clear labels or reference lines, merely served as decoration. I aim to solve some of these problems by providing an easy-to-use plotting interface for the ROC curve that provides sensible defaults.

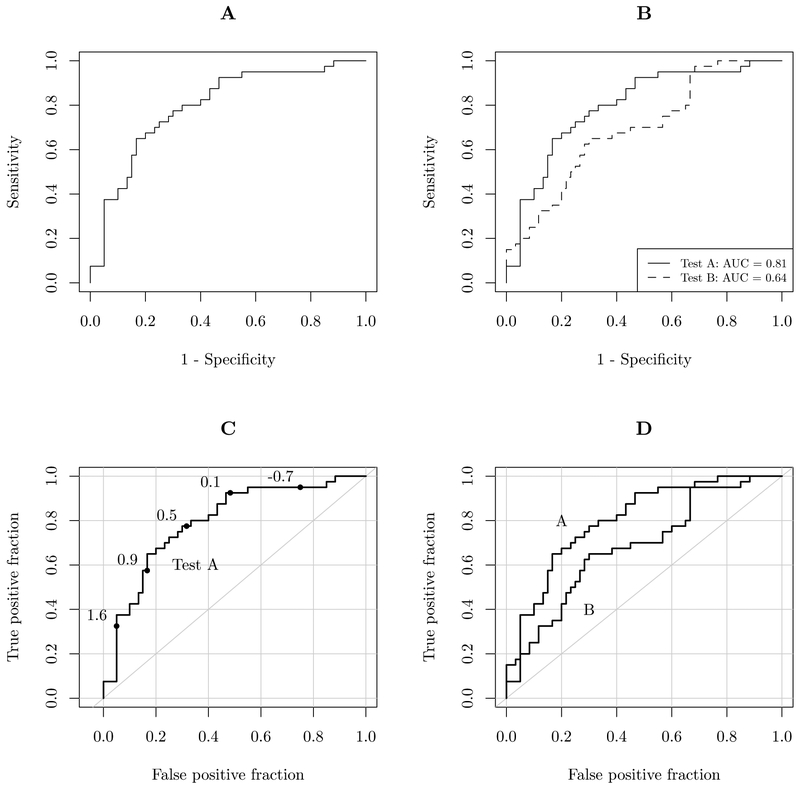
The panels of Figure 1 illustrate the most common styles of ROC curve plots, and the associated design elements. I favor the use of grid lines and a diagonal reference line to facilitate accurate readings off of the axes. Direct labels are preferred over legends because they omit the additional cognitive step of matching line types or colors to labels. The plotROC package additionally provides plotting of cutoff values, which are displayed interactively with the web-based output option, and direct labels for print use. Exact confidence regions for points on the ROC curve are optionally calculated and displayed. Additionally, the use of axis scales adjusted to be denser near the margins 0 and 1 facilitates accurate reading of FPF and TPF values. In medical applications, it is often necessary to have a very low FPF (less than 10%, for instance), therefore the smaller scales are useful for accurately determining values near the margins. The next section details the usage of the plotROC R package and these features.

Figure 1:

Illustration of design choices in plotting ROC curves. Panel A shows a sparse ROC curve, with no design additions inside the plotting region. The plot results in more white space than anything else. It is difficult to accurately determine values without reference lines. Panel B shows a plot comparing 2 curves, with different line types and a legend. AUC values are also given in the legend. Panels C and D add grid lines, diagonal reference lines, and direct labels.

The vast majority of the figures that were reviewed looked more like those in panels A and B than those in C and D. While plots like this do technically display the trade-offs between false and true positives, they minimize the amount of useful information that can be displayed in the space needed to plot a ROC curve. The plots created by plotROC attempt to increase the amount of information displayed in ROC charts that would otherwise be mostly white space. This is useful not only for print media, where space is limited, but also during data analysis. The analyst can quickly and easily view information that would otherwise be obscured by standard plotting software. The interactive features take this one step further, enhancing the plots with high density and easily accessible supplementary information.

2. Usage of the package

2.1. shiny application

A shiny application (Chang, Cheng, Allaire, Xie, and McPherson 2017) was created in order to make the features more accessible to non-R users. A limited subset of the functions of plotROC can be performed on an example data set or on data that users upload to the website. Resulting plots can be saved to the users’ machine as a PDF or as a stand-alone HTML file. It can be used in any modern web browser with no other dependencies at the website here: http://sachsmc.shinyapps.io/plotROC.

2.2. Installation and loading

Users can install the latest version of plotROC from CRAN. It can also be downloaded or installed from https://github.com/sachsmc/plotROC, where active development will take place. plotROC also requires at least version 2.0.1 of ggplot2, also available from CRAN.

R> install.packages(c(“ggplot2”, “plotROC”))

R> library(“plotROC”)

2.3. Quick start

After installing, the interactive shiny application can be run locally.

R> shiny_plotROC()

2.4. Command line basic usage

I start by creating an example data set. There are 2 markers, one that is moderately predictive and one that is not as predictive.

R> set.seed(2529)

R> D.ex <− rbinom(200, size = 1, prob = 0.5)

R> M1 <− rnorm(200, mean = D.ex, sd = 0.65)

R> M2 <− rnorm(200, mean = D.ex, sd = 1.5)

R> test <− data.frame(D = D.ex, D.str = c(“Healthy”, “Ill”)[D.ex + 1],

+  M1 = M1, M2 = M2, stringsAsFactors = FALSE)

The roc geom

As of version 2.0.1, the ggplot2 package (Wickham 2009) exports the previously internal functions Geom and Stat. This enables developers to create their own statistical transformations (stats) and geometric layers (geoms), while enjoying all of the other features of ggplot2. I have implemented the empirical ROC curve estimate and the calculation of exact confidence regions as statistical transformations: stat_roc and stat_rocci, respectively. I have also defined geometric layers for the ROC curve and confidence regions for the ROC curve: geom_roc and geom_rocci, respectively. For further discussion and details of the grammar of graphics as implemented in ggplot2, I refer readers to Wickham (2010) and the ggplot2 vignettes.

To use the ROC geometric layer, I use the ggplot function to define the aesthetic mappings, and the geom_roc function to add a ROC curve layer. The geom_roc function requires that the named aesthetics d for disease status, and m for marker be present in the aes function call inside ggplot. By default, the ROC geom and stat are linked, so that when geom_roc is called, stat_roc does the computation, and when stat_roc is called, geom_roc is used to plot the layer. The disease status need not be coded as 0/1, but if it is not, stat_roc assumes (with a warning) that the lowest value in sort order signifies disease-free status.

R> basicplot <− ggplot(test, aes(d = D, m = M1)) + geom_roc()

The geom_roc layer includes the ROC curve line combined with points and labels to display the values of the biomarker at the different cut points. It accepts the argument n.cuts to define the number of cut points to display along the curve. Labels can be suppressed by using n.cuts = 0 or labels = FALSE, however points will be displayed in the latter case. The size of the labels and the number of significant digits can be adjusted with labelsize and labelround, respectively.

R> ggplot(test, aes(d = D, m = M1)) + geom_roc(n.cuts = 0)

R> ggplot(test, aes(d = D, m = M1)) + geom_roc(n.cuts = 5,

+   labelsize = 5, labelround = 2)

R> ggplot(test, aes(d = D, m = M1)) + geom_roc(n.cuts = 50, labels = FALSE)

Confidence regions and the rocci geom

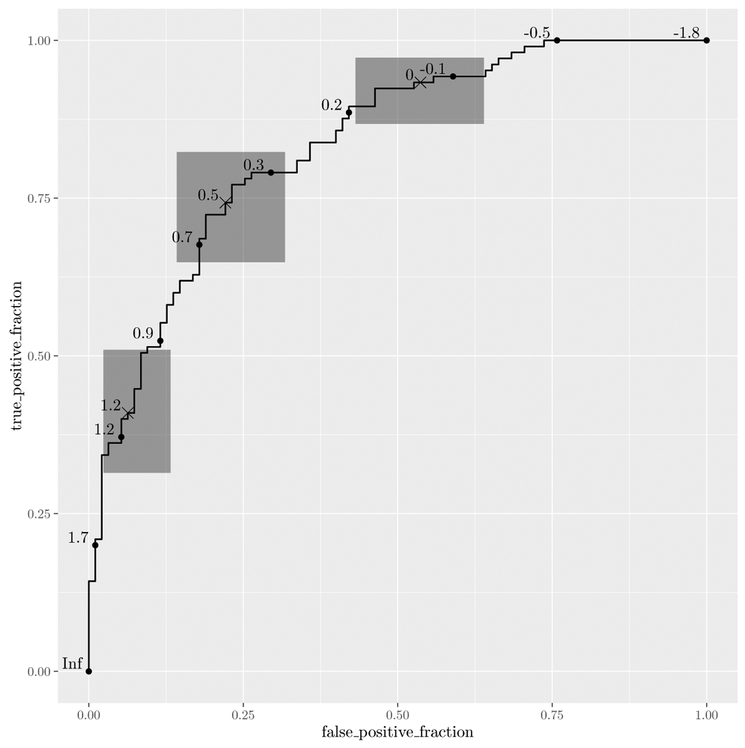
It is common to compute confidence regions for points on the ROC curve using the Clopper and Pearson (1934) exact method. Briefly, exact confidence intervals are calculated for the FPF and TPF separately, each at level $1-\sqrt{1-\alpha }$. Based on Result 2.4 from Pepe (2003), the cross-product of these intervals yields a 100 · (1 − α) percent rectangular confidence region for the pair.

This is implemented in stat_rocci and displayed as a geom_rocci layer. These both require the same aesthetics as the ROC geom, d for disease status and m for marker. By default, a set of 3 evenly spaced points along the curve are chosen to display confidence regions. Points corresponding to the confidence regions are distinguished from the others with a different symbol. You can select points by passing a vector of values in the range of m to the ci.at argument. By default, the significance level α is set to 0.05, this can be changed using the sig.level option. An example is shown in Figure 2.

Figure 2:

Illustration of plotROC with exact confidence regions.

R> basicplot + geom_rocci()

R> basicplot + geom_rocci(sig.level = 0.01)

R> ggplot(test, aes(d = D, m = M1)) + geom_roc(n.cuts = 0) +

+   geom_rocci(ci.at = quantile(M1, c(0.1, 0.4, 0.5, 0.6, 0.9)))

Styles and labels

The same objects like basicplot with roc and/or rocci layers can be treated like any other ‘ggplot’ objects. They can be printed to display the figure, and other layers can be added to the plot. I provide the function style_roc() which is a layer containing a theme, modified grid lines, and axes. Adding the style_roc() layer to the ‘ggplot’ object creates a plot with sensible defaults for use in print. This function has options for the number and location of major and minor breaks, addition of the diagonal guideline, axis labels, and any theme object created for use with ggplot2 can be supplied.

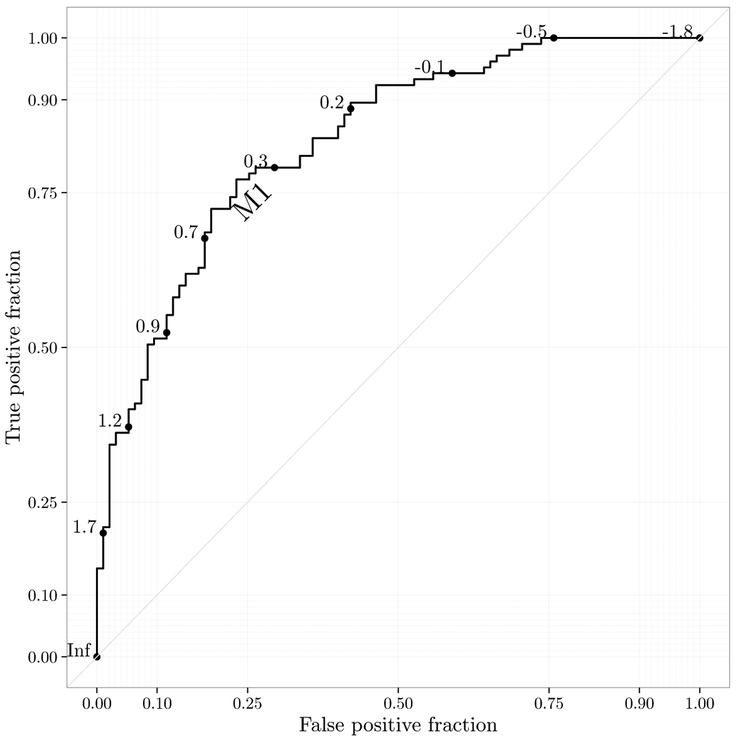
The direct_label function takes a ‘ggplot’ object as an argument and annotates the figure with a direct label with an automatically chosen location. It attempts to intelligently select an appropriate location for the label, but the location can be adjusted with nudge_x, nudge_y and label.angle. If the labels argument is NULL, it will take the name from the mapped aesthetic. A simple example with the default options is shown in Figure 3.

Figure 3:

Illustration of ROC curve plot generated by plotROC with the styles and direct labels applied for use in print.

R> direct_label(basicplot) + style_roc()

R> basicplot + style_roc(theme = theme_grey, xlab = “1 - Specificity”)

R> direct_label(basicplot, labels = “Biomarker”, nudge_y = −0.1)

Interactive ROC plots

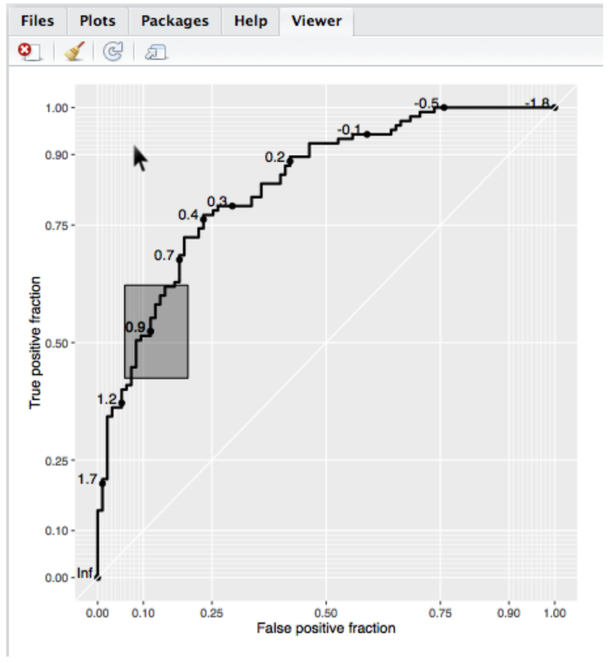
The basicplot object, which is of class ‘ggplot’, can be used to create an interactive plot and display it in the RStudio viewer or default web browser by passing it to the plot_interactive_roc function. Give the function an optional path to an HTML file as an argument called file to save the interactive plot as a complete web page. A screen shot of an interactive plot is shown in Figure 4. Hovering over the display shows the cutoff value at the point nearest to the cursor. Clicking makes the cutoff label stick until the next click, and if confidence regions are available, clicks will also display those as grey rectangles. By default, plot_interactive_roc removes any existing rocci geom and adds a high-density layer of confidence regions. This can be suppressed by using the add.cis = FALSE option. The points and labels layer of the roc geom can be hidden by using the hide.points = TRUE option. Then, points and labels will be displayed only when the mouse is hovering over the plotting region. Also by default, the style_roc function is applied, the settings can be modified by passing a call to that function or setting it to NULL.

Figure 4:

Screen shot of an interactive plot created with plotROC being displayed in the RStudio viewer. Hovering the mouse cursor over the plot causes the cutoff label nearest to the cursor to be displayed. Clicking will display a confidence region, if available, and make the label stick until the next click. For live examples, see the package vignette, or go to http://sachsmc.github.io/plotROC.

R> plot_interactive_roc(basicplot)

R> plot_interactive_roc(basicplot, hide.points = TRUE)

R> plot_interactive_roc(basicplot, style = style_roc(theme = theme_bw))

Users can export an interactive ROC plot by using the export_interactive_roc function, which returns a character string containing the necessary HTML and JavaScript. The JavaScript source can be omitted by using the omit.js = TRUE option. Users may wish to do this when there are multiple interactive figures in a single document; the source only needs to be included once. The character string can be copy-pasted into an HTML document, or better yet, incorporated directly into a dynamic document using knitr (Xie 2017). In a knitr document, it is necessary to use the cat function on the results and use the chunk options results = “asis” and fig.keep = “none” so that the interactive plot is displayed correctly. For documents that contain multiple interactive plots, it is necessary to assign each plot a unique name using the prefix argument of export_interactive_roc. This is necessary to ensure that the JavaScript code manipulates the correct SVG elements. For examples of interactive plots and how to incorporate them into knitr documents, see the package vignette (vignette(“examples”, package = “plotROC”)) or the web page https://sachsmc.github.io/plotROC/. The next code block shows an example knitr chunk that can be used in an .Rmd document to display an interactive plot.

′ ′ ′ {r int-no, results = “asis”, fig.keep = “none”}

cat(

 export_interactive_roc(basicplot, prefix = “a”)

 )

′ ′ ′

Multiple ROC curves

If you have grouping factors in your data set, or you have multiple markers measured on the same subjects, you may wish to plot multiple ROC curves on the same plot. plotROC fully supports faceting and grouping as done by ggplot2. In my example data set, there are 2 markers measured in a paired manner:

R> head(test)

  D   D.str     M1     M2

1  1    Ill  1.48117155  −2.50636605

2  1    Ill  0.61994478  1.46861033

3  0  Healthy  0.57613345  0.07532573

4  1    Ill  0.85433197  2.41997703

5  0  Healthy  0.05258342  0.01863718

6  1    Ill  0.66703989  0.24732453

These data are in wide format, with the 2 markers going across 2 columns. ggplot2 requires long format, with the marker result in a single column, and a third variable identifying the marker. I provide the convenience function melt_roc to perform this transformation. The arguments are the data frame, a name or index identifying the disease status column, and a vector of names or indices identifying the markers. Optionally, the names argument gives a vector of names to assign to the marker, replacing their column names. The result is a data frame in long format.

R> longtest <- melt_roc(test, “D”, c(“M1”, “M2”))

R> head(longtest)

   D      M   name

M11  1  1.48117155    M1

M12  1  0.61994478    M1

M13  0  0.57613345    M1

M14  1  0.85433197    M1

M15  0  0.05258342    M1

M16  1  0.66703989    M1

Then, the data set can be passed to the ggplot function, with the marker name given as a grouping or faceting variable. Some examples of its usage are given below.

R> ggplot(longtest, aes(d = D, m = M, color = name)) + geom_roc()

R> ggplot(longtest, aes(d = D, m = M)) + geom_roc() + facet_wrap(~ name)

R> ggplot(longtest, aes(d = D, m = M, linetype = name)) + geom_roc() +

+   geom_rocci()

R> ggplot(longtest, aes(d = D, m = M, color = name)) + geom_roc()

R> pairplot <- ggplot(longtest, aes(d = D, m = M, color = name)) +

+  geom_roc(show.legend = FALSE)

R> direct_label(pairplot)

R> pairplot + geom_rocci()

R> pairplot + geom_rocci(linetype = 1)

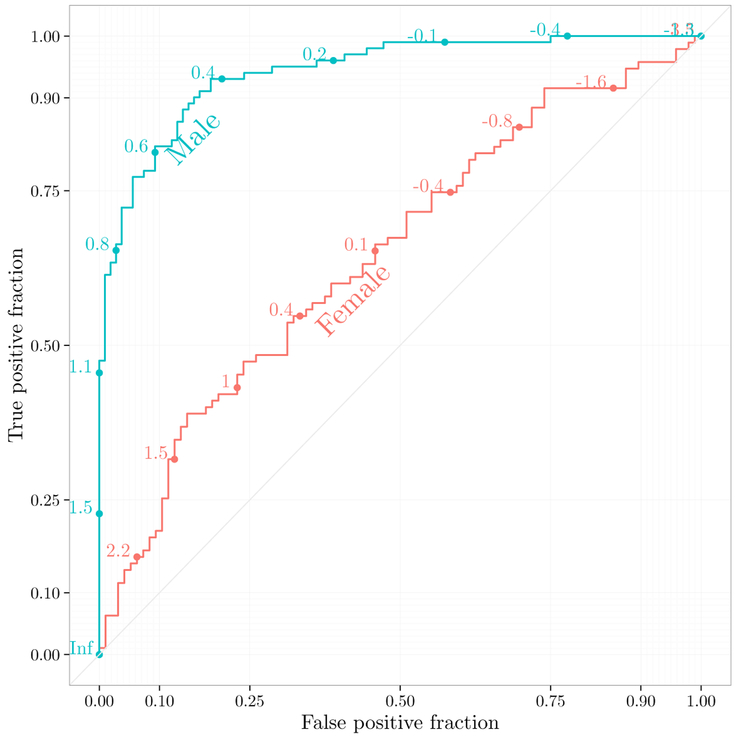
Showing multiple curves is also useful when there is a factor that affects the classification accuracy of the test. Let us create another example data set.

R> D.cov <- rbinom(400, 1, 0.5)

R> gender <- c(“Male”, “Female”)[rbinom(400, 1, 0.49) + 1]

R> M.diff <- rnorm(400, mean = D.cov,

+   sd = ifelse(gender == “Male”, 0.5, 1.5))

R> test.cov <- data.frame(D = D.cov, gender = gender, M = M.diff)

R> bygend <- ggplot(test.cov, aes(d = D, m = M, color = gender)) +

+   geom_roc(show.legend = FALSE)

R> direct_label(bygend) + style_roc()

This example is displayed in Figure 5. Interactive versions of the plots with grouping and faceting are fully supported.

Figure 5:

Illustration of plotROC with multiple curves.

2.5. Advanced options

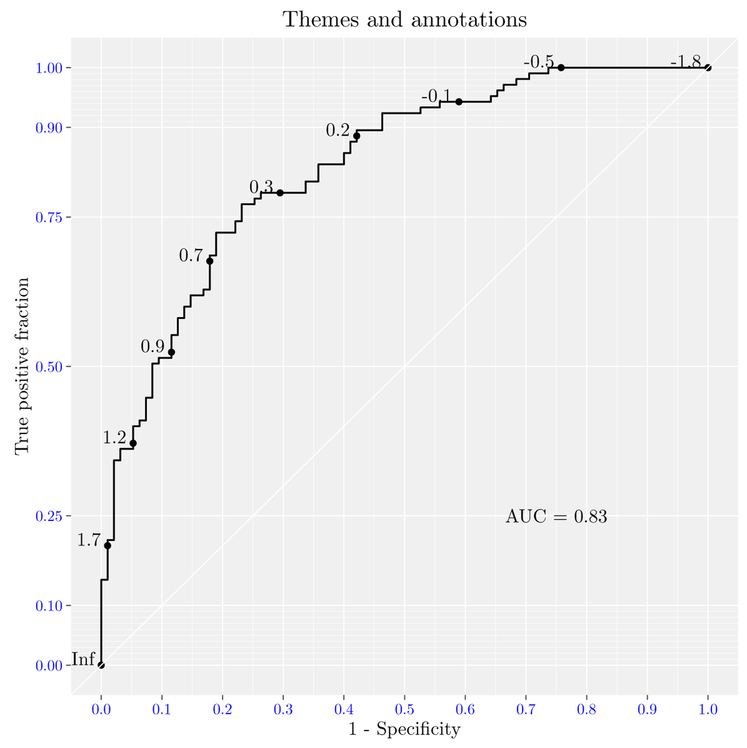
Themes and annotations

plotROC uses the ggplot2 package to create the objects to be plotted. Therefore, users can add themes and annotations in the usual ggplot2 way. A figure with a new theme, title, axis label, and AUC annotation is shown in Figure 6. plotROC provides the convenience function calc_auc that takes a ‘ggplot’ object that has a roc layer, extracts the data, and calculates the AUC.

Figure 6:

Using ggplot2 themes and annotations with plotROC objects.

R> annotate <− basicplot + style_roc(theme = theme_grey) +

+   theme(axis.text = element_text(color = “blue”)) +

+   ggtitle(“Themes and annotations”) + annotate(“text”, x = 0.75, y = 0.25,

+   label = paste(“AUC =”, round(calc_auc(basicplot)[“AUC”], 2))) +

+   scale_x_continuous(“1 − Specificity”, breaks = seq(0, 1, by = 0.1))

The results are compatible with all other ggplot2 layers and functions, and interactive versions are supported as long as there is a roc layer present.

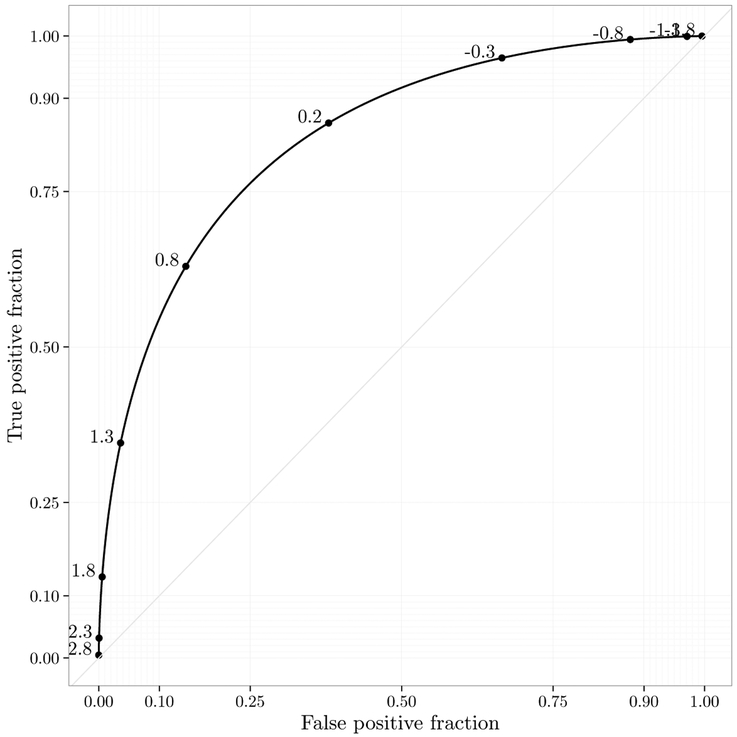
Other estimation methods

By default calculate_roc computes the empirical ROC curve. There are other estimation methods out there, as summarized in the introduction. Any estimation method can be used, as long as the cutoff, the TPF and the FPF are returned. Then you can simply pass those values in a data frame to the ggplot function and override the default statistical transformation to stat_identity. For example, let us use the binormal method to create a smooth curve. This approach assumes that the test distribution is normal conditional on disease status.

R> D.ex <− test$D

R> M.ex <− test$M1

R> mu1 <− mean(M.ex[D.ex == 1])

R> mu0 <− mean(M.ex[D.ex == 0])

R> s1 <− sd(M.ex[D.ex == 1])

R> s0 <− sd(M.ex[D.ex == 0])

R> c.ex <− seq(min(M.ex), max(M.ex), length.out = 300)

R> binorm.roc <− data.frame(c = c.ex, FPF = pnorm((mu0 - c.ex)/s0),

+   TPF = pnorm((mu1 - c.ex)/s1))

R> binorm.plot <− ggplot(binorm.roc, aes(x = FPF, y = TPF, label = c)) +

+   geom_roc(stat = “identity”) + style_roc()

The example is shown in Figure 7. Interactive plots with stat = “identity” are not currently supported. Another potential use of this approach is for plotting time-dependent ROC curves for time-to-event outcomes estimated as described in Heagerty, Lumley, and Pepe (2000). Here is an example using the survivalROC package (Heagery and Saha-Chaudhuri 2013) for estimation:

Figure 7:

Illustration of smooth binormal ROC curve.

R> library(“survivalROC”)

R> survT <− rexp(350, 1/5)

R> cens <− rbinom(350, 1, 0.1)

R> M <− −8 * sqrt(survT) + rnorm(350, sd = survT)

R> sroc <− lapply(c(2, 5, 10), function(t) {

+   stroc <− survivalROC(Stime = survT, status = cens, marker = M,

+    predict.time = t, method = “NNE”, span = 0.077)

+   data.frame(TPF = stroc[[“TP”]], FPF = stroc[[“FP”]],

+    c = stroc[[“cut.values”]], time = rep(stroc[[“predict.time”]],

+    length(stroc[[“FP”]])))

+  })

R> sroclong <− do.call(rbind, sroc)

R> survplot <− ggplot(sroclong, aes(x = FPF, y = TPF, label = c,

+    color = time)) + geom_roc(labels = FALSE, stat = “identity”)

3. How it works

plotROC makes use of ggplot2 (Wickham 2009), gridSVG (Murrell and Potter 2017), and d3.js (Bostock, Ogievetsky, and Heer 2011) to create interactive plots. The first step in the process is to create ‘ggplot’ objects with roc and/or rocci layers. They can be plotted and inspected in the R console. These form the basis for both the print versions and the interactive versions of the plots. Basic styling and labeling can be added with the style_roc and direct_label functions.

plotROC makes interactive plots by first converting the ‘ggplot’ object into a scalable vector graphic (SVG) object with the gridSVG::grid.export function. This function maps each element of the plot to a corresponding element of the SVG markup language. Interactivity is then added using d3.js and JavaScript to manipulate those SVG elements in response to users’ input. The main interactive feature is to display the cutoff labels at the points on the ROC curve closest to the mouse cursor.

There are many ways to solve this with d3.js, but Voronoi polygons are a convenient and efficient way to map the cursor location to approximately the nearest point on the ROC curve. For the set of cutoff points along the ROC curve, the d3.geom.voronoi function chain computes a set of polygons overlaying the plotting region such that the area of each polygon contains the region of the plot closest to its corresponding cutoff point. Hover events are bound to the polygons so that when the mouse cursor moves around the plotting region, the closest point on the ROC curve is made visible. Similarly, click events are bound to the polygons so that the appropriate confidence region is made visible upon clicking. The SVG code and all necessary JavaScript code is returned in the character string provided by export_interactive_roc.

This approach is similar to what is done in the gridSVG grid.animate function, which uses the SVG <animate /> tags. However, d3.js provides a much richer set of features. There are several other R packages that aim to create interactive figures. The authors of animint (Hocking, VanderPlas, Sievert, Ferris, Tsai, and Khan 2017) created an extensive JavaScript library that creates plots in a similar way as ggplot2. A set of interactive features can be added to plots using d3.js. ggvis (Chang and Wickham 2016), rCharts (Reinholdsson, Russell, and Vaidyanathan 2014), and the more recently released htmlwidgets (Vaidyanathan, Cheng, Allaire, Xie, and Russell 2016) all leverage existing charting libraries written in JavaScript. qtlcharts (Broman 2017) uses a set of custom JavaScript and d3.js functions to visualize data from genetic experiments. Their general approach is to manipulate the data and record plotting options in R, and then pass those objects to the charting libraries or functions that handle the rendering and interactivity. plotROC lets R do the rendering, allowing the figures to be consistent across print and web-based media, and retaining the distinctive R style. This also allows users to manipulate the figures directly in R to suit their needs, using tools that are more accessible and familiar to most R users. Then, the JavaScript adds a layer of interactivity to the rendered figures.

4. Discussion

Here I have illustrated the usage and described the mechanics of a new R package for creating ROC curve plots. The functions are easy to use, even for non-R users via the web application, yet have sufficient flexibility to meet the needs of power users. My approach to creating interactive plots differs from other interactive charting packages. I found that existing approaches did not meet the highly specialized needs of plotting ROC curves. While ROC curve plots can technically be created with even the most basic plotting tools, I find that specialized functions make the results clearer and more informative. The functions are integrated into the existing and popular ggplot2 package, so that all the benefits and features therein can be used effectively.

Computational details

This manuscript is completely reproducible using the source files. The output below indicates the R packages and versions used. Compiling the PDF output also requires pandoc version1.13.1 and pdfLATEX.

R> sessionInfo()

R version 3.3.1 (2016-06-21)

Platform: x86_64-apple-darwin13.4.0 (64-bit)

Running under: OS X 10.11.5 (El Capitan)

locale:

[1]  en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages

:

[1]  methods  stats  graphics  grDevices  utils  datasets base

other attached packages:

[1]  survivalROC_1.0.3  plotROC_2.0.2  ggplot2_2.1.0  xtable_1.8–2

[5]  stringr_1.0.0    knitr_1.13

loaded via a namespace (and not attached):

 [1]  Rcpp_0.12.5    digest_0.6.9    grid_3.3.1

 [4]  plyr_1.8.4     gtable_0.2.0    formatR_1.4

 [7]  magrittr_1.5    evaluate_0.9    scales_0.4.0

 [10] highr_0.6     stringi_1.1.1    tikzDevice_0.10–1

 [13] labeling_0.3    tools_3.3.1    munsell_0.4.3

 [16] colorspace_1.2–6  filehash_2.3