Neural signatures of co-occurring reading and mathematical difficulties

Abstract

Impaired abilities in multiple domains is common in children with learning difficulties. Co-occurrence of low reading and mathematical abilities (LRLM) appears in almost every second child with learning difficulties. However, little is known regarding the neural bases of this combination. Leveraging a unique and tightly controlled sample including children with LRLM, isolated low reading ability (LR), and isolated low mathematical ability (LM), we uncover a distinct neural signature in children with co-occurring low reading and mathematical abilities differentiable from LR and LM. Specifically, we show that LRLM is neuroanatomically distinct from both LR and LM based on reduced cortical folding of the right parahippocampal gyrus, a medial temporal lobe region implicated in visual associative learning. LRLM children were further distinguished from LR and LM by patterns of intrinsic functional connectivity between parahippocampal gyrus and brain circuitry underlying reading and numerical quantity processing. Our results critically inform cognitive and neural models of LRLM by implicating aberrations in both domain-specific and domain-general brain regions involved in reading and mathematics. More generally, our results provide the first evidence for distinct multimodal neural signatures associated with LRLM, and suggest that this population displays an independent phenotype of learning difficulty that cannot be explained simply as a combination of isolated low reading and mathematical abilities.

Introduction

Children with learning difficulties often manifest poor performance in multiple domains (Lewis, Hitch, & Walker, 1994; Devine et al., 2013); however, their learning problems are typically considered within specific cognitive domains. For example, low reading abilities (LR) are widely thought to originate from a particular problem in representing the sound structure, or phonology, of language, negatively impacting the mapping of these sounds to orthographic representations (Wagner & Torgesen, 1987). Similarly, low mathematical abilities (LM) are thought to originate from difficulties in processing quantities (Butterworth, Varma, & Laurillard, 2011) or mapping numeric symbols to mental representations of magnitudes (Rousselle & Noël, 2007), resulting in calculation deficits relative to their peers (Szűcs & Goswami, 2013).

An often overlooked fact is that learning difficulties in reading and mathematics have co-occurrence rates of 40% or higher (Lewis et al., 1994); however, the cognitive and brain bases of combined low reading and mathematical abilities (LRLM) is poorly understood. From a cognitive perspective, LRLM could be driven by: (a) domain-specific problems, separately affecting reading and mathematics-specific functions, which are expressed additively in children with LRLM, (b) domain-general problems, in which difficulties in reading and math are secondary to difficulties in general cognitive skills, such as memory, necessary for both domains (Gathercole et al., 2016; Mammarella et al., 2017; Szűcs, 2016; Wang & Gathercole, 2013), or (c) a combination of domain-specific and domain-general problems. Results from behavioral studies have not conclusively identified the contributions of domain-specific and general problems to LRLM. Studies have consistently shown that LRLM is associated with both domain-specific (Peterson & Pennington, 2012) and domain-general difficulties (Landerl, Fussenegger, Moll, & Willburger, 2009); however it is unclear whether domain-general difficulties in LRLM are sufficient to account for both low reading and mathematical abilities. Therefore, it remains unknown whether cognitive and neural features in LRLM are comparable to additive LM and LR difficulties, or whether LRLM is characterized by a distinguishable set of cognitive and/or neural features.

Structural and functional brain imaging research provides an alternative approach to investigating commonalities and differences between individuals with LRLM and individuals with isolated LR and LM. Although there is extensive evidence describing the brain basis of both LR (Shaywitz & Shaywitz, 2008) and LM (Ashkenazi, Black, Abrams, Hoeft, & Menon, 2013), the neurobiological signature of LRLM has not been explored. A recently proposed framework identifies three hypotheses that may explain the neural bases of LRLM (Ashkenazi et al., 2013). First, a domain-specific hypothesis states that additive problems in brain areas associated with both LR (i.e., left occipito-temporal and temporo-parietal cortices; (Hoeft et al., 2007; Skeide et al., 2016)) and LM (i.e., parietal and prefrontal cortices; (Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007)) underlie LRLM. Second, a domain-general hypothesis posits that aberrations in brain structures serving attention or working memory, instantiated in ventro- and dorsolateral prefrontal cortices and medial temporal regions, underlie LRLM. Third, a phonological hypothesis postulates that aberrations to temporal cortex, resulting in difficulties in phonological processing systems, that are involved in mapping verbal codes (e.g., number words) to quantity representations, and in memorizing verbal arithmetic facts, preclude both normal reading and mathematical skill acquisition (Geary, 2004; Ashkenazi et al., 2013).

Here, we tested these competing hypotheses using a unique dataset that included four tightly controlled groups of children: LR, LM, LRLM, and typically-developing (TD). We first used voxel- and surface-based morphometric analyses (Greve et al., 2014; Tucholka, Fritsch, Poline, & Thirion, 2012) to examine anatomical differences in the cortices of LR, LM, LRLM and TD groups. We then examined differences in intrinsic functional connectivity across these groups to identify functional brain circuitry that distinguishes the LRLM group. We predicted that a domain-specific basis for LRLM would be manifested in additive problems consistent with both LR and LM groups, including structural and functional aberrations in left occipito-temporal and temporo-parietal cortices, as well as bilateral parietal and prefrontal cortices (Price et al., 2007; Skeide et al., 2016). Alternatively, a domain-general basis for LRLM would manifest in aberrations to ventro- and dorso-lateral prefrontal regions subserving working memory and attention (LaBar, Gitelman, Parrish, & Mesulam, 1999), or medial temporal lobe regions involved in associative learning (Aminoff, Kveraga, & Bar, 2013). Finally, a phonological basis for LRLM would manifest as problems in phonological and object processing regions in temporo-parietal and occipito-temporal cortices similar to LR, with secondary effects in parietal and frontal regions serving mathematical cognition.

Materials and Methods

Participants

Our goal was to identify well-matched LR, LM, LRLM, and TD control groups from a cohort of 129 children, between the ages of 7 and 12, who had complete neuropsychological and structural brain imaging datasets from a multiyear brain imaging study of learning disabilities. All 129 children had full-scale IQ ≥ 80 to ensure no general intellectual disability (American Psychiatric Association, 2013), and no formal diagnosis of attention-deficit/hyperactivity disorder, which is often co-morbid with learning difficulties (Margari et al., 2013). To ensure interpretable structural brain imaging results, we scrutinized the integrity of structural brain imaging data in all eligible participants and subsequently excluded 46 participants based on poor quality of structural images (Ducharme et al., 2016; see Structural MRI data acquisition and analysis).

LRLM, LR, and LM Categorization

To identify individuals with LR, LM, and LRLM in this sample of 83 eligible children, we used a normed-based cut-off criterion consistent with previous studies of learning difficulties (Bruck, 1992; Evans, Flowers, Napoliello, Olulade, & Eden, 2014; Krafnick, Flowers, Luetje, Napoliello, & Eden, 2014; Olulade, Flowers, Napoliello, & Eden, 2013).

The LR group consisted of children who had at least average mathematical skills (32^nd percentile, standardized test score ≥ 93) but performed below the 30^th percentile, either in a real word or a pseudoword reading accuracy test (standardized test score ≤ 92). The LM group consisted of children who had at least average reading skills (≥ 93) but mathematical skills that were below the 30^th percentile (≤ 92). The LRLM group consisted of children who performed below the 30^th percentile (≤ 92) either in a real word or a pseudoword reading test and in a basic mathematical test. The TD group consisted of children that had both at least average reading and mathematical skills (≥ 93) (Table 1; see Psychometric assessment section for details).

Table 1. Groupinclusion table.

	LR	LM	LRLM	TD
Full-scale IQ	> 80	> 80	> 80	> 80
Word reading skills	≤92	≥ 93	≤ 92	≥ 93
Mathematical skills	≥ 93	≤92	≤ 92	≥ 93

Psychometric assessment

Real word reading and mathematical skills were assessed either with the Wechsler Individual Achievement Test (WIAT-II; Word Reading / Numerical Operations subtests; (Wechsler, 2001)) or the Woodcock-Johnson Tests of Cognitive Abilities (WJ-III; Letter-Word Identification / Calculation subtests; (Woodcock, McGrew, & Mather, 2001)). Correlation between WIAT-II and WJ-III was R = 0.90 for the reading subscales and R = 0.72 for the calculation subscales. Pseudoword reading skills were assessed with the Word Attack subtest of the WJ-III. IQ scores were determined using the Wechsler Abbreviated Scale of Intelligence (WASI; (Wechsler, 1999)). Working memory measures included the Block Recall, Digit Recall and Backward Digit Recall subtests of the Working Memory Test Battery for Children (WMTB-C; (Pickering & Gathercole, 2001)) or the Automated Working Memory Assessment (AWMA; (Alloway, 2007)).

Between-group comparisons of all demographic and psychometric data were performed either by running one-way analyses of variance or independent-samples T-tests. Within-group comparisons were performed by running one-sample T-tests. Non-parametric Kruskal-Wallis H tests or Mann-Whitney U tests were carried out in case the data were not normally distributed, variance was inhomogeneous, or the sphericity assumption was violated. Within-group comparisons of non-normally distributed data were carried out by running Wilcoxon signed-rank tests.

Structural MRI data acquisition and analysis

T1-weighted spoiled gradient recalled inversion recovery images were acquired on a 3T General Electric Signa scanner at a single site. Data from 26 participants was acquired with the following protocol using a 1-channel head coil: repetition time TR = 8.36ms; echo time TE = 1.78ms; inversion time TI = 300ms; flip angle FA = 15°; bandwidth = 122.11kHz; voxel size = 1.5×0.9×1.1mm³). Data from 13 participants was acquired with an 8-channel head coil; repetition time TR = 5.90ms; echo time TE = 1.95ms; inversion time TI = 400ms; flip angle FA = 11°; bandwidth = 244.14kHz; voxel size = 0.9×0.9×1.0mm³). Data from the remaining 9 participants was acquired with a slightly different protocol but the same 8-channel head coil; repetition time TR = 8.36ms; echo time TE = 1.78ms; inversion time TI = 300ms; flip angle FA = 15°; bandwidth = 122.11kHz; voxel size = 1.5×0.9×1.1mm³). Importantly, the distribution of protocols over the four study groups did not differ (Χ²(3) = 0.08, P = 0.994): Protocol 1: N_LR=6, N_LM=6, N_LRLM=6, N_TD=7; Protocol 2: N_LR=1, N_LM=3, N_LRLM=4, N_TD=1; Protocol 3: N_LR=4, N_LM=3, N_LRLM=2, N_TD=4.

All T1 images were visually inspected for artifacts and anatomical abnormalities (Ducharme et al., 2016) before their qualities were rated automatically by quantifying noise, inhomogeneity and resolution using the Computational Anatomy Toolbox (CAT) (http://dbm.neuro.uni-jena.de/cat) implemented in the Statistical Parametric Mapping 12 (SPM 12) software (http://fil.ion.ucl.ac.uk/spm/). To be included in further analyses, an image had to yield at least a summarized rating of ≥ 73.33 (considered as satisfactory within the CAT framework). Image quality did not differ significantly between groups (F(3,43) = 0.98, P = 0.412).

The images were first normalized to an age-specific template in Montreal Neurological Institute (MNI) space. This template was generated from the T1 data of the sample by employing the Diffeomorphic Anatomical Registration Through Exponentiated Lie Algebra (DARTEL) algorithm. Next, the images were segmented into gray matter, white matter, CSF, dura, non-brain soft tissue and air. Tissue probability maps used as priors for the segmentation were created from the T1 data of an independent reference sample with a comparable age and sex distribution using the Template-O-Matic Toolbox Version 8 (https://irc.cchmc.org/software/tom/downloads.php).

We computed gray matter volume maps that were modulated for non-linear effects to preserve local volumetric values, while accounting for individual differences in total intracranial volume. Total intracranial volume did not differ significantly between groups (F(3,43) = 0.42, P = 0.740). Finally, the volumetric images were smoothed with an 8mm full-width at half-maximum (FWHM) Gaussian kernel. In the analysis, we also employed surface-based methods, which more accurately reflect cortical geometry and have proven to be more powerful and reliable in detecting effects than volume-based methods, with fewer subjects required to achieve similar levels of significance (Greve et al., 2014; Tucholka et al., 2012). We estimated cortical thickness by applying a projection-based thickness method (Dahnke, Yotter, & Gaser, 2013) and local surface complexity by applying spherical harmonic constructions (Yotter, Nenadic, Ziegler, Thompson, & Gaser, 2011), both of which are implemented in CAT. In accordance to the matched filter theorem, the cortical thickness data were smoothed using a 10mm FWHM Gaussian kernel whereas the cortical surface complexity data were smoothed using a 20mm FWHM Gaussian kernel to optimally capture features in distances between sulci and gyri (about 20-30mm in the adult brain). All images were statistically analyzed as between-group T-contrasts in the framework of the flexible factorial design implemented in SPM 12. Between-group T-contrasts were set up to test for additive effects of LR (−LR +LM −LRLM +TD and +LR −LM +LRLM −TD), additive effects of LM (+LR −LM −LRLM +TD and −LR +LM +LRLM −TD) and specific effects of LRLM (+LR +LM −LRLM +TD and −LR −LM +LRLM −TD) on gray matter macrostructure. To correct for multiple testing, we combined a height threshold of P < 0.001 with a spatial extent threshold of P < 0.05 that was corrected by applying the false-discovery-rate (FDR) method. Significant clusters were identified anatomically based on the Automated Anatomical Labeling Atlas (http://www.gin.cnrs.fr/AAL). Image quality was unrelated to cortical surface complexity (R = −0.02, P = 0.916).

Functional MRI data acquisition and analysis

Resting-state fMRI data were acquired using T2*-sensitive gradient echo spiral-in/ spiral-out pulse sequences on a 3T General Electric Signa scanner at a single site. Data from 21 participants was acquired using a 1-channel head coil with the following protocol: field of view = 200×200; matrix size = 64×64×31; number of volumes = 240; voxel size = 3.1×3.1×4mm³). Data from 10 participants was acquired using an 8-channel head coil and the following parameters; field of view = 220×220; matrix size = 64×64×29; number of volumes = 180; voxel size = 3.1×3.1×4mm³). Data from the remaining 8 participants was acquired using the same 8-channel head coil and the following parameters; field of view = 220×220; matrix size = 64×64×29; number of volumes = 180; voxel size = 3.4×3.4×4mm³). All other parameters, including TR = 2.000ms and TE = 30ms was the same across all participants. The distribution of protocols over the four study groups did not differ (Χ²(3) = 1.35, P = 0.718): Protocol 1: N_LR=4, N_LM=5, N_LRLM=5, N_TD=6; Protocol 2: N_LR=0, N_LM=3, N_LRLM=4, N_TD=1; Protocol 3: N_LR=4, N_LM=3, N_LRLM=0, N_TD=3.

fMRI data were available for 41 out of 48 subjects. First, all images were visually inspected for artifacts and anatomical abnormalities. Next, to ensure comparability of the data, all datasets containing 240 volumes were reduced to 180 volumes by cutting off the last 60 volumes. Additionally, the two most ventral slices of all datasets containing 31 slices (covering the brainstem ventral to the cerebellum) were cut off so that all datasets comprised of 29 slices. Two cutoff criteria for head motion were defined a priori to minimize the confounding influence of head motion: 1. Mean distance between consecutive frames, i.e., mean framewise displacement (FD), had to be <0.2 mm. Maximum distance between consecutive frames, i.e., maximum FD, had to be <0.8 mm. Two datasets could not be included in further analyses because they violated the former criterion. The final sample of 39 participants comprised 9 LR, 11 LM, 9 LRLM and 10 TD individuals. Maximum FD in the final sample of 39 participants was 0.79 mm, and mean FD was 0.12 mm (SD = 0.05 mm). Mean FD was not significantly correlated with the variables of interest (word reading skills: R = 0.12, P = 0.483; mathematical skills: R = −0.12, P = 0.500) and did not differ significantly between groups (Χ²(3) = 2.10, P = 0.553).

Preprocessing was conducted using SPM12 and the FMRIB software library (FSL) version 5.0 (http://fsl.fmrib.ox.ac.uk). The first 4 volumes of each dataset were discarded to allow for MR signal stabilization. Then, the remaining images were slice-timing corrected by interpolating them and resampling them to the slice at the mid-time point of each TR. Next, the images were motion-corrected by: (1) realigning them to the first volume, (2) regressing out 3 translational and 3 rotational parameters of each volume and its preceding volume as well as the square of each of these values, and (3) regressing out the FD of each volume. Mean signals of the white matter and the cerebrospinal fluid and linear and quadratic trends of the gray matter signal were also regressed out in this model to control for physiological noise. Residual time series were temporally band-pass filtered with an ideal rectangular filter (0.01 – 0.1Hz). Subsequently, all images were resampled to a spatial resolution of 1.5×1.5×1.5 mm³ and normalized to the MNI template specified above. The images were spatially smoothed by applying a 6 mm FWHM Gaussian kernel.

ROIs for the functional connectivity analysis were created using the MarsBar toolbox (http://marsbar.sourceforge.net). A sphere of radius 3mm was placed at the peak MNI coordinate in the right parahippocampal gyrus (rPHG) (+33 −39 −12) obtained from the cortical surface complexity analysis. Four additional spheres were placed at the peak MNI coordinates of brain areas that repeatedly revealed activation differences in previous task-based fMRI studies when comparing children with low reading or low mathematical ability, respectively, against TD individuals (see Results for details). Established reading-related ROIs included left-hemisphere posterior fusiform gyrus (lpFFG; MNI coordinates: −31 −69 −10; (Hoeft et al., 2007)) and planum temporale (lPT; MNI coordinates: −44 −28 +10; (Blau et al., 2010)), and mathematics-related areas included right-hemisphere intraparietal sulcus (rIPS; MNI coordinates: +33 −50 +52; (Price et al., 2007)) and left-hemisphere prefrontal cortex (lPFC; MNI coordinates: −13, +54, −2; (Price et al., 2007)).

Custom Matlab scripts (https://www.mathworks.com) were used for carrying out the following analysis steps. Hemodynamic time courses of each ROI were computed by averaging the BOLD signals of all voxels within the spheres. Subsequently, we created single-subject functional connectivity matrices by calculating bivariate Pearson correlations between the signal-intensity time courses of each pair of seeds. This was done first for the rPHG and the 2 reading-related ROIs and then separately for the rPHG and the 2 mathematics-related ROIs. After converting the single-subject R matrices to Z matrices by applying Fisher's R-to-Z transformation, between-group comparisons of the functional connectivity indices were performed by running independent-samples T-tests. The significance threshold of P < 0.05 was FDR-corrected.

Binary logistic regression

To examine whether the strength of functional connectivity of the rPHG to brain circuitry known to support reading and mathematical function distinguish LRLM group membership, binary logistic regression was performed. We first calculated connectivity strength between ROIs identified in the functional connectivity analysis, and then calculated Pearson correlation coefficients for each subject for the following six connections: (1) rPHG to lFFG; (2) rPHG to lPT; (3) lFFG to lPT; (4) rPHG to rIPS; (5) rPHG to lPFC; and (6) rIPS to lPFC. We then used binary logistic regression to model the relationship between the dependent variable, which was group membership in either LM vs. LRLM or LR vs. LRLM, and the independent variables, which were Z-scores describing the strength of connectivity for the six aforementioned connections. Separate regression models were run for LM vs. LRLM and LR vs. LRLM analyses. SPSS software (IBM) was used for all regression analyses.

Results

Group characteristics: reading and mathematical skills

Reading skills differed significantly between groups (Χ²(3) =36.91, P < 0.001, Cohen's D = 3.9) with LR scoring significantly below LM (Z = 4.07, P < 0.001) and TD (Z = 4.07, P < 0.001) but above LRLM (Z = 3.03, P = 0.002) (Figure 1A). Additionally, mathematical skills differed significantly between groups (Χ²(3) =34.66, P < 0.001, Cohen's D = 3.39) with LM scoring significantly below LR (Z = 4.07, P < 0.001) and TD (Z = 4.16, P < 0.001) but not LRLM (Z = 0.61, P = 0.543) (Figure 1B). Within-group differences between reading and mathematical skills were only significant in LR (Z = 2.93, P = 0.003) and in LM (Z = 3.06, P = 0.002) but not in LRLM (Z = 1.34, P = 0.181) and TD (Z = 0.67, P = 0.504) (Table 2). These results show clear dissociation between LR, LM, LRLM and TD groups, with LR and LM groups showing domain specific weaknesses and LRLM showing significant weaknesses in both reading and mathematical domains.

Figure 1.

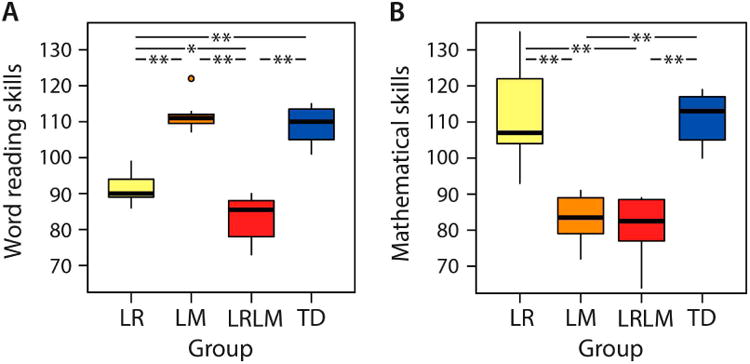
Group-wise word reading skills (A) and mathematical skills (B). From left to right: Yellow bar: children with low reading ability (LR), orange bar: children with low mathematical ability (LM), red bar: children with both low reading and mathematical ability (LRLM), blue bar: typically developing (TD) children with at least average ability. Horizontal lines within the bars represent the group median. Vertical lines at the top and the bottom of the bars depict the standard deviation. Dots indicate single cases that are more than 1.5 standard deviations away from the group mean. Asterisks mark significant between-group differences (single asterisk: P < 0.005; double asterisk: P < 0.001).

Table 2. Demographic and psychometric results.

	LR11	LM11	LRLM11	TD11	Δ12
Age1	8.67±0.62	8.88±1.19	9.04±1.47	8.70±0.63	F(3,43)=0.31, P=0.819
Sex2	4m/7f	6m/6f	4m/8f	6m/6f	Χ2(3)=1.11, P=0.775
Handedness3	11/0	12/0	9/1	12/0	Χ2(3)=3.50, P=0.321
Maternal education4	3.64±1.29	3.83±1.12	3.75±0.75	3.55±1.21	Χ2(3)=0.40, P=0.939
Performance IQ5	99.45±13.43	101.92±17.14	102.67±11.04	106.50±9.08	F(3,43)=0.58, P=0.629
Verbal IQ5	101.00±11.45	107.67±11.05	101.25±11.32	108.42±9.87	F(3,43)=1.58, P=0.209
Full-scale IQ5	100.27±12.83	105.42±12.09	102.42±10.23	108.00±6.48	F(3,43)=1.17, P=0.331
Visuospatial sketchpad6	94.20±12.47	88.42±10.27	87.30±18.57	96.09±14.61	F(3,39)=0.99, P=0.407
Phonological loop7	89.89±15.02	101.27±15.32	96.40±15.08	92.82±18.17	F(3,39)=0.96, P=0.424
Central executive8	89.60±11.08	91.92±16.18	83.20±13.09	95.82±12.09	F(3,39)=1.63, P=0.198
Word reading skills9	91.64±4.32	111.42±3.78	83.42±5.88	109.00±5.10	Χ2(3)=36.91, P<0.001*
Mathematical skills10	111.82±13.49	83.33±6.23	80.83±8.31	111.08±6.69	Χ2(3)=34.66, P<0.001*

¹years

²m=male/f=female

³right-handers/left-handers (if < 12 data unavailable)

⁴5-point scale: 1= partial high school, 2= high school graduate, 3= partial college, 4= college graduate, 5= graduate degree

⁵Wechsler Abbreviated Scale of Intelligence (WASI)

⁶Automated Working Memory Assessment (AWMA) block recall / Working Memory Test Battery for Children (WMBT-C) block recall (unavailable for 4 participants)

⁷Automated Working Memory Assessment (AWMA) digit recall / Working Memory Test Battery for Children (WMBT-C) digit recall (unavailable for 4 participants)

⁸Automated Working Memory Assessment (AWMA) backward digit recall / Working Memory Test Battery for Children (WMBT-C) backward digit recall (unavailable for 4 participants)

⁹Wechsler Individual Achievement Test (WIAT-II) word reading / Woodcock-Johnson (WJ-III) letter-word identification

¹⁰Wechsler Individual Achievement Test (WIAT-II) numerical operations / Woodcock-Johnson (WJ-III) calculation

¹¹RD= reading deficits, MD= mathematical deficits, RDMD= reading and mathematical deficits, TD= typically developing

¹²one-way ANOVA or Kruskal-Wallis H test,

^*significant (two-sided P value)

Whole-brain gray matter morphometry

Gray matter volume, cortical thickness and cortical surface complexity were computed for LR, LM, LRLM, and TD groups. A significant difference of group means was found in cortical surface complexity, but not in gray matter volume and cortical thickness (height threshold of P < 0.001 and a family-wise-error (FWE) corrected spatial extent threshold of P < 0.05). A significant effect was identified as a specific reduction in surface complexity of LRLM compared to LR, LM and TD. This effect was localized to the right parahippocampal gyrus (rPHG) (MNI coordinates: +33 −39 −12; 554 vertices; Cohen's D > 0.8; Cohen's D_MAX = 1.26; achieved power: 0.60- 0.91; Figure 2).

Figure 2.

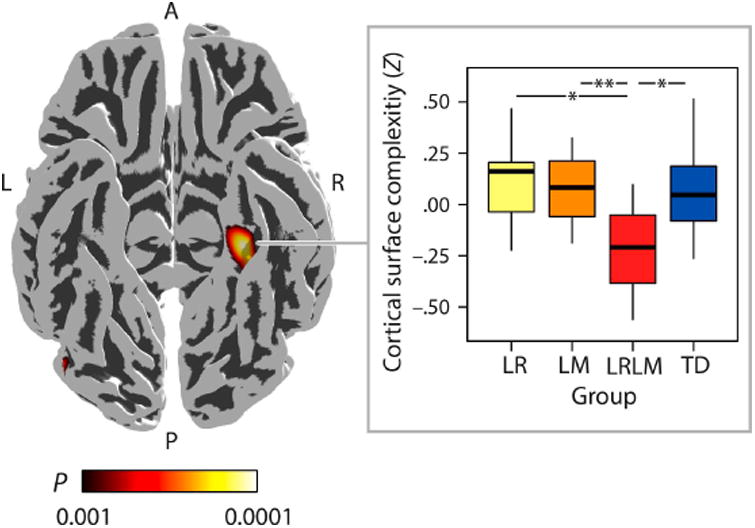
Whole-brain cortical surface complexity results. Compared to children with isolated low reading ability (LR), low mathematical ability (LM) and typically developing children (TD), children with co-occurring difficulties (LRLM) showed significantly reduced cortical surface folding of the right parahippocampal gyrus (MNI coordinates: +33 −39 −12; 511 vertices). L = left, R = right, A = anterior, P = posterior. The color bar illustrates the P-values of the T-contrast (+LR +LM −LRLM +TD) that was thresholded at height P < 0.001 with false-discovery-rate (FDR) corrections at a spatial extent threshold of P < 0.05. Effect sizes at each vertex yielded Cohen's D > 0.8. Group-wise medians (horizontal lines within the bars) and standard deviations (vertical lines at the top and the bottom of the bars) of the cortical surface complexity (Z scores) within the cluster are visualized in the boxplot. From left to right: Yellow bar: children with low reading ability (LR), orange bar: children with low mathematical ability (LM), red bar: children with both low reading and mathematical ability, blue bar: typically developing (TD) children. Asterisks mark significant between-group differences (single asterisk: P < 0.005; double asterisk: P < 0.001).

To examine whether reduced cortical folding of the LRLM vs. the LR sample reflects overall lower reading abilities in the LRLM sample, we performed a post hoc analysis of variance on these two samples with the factor group and cortical surface complexity as the dependent variable. Group differences remained statistically significant after covarying out reading test scores (F(2, 20) = 6.72, P = 0.006).

Intrinsic functional connectivity of math and reading circuits in LRLM

Structural findings indicated LRLM being characterized by abnormalities in rPHG, a region known to be involved in long-term memory formation (Aminoff et al., 2013; Kirchhoff, Wagner, Maril, & Stern, 2000; Nenert, Allendorfer, & Szaflarski, 2014; Schon, Hasselmo, Lopresti, Tricarico, & Stern, 2004). However, it is unclear how deficiencies in this region might impact domain-specific reading and mathematics in this population. Therefore, our next goal in the analysis was to investigate the possible role of rPHG in domain-specific functions by examining intrinsic brain connectivity linking rPHG to brain regions known to support reading and mathematics. We focused our analysis on functional interactions between rPHG and two structures that have been implicated in reading, including left-hemisphere posterior fusiform gyrus (lpFFG; (Hoeft et al., 2007)) and planum temporale (lPT; (Blau et al., 2010)), as well as two structures that have been implicated in mathematical function, including right-hemisphere intraparietal sulcus (rIPS; (Price et al., 2007)) and left-hemisphere prefrontal cortex (lPFC; (Price et al., 2007)).

Results show that functional connectivity between rPHG and cortical structures implicated in reading and mathematical function distinguished the LRLM group from LR, LM, and TD groups. First, analysis of functional connectivity between rPHG and reading-related cortical structures revealed weaker connectivity between rPHG and lpFFG in the LRLM group compared to LR, LM and TD groups (P < 0.05, FDR corrected; Cohen's D = 0.50-0.89; Figure 3A). Additionally, the LRLM group also showed weaker connectivity compared to the LR group for both the rPHG to lPT and lFFG to lPT connections (P < 0.05, FDR corrected; Cohen's D = 0.67 and 1.43; Figure 3A, left matrix). Next, functional connectivity analysis between rPHG and mathematics-related cortical structures showed that the LRLM group had reduced connectivity between rPHG and rIPS compared to LR, LM and TD groups (P < 0.05, FDR corrected; Cohen's D = 0.78-1.06) (Figure 3B).

Figure 3.

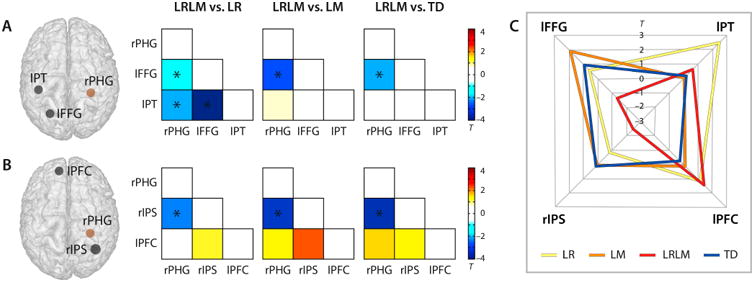
Intrinsic functional connectivity in combined LRLM group vs. the three other groups. (A) Schematic illustration of the right parahippocampal gyrus (rPHG) seed region (brown sphere), and two target regions (black spheres) know from the literature to be related to reading (lFFG: left posterior fusiform gyrus, lPT: left planum temporale). (B) Schematic illustration of the right parahippocampal gyrus (rPHG) seed region (brown sphere), and to target regions know from the literature known to be related to mathematical processing (rIPS: right intraparietal sulcus, lPFC: left prefrontal cortex) (black spheres). The corresponding matrices display the results of pair-wise group comparisons of Pearson correlation coefficients quantifying the associations of mean hemodynamic signal timecourses for each pair of regions. The color bars depict the T-statistics of the independent-sample T-tests. Significant group differences passing a false-discovery-rate (FDR) corrected threshold of P < 0.05 are indicated by asterisks. LR = children with isolated low reading ability, LM = children with isolated low mathematical ability, LRLM = children with co-occuring difficulties, TD = typically developing children. (C) Polar plot showing the mean functional connectivity (Z values) between the rPHG seed region and all four target regions for all four groups.

Functional connectivity fingerprints showing group connectivity between rPHG and nodes of reading and mathematics circuits were constructed for LR, LM, LRLM and TD groups (Figure 3C). Results show a distinct connectivity profile for the LRLM group (red) with pronounced weaknesses in connectivity between rPHG and lFFG and rIPS compared to the other three groups.

Functional connectivity discriminates LRLM group membership

The final goal of the analysis was to examine whether the strength of intrinsic connectivity between rPHG and brain circuitry known to support reading and mathematical function is sufficient to discriminate LRLM group membership. First, we performed a multinomial logistic regression analysis using group as the dependent variable (with the categories LR, LM and LRLM) and functional connectivity values for six connections (see off-diagonal connections in Figure 3 matrices) as covariates. Functional connectivity indices significantly distinguished between the three groups (Χ²(6) = 24.05, P = 0.020). Finally, to determine the degree to which differences between LRLM and the remaining groups contributed to this effect, we performed binary logistic regression using two separate models. In the first regression model, group membership in LM vs. LRLM acted as the dependent variable, and functional connectivity values served as covariates. In the second regression model, we set group membership in LR vs. LRLM as the dependent variable. Results from binary logistic regression analyses showed that the strength of these functional connections discriminates the LRLM group from both the LM group (Χ²(6) = 15.37, P = 0.018) and the LR group (Χ²(6) = 23.51, P < 0.001).

Discussion

Low reading and mathematical abilities are typically considered within their respective domains; as such, little is known regarding the brain mechanisms underlying frequent co-occurrence of these difficulties in school-aged children. Here, we have identified a distinct neural signature for children with low abilities in reading and mathematical cognitive domains. Specifically, we have shown that LRLM is both neuroanatomically distinct from LM and LR groups based on reduced cortical surface complexity in the rPHG and functionally distinct from these groups based on unique profiles of intrinsic functional connectivity linking the rPHG and specialized regions for reading and mathematical processing. Together, these results provide novel support that children struggling with combined reading and mathematical difficulties display a distinct neurocognitive profile relative to both LR and LM groups, and suggest that cognitive and neural models of LM and LR require additional refinement to distinguish and characterize this large sub-population of children with multiple difficulties.

Phenotypic specificity of LRLM

Our sample of children with LRLM showed reduced reading abilities compared to children with LR but comparable math skills compared to individuals with LM. This particular cognitive profile is consistent with results reported from several independent samples across different languages (Supplementary Tables S1 and S2). The consistency of this finding suggests that reduced reading abilities in individuals with comorbid reading and math difficulties compared to children with LR reflects an important feature of this population, and that the samples described in the current study are appropriate representations of these low performing groups. Nevertheless, we performed additional analyses to examine the possibility that reduced cortical folding in the LRLM vs. LR sample does not simply reflect overall lower reading abilities in the LRLM sample, and results continued to show reduced cortical folding in the LRLM compared to LR group after controlling for behavioral differences in reading ability.

A role for the rPHG and memory systems in LRLM

Whole-brain gray matter morphometry analysis showed that LRLM children had significantly reduced surface complexity of rPHG, a key node of the brain's memory system (Aminoff et al., 2013; Kirchhoff et al., 2000; Nenert et al., 2014; Schon et al., 2004), compared to LR, LM and TD children (Figure 2); however all groups showed comparable cortical thickness in this region. The cortical surface complexity measure applied here is particularly sensitive to local differences in cortical folding (Yotter et al., 2011), suggesting that in individuals with LRLM, the rPHG surface is misfolded despite normal thickness.

We then tested the hypothesis that such morphometric abnormalities in the medial temporal lobe contribute to aberrant functional connectivity between the PHG and domain-specific regions subserving reading and mathematics (Figure 3). From a functional neuroanatomical perspective, it should be noted that the rPHG has been consistently implicated in the associative encoding of complex visuospatial information in long-term memory (Aminoff et al., 2013; Kirchhoff et al., 2000; Nenert et al., 2014; Schon et al., 2004). However, the rPHG is seldom associated with LR or LM, and structural alterations in this region have only been sporadically reported in the context of learning disorders (Rotzer et al., 2008; Rykhlevskaia, Uddin, Kondos, & Menon, 2009). What, then, might be the role of the rPHG in LRLM? Perhaps becoming literate and acquiring arithmetic skills both require, and result in, visual memory formation, including associative encoding of symbolic stimuli. Specifically, these associative processes require that visual symbolic stimuli be paired with mental representations of phonological information during reading acquisition and with magnitude information during mathematical skills acquisition. Consistent with this view, several previous studies have demonstrated a key role for medial temporal lobe structures in both reading and mathematical learning. For example, in the reading domain, increased gray matter volume in the right medial temporal lobe has been shown to accompany vocabulary learning (Bellander et al., 2016). Similarly, in the mathematical domain, the developmental trajectory from the reliance on counting to more mature memory-based fact retrieval strategies for calculation is marked by increased neocortical functional connectivity of the right hippocampus (Qin et al., 2014). Moreover, it has been shown that hippocampal volume predicts performance improvements in reading and mathematics (Hoeft et al., 2011; Supekar et al., 2013). Based on this evidence, we suggest that the PHG plays an important role in the associative encoding of both orthographic and numeric symbolic stimuli, and that reduced structural integrity of this neural structure adversely affects these key associative processes in LRLM.

Implications for neural models and theories of LRLM

A primary goal of the current study was to test differential predictions of neural models of LRLM described in a theoretical framework proposing domain-specific, domain-general, or phonological processing pathways to theses difficulties (Ashkenazi et al., 2013). Structural results from gray matter morphometry showed reduced cortical surface complexity in rPHG, and, given the putative role of the rPHG in visuo-spatial memory, are consistent with a domain-specific model of LRLM. However, results from functional connectivity and logistic regression analyses revealed distinct patterns of intrinsic connectivity linking rPHG to domain-specific cortical regions implicated in reading and mathematics in LRLM. Together, these results support a hybrid neural model of LRLM, fusing elements of the domain-specific and domain-general models. Specifically, LRLM is characterized by a primary problem in a domain-general structure underlying visuo-spatial memory (rPHG) (Aminoff et al., 2013; Kirchhoff et al., 2000; Nenert et al., 2014; Schon et al., 2004); however, weak intrinsic functional interactions between the rPHG and domain-specific regions serving reading and mathematics further distinguishes LRLM from LR and LM children. We suggest that simplistic models of LRLM may be insufficient to account for the heterogeneity of cognitive profiles seen within this population with comorbid learning difficulties. An important direction for future work informing cognitive (Landerl et al., 2009; Wilson et al., 2015) and neural models (Ashkenazi et al., 2013) of LRLM is to incorporate a multidimensional approach to studying cognitive function in this population that simultaneously considers interactions between domain-specific and domain-general function.

Developmental origins of neural basis of LRLM

When assessed together, surface-based and volumetric methods allow for the distinction between cortical thickness and gyral complexity as they provide complementary information about the timing and nature of disrupted neurodevelopmental processes (Schaer and Eliez, 2009). Atypical cortical surface complexity is thought to arise early in development (Giménez et al., 2006; Haukvik et al., 2012; Kesler et al., 2006; Schaer et al., 2009) while changes in cortical thickness undergo constant maturation through adulthood via pruning and learning-dependent plasticity (Shaw et al., 2006, 2008). Our finding of reductions in cortical surface complexity, but not thickness, is suggestive of early focal problems in LRLM individuals. This finding might also explain why LRLM children are vulnerable to difficulties in multiple cognitive domains. Whether such aberrations in the medial temporal lobe manifest early in development, and how this weakness in turn disrupts the communication between relevant cortical networks supporting reading and mathematical information processing remains to be investigated using appropriate longitudinal study designs in younger children (Kraft et al., 2016; Skeide et al., 2016). In addition, further research is also needed to examine whether early disruption of medial temporal lobe organization also contributes to learning difficulties in multiple other cognitive domains.

Diagnostic distinction between “low abilities” and “learning disabilities”

Here we have applied a relatively liberal criterion for grouping children with learning difficulties. However, unlike previous studies applying similar diagnostic criteria (Olulade et al., 2013; Evans et al., 2014; Krafnick et al., 2014), participants of our study were not labeled “learning disabled”; rather these children were characterized as “low reading and mathematical abilities.” Nevertheless, we argue that the reported findings are relevant to our understanding of learning disabilities given the empirical evidence for quantitative rather than qualitative differences between disabilities and low abilities. In particular, several recent functional and structural MRI studies suggest that the core neural indices of reading disability can be robustly identified across liberal and conservative criteria (e.g., Clark et al., 2014; Finn et al., 2014). Moreover, several available data sources indicate that the trajectory from average to below-average performance is continuous, rather than categorical in nature (Peterson & Pennington, 2012); therefore, we argue that applying the criteria described in our manuscript will provide important and novel information regarding structural and functional brain differences underlying reading and mathematical abilities. Nevertheless, follow-up work is needed to determine whether our results generalize to clinical samples involving subjects with an official diagnosis of reading disability (developmental dyslexia) or mathematical disability (developmental dyscalculia).

Conclusion

Here we have described, for the first time, a distinct brain signature of co-occurring low reading and mathematical ability in the developing brain. Results indicate that LRLM is distinguished by structural aberrations within a domain-general medial temporal lobe region and intrinsic functional connectivity reductions in circuits linking specific medial temporal lobe regions to domain-specific regions critical for reading and mathematics. Our findings inform models of LRLM by suggesting that this population displays an independent phenotype of learning difficulty that cannot be explained as a combination of isolated low reading and mathematical ability.

Research Highlights.

• Cortical morphometry and intrinsic functional connectivity were examined in children with low reading and/or mathematical abilities (LRLM) and typically developing children.

• Children with LRLM showed reduced cortical folding in right parahippocampal gyrus compared to comparison groups.

• Children with LRLM showed aberrant patterns of intrinsic functional connectivity between right parahippocampal gyrus and brain regions that support reading and numerical processing.

• Evidence for an independent neural signature of co-occurring low reading and mathematical abilities characterized by aberrations to both domain-general and domain-specific brain regions.