Prediction of CB[8] host-guest binding free energies in SAMPL6 using the double-decoupling method

Abstract

This study reports the results of binding free energy calculations for CB[8] host-guest systems in the SAMPL6 blind challenge (receipt ID 3z83m). Force-field parameters were developed specific for each of host and guest molecules to improve configurational sampling. We used quantum mechanical (QM) implicit solvent calculations and QM force matching to determine non-bonded (partial atomic charges) and bonded terms, respectively. Free energy calculations were carried out using the double-decoupling method (DDM) combined with Hamiltonian replica exchange method (HREM) and Bennett acceptance ratio (BAR) method. The root mean square error (RMSE) of the predicted values using DDM with respect to the experimental results was 4.32 kcal/mol. The coefficient of determination (R²) and Kendall rank coefficient (τ) were 0.49 and 0.52, respectively, highest of all submissions. In addition, these were compared to the results obtained by umbrella sampling (US) and weighted histogram analysis method (WHAM). Overall, DDM achieved a higher prediction accuracy than the US method. Results are discussed in terms of parameterization and free energy simulations.

1. INTRODUCTION

Binding free energy calculations using molecular simulations provide a way to understand the binding affinity between proteins and ligands at the atomic level. The ability to predict binding affinities of ligands to proteins is crucial for understanding a comprehensive profile of protein interactions with not only naturally occurring activators and inhibitors in cells but also synthesized drug-like small molecules. For this reason, many computational methods for calculating binding free energy have been developed and are increasingly used in the fields of drug discovery, biochemical engineering, and nanotechnology [1,2]. This is especially important for early-stage drug discovery [1–3]. Accurate molecular modeling and virtual screening based on the prediction of protein-ligand binding free energies can accelerate hit-to-lead and lead optimization processes. Furthermore, the ability to predict binding free energy can be used to evaluate selectivity and off-target interactions of leads, enabling in silico testing of potential target toxicity, side-effects, and resistance in drug development steps

While many computational techniques have been developed [3–5], challenges persist for the quest of optimal methods for the molecular modeling, force field development and free energy simulations. However, it is difficult to rank superiority of current state-of-the-art methods, as most approaches are assessed on different systems.

The Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) blind challenge [6] provides a unique platform for validating computational methods for predicting protein-ligand binding free energies in an unbiased manner. Since SAMPL3 in 2011, the scope of the SAMPL challenge has expanded from calculating solvation free energies (SAMPL1) [6] and tautomeric states of drug-like small molecules (SAMPL2) [7] to predicting binding free energies of host-guest systems (SAMPL3–6) [8–11].

Host-guest systems are useful models for testing computational methods for predicting binding free energies of drug-like small molecules. Host molecules used in SAMPL challenges are smaller (~100 non-hydrogen atoms) and have fewer conformational degrees of freedom than proteins, which significantly reduces the complexity and cost of computations. Hence, it is beneficial in terms of circumventing the quasi-nonergodicity problem in protein-ligand binding affinity predictions [5,12], as the incomplete sampling due to the slow structural reorganizations can affect the simulation results to a significant degree [5,12–14].

Cucurbit[8]uril (CB[8]) [15,16] is a macrocyclic methylene-bridged glycoluril oligomer (CB[n] family) containing eight glycoluril units. The CB[n] family has attracted considerable research interest recently due to their rich structural and chemical functionality. Validating computational methods for calculating binding free energies of the CB[8] host-guest systems are important for both developing tools to accurately predict protein-ligand binding affinities and supporting experimental studies on developing CB[8] as drug delivery carriers, molecular switch and catalyst [15,16].

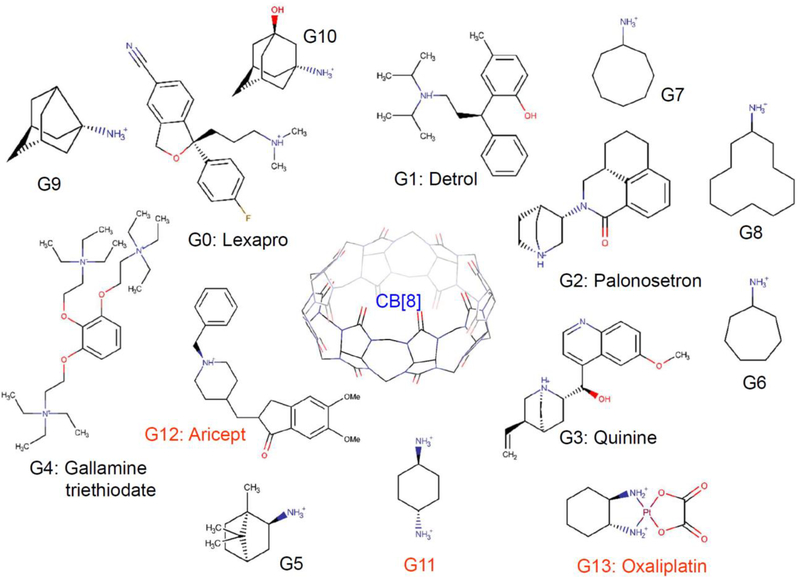
CB[8] was previously used as the host molecule in the SAMPL3 challenge with two guest molecules and now it is extensively dealt in the current SAMPL6 challenge with fourteen guest molecules, including FDA-approved drugs (Fig. 1). In the current challenge, eleven guests (G0-G10) are included in the main challenge and three guests (G11-G13) are offered as bonus cases, having the possibility of a 1:2 or 1:3 stoichiometry between host and guest. A blinded dataset using isothermal titration calorimetry (ITC) was provided by the SAMPL6 organizers following the submission of calculated binding free energies [17].

Fig. 1.

The structures of the host (CB[8]) (blue) and guests (G0-G13). G11-G13 (red) are bonus molecules.

Learning from previous experiences on SAMPL host-guest binding affinity prediction challenges, we focus on understanding the effects of two major sources of error in this study, 1) force-field parameters and 2) free energy simulation methods. Utilizing the classical molecular mechanics potential energy functions used in Chemistry at HARvard Molecular Mechanics (CHARMM) [18], we generated parameters ‘specific’ for each of host and guest molecules. Although this approach inherently negates transferability, it is expected that the gains in conformational degrees of freedom will improve sampling in bound and unbound states. To investigate the limitations of free energy methods, we compared results from two methods based on different sampling approaches, i.e., double-decoupling method (DDM) [19,20] used with Hamiltonian replica exchange method (HREM) [21] and Bennett acceptance ratio (BAR) [22] (method 1) and umbrella sampling (US) method [23] combined with weighted histogram analysis method (WHAM) [24,25] (method 2).

The paper is organized as follows—Section 2 describes the force field parameterization (Section 2.1), i.e., calculations of partial atomic charges (Section 2.1.1) and generation of bonded parameters (Section 2.1.2), methods used for docking and molecular dynamics (MD) simulations (Section 2.2), and free energy simulations (Section 2.3) such as DDM (Section 2.3.1) and the US method (Section 2.3.2). Section 3 begins with results of DDM (Section 3.1) and the results are compared to those using the US method in Section 3.2. Section 4 combines the Discussion and Conclusions.

2. METHODS

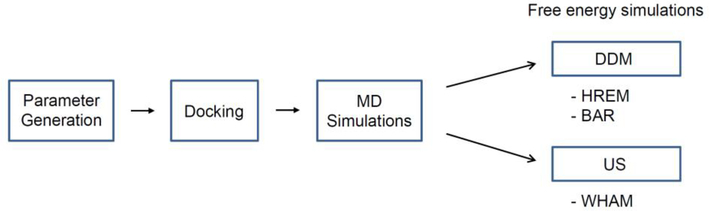
The workflow for calculating the binding free energy is shown in Fig. 2. We first generated force field parameters for the host and guest molecules and then initial binding poses for host-guest complexes were obtained via molecular docking. Systems consisting of a guest molecule or a host-guest complex were subjected to MD simulations. Free energy simulations were started from the last coordinates of the MD simulations. All simulations were performed with CHARMM (c41b1 and c41b2).

Fig. 2.

Workflow of the binding free energy calculations.

2.1. Parameterization

Force-field parameters were generated based on the classical molecular mechanics potential energy functions used in CHARMM [18,26–28]. Given R, the vector of the coordinates of the atoms, the non-bonded and bonded parts are evaluated by electrostatic and van der Waals (vdW) interactions (eq. 1) and bond, Urey-Bradley, angle, dihedral and improper dihedral terms (eq. 2), respectively.

$$U{(\mathit{R})}_{\mathit{nonbond}}=\sum _{\mathit{nonbond}}\frac{q_i{q}_j}{4\pi {\epsilon }_0{r}_{ij}}+{\epsilon }_{ij}\left[{\left(\frac{R_{\text{min}ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{\text{min}ij}}{r_{ij}}\right)}^6\right]$$ (1)

$$U{(\mathit{R})}_{\mathit{bond}}=\sum _{\mathit{bond}}{K}_b{\left(b-b_0\right)}^2+\sum _{\mathit{UB}}{K}_{UB}{\left(S-S_0\right)}^2+\sum _{\mathit{angle}}{K}_{\theta }{\left(\theta -{\theta }_0\right)}^2+\sum _{\mathit{dihedral}}{K}_{\chi }(1+\cos (n\chi -\delta ))+\sum _{\mathit{improper}}{K}_{imp}{\left(\phi -{\phi }_0\right)}^2$$ (2)

The first term on the right hand side of eq. 1 refers to the electrostatic interactions, given by Coulomb’s law where q_i and q_j are partial atomic charges of atoms i and j, r_ij is the distance between them and ɛ₀ is the vacuum permittivity (≈ 8.854 × 10⁻¹² F/m) [29]. In the second term, vdW interaction is treated by standard 6–12 Lennard-Jones (L-J) function where R_minij and ɛ_ij is the distance at the minimum of the L-J function and the depth of the minimum, respectively. For the host and guests (G0-G12), the L-J parameters provided by CHARMM General Force Field (CGenFF) program [28] were used, while the parameters for G13 were adopted from a modeling study for platinum atom (Pt (II)) [30]. The L-J parameters between pairs of different atoms are obtained via the LorentzBerthelot combination rules [31], in which ɛ_ij values are based on the geometric mean of ɛ_i and ɛ_j and R_minij values are based on the arithmetic mean between R_mini and R_minj.

In eq. 2, K_b, K_UB, K_θ, K_χ and K_imp are the bond, Urey-Bradley, angle, dihedral angle, and improper dihedral angle force constant, respectively; b, S, θ, χ and φ are the bond length, Urey-Bradley 1,3-distance, bond angle, dihedral angle and improper torsion angle, respectively, with the subscript zero representing the equilibrium values for the individual terms. More details of the potential energy function can be obtained from references 25–27.

2.1.1. Partial atomic charges

Partial atomic charges in eq. 1 were obtained via QM calculations. Equilibrium geometries for the host CB[8] and guest molecules G0-G12 were optimized using the B3LYP density functional theory [32,33] and Møller-Plesset second-order perturbation theory (MP2) [34], respectively, with Pople’s split-valence double zeta plus polarization basis sets (6–31G(d)) [35,36]. Following, single point calculations were carried out to determine electrostatic potential (ESP) charges based on MP2/6–31G(d) densities. ESP charges were redistributed so that equivalent atoms have the same partial charge using the restrained electrostatic potential (RESP) charge fitting procedure [37]. In the case of G13, triple-zeta quality correlation consistent basis sets (cc-pVTZ) [38] with the respective relativistic pseudopotential for Pt (cc-pVTZ-PP) [39] were used. Geometry optimizations were performed using B3LYP and ESP charges were obtained based on MP2 densities, using an atomic radius of 2.0 Å for Pt. All calculations were performed with the solvation model based on density (SMD) implicit solvent model [40]. Electronic structure calculations and charge fitting were performed using Gaussian16 [41] and Antechamber [42], respectively.

2.1.2. Bonded parameters

Bonded parameters in eq. 2 were determined by force-matching to QM forces. To generate classical conformational ensembles of the host and guests, Langevin dynamics (LD) simulations were performed in gas-phase (i.e., no tapering of non-bonded contributions), with a timestep of 1 fs, a temperature of 298.15 K, a collision frequency of 5 ps⁻¹, a coordinate saving frequency of 1 ps, and preceded by 500 ps of equilibration. L-J parameters and initial bonded parameters were used directly from CGenFF program. A total of 10,000 snapshots (i.e., 10 ns production run) were collected for each system (excluding G13) and B3LYP/631(d) forces were calculated for each point, which in turn was subjected to force-matching using the ForceSolve program [43,44]. Partial charges and L-J parameters were fixed during force-matching. For G13, classical ensemble generation proceeded in a similar manner to the systems of G0-G12, with exception of 20,000 snapshots collected from 5 ns of LD simulations. Palladium (Pd) (II) was used as a substitute for the complex coordinated Pt(II). The semi-empirical QM method, MNDO(d) [45] was used to perform LD simulations and the force matching was performed using B3LYP/LANL2DZ forces [46–48].

2.2. Docking and molecular dynamics simulations

Initial biding poses for the systems of the host-guest complex were obtained via molecular docking using GalaxyDock-HG program, which was developed based on the GalaxyDock2 program [49,50]. In cases of a 1:2 or 1:3 stoichiometry between host and guest (G11-G13) and in the absence of parameters (i.e., Pt(II) for G13), we alternatively resorted to manual docking, followed by short MD simulations to find lowest-energy binding poses.

The systems of host-guest complex and guest-only were then solvated using preequilibrated TIP3P water boxes (cubic, l = ~ 50 Å). We added additional Na⁺ and Cl⁻ ions (i.e., three of each) to reach the experimental [Na⁺] of the 25 mM sodium phosphate buffer at pH 7.4 and 298.15 K, in addition to neutralizing Cl⁻ ions for positively charged guest molecules. Systems were then subjected to MD simulations. They were minimized using the steepest descent (50,000 steps) and adopted basis Newton Raphson methods (500,000 steps), heated to 298.15 K over 100 ps, and then simulated for 50 ns under constant number, pressure, and temperature (NPT) ensemble at 298.15 K and 1 atm using the Nosé-Hoover thermostat [51]. The integration time step was 1 fs, and coordinate sets were saved every 10 ps. Electrostatics were evaluated using particle-mesh Ewald (PME) with ca. one grid point per angstrom (Å), a sixth–order spine interpolation for the complementary error function, a κ value of 0.36, and a 12 Å real space cutoff. The vdW term used a standard 6–12 LJ form, with force-switched truncation over the range 10–12 Å. The SHAKE constraint method [52] was applied to the covalent bonds between the hydrogen and oxygen atoms in TIP3P waters, with the default tolerance (1.0×10^–10 Å).

2.3. Free energy simulations

We partitioned the free energy simulation scheme into two parts: 1) DDM [19,20] combined with HREM [21] and BAR [22] (method 1) and 2) US method [23] used with WHAM [24,25] (method 2). All the simulations were repeated three times using different randomly assigned initial velocities to estimate statistical error.

2.3.1. Double-decoupling method

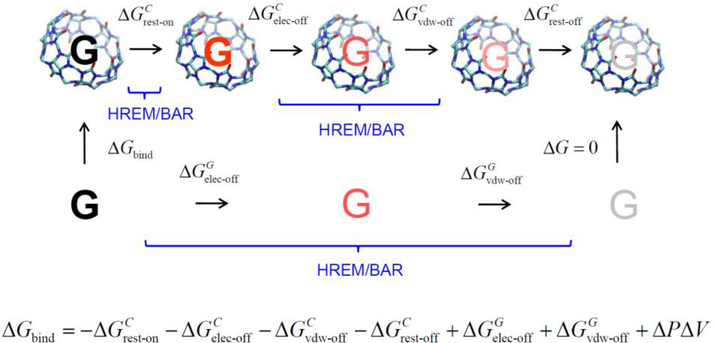
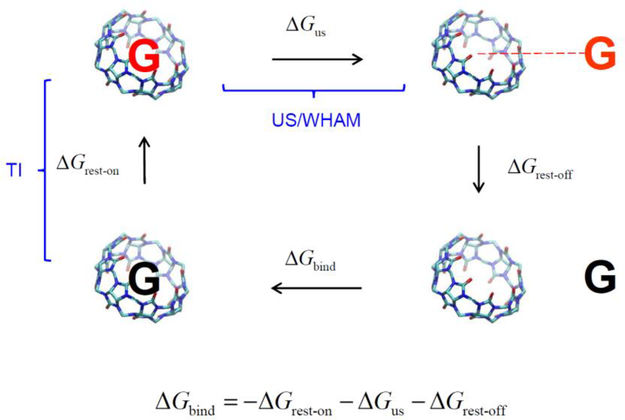
The binding free energies for all the host-guest systems including three bonus cases were calculated based on the DDM [19,20]. The thermodynamic analysis that underlies DDM is summarized in Fig. 3. The top pathway denotes the annihilation of the guest from the host-guest complex in solution and the bottom is the annihilation of the guest from the solution, where the electrostatic and vdW interactions of the guest have been turned off alchemically, gradually converting the guest into an ideal-gas molecule. The corresponding free energy changes denoted respectively by ΔG_{elec −off} and ΔG_{vdw −off}, with the superscript ‘C’ and ‘G’ representing the host-guest complex and guest-only, respectively. The free energy changes of the two alchemical pathways combine to yield the “absolute free energy of binding” [19,20].

Fig. 3.

The thermodynamic cycle used in double decoupling method (DDM).

ΔG_bind is the (absolute) binding free energies. ΔG_{rest −on}, ΔG_{rest −off}, ΔG_{elec −off} and ΔG_{vdw −off} are free energy changes due to applying and releasing the restraint and to turning-off electrostatic and vdW interactions, respectively. Superscript ‘C’ and ‘G’ respectively denote the host-guest complex and guest-only. ΔPΔV is the work associated with pressure and volume differences between the top and bottom paths.

The free energy changes were computed as follows: Equilibrium simulations of states of interest and intermediate states were performed using the HREM [21] to enhance configurational sampling. The simulations were done under constant number, volume, and temperature (NVT) ensemble at 298.15 K. The integration time step was 1 fs, and coordinate sets were collected every 1 ps. The other simulation conditions were the same as the MD simulations (Section 2.2). Statistical analysis of energetic information collected from simulation samples was done using BAR method [22].

For systems of host-guest complexes, a harmonic restraint in the form of U(r) = K_f(r_i − r_j)² was applied to the distance between the reference positions r_i and r_j of atom i (for host) and atom j (guest). These atoms were selected to form the shortest distance between the host and guest. The free energy cost for applying the restraint ($\mathrm{\Delta }{G}_{\text{rest}–\text{on}}^C$) was calculated by HREM simulations using 6 replicas (R1-R6). The force constant K_f was gradually increased over R1-R6 to reach the final force constant K_f of 0.4–2.0 kcal/mol/rad². The energetic information was analyzed via the BAR method [22].

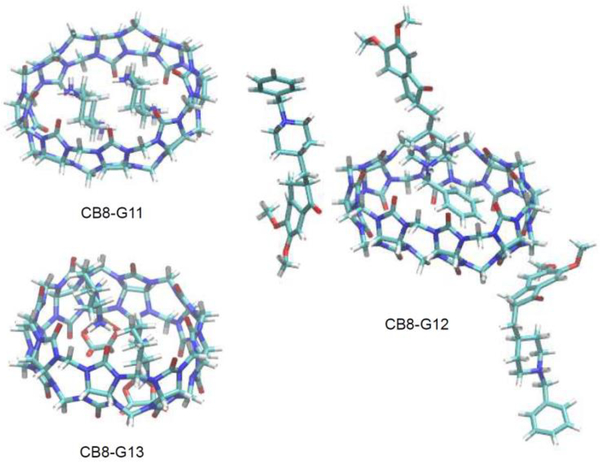
To calculate the contributions of the electrostatic ($\mathrm{\Delta }{G}_{\text{elec}–\text{off}}^C$) and van der Waals interactions ($\mathrm{\Delta }{G}_{\text{vdW}–\text{off}}^C$), we performed HREM simulations using 60 replicas (R6-R65), followed by analysis with the BAR method. The electrostatic interactions were gradually scaled down for the R6-R16 and then vdW interactions were gradually turned off for R16-R65. The restraint between the host and guest remain the same as in R6. The simulation for each replica was performed for 1 ns, to a total of 60 ns. In cases of binding of two or three guests to the host cavity (i.e., G11-G13), only one guest molecule was decoupled in the presence of other guests in the cavity to yield the second or third binding free energies. Representative binding configurations are shown in Fig. 4.

Fig. 4.

Representative configurations of the multiple guest binding mode for G11-G13: G11 (top left), G12 (right), and G13 (bottom left). Waters and ions are not displayed. For G11 and G13, two guest molecules are simultaneously bound in the cavity of the host CB[8] (spherical shape). Only one G12 molecule can be bound in the cavity in the presence of two other molecules interacting with portal regions of the host.

Free energy costs upon applying restraints between the host and guest were corrected for the standard state (i.e., restraint correction). The free energy for releasing the restraint was assumed as $\mathrm{\Delta }{G}_{\mathit{rest}–\mathit{off}}^c=-k_{B}T\ln (V_0/V_{\mathit{eff}})$ [19,20,53,54]. k_B is the Boltzmann constant and T the temperature in Kelvin. V₀ is the estimated standard state volume for an ideal gas at 298.15 K (1649.76 ų). V_eff was estimated using the equation, $V_{eff}=\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi (r_{\mathit{max}}^3-r_{\mathit{min}}^3)$. The maximum (r_max) and minimum (r_min) distances between the reference atoms were estimated as the upper and lower limits of the middle 95% of the distance distribution. The distribution was calculated using CORREL module in CHARMM for the 1 ns trajectory of replica R65, where both electrostatic and vdW forces are completely turned off.

The free energy changes due to the electrostatic and vdW interactions of the guest-only systems were calculated with HREM/BAR simulations for 60 replicas (r1-r60) using the same procedure as the host-guest system through replicas R6-R65. The electrostatic and vdW interactions were gradually scaled down for the r1-r11 and r11-r60, respectively.

The work associated with pressure (ΔP) and volume (ΔV) differences between the alchemical pathways of the host-guest complex and guest-only (i.e., ΔPΔV correction) was accounted as described below. As the relationship between pressure and intermediate state was linear for both pathways, the correction factor was estimated as the difference between the average pressure over R6-R65 and the average pressure over r1-r60. The volume difference was considered as the volume of each guest in the last coordinate of the MD simulation of the guest-only system. It was calculated using the CORMAN module in CHARMM. The work associated with ΔPΔV in a unit of atm·Å³ was scaled to kcal/mol.

The (absolute) binding free energy (ΔG_bind ) was obtained by using the following thermodynamic cycle:

$$\mathrm{\Delta }{G}_{\text{bind}}=-\mathrm{\Delta }{\text{G}}_{\text{rest}–\text{on}}^C-\mathrm{\Delta }{\text{G}}_{\text{elec}-\text{off}}^C-\mathrm{\Delta }{\text{G}}_{\text{vdW}-\text{off}}^C-\mathrm{\Delta }{\text{G}}_{\text{rest}–\text{off}}^C+\mathrm{\Delta }{\text{G}}_{\text{elec}-\text{off}}^G+\mathrm{\Delta }{\text{G}}_{\text{vdW}-\text{off}}^G+\Delta P\Delta V$$ (3)

2.3.2. Umbrella sampling method

Umbrella sampling (US) was used to calculate the binding free energies for G0-G11 (1:1 binding cases) [23,55–64]. The calculations were done using the same initial coordinates and force-field parameters as used in DDM. The thermodynamic cycle used in the US method is presented in Fig. 5.

Fig. 5.

The thermodynamic cycle used in umbrella sampling method.

ΔG_bind is the (absolute) binding free energy and ΔG_us denotes the free energy cost to pull the guest molecule from the binding pocket to outside the host molecule. ΔG_{rest −on} and ΔG_{rest −off} are free energy changes due to applying and releasing the harmonic restraint, respectively.

A series of MD simulations were performed on a host-guest complex with the harmonic distance restraint between the centers of masses of the host and the guest molecules. The biasing potential in the i-th simulation window is $W_i(\mathit{r})=\frac{1}{2}{K}_i{(\mathit{r}-{\mathit{r}}_{\mathit{i}}^{\mathbf{0}})}^2$, where K_i is the force constant, r is the reaction coordinate and ${\mathit{r}}_{\mathit{i}}^{\mathbf{0}}$ is the reference distance for the i-th sampling window. The full range of the reaction coordinate is covered using approximately 100 windows.

Starting from the initial binding pose obtained from molecular docking—followed by MD simulations, the guest molecule was gradually moved along the reaction coordinate towards outside of cavity by incrementing the reference distance $r_i^0$ at a speed of 0.2 Å every step, until the guest was fully dissociated. In most cases, for each sampling window, a 500 ps simulation was performed, starting from the last configuration of the previous sampling window. The first 250 ps in each run were treated as equilibration, which allowed the system to adjust to the current umbrella potential.

The biased probability distributions of the distance P′(r_i) collected in sampling windows were unbiased using WHAM [24]. The WHAM program (version 2.0.9.1) implemented by Grossfield [25] was used to obtain the unbiased distribution (r_i) and the associated potential of mean force (PMF), indicated by ΔG_us.

The free energy cost for imposing the restraint (ΔG_{rest −on}) was calculated using thermodynamic integration (TI) method. The harmonic force constant K_i was gradually increased from 0 to 30 kcal/mol/rad² over 30 λ states. For each λ state, we performed an equilibration for 20 ps and a production increment of 180 ps. The simulations were performed in the NVT ensemble by using LD with a timestep of 1 fs, a temperature of 298.15 K, a collision frequency of 1 ps⁻¹, and a coordinate saving frequency of 1 ps⁻¹. The restraint correction was done in a similar manner to the DDM to yield the free energy for releasing the restraint (ΔG_{rest −off}).

The (absolute) binding free energy (ΔG_bind ) was obtained via the thermodynamic cycle:

$$\mathrm{\Delta }{G}_{\text{bind}}=-\mathrm{\Delta }{G}_{\text{rest}–\text{on}}-\mathrm{\Delta }{G}_{\text{us}}-\mathrm{\Delta }{G}_{\text{rest}–\text{off}}$$ (4)

3. RESULTS

3.1. Prediction accuracy of computed values using the double-decoupling method

Table 1 shows computed binding free energy (ΔG_bind ) using DDM and the values of the thermodynamic terms. We assumed a 1:1 stoichiometry between the host and guest for eleven guest molecules included in the main challenge (G0-G10), whereas both single and multiple binding modes were considered for three bonus cases (G11-G13).

Table 1.

Free energy values of each of thermodynamic terms in double decoupling method (method 1).

Guest	$\mathbf{\Delta }{\mathbf{G}}_{\mathbf{rest}–\mathbf{on}}^{\mathit{C}}$	$\mathbf{\Delta }{\mathit{G}}_{\mathbf{elec–off}}^{\mathit{C}}$	$\mathbf{\Delta }{\mathit{G}}_{\mathbf{vdw}–\mathbf{off}}^{\mathit{C}}$	$\mathbf{\Delta }{\mathbf{G}}_{\mathbf{rest-off}}^{\mathit{C}}$	$\mathbf{\Delta }{\mathbf{G}}_{\mathbf{elec–off}}^{\mathit{G}}$	$\mathbf{\Delta }{\mathit{G}}_{\mathbf{vdw}–\mathbf{off}}^{\mathit{G}}$	ΔPΔV	ΔGbind	ΔGexpt
G0	0.83 ± 0.06	−23.75 ± 0.03	−10.02 ± 0.95	−1.66 ± 0.02	−26.56 ± 0.03	−40.73 ± 0.05	24.63	−8.05 ± 0.88	−6.69 ± 0.05
G1	0.10 ± 0.04	24.24 ± 0.15	−47.94 ± 1.31	−1.83 ± 0.03	19.43 ± 0.20	−67.54 ± 0.03	21.25	−1.43 ± 1.51	−7.65 ± 0.04
G2	0.84 ± 0.05	−2.96 ± 0.06	−19.81 ± 0.20	−1.50 ± 0.01	−6.67 ± 0.01	−48.80 ± 0.07	21.79	−10.25 ± 0.20	−7.66 ± 0.05
G3	0.37 ± 0.06	−18.83 ± 0.04	−44.21 ± 0.99	−1.49 ± 0.01	−22.34 ± 0.05	−76.03 ± 0.16	23.39	−10.82 ± 0.85	−6.45 ± 0.06
G4	2.01 ± 0.13	−56.13 ± 0.19	−38.10 ± 0.11	−1.46 ± 0.00	−60.58 ± 0.08	−78.37 ± 0.56	39.85	−5.42 ± 0.51	−7.80 ± 0.04
G5	1.03 ± 0.08	26.31 ± 0.05	4.98 ± 0.11	−0.43 ± 0.01	25.59 ± 0.08	−22.59 ± 0.08	12.60	−16.29 ± 0.34	−8.18 ± 0.05
G6	2.10 ± 0.05	46.88 ± 0.19	8.86 ± 0.08	−1.52 ± 0.02	47.25 ± 0.06	−11.84 ± 0.01	9.18	−11.73 ± 0.23	−8.34 ± 0.05
G7	1.11 ± 0.02	45.69 ± 0.07	10.38 ± 0.07	−0.82 ± 0.01	46.81 ± 0.03	−13.50 ± 0.08	9.71	−13.34 ± 0.14	−10.00 ± 0.10
G8	1.16 ± 0.40	36.29 ± 0.07	8.21 ± 0.33	−1.97 ± 0.02	32.23 ± 0.03	−22.74 ± 0.01	14.54	−19.67 ± 0.30	−13.50 ± 0.04
G9	1.50 ± 0.05	101.92 ± 0.18	11.74 ± 0.12	−1.37 ± 0.00	100.09 ± 0.04	−9.79 ± 0.05	9.63	−13.87 ± 0.13	−8.68 ± 0.08
G10	1.83 ± 0.07	122.60 ± 0.04	15.10 ± 0.30	−1.44 ± 0.00	126.17 ± 0.03	−11.27 ± 0.13	11.43	−11.76 ± 0.20	−8.22 ± 0.07
G11	3.10 ± 0.06	104.23 ± 0.16	9.23 ± 0.06	−1.48 ± 0.01	106.86 ± 0.06	−9.74 ± 0.08	10.26	−7.70 ± 0.21	−7.77 ± 0.05
G11*	2.17 ± 1.04	94.91 ± 0.59	−4.18 ± 0.61	−1.60 ± 0.02	106.86 ± 0.06	−9.74 ± 0.08	9.71	15.54 ± 2.21	N/A
G12	8.22 ± 1.13	−23.63 ± 0.08	−29.05 ± 0.66	−1.50 ± 0.00	−27.94 ± 0.03	−58.74 ± 1.60	26.83	− 13.90 ± 2.40	− 9.86 ± 0.03
G13	0.77 ± 0.08	226.92 ± 0.16	6.04 ± 0.11	−1.87 ± 0.02	225.54 ± 0.04	−12.55 ± 0.15	14.09	−4.79 ± 0.36	−7.11 ± 0.03
G13*	2.32 ± 0.24	232.26 ± 0.31	−1.68 ± 0.14	−1.77 ± 0.00	225.54 ± 0.04	−12.55 ± 0.15	14.00	−4.11 ± 0.27	N/A

ΔG_bind and ΔG_expt are the computed and experimental binding free energies, respectively. ΔG_{rest –on} and ΔG_{rest –off} are the free energy changes due to applying and releasing the restraint and ΔG_{elec –off} and ΔG_vdw–off denote the contributions of electrostatic and vdW interactions, respectively. Superscript ‘C’ and ‘G’ respectively denote the host-guest complex and guest-only. ΔPΔV denotes the work associated with differences in pressure and volume between the alchemical pathways of the host-guest complex and guest-only. All standard errors for ΔPΔV are less than 10⁻² kcal/mol. Means and standard errors are obtained from three independent simulations using different randomly assigned initial velocities.

^*Represents values for the second guest molecule.

The mean absolute error (MAE) and root mean square error (RMSE) with respect to experiment were 3.82 and 4.32 kcal/mol, respectively (see Table 2 and Fig. 6). The slope of the linear regression line (indicated by s) was 1.92. Pearson correlation coefficient (r) [65] was 0.70 with the p-value of 0.0042 (two-tailed test; n=14, α=0.05), indicating that the linear correlation between the experimental and computed values is statistically significant at the level of significance of 0.05. The corresponding coefficient of determination (R²) was 0.49. Although the correlation between DDM predictions and experiment was the highest amongst the SAMPL6 submissions, the linear correlation (r) is generally considered moderate and the accuracy of the linear regression model (measured by R²) in not satisfactory—51% of the variance in the experimental value still cannot be predicted by the computed value.

Table 2.

Comparison of computed and experimental free energy.

Method	RMSE	MAE	s	r	R2	τ	ρ
DDM*	4.32	3.82	1.92	0.70a	0.49	0.52b	0.75c
DDM**	4.45	3.89	1.77	0.67d	0.45	0.48e	0.73f
US**	5.94	4.99	0.82	0.41g	0.17	0.15h	0.24i

^*Results including all guest molecules (G0-G13).

^**Results of guest molecules G0-G11.

RMSE and MAE are the root mean square error and mean absolute error between computed and experimental values, respectively.

s denotes the slope of the linear regression line.

r, τ, ρ is Pearson, Kendall, and Spearman correlation coefficient, respectively.

R² is correlation coefficient of determination.

^ap-value of 0.0042 with a confidential interval of [0.27, 0.90] (two-tailed test; n=14, α=0.05 with Fisher z-transformation)

^bp-value of 0.010 with a confidential interval of [0.12, 0.91] (two-tailed test; n=14, α=0.05)

^cp-value of 0.0020 (two-tailed test; n=14, α=0.05)

^dp-value of 0.015 with a confidential interval of [0.15, 0.90] (two-tailed test; n=12, α=0.05 with Fisher z-transformation)

^ep-value of 0.028 with a confidential interval of [0.05, 0.92] (two-tailed test; n=12, α=0.05)

^fp-value of 0.0074 (two-tailed test; n=12, α=0.05)

^gp-value of 0.19 with a confidential interval of [−0.21, 0.80] (two-tailed test; n=12, α=0.05 with Fisher z-transformation)

^hp-value of 0.49 with a confidential interval of [−0.28, 0.58] (two-tailed test; n=12, α=0.05)

ⁱp-value of 0.46 (two-tailed test; n=12, α=0.05)

Note that the computed first binding free energy value of G11 (−7.70 ± 0.21 kcal/mol) was used for the analysis.

In case of G12, the computed value was compared with the first binding free energy of experiment (−9.86 ± 0.03 kcal/mol).

For G13, the average of the first and second binding free energy (−4.45 ± 0.19 kcal/mol) was compared to the experimental value (7.11 ± 0.03 kcal/mol).

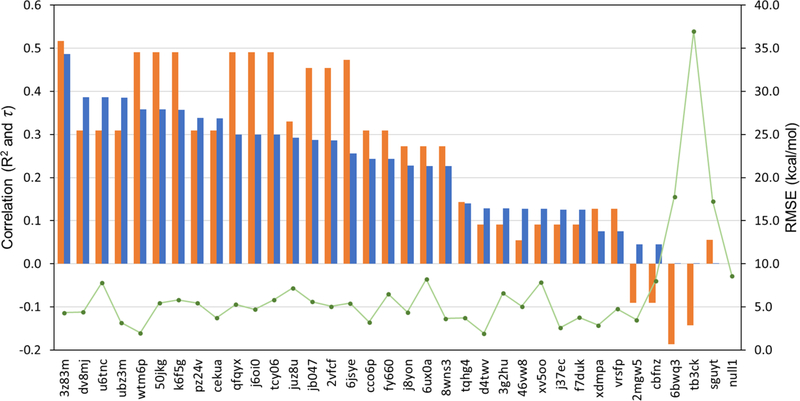
Fig. 6.

Relative performance of our approach (receipt ID 3z83m) with respect to τ (orange bar), R² (blue bar) and RMSE (green marker). The x-axis denotes receipt ID of all submissions. Further statistical analysis can be found in an overview paper for the SAMPL6 host-guest binding affinity prediction challenge in the same issue [11].

In addition, the similarity between the ranks of experimental and computed values were evaluated (Table 2). The Kendall rank correlation coefficient (τ) [66] was 0.52. The p-value of the two-tail test at n=14 and α=0.05 was 0.010, proving a statistically significant rank order correlation between two sets at the 95% confidence level. The Spearman correlation coefficient (ρ) (i.e., the Pearson’s r on the ranks of the data) was 0.75 (p-value = 0.0020; two-tailed test at n=14 and α=0.05). Altogether, this indicates that the rank ordering is robust, as there is at most a 5% chance that this similarity in rank order is due to unknown factors.

It is worth noting that our submission for bonus cases (G11-G13) was the top result in terms of error with respect to experimental results. The MAE and RMSE of our predictions with respect to experiment were 2.26 and 2.79 kcal/mol, respectively. The absolute errors for G11, G12, and G13 were 0.07, 4.04, 2.66 kcal/mol, respectively, while the MAE reported for each molecule for all six participants was 6.44 (for G11), 18.84 (G12), and 11.67 kcal/mol (G13).

For G11, we tested host:guest binding ratios of 1:1 and 1:2. ΔG_bind values of the first and second guest were −7.70 ± 0.21 (mean and standard error) and 15.54 ± 2.21 kcal/mol, respectively, proving that binding of the second guest is energetically unfavorable. Therefore, we submitted only ΔG_bind obtained via 1:1 binding mode, excluding the second ΔG_bind. This is confirmed by the ITC experiment provided by organizers [17] and the submitted value was very close to the experimental result (−7.77 ± 0.05 kcal/mol). We investigated 1:1 – 1:3 binding modes for G12, given that in the ITC experiment the final concentration of guest was approximately three times greater than the host concentration (i.e., 0.0729 mM (for CB[8]) and 0.271 mM (G12)) [17]. However, it became clear that having two or three guests in the host cavity was energetically unfavorable. Instead, we calculated a binding free energy of a guest bound to the cavity of the host in the presence of two other molecules interacting with portal regions of the host, based on observations from MD trajectories (Fig. 4). In the case of G13, both the first and second binding free energies had energetically favorable values (i.e., −4.79 ± 0.36 and −4.11 ± 0.27, respectively). Therefore, the averaged value over the first and second binding free energies (−4.45 ± 0.19 kcal/mol) was taken as the final binding free energy.

3.2. Comparison between the double decoupling and umbrella sampling method

We conducted a follow-up study on 1:1 binding cases (i.e., G0-G11) after the SAMPL6 submission. To investigate the limitations of free energy simulation methods, we used a different strategy (US method), which considers the PMF as a function of the physical separation of the host and guest [23,55–64]. The (absolute) binding free energies (ΔG_bind ) determined using the US method are summarized in Table 3. The performance of the DDM and US methods, with respect to experiment, are compared for twelve hostguest systems (Table 2 and Fig. 7). The correlations between the two methods are presented in Table 4.

Table 3.

Free energy values of each of thermodynamic terms in umbrella sampling method (method 2).

Guest	ΔGrest–on	ΔGus	ΔGrest–off	ΔGbind	ΔGexpt
G0	2.41 ± 0.19	18.56 ± 0.90	−0.31 ± 0.14	−20.67 ± 0.93	−6.69 ± 0.05
G1	2.42 ± 0.06	5.97 ± 0.64	−0.41 ± 0.18	−7.98 ± 0.85	−7.65 ± 0.04
G2	1.99 ± 0.04	13.53 ± 1.04	−0.84 ± 0.02	−14.68 ± 1.05	−7.66 ± 0.05
G3	4.01 ± 0.21	7.74 ± 0.15	−0.52 ± 0.02	−11.23 ± 0.19	−6.45 ± 0.06
G4	2.08 ± 0.05	9.86 ± 0.82	−0.39 ± 0.06	−11.55 ± 0.87	−7.80 ± 0.04
G5	1.69 ± 0.01	13.54 ± 0.95	−1.34 ± 0.12	−13.89 ± 0.83	−8.18 ± 0.05
G6	1.87 ± 0.02	10.87 ± 0.56	−1.25 ± 0.17	−11.49 ± 0.74	−8.34 ± 0.05
G7	1.80 ± 0.03	12.22 ± 1.07	−1.26 ± 0.06	−12.77 ± 1.00	−10.00 ± 0.10
G8	1.60 ± 0.01	19.36 ± 0.93	−0.82 ± 0.14	−20.14 ± 0.78	−13.50 ± 0.04
G9	1.65 ± 0.01	12.66 ± 1.04	−1.14 ± 0.04	−13.18 ± 1.02	−8.68 ± 0.08
G10	2.63 ± 0.03	9.74 ± 0.10	−1.10 ± 0.11	−11.26 ± 0.10	−8.22 ± 0.07
G11	4.07 ± 0.04	8.46 ± 0.45	−0.49 ± 0.27	−12.04 ± 0.39	−7.77 ± 0.05

ΔG_bind and ΔG_expt are the computed and experimental binding free energies, respectively. ΔG_{rest –on} and ΔG_rest–off are respectively free energy changes due to applying and releasing the harmonic restraint. ΔG_us denotes the free energy cost to pull the guest molecule from the binding pocket to outside the host molecule. Means and standard errors are obtained from three independent simulations using different randomly assigned initial velocities.

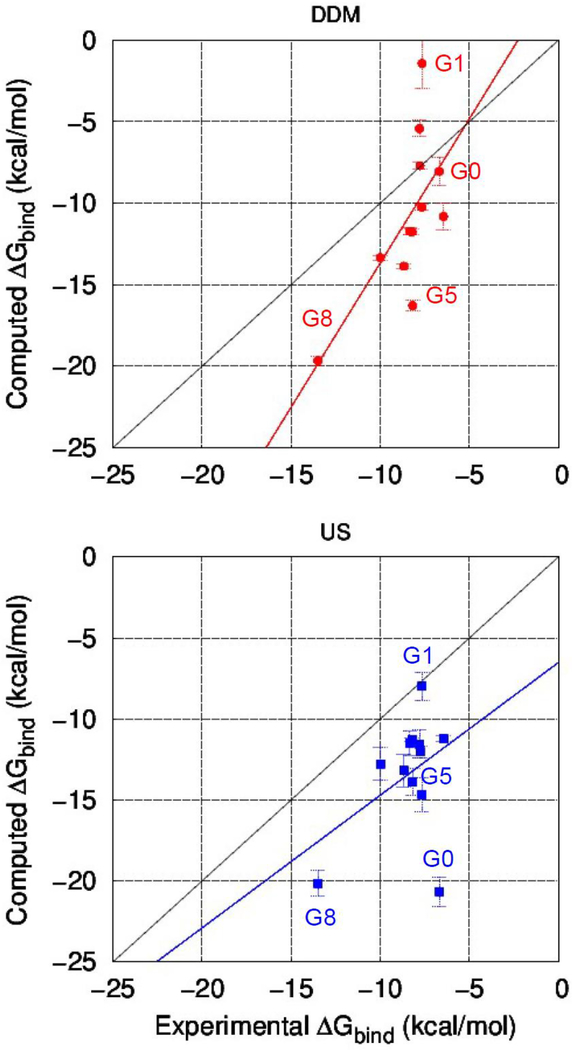
Fig. 7.

Correlations between experimental and computed free energies using method 1 (DDM) (top) and method 2 (US method) (bottom). Computed values are presented as the mean and standard error (error bar) with linear regression line; red for double decoupling method and blue for umbrella sampling method. Solid black line denotes a perfect positive correlation. G12 and G13 are not included.

Table 4.

Correlations between the method 1 (DDM) and 2 (US method).

RMSE	s	r	R2	τ	ρ
4.88	0.68	0.51a	0.26	0.36b	0.41c

s denotes the slope of the linear regression line.

r, τ, ρ is Pearson, Kendall, and Spearman correlation coefficient, respectively.

R² is correlation coefficient of determination.

^ap-value of 0.09 with a confidential interval of [−0.09, 0.84] (two-tailed test; n=12, α=0.05 with Fisher z-transformation)

^bp-value of 0.10 with a confidential interval of [−0.07, 0.80] (two-tailed test; n=12, α=0.05)

^cp-value of 0.19 (two-tailed test; n=12, α=0.05)

Note that correlations were obtained from results of G0 – G11.

The first binding free energy value of G11 was used for the analysis.

DDM achieved a relatively higher accuracy than the US method in terms of error with respect to experiment. The MAE and RMSE were 3.89 and 4.45 (for DDM) and 4.99 and 5.94 kcal/mol (for US), respectively (see Table 2). In addition, correlations were higher in results obtained with DDM than with the US method, with exception of the slope of linear regression (s = 1.77 for DDM and 0.82 for US). While computed binding free energies (ΔG_bind ) using DDM illustrated a statistically significant linear relationship with the experiment, the values via the US method did not. In case of DDM, Pearson’s r was 0.67 with p-value of 0.015 (two-tailed test; n=12, α=0.05), indicating that there is a statistically significant linear relationship between the experimental and computed values at the level of significance of 0.05. The corresponding coefficient of determination (R²) was 0.45. For the US method, r was 0.41 (R² = 0.17) with p-value of 0.19 (n=12, α=0.05).

Moreover, the similarity between the ranks of experimental and computed values was higher in DDM than US method. For DDM, the Kendall’s τ was 0.48. The p-value of the two-tail test at n=12 and α=0.05 was 0.028, proving a statistically significant rank order correlations between two sets at the 0.05 confidence level. The Spearman’s ρ was 0.73 (p-value = 0.0074; two-tailed test at n=12 and α=0.05). For the US method, the τ and ρ were 0.15 and 0.24, which are far below the critical values of the level of significance of 0.05.

The correlations between the two methods were moderate. The RMSE between DDM and US methods was 4.88 kcal/mol and the slope of the linear regression line was 0.68 (Table 4). Pearson‘s r was 0.51 with the p-value of 0.09 (two-tail test; n=12 and α=0.05). The rank correlation coefficients, τ and ρ were 0.36 and 0.41 with p-values 0.10 and 0.19 (two-tail test; n=12 and α=0.05), respectively.

4. DISCUSSION AND CONCLUSIONS

In an attempt to improve the force-field accuracy, we generated tailored force-field parameters ‘specific’ to each host and guest molecule. Namely, even if different molecules have same atom types, each parameter is slightly different, according to QM calculations of each molecule. Although this approach inherently negates transferability, it is expected that the gains in configurational degrees of freedom will improve sampling in bound and unbound states. However, as a derivative for classical molecular mechanics models, the parameters do not account for polarizability.

Partial charges were obtained from QM calculations. The structure of CB[8] was optimized with density functional theory (i.e., B3LYP/6–31G(d)) whereas the geometry-optimized structures for guests (G0-G12) were obtained using MP2/6–31G(d). MerzKollman ESP charges were obtained for each optimized structure, and these are processed through the antechamber RESP facility to symmetrize charge distribution amongst topologically equivalent atoms. However, partial charges for the bonus guest molecule G13 needed special consideration as the guest contained a platinum (Pt II) atom which required the use of effective core potentials. In the case of G13, triple-zeta quality correlation consistent basis sets (cc-pVTZ) with the respective relativistic pseudopotential for Pt (cc-pVTZ-PP) [39] were used, based on an effective pseudopotential-based composite method, rp-ccCA [67]. Geometry optimizations were performed using B3LYP and ESP charges were obtained based on MP2 densities, using an atomic radius of 2.0 Å for Pt. All QM calculations were carried out using the SMD implicit solvent (water) model [40,68], to include approximate solvent effects on the partial charge calculations in hopes to provide a reasonable description of the solute in solution. As a continuum solvation method, the SMD model is unique in contrast to other implicit models because it uses the solute’s charge density rather than partial atomic charges, allowing the method to be used with wavefunction theory and density functional theory methods [40]. The parameterization of the boned part for G13 proved a more difficult challenge, as parameters for Pt (II) complexes are not readily available classically. As a work around, Palladium (Pd) (II) was used as a substitute for the complex coordinated Pt (II), with the assumption that discrepancies in internal degrees of freedom between exchanging Pd (II) and Pt (II) are minimal and are reasonably close in vibrational motions.

Although the tailored parameterization approach ideally would improve sampling which in turn allows more accurate prediction of the binding free energy, we had unexpected technical problems in the parameterization process via software issue. First, improper dihedral terms assigned by force-matching were not utilized in free energy simulations. The ForceSolve program creates additional improper dihedrals based on the bond connectivity other than those existing in the CHARMM force field and these additional parameters were not read from the CHARMM program. For instance, in the CB[8] host, the original CHARMM topology assigns a single improper dihedral centered on the carbonyl carbon, to ensure planarity of the associated oxygen and the two nitrogen atoms attached to the carbon. However, the force-matching procedure generates all possible combinations of atoms with a bond connectivity of three to yield an additional improper dihedral onto the nitrogen atoms between the CB[8] carbonyls, for a total of two improper dihedral parameters. This new nitrogen-centered improper dihedral was not utilized since it was not in the initial CHARMM topology file used to generate the initial systems. However, this solely manifested in the aromatic substituents of the guest systems, and thus caused some minor excessive flexibility in planar rings. They maintained reasonable structural features and did not significantly impact either the binding poses nor the non-bonded interactions between the host and guest. These issues were corrected after the SAMPL6 challenge. Second, we found a dihedral overwriting parser problem. For singly defined dihedrals (i.e., a dihedral with one associated multiplicity), the overwriting occurred as expected. However, dihedral terms containing dihedral multiplicities were to be a combination of CHARMM and force-matched parameter. For example, after reading in a CHARMM parameter set, and following with the appending of the force-matched parameter set, a dihedral with multiplicity of n = 2, 3 and 6 would take the n = 6 dihedral parameter from the force-matched set. This resulted in a dihedral that has CHARMM dihedral parameters for n = 2 and 3, and a force-matched dihedral parameter for n = 6. This is a bug associated with CHARMM and the exact cause is still uncertain. Last, overlap between same parameter types in host and guest occurred in reading parameters. Further discussion on the parameterization issue can be found in the work of Hudson et al., also in this issue [69].

Free energy simulations using two well-known methods, alchemical (DDM) and US method, were considered for side by side comparison. The methods are based on different perturbation techniques. In DDM, the complex of host and guest is gradually separated via an alchemical transformation, while in the US method, the complex is separated along a physically realizable path (reaction coordinate) such as the distance between host and guest. In addition, these methods are combined with different sampling and analysis approaches. For DDM, equilibrium simulations of states of interest and intermediate states were performed using HREM to enhance configurational sampling and statistical analysis of the energetic information collected from sampling was performed using the BAR method. On the other hand, non-Boltzmann sampling was used for the US method. A non-Boltzmann weighting function was added to each window to acquire adequate statistics about low-energy configurations. The obtained biased probability distributions accumulated in these sampling windows were unbiased using WHAM to yield the PMF.

In both cases, starting with plausible binding poses are essential for accurate predictions, given that both DDM and US method aim to calculate “absolute” binding free energies, which are the free energy differences between two thermodynamics states—the ligand restricted to the host (bound state) and the unrestricted ligand, free to explore all the possible conformations (unbound state). From a sampling perspective, energetically unfavorable initial binding poses lead to insufficient sampling of the low-energy bound states. Therefore, we conducted molecular docking to obtain low-energy initial binding poses (in the context of the force-field) for extensive free energy simulations (i.e., DDM and US method). Docking algorithms are designed to estimate binding affinities between proteins and ligands using phenomenological scoring functions based on (nearly) rigid representations of the molecules. Although comparative studies (including SAMPL challenges) consistently illustrate that binding free energies obtained from docking simulations poorly correlate with experiment [8–10,70,71], if used properly, molecular docking approaches offer useful intuitions such as plausible configurations of a protein-ligand complex in a fast and computationally inexpensive way.

We used the GalaxyDock-HG program for docking simulations for most host-guest systems. The program finds binding poses of host and guest via global optimizations of the AutoDock4 energy [72] using the conformational space annealing (CSA) algorithm [73]. The energy is evaluated in the continuous space instead of interpolating energy values at the grid points as in the GalaxyDock2 program and the initial set of conformations for CSA was generated by random perturbations of initial structures unlike the geometry-based pre-docking used in GalaxyDock2. For cases of binding of two or three guests to the host or the absence of parameters (i.e., Pt(II) for G13), we alternatively resorted to manual docking followed by short MD simulations to find lowenergy binding poses.

In free energy calculations, corrections for free energy changes due to pressure (P) and volume (V) differences—referred to as “ΔPΔV correction” (for DDM) and free energy costs for releasing restraints— “restraint correction” (for both DDM and US method) were accounted. For “ΔPΔV correction”, the work associated with the differ in pressure and volume between the intermediate states of host-guest complex and guest-only was corrected for the standard state. Specifically, $U_i^C\left(\mathit{R}\right)$ and $U_i^G\left(\mathit{R}\right)$, the potential energy of i-th state of host-guest complex and that of guest-only system were, respectively, replaced with $U_i^C\left(\mathit{R}\right)+P_i^C{V}_i^C$ and $U_i^G\left(\mathit{R}\right)+P_i^G{V}_i^G$. Although applying artificial restraint is useful to avoid sampling problems due to complex energy barriers along the alchemical pathway, this causes the loss of positional and orientational freedom and ultimately alters the free energy. Corresponding free energy for releasing the restraint can be estimated as the ratio between the standard state volume for an ideal gas (V₀) and an effective volume of a guest molecule (V_eff), namely, $\mathrm{\Delta }{G}_{\mathit{rest}–\mathit{off}}^c=-k_{B}T\ln (V_0/V_{\mathit{eff}})$ [19,20,53,54]. In bound states for both DDM and US method, imposing the restraint confines the guest molecule to a small volume, i.e., V_eff < V₀, and corresponding free energy for releasing the restraint (ΔG_rest−off) is negative. On the other hand, in US scheme, when guest molecules are dissociated from the host beyond certain distance (i.e., r ≈ 20 Å) V_eff values become larger than V₀ to yield the positive ΔG_rest−off values. It is worth pointing out, however, the resulting binding free energies (ΔG_bind) (in cases of positive ΔG_rest−off values) are (almost) same as those with negative ΔG_rest−off values because ΔG_us decreases with the increase in ΔG_rest−off. We confirmed that ΔG_bind values did not depend on the final dissociation distance—the variances of calculated ΔG_bind values beyond a “cutoff limit” (approximately 10 Å) were negligible. The configurations of the distances between the host and guest greater than the “cutoff limit” can be considered as “fully dissociated” states, in which the host and guest are separated by multiple water layers.

We note that in US simulations some systems needed special consideration for sampling. In an effort to achieve a well-converged PMF, we confirmed the ‘pulling-out (starting from the bound state)’ schemes by comparing with ‘pushing-in (from the unbound state)’ simulations. In cases of PMF profiles of pulling-out simulations (500 ps for each window) were not consistent with those based on pushing-in simulations (i.e., CB8-G0, CB8-G4 and CB8-G10), we performed a 1 ns simulation for each window to achieve the consistency. For the other systems, the consistency was observed with 200 ~ 500 ps simulation for each window. Even though applying a force to separate the host and guest is effective in producing representative unbound states, this can create nonnative unbound states. In addition, the initial coordinate for pulling-out simulations is not uniquely defining the bound state. Therefore, collected distributions that are under-sampled can lead to a poorly-converged PMF. Although the consistency of the PMF profiles is not sufficient to demonstrate that a simulation is well-sampled and converged, it is necessary to confirm the convergence [74]. Further discussion on the US method can be found in a companion paper by Nishikawa et al. in the same issue [75].

Using Na⁺ and Cl⁻ ions in simulations as an alternative to the sodium phosphate buffers used in the ITC experiment could be another source of error in the binding free energy calculations. This approach negates the properties of phosphate in solution such as specific electrostatic interactions with the host and guest molecules and with ions [76–78] and the kosmotropic behavior [79,80]. However, unfortunately we lack a better alternative than using Cl⁻ (instead of phosphate) as the reliable force-field parameters for phosphates and interacting ions are still under development [81–83,78].

The current results demonstrate limitations of the DDM and US method based on classical force-fields for predicting the experimental binding free energies. Although the correlation of the results from the DDM approach with respect to experiment, was strongly statistically significant and highest among all submissions, almost half of the variance in the experimental value still cannot be predicted by the computed values. Still many theoretical and practical issues associated with our methodology used in the SAMPL6 challenge remain unresolved. We have developed force-field parameters specific for each of host and guest molecules to best reproduce QM properties such as partial charges and forces. However, as a derivative of CHARMM classical force-field parameters, the parameters do not account for polarizability. This would be the major weakness of the force-field parameters used in this study. From the comparison of results of DDM and US methods, we have learned that methodology limitations are not negligible. Although both methods based on the same initial binding poses and force-field parameters, the correlation between the two methods is not significant. Inaccuracies in both configurational sampling and statistical analysis for collected energetic information could be another major source of errors in binding free energy predictions.