Multi-Pathway Multi-Echo (MPME) imaging: all main MR parameters mapped based on a single 3D scan

Abstract

Purpose:

Quantitative parameter maps, as opposed to qualitative grayscale images, may represent the future of diagnostic MRI. A new quantitative MRI method is introduced here that requires a single 3D acquisition, allowing good spatial coverage to be achieved in relatively short scan times.

Methods:

A multi-pathway multi-echo (MPME) sequence was developed, and at least three pathways with two echo times were needed to generate T₁, T₂, T₂*, B₁⁺ and B₀ maps. The method required the central k-space region to be sampled twice, with the same sequence but with two very different nominal flip angle settings. Consequently, scan time was only slightly longer than that of a single scan. MPME data were reconstructed into parameter maps, for phantom as well as brain acquisitions, in five healthy volunteers at 3T. Spatial resolution, matrix size and FOV were 1.2×1.0×1.2mm³, 160×192×160 and 19.2×19.2×19.2cm³ (whole brain), acquired in 11.5 min with minimal acceleration. Validation was performed against T₁, T₂ and T₂* maps calculated from gradient-echo and spin-echo data.

Results:

In Bland-Altman plots, bias and limits of agreement for T₁ and T₂ results in vivo and in phantom were: −2.9/±125.5ms (T₁ in vivo), −4.8/±20.8ms (T₂ in vivo), −1.5/±18.1ms (T₁ in phantom), and −5.3/±7.4ms (T₂ in phantom), for ROIs including given brain structures or phantom compartments. Due to relatively-high noise levels, the current implementation of the approach may prove more useful for ROI-based as opposed to pixel-based interpretation.

Conclusions:

We proposed a novel approach to quantitatively map MR parameters based on an MPME acquisition.

Introduction

MR images are not typically quantitative in nature, in the sense that voxel values are associated with arbitrary grayscales rather than clear physical quantities. While contrast can be manipulated to great effect to produce clinically-useful images, one rarely obtains maps of the actual physical parameters that determine contrast. As imaging strategies and acceleration techniques continue to evolve, routine MR images may become more quantitative in nature, with values that have actual units and physical meaning. Existing quantitative imaging methods include the use of a multi-echo spin-echo (or gradient-echo) sequence to measure T₂ (or T₂*) (1,2). Alternately, the signal equation in phase-cycled SSFP and ‘dual echo in the steady state’ (DESS) (3) involves T₂ along with several other parameters, and strategies can be developed to generate T₂ maps from these signals (4–8). The ‘Gradient-Echo Sampling of FID and Echo’ (GESFIDE) method (9) jointly measures T₂ and T₂* by acquiring both free induction decay (FID) as well as spin echo signal. We adapted a GESFIDE-like strategy to a multi-echo DESS sequence (10), which is faster than the spin-echo based method originally used for GESFIDE. T₁, on the other hand, can be measured by sampling the recovery that follows an inversion pulse (11), for example using a Look-Locker sequence (12), or fitting data acquired with varied TR and/or flip angle settings (13–15). Some methods can capture both T₁ and T₂ jointly, for example DESPOT (16,17) and the ‘Triple echo in the steady state’ (TESS) method (18). More recently, MR fingerprinting (19–21) has received much attention and has been employed in a variety of contexts.

The proposed method relies on the use of a Multi-Pathway Multi-Echo (MPME) sequence. Multi-echo imaging is commonplace on commercial scanners, and multi-pathway imaging is sometimes performed with DESS (3), TESS (18) and in thermometry (22). But the only prior MPME work appears to be our own two-pathway multi-echo approach for T₂, T₂* and B₀ mapping (10). The present three-pathway multi-echo pulse sequence can be seen equally well as adding a third pathway to our two-pathway prior work from (10), or adding multi-echo capability to TESS (18). We show here that a single 3D MPME acquisition, supplemented with a quickly-acquired central k-space region using the same sequence but a very different flip angle setting, suffices to map T₂, T₂*, T₁, B₀, B₁⁺ and M₀.

One weakness common to many prior approaches comes from the assumption that the flip angle is known. While MRI protocols include a nominal value for the flip angle, and that prescan procedures attempt to scale the B₁⁺ field appropriately, flip angles in MRI vary spatially and are always at best only approximately equal to the nominal user-input value, especially at higher field strengths. A reliable estimate of flip angle is often necessary to achieve a reliable measurement of T_1. The B₁⁺ field could be measured separately, for example with the Bloch-Siegert method (23,24), at the cost of extra scan time. A major strength of the present approach is that it does not assume the flip angle to be known and naturally generates spatially-varying 3D flip angle maps. On the other hand, a major weakness of the approach is that noise gets amplified from one reconstruction step to the next; for this reason, in its current implementation at least, the approach may be more appropriate for ROI-based as opposed to pixel-based interpretation.

The method was tested in simulations, phantom scans and five healthy volunteer brain exams. Validation was performed against T₂ and T₁ maps calculated from multiple spin-echo acquisitions.

Methods

Multi-Pathway Multi-Echo (MPME) pulse sequence

Steady-state sequences do not have RF spoiling; for this reason, they may generate many different signal pathways (25,26). These sequences can be balanced or unbalanced, depending on whether their gradient waveforms have zero total area or not, respectively. The total gradient area determines the k-space separation between pathways, which means that for balanced sequences this separation is zero and all pathways overlap near k-space center. Such multi-layer overlap creates good SNR, but also leads to well-known ‘dark-band artifacts’ wherever pathway signals interact destructively. Balanced steady-state sequences are known as bSSFP (Balanced Steady-State Free Precession) or by their vendor-specific names such as True-FISP (Fast Imaging with Steady-state Precession), FIESTA (Fast Imaging Employing Steady-state Acquisition) or bFFE (balanced Fast Field Echo), for example.

On the other hand, in the case of unbalanced steady-state sequences, most pathway signals are displaced to faraway locations in k-space, beyond the sampled region. These sequences typically sample only one pathway, the one that remained near k-space center, the so-called 0^th or FISP pathway. The DESS (Dual Echo in the Steady State) sequence (3) is an exception, as it samples both the 0^th and –1^st pathway (also called PSIF, for inverted FISP). The TESS sequence (18) goes one step further as it samples the +1^st pathway as well.

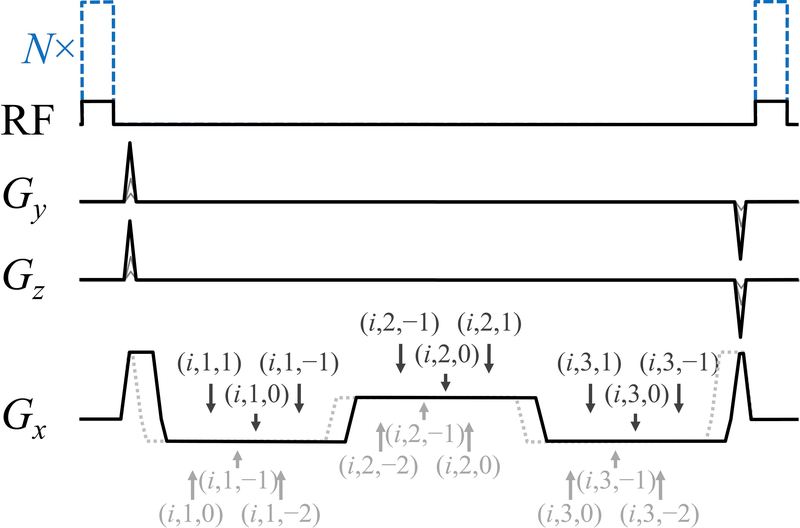
Our MPME pulse sequence is depicted in Fig. 1. Only the G_x gradient waveform is unbalanced, i.e., the G_y and G_z waveforms have zero total area. As a consequence, pathway signals were separated by a k_x increment D_kx = −γ × A_Gx, where γ is the gyromagnetic ratio and $A_{Gx}={\int }_{t=0}^{TR}{G}_x\left(t\right)dt$. The MPME sequence was designed such that each readout window captured three different pathways: the +1^st, 0^th and −1^st pathway (black G_x waveform in Fig. 1), or the 0^th, −1^st and −2^nd pathway (dashed gray G_x waveform). The sequence is depicted in Fig. 1 for N_TE = 3 readout windows, of alternating polarity.

Fig. 1.

: A three-pathway three-echo version of our MPME sequence is depicted here. Using a (i, j, k) notation to represent the j^th echo from the k^th pathway during the i^th scan, the timing of all pathway and echo acquisitions is displayed with arrows, for two acquisition scenarios: [1,0,−1] (solid black line in G_x channel) and [0,−1,−2] (dotted gray line). In the RF channel, black lines indicate the smaller flip angle acquisition, i=1, while dashed blue lines indicate the larger flip angle acquisition, i=2. Only three of these magnetization states are needed for the proposed processing to be carried out, which explains why either a [0,−1,−2] or a [1,0,−1] scheme can be chosen.

The G_x waveform as drawn in Fig. 1 consisted of 5 separate lobes, whose relative areas must be precisely set for the desired pathways to be obtained. In units of −A_Gx, the 5 lobes had an area of +1.5:−3:+3:−3:+0.5 for the +1^st, 0^th and −1^st pathways to be sampled, see black G_x waveform in Fig. 1. Alternately, to sample the 0^th, −1^st and −2^nd pathways, areas of +0.5:−3:+3:−3:+1.5 were employed instead, see dashed gray G_x waveform in Fig. 1. A notation (i, j, k) is employed here to represent signal from the k^th pathway (ranging from −2 to 1), j^th echo (from 1 to N_TE) and i^th scan. Scan number i=1 was acquired using a relatively low flip angle setting (black RF waveform in Fig. 1) while scan i=2 was obtained with a much larger flip angle setting (dashed blue RF waveform in Fig. 1). The two scans were performed either serially, or in TR-interleaved fashion, as further detailed below. In our favored implementation only a small central region in the k_y-k_z plane was acquired for the i=2 scan. In such case, with one scan much shorter than the other, the two scans had to be performed in serial fashion (as opposed to TR-interleaved).

Reconstruction step 1: Evaluating B₀

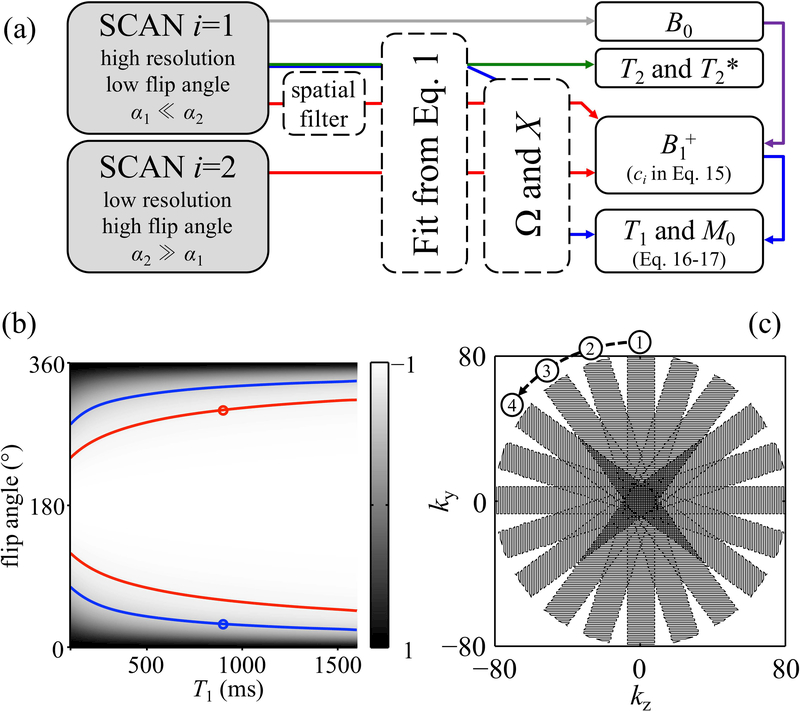
Reconstruction was performed in Matlab, on a 64-bit linux machine (Intel i7–4820K 3.7GHz × 4, 64GB of memory), and called functions from the freely-downloadable fast imaging library available from the National Center for Image Guided Therapy (27). Data acquired with an MPME sequence were converted into B₀ maps in a fairly standard manner (10), i.e., by analyzing the phase evolution from one echo to the next. More specifically, both positive and negative pathway signals experience the same off-resonance effects, and as such, all pathway signals could jointly contribute toward evaluating B₀. These different signals were combined through a weighted linear regression, in a manner similar to Equation 11 of Ref. (10). Because the scan i=2 had low spatial resolution in most results obtained here, and as depicted with a gray line in the flowchart from Fig. 2a, this operation was performed based on the i=1 scan only.

Fig. 2.

: a) The main reconstruction steps are shown here, in a color-coded manner, for our preferred implementation. Gray line: The complex multi-echo data from scan i=1 is employed toward evaluating B₀. Green line: R₂ and R₂′, or equivalently T₂ and T₂*, were mapped by fitting the data from the full-resolution i=1 scan to Eq. 1. Red lines: Both datasets, with high and with low nominal flip angle values, were employed toward evaluating B₁⁺, i.e., the flip angle, whose cosine appears as c_i in Eq. 15. The i=1 higher spatial resolution data were filtered to match those of the i=2 scan, and both datasets were used toward solving for c_i in Eq. 15. B₀ was further employed in the process, as indicated with the purples line, to account for off-resonance effects (see Eq. 8). Blue lines: Using B₁⁺ as evaluated above, the higher resolution i=1 data were employed to map T₁ and M₀, through Eq. 16 and 17, respectively. In (b), the mixing factor, X, is mapped here for a number of different combinations of flip angle and T₁ values. For a given voxel, one MPME acquisition allows one value of the mixing factor to be calculated, which is not sufficient to pinpoint both α₁ and T₁ (e.g., see blue lines). However, if a 2^nd scan is performed with a quantifiably-different flip angle setting, for example α₂ = 10×α₁, a second mixing factor value is obtained (e.g., see red lines), and T₁ as well as α₁ can be evaluated (see blue circle). The sampling strategy in the k_y-k_z plane, for in vivo scans, is shown in (c). The PROPELLER-like scheme, with oversampling near k-space center, provides extra robustness to motion. The covered region was circular in shape, with a 10-fold oversampled center and a periphery under-sampled by 40%. Overall, the number of phase encodes and corresponding scan time were adjusted to match those of a Cartesian scheme.

Reconstruction step 2: Evaluating T₂ and T₂*

Consider one voxel, from coil-combined images, with signal S_i,j,k. These signals depended on TE_i,j,k, the echo time at which they were sampled:

$$\left|S_{i,j,k}\right|=\{\begin{array}{cc}\left|F_{i,k}^{+}\right|\times e^{-\left(R_2+R_2^{\prime }\right)\times T{E}_{i,j,k}},& k\ge 0\\ \left|F_{i,k}^{+}\right|\times e^{-\left(R_2-R_2^{\prime }\right)\times T{E}_{i,j,k}},& k<0\end{array}$$ [1]

where R₂ and R₂′ represent irreversible and reversible decay, respectively, such that T₂ = 1/R₂ and T₂* = 1/(R₂+R₂′). The meaning of $\left|F_{i,k}^{+}\right|$ will be clarified when defining F states below, but at this point it can simply be viewed as a real-valued constant for a given scan i and pathway k. Because signals from negative pathways prove similar to a spin-echo on its way to formation, reversible decay is in the process of being corrected and as such, R₂′ appeared with a minus sign in Eq. 1 for cases k < 0. In contrast, for positive pathways, both R₂ and R₂′ combine with a same sign thus giving rise to T₂* decay, as seen in Eq. 1 for cases k ≥ 0.

As shown in our prior work (10), Eq. 1 can be solved for R₂ and R₂′ (or equivalently, T₂ and T₂*), for example by taking the natural logarithm of Eq. 1 and solving the resulting system of linear equations. In (10), a single scan and only two pathways were needed to map R₂ and R₂′. The third pathway obtained here can be included in the solution to Eq. 1, for improved SNR. Information from different pathways and/or scans should be combined in an SNR-optimum manner, using the signal strength |S_i,j,k| as a weight. As in Step 1 above, and as shown with a green line in the flowchart from Fig. 2a, T₂ and T₂* maps were evaluated here based on the i=1 data alone because the i=2 scan typically had lower spatial resolution.

Step 3: Calculating the magnetization states F and Z

The derivation below employs a notation for magnetization states that is very similar to that originally introduced by Hennig (25,28). F_k and Z_k represent the transverse and longitudinal magnetization for pathway k, respectively. The superscripts −, + and ⇒ are further used here to distinguish between magnetization states just before, just after and a time TR after an RF pulse, respectively.

The signal immediately after an idealized zero-length RF pulse would be $\left|F_{i,k}^{+}\right|$, as obtained when setting TE to zero in Eq. 1. Similarly, Eq. 1 also allows $\left|F_{i,k}^{\Rightarrow }\right|$ to be evaluated, by setting TE equal to TR and replacing both R₂ and R₂′ by their values as found in Step 1, above. The phase of these complex-valued F states is not known at this point, but as explained later this will not cause any problem here. At steady-state, the magnetization states just before an RF pulse (i.e., those with a ‘−’ superscript) are closely related to those a time TR after the RF pulse (i.e., those with a ‘⇒’ superscript); however, as explained further below, the details of this relation depend on whether the scans i=1 and i=2 were obtained in a sequential vs. an interleaved manner, hence the need to consider both − and ⇒ superscripts at this point.

Unlike transverse F states, longitudinal Z states cannot readily be sampled by a pulse sequence, at least not without interrupting the steady-state. The longitudinal states $Z_{i,k}^{+}$ and $Z_{i,k}^{\Rightarrow }$ are linked through T₁:

$$Z_{i,k}^{\Rightarrow }=\{\begin{array}{cc}{Z}_{i,k}^{+}{e}^{-T{R}_i/T_1},& \left|k\right|>0\\ M_0\left(1-e^{-T{R}_i/T_1}\right)+Z_{i,0}^{+}{e}^{-T{R}_i/T_1},& k=0\end{array}$$ [2]

The 0^th and non-zero pathways behave differently with respect to T₁, as the latter represents dephased magnetization states decaying with T₁ while the k = 0 pathway represents a magnetization vector recovering with T₁. As described in (28), all Z states had Hermitian symmetry with respect to k:

$$Z_{i,k}^{{\rm O}}=\overline{Z_{i,-k}^{{\rm O}}},$$ [3]

where Ο is a placeholder for ‘+’, ‘−’ or ‘⇒’ superscripts, and the notation $\overline{Z}$ represents the complex conjugate of Z. Still from Ref. (28), the Z_i,k and F_i,k states just before and after an RF pulse were related through:

$$F_{i,k}^{+}=\{\begin{array}{cc}{F}_{i,k}^{-}{\cos }^2\left({\alpha }_i/2\right)-\overline{F_{i,-k}^{-}}{\sin }^2\left({\alpha }_i/2\right)+Z_{i,k}^{-}\sin \left({\alpha }_i\right),& \left|k\right|>0\\ F_{i,0}^{-}\cos \left({\alpha }_i\right)+Z_{i,0}^{-}\sin \left({\alpha }_i\right),& k=0\end{array}$$ [4]

where α_i is the flip angle for i^th scan. As in Eq. 2, Eq. 4 had different form for the 0^th pathway because it represents a refocused vector rather than a dephased distribution of vectors. Equation 15 of Ref. (28) provided another relationship between Z_i,k and F_i,k states, before and after an RF pulse:

$$Z_{i,\pm k}^{+}=F_{i,\pm k}^{-}\sin \left({\alpha }_i\right)+Z_{i,\pm k}^{-}\cos \left({\alpha }_i\right).$$ [5]

Adding the +k and −k versions of Eq. 5, and employing the symmetry from Eq. 3, one obtains:

$$Z_{i,k}^{+}=Z_{i,k}^{-}\cos \left({\alpha }_i\right)-\left(F_{i,k}^{-}+\overline{F_{i,-k}^{-}}\right)\sin \left({\alpha }_i\right)/2.$$ [6]

Finding both $Z_{i,k}^{-}$ and $Z_{i,-k}^{-}$ for the |k| > 0 case from Eq. 4, and relating them through Eq. 3, an equation is obtained that involves only F states:

$$F_{i,k}^{+}-\overline{F_{i,-k}^{+}}-F_{i,k}^{-}+\overline{F_{i,-k}^{-}}=0.$$ [7]

Step 4: Evaluating the flip angles, or more precisely, their cosine value

As shown with red lines in Fig. 2a, data from both i=1 and i=2 scans were employed toward mapping B₁⁺, i.e., the flip angle map. A spatial filter was applied to the i=1 data, to bring spatial resolution down to the level of the i=2 data. As a result, reconstructed flip angle maps had low spatial resolution, which should not be a problem as B₁⁺ is expected to vary smoothly in space.

The main difference between scans i=1 and i=2, besides spatial resolution, is their nominal flip angles, ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_2$, and also possibly their TR settings, TR₁ and TR₂. The ‘true’ flip angle values differ from their corresponding nominal values, ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_2$, for two main reasons: First, the strength of the RF field, B₁⁺, varies spatially and essentially ‘scales’ the non-selective RF waveforms depicted in Fig. 1. If such spatially-variable scaling were the only issue, the ratio of nominal flip angles, ${\widehat{\alpha }}_2/{\widehat{\alpha }}_1$, would still be correct. However, as described in more detail below, off-resonance effects can further affect the flip angle values, in a non-linear fashion.

The flip angles α₁ and α₂ are defined here as the ‘true’ flip angles associated with nominal flip angles ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_2$ whenever/wherever the offset frequency, Δf, is null, leading to ${\alpha }_2/{\alpha }_1={\widehat{\alpha }}_2/{\widehat{\alpha }}_1$. More generally, for cases where Δf is non-zero, a nutation function v(α,Δf) is introduced below to account for off resonance effects on the cosine of these flip angles:

$$c_1=\nu \left({\alpha }_1,\mathrm{\Delta }f\right);c_2=\nu \left({\alpha }_2,\mathrm{\Delta }f\right)=\nu \left({\widehat{\alpha }}_2/{\widehat{\alpha }}_1\times {\alpha }_1,\mathrm{\Delta }f\right),$$ [8]

where v(α_i,0) = cos(α_i) wherever Δf = 0. In practice, a one-time application of a Bloch equation simulation was used to generate a two-dimensional v(α₁, Δf) matrix, specific to the shape of the RF waveform being employed (see Fig. 1). In the flowchart from Fig. 2a, the fact that the cosines c₁ and c₂ had a dependency on Δf is captured using a purple arrow.

From Eq. 2, because T₁ must be the same for both scans, one obtains:

$$Z_{1,k}^{+}\times {\left(Z_{2,k}^{\Rightarrow }\right)}^{T{R}_1/T{R}_2}-{\left(Z_{2,k}^{+}\right)}^{T{R}_1/T{R}_2}\times Z_{1,k}^{\Rightarrow }=0.$$ [9]

A factor Ω_i,k is defined whose effect is that of a scaling factor, for a given scan i and pathway k:

$${\mathrm{\Omega }}_{i,k}=F_{i,k}^{-}+\overline{F_{i,-k}^{-}}.$$ [10]

Furthermore, a most-useful quantity X_i,k, named here ‘mixing factor’, is defined as:

$$X_{i,k}=1-\frac{2\times \left(F_{i,k}^{-}-F_{i,k}^{+}\right)}{{\mathrm{\Omega }}_{i,k}}.$$ [11]

The mixing factor captures how +k and –k transverse magnetization states get intermixed when an RF pulse is played out. Please note that the factors Ω_i,k and X_i,k as defined above involve only transverse magnetization states F, and as such can be calculated from acquired data, through Eq. 1. Equations 4 and 11 were combined along with the trigonometric identity cos(α) = 2×cos²(α/2) – 1:

$$Z_{i,k}^{-}=\frac{{\mathrm{\Omega }}_{i,k}}{2\times \sin \left({\alpha }_i\right)}\times \left(X_{i,k}-c_i\right);\left|k\right|>0,$$ [12]

Replacing $Z_{i,k}^{-}$ in Eq. 6 with the expression from Eq. 12 one can obtain:

$$Z_{i,k}^{+}=\frac{{\mathrm{\Omega }}_{i,k}}{2\times \sin \left({\alpha }_i\right)}\times \left(X_{i,k}{c}_i-1\right);\left|k\right|>0.$$ [13]

In a sequential acquisition, whereby the same flip angle is used in consecutive TRs, the steady-state condition is simply:

$$Z_{i,k}^{\Rightarrow }=Z_{i,k}^{-}.$$ [14]

Replacing all of the longitudinal Z states in Eq. 9 with their corresponding expressions from Eqs 12–14, one obtains with some effort:

$${\left(X_{1,k}{c}_1-1\right)}^{\frac{T{R}_2}{T{R}_1}}\times \left(X_{2,k}-c_2\right)-\left(X_{2,k}{c}_2-1\right)\times {\left(X_{1,k}-c_1\right)}^{\frac{T{R}_2}{T{R}_1}}=0;\left|k\right|>0.$$ [15]

Replacing c₂ in Eq. 15 with its expression from Eq. 8, one obtains an equation of a single unknown, α₁, which can readily be solved numerically. Reconstructed maps of α₁ had the same low spatial resolution as the acquired i=2 data, and were then further fitted to a polynomial to help suppress noise.

Please note that acquired MRI data actually enter Eq. 15 only though the form of the mixing factor X_i,k. Using a setting of k=−1 in Eq. 10 and 11, X_i,k and Ω_i,k then involve only $\left|F_{i,-1}^{-}\right|$, $\left|F_{i,-1}^{+}\right|$ and $\left|F_{i,1}^{-}\right|$, all of which can be calculated from the −2^nd, −1^st and 0^th pathway acquisition (gray dashed G_x waveform in Fig. 1). Using a k=1 setting instead, X_i,k and Ω_i,k involve $\left|F_{i,-1}^{+}\right|$, $\left|F_{i,1}^{-}\right|$ and $\left|F_{i,1}^{+}\right|$, all of which can be calculated from the −1^st, 0^th and +1^st pathway acquisition (black G_x waveform in Fig. 1).

Because Eq. 15 involves only the cosine of the flip angles, and that cos(θ) = cos(n×2π+θ) = cos(n×2π−θ) where n is an integer, an infinite number of degeneracies can be expected on flip angle values. The normal mode of operation for the proposed method is to use a smaller α₁ << 180^o, and a much larger α₂ ⊰ [180^o 360^o], in which case the complex value of $F_{1,0}^{+}$ is about 180° out of phase with that of $F_{2,0}^{+}$. If $F_{1,0}^{+}$ and $F_{2,0}^{+}$ were found to be in phase instead, it would be assumed that α₂ got so large as to reach/exceed 360^o, and lies in the [360^o 540^o] interval instead. Accordingly, using the relative phase of $F_{1,0}^{+}$ and $F_{2,0}^{+}$ as a guide, the flip angles can be evaluated without degeneracy as long as α₁ remains non-zero, positive and smaller than 180^o, and that α₂ remains within the [180^o 540^o] interval.

In Fig. 2b, the mixing factor X was simulated over a range of T₁ and flip angle settings (with T₂=100 ms, TR=30 ms) to provide a visual representation of how the proposed method works. One MPME scan allows the mixing factor X to be calculated through Eq. 11, but a single X value would not suffice to pinpoint both α and T₁ (e.g., see blue lines in Fig. 2b). But two scans along with a known relation between them, for example α₂ = 10×α₁, does allow a solution to be found (e.g., see ‘○’ marks in Fig. 2b).

Step 5: Evaluating T₁ and M₀

As shown with blue lines in Fig. 2a, Ω_1,k and X_1,k were evaluated, through Eq. 10–11, based on full-resolution i=1 data. Ω_1,k and X_1,k, along with c₁ as found above, were then employed toward calculating T₁ and M₀. More specifically, combining Eq. 2 with Eqs 12–14, one obtains:

$$T_{1,i,k}=T{R}_i/\ln \left(\frac{Z_{i,k}^{+}}{Z_{i,k}^{\Rightarrow }}\right)=T{R}_i/\ln \left(\frac{X_{i,k}\times c_i-1}{X_{i,k}-c_i}\right);\left|k\right|>0.$$ [16]

Using the k=0 case from Eqs 2 and 4, along with Eqs 6, 14 and 16, as well as the fact that $F_{i,0}^{-}$ represents refocused magnetization and can be assumed to be real-valued without loss of generality, one obtains:

$$M_{0,i,k}=\left|\frac{\left(\left(F_{i,0}^{+}-c_i\times F_{i,0}^{-}\right)+\left(F_{i,0}^{-}-c_i\times F_{i,0}^{+}\right)\times e^{-\frac{T{R}_i}{T_1}}\right)}{\sqrt{1-c_i{}^2}\times \left(1-e^{-\frac{T{R}_i}{T_1}}\right)}\right|,$$ [17]

where the identity $\sin \left({\alpha }_i\right)=\pm \sqrt{1-{\cos }^2\left({\alpha }_i\right)}$ was employed. Given that M₀ must be positive the ambivalence in sign was resolved by applying an absolute value operator. M₀ is found through Eq. 17 using known F states, along with c_i and T₁ values as found above. It is worth noting that M₀ is unavoidably weighed by the receive-coil sensitivity, and thus is not a truly quantitative proton density map, and for this reason will be referred to as C×M₀ below. Equations 14 through 17, above, apply to cases where the low and high flip angle scans are performed in a sequential manner; in contrast, equations A1 through A5 in the Appendix apply to cases where these two scans would be performed in an interleaved manner instead.

On performing all of the processing above using real (non-complex) F states

The F and Z magnetization states used throughout the derivations above were complex numbers. A great simplification came from realizing that real numbers could be used instead. With the MPME sequence from Fig. 1, the longitudinal magnetization was always flipped to the x or ‘real’ axis in the transverse plane, and in an ideal case all signals S_i,j,k should have been real. In reality, variations in B₀ and B₁ fields made the measured signals complex in nature. But as confirmed through simulations, such variations affected only the phase of F states and not their magnitude. In other words, by ignoring the phase of F states one merely ignores undesired B₀ and B₁ frequency and phase variations unrelated to the derivations above.

Of course, phase information was valuable, and was employed in usual ways toward frequency mapping. But idealized real-valued F states free of phase errors were obtained here by taking the magnitude of complex ones, and adjusting polarity as follows:

$$\begin{gathered} F_{i,k}^{\mathrm{O}}=+\left|F_{i,k}^{\mathrm{O}}\right|,k\ge 0 \\ {F}_{i,k}^{\mathrm{O}}=-\left|F_{i,k}^{\mathrm{O}}\right|,k<0 \end{gathered}$$ [18]

where Ο is a placeholder for ‘+’, ‘−’ or ‘⇒’ superscripts. Even in cases where RF chopping was used Eq. 18 was still valid: while RF chopping might swap α_i for −α_i, it would not affect c_i in the equations above, as cos(α_i) = cos(−α_i). Using Eq. 18 and performing all steps above on real rather than complex numbers led to a vastly simplified and more robust implementation.

Simulated acquisition with the proposed MPME sequence

Signals from the MPME sequence in Fig. 1 were simulated as follows. Isochromats were rotated to represent RF pulses, frequency offsets and unbalanced gradients, while T₂ and T₁ recovery were applied. Several different frequency offsets were simulated and combined with Lorentzian weighting to simulate the effect of R₂′. Five hundred TR periods were simulated to reach steady-state before signals were ‘sampled’. To validate the simulation program, simulated MPME signals were compared to acquired ones. Simulations were performed using the nominal flip angle value, as well as ±10% the nominal value, as the nominal flip angle value cannot be expected to be accurate. A number of experiments were performed using an fBIRN phantom (29), with flip angle = 15°, 20°, and 30°; TR = 25 ms, 35 ms, and 45 ms, and with either [0,−1,−2] or [1,0,−1] pathway acquisitions (see Fig. 1). Signal strength was averaged spatially over the phantom and compared with simulated signals with Bland-Altman plots. Once validated, the simulated version of the MPME pulse sequence helped provide insights about the overall method, as shown in Results.

Parameter mapping from noiseless simulated data – looking for degeneracies

The same reconstruction code was used to convert either simulated or acquired MPME signals into basic MR parameters, namely T₂, T₂*, T₁, B₀, B₁⁺ and M₀. In a first step, noiseless simulations were performed to help confirm that the proposed algorithm seems effectively free of degeneracies or local minima. Simulations were made while modifying the MR parameters over a range of values: T₁ from 300 to 1800 ms (in 100 ms steps), T₂ from 30 to 120 ms (in 10 ms steps), T₂*= 0.8×T₂, and Δf from −100Hz to +100Hz (in 25 Hz steps). The simulated acquisition parameters were α₁ = 15^o, α₂ = 22×α₁, TR₁ = TR₂ = 25 ms, and N_TE = 3 echoes uniformly distributed across TR. MR parameters were computed based on the simulated MPME signals, and then compared to the known ‘true’ values.

Parameter mapping from noisy simulated data – parameter optimization

Simulations with added noise were performed to help optimize the imaging parameters. Simulations were made over a range of TR₁ from 15 to 50 ms, TR₂ also from 15 ms to 50 ms, α₁ from 10^o to 30^o, α₂ from 310^o to 350^o, using N_TE = TR/8ms. MR parameters typical of brain imaging were selected, T₁/T₂/T₂* = 1500/70/60 ms (30–32), with Δf = 0. Each pathway and echo signal, in turn, was disrupted by a small perturbation equal to +0.1% and then −0.1% of M₀. A setting was sought for the acquisition parameters TR₁, TR₂, α₁ and α₂ that would minimize T₁ errors, as caused by the perturbations. After the acquisition parameters were set, Gaussian noise (SNR = 30) was added to the simulated signals and noise propagation, from one parameter-mapping step to the next, was evaluated.

Phantom data

Scans were performed on a Siemens Trio 3T system with a product 8-channel knee coil (Invivo Corporation, Gainesville, FL, USA) and the pulse sequences from Fig. 1, with hard RF pulses (see Fig. 1). A sequential acquisition was performed using a [1,0,−1] pathway scheme with parameters from Table 1. Data from the [1,0,−1] scheme were processed using a k=1 setting in Eqs 10–11. A multi-compartment gel phantom was built specifically for these experiments, using gelatin (Knox, E.D. Smith Foods, ON, Canada) doped with a gadolinium contrast agent (Magnevist, Bayer HealthCare LLC, NJ, USA). The concentration of contrast agent in the gel was varied from one compartment to the next.

Table 1:

Acquisition parameters: MPME scans for phantoms and healthy volunteers

	Number of TE	Pathway spacing time (ms)	TR (ms)	Flip angle (°)	BW/pixel (Hz)	Voxel size (mm3)	FOV size (cm3)	Scan time (min)
Gelatin phantom	3	1.86	25	15/330	539	1×0.5×1	16×16×16	11:24
Subjects A-D Subject E	3 same	2 same	25 same	15/330 same	501 same	1.2×1×1.2 same	19.2×19.2×19.2 21.1×19.2×21.1	11:26 13:39

In our favored implementation, only the central k-space region was sampled for the i=2 scan, which nearly halved scan time as compared to fully sampling both scans. More specifically, only 25% of the k_y and of the k_z axis were sampled for the i=2 scan, a 16× reduction compared to full sampling. Having one scan that requires 16× less TR intervals than the other is not compatible with a TR-interleaved acquisition of the two, and for this reason the sequential acquisition associated with Eqs 15–17 was preferred here; the TR-interleaved scheme is presented in the Appendix. The [1,0,−1] scheme was selected here, although the [0,−1,−2] scheme appeared to be mostly equivalent in terms of quality of calculated parameter maps.

In vivo brain data

Five healthy volunteers (4 males and 1 female, age: 27.2±4.1 years old) were imaged following informed consent using an IRB-approved protocol, with same scanner and a product 12-channel head coil. In early results, motion artifacts were seen emanating from ventricles and CSF-containing regions. For this reason, a more motion-robust coverage of the k_y-k_z plane was developed for in vivo data compared to phantom data, loosely inspired from the ‘periodically rotated overlapping parallel lines with enhanced reconstruction’ (PROPELLER) method (33,34). As shown in Fig. 2c, the central k_y-k_z region was oversampled using overlapping ‘blades’ to improve motion robustness, assuming irregular events with respect to k-space acquisition were averaged out. The phase-encoding scheme was designed such that all k-space samples fell on Cartesian coordinate. Ten blades were used to cover the k-space, while the width was reduced by 40% to match the overall scan time of a Cartesian scan: As an example of a 160×160 acquisition matrix, the k_y-k_z pattern from Fig. 2c had 25664 phase encodes, leading to 0.25% increase in scan time as compared with the Cartesian scheme. K-space density correction was applied prior to a conjugate gradient-based parallel imaging reconstruction method (35,36). The readout direction was oriented in the superior-inferior direction, and the FOV was set large enough along the left-right and anterior-posterior directions to encompass the entire cross section of the head.

As explained in the text above Eq. 8, one would expect the relationship ${\alpha }_2/{\alpha }_1={\widehat{\alpha }}_2/{\widehat{\alpha }}_1$ to hold wherever the offset frequency, Δf, is null. However, for in vivo scans, one further scaling factor had to be introduced:

$${\alpha }_2/{\alpha }_1=\beta \times {\widehat{\alpha }}_2/{\widehat{\alpha }}_1$$ [19]

This factor β was determined through one single fit involving all available in vivo data.

Validation

In addition to our MPME scans, a series of gradient-echo and spin-echo images were acquired for multiple TE settings, for a single centrally-located 2D axial slice. Moreover, several inversion-recovery spin-echo (IR-SE) images were obtained for the same slice while varying the inversion time. Parameters for the validation scans are summarized in Table 2.

Table 2:

Acquisition parameters for validation scans

	Sequence:	TE (ms)	TR (ms)	TI (ms)	Flip angle (°)	BW/pixel (Hz)	Voxel size (mm3)
Gelatin phantom	2D IR-SE	10	5000	50, 100, 200, 400, 800, 1600, 3200	180–90-180	183	1×1×3
	2D SE	20, 30, 60, 120, 200	1500	N/A	90–180	183	1×1×3
in vivo	2D IR-SE	10	2500	50, 300, 800, 1600, 2400	180–90-180	473	1.2×1.2×4
	2D SE	25, 50, 90, 150	800	N/A	90–180	501	1.2×1.2×4
	2D GRE	16, 24, 32, 40, 48, 56, 64, 72	800	N/A	60	501	1.2×1.2×2

Log-linear fitting allowed T₂* and T₂ maps to be calculated from the gradient-echo and spin-echo data, respectively, while T₁ maps were generated using a non-linear least-square fit of the IR-SE data. These independently-obtained T₂*, T₂, and T₁ maps were used as reference standards toward validating the present parameter-mapping method. The reference T₁ maps were further employed to help fit for β in Eq. 19: a value for β was sought that minimized T₁ errors for all five volunteers jointly. The same β value was then employed in the reconstruction of all MPME in vivo datasets.

Because they were generated in a standard manner, B₀ maps were not further validated. As for C×M₀ and B₁⁺, the value of all MR parameters were so intertwined in the equations above that not all of them may require independent testing; although not explicitly validated here, obtaining correct values for T₂*, T₂, and T₁ would strongly suggest that C×M₀ and B₁⁺ values may be correct as well, given how tightly these parameters are interconnected.

Results

Simulated results

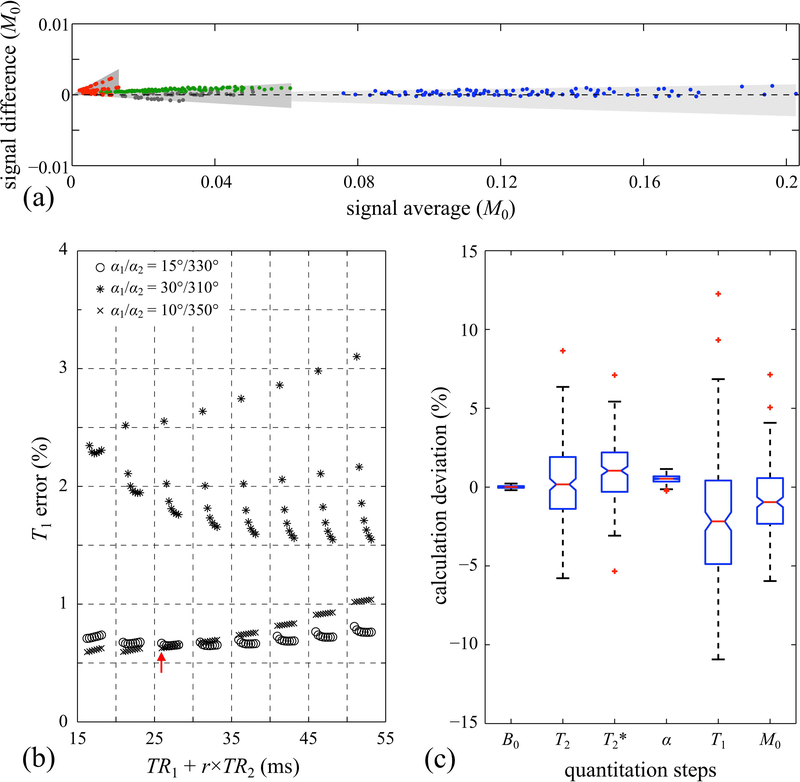
The Bland-Altman plot in Fig. 3a compares simulated and acquired signal strengths, for signal pathways ranging from −2 to +1. One single global fit/scaling was performed to make M₀ in the acquired data match the (arbitrary) value for M₀ employed in the MPME simulation code. The good agreement obtained in Fig. 3a was interpreted as a validation of the MPME simulation code.

Fig. 3.

: (a) Signals acquired and spatially-averaged over an fBIRN gel phantom were compared in a Bland-Altman manner with corresponding MPME simulations. Overall, the good agreement between simulated and sampled MPME data was interpreted as validation of the simulation. Red, gray, blue, and green circles represent data from the −2^nd, −1^st, 0^th, and 1^st pathways, respectively. Gray shaded areas were drawn to show the effect of varying the simulated flip angle from −1% to +1% of the nominal values. In (b), simulated MPME with added noise were converted into T₁ estimates, for a number of different TR₁, TR₂, α₁ and α₂ settings. A solution was sought that would lead to relatively small T₁ errors and relatively short scan times. The red arrow points to the practical solution selected here for in vivo scans. The parameter r represents the ratio in matrix size between scans i=2 and i=1, which is 1/16 here, such that (TR₁+r×TR₂) as plotted on the horizontal axis is proportional to total scan time. (c) Deviations from the ground truth at each quantitation step were simulated and are displayed in a box-and-whisker plot, showing how noise propagates from one processing step to the next. Red ‘+’ markers, whiskers and boxes indicate, respectively, outliers, min/max values, and the 1^st and 3^rd quartiles.

In noiseless simulations, the precise value of all mapped parameters could be recovered in all simulated cases, suggesting there is no degeneracy in the solution. More specifically, the maximum deviation for T₁ and T₂ was 0.014% and 0.006%, respectively.

Results from noisy simulations are shown in Fig. 3b. The horizontal axis, TR₁+r×TR₂, where r is the ratio in k-space coverage between scan i=1 and i=2, is proportional to overall scan time. As such, a solution reasonably close to the lower left corner in Fig. 3b was sought, which would provide small T₁ errors with relatively short scan time. Based on these results, a setting of TR₁=25 ms, TR₂=25 ms, r=1/16, ${\widehat{\alpha }}_1$=15° and ${\widehat{\alpha }}_2$=330° was selected for in vivo scans. Using these parameters and added Gaussian noise, Fig. 3c shows noise propagation through the proposed processing steps, as the different quantitative parameters get evaluated in turn.

Phantom results

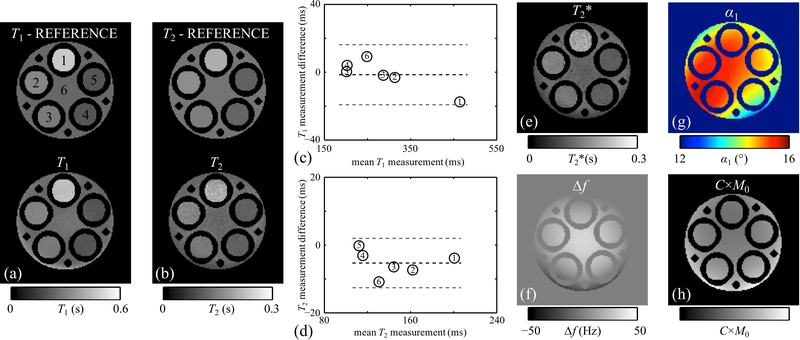
Phantom results are shown in Fig. 4, for a [1,0,−1] sequential acquisition. Validation in Fig. 4c,d shows good agreement with the spin-echo reference standard. The bias and the limits of agreement for T₁ and T₂ measurements were: −1.5/±18.1ms and −5.3/±7.4ms, respectively. No scaling factor β (Eq. 19) was required for phantom scans, i.e., β = 1 for all phantom datasets.

Fig. 4.

: (a,b) T₁ and T₂ maps derived from spin-echo data were compared to those obtained with the proposed approach, for a given 2D slice in a custom-made multi-compartment gelatin phantom. (c,d) Agreement was tested using Bland-Altman plots. Black and gray dashed lines represent the bias and limits of agreement, respectively. (e-h) Quantitative maps of T₂*, offset frequency, flip angle and sensitivity-weighted proton density were also reconstructed, using the proposed methodology.

In vivo brain results

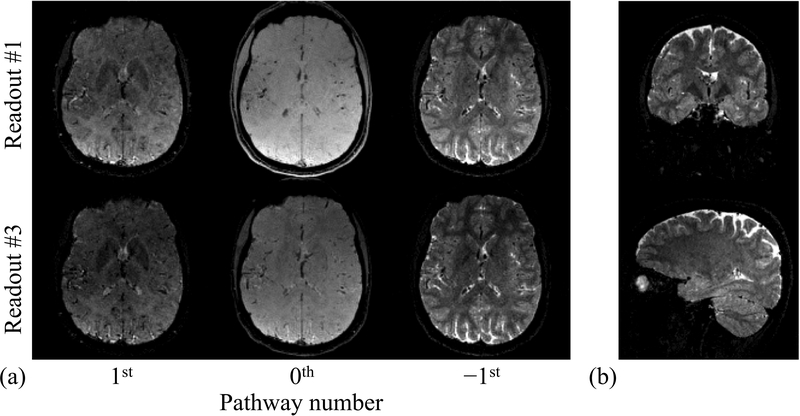
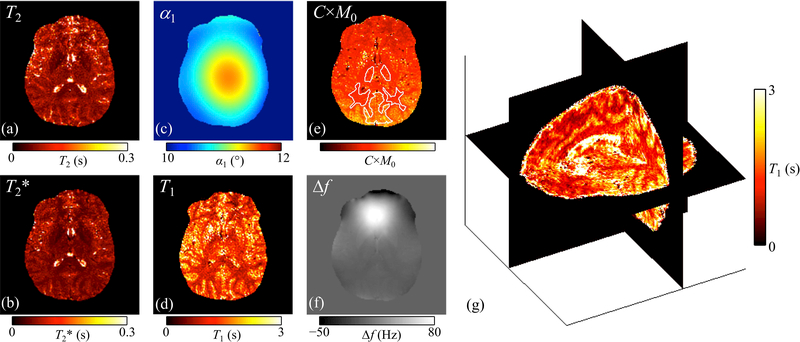
Scan parameters, as optimized through the simulation above, are listed in Table 1. One of the volunteers was imaged with a FOV 10% larger in both phase-encoding directions, due to larger head size, resulting in a slightly longer acquisition time (see Table 1). Figure 5 shows examples of individual pathway images, and reconstructed MR parameter maps are shown in Fig 6, for one given slice from one given volunteer. The display in Fig. 6g is meant to visually emphasize the 3D nature of the parameter maps reconstructed here. Overall, the noise level of the reconstructed 3D maps tended to be high, which can be considered a weakness of the approach as currently implemented.

Fig. 5.

: Images are shown for three different pathways at two different echo times, for one axial slice (out of 160) and one subject (out of 5). These images provide drastically different tissue contrasts, allowing the present method to function. In (b), images that correspond to the 2^nd readout (out of 3) of the −1^st pathway are shown, in coronal and sagittal views.

Fig. 6.

: (a-f) Reconstructed parameter maps are shown, for one given slice from one given subject (subject #1). The slice shown here was further involved in the Bland-Altman validation process in Fig. 7. More specifically, this slice was further imaged with 2D spin-echo and gradient-echo sequences, and the ROIs used for validation are shown in (e), overlaid on the C×M₀ map using white contours. A 3-plane visualization of the whole-brain T₁ map is shown in (g) to emphasize the 3D nature of the reconstructed results.

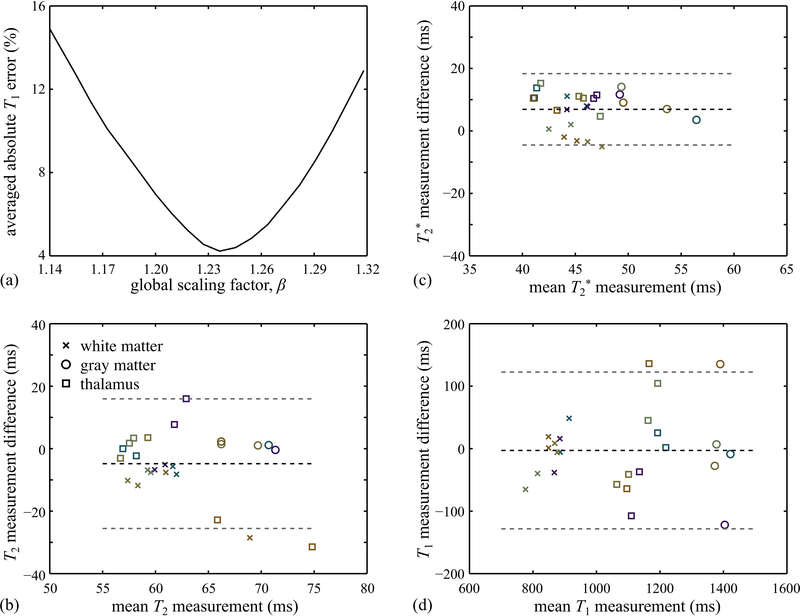
ROIs were drawn for validation purposes (e.g., white contours in Fig. 6e) in both MPME results and reference gradient echo and spin echo results, to enclose specific brain structures. While the choice ${\widehat{\alpha }}_2/{\widehat{\alpha }}_1$ = 330°/15° = 22 should arguably have led to α₂/α₁ = 22, the plot in Fig. 7a shows that minimized T₁ errors is achieved with β = 1.24, as defined in Eq. 19. The same β was employed here for all in vivo datasets. Bland-Altman plots comparing MPME results to reference results are presented in Fig. 7b-d for T₂, T₂* and T₁, respectively.

Fig. 7.

: (a) Absolute T₁ measurement errors (%), averaged over all volunteers and all tissue types, were calculated for values of the calibration factor β (as defined in Eq. 19) ranging from 1.14 to 1.32. A clear minimum was obtained near β=1.24, and this calibration value for β was employed for all in vivo results presented here. (b-d) T₂, T₂* and T₁ values, averaged over ROIs corresponding to different tissue types (see Fig. 6e), were obtained both for the proposed method as well as for the reference (GRE- and SE-based) scans. In the resulting Bland-Altman plots, the markers ‘×’, ‘○’ and ‘□’ represent white matter, gray matter and thalamus tissues, respectively. Five different colors were used to distinguish between the five Subjects. Black and gray dashed lines represent the bias and limits of agreement, respectively.

Discussion

A method was introduced for parameter mapping based on a MPME pulse sequence. As seen in Fig. 5, the pathway images acquired with this sequence had full brain coverage, overall good quality, diversified contrasts and good resolution (1.2×1.0×1.2 mm); as such, these images might have intrinsic diagnostic value beyond the processed maps that can be derived from them. Using the present equations, these MPME images were converted into 3D quantitative maps for T₂, T₂*, T₁, B₀, B₁⁺ and C×M₀ (i.e., M₀ weighed by the receive-coil sensitivity). The main weakness of the proposed approach, as currently implemented, was noise amplification from one processing step to the next, which led to visibly-noisy parameter maps for in vivo results. For this reason, the present method might currently be restricted to ROI-based applications such as tissue characterization, as these would enable some degree of noise averaging to occur over the ROI. In future work, several approaches may be envisioned to help control noise amplification. Most notably, a regularization scheme tailored to the present equations might be devised to potentially lower noise levels to a considerable extent. Alternately, convolutional neural networks might prove well-suited to the conversion of acquired MPME images into parameter maps in an SNR-advantageous manner.

Scan time was relatively long here, about 12 min for full brain coverage. As suggested by Fig. 3b, shorter TR settings might be achievable at little to no cost in terms of T₁ precision. Furthermore, readily available acceleration methods could be included at a cost in SNR; especially if noise amplification could be better controlled (paragraph above), reductions in scan time might be achieved in a simple manner with parallel imaging, for example. Other limitations included partial voluming, which was not accounted for here. In principle at least, because the proposed approach is analytical in nature, it should be possible to acquire more data and resolve partial voluming effects. Furthermore, while many interesting MR parameters were mapped others were not, such as the apparent diffusion coefficient (ADC), for example. Because gradient pulses were fairly small and/or quickly rephased here, the data did not capture diffusion effects in any practical manner. Furthermore, the need for a calibration factor β in Eq. 19 is not explained here; this calibration was performed once and for all and the same value was employed for all in vivo datasets. Other limitations included a small number of healthy subjects (five), in a single application (brain), and a small loss of resolution from the circular coverage in the k_y-k_z plane (see Fig. 2c) as opposed to a full, square coverage.

The use of very large flip angles in the partially-sampled i=2 scan, with nearly 360^o of rotation, would suggest that high specific absorption rate (SAR) might be a problem with the proposed approach. In fact, three factors combine to make SAR a minor issue here: TR is not particularly short, hard pulses were employed, and most of the acquisition time is actually spent on the full-resolution small flip angle scan. However, as a limitation, the low-flip angle RF pulse had to be played here with longer duration and lower voltage than would otherwise have been necessary, because its duration was matched to that of the larger pulse (see Fig. 1). Please note that in the present method, a small negative flip angle could not replace a large positive one, for example −10^o instead of +350^o. This is because flip angles are not assumed to be correct and B₁⁺ is actually being mapped. Imagine a location where B₁⁺ would happen to be only 90% of its full expected value; in such location, nominal −10^o and 350^o pulses would turn out as −9^o and 315^o instead, two very different angles.

The main contribution of the present work might arguably be the set of equations derived here, which demonstrate that MPME acquisitions capture the information required for parameter mapping. The manner in which the parameter maps are generated, whether by solving small sets of equations in a serial manner as proposed here, or possibly through a regularized numerical solution, or a convolutional neural network, may evolve and improve in future work. While some of these processing strategies may prove more SNR-advantageous than others, in all cases the present equations should remain relevant, as they demonstrate that MPME scans capture the information content needed for parameter mapping. Lastly, the proposed method functions in a manner very distinct from prior quantitative imaging methods, offering a different set of strengths and weaknesses; as such, it might in time play a key role in hybrid methods combining different strategies for added performance.

Conclusion

A multi-pathway multi-echo sequence and associated processing were developed for quantitative MRI, and maps of T₂, T₂*, T₁, B₀, B₁⁺ and C×M₀ were generated.

Appendix

While the present method involves a lower and higher flip angle scan, these two scans can be acquired in sequential or interleaved fashion. Equations presented in the main body of the text were for the sequential case, while their equivalent for the interleaved case are presented here instead. For a TR-interleaved acquisition, whereby the flip angle flip-flops between two very different values from TR to TR, the steady-state condition is:

$$\left(\mathrm{TR-interleaved}\right)Z_{i,k}^{\Rightarrow }=Z_{h(i),k}^{-},$$ [A1]

where h(1) = 2 and h(2) = 1. Using Eq. A1 instead of Eq. 14, the TR-interleaved equivalent of Eq. 15 became:

$$\left(\mathrm{TR-interleaved}\right)\begin{array}{c}{\left({\mathrm{\Omega }}_{1,k}\times \sin \left({\alpha }_2\right)\right)}^{\left(\frac{T{R}_2}{T{R}_1}+1\right)}\times {\left(X_{1,k}{c}_1-1\right)}^{\frac{T{R}_2}{T{R}_1}}\times \left(X_{1,k}-c_1\right)-\\ {\left({\mathrm{\Omega }}_{2,k}\times \sin \left({\alpha }_1\right)\right)}^{\left(\frac{T{R}_2}{T{R}_1}+1\right)}\times \left(X_{2,k}{c}_2-1\right)\times {\left(X_{2,k}-c_2\right)}^{\frac{T{R}_2}{T{R}_1}}=0;\left|k\right|>0.\end{array}$$ [A2]

In the special case where TR₁ = TR₂, Eq. A2 simplifies to:

$$\left(\mathrm{TR-interleaved}\right)\begin{array}{c}{\mathrm{\Omega }}_{1,k}^2\times \left(1-c_2{}^2\right)\times \left(X_{1,k}{c}_1-1\right)\times \left(X_{1,k}-c_1\right)-\\ {\mathrm{\Omega }}_{2,k}^2\times \left(1-c_1{}^2\right)\times \left(X_{2,k}{c}_2-1\right)\times \left(X_{2,k}-c_2\right)=0;\left|k\right|>0.\end{array}$$ [A3]

Like for Eq. 15 in the sequential case, c₂ was replaced by its expression from Eq. 8, and Eq. A3 could be solved for α₁.

Relationships similar to Eq. 16–17 were also obtained for the TR-interleaved case, using the steady-state definition from Eq. A1 rather than that from Eq. 14:

$$\left(\mathrm{TR-interleaved}\right)T_{1,i,k}=\left|\pm T{R}_i/\ln \left(\frac{{\mathrm{\Omega }}_{i,k}\times \sqrt{1-c_{h(i)}{}^2}\times \left(X_{i,k}{c}_i-1\right)}{{\mathrm{\Omega }}_{h(i),k}\times \sqrt{1-c_i{}^2}\times \left(X_{h\left(i\right),k}-c_{h(i)}\right)}\right)\right|;\left|k\right|>0,$$ [A4]

$$\left(\mathrm{TR-interleaved}\right)M_{0,i,k}=\left|\frac{\left(F_{h(i),0}^{+}-c_{h(i)}\times F_{h(i),0}^{-}\right)/\sqrt{1-c_{h(i)}{}^2}+\left(F_{i,0}^{-}-c_i\times F_{i,0}^{+}\right)\times e^{-\frac{T{R}_i}{T_1}}/\sqrt{1-c_i{}^2}}{\left(1-e^{-\frac{T{R}_i}{T_1}}\right)}\right|.$$ [A5]