Wave-LORAKS: Combining Wave Encoding with Structured Low-Rank Matrix Modeling for More Highly Accelerated 3D Imaging

Abstract

Purpose:

Wave-CAIPI is a novel acquisition approach that enables highly-accelerated 3D imaging. This paper investigates the combination of Wave-CAIPI with LORAKS-based reconstruction (Wave-LORAKS) to enable even further acceleration.

Methods:

LORAKS is a constrained image reconstruction framework that can impose spatial support, smooth phase, sparsity, and/or parallel imaging constraints. LORAKS requires minimal prior information, and instead uses the low-rank subspace structure of the raw data to automatically learn which constraints to impose and how to impose them.

Previous LORAKS implementations addressed 2D image reconstruction problems. In this work, several recent advances in structured low-rank matrix recovery were combined to enable large-scale 3D Wave-LORAKS reconstruction with improved quality and computational efficiency.

Wave-LORAKS was investigated by retrospective subsampling of two fully-sampled Wave-encoded 3D MPRAGE datasets, and comparisons were made against existing Wave reconstruction approaches.

Results:

Results show that Wave-LORAKS can yield higher reconstruction quality with 16×-accelerated data than is obtained by traditional Wave-CAIPI with 9×-accerated data.

Conclusion:

There are strong synergies between Wave encoding and LORAKS, which enables Wave-LORAKS to achieve higher acceleration and more flexible sampling compared to Wave-CAIPI.

INTRODUCTION

Obtaining high-quality MR images in a short period of time is difficult because of practical tradeoffs between data acquisition speed, signal-to-noise ratio (SNR), and spatial resolution. As a result, improving the speed of an MRI scan has been one of the major goals of the research community since the very early days of the field. There have been three principal approaches to increasing the acquisition speed of a high-quality conventional MR image: (i) improved hardware (e.g., higher magnetic field strengths, high-efficiency receiver coils, etc.) and optimized sequence parameters (flip angles, repetition times, etc.) to maximize SNR while achieving desired image constrast; (ii) improved methods for rapidly encoding spatial information (e.g., efficient Cartesian and non-Cartesian k-space trajectories, spatial encoding using multiple receiver coils simultaneously, etc.); and (iii) improved image reconstruction methods that allow extraction of high-quality information from sparsely-sampled and/or noisy data. These three approaches are often synergistic, and can yield massive further speed improvements when they are combined together in appropriate ways.

This work explores the potential synergies that can be obtained when a recent promising spatial encoding approach, i.e., Wave-CAIPI (1–4), is combined with a recent promising image reconstruction approach, i.e., LORAKS (5–8). These approaches have each separately been demonstrated to enable highly accelerated imaging, but have not been previously used together. As will be shown, our results suggest that their combination (which we call Wave-LORAKS) can enable substantial further acceleration of high-resolution 3D MRI beyond what has previously been possible.

While the combination of Wave-CAIPI with LORAKS is straightforward in principle, a substantial challenge is that Wave-CAIPI data requires reconstruction of large-scale 3D datasets, which necessitates computational efficiency. On the other hand, existing LORAKS implementations have been designed for smaller scale 2D reconstruction problems and have not prioritized computational efficiency (9). To overcome computational issues, this paper reports several modifications to existing LORAKS implementations that substantially reduce the computational requirements for Wave-LORAKS. While these modifications are straightforward based on previous literature, their combination is necessary to enable our current investigation of Wave-LORAKS.

One ingredient of our new implementation is the previous autocalibrated LORAKS approach (10), which uses autocalibration data to pre-estimate the nullspace of the LORAKS matrix prior to reconstruction. This prior knowledge can be used to simplify image reconstruction, reducing a complicated nonconvex optimization problem to a much-easier linear least squares problem. The idea of simplifying optimization by pre-estimating subspaces from autocalibration data has a long history in low-rank MRI reconstruction for both convolution-structured (11,12) and unstructured (13–15) low-rank matrices. While autocalibrated LORAKS (10) is inspired by all of these previous methods, it is a direct generalization of and most closely resembles the previous PRUNO approach (12). Similar autocalibration ideas have also been used in several subsequent publications (16–18). Another ingredient of our new implementation is the use of fast Fourier transforms (FFTs) for implementing matrix-vector multiplications with high-dimensional structured low-rank matrices, as originally proposed by Ongie and Jacob (19). We have recently made both of these ingredients available to the community through a new public open-source LORAKS software release (20).

A preliminary account of portions of this work was previously presented in Ref. (21).

THEORY

This section provides a detailed review of the relevant previous literature (to give appropriate context and rationale for our reconstruction setup), and also describes the implementation choices we have made for the specific version of Wave-LORAKS investigated in this work.

Wave-CAIPI

Wave-CAIPI is a recent data acquisition technique that enables parallel imaging at high acceleration factors with minimal g-factor penalty (1–4). Like 2D CAIPIRINHA (22), Wave-CAIPI for volumetric 3D imaging chooses its phase encoding positions to lie on a 2D lattice in k-space, while the readout gradient is used to encode the third dimension. Lattice sampling of k-space leads to periodic aliasing on a reciprocal lattice in the image domain, and careful design of this aliasing pattern can help to reduce the resulting parallel imaging g-factor in an accelerated acquisition (22).

However, distinct from 2D CAIPIRINHA (in which the readout follows a straight-line path through k-space), Wave-CAIPI employs a 3D corkscrew-shaped non-Cartesian readout trajectory. The choice to use this kind of readout was inspired by the earlier bunched phase encoding approach (23), and has the effect of spreading aliasing across all 3 spatial dimensions. This makes more efficient use of the additional spatial encoding provided by 3D coil sensitivity profiles, and leads to even further reduction in the parallel imaging g-factor.

The reduced g-factor means that Wave-CAIPI has major implications for highly-accelerated MRI. For example, Polak et al. (4) have demonstrated 9× accelerated high-resolution MPRAGE imaging¹ with an average g-factor of only 1.06 at 3T. This enables an acquisition lasting only 72 seconds, which is a substantial improvement over a fully-sampled acquisition which would take nearly 11 minutes to acquire.

Similar to traditional SENSE parallel imaging reconstruction (25, 26), most of the previous Wave-CAIPI implementations (1–4) perform image reconstruction using a least-squares formulation:

$$\widehat{\mathbf{m}}=\arg \underset{\mathbf{m}\in {ℂ}^N}{\min }\Vert \mathbf{Em}-\mathbf{w}{\Vert }_2^2,$$ [1]

where $\mathbf{m}\in {ℂ}^N$ is the vector of voxel values for the unknown 3D image to be estimated, $\mathbf{E}\in {ℂ}^{M\times N}$ represents the data acquisition model (including the effects of sensitivity encoding and non-Cartesian Fourier encoding), and $\mathbf{w}\in {ℂ}^M$ is the vector of measured data samples collected from all receiver coils. Due to system imperfections in the MRI scanner (e.g., gradient imperfections that perturb the nominal k-space trajectory), it has proven useful to use a simple autocalibrated point-spread function model when constructing the E matrix instead of trusting the acquisition to be faithful to the nominal k-space trajectory (3,4).

Beyond these least-squares reconstruction approaches, Wave-CAIPI has also previously been combined with an existing advanced reconstruction approach that uses ${\mathcal{l}}_1$-regularization to promote transform-domain sparsity (27, 28). Because the use of ${\mathcal{l}}_1$-regularization was inspired by compressed sensing (CS) (29), this approach to Wave reconstruction is known as CS-Wave (27, 28). The version of CS-Wave we will compare against later in this paper is formulated as (28)

$$\widehat{\mathbf{m}}=\arg \underset{\mathbf{m}\in {ℂ}^N}{\min }\Vert \mathbf{Em}-\mathbf{w}{\Vert }_2^2+\lambda TV(\mathbf{m}),$$ [2]

where TV (·) represents the standard 3D total variation (TV) regularization penalty that encourages the reconstructed image to have sparse edges, and λ is a user-selected regularization parameter. CS-Wave enables higher acceleration factors than Wave-CAIPI. Instead of using the strict lattice sampling pattern used in Wave-CAIPI, CS-Wave is generally used with a partially random phase encoding pattern (27, 28).

LORAKS and Wave-LORAKS

For the sake of simplicity and clarity, our description will focus solely on the theoretical justifications, mathematical notation, and problem formulation conventions from our previous LORAKS work (5–8). However, we should note that some of the capabilities and features we describe for LORAKS are also shared by related methods that use similar concepts and methodology (16,30,31).

LORAKS is a powerful and flexible constrained reconstruction framework that can integrate classical image support constraints, smooth phase constraints, sparsity constraints, and parallel imaging constraints into a single unified subspace constraint. The basic foundation of LORAKS is that, if one or more of the aforementioned constraints is applicable to a given image, then the fully-sampled Fourier data of that image should be linearly predictable.

Linear-prediction relationships are nothing new in the constrained MR image reconstruction literature. For example, linear prediction has been exploited in some of the earliest constrained reconstruction papers in the field (11, 32), and is the cornerstone of modern widely-used image reconstruction methods like GRAPPA (33) and SPIRiT (34). However, it’s been known for a long time that linear predictability is intimately related to the existence of structured low-rank matrices (11). This fact opens new doors for MR image reconstruction, especially when combined with the explosion of recent theory and methods that demonstrate the possibility of reconstructing low-rank matrices from sparsely sampled data (35). LORAKS is one such MR image reconstruction method, which uses the principles of linear predictability to construct low-rank matrices, while simultaneously using the principles of structured low-rank matrix recovery to infer missing data.

Compared to classical linear-prediction methods, LORAKS has been shown to have several notable features:

• While linear-prediction relationships can exist in the data for various reasons (e.g., support, phase, sparsity, parallel imaging, etc.), using LORAKS does not require specific prior knowledge about which of these constraints are applicable. Instead, LORAKS attempts to learn all of the relevant local linear-prediction relationships that may exist in k-space (regardless of their source). LORAKS imposes all of these learned relationships simultaneously, while remaining agnostic to the original source of these relationships. This allows LORAKS to be flexible and adaptable enough to work across a range of different image reconstruction scenarios without the need for substantial adaptations in the problem formulation.

• The use of low-rank matrix completion means that LORAKS is compatible with a wide range of sampling patterns, both conventional and unconventional. For example, previous work has demonstrated that LORAKS can successfully reconstruct images from “silly” sampling patterns that have been selected for aesthetic purposes (e.g., based on the logo of our institution (7,8)). While we don’t recommend the use of “silly” sampling, these new capabilities offer exciting new opportunities for improving the design of k-space sampling patterns.

• We have frequently observed that LORAKS-based reconstruction outperforms sparsity-based CS reconstruction (5–8). We also note that LORAKS is just regularization, and can be synergistically combined with other regularization penalties for further improvements in image reconstruction quality, although this generally comes at the expense of increased computational burden.

• While LORAKS is compatible with calibrationless acquisition, it can also easily be used with calibration information when it is available (10,18,36) for even further improvements in reconstruction quality and computational efficiency.

While many different flavors of LORAKS have been proposed over the past several years, the version we investigate for Wave-LORAKS makes use of prior information about the coil sensitivity maps (36), which leads to the following problem formulation:

$$\widehat{\mathbf{m}}=\arg \underset{\mathbf{m}\in {ℂ}^N}{\min }\Vert \mathbf{Em}-\mathbf{w}{\Vert }_2^2+\lambda J(\mathcal{P}(\mathbf{m})),$$ [3]

where the operator $\mathcal{P}(\cdot ):{ℂ}^N\to {ℂ}^{Q\times S}$ takes an image as input and constructs a structured matrix (typically with Hankel and/or Toeplitz structure) out of the Nyquist-sampled k-space data corresponding to this input, and $J(\cdot ):{ℂ}^{Q\times S}\to ℝ$ is a cost function that penalizes matrices with large rank. As before, λ denotes a regularization parameter.

There are several additional choices that must be made to fully specify the Wave-LORAKS approach. The following subsections describe the specific choices that we made, as well as the rationale we used to make decisions when we had multiple alternatives to choose from. As described below, the Wave-LORAKS choices we made are largely based on approaches and insights that have already been described in previous work, although the specific combination we have used in this work is distinct from previous approaches. Due to space limitations, our description of existing work is largely presented conceptually at a high-level, and we refer interested readers to the corresponding references for additional details.

Choice of LORAKS Matrix

There are several different possible ways of choosing the structured matrix construction operator $\mathcal{P}(\cdot )$ in Eq. [3]. For single-channel data, early LORAKS work described three different construction methods, which were called the C, G, and S matrix constructions (5,9). The C matrix is a simple convolution-structured matrix that can be used to impose image-domain support constraints and can be viewed as a single-channel version of the matrix appearing in PRUNO/SAKE/ESPIRiT (12,30,37), while the G and S matrices have more complicated structure that allows them to impose both support and smooth phase constraints simultaneously (5,9). In multi-channel datasets, parallel imaging constraints can be additionally included by stacking the single-coil C, G, or S matrices for each coil next to one another in a larger matrix (6,12,30,37). Other matrix constructions are also possible that impose sparsity constraints (7,11,16,31).

In our experience, the parallel imaging version of the S matrix (imposing support, smooth phase, and parallel imaging constraints simultaneously) consistently leads to the best image reconstruction performance in most cases (5–8), and would be a natural choice to use for Wave-CAIPI. However, a computationally efficient version of S-based LORAKS was not available at the time we originally performed the research reported in this paper.² Since computational efficiency is important for large-scale 3D Wave-LORAKS, we focus in this work on the parallel imaging version of the C matrix, which is substantially easier to manipulate. While the C matrix is normally incapable of incorporating smooth phase constraints, it is possible to use phase constraints with the C matrix by using the concept of virtual conjugate coils (8,38,39). In our experience, combining the C matrix with virtual conjugate coils does not lead to substantially worse image reconstruction error values than using the S matrix (8,20).

Similar to previous work (8, 38, 39), our use of virtual conjugate coils is motivated by the complex conjugation property of the Fourier transform. Let $s_{\mathcal{l}}(\mathbf{x})$ denote the spatially-varying coil sensitivity for the $\mathcal{l}\text{th}$ channel and m(x) represents the desired image, and let $G_{\mathcal{l}}(\mathbf{k})$ denote the Fourier transform of $s_{\mathcal{l}}(\mathbf{x})m(\mathbf{x})$. The conjugation property of the Fourier transform implies that if we construct virtual conjugate coil data $D_{\mathcal{l}}(\mathbf{k})$ according to $D_{\mathcal{l}}(\mathbf{k})\triangleq \overline{G_{\mathcal{l}}(-\mathbf{k})}$ where the bar denotes complex conjugation, then this virtual coil data will be equal to the Fourier transform of $\overline{{\tilde{s}}_{\mathcal{l}}(\mathbf{x})m(\mathbf{x})}$, which can be rewritten in terms of the standard SENSE model as ${\tilde{s}}_{\mathcal{l}}(\mathbf{x})m(\mathbf{x})$ for some “virtual” coil sensitivity profile ${\tilde{s}}_{\mathcal{l}}(\mathbf{x})$ defined by

$${\tilde{s}}_{\mathcal{l}}(\mathbf{x})=\overline{s_{\mathcal{l}}(\mathbf{x})}\exp (-i2\angle m(\mathbf{x})),$$ [4]

where ∠ m(x) is the phase of m(x). Constructing virtual conjugate coils in this way allows us to double the effective number of channels we’ve measured data from (increasing the amount of spatial encoding and the amount of information content that can potentially be extracted from the data), while also facilitating the use of smooth phase constraints (which classically lead to linearprediction relationships between opposite sides of k-space) (8,38,39).

Let ${\mathcal{P}}_C(\cdot )$ denote the operator that constructs the standard C-matrix from single-channel Nyquist-sampled k-space data (5). Also assume that we measure data from L coils, and that multiplying an image m with the sensitivity map from the $\mathcal{l}\text{th}$ coil can be represented by the matrix-vector multiplication ${\mathbf{R}}_{\mathcal{l}}\mathbf{m}$, where ${\mathbf{R}}_{\mathcal{l}}\in {ℂ}^{N\times N}$ is a diagonal matrix with diagonal entries equal to the sensitivity map values for each voxel. Additionally, let $\mathbf{F}\in {ℂ}^{N\times N}$ denote the Cartesian Nyquist-sampled Fourier transform operator. Combining parallel imaging and virtual coil ideas (6,8,12,30,37–39), the $\mathcal{P}(\cdot )$ operator we use for Wave-LORAKS in Eq. [3] is defined by concatenating C-matrices corresponding to different real and virtual coils according to

$$\mathcal{P}(\mathbf{m})=\left[{\mathbf{C}}_1,{\mathbf{C}}_2,\dots ,{\mathbf{C}}_L,{\mathbf{D}}_1,{\mathbf{D}}_2,\dots ,{\mathbf{D}}_L\right],$$ [5]

where

$${\mathbf{C}}_{\mathcal{l}}\triangleq {\mathcal{P}}_C\left({\mathbf{FR}}_{\mathcal{l}}\mathbf{m}\right)$$ [6]

is the C matrix for the $\mathcal{l}\text{th}$ real coil, and

$${\mathbf{D}}_{\mathcal{l}}\triangleq {\mathcal{P}}_C\left(\mathbf{F}\overline{\left({\mathbf{R}}_{\mathcal{l}}\mathbf{m}\right)}\right)$$ [7]

is the C matrix for the corresponding virtual conjugate coil.

Due to its structure, the matrix constructed according to Eq. [5] is expected to have nullspace vectors associated with support constraints, smooth phase constraints, and parallel imaging constraints.

Use of Autocalibration

LORAKS approaches that have been used with calibrationless sampling have generally used nonlinear/nonconvex penalty functions J(·) (5,6), since this enables the linear-prediction relationships to be learned automatically during the optimization procedure. However, substantial computational accelerations are possible if densely-sampled autocalibration (ACS) data is available, since this data can be used to pre-learn the linear-prediction relationships for the specific image of interest (10). The specific variation of this idea that we describe below for Wave-LORAKS is a direct adaptation of the previous autocalibrated LORAKS approach (10). In particular, we choose J(·) in Eq. [3] to be a simple autocalibrated linear least-squares penalty (10,12), which leads to:

$$\widehat{\mathbf{m}}=\arg \underset{\mathbf{m}\in {ℂ}^N}{\min }\Vert \mathbf{Em}-\mathbf{w}{\Vert }_2^2+\lambda \Vert \mathcal{P}(\mathbf{m})\mathbf{N}{\Vert }_F^2,$$ [8]

where ∥ ⋅ ∥_F denotes the standard Frobenius norm, and the columns of the matrix $\mathbf{N}\in {ℂ}^{S\times T}$ are estimates of the approximate nullspace vectors of the matrix $\mathcal{P}(\mathbf{m})$. By construction, Eq. [8] encourages the rows of the matrix $\mathcal{P}(\mathbf{m})$ to be orthogonal to a T-dimensional subspace defined by N.

If we have a subregion of k-space that is sampled at the Nyquist-rate on a Cartesian grid (i.e., ACS data), then we can estimate N by forming a structured LORAKS matrix from the zero-padded ACS data (10,12,37). In particular, the LORAKS matrix formed from zero-padded ACS data will contain a fully-sampled submatrix (because the ACS data is fully sampled), and we choose the columns of N to be an orthonormal basis (obtained using the singular value decomposition) for the approximate nullspace of this submatrix. Since the submatrix will generally be only approximately low-rank, the dimension T of the approximate nullspace is a parameter that should be selected by the user. The matrix N obtained in this way implicitly encodes the linear-prediction relationships that are observable in the ACS measurements (10).

For Wave-LORAKS, the need to acquire conventional ACS data (i.e., Cartesian data sampled at the Nyquist rate) would substantially reduce experimental efficiency. To avoid this problem, we instead generate synthetic ACS data by performing an initial unregularized SENSE reconstruction using Eq. [1], and then simulating Cartesian Nyquist-sampled k-space data for each coil using the SENSE forward model. We estimate coil sensitivity profiles for this initial SENSE reconstruction by applying ESPIRiT (37) (with automatic masking of the sensitivity profiles based on the image support) to data measured with a rapid low-resolution prescan that takes about 2 seconds to acquire. Since the SENSE reconstruction will be most accurate in densely-sampled regions of k-space, we only generate synthetic ACS data for low-frequency regions of k-space (i.e., the region of k-space that has the highest SNR and is sampled most densely by the sampling patterns we’ve considered).

Fast Optimization

The optimization problem we wish to solve in Eq. [8] has the form of a simple linear least-squares problem,³ and we use the conjugate gradient algorithm (40) to solve it. This is an efficient iterative algorithm that is also commonly used for solving unregularized SENSE (26) and Wave-CAIPI reconstruction problems (1).

These kinds of iterative algorithms become especially efficient when there are fast algorithms for implementing matrix-vector multiplication. It has already been established (1) that there are efficient ways to implement matrix-vector multiplication with the E matrix (based on convolution with a point-spread function model of the acquisition, which can be implemented using the fast Fourier transform (FFT) for computational efficiency). However, one of the challenges associated with implementing the LORAKS reconstruction is that the matrix $\mathcal{P}(\mathbf{m})$ can be many times larger than the original image m. This is particularly problematic for large-scale problems like those we consider in this work. For example, for one of the 3D Wave-CAIPI datasets we consider later in this paper (i.e., Dataset 1), the vector w occupies around 17 GB (in single precision, and without coil compression), while the corresponding LORAKS matrix can require up to 1300 GB or more of memory, which can be difficult for modern computers to accommodate. In addition to these memory issues, our previous LORAKS implementation (9) of the C matrix operator ${\mathcal{P}}_C(\cdot )$ is sufficiently fast for smaller-scale 2D problems, but is relatively slow at building the large matrices associated with 3D problems.

However, it has recently been observed (19) that the convolutional structure of this kind of matrix allows computations involving ${\mathcal{P}}_C(\cdot )$ to be performed using simple convolution operations (which can also be implemented efficiently using the FFT), without the need for explicitly forming the large-size LORAKS matrix. The structured low-rank matrix used in Ref. (19) has nearly identical structure to the LORAKS C matrix, with the primary difference being the shape of the neighborhood system used to form the structured low-rank matrix. In particular, LORAKS generally uses circular neighborhoods to ensure isotropic resolution characteristics (5), while Ref. (19) uses rectangular neighborhoods similar to the rectangular kernel shapes used by methods like GRAPPA (33) and SPIRiT (34). Since this difference in the neighborhood system does not change the form of the computation and because we are using the C matrix in this work, it becomes possible for us to use the exact same FFT-based approach described previously (19) in our implementation of Wave-LORAKS. A more detailed description and an example software implementation of this FFT-based approach is available from Ref. (20). It should be noted that this FFT-based approach is based on certain approximations (19). However, both the results of Ref. (19) and our past experience (20) suggest that these approximations have a nearly negligible effect on image reconstruction quality for the type of imaging scenario considered in this paper.

METHODS

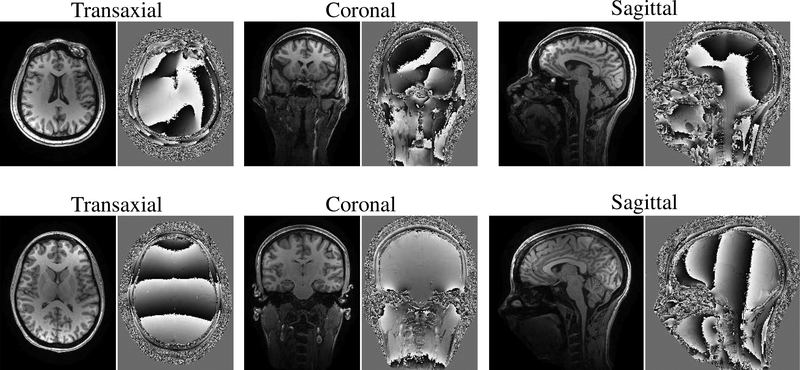
Two in vivo human brain Wave-encoded MPRAGE datasets were acquired using a Siemens 3T Connectom scanner with a 32 channel headcoil. Both datasets were acquired “unaccelerated,” with phase encoding positions placed on a fully-sampled Cartesian grid at the Nyquist rate. Due to the use of Wave encoding, these datasets were oversampled along the readout dimension. Dataset 1 was acquired assuming a nominal image matrix size of 240 × 240 × 192 voxels (with 1 mm³ isotropic resolution). This data was acquired with 6× oversampling along the readout, corresponding to a k-space matrix (readout × phase encode 1 × phase encode 2 × coil) size of 1440 × 240 × 192 × 32. Additional acquisition parameters include: readout duration 5.04 ms, maximum slew rate 180 mT/m/s, maximum gradient amplitude 9.6 mT/m, 15 sinusoidal Wave cycles, flip angle 9° and TR/TE/TI = 2500/3.52/1100 ms. Dataset 2 was acquired assuming an image matrix size of 256 × 256 × 192 voxels (again with with 1 mm³ isotropic resolution). This data was acquired with 3× oversampling along the readout, corresponding to a k-space matrix size of 768 × 256 × 192 × 32. Additional acquisition parameters include: readout duration 5.07 ms, maximum slew rate 175 mT/m/s, maximum gradient amplitude 9.4 mT/m, 15 sinusoidal Wave cycles, flip angle 8°, and TR/TE/TI = 2500/3.48/1100 ms. To reduce later computational complexity, the original 32 channels were coil compressed down to 16 virtual channels. Even with this coil compression, the datasets are still both very large. Specifically, the coil-compressed single-precision raw data for Datasets 1 and 2 respecitively occupies 7.8 GB and 4.2 GB of memory. Basic Wave-CAIPI reconstructions of the fully-sampled Datasets 1 and 2 are shown in Fig. 1.

Figure 1.

Gold standard magnitude and phase images for Dataset 1 (top row) and Dataset 2 (bottom row). Images are shown for three representative orthogonal views.

These two fully-sampled Wave datasets were used to define gold standard reference images, and were also retrospectively undersampled to allow evaluation and comparison of different acceleration techniques. Retrospective undersampling was only performed along the two phase encoding dimensions, while the readout dimension was always fully sampled.

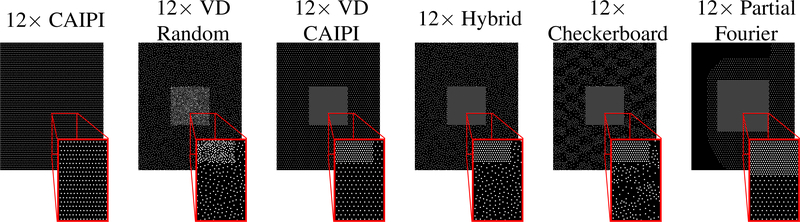
One of the potential advantages of Wave-LORAKS is that LORAKS is compatible with a wide variety of different sampling strategies. However, since we do not know what the optimal undersampling strategy should be in this case, we performed an initial study of different k-space undersampling strategies with 12× acceleration. We specifically compared the following:

• CAIPI sampling. This is a standard approach in which k-space is sampled on a uniform lattice, and was used in earlier Wave-CAIPI work (4).

• Variable density (VD) random sampling. K-space was randomly undersampled using a Poisson disc sampling distribution (41). The central 72 × 72 region of Dataset 1 and the central 74 × 74 region of Dataset 2 was sampled at a 4× higher sampling density than the other portions of k-space to account for the fact that low-frequencies generally contain a substantially higher amount of information content than high frequencies. This is a standard approach for compressed sensing, and was used in earlier CS-Wave work (27,28).

• VD CAIPI sampling. This approach is similar to CAIPI, except that the central 72 × 72 region of Dataset 1 and the central 74 × 74 region of Dataset 2 was sampled at a 4× higher sampling density than the other portions of k-space. Both the central and high frequency regions of k-space were sampled using a uniform lattice (CAIPI) pattern.

• Hybrid sampling. This approach can be viewed as a hybridization of VD random sampling and VD CAIPI sampling. Specifically, we used lattice (CAIPI) sampling for the central 72 × 72 region of Dataset 1 and the central 74 × 74 region of Dataset 2, and used random Poisson disc undersampling in high frequency regions.

• Checkerboard sampling. This is an unconventional form of partial Fourier acquisition that was introduced in Ref. (6). Like conventional partial Fourier approaches, one side of k-space is sampled densely while the opposite side of k-space is sampled more sparsely. However, unlike conventional partial Fourier acquisition, the denser and sparser regions are distributed on both sides of k-space in an alternating checkerboard pattern, with random Poisson disc sampling within each checkerboard square. As with VD CAIPI and Hybrid sampling, we used denser lattice (CAIPI) sampling for the central 72 × 72 region of Dataset 1 and the central 74 × 74 region of Dataset 2.

• Partial Fourier sampling. In this case, we combined VD CAIPI with a more conventional partial Fourier acquisition approach. Specifically, we started with a VD CAIPI pattern, and then removed samples from the edge of one side of k-space. To maintain the same acceleration factor as VD CAIPI, we increased the size of the central densely-sampled region of k-space to 96 × 96 for both datasets.

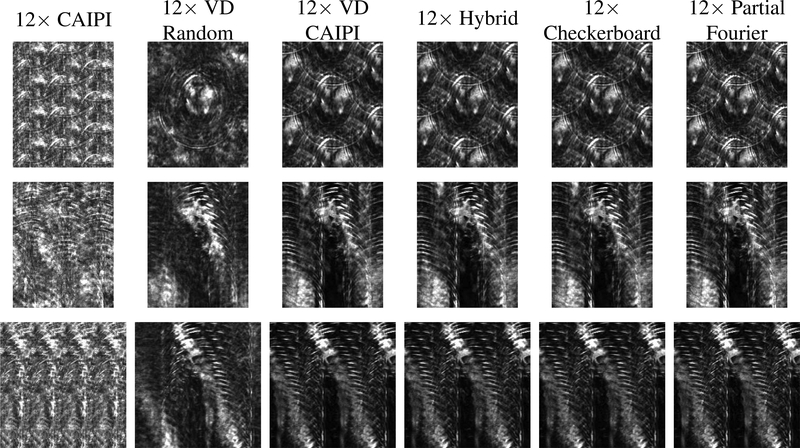
Due to the difference in matrix size for Datasets 1 and 2, we retrospectively undersampled these datasets using different sampling pattern realizations, as illustrated in Fig. 2 and Supporting Information Fig. S1. For reference, images showing the 3D aliasing patterns corresponding to each of these different sampling patterns are shown in Fig. 3 and Supporting Information Fig. S2.

Figure 2.

Different 12× accelerated sampling patterns used with Dataset 1. (This figure contains high resolution detail that may not print clearly on certain printers. Readers may prefer to view the electronic version of this figure.)

Figure 3.

Images showing the 3D aliasing patterns corresponding to the sampling patterns from Fig. 2 for Dataset 1. We show (top row) axial, (middle row) coronal, and (bottom row) sagittal views that are matched to the 3 orthogonal views shown in Fig. 1.

For each sampling pattern, reconstructions were performed using traditional Wave-CAIPI reconstruction (Eq. [1]), Wave-CS reconstruction using TV regularization (Eq. [2]), and our proposed Wave-LORAKS approach (Eq. [8]), with optimization performed in MATLAB on a desktop computer with an Intel Xeon E5–1620 3.7 GHz quad core CPU processor and 96GB of RAM. Image quality was judged qualitatively and quantitatively. For quantitative comparisons, we computed the normalized root-mean-squared error (NRMSE) and the high frequency error norm (HFEN). The HFEN is based on computing the NRMSE of a high-pass filtered version of the image (42), and provides more insight than NRMSE into how well the reconstruction has preserved the high frequency edges and textures of the image. Since we wanted to emphasize errors that occured within the brain parenchyma and do not care about errors that occur outside the brain, we applied a brain mask (generated using BrainSuite (43)) to the reconstructed images prior to computing NRMSE and HFEN.

After this initial comparison of different sampling patterns, we also compared Wave-CAIPI, CS-Wave, and Wave-LORAKS at 16× acceleration. For simplicity, we only performed reconstructions using the “best” undersampling approach for Wave-LORAKS (as determined based on the results of the previous comparison at 12× acceleration), while Wave-CAIPI and CS-Wave reconstructions were performed with the sampling patterns proposed for them in previous literature (i.e., CAIPI sampling for Wave-CAIPI, and Hybrid sampling for CS-Wave).

To ensure a fair comparison, regularization parameters for CS-Wave were optimized independently for each sampling pattern to minimize NRMSE. On the other hand, reconstruction parameters for Wave-LORAKS were set relatively coarsely. Specifically, Wave-LORAKS was implemented with a LORAKS neighborhood radius of 4 and a matrix rank of 2000 for both datasets, and we used λ = 1 for Dataset 1 and λ = 0.5 for Dataset 2. These coarsely-selected Wave-LORAKS parameters were used uniformly across all sampling patterns, without adaptation to the unique characteristics of each dataset.

RESULTS

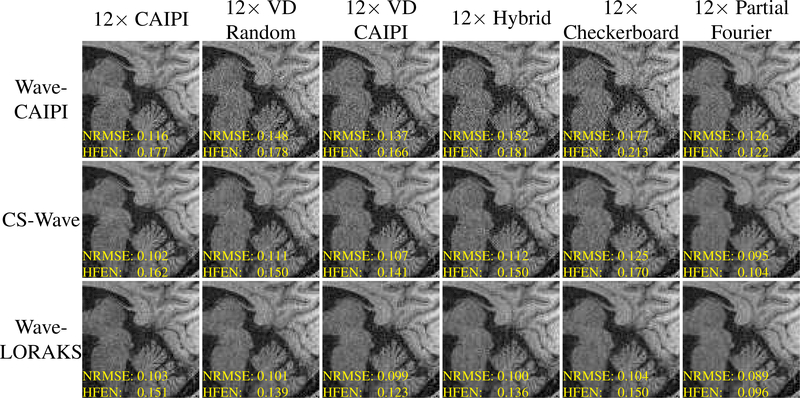
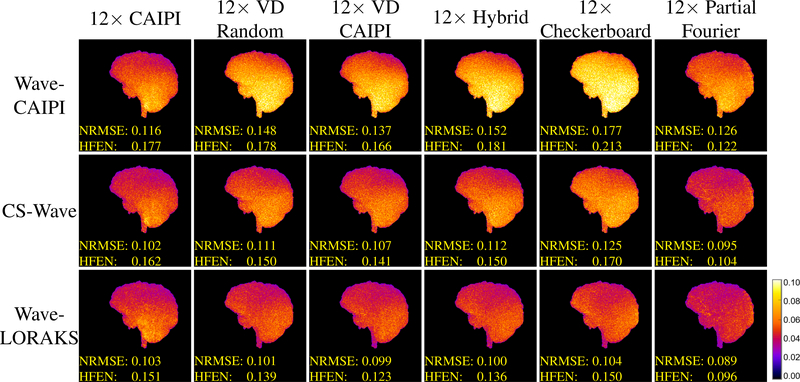
Figure 4 shows a zoomed-in version of a representative slice of the 3D reconstructions obtained from Dataset 1, while Figs. 5 and 6 respectively show maximum-intensity projection (MIP) images of the 3D error images for both datasets. The MIP was computed after applying the previously mentioned brain mask. As can be seen, the Wave-CAIPI reconstructions have the highest errors with respect to both NRMSE and HFEN, and have a “noisy” appearance as may be expected from an unregularized reconstruction of highly-undersampled data. On the other hand CS-Wave and Wave-LORAKS both have substantially lower errors. Interestingly, Wave-LORAKS outperformed Wave-CAIPI and CS-Wave for almost all undersampling patterns. The one exception was that CS-Wave had a slightly smaller NRMSE for CAIPI sampling.

Figure 4.

Reconstructions of a representative sagittal slice from Dataset 1 using different reconstruction techniques and different 12× accelerated undersampling patterns. For easier visualization, we have zoomed-in on a region that shows a variety of important anatomical features that exhibit structure across a variety of different spatial scales, including the brain stem, cerebellum, corpus callosum, and portions of the occipital and parietal lobes.

Figure 5.

Maximum intensity projections of the 3D error images associated with reconstructions of Dataset 1 using different reconstruction techniques and different 12× accelerated undersampling patterns. The color scale has been normalized so that a value of 1 corresponds to the maximum intensity of the image within the brain mask.

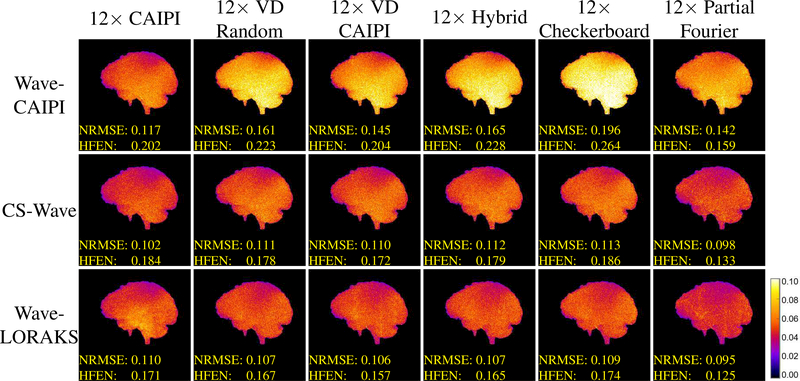
Figure 6.

Maximum intensity projections of the 3D error images associated with reconstructions of Dataset 2 using different reconstruction techniques and different 12× accelerated undersampling patterns. The color scale has been normalized so that a value of 1 corresponds to the maximum intensity of the image within the brain mask.

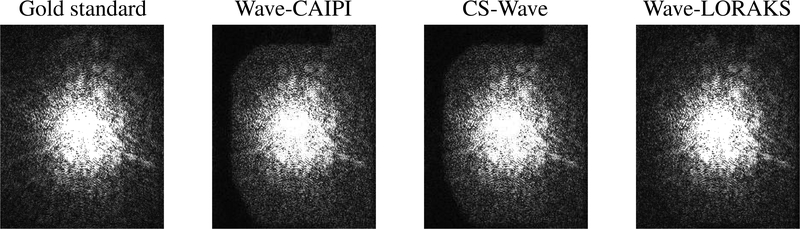
When we compare different sampling patterns for Wave-CAIPI, we observe that traditional Wave-CAIPI has the lowest NRMSE with traditional CAIPI undersampling, as might be expected based on the the excellent g-factor characteristics of CAIPI for traditional reconstruction approaches (22). However, surprisingly, we observe that Wave-CAIPI has the lowest HFEN with partial Fourier sampling. This result is surprising because Wave-CAIPI does not make use of phase constraints, and is not expected to be able to extrapolate the missing high-frequency information. Closer examination of this result suggests that Wave-CAIPI actually does have substantial high-frequency errors as can be seen in Fig. 7. Our surprising HFEN results can be explained by the fact that the Laplacian of Gaussian filter used in the definition of the HFEN (42) is actually a bandpass filter that suppresses both low-frequencies and high-frequencies, while emphasing mid-range frequencies.

Figure 7.

Reconstructed k-space data obtained by applying different reconstruction methods to a subsampled version of Dataset 1, using the 12× partial Fourier undersampling pattern from Fig. 2. Both Wave-CAIPI and CS-Wave demonstrate significant errors in the high-frequency region of one side of k-space. This side of k-space was not measured because of partial Fourier sampling.

When we compare different sampling patterns for CS-Wave and Wave-LORAKS, we observe that Partial Fourier sampling yields the smallest NRMSE and HFEN values in both cases. This result may be expected for Wave-LORAKS, because the good performance of LORAKS with partial Fourier acquisition is consistent with previous literature (5,6,36). However, this result is surprising for CS-Wave, which does not impose smooth phase constraints and is not expected to accurately extrapolate the missing side of k-space. Closer examination suggests that CS-Wave with partial Fourier sampling has substantial errors on the missing side of k-space (as seen in Fig. 7), but is still able to have lower overall NRMSE and HFEN values than CS-Wave with other sampling patterns because of smaller errors in the mid-frequency range. We suspect that CS-Wave is benefitting from the fact that Partial Fourier sampling has dense sampling over a larger region of central k-space than is used by the other sampling schemes. Surprisingly, Hybrid sampling (which we expected to demonstrate the best performance for CS-Wave based on previous literature) was slightly outperformed by CAIPI, VD CAIPI, and VD Random sampling with respect to NRMSE, and was slightly outperformed by VD Random and VD CAIPI sampling with respect to HFEN. However, in all of these cases, the performance of Hybrid sampling was not substantially worse than the alternative choices.

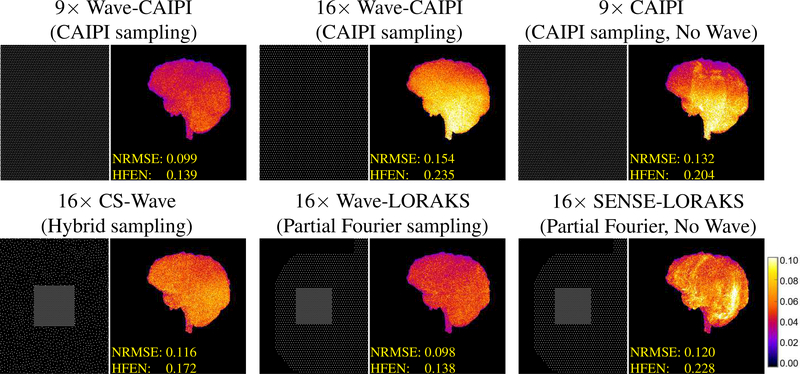
Figure 8 shows results with 16× acceleration, using CAIPI sampling for Wave-CAIPI, Hybrid sampling for CS-Wave, and Partial Fourier sampling for Wave-LORAKS. For reference, we also show Wave-CAIPI results with 9× accelerated CAIPI sampling, which is the acceleration rate and sampling strategy considered in previous Wave-CAIPI papers (1,4). We observe in this case that 16× accelerated Wave-LORAKS has substantial advantages relative to the other two 16× accelerated reconstructions. Perhaps surprisingly, the 16× accelerated Wave-LORAKS reconstruction even outperforms the 9× accelerated Wave-CAIPI reconstruction with respect to the NRMSE and HFEN quantitative error metrics. This demonstrates that Wave-LORAKS can enable substantially more acceleration than Wave-CAIPI without a corresponding loss of image quality. For additional reference, we also show results obtained using traditional 9× accelerated CAIPI and 16× accelerated SENSE-LORAKS without Wave encoding. Since we did not acquire data without Wave encoding, this data was simulated based on the fully-sampled gold standard reference image. As can be seen, results are substantially worse when Wave encoding is not used. This confirms that Wave encoding is also an important ingredient of the Wave-LORAKS approach.

Figure 8.

Maximum intensity projections of the 3D error images associated with reconstructions of Dataset 1 using 16× accelerated data. The color scale is normalized to match Fig. 5. (This figure contains high resolution detail that may not print clearly on certain printers. Readers may prefer to view the electronic version of this figure.)

On our computer, the 16× accelerated reconstructions shown in Fig. 8 took about 45 minutes for Wave-CAIPI and about 5.5 hours for CS-Wave using an efficient implementation based on the alternating directions method of multipliers (28). For comparison, our fast Wave-LORAKS implementation takes approximately 2.5 hours. Even though our implementation is still at the proof-of-principle stage and has not been fully optimized, we still observe a major speed advantage relative to CS-Wave. We believe that there are many opportunities for further improving reconstruction speed by using better hardware, more efficient programming languages, and smarter algorithms.

DISCUSSION

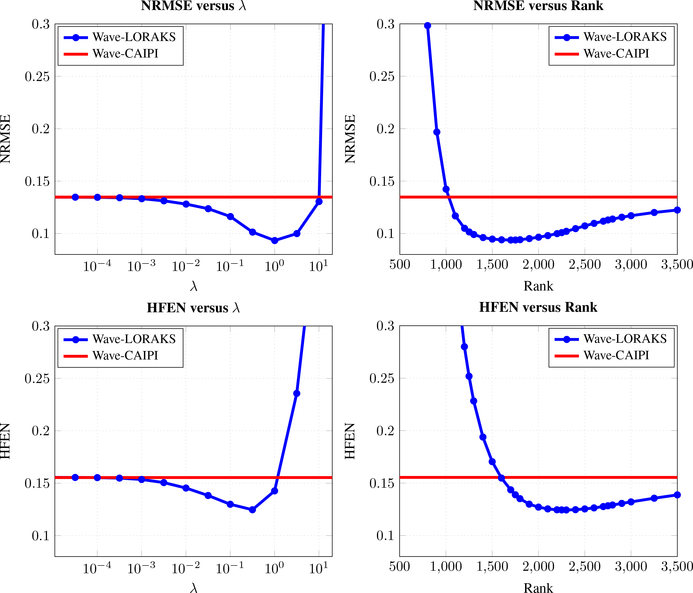
Wave-LORAKS has a few reconstruction parameters that need to be selected, and it is worthwhile to understand how sensitive the Wave-LORAKS reconstruction is to the choice of these parameters. Figure 9 examines how the NRMSE and HFEN error metrics change as a function of the regularization parameter λ and the LORAKS matrix rank, in the context of reconstructing Dataset 1 from 12× accelerated VD CAIPI data. For reference, we also show the NRMSE and HFEN values obtained from traditional unregularized Wave-CAIPI. These plots demonstrate that Wave-LORAKS outperforms traditional Wave-CAIPI over a wide range of different λ and matrix rank values, with the results being slightly more sensitive to λ than they are to the choice of matrix rank. As a result, we infer that careful parameter tuning is not essential to the good performance of Wave-LORAKS, and that Wave-LORAKS is likely to provide benefits as long as parameters are set in a reasonable way. While we selected reconstruction parameters for Wave-LORAKS coarsely and manually in this work, an automatic data-adaptive parameter selection approach would also be a viable and potentially valuable strategy (44,45), although would be expected to incur substantial additional computational costs.

Figure 9.

(top) NRMSE and (bottom) HFEN reconstruction error metrics as a function of the (left) regularization parameter λ and (right) LORAKS matrix rank, for reconstruction of Dataset 1 with 12× accelerated VD CAIPI sampling.

All of the results shown so far were based on a LORAKS neighborhood radius of 4. The neighborhood radius is a LORAKS parameter that is analogous to the k-space kernel size in GRAPPA and ESPIRiT (33,37). As has been discussed in previous papers (5,6), selection of this radius represents a balance between multiple factors. On the one hand, larger values of the radius mean that the low-rank model will be more flexible and better able to accommodate rapid spatial variations in the image support, phase, or parallel imaging constraints. On the other hand, this additional flexibility also means that the LORAKS model will have a larger number of degrees-of-freedom, and can be more prone to overfitting. At the same time, the size of the LORAKS matrices (and therefore, the amount of memory required if the matrices were formed explicitly) grows in proportion to the square of the neighborhood radius. This last fact may be the most important one to consider in scenarios where computational resources are limited. Table investigates the effects of different neighborhood radius choices for the same context considered in the previous paragraph. As can be observed, the NRMSE and HFEN both seem to reduce very slightly as we increase the neighborhood radius from 2 to 4, although this improvement in reconstruction quality is somewhat offset by very substantial increases in computation time. Interestingly, with a neighborhood radius of 2, the Wave-LORAKS reconstruction time of 0.99 hours is not too much larger than that of the much simpler Wave-CAIPI reconstruction (0.75 hours), while the Wave-LORAKS reconstruction quality is substantially better (i.e., Wave-LORAKS gives an NRMSE of 0.108, while Wave-CAIPI gives an NRMSE of 0.137 with the same data). Comparing memory usage, we observe that the use of FFT-based matrix multiplication substantially reduces the amount of memory required for LORAKS reconstruction compared to what would be required from our original implementation that explicitly constructs large-scale LORAKS matrices. However, it should also be noted that our FFT-based Wave-LORAKS implementation still requires more memory than Wave-CAIPI.

We would hypothesize that the trend of reduced NRMSE with larger neighborhood radii will not continue indefinitely, and we would eventually start to see increased NRMSE for larger radius values. However, we have not explored this regime because of the increased computational complexity associated with larger neighborhood radius values.

The results shown in this paper were based on retrospective undersampling of a “fully sampled” dataset that took roughly 10 minutes to acquire. Specifically, Dataset 1 took 10 minutes to acquire while Dataset 2 took 10.67 minutes to acquire. The fact that we can achieve high quality reconstruction results with 16× undersampling suggests that a prospective Wave-LORAKS acquisition of this kind of data could be roughly 40 seconds long, which is a substantial improvement over the previous state-of-the-art. Future prospective implementations of Wave-LORAKS with the MPRAGE sequence will need to account for T1-blurring effects when designing the phase encode acquisition order, due to the fact that the MPRAGE sequence uses an echo train. However, accounting for these effects with highly-structured sampling (like the CAIPI-based Partial Fourier sampling pattern that worked the best with Wave-LORAKS) is more straightforward than it would be for the VD Random or Hybrid sampling patterns that are better suited for compressed sensing methods like CS-Wave.

We observed in this work that Partial Fourier sampling appeared to be the best sampling scheme for Wave-LORAKS in the context of this application. However, it should be noted that we only considered a restricted class of sampling patterns, and did not perform an exhaustive evaluation of every imaginable sampling strategy. Exploring optimal sampling strategies remains an interesting topic for future research.

While this work focused on 3D Wave acquisition, we believe that it would be straightforward to apply the same ideas to simultaneous multislice (SMS) wave data (2). In particular, there already exists an SMS formulation for LORAKS (46) that can be easily adapted to this purpose.

Finally, we should mention that while we compared Wave-LORAKS against CS-Wave in this paper, it would also be possible to use LORAKS synergistically with other regularization constraints for even further improvements in reconstruction performance, at the cost of increased computational complexity. Specifically, because the LORAKS constraint is just regularization, it is easy to append additional regularization terms (e.g., TV or wavelet regularization) to the Wave-LORAKS objective function in Eq. [8]. Another potentially interesting extension would be the combination of Wave encoding and LORAKS in the context of multi-contrast imaging, since recent work has shown that LORAKS constraints can also be very beneficial when reconstructing multi-contrast datasets (17).

CONCLUSION

This work introduced and evaluated a new Wave-LORAKS approach for highly accelerated MRI. Our experimental results indicate that Wave-LORAKS is quite powerful relative to standard WaveCAIPI. Specifically, the Wave acquisition and LORAKS reconstruction combine synergistically, allowing even higher acceleration factors than Wave-CAIPI without a loss of image quality, while also enabling higher flexibility in the choice of sampling patterns. While the improved performance of Wave-LORAKS comes at the expense of some additional computational complexity, we believe that these computational costs can largely be mitigated using appropriate tuning of the LORAKS neighborhood radius combined with a more efficient numerical implementation.

Supplementary Material

Supporting Information Figure S1.

Different 12× accelerated sampling patterns used with Dataset 2. (This figure contains high resolution detail that may not print clearly on certain printers. Readers may prefer to view the electronic version of this figure.)

Supporting Information Figure S2.

Images showing the 3D aliasing patterns corresponding to the sampling patterns from Fig. S1 for Dataset 2. We show (top row) axial, (middle row) coronal, and (bottom row) sagittal views that are matched to the 3 orthogonal views shown in Fig. 1.

Table 1:

The effect of the LORAKS neighborhood radius on NRMSE, memory usage, and computation time for reconstruction of Dataset 1 with 12× accelerated VD CAIPI sampling. For reference, values corresponding to Wave-CAIPI reconstruction are also shown.

	Wave-LORAKS			Wave-CAIPI
Neighborhood Radius	2	3	4
NRMSE	0.108	0.102	0.098	0.137
HFEN	0.133	0.127	0.124	0.166
Compute Time (hours)	0.99	1.52	2.48	0.75
Memory Usage (FFT-based implementation)	80 GB	80 GB	80 GB	33 GB
Matrix size (original implementation)	90 GB	320 GB	650 GB