Interactions of Flicker and Motion

Abstract

We present a series of novel observations about interactions between flicker and motion that lead to three distinct perceptual effects. We use the term flicker to describe alternating changes in a stimulus’ luminance or color (i.e. a circle that flickers from black to white and visa-versa). When objects flicker, three distinct phenomena can be observed: (1) Flicker Induced Motion (FLIM) in which a single, stationary object, appears to move when it flickers at certain rates; (2) Flicker Induced Motion Suppression (FLIMS) in which a moving object appears to be stationary when it flickers at certain rates, and (3) Flicker-Induced Induced-Motion (FLIIM) in which moving objects that are flickering induce another flickering stationary object to appear to move. Across four psychophysical experiments, we characterize key stimulus parameters underlying these flicker-motion interactions. Interactions were strongest in the periphery and at flicker frequencies above 10Hz. Induced motion occurred not just for luminance flicker, but for isoluminant color changes as well. We also found that the more physically moving objects there were, the more motion induction to stationary objects occurred. We present demonstrations that the effects reported here cannot be fully accounted for by eye movements: we show that the perceived motion of multiple stationary objects that are induced to move via flicker can appear to move independently and in random directions, whereas eye movements would have caused all of the objects to appear to move coherently. These effects highlight the fundamental role of spatiotemporal dynamics in the representation of motion and the intimate relationship between flicker and motion.

Introduction

The neural basis of visual motion perception is grounded in computations and processes that operate on spatiotemporal changes of feature-level information across the visual field (Adelson & Bergen, 1985; Lu & Sperling, 1995; van Santen & Sperling, 1984; Ullman, 1979; Watson & Ahumada, 1985). Neurons that are selective to transient changes (i.e. a sudden change in luminance) within their receptive fields serve as the earliest stage of a visual motion processing hierarchy that extracts local directionality, speed, and global motion velocities to ultimately represent our experience of a moving object (Braddick et al., 2001; Pack & Born, 2001; Pack, Livingstone, Duffy, & Born, 2003; Sincich & Horton, 2005). However, not all transient changes in the visual scene arise from motion across the retina. Sudden appearances, changes in illumination, and even eye-blinks can cause transient changes in the visual scene at locations of stationary objects (Volkmann, 1986). Given the fact that temporal transients are such a fundamental input for motion perception, it is perhaps not surprising that non-directional transients can lead to percepts of motion and activate motion selective areas of cortex (i.e. hMT+; Sunaert, Van Hecke, Marchal, & Orban, 1999; Tootell et al., 1995). This is most commonly observed with stationary, counter-phase flickering patterns such as checkerboards (see Video 1) or checker-rings (Video 2) which evoke strong percepts of motion despite the fact that the flickering elements are in fact stationary. These flickering-pattern motion percepts arise from the manner in which the visual motion processing hierarchy solves the motion correspondence problem (Anstis, 1970; Attneave, 1974; Ullman, 1979), which is itself a key focus of interest to vision scientists. In this paper, we introduce a new class of flicker-motion interactions that are not based on the correspondence problem, which differentiates them from these classic, pattern-based examples. Here we describe the results of four psychophysical experiments and a series of stimulus demonstrations that reveal three distinct flicker-motion interactions: (1) Flicker Induced Motion (FLIM) in which one or more stationary objects appear to move when they flicker at certain rates; (2) Flicker Induced Motion Suppression (FLIMS) in which one or more moving objects appear to be stationary when they flicker at certain rates, and (3) Flicker-Induced Induced-Motion (FLIIM) in which moving objects that are flickering induce other stationary flickering objects to appear to move.

This project was motivated by observations made while studying a visual illusion called the Wandering Circles (Blair, Strother, & Caplovitz, 2014; Blair, Erlikhman, & Caplovitz, submitted) which was a top-10 finalist of the 2015 Best Visual Illusion of the Year contest sponsored by the Neural Correlates Society and can be viewed at their website: http://illusionoftheyear.com/2015/06/the-wandering-circles/ or in the re-created version shown in Video 3. In the Wandering Circles illusion, four stationary circles that flicker from light to dark appear to move in independent and seemingly random directions. The effect is strongest in the periphery, when the object is flickering at an intermediate rate of 10 Hz (compared to 2 or 30 Hz), and is particularly strong when the edges of the object induce the Craik-O’Brien-Cornsweet illusion (Cornsweet, 1970; Craik, 1966; O’Brien, 1958) and which undergo polarity reversals as they flicker¹ (Figure 1). This illusion is of particular interest for two reasons: (1) Like the illusion of motion observed in counter-phase flickering patterns, there is no net motion in the image; however, unlike counter-phase flicker, the illusory motion observed in the Wandering Circles does not arise from the correspondence problem. This is because the flickering circles are unitary in nature (i.e. not comprised of patterned textures) and thus there is no correspondence problem to solve. Furthermore, random dot patterns that flicker in counterphase can be seen to move in the same direction as eye movements and the effect can be explained by reverse-phi motion (Spillmann, Anstis, Kurtenbach, & Howard, 1997). In the Wandering Circles illusion, there are multiple flashing circles presented simultaneously, each of which appears to move independently in random directions. The effects therefore cannot be explained by eye movements since microsaccades leading to a shift of the retinal image would move all circles in the same direction across the retina at the same time. This suggests a more complicated interaction between form, position, and motion mechanisms in the illusion. (2) The illusory motion observed in the Wandering Circles involves the perceived shift of their positions both relative to each other and within the visual scene. This again stands in contrast to the motion observed in counter-phase flicker, which appears internal to patterns and does not invoke positional displacement.

Figure 1.

The “Flickering Cornsweet” stimulus used in the Wandering Circles illusion.

The wandering nature of the Wandering Circles illusion is more in line with a second class of motion illusions called motion-induced position shifts, which describe a wide range of stimuli in which the presence of directional visual motion can influence the perceive location of objects in the visual scene. For example, a stationary Gabor patch with an internal drift (i.e., continuously and smoothly changing phase) will appear to move in the direction of the drift, orthogonal to its orientation (Chung, Patel, Bedell, & Yilmaz, 2007; De Valois & De Valois, 1991; Mather & Pavan, 2009). One way of describing the effect is that the internal motion signal is “captured” by the contours of the object. Such motion-capture effects can arise even when the motion pattern is created by random dots or when the object’s contours are illusory (Ramachandran, 1987; Ramachandran & Anstis, 1988, 1990; Ramachandran & Inada, 1985). If an internally drifting Gabor patch is also set in motion, as in the infinite regress and double-drift illusions, then the perceived position of the patch from moment to moment is offset by a large amount relative to the true position and the position error increases across animation frames (Lisi & Cavanagh, 2015; Tse & Hsieh, 2006). Perceived object position can also be altered by the motion of distant objects. For example, in the flash-drag effect, lines flashed near, but not overlapping with a rotating radial grating appear displaced in the direction of the grating’s motion (Whitney & Cavanagh, 2000, 2002; for a review, see Whitney, 2002). Even larger position shifts can be induced in the flash-grab effect where a stimulus is flashed on top of a rotating pattern right at the moment when the pattern changes rotation directions (Cavanagh, & Anstis, 2013). The overlapping stimulus appears displaced in the direction of rotation of the pattern after the switch – it’s motion “grabs” the flashed stimulus.

The positional displacements observed in the Wandering Circles draws an obvious connection to these motion-induced position shifts. However, unlike all of these other examples, the Wandering Circles do not, at the level of the image, contain a directional motion signal that induces the position shift. Instead, at the level of the image, the Wandering Circles contain non-directional motion signals (i.e. non-directional temporal transients induced by the flicker). As such, we refer to the Wandering Circles illusion as an example of ‘Flicker-Induced Motion’ (FLIM)². We note that, albeit weaker, FLIM and the related effects described below can occur even if the circles are defined by uniform black/white surfaces with crisp edges.

Inspired by the Wandering Circles, we developed a variant in which a single stationary, flickering circle appears with other, flickering, but moving circles (Video 4). As in the Wandering Circles illusion, the stationary circle’s position appears to jitter. We refer to this induced motion effect as “Flicker-Induced Induced Motion” or FLIIM because the effect goes away if the circles are not flickering and the presence of the other flickering and moving circles enhances the perceived illusory motion above and beyond what would be observed if there were no physically moving circles (e.g. FLIM). In a series of four psychophysical experiments, we explored the stimulus properties that influence the strength of the induced motion, and in the process revealed a third flicker-motion interaction that we call “Flicker-Induced Motion Suppression” (FLIMS), in which flickering circles that are physically moving will appear to be stationary. This effect is the opposite of FLIM and in our experiments tends to be observed more often. Taken together, these three effects: FLIM, FLIMS, and FLIIM highlight the fundamental role of temporal transients in motion perception and, as will be discussed in the general discussion, the need for models of motion perception to move away from computations that operate at the level of the image and towards computations that operate at the level of neural representations of the image.

Experiment 1

The purpose of the experiment was to quantify the basic characteristics of interactions between flicker and motion. The design was similar to that used for Blair et al. (submitted). Participants were presented with four flickering circles, three of which would subtly move in random directions while one would remain stationary. Participants were instructed to identify the location of the stationary circle. Performance on this task was examined as a function of eccentricity and flicker rate.

Methods

Participants

Nineteen undergraduate or graduate students (twelve male, seven female) from the University of Nevada, Reno (UNR) and University of California, Los Angeles (UCLA) participated in the experiment for course credit. Ten participated in the far eccentricity condition and nine in the near eccentricity condition. Data from five participants in the far condition was collected at UCLA. All other data were collected at UNR. Two locations were used because of some difficulty in recruiting a sufficient number of participants at UNR at the time the study was conducted. Ages ranged from 20 to 32, with a mean of 24.1. All participants had normal or corrected-to-normal vision and provided informed consent and all experiments were conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Apparatus

Stimuli were created and shown using MATLAB (Mathworks Inc., Natick, MA) and Psychophysics Toolbox (Brainard, 1997; Pelli, 1997). At UNR, Stimuli were displayed on a Dell Triniton CRT monitor connected to a 2.5 GHz Mac Mini with an Intel HD Graphics 4000 graphics processor and 768 MB of DDR3 VRAM. The computer used Matlab 2017b, MacOS High Sierra, and Psychtoolbox verison 3.0.14. The refresh rate of the monitor was set to 85 Hz. The resolution was 1024×768. Participants sat a distance of 74 cm with their head stabilized with a chinrest. The experimental setup was the same at UCLA except that the computer was a MacPro 5 with a 2.66 GHz Quad-Core Intel Xeon processor, an NVidia GeForce GT120 graphics card, and a Viewsonic G250 CRT monitor. The computer used Matlab 2010a, MacOS 10.6, and Psychtoolbox version 3.0.9

Stimulus

Four circles (diameter = 4.5°) appeared on a gray (43.37 cd/m²) background, one in the center of each quadrant of the screen. Starting position was jittered independently for each circle in a random direction by a random amount between 0 and 18 arcmin. The distance from the center of the screen to the center of each circle was 3° in the near eccentricity condition and 4.5° in the far condition. The circles were all the same color, either black (2.35 cd/m²) or white (152.8 cd/m²). The circles alternated between the two colors at frequencies of 0 (no flicker), 1.98, 3.86, 5.67, 6.54, 7.73, 8.50, 9.44, 10.62, or 12.14 Hz. Color change was instantaneous (i.e. square wave modulation). For the no flicker, 0 Hz, condition, half of the trials had all black circles and half had all white. A white fixation spot was shown continuously in the middle of the screen (diameter = 18.1 arcmin). On each trial, one of the circles was randomly designated as the target, stationary circle, and the other three were designated as moving. On each frame, the three moving circles were translated in a random direction by 1.8 arcmin. Each circle’s direction of motion was independent. The motion of the circles, because it occurred with each frame refresh, was not tied to their flicker frequency.

Procedure

Participants were instructed to identify the quadrant that contained the stationary circle. Each experimental trial began with a gray screen with a central fixation spot. The circles then appeared for 1 s. Circles moved as soon as they appeared. After 1 s, the circles disappeared and each of the four quadrants was labeled with a number 1, 2, 3, or 4. Participants indicated which of the four quadrants contained the stationary circle by pressing the corresponding number key. There was no time limit for making a response. After a keypress, a blank screen again appeared for 1 s and the next trial began. Each of the 10 frequencies was repeated 20 times in a random order for a total of 200 trials. A rest break was given every 100 trials. The two eccentricity conditions were run between-subjects.

There were ten practice trials at the beginning of the experiment in which no circles flickered and the non-target circles moved at a faster rate of 5.4 arcmin per frame. This was considered an easy setting and was used to make sure that participants understood the task.

Results and Discussion

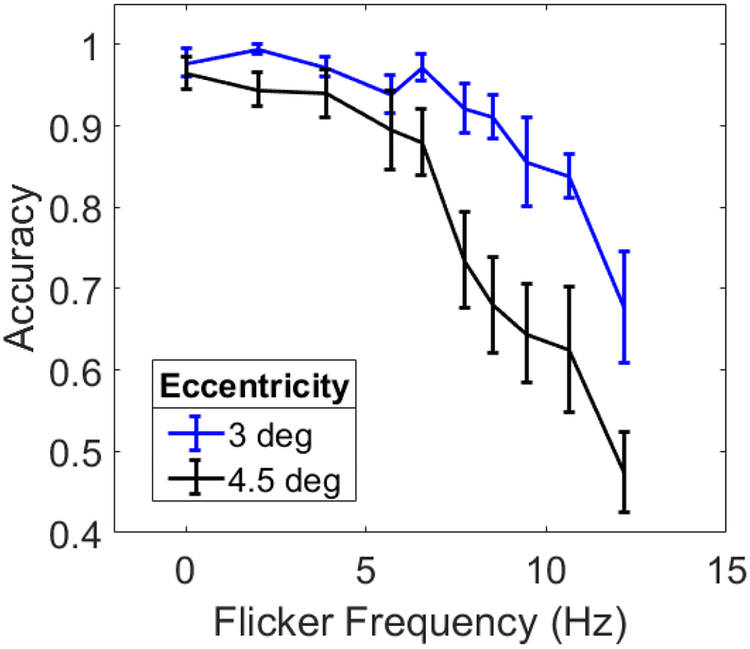
The results are shown in Figure 2. The data were submitted to a 2 (eccentricity) × 10 (flicker frequency) mixed ANOVA. All ANOVAs shown here and in all subsequent experiments were Greenhouse-Geisser corrected. There were main effects of eccentricity (F(1,17)=7.49, p=0.0140η_p²=0.306) and flicker frequency (F(4.0,68.0) = 37.57, p<0.001, η_p²=0.688), and an interaction (F(4.0,68.0)=4.38, p=0.003, η_p²=0.205). Accuracy was unaffected by flicker for frequencies up to ~6 Hz. For higher frequencies, performance continuously decreased, ultimately dropping to 67.8% and 47.5% in the near and far eccentricity conditions respectively at the fastest flicker rate tested of 12.14 Hz. Across all frequencies, stationary targets were harder to identify when the circles were presented peripherally. When no circles were flickering (0 Hz condition), performance was near ceiling at 97.8% in the near condition and 96.5% in the far condition (chance performance was 25%) even though amount of movement was relatively small (<2 arcmin per frame) and the presentation time was short (1 s).

Figure 2.

Accuracy as a function of flicker frequency for Experiments 1. Black and blue curves are data from experiment 1 at far (4.5 deg) and near (3 deg) eccentricities respectively. Error bars are standard errors. The 0 Hz point corresponds to no flicker.

To check for possible effects of testing location on performance, the data from the far condition were split by location (UNR and UCLA) and analyzed with a mixed ANOVA with location as a between-subjects factor. There was a main effect of frequency (F(3.15,25.12) = 30.53, p<0.001, η_p²=0.792), but no effect of location (F(1,8) = 1.27, p=0.293, η_p²=0.137) and no interaction between frequency and location (F(3.15,25.12)=1.30, p=0.296, η_p²=0.140), indicating that different testing environments did not affect the data.

In summary, despite the fact that the task was trivially easy in the no flicker condition, participants’ ability to identify the stationary circle was significantly impaired when the circles were flickering at rates above ~6 Hz. This is the FLIM (flicker-induced motion) effect. FLIM was stronger when the circles were presented farther from fixation. Why might flicker lead to a perception of motion? In the image, there is no displacement of a luminance-defined edge during flicker, which would typically serve as input to models of motion processing (Adelson & Bergen, 1985; Adeslon & Movshon, 1982; Hildreth, 1984; Marr & Ullman, 1981; van Santen & Sperling 1984; Watson & Ahamuda, 1985). Under normal circumstances, any changes in scene luminance that are not the result of motion, such as turning a light on or off or the sudden appearance of an object are noise to the motion system. For flickering circles, motion signals would be produced in all directions for motion energy detectors (Adelson & Bergen, 1985; Watson & Ahumada, 1985) and flickering stimuli do indeed activate direction-sensitive complex and hypercomplex cells in primary visual cortex (Qian & Andersen, 1994). Feedback from MT may play a suppressive, noise-reducing role in attenuating such signals when they arise from spatially and temporally uncorrelated stimuli (Pack & Born, 2001; Qian & Andersen, 1994). Flicker also stimulates neurons in hMT/V5+, but to a lesser extent (Goebel, Khorram-Sefat, Muckli, Hacker, & Singer, 1998; Sunaert, et al., 1999; Tootell et al., 1995). Perhaps the illusory jitter arises from not quite uniform distributions of motion energy around each circle. Neural noise might elevate the activity of some direction-sensitive units while attenuating others. Such an imbalance might produce net motion energy in a particular direction. Importantly, this motion would be “in the system” and not in the image. Because the noise is random, this would produce net motion signals in different directions over time, resulting in a “wandering” effect.

Experiment 2

As considered above, and in general, motion perception is dominated by the processing of spatiotemporal changes in luminance, i.e., first-order motion (Lu & Sperling, 1995). However, motion can also be experienced from the processing of spatiotemporal changes in non-luminance features such as color. In Experiment 2 we investigated whether the FLIM effect observed in Experiment 1 was isolated to first-order motion processing and the neural pathways that underlie it. To accomplish this, we applied the same basic paradigm as above using isoluminant red-green flickering circles instead of black-white ones.

Methods

Participants

Participants were seven (three male, three female, one not reported) new undergraduate students from the University of Nevada, Reno. Ages ranged from 20 to 26 with a mean of 22.7. All reported having normal or corrected-to-normal vision and provided informed, written consent and all experiments were conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Stimuli and Procedure

The experiment consisted of two phases. In the first phase, isoluminant settings were determined independently for each participant. Four circles, similar to those used in the experiment, were shown on a gray background and set to flicker at 10 Hz. On each trial, all of the circles were either red or green. Participants adjusted the intensity of the corresponding color channel by pressing up or down arrow keys while maintaining fixation on a central fixation spot. The circles were considered isoluminant with the gray background when flicker was perceived to be minimal (Kaiser & Boynton, 1996; Kleinholdermann, Franz, Gegenfurtner, & Stockmeier, 2009). Once a participant was satisfied with their calibrated setting, they could press a key to save the color value. This calibration procedure was repeated three times each for red circles and for green circles. The average of the three calibration settings for each color was then used as the isoluminant RGB color setting for the circles in the next phase of the experiment.

The second phase was almost the same as Experiment 1, but with red/green isoluminant color changes instead of white/black. The same 10 flicker frequency values were used. The maximum flicker frequency (12.14 Hz) was well below the 25 Hz critical flicker fusion frequency for isoluminant stimuli (De Lange, 1958; Kelly, 1971; Matin, 1968). For both phases of the experiment, the larger eccentricity of 4.5° was used, which had produced larger effects in the previous experiment.

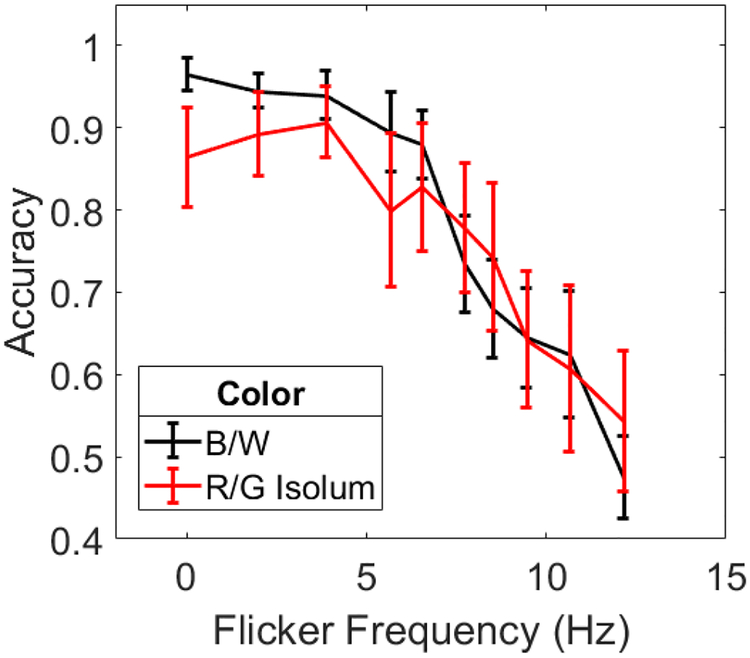
Results and Discussion

The results are shown in Figure 3, with data from the same eccentricity condition in Experiment 1 replotted for ease of comparison. Flicker defined by isoluminant color changes produced a similar pattern of results as black and white contrast polarity reversals in Experiment 1. The data were submitted to a 2 (color change type) × 10 (flicker frequency) mixed ANOVA. There was a main effect of flicker frequency (F(3.4,47.5) = 18.81, p<0.001, η_p²=0.573) and of color change type (F(1,14) = 5.35, p=0.035, η_p²=0.276), but no interaction (F(3.4,47.5) = 0.98, p=0.420, η_p²=0.065). The difference between isoluminant and non-isoluminant conditions can be seen at lower flicker frequencies: performance in the isoluminant condition was worse at flicker rates of 0–6 Hz and comparable at higher frequencies. This is consistent with previous findings that motion detection thresholds are similar for isoluminant and non-isoluminant drifting sine gratings at high temporal frequencies, but thresholds are elevated for isoluminant stimuli at low temporal frequencies (Derrington & Henning 1993; Gegenfurtner & Hawken, 1995; Henning & Derrington, 1994).

Figure 3.

Accuracy as a function isoluminant flicker frequency from Experiment 2 (red curve). Data from the far condition in Experiment 1 are replotted for comparison (black curve). Error bars are standard errors. The 0 Hz point corresponds to no flicker.

In summary, a very similar pattern of results was obtained for chromatically-defined flicker, suggesting that the neural mechanisms underlying FLIM may not be restricted to the first-order motion processing pathway. Instead, FLIM may be a second- or higher-order motion process. Color-opponent cells in V1, for example, respond to chromatic flicker (Gur & Snodderly, 1997; Jiang, Zhou, & He, 2007) and may be the locus of motion signals in FLIM. Alternatively, chromatically-defined motion might be detected by the same second-order motion mechanisms that induce motion signals in the black and white version of the stimulus (Baker Jr., Boulton, & Mullen, 1998; although see Mullen, Yoshizawa, & Baker Jr., 2003) and so FLIM may be a more fundamental process that arises in both first- and second-order motion pathways. The results of the first two experiments cannot distinguish between these two alternatives. We return to a discussion of the possible neural mechanisms underlying FLIM in the General Discussion.

Experiment 3

In Experiments 1 and 2, increasing the flicker frequency decreased the ability of observers to detect the stationary circle. We consider two possible explanations for this effect: (1) Flicker-Induced Motion (FLIM): at rates above ~6 Hz, the stationary circle appears to move, and (2) Flicker-Induced Motion Suppression (FLIMS): at rates above ~6 Hz, the moving circles appeared stationary, making it difficult to identify the one that was in fact stationary. These effects are not mutually exclusive and may have occurred concurrently. In order to test for these effects, we simplified the display to show only a single stationary or moving circle. The circle was still presented in the periphery, in the center of a random quadrant, and observers simply had to say whether the circle was moving or not. If lower accuracy in Experiments 1 and 2 was due only to FLIM, then the stationary circle should sometimes appear to move, leading to worse performance than for a moving circle flickering at the same rate. If stationary circles were harder to identify solely due to motion suppression of the moving circles (FLIMS), then the opposite pattern of results should obtain: a single moving circle will sometimes appear to be stationary, and stationary circles will always be seen as stationary. If both FLIM and FLIMS influenced performance in Experiment 1, then a combination of the two effects would be seen: a single stationary circle would sometimes appear to be moving and a single moving circle would sometimes appear to be stationary.

Methods

Participants

Participants were eight undergraduate students (three male, five female) at the University of California, Los Angeles, recruited through the subject pool and who participated for course credit. Ages ranged from 18 to 22 with a mean of 19.6. All participants reported having normal or corrected-to-normal vision and provided informed consent and all experiments were conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Stimuli and Procedure

The apparatus was the same as described in Experiment 1, except that the monitor refresh rate was set to 60 Hz. Instead of four circles, only one circle was shown on a given trial. The circle could appear in the center of any of the four quadrants. The quadrant was selected randomly on each trial. Three eccentricities (distance from center of screen to center of circle) were used: 3°, 4.5°, and 6°. The circles flickered at one of three rates: no flicker (0 Hz), slow (2 Hz), and fast (15 Hz). On half of the trials, the circle moved in a random direction by 1.8 arcmin every frame; on the other half of the trials the circle was stationary. There were therefore 2 (motion types) × 3 (eccentricities) × 3 (flicker frequencies) = 18 unique trials. Each trial type was repeated 20 times. The presentation order of the trials was random. Participants were instructed to report whether or not the circle was moving. The experiment began with 10 practice trials, half of which contained moving circles and half stationary. In the practice trials with moving circles, the circles moved at a rate of 5.4 arcmin per frame as in the previous experiments. In all of the practice trials, the circles were not flickering.

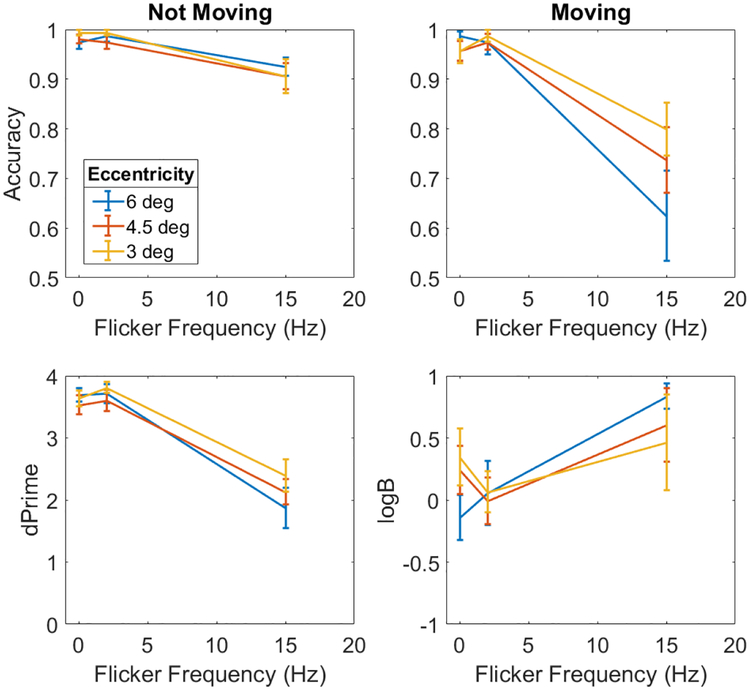
Results and Discussion

Data were split by physically stationary and moving trials (Figure 4, top row). When the circle was not flickering or was flickering at 2 Hz, observers were able to identify whether it was stationary or not most of the time, irrespective of eccentricity (accuracy > 95%). However, when the circle flickered at a rate of 15 Hz, performance dropped to 91% for the stationary circle and 72% for the moving circle. The data were submitted to a 2 (motion) × 3 (eccentricity) × 3 (flicker frequency) ANOVA. There was no main effect of motion (F(1.0,7.0) = 0.98, p=0.369, η_p²=0.117) or flicker frequency (F(1.11,7.78) = 1.19, p=0.315, η_p²=0.146), but there was a main effect of eccentricity (F(1.11,7.76) = 14.72, p=0.005, η_p²=0.678). There was also a two-way interaction between movement and flicker frequency (F(1.41,9.88) = 25.78, p<0.001,η_p²=0.786), but not between movement and eccentricity (F(1.46,10.2) = 0.65, p=0.494, η_p²=0.085) or between eccentricity and flicker frequency (F(1.73,12.14) = 2.10, p=0.168, η_p²=0.231). There was a three-way interaction between motion, eccentricity, and flicker frequency (F(1.68,11.74) = 12.41, p=0.002, η_p²=0.639). From Figure 4, one can see that eccentricity did not influence performance for stationary circles, but it did for moving circles, with worsening performance at greater eccentricities. Likewise, flicker frequency had a greater effect on the perception of moving circles. The effect of eccentricity was most pronounced for moving circles flickering at 15 Hz.

Figure 4.

Top row: Accuracy in saying whether a single circle is not moving (left) or moving (right) as a function of flicker frequency and eccentricity. Bottom row: The accuracy data converted to sensitivity (left) and bias (right). Error bars are standard errors.

The difference in performance between moving and non-moving circles may reflect a response bias on the part of the observers to report the circles as non-moving more often. This would decrease performance when the circles were actually moving and increase performance when they were not. To test this possibility, a signal detection analysis was performed in which accuracy data from both kinds of trials were combined into a single sensitivity measure (d’). Response bias was quantified as logβ where positive values corresponded to a bias to say “moving”, negative values to a bias to “not moving”, and a logβ of 0 indicated no response bias. These results are shown in the bottom row of Figure 4. Separate 3 (eccentricity) × 3 (flicker frequency) repeated-measures ANOVAs were run for the two measures. For sensitivity, there was a main effect flicker frequency (F(1.20,8.39) = 66.53, p<0.001, η_p²=0.905), but no main effect eccentricity (F(1.55,10.86) = 1.31, p=0.299, η_p²=0.158) and no interaction (F(2.02,14.14) = 1.02, p=0.388, η_p²=0.127). Sensitivity was lower for the 15 Hz flicker than for the other flicker rates, but was still relatively high (d’ = 2.13), suggesting that the difficulty in distinguishing stationary and moving circles at high flicker rates was not solely due to response bias.

However, there was also a change in response criterion as a function of flicker frequency (F(1.50,10.50) = 4.38, p=0.050, η_p²=0.385), but no effect of eccentricity (F(1.47,10.31) = 0.40, p=0.921, η_p²=0.006) and no interaction (F(1.90,13.32) = 1.28, p=0.307, η_p²=0.155). While observers were mostly unbiased in their responses at 0 and 2 Hz flicker rates, there was a strong positive bias to respond “not moving” at the 15 Hz frequency. That is, when the discrimination task was difficult, observers had a tendency to say that the circle was not moving. This accounts for the higher overall accuracy in the case when the circle was stationary. Nevertheless, the fact that sensitivity was lower at 15 Hz than at other frequencies indicates that it was harder to tell whether the circle was moving or not, and not only that observers were more biased to make “not moving” responses. Importantly, response bias was not constant across all flicker rates.

The two patterns of responses suggest that there may be two complementary effects affecting performance. First, stationary circles appear to move when flickering at a relatively high rate, which we refer to as Flicker-Induced Motion (FLIM). There is also a complementary effect by which moving circles appear stationary – Flicker-Induced Motion Suppression (FLIMS). FLIMS appears to have a larger impact on perception than FLIM: the former leading to a reduction in performance of 30%, while the latter led to a reduction of only 10% at high flicker rates. However, this difference can in part be explained by an increased bias to respond “not moving” when the task is difficult (i.e., at 15 Hz).

Experiment 4

In Experiment 1, observers were asked to identify the stationary circle. The results of Experiment 3 indicate that the drop in performance at higher flicker rates could arise from both FLIM (that all appear to be moving) or FLIMS (they all appear to be stationary). Rather than attempt to make inferences about the contributions of each from the data obtained above, in this experiment we changed the task to have the participants more directly report what they were experiencing. Instead of being asked to identify the stationary circle, participants were asked to report when all four circles appeared to be moving or not. We additionally manipulated the number of circles that were moving from none to all four. FLIM should increase the proportion of “all moving” responses, while FLIMS would reduce the number.

By systematically increasing the number of moving circles, it is also possible to examine whether FLIM and FLIMS were additive in nature. In Experiment 3, a single stationary circle appeared to move 10% of the time. If four stationary circles are shown, it is unclear whether the effect of flicker applies to the entire visual field, so that all four circles would also appear to move 10% of the time, or whether each circle appears to move independently from the rest, so that the probability of all four appearing to move simultaneously would be 0.1⁴ = 0.01%. Likewise, the more moving circles there are, the more likely it could be that the motion of at least one of them is suppressed. In Experiment 3, FLIMS had a much larger effect on perceived motion than FLIM. We may therefore expect that as there are more moving circles added to the display, the less likely it would be that all of them would be perceived to be moving at the same time.

Methods

Participants

Participants were nine (four male, five female) new undergraduate students at the University of California, Los Angeles, recruited through the subject pool and who participated for course credit. Ages ranged from 18 to 22 with a mean of 20.9. All participants reported having normal or corrected-to-normal vision and provided informed consent and all experiments were conducted in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki). All participants were naïve to the purposes of the experiment.

Stimuli and Procedure

The apparatus was the same as in Experiment 3. The displays were similar to those used in Experiment 1, except that instead of only a single stationary circle and three moving circles, there could be 0, 1, 2, 3, or 4 moving circles. In all cases, all four circles were always shown. The participants’ task was to say whether all four of the circles were moving or not (i.e., fewer than four). Three flicker frequencies were used, as in Experiment 3: 0 (no flicker), 2, and 15 Hz. The largest eccentricity from Experiment 3 of 6° was used since this produced the strongest effects.

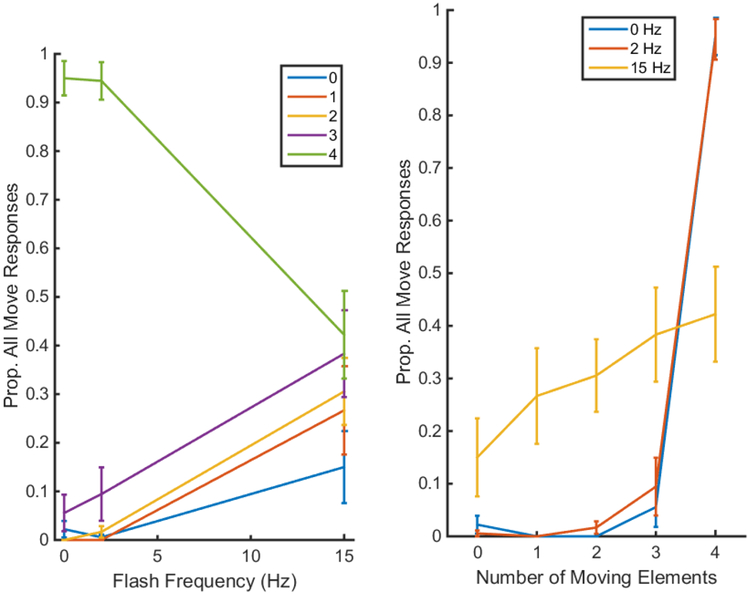
Results and Discussion

The results of Experiment 4 are shown in Figure 5. The data are displayed in two ways: as a function of flash frequency (left panel) and as a function of the number of moving circles. In both cases, the y-axis shows the proportion of “all moving” responses. This was the correct response only when all four circles were actually moving. For all other conditions, this was the incorrect response. The data were submitted to a 3 (flicker frequency) × 5 (number of moving circles) repeated-measures ANOVA. There was a main effect of element number (F(1.97,15.73) = 171.0, p<0.001, η_p²=0.955) and an interaction between element number and flicker frequency (F(2.53,20.23) = 58.90, p<0.001, η_p²=0.880), but there was no main effect of flicker frequency (F(1.02,8.12) = 1.51, p=0.254, η_p²=0.159).

Figure 5.

Left: Proportion of “all moving” responses as a function of flash frequency and total number of moving circles: 0 – blue, 1 – red, 2 – yellow, 3 – purple, and 4 – green. Right: the same data, but now with the number of moving circles on the x-axis and different lines representing the different flash frequencies: 0 Hz – blue, 2 Hz – red, 15 Hz – yellow. Error bars are standard errors.

Looking at the left panel, several interesting patterns emerge. First, when the circles were all moving and not flickering, observers were able to do the task very well, correctly identifying them as all moving 95% of the time and having a similar accuracy when fewer than four circles were moving (<5% being reported as all moving). As the flicker rate increased, the proportion of the time that all four actually moving circles were seen as moving decreased, to an average response rate of 42% at 15 Hz, while the proportion of time that fewer than four circles were perceived to all be moving at 15 Hz increased. At 15 Hz, the more circles that were moving (indicated by the differently colored lines), the more likely the observer was to respond that all four were moving. Interestingly, even when none of the circles were moving (blue line), but were flickering at 15 Hz, 15% of the time observers still said that all four were moving! This replicates the results from Experiment 3 with a single stationary circle. Most important was the observation that three moving and one stationary circle (purple line) appeared to all be moving as often (38%) as four moving circles (green line; Wilcoxon signed rank test, p=0.328). That is, for the condition that was used in Experiment 1, the stationary circle appeared to be moving. This indicates that FLIM is a contributing factor to the observed flicker-rate decrease in performance observed in Experiment 1.

Even more pronounced is the fact that in the four-moving circle 15 Hz condition, observers only reported seeing all four circles move on average 42% of the time. This is a striking demonstration of flicker induced motion suppression (FLIMS). However, if motion suppression was the only factor affecting perception in these displays, then the condition with three moving and one stationary circle should have sometimes appeared as two or fewer moving circles and therefore the proportion of “all moving” responses would have been even lower than when all were moving. Because the proportion of “all moving” responses were similar for the two conditions, a flicker-induced motion (FLIM) effect must also have contributed.

Of note is the observation that at 15 Hz, as the number of moving circles increases, the likelihood of reporting “all-moving” also increases. This can be readily observed in the right panel of Figure 5, which replots the data, showing the proportion of “all moving” responses as a function of the number of elements instead of flicker frequency. On the one hand, this is not surprising because a display with three moving circles is more similar to a display with four moving circles than a display with just one moving circle. On the other hand, this pattern of results suggests that the FLIM and FLIMS effects are not independently additive. If FLIM applied to each circle independently, then based on the results of Experiment 3, at 15 Hz, there would be a 10% chance that each stationary circle would appear to move. This would thus predict a response rate of 10% in the 3 moving circle condition, 1% in the 2 moving circle condition, 0.1% in the 1 moving circle rate and 0.01% in the 0 moving circle condition. Obviously, the observed rate of seeing ‘all moving’ greatly exceeds these predictions. As more moving elements are added, the more likely the remaining stationary circles are to appear to be moving. One interpretation of this is that global motion signals are spread across the synchronously flickering objects in the display. Because this only occurred at high flicker rates, we refer to this as flicker-induced induced motion (FLIIM).

General Discussion

The experiments presented in this paper set out to characterize the stimulus properties that affected the perception of illusory motion in a variant of the Wandering Circles illusion (Blair et al., 2014, submitted). We found that stationary circles that flickered at a rate of at least 6 Hz were perceived to be moving. This effect was stronger in the periphery and also occurred for red-green isoluminant color changes (Experiments 1 and 2). In Experiment 3, we showed that the empirical results obtained in Experiment 1 and 2 arise from distinct perceptual effects. First, a single, stationary, flickering circle will sometimes appear to move; this is flicker-induced motion (FLIM). Second, a moving, flickering circle will sometimes appear stationary; this is flicker-induced motion suppression (FLIMS). In Experiment 4, observers reported that displays that contained three moving and one stationary circle appeared to have four moving circles as often as when they were actually shown four moving circles. That is, difficulty in identifying which of four circles was actually stationary in Experiments 1 and 2 was not due solely to FLIMS, but also to FLIM. Importantly, the more circles that were moving in Experiment 4, the more likely observers were to say that all four circles were moving, suggesting that motion in many areas of a display spread to other regions that were flickering in synchrony; this is flicker-induced induced motion (FLIIM). This latter effect further distinguishes the current displays from the Wandering Circles illusion, in which all objects are stationary. Another distinguishing factor is that FLIIM can be seen from filled-in circles with crisp edges that undergo contrast polarity reversals; the Wandering Circles illusion, in contrast, is very weak with such stimuli and is best observed with “Cornsweet” circles. Below, we consider each of the three effects, FLIM, FLIMS, and FLIIM in turn.

Flicker-Induced Motion (FLIM)

FLIM reveals an interesting interaction between flicker, position, and motion perception. Flicker creates large omni-directional motion signals at the boundaries of the circles. In the image, these motion signals cancel out for stationary circles, resulting in net zero motion. Nevertheless, these circles are perceived to be moving, suggesting that somewhere in the visual system, there is still some net directional motion energy. There are several possible mechanisms for how this may arise. Greater positional uncertainty in the periphery may cause sequentially presented circles to be represented in overlapping, but not perfectly matching spatial locations (Levi & Klein, 1990; Westheimer, 1982). Bocianski, Müsseler, and Erlhagen (2008) found that successively flashed targets are indeed mislocalized in the periphery and that the effects are stronger when attention is divided across multiple objects, as in our study (Bocianski, Müsseler, & Erlhagen, 2010). Because the circles are changing in contrast polarity, a black circle in one position followed by a white circle in an apparently nearby position could produce a second-order motion signal, which would result in FLIM (Cavanagh & Mather, 1989; Chubb & Sperling, 1989). However, a purely second-order-motion-based account would need to account for the fact that some second-order motion is suppressed or impaired in the periphery (Pantle, 1992; Smith, Hess, & Baker, 1994; Zanker 1992) and that second-order motion mechanisms are somewhat insensitive to temporal frequency (Seiffert & Cavanagh, 1998), while FLIM only occurs at higher flicker frequencies.

Perceived motion in a stationary pattern can also occur following adaptation to dynamic noise (Murakami & Cavanagh, 1998, 2001). The effect can be produced with a center-surround configuration in which either the center or the surround is dynamic, while the other is static. Following adaptation, the un-adapted region of a static test pattern appears to move, while the adapted region – where the dynamic pattern was shown – appears static. This aftereffect gradually fades after several seconds. If the adapting stimulus consists of a dynamically changing background and several disconnected static regions, then, following adaptation, the static, un-adapted regions will all appear to move coherently, suggesting that the effect may be due to eye movements. In contrast, FLIM can occur for a single, stationary circle, with no positional motion in the image and does not fade with prolonged viewing, indicating that the effect is not due to adaptation. Most importantly, however, as in the Wandering Circles illusion, when there are multiple flickering, stationary objects, all can appear to move in different random directions, suggesting that the effect is not entirely due to eye movements.

Illusory motion can also occur “on-line”, without adaptation, by having a static central region surrounded by a flickering annular region (Murakami, 2003). The static region appears to move, but the flickering region appears stationary. Unlike the displays used to produce the motion aftereffect described above, there is no dynamic noise in this stimulus. Another difference is that the spatial configuration of this on-line motion stimulus is important – if the flickering and static regions are placed side-by-side, no illusory jitter is seen (Park, Bedggood, Metha, & Anderson, 2017). Furthermore, as with other flickering stimuli, the flicker suppresses motion perception within the flickering region. In our displays, the entire object was flickering; the only non-flickering region was the background. It is in theory possible that in the experiments described in this manuscript the flicker of the circles made the background appear to move, which in turn made the circles appear to move relative to it. However, the background covered the entire screen and therefore would have been perceived to move in one direction and therefore all of the circles would also have been perceived to move coherently, but that was not the case. Finally, we note that there are a number of other illusions in which motion can be perceived from stationary patterns, both with and without eye- and head-motion. A list of many of these can be found in Kitaoka and Ashida (2007). Motion aftereffects can also result from implied motion in stationary images (Winawer, Huk, & Boroditsky, 2008). In FLIM, however, no illusory motion or induced motion occurs when the circles are static and not flickering.

Flicker-Induced Motion Suppression (FLIMS)

In Experiment 3, we found that moving, flickering circles were often perceived as stationary. This is in agreement with previous work that found reduced motion detection thresholds for high-contrast flickering stimuli in the periphery (Bedell & Johnson, 1995). The same mechanism that produces FLIM in stationary circles may account for suppression of motion in moving circles. Omni-directional motion signals generated by high-contrast flicker may swamp out any local real signals, especially since the motion is not coherent across frames since the circles physically move in random directions.

Flicker-induced motion suppression can also occur when many moving dots undergo color or size changes (Churan & Ilg, 2002; Peirce, 2013). This is the converse of Motion-Silencing, a particularly compelling effect in which the rate of luminance, size, or color changes of moving dots appears to be slower than it is (Suchow & Alvarez, 2011). One possible source of silencing in both versions of the effect may be crowding (Turi & Burr, 2013). In our experiments, however, there were only four large circles that were far apart. FLIMS also increased with eccentricity where crowding would be weaker. An alternative explanation of motion silencing is that flicker is misattributed as a motion signal when real motion is present (Choi, Bovik, & Cormack, 2014, 2016). This was used to explain why the perception of flicker might be silenced or reduced, but it might also explain why motion is suppressed in the same stimulus (Peirce, 2013). These phenomena are described by a standard motion energy model (Adelson & Bergen, 1985) which would need to be extended to account for FLIMS under isoluminant changes in Experiment 2.

Similar flicker-induced motion interference effects have been observed in visual temporal order judgments (Cass & Van der Burg, 2014; Talbot, Van der Burg, & Cass, 2017). The perception of which of two dots was first to reverse polarity can be disrupted when surrounded by flickering, dynamic distractors. This “remote temporal camouflage” effect does not occur cross-modally (i.e. if the task is to say whether a sound was played first or whether a dot changed color first). One explanation that is very similar to what we propose here is that long-range apparent motion signals created by the sequential polarity reversals of the target dots are disrupted or suppressed by additional motion signals, dampening the signal-to-noise ratio. Extraneous motion can also impact the recovery of spatiotemporally defined surfaces that depend on local motion signals to recover shape boundaries (Cunningham, Shipley, & Kellman, 1998; Shipley & Kellman, 1997).

Flicker-induced motion suppression is also consistent with interaction between multiple temporal channels in the visual system (Anderson & Burr, 1985; Cass & Alais, 2006; Hess & Snowden, 1992). A mask flickering at frequencies greater than 6Hz suppresses the perception of an overlapped target which is flickering at a lower frequency (1 Hz), but not vice versa (Cass & Alais, 2006). This asymmetry in temporal frequency masking may play a role in motion deblurring: high frequency inhibition of lower frequency signals reduces the amount of smearing and sharpens the signal of longer duration motion stimuli (Burr & Morgan, 1997). Consistent with this account, in Experiments 1 and 2, the ability to detect a slowly moving, flickering stimulus begins to deteriorate at flicker rates of about 6 Hz. This may be the first demonstration of such low-frequency motion suppression in an actually moving stimulus as other studies typically use stationary, overlapping mask stimuli.³

Flicker-Induced Induced Motion (FLIIM)

The more moving circles there were in the displays in Experiment 4, the more likely that all of them were to be perceived as moving. This effect may be related to the grouping of spatially distant image regions by temporal synchrony (Alais, Blake & Lee 1998; Lee & Blake, 1999; Sekuler & Bennet 2001; Usher & Donnelly 1998). We did not explore whether the stationary and moving objects had to flicker at the same frequency or not – in all experiments, objects flickered in phase. Nor did we explore whether induced motion could occur if only the stationary object was flickering, or if only the moving objects were flickering, or if none of the objects were flickering, but the background was. These stimulus parameters are a fruitful area for future research.

Summary

The flicker-motion interaction effects revealed in our experiments and the Wandering Circles illusion can be informative for traditional models of motion perception that analyze the motion energy in an image (e.g. Adelson & Bergen, 1985). Stationary, flickering circles produce no net directional motion energy: contrast polarity or color reversals at the object boundary create uniform motion signals in all directions. Nevertheless, they are perceived to be moving in random directions. One possible explanation for the effects could be the addition of internal noise. Random amounts of noise added to different units with sensitivities for different motion directions could tip the balance in favor of one direction over another. If the noise added to the input motion signal is random and changing over time, this could cause the circles to appear to continuously move in new directions, accounting for the wandering-motion percept, as opposed to a continuous drift in a single direction. The independent motion of the circles could be explained by the noise being added locally and early on during visual processing. In contrast, if motion energy was first computed across the entire visual field and then a single noise signal was added uniformly across the entire visual field, then all of the circles would appear to move in the same direction.

There are several other sources of information that could manifest as ‘noise’ and contribute to the seemingly random direction of motion. For example, subtle heterogeneities in motion sensitivity and directional turning across the visual field (Born & Bradley, 2005) could lead a no-net-directional-motion stimulus to have net-directional motion in the brain. Combined with non-constant rates of adaptation, the resultant motion-percept would be expected to be dynamically changing and potentially seem random. Our data suggest that another source of information comes from nearby moving objects and is consistent with motion interference effects observed in similar paradigms (e.g. Cass & Van der Burg, 2014). FLIIM describes the effect of distant moving objects having an effect on the perceived motion of a stationary object. Such long-range contextual effects are currently not commonly incorporated in motion models. As indicated above, such effects remain largely unexplored, and may be influenced by such factors as uniformity of motion, amount of motion, distance between the objects, similarity between the objects, etc. For example, if the moving object was a triangle, perhaps its motion would be less likely to “spread” to circles than to other triangles. Another possibility is that the addition of more identical objects makes the entire set of objects appear more like a texture or separate surface that lies on top of a background, and therefore more likely to be grouped together and share properties. Such factors may speak to intermediate- and higher-level interactions between motion and form and scene processing.