Human social motor solutions for human–machine interaction in dynamical task contexts

Significance

Human–machine interaction (HMI) is becoming ubiquitous within today’s society due to rapid advances in interactive virtual and robotic technologies. Ensuring the real-time coordination necessary for effective HMI, however, requires both identifying the dynamics of natural human multiagent performance and formally modeling those dynamics in ways that can be incorporated into the control structure of artificial agents. Here, we used a dyadic shepherding task to demonstrate that the dynamics of complex human multiagent activity cannot only be effectively modeled by means of simple, environmentally coupled dynamical motor primitives but that such models can be easily incorporated into the control structure of artificial agents to achieve robust, human-level HMI performance.

Abstract

Multiagent activity is commonplace in everyday life and can improve the behavioral efficiency of task performance and learning. Thus, augmenting social contexts with the use of interactive virtual and robotic agents is of great interest across health, sport, and industry domains. However, the effectiveness of human–machine interaction (HMI) to effectively train humans for future social encounters depends on the ability of artificial agents to respond to human coactors in a natural, human-like manner. One way to achieve effective HMI is by developing dynamical models utilizing dynamical motor primitives (DMPs) of human multiagent coordination that not only capture the behavioral dynamics of successful human performance but also, provide a tractable control architecture for computerized agents. Previous research has demonstrated how DMPs can successfully capture human-like dynamics of simple nonsocial, single-actor movements. However, it is unclear whether DMPs can be used to model more complex multiagent task scenarios. This study tested this human-centered approach to HMI using a complex dyadic shepherding task, in which pairs of coacting agents had to work together to corral and contain small herds of virtual sheep. Human–human and human–artificial agent dyads were tested across two different task contexts. The results revealed (i) that the performance of human–human dyads was equivalent to those composed of a human and the artificial agent and (ii) that, using a “Turing-like” methodology, most participants in the HMI condition were unaware that they were working alongside an artificial agent, further validating the isomorphism of human and artificial agent behavior.

Many human behaviors are performed in a social setting and involve multiple agents coordinating their actions to achieve a shared task goal. Such multiagent coordination occurs when two or more individuals move heavy furniture up a flight of stairs, when family members work together to catch an escaped pet, or when teammates perform an offensive attack against an opposing team in football or rugby. Indeed, multiagent coordination is a ubiquitous part of everyday life that not only fosters new and more efficient modes of behavioral activity but also, plays a fundamental role in human perceptual motor development and learning as well as human social functioning more generally (1–6).

Due to rapid advancements in interactive virtual reality (VR) and robotics technologies, opportunities for the inclusion of artificial agents in multiagent contexts is also rapidly increasing within today’s society [i.e., human–machine interaction (HMI)]. The potential applications of HMI include behavioral expertise training and perceptual motor rehabilitation (7, 8), enhancing prosocial functioning in children with social deficit disorders (9), and assisting the elderly and individuals with disabilities with daily life activities (10, 11). Like effective human–human interaction, the effectiveness of HMI systems within these contexts depends on the ability of artificial agents to respond and adapt to the movements and actions of human coactors in a natural and seamless manner (12–17). One approach to ensuring the kind of robust HMI required to achieve and enhance real-world task outcomes is to identify and model the embedded perceptual motor coordination processes or task/behavioral dynamics that define adaptive human multiagent task activity (18–22).

Unfortunately, the body of research aimed at formally modeling the dynamics of goal-directed multiagent perceptual motor activity for HMI applications remains rather small (13, 23–25). This is due, in part, to the assumed complexity of such behavior (i.e., the high dimensionality of the possible perceptual motor control solutions that can define a given multiagent environment task scenario) (26, 27). In contrast to this assumption, however, there is now a growing body of research within the biological, motor control, and cognitive sciences that has revealed that a large number of goal-directed human perceptual motor behaviors are constituted by just two fundamental movement types (28–30): discrete movements, such as when one reaches for an object or target location, taps a piano key, or throws a dart; and rhythmic movements, such as when one walks, waves a hand, or hammers a nail.

The collective implication of this previous work is that the task/behavioral dynamics of human perceptual motor behavior, including coordinated multiagent activity (31), can often be modeled by composing the elemental behaviors of two basic types of dynamical systems, namely point attractors [for modeling discrete movements or actions (20, 32–34)] and limit cycles [for modeling rhythmic movements or actions (35–38)]. The general hypothesis is that, given the right generative formulation and interagent or environmental coupling terms, the spatiotemporal patterning of a large number of human end effector or multijoint limb movements can be modeled using these dynamical motor primitives (DMPs) (22). Consistent with this latter hypothesis, these DMPs have been used to model a wide range of human actions [e.g., reaching, cranking, waving, drumming, racket swinging, obstacle avoidance, route navigation (20, 39–41)], including several dyadic social motor behaviors (18, 19, 42).

Relatedly, low-dimensional dynamical systems composed of point attractor and limit cycle primitives are hypothesized to be a suitable control architecture for embodied artificial agents to produce “human-like” behavior. At the level of individual (nonsocial) action, Ijspeert et al. (29, 39) have provided preliminary support for this hypothesis, demonstrating how task-specific models composed of point attractor and limit cycle dynamical primitives can be used to generate human-like reaching, obstacle avoidance, drumming, and racket-swinging behavior in simulated virtual end effector systems or multijoint robotic arms. A dyadic interpersonal rhythmic coordination task (43) demonstrated how a virtual avatar embodying a coordinative model capable of mirroring discrete finger flexion extensions as well as rhythmic, oscillatory behavior reproduced the same stable behaviors seen in the interpersonal behavioral synchrony literature (18, 44–47). Furthermore, this virtual avatar was capable of steering novices to adopt difficult to produce coordinative patterns (23). Moreover, some participants attributed agency to the virtual avatar, providing preliminary support for the effectiveness of such models to produce human-like behavior when appropriately coupled to other human coactors (43, 48).

DMPs for Complex Multiagent Tasks: A Shepherding Example

Previous research modeling and designing artificial systems utilizing DMPs has focused on either nonsocial or minimally goal-directed task contexts (although refs. 42 and 49 discuss modeling more complex task contexts). The aim of this work was to expand the feasibility of DMPs for HMI by demonstrating the effectiveness of such an approach within the context of a complex, goal-directed multiagent task. An excellent paradigmatic example of multiagent activity found in several species is group corralling and containment, which is oftentimes seen in animal shepherding and hunting behavior (50–52). Such shepherding and containment behavior require the coordination of multiple coactors to control a dynamically changing environment (e.g., the containment of herds of animals or fleeing prey). To solve the task, coactors must divide the task space appropriately and switch between multiple behaviors depending on changing environmental states (e.g., transitioning between prey pursuit and herd containment). Such behavior is not only necessary for the survival of certain predators but has applications in robotic crowd control, security, and environment hazard containment systems (52–55). Furthermore, parallels can be made to other human group behaviors, such as military and team sports performance that requires problem solving and decision making among multiple actors.

Human dyadic shepherding has been recently investigated as a paradigmatic example of complex goal-directed dyadic coordination in our previous work (19). Inspired by previous work utilizing a single-player object control task (56), the shepherding task required human dyads, standing on opposite sides of a game field projected on a tabletop display, to cooperatively herd, corral, and contain simulated “sheep” agents (rolling brown spheres) within a predefined target region (the red circles in Fig. 1 A and B). The participants controlled virtual “sheepdogs” (blue and orange cubes in Fig. 1 A and B) using a handheld motion sensor. Sheep movement entailed both stochastic and deterministic qualities. When left undisturbed, each sheep would exhibit Brownian motion, randomly rolling around the game field. However, when a participant’s hand/sheepdog came within a specific distance of the sheep, the sheep would react by moving in the opposite direction, away from the participant’s hand/sheepdog location. The level of task difficulty was manipulated by changing herd size (i.e., three, five, or seven sheep), with participants given the task goal of keeping the sheep within the target region for as long as possible during 1-min trials. A successful trial was deemed to have occurred if participants were able to contain the sheep for 70% of the last 45 s of each trial (i.e., 31.5 s within the last 45 s). Finally, task failure was also deemed to occur (and trials ended early) if any one sheep reached the outer fence of the game field or if all sheep moved too far outside the target region (where “too far” was defined as beyond the outside perimeter of the light gray annulus surrounding the target region in Fig. 1 A and B).

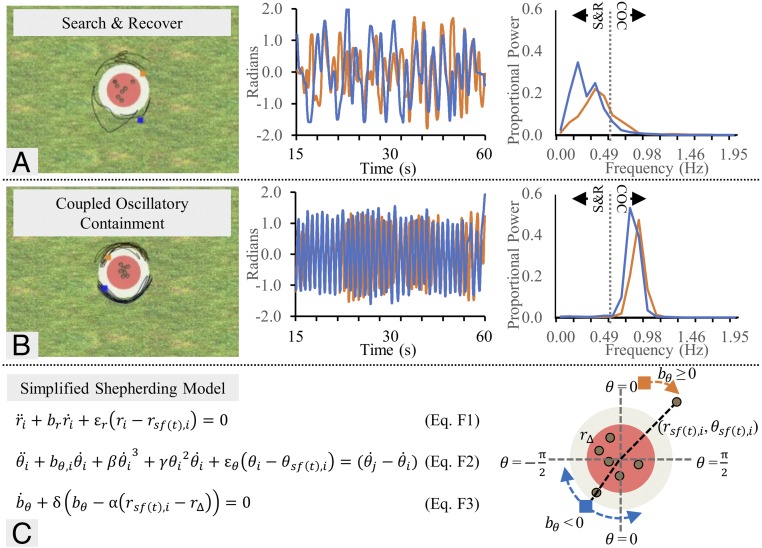
Fig. 1.

Observed behaviors and simplified model for the multiagent shepherding task. (A and B) Depiction of successful S&R and COC (Left). The black line trajectory indicates the previous 5 s of behavior. Timeseries during one successful trial of each angular component of the participant’s position (Center) and corresponding power spectra (Right), with a 0.5-Hz frequency boundary used to distinguish between S&R and COC behavioral modes. (C) Simplified shepherding model developed to describe behavior seen in ref. 19) (Materials and Methods has the more detailed model equations used for this study). Eq. F1 is a linear damped mass spring equation that reduces the difference between agent i’s current radial distance, $r_i$, to the radial distance, $r_{sf\left(t\right),i}$, of the farthest sheep on agent i’s one-half of the game field at time t plus a fixed distance, $r_{\min }$, to ensure repulsion toward the center. Eq. F2, excluding, $\beta {\dot{\theta }}_i^3+\gamma {\theta }_i^2\dot{{\theta }_i}$, is identical to Eq. F1 but for the control of agent i’s angular movement, ${\theta }_i$. The inclusion of the terms $\beta {\dot{\theta }}_i^3+\gamma {\theta }_i^2\dot{{\theta }_i}$ convert the linear damped mass spring to a nonlinear system with behavior that can exhibit both point attractor dynamics (akin to Eq. F1) when $b_{\theta i}>0$ and limit cycle dynamics when $b_{\theta i}\le 0$ (the blue agent in C, Right). The dissipative coupling function on the right side of Eq. F2 ensures oscillatory synchronization between agent i and partner j. Eq. F3 is a parameter-dynamic function that determines the value of parameter $b_{\theta i}$, such that $b_{\theta i}$ will be attracted to a value that is less than or equal to zero when the radial distance of agent i’s farthest sheep $r_{sf\left(t\right),i}\le r_{\mathrm{\Delta }}$. Materials and Methods has more details, including human- and task-specific modifications for the experiments presented in this paper.

Initially, all dyads adopted a search and recover (S&R) mode of behavior, which involved each participant discretely moving toward and herding the sheep farthest from the target region on their side of the game field. After varying lengths of game play, however, a small subset of dyads spontaneously discovered a second and more effective mode of behavior termed coupled oscillatory containment (COC). This mode of behavior involved both participants in a dyad moving in a rhythmic, semicircular manner around the sheep, essentially forming a virtual wall around the herd (Fig. 1 A and B has depictions of S&R and COC behavior, respectively). Consistent with the dynamic stabilities of intra-/interpersonal rhythmic interlimb coordination (35, 44, 57), dyads exhibited both in-phase (0°) and antiphase (180°) patterns of COC coordination. In addition to COC behavior resulting in higher containment times and better herd control (i.e., less herd spread) compared with S&R behavior, COC was also more likely to be discovered and adopted by dyads as task difficulty increased (i.e., as herd size increased). In other words, the less effective dyads were at herding the sheep via the S&R mode of behavior, the more likely they were to spontaneously discover COC behavior. In fact, the discovery of COC behavior was equated to a kind of “eureka” or sudden insight moment for participants, with those dyads that discovered COC behavior achieving nearly 100% containment success after its discovery.

Both S&R and COC behaviors reflect task-specific realizations of environmentally coupled point attractor and limit cycle dynamics. This is illustrated in Fig. 1C, where the system equations (Eqs. F1–F3 in Fig. 1C) for the time-evolving end effector movements of each ith agent’s hand/sheepdog (where i = 1–2) are defined in polar coordinates with respect to the center of the target containment region, $\left(r_i,{\theta }_i\right)=\left(\mathrm{0,0}\right)$. As a generalizable model of two-agent S&R and COC shepherding behavior (Materials and Methods has experiment-/task-specific adaptions and expanded description), a discrete or point attractor damped mass spring equation (Eq. F1 in Fig. 1C) is used to define an agent’s radial distance from the center of the game field, and a nonlinear hybrid system, capable of both discrete (point attractor) and rhythmic (limit cycle) behavior (Eq. F2 in Fig. 1C) (ref. 36 has details), is used to define an agent’s polar angle dynamics. Note that, during agent i’s S&R behavior, the sheep farthest from the center of the game field at time t [denoted by the subscript sf(t),i] on that agent’s side of the field defines the target location (i.e., attractor location) of the sheep in both Eq. F1 in Fig. 1C (radial target coordinate, where distance $r_{\min }$ is the agent’s preferred minimum distance away from the sheep, ensuring repulsion of the sheep toward the target region) and Eq. F2 in Fig. 1C (polar angle coordinate). That is, each agent is coupled to the movements of the farthest sheep on their side of the field. The agents are also coupled to each other via a dissipative coupling function in Eq. F2 in Fig. 1C. This interagent coupling (44, 45) ensures stable in-phase synchronization during COC behavior and reflects the natural behavioral synchrony phenomena commonly observed between interacting agents more generally (ref. 47 has a review). Key to the differential enactment of S&R vs. COC behavior, however, is $b_{\theta i}$ (the parameter of the linear damping term in Eq. F2 in Fig. 1C), which is modulated by the radial distance of an agent’s “farthest sheep”: r_sf(t),i (Eq. F3 in Fig. 1C). In short, when agent i’s farthest sheep is outside the target region, $b_{\theta i}$ ≥ 0, agent i’s polar angle, ${\theta }_i$, is simply attracted to the angular position of the farthest sheep [${\theta }_{sf\left(t\right),i}$]$.$ Hence, when $b_{\theta i}$ ≥ 0, agent i exhibits S&R-type behavior. However, when agent i’s farthest sheep is corralled inside the target containment region, the value of $b_{\theta i}$ changes from positive to negative, and a Hopf bifurcation* occurs, such that, for $b_{\theta i}$ < 0, agent i’s polar angle dynamics are defined by limit cycle behavior. Accordingly, when both agent’s sheep are within the containment region, COC behavior results.

This Study

Across two experiments, this study tested whether low-dimensional models consisting of fixed point and limit cycle DMPs can, when embodied in the control architecture of a virtual avatar working alongside human novices, achieve robust HMI in more complex, goal-directed multiagent task contexts—in this case, within the context of a dyadic shepherding task (19). These experiments compared novice human participants completing the dyadic shepherding task with either another human coactor or a virtual artificial agent whose end effector movements were controlled by task-specific relations of the shepherding model detailed in Fig. 1C (again, Materials and Methods has details about the task-specific modifications). Pursuant to the primary aim, the study sought to determine whether novice participants, when working with the artificial agent, can learn to adopt and maintain COC behavior in a way comparable with human–human COC discoverers as an efficient means to complete the shepherding task. Furthermore, the study sought to determine whether interacting with the artificial agent is perceived as natural by assessing participant believability that their partner was a human coactor.

For experiment 1, the same tabletop shepherding task used by Nalepka et al. (19) was used. However, in contrast to Nalepka et al. (19), participants completed the task within a fully immersive VR environment. Participants viewed the shepherding task environment from a first-person perspective via an Oculus Rift head-mounted display and completed the task by controlling the end effector movements of a humanoid crash test dummy avatar using a handheld motion sensor. A participant’s coactor was also represented as a humanoid crash test dummy avatar (Fig. 2A). To validate this VR setup, we first instructed dyads of novice participants to complete the VR shepherding task together (experiment 1a), with the expectation that these novice dyads would exhibit the same (i.e., replicate) behavioral dynamics observed by Nalepka et al. (19). After this, experiment 1b compared the behavioral dynamics and performance of novices who completed the shepherding task together with the artificial agent (i.e., the model-controlled crash test dummy) with those who worked together with an expert confederate participant. For both conditions, the confederate posed as a naïve participant who sat beside participants in the waiting area. Participants were taken to one room, while the confederate (who participants were told would be their partner) was taken to an adjacent laboratory. Participants were not allowed to verbally communicate with each other (in any condition), and for both the artificial agent and confederate conditions (experiment 1b), participants were told that their partner would complete the task remotely from an adjacent laboratory. Accordingly, during a postexperiment funnel debriefing session (61), we also assessed whether the novice participants remained in belief that they were working with a human during the experiment or if there was suspicion that they were working alongside an artificial agent (a Turing-like test).

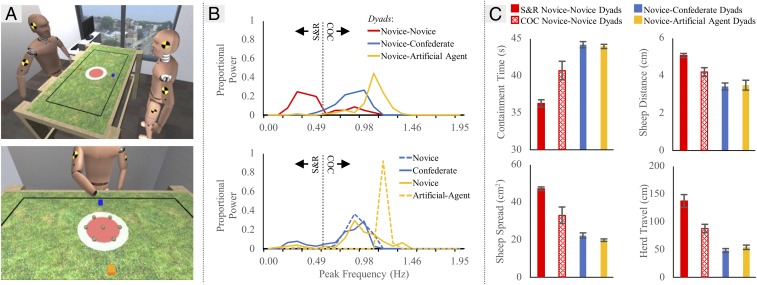
Fig. 2.

Experiment 1 setup, behaviors, and results. (A) Depiction of the shepherding task used in experiment 1 modeled after the experimental room in which testing took place (19) (Upper). First-person perspective of the shepherding task with initial sheep (modeled as spheres) arrangement (Lower). The sheepdogs (orange and blue cubes) were controlled via the movements of a handheld motion sensor on a tabletop of similar dimension. The goal was to contain the sheep within the red target region. (B, Upper) Average power spectra across participants in each dyad type (novice–novice in experiment 1a; novice–confederate and novice–artificial agent in experiment 1b) calculated from the last 45 s of all successful trials. (B, Lower) Average power spectra of each participant type in the novice–confederate and novice–artificial agent conditions. (C) Shepherding performance metrics for successful trials across behavioral mode and condition: S&R novice–novice dyads—dyads that only exhibited successful S&R behavior; COC novice–novice dyads—performance during COC-classified trials from dyads that discovered COC behavior; and novice–confederate and novice–artificial agent dyads—performance during successful COC-classified trials from dyads in both conditions. Performance metrics were containment time—the amount of time (seconds) that all sheep were contained within the red target region; sheep distance—the mean sheep distance from the center of the target region; herd spread—the average herd spread (centimeters squared) measured by computing the convex hull formed by all of the sheep (the convex hull is defined by the smallest convex polygon that can encompass an entire set of objects, like a rubber band placed over a set of pegs); and herd travel—defined as the cumulative distance (centimeters) that the herd’s COM moved during the trial. The herd’s COM was computed by taking the mean sheep’s position. Error bars represent SE.

For experiment 2, novice–novice and novice–artificial agent dyads completed a less constrained version of the shepherding task, in which all of the sheep (now scattered randomly across the game field) still needed to be herded together in the same region but the location of this region was not specified (i.e., participants were free to self-choose where they herded the sheep). In addition to further validating whether the proposed shepherding model could be used for robust HMI, this second experiment also provided a test of whether S&R and COC modes of behavior generalized across different, less constrained task contexts.

For both experiments, testing lasted for a maximum of 45 min or until a dyad performed eight successful trials. For experiment 1, a trial was considered successful if a dyad was able to contain the herd within the target region at the center of the game field for 70% of the last 45 s of each 1-min trial (i.e., 31.5 s within the last 45 s). Trials ended early (with no score) if any one sheep reached the bordering fence or if all sheep dispersed too far from the center (Materials and Methods has more details). For experiment 2, a trial was considered successful if a dyad was able to contain the herd within a similar area to experiment 1—but could do so anywhere within the game field for 70% of the last 45 s of each 2-min trial. Trials were 2 min in length to allow extra time for participants to collect the sheep, which (unlike experiment 1) were randomly scattered throughout the task environment. Because no containment region was visible in experiment 2, participants received visual feedback when the sheep were considered adequately contained (i.e., the color of the sheep turned from brown to red). A video summarizing the behaviors observed in experiments 1 and 2 as well as a web-based, interactive demonstration version of the experimental task and artificial agent behavior can be found at https://github.com/MultiagentDynamics/Human-Machine-Shepherding/.

Results

Experiment 1a.

Fifteen novice–novice dyads were recruited to complete the shepherding task in the VR environment with the centrally located target region specified (Fig. 2A). Overall, the behavioral dynamics exhibited by these novice–novice dyads replicated the findings of Nalepka et al. (19). All dyads initially adopted the S&R mode of behavior, but not all were able to successfully complete the task, with only nine (60%) of dyads reaching eight successful containment attempts within the 45-min testing period (M = 29.06 min needed, SD = 6.89). Importantly, a small subset of successful dyads (n = 3) discovered and transitioned to COC behavior over the course of experimental testing (M = 7 COC trials of 8, SD = 1.73). In such trials, a dyad’s behavior was classified as COC when both participants exhibited a spectral peak ≥0.5 Hz (M = 0.77 Hz, SD = 0.12) (19) (Materials and Methods has more details). As observed in Nalepka et al. (19), nearly all COC behavior was constrained to a stable in-phase (0°) or antiphase (180°) pattern of coordination, with only one COC-classified trial exhibiting no stable relative-phase relationship. Finally, shepherding performance was superior for COC behavior compared with S&R behavior (Fig. 2C). That is, the novice–novice dyads that adopted COC behavior were able to contain the sheep for a greater period (containment time P = 0.004, d = 2.56), which was the explicit task goal, as well as keep the sheep closer to the center of the containment region (sheep distance P = 0.005, d = 2.63) and minimize the overall movement of the herd (herd travel P = 0.03, d = 2.25).

Experiment 1b.

Eleven participants completed the virtual shepherding task together with the coacting virtual avatar whose end effector movements were artificially (model) controlled. Another 10 participants completed the virtual shepherding task together with the coacting virtual avatar who was controlled by the expert human–confederate. As expected, the results demonstrated that novices were able to successfully complete the shepherding task together with the artificial agent, including learning to use COC behavior, and reached performance levels equivalent to those exhibited by novice–confederate dyads. More specifically, 20 of 21 dyads (95.23%) achieved task success—completing eight successful herding trials within the 45-min testing period—with all novice participants utilizing COC behavior for at least one-half of all successful trials (M = 6.90 trials, SD = 1.25). Furthermore, although the lone dyad that did not achieve eight successful trials was in the novice–artificial agent condition, the dyad obtained two successful trials during the 45-min period—one of which the novice performed COC-classified behavior.

With respect to task performance, dyads in both the artificial agent and confederate conditions reached success in a similar amount of time (confederate: M = 8.62 min, SD = 1.63; artificial agent: M = 9.32 min, SD = 1.16; P = 0.29, d = 0.49). Moreover, novices who completed the task with the artificial agent also achieved levels of herding performance (i.e., herd containment time, sheep distance from the center, herd spread, and herd travel) equivalent to those novices who completed the task with the confederate (all P ≥ 0.15). The equivalence of novice–confederate and novice–artificial agent performance compared with novice–novice performance can be discerned from an inspection of Fig. 2C.

Finally, during the postexperiment debriefing session, seven (63.64%) of novices who completed the task with the artificial agent thought that they were completing the task together with a human and did not note anything odd in their partner’s behavior. The remaining four (36.36%) novices indicated that they suspected that their partner may not have been human (i.e., computer driven). Common statements from these latter participants were “my partner moved too quickly” and “I didn’t understand why they worked harder than they had to.” Interestingly, one novice who completed the task with the confederate thought at times that the behavior was “computer like.”

The statements regarding the artificial agent moving “too quickly” (Fig. 2B) were due to the artificial agent having a greater peak oscillatory frequency (M = 1.18 Hz, SD = 0.01) than the confederate (M = 0.90 Hz, SD = 0.08; P < 0.001, d = 4.82). Likewise, novices completing the task with the artificial agent attempted to frequency match with their partner, as they also exhibited faster oscillatory behavior (M = 0.98 Hz, SD = 0.14) than their peers working with the confederate (M = 0.86 Hz, SD = 0.09; P = 0.04, d = 1.02). Despite attempts to frequency match with the artificial agent, the frequency difference in novice–artificial agent dyads was greater (M = 0.22 Hz difference, SD = 0.11) than those in the novice–confederate condition (M = 0.05 Hz difference, SD = 0.06; P = 0.001, d = 1.87). This resulted in less stable coordinative relative-phase relationships within novice–artificial agent dyads compared with novice–confederate dyads (P = 0.001, d = 2.01)—consistent with past research indicating that incidental/unintentional rhythmic coordination is less likely to occur and is less stable when it does occur as the frequency difference between movements increases (62). It was because of this oscillatory frequency difference that novice–artificial agent dyads had more successful trials that deviated from in-phase/antiphase coordination (M = 4.94 normalized trials, SD = 2.46) than for novice–confederate dyads (M = 0.72 normalized trials, SD = 0.80; Mann–Whitney U = 63, P = 0.001).

It should be noted that, although coupled human–human dyads are typically attracted toward in-phase or antiphase patterns of COC behavior, such stable relative-phase relationships are not essential for task success. Rather, they are simply a natural consequence of the visual informational coupling that constrains the rhythmic movements of interacting individuals to in-phase and antiphase patterns of behavioral coordination (i.e., synchronization) more generally (47). Indeed, task success for COC is due to this behavioral mode creating a spatiotemporal perimeter around the herd, with any interagent relative-phase relationship ensuring task success.

Experiment 2a.

As noted above, the task goal in experiment 2 was for novice–novice and novice–artificial agent dyads to corral all of the sheep together anywhere within the game field. That is, no target region was specified a priori, and dyads were free to self-choose where to contain the sheep. The sheep were considered contained or successfully herded together when they were all within 19.2 cm of each other, consistent with the containment demands in experiment 1. When this happened, the color of the sheep changed from brown to red, providing visual feedback to participants that the sheep had been successfully herded together. At the start of each trial, the sheep were randomly scattered throughout the task environment (Fig. 3A shows an example initial arrangement); again, a trial was considered successful if the herd remained within 19.2 cm of each other for a minimum of 70% of the last 45 s of each 2-min trial.

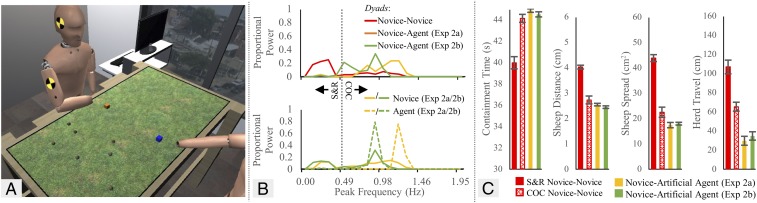
Fig. 3.

Experiment 2 setup, behaviors, and results. (A) Depiction of experiment 2 with an example initial sheep arrangement. Participants were instructed to contain sheep within an area equivalent to the red circle depicted in Fig. 2A centered on the sheep herd’s COM. Participants received visual feedback regarding sufficient containment by changing the sheep’s color to red. (B, Upper) Average power spectra across participants in each dyad type [novice–novice, novice–artificial agent (experiment 2a), and novice–artificial agent (experiment 2b)] calculated from the last 45 s of all successful trials. (B, Lower) Average power spectra of each participant type for the novice–artificial agent condition. (C) Performance metrics across behavioral mode and condition: S&R novice–novice dyads—dyads that only exhibited successful S&R behavior; COC novice–novice dyads—performance during COC-classified trials from dyads that discovered COC behavior; and novice–artificial agent dyads (experiments 2a and 2b)—performance during successful COC-classified trials. Performance metrics were defined as in experiment 1 with the following exceptions: containment time now referred to the amount of time that all sheep were within the 19.2-cm circle centered on the herd’s current COM location, and sheep distance now referred to the mean sheep distance (centimeters) from the herd’s current COM location. Error bars represent SE.

Overall, the participants in experiment 2 exhibited the same behavioral dynamics observed in Nalepka et al. (19) and experiment 1; 13 of 19 (61.90%) novice–novice dyads successfully completed the unconstrained shepherding task (i.e., performed eight successful trials within the 45-min testing period), with a mean completion time of 27.69 min (SD = 7.25). All 13 of the novice participants completing the task with the artificial agent achieved task success and did so in significantly less time than novice–novice dyads (P = 0.002, d = 1.35), with novice–artificial agent dyads having a mean completion time of 19.69 min (SD = 4.23).

With regard to COC discovery, 6 of 13 (46.15%) novice–novice dyads exhibited predominantly COC behavior for at least three successful trials (M = 5.17, SD = 1.72), whereas 12 of 13 (92.31%) novices completing the task with the artificial agent discovered the COC solution (2 dyads had one successful COC trial, and the remaining dyads had ≥4 successful trials; M = 6.00 trials, SD = 2.63). Consistent with experiment 1, dyads that used COC behavior contained the sheep for a longer period than dyads that only adopted S&R behavior while also keeping the sheep closer together and minimizing herd movement (all P < 0.001, d ≥ 2.53).

As in experiment 1, novice–artificial agent dyads were unable to frequency match (M = 0.27 Hz difference, SD = 0.18) to the extent that novice–novice dyads did (M = 0.05 Hz difference, SD = 0.08; P = 0.002, d = 1.63). Similar to experiment 1, this was due to the artificial agent producing a significantly greater peak oscillatory frequency (M = 1.19 Hz, SD = 0.02) compared with novices in the dyad (M = 0.91 Hz, SD = 0.18) (Fig. 3B), who did not differ in the average frequency of novice–novice dyads that discovered COC (M = 0.90 Hz, SD = 0.16; P = 0.88, d = 0.08). Furthermore, novice–novice dyads that discovered COC behavior had less deviation from predominantly in-phase/antiphase coordination (M = 1.06 normalized trials, SD = 1.27) than novice–artificial agent dyads (M = 5.47 normalized trials, SD = 2.29; Mann–Whitney U = 4.50, P = 0.003). Similar to experiment 1, this discrepancy was due to a greater magnitude of relative-phase variability for novice–artificial agent dyads compared with novice–novice dyads (P = 0.02, d = 1.67).

Finally, the herding performance of novice–novice and novice–artificial agent dyads that discovered and adopted COC was comparatively similar (Fig. 3C). Although novice–artificial agent dyads kept the sheep to a smaller area (herd area P = 0.02, d = 1.18) and stabilized their mean movement to a greater degree (herd travel P < 0.001, d = 2.57), dyads in both groups reached near ceiling on the explicit task goal measure of containment time (P = 0.06, d = 0.94). Novice–novice and novice–artificial agent dyads also exhibited equivalent performance regarding the mean sheep distance away from the herd’s center of mass (COM; P = 0.17, d = 0.17).

Experiment 2b.

Following the inability of the artificial agent to frequency match with participants in experiments 1 and 2a, a new sample of 20 naïve participants completed the same shepherding task as in experiment 2a but with a modified artificial agent capable of adapting its movement frequency during COC behavior. One participant could not complete the task within the 45 min allotted, and one participant was excluded from analysis for adopting an individualistic strategy, which involved circling around the entire herd. For the latter participant, although this behavior had been witnessed by two dyads in ref. 19, this behavior was outside what was typically observed in ref. 19 as well as experiments 1 and 2a, and therefore, the behavior of this participant was excluded from analysis.

Of the remaining 18 participants, 14 (77.78%) utilized COC behavior at least once (one participant had one successful COC trial, and one had two, while the remaining 12 had at least five successful COC trials; M = 7.25). Importantly, for successful COC trials, the average frequency difference between the novice and artificial agent during COC behavior was 0.04 Hz (SD = 0.05). This was not significantly different from the frequency difference observed between novice–novice dyads in experiment 2a (P = 0.86, d = 0.08), confirming that the frequency adaptations to the original shepherding model were successful (Fig. 3B). The resulting effect was an overwhelming predominance of stable in-phase and antiphase behavior, such that only 1 (0.01%) trial of a total of 90 successful COC trials deviated from in-phase/antiphase behavior. The resulting effect on participant interaction with the artificial agent was that, although participants in experiment 2b were told that their partner was a computer-controlled artificial agent, 7 (38.89%) of 18 participants indicated afterward that, at times, they thought that they were completing the task alongside an actual human coactor. These findings are, therefore, consistent with findings of refs. 43 and 48, which also indicated that participants attribute human agency to interactive artificial agents that exhibit human-like behavioral dynamics.

Discussion

This study tested the efficacy of DMPs as a suitable control architecture for interactive artificial agents completing complex and dynamic multiagent tasks with human coactors. For this study, a dyadic shepherding task was used, which captures the key features of goal-directed multiagent activity, including task division, decision making, and behavioral mode switching (19). Two experiments were conducted in which novice human participants were required to complete the shepherding task with either another human actor or a virtual artificial agent whose end effector movements were defined by a low-dimensional dynamical model composed of environmentally coupled point attractor and limit cycle dynamics.

As expected, the results revealed that HMI performance was equivalent to human–human performance, with human–human and human–artificial agent systems exhibiting the same robust patterns of S&R and COC behavior that characterized the performance of human dyadic shepherding (19). Moreover, S&R and COC behaviors were observed in both defined (experiment 1) and undefined (experiment 2) containment contexts, which not only further highlights the robust generalizability of these two behavioral modes but also, indicates that the emergence of COC behavior is not simply a function of specifying a circular target region [as was the case in experiment 1 and in the original study by Nalepka et al. (19)]. In both task contexts, optimal performance involved immobilizing the sheep together as a collective herd by applying lateral forces evenly distributed around a predefined or self-selected area of containment. Of particular significance is that a qualitatively similar behavioral strategy is observed across a range of other animal herding and hunting systems—such as the formation of a circle around lone prey in wolf pack hunting (50) or the creation of a “bubble net” to encircle herring in group humpback whale hunting (51)—despite differences in morphological and environmental constraints acting on these disparate animal systems. In sheepdog herding contexts specifically, similar patterns of (S&R-like) pursuit and (COC-like) oscillatory behavior are also observed (52, 63, 64). Such patterns are also common in many team sports contexts (65, 66), implying that the patterns of S&R and COC behavior observed here reflect context-specific realizations of the lawful dynamics that define functional shepherding behavior more generally (20, 31).

With respect to the latter claim, we freely acknowledge that the current tabletop, laboratory-based task methodology used in this study prevents any definitive conclusions regarding the degree to which the S&R and COC behavioral modes of shepherding behavior observed here might transfer to more real-world or complex multiagent shepherding task environments. Future research could address this limitation by investigating shepherding problems in larger shepherding environments and from a first-person perspective (i.e., where individuals must move by walking or running around a large area or field). The shepherding task could also be expanded to require individuals to transition from collection and containment to sheep transportation (i.e., moving a herd from one location to another). Furthermore, online perturbations, like the introduction of new sheep or altering team composition and member capabilities, could be introduced, which may lead to role differentiation and role switching for task success. Together, these more complex shepherding scenarios would help to further detail not only the lawful processes that promote the emergence of stable and robust multiagent shepherding behavior but also, other forms of everyday multiagent or social motor coordination.

Although most participants discovered and maintained COC behavior when working alongside the artificial agent, it is important to appreciate that one participant (7.69%) in experiment 2a and four (21.05%) participants in experiment 2b completed the task without adopting COC behavior, indicating that the emergence and maintenance of COC behavior may depend on specific interactions or contextual experiences with the task environment. By scaffolding interactive environments as a comember of a team (or as a “teacher” or “coach” embedded in the task context), artificial agents can potentially serve a promising role in implicit skill acquisition contexts, an alternative to utilizing artificial systems for explicit “trajectory shaping” of ideal behaviors (67, 68). Alternatively, artificial agents embodying human-like dynamics can take the role of humans in situations where recruitment is difficult, such as large-scale training exercises, or provide more varied team composition or role assignment for more robust team coordination in light of perturbations (69). As demonstrated by human “dynamic clamp” methodologies, the use of artificial agents as members of dyadic or group contexts can also allow researchers to deduce unidirectional effects of the (artificial) member on the rest of the group to better understand the processes underlying social interactions and diagnosis of social disorders (23, 43, 48, 70). Outside of using assistive artificial systems for skill acquisition or training to prepare for future social encounters, embodying robotic systems with human-like dynamics may facilitate action prediction and safety in domains, such as advanced manufacturing (e.g., handing objects from robot to human), where the movement capabilities of such systems are not readily apparent (71, 72).

Although most participants were unaware that they were working alongside an artificial agent in experiment 1b, the few participants who detected the artificial agent noted that its behaviors during COC were “too quick.” This deficit in the human-like nature of the proposed model was addressed in experiment 2b by including an adaptive frequency function (i.e., frequency parameter dynamics) that operated to match a human actor’s natural movement frequency (73). The resulting effect led a subset of participants to attribute human agency to the artificial agent, although they were informed that it was a computer-controlled player. It remains unclear whether this attribution was due to the artificial agent’s ability to modulate its movement frequency or the increased occurrence of stable in-phase and antiphase COC behavior that such frequency modulation afforded. Regardless, consistent with refs. 43 and 48, a combination of adaptive frequency dynamics and modulations in interagent coupling strength does seem to facilitate the naturalness of HMI (14, 43, 48). Recent work by ref. 74 has provided additional support for the tangible benefits for such adaptions in HMI, demonstrating how the use of dynamical primitives can be extended to include “interaction primitives” that promote movement adaptation to particular user styles to facilitate physical human–robot interaction during a high five or object handover task. This is to be expected, however, given that interacting individuals tend to spontaneously and reciprocally adapt their behaviors during social interaction (45, 47, 75). Indeed, when producing rhythmic movements with another person, individuals naturally adapt their movement frequencies to be in alignment (i.e., exhibit frequency entrainment) (45, 76), with such frequency modulation lingering in “social motor memory” even after the interaction has ended (75, 77). In other social motor tasks, participants who resemble similar “motor signatures” are known to coordinate their behaviors more than those who are dissimilar (14, 45, 75, 78). Such movement adaptation has numerous social and emotional consequences (79) and is associated with increased rapport and the success of future interactive task performance (80). Thus, one could hypothesize that it is this movement modulation and reciprocal entrainment that led to attributions of human agency observed in this study. This hypothesis could be tested in future research as well as whether reciprocal adaptation might also operate to increase the degree to which human actors accept or trust interactive artificial agents (12).

In conclusion, this study demonstrated the usefulness of a human-inspired model of multiagent coordination for HMI and provides clear evidence that the task/behavioral dynamics of complex human multiagent coordination can be generatively modeled from a relatively simple set of DMPs. Consistent with previous research demonstrating how individual (single-agent) perceptual motor behavior can be effectively modeled using similar dynamical primitives (39, 41) or low-dimensional task-dynamic models (20, 21, 31), the implication is that the organization and context-specific regularity or control of embedded single-agent or multiagent perceptual motor behavior are often a natural and emergent consequence of the physical, informational, and task goal constraints that define a given task context (21, 22, 31). In conjunction with contemporary system optimization methods and reinforcement and machine-based learning approaches, it therefore seems clear that models composed of interactive or coupled dynamical primitives not only hold great promise for the development of robust, human-centered HMI systems but also, have the potential to provide a generalized modeling framework for understanding how and why the dynamic patterns of goal-directed, human multiagent environment activity emerge within a given task context. Indeed, while it might be difficult to deduce the “equations of mind” (81, 82) from DMP models alone, exploring the generative potential of such models with regard to capturing the dynamic stabilities of human and social activity will likely provide insights about how intentional and cognitive states emerge and operate to shape and enhance the lawful dynamics that define (multi-)agent environment task performance.

Materials and Methods

Shepherding Model.

Eqs. F1–F3 in Fig. 1C were modified to account for human-specific adaptations observed in ref. 19. The equations governing the radial and angular components of the agent’s movement were modified as follows:

$${\ddot{r}}_i+b_r\dot{r_i}+{\epsilon }_r\left(r_i-\xi \left(r_{sf\left(t\right),i}+r_{\min }\right)-\left(1-\xi \right)(r_{\mathrm{\Delta }}+r_{\min })\right)=0$$ [1]

$$\ddot{{\theta }_i}+b_{\theta }\dot{{\theta }_i}+\beta {\dot{\theta }}_i^3+\gamma {\theta }_i^2\dot{{\theta }_i}+{\epsilon }_{\theta }({\theta }_i-\xi \left({\theta }_{sf\left(t\right),i}\right))=(1-\xi )\left(\dot{{\theta }_i}-{\dot{\theta }}_j\right)\left(A+B{\left({\theta }_i-{\theta }_j\right)}^2\right).$$ [2]

For Eq. 1, variables $r_i$, $\dot{r_i}$, and ${\ddot{r}}_i$ represent the radial component of agent i’s (i = 1, 2) current position, velocity, and acceleration at time t, respectively. Parameters $b_r$ and ${\epsilon }_r$ are linear damping and stiffness terms, respectively, for the damped mass spring function. Eq. 1 reduces the difference between agent i’s current radial distance ($r_i$) and the distance of the targeted sheep on agent i’s side of the game field [$r_{sf\left(t\right),i}$]. To ensure that the targeted sheep is repelled toward the correct direction, agent i maintained a distance $r_{\min }$ away from $r_{sf\left(t\right),i}$.

For Eq. 2, variables ${\theta }_i$, ${\dot{\theta }}_i$, and ${\ddot{\theta }}_i$ represent the angular component of agent i’s current position, velocity, and acceleration at time t, respectively. Parameters $b_{\theta }$ and ${\epsilon }_{\theta }$ are the linear damping and stiffness terms, respectively. The Rayleigh ($\beta {\dot{\theta }}_i^3$) and van der Pol ($\gamma {\theta }_i^2\dot{{\theta }_i})$ escapement terms allow for oscillatory behavior to emerge (36). The coupling function to the right of Eq. 2 couples the angular component of agent i’s position and velocity to those of their partner j (35). The format of the coupling function allows for the model’s angular movements of both agents to achieve the stable in-phase and antiphase modes of behavior observed in ref. 19 and during interpersonal rhythmic coordination more generally (35, 47) when the resonant frequency between agents is sufficiently small. Parameters A and B index coupling strength, such that |4B| > |A| allows for both stable in-phase and antiphase solutions to emerge.

Parameter $b_{\theta }$ was modulated to allow for behavioral mode switching from S&R and COC behavior. The rate of change of $b_{\theta }$, ${\dot{b}}_{\theta }$, was modeled with Eq. 3, where $\delta$ and $\alpha$ are fixed parameters that determine the rate of change of $b_{\theta }$, while $r_{\mathrm{\Delta }}+r_{\min }$ is the radial distance that demarcated S&R and COC behavior:

$${\dot{b}}_{\theta }+\delta \left(b_{\theta }-\alpha (r_{sf\left(t\right),i}-(r_{\mathrm{\Delta }}+r_{\min })\right)=0.$$ [3]

Critically, the model exhibited S&R behavior when $r_{sf\left(t\right),i}\ge r_{\mathrm{\Delta }}$ and COC behavior when $r_{sf\left(t\right),i}<r_{\mathrm{\Delta }}$. Furthermore, when performing COC behavior, the model’s radial and angular components were no longer coupled to the targeted sheep [sf(t),i] but instead, performed oscillatory movements around the herd (centered at θ = 0) at a fixed distance away from the containment region ($r_{\mathrm{\Delta }}+r_{\min }$). To account for this, a Heaviside function (Eq. 4) was included to determine when the model would pursue sf(t),i (note also the $\xi$ terms in Eqs. 1 and 2). Note that, although the inclusion of $\xi$ in Eq. 2 is not necessary for successful shepherding performance, it ensured a characteristic of human shepherding performance found in ref. 19, where participants maintain the center of their oscillatory behavior along the parasagittal plane:

$$\xi =\{\begin{array}{c}0,\\ 1,\end{array}\begin{array}{c}{r}_{sf\left(t\right),i}<r_{\mathrm{\Delta }}\\ r_{sf\left(t\right),i}\ge r_{\mathrm{\Delta }}\end{array}.$$ [4]

For experiment 1, the origin (pole) of each agent’s polar task space was located at the center of the game field, and the 0° reference direction (polar axis) for each agent was defined by the ray from the pole to the agent’s side of the game field. For experiment 2, each agent’s pole at time t was defined at the herd’s current COM location, which was calculated as the average sheep position at that time t. The radial component was measured as the distance (in meters) from the pole, and the angular component was specified as defined above and illustrated in Fig. 1C. This ensured that the stability of in-phase and antiphase coordination was represented accurately during the shepherding task. Additionally, to add stochasticity to the agent’s behavior, an additional movement noise term, (η_r, η_θ) = (±1$\text{m}/{\text{s}}^2$, ±$1\text{rad}/{\text{s}}^2$), was added to Eqs. 1 and 2.

The determination of the targeted sheep, sf(t),i, was different between experiments due to changes in task constraints (Apparatus and Task has more detail). For experiment 1, because a trial would end prematurely if a sheep made contact with the surrounding fence, sf(t),i was defined as the sheep on agent i’s side of the game field that had the largest ratio of $\text{distance from center}/\text{distance from fence}$. For experiment 2, this constraint was removed from the task, and therefore, sf(t),i was defined as the sheep on agent i’s side of the game field that was farthest from the sheep’s COM.

Eqs. 1–4 were the finalized model used in experiments 1b and 2. The parameter values utilized were as follows: $b_r=10.9987$, ${\epsilon }_r=98.70672$, $r_{\mathrm{\Delta }}=0.062$, $r_{\min }=0.061539$, $\beta =0.161641$, $\gamma =7.22282$, ${\epsilon }_{\theta }=61.6225$, A = −0.2, B = −0.2, $\delta =23.08993$, and $\alpha =80.59288$. The values were the result of a parameter search using a genetic evolutionary algorithm, where the environment from experiment 1 was used to assess parameter fitness. Parameters $r_{\mathrm{\Delta }}$ and $r_{\min }$ were then adjusted manually to match observations from ref. 19, while A and B were fixed constants set to −0.2.

Following the results from experiments 1 and 2a, Eq. 5 was included to adapt the artificial agent to individual differences in the frequency of movement during COC (43, 73):

$$\dot{\omega }-v\left({\omega }_0-\omega \right)-(1-\xi )\kappa {\theta }_j\frac{\dot{{\theta }_i}}{\sqrt{{\theta }_i^2+{\dot{{\theta }_i}}^2}}=0.$$ [5]

In Eq. 5, $\omega =\sqrt{{\epsilon }_{\theta }}$, and thus, Eq. 5 affected the time-varying nature of ${\epsilon }_{\theta }$ in Eq. 2. Parameter ${\omega }_0$ was set to be the preferred frequency of the model, which was set to 5.652 $\text{rad}/\text{s}$. This value was determined from the relationship $\omega /2\pi$ = frequency (36), which was, on average, 0.90 Hz for novice–novice dyads in experiment 2a. During S&R behavior, $\omega$ approached ${\omega }_0$, where $v$ is the parameter relaxation time. During COC behavior, $\omega$ was also influenced by the current angular position, ${\theta }_j$, of the human participant, where $\kappa$ is the coupling strength of the participant’s influence. For experiment 2b, $v=1$, and $\kappa =2$. In simulation, these parameter values reached $\omega$ convergence between two coupled artificial agents, where the artificial agent with ${\omega }_0=5.652$ adapted its oscillatory frequency to another agent with natural frequency that was within 0.2-Hz difference, consistent with what is found in the human literature of incidental visual coordination (62).

Participants.

Participants were recruited from the University of Cincinnati (experiments 1 and 2a) and Macquarie University (experiment 2b) in exchange for partial course credit as part of a psychology course requirement. Informed consent was obtained at the beginning of the experiment session. The task, procedure, and methodology were reviewed and approved by the institutional review boards of the University of Cincinnati and Macquarie University. All participants were right handed and were naïve to the task and purpose of the experiment.

Experiment 1.

Thirty undergraduate students (15 female, 15 male), recruited into 15 dyads, completed the novice–novice condition (experiment 1a). Twenty-one undergraduate students (8 female, 12 male, 1 undisclosed) participated in experiment 1b. Each participant was randomly assigned to complete the experiment with a confederate (10 participants) or with the artificial agent (11 participants). The participants ranged in age from 18 to 23 y old.

Experiment 2a.

Fifty-two undergraduate students (35 female, 17 male) participated in experiment 2. Thirty-eight participants were recruited into 19 dyads, while the remaining 14 participants completed the experiment together with the artificial agent. The participants ranged in age from 17 to 23 y old. One participant in the novice–artificial agent condition was later excluded due to a computer malfunction.

Experiment 2b.

Following the findings of experiments 1 and 2a, an additional 20 undergraduate students (12 female, 8 male) were recruited to complete the shepherding task from experiment 2 alongside a modified version of the artificial agent capable of adapting its movement frequency during COC. The participants ranged in age from 18 to 25 y old.

Apparatus and Task.

For both experiments, the task was designed using the Unity 3D game engine (version 5; Unity Technologies) and presented to participants via the Oculus Rift DK2 (VR) headset (Oculus VR). The virtual environment was modeled such that there was a 1:1 mapping between the virtual and real experimental testing rooms. While wearing the VR headsets, the task was presented on the virtual tabletop colocated with a physical table in the real environment—the real table provided a physical surface for participants to move their handheld sensors on while controlling the end effector movements of their virtual avatar in the virtual environment. Participants used wireless LATUS motion-tracking sensors operating at 96 Hz (Polhemus Ltd.). Participants moved the sensors along the tabletop, and their hand movements translated 1:1 to the movements of the agent-controlled end effector/sheepdog (modeled as a cube). In the virtual world, participants were embodied as “crash test dummies” whose motion was controlled using an inverse kinematic calculator given the inputs from the participant’s hand and head position (3D model and calculator supplied by RootMotion). Separate computers were used to power the VR headsets, and a local area network was used to transfer data using Unity 3D’s UNET server-authoritative protocol. Agent- and task-state variables were updated at 50 Hz. Only hand position data were transferred across the network to control for the lack of head motion dynamics in the artificial agent condition.

The task involved participants corralling and containing seven autonomous and reactive sheep (modeled as spheres, 2.4-cm diameter). The sheep exhibited Brownian dynamics, where a randomly directed force would be applied at a rate of 50 Hz if left alone. To contain the sheep, agents had to move their sheepdog/cube near the sheep. If either sheepdog was within 12 cm of the sheep, the Brownian force was replaced with a repulsive force directly away from the agent’s sheepdog at a rate inversely proportional to the distance between the sheep and the agent-controlled cube. The code used for the shepherding task and sheep dynamics can be found at https://github.com/MultiagentDynamics/Human-Machine-Shepherding/ (83).

Experiment 1.

Participants were instructed to contain the sheep within the centrally located red containment circle (19.2-cm diameter) (Fig. 2A). The game field was a fenced area measuring 1.17 × 0.62 m. Trials were 60 s in duration, and participants were instructed to keep the sheep contained within the red circle for at least 70% of the last 45 s of the trial. The sheep were considered contained if all of the sheep had at least some part of their sphere within the 19.2-cm containment circle. At the end of each trial, participants received visual feedback on their containment percentage. Participants were informed that, to complete the shepherding task successfully, they needed to complete eight successful trials within the 45-min testing period. As an incentive to cooperate with their partner, participants were informed that the experiment would automatically end after eight successful trials had been completed and that they would receive full research credit even if it occurred well before the 45-min testing period (otherwise, the program closed automatically after 45 min).

At the start of a trial, the sheep would appear within the containment region (Fig. 2A has the initial arrangement). Trials lasted a maximum of 60 s but would end early if one of two things occurred during a trial: if a sheep managed to collide with the surrounding fence or if all sheep managed to escape the centrally located area measuring 28.8 cm in diameter (displayed as the white annulus surrounding the red containment region). If a trial ended prematurely, no score was given for that trial. When a trial ended, the sheep and the participant’s partner disappeared. To initiate the next trial, both participants moved their cubes to a designated start location 24 cm from the center of the game field on their respective side of the game field.

Experiment 2.

The task was modified from experiment 1. The task space was expanded to cover a fenced area of 1.5 × 0.8 m. No containment circle was displayed to participants. Instead, the containment circle (19.2-cm diameter) was invisible and centered on the sheep’s COM, calculated as the mean position of the sheep at time t. The artificial agent’s polar task space was also dynamically centered on the sheep’s COM as opposed to the center of the game field as in experiment 1. For each trial, the sheep were randomly scattered across a 0.5 × 0.8-cm boxed region centered on either the left, center, or right one-third of the task space (Fig. 3A has an example initial arrangement). Unlike experiment 1, no premature trial failure conditions were applied. If a sheep contacted the bordering fence, a repulsive force was applied to the sheep orthogonal to the fence, causing the sheep to move toward the field. Finally, the trial length was increased to 2 min to allow for additional time to collect the sheep.

Participants were informed that the task goal was to bring the randomly scattered sheep together. If all of the sheep were sufficiently contained, participants received visual feedback that the sheep were adequately contained by changing the sheep’s color from brown to red. To discourage participants from taking advantage of the limited size of the task space, participants only received visual feedback if the herd’s COM was at least 10.8 cm from the bordering fence. Participants received a point if the sheep were within the invisible 19.2-cm circle centered on the herd’s COM for at least 70% of the last 45 s of the trial. Like in experiment 1, the sheep were considered contained if all of them had some portion of their sphere within the (invisible) containment area. As with experiment 1, participants had 45 min to obtain eight successful trials.

Procedure.

Experiment 1.

Before consent, participants sat in the waiting area together (experiment 1a) or alongside a confederate coinvestigator, who posed as a participant, (experiment 1b). Both individuals were brought into the suite and were either taken to the same room (experiment 1a) or directed to one of two experimental rooms (experiment 1b). After consent, participants were given the VR headset and the motion tracker to be used in their right hand. The rules and goal of the task were explained to participants, and participants proceeded to move through the experiment at their own pace with their partner virtually present on the opposite side of the table. Note that participants in the novice–novice condition were told that they could not talk to each other, and the experimenter enforced this no talking rule.

For experiment 1b, participants were always sent to the same experimental room, and while they were reviewing the consent form, the coinvestigator was walked to an adjacent room by the experimenter. The experimenter returned to the room with the participant and told the participant that the partner was to be supervised by another experimenter, while the lead experimenter remained in the room with the participant to answer any questions that the participant had. The participant’s partner was either controlled by the confederate or the artificial agent. The confederate had knowledge of the S&R and COC behavioral modes. Also, the confederate was told to implement COC behavior when the sheep were within the containment region and to not encroach on the novice participant’s side of the task space. After the conclusion of the task, participants were funnel debriefed as to the purpose of the experiment and asked whether they had any doubts that they were completing the task with a human partner at any time during the experiment.

Experiment 2.

Participants were either recruited as dyads (in the novice–novice condition) or as individuals (in the novice–artificial agent condition and for experiment 2b). Participants in the novice–novice condition completed the task together in separate rooms and were told that they were working together to complete the shepherding task. Participants in the novice–artificial agent condition and experiment 2b were told that they would be working alongside an artificial agent. For participants working with the artificial agent, the capabilities of the artificial agent were never disclosed; participants were only informed that the agent was there to assist them in completing the shepherding task. After consent, participants were given their respective VR headsets and handheld motion controllers. The rules and goal of the task were explained to participants, and participants proceeded to move through the experiment at their own pace. After completion, participants were debriefed as to the purpose of the experiment.

Data Reduction, Preprocessing, and Measures.

Consistent with analyses performed by Nalepka et al. (19), positional (x,y) values of the handheld sensor were converted to polar (r,θ) coordinates. For each respective agent, the angular component was centered on the intersection of the agent’s sagittal and transverse planes, with values of ($-3\pi /2,3\pi /2$) in the game field. This allowed for accurate representation of an agent’s movement, including sagittal plane crossings on the partner’s side of the game field. All analyses were conducted on the last 45 s of the trial.

COC Classification.

COC behavior was defined by the presence of a strong oscillatory component operationalized as a peak frequency component between 0.5 and 2 Hz. S&R behavior was classified as having a peak oscillatory frequency below 0.5 Hz. Welsh’s power spectral density estimates (MATLAB’s pwelch function) were conducted to determine the oscillatory frequency with the most power between 0 and 2 Hz. The angular component of agent movements was low-pass filtered at 10 Hz using a fourth-order Butterworth filter and linearly detrended. The analysis was windowed at 512 samples, with 50% overlap. For COC classification in experiment 1, the polar coordinate axis was aligned with the center of the containment region. For COC classification in experiment 2, the polar coordinate axis was centered on the sheep herd’s COM.

In addition to a strong oscillatory component, a second feature of COC behavior is the emergence of a stable in-phase or antiphase relative-phase relationship (19). To determine the pattern and degree of coordination among dyads, instantaneous relative-phase analysis was conducted on the angular time series of dyads. The relative-phase angles that occurred within a dyad were determined using the Hilbert transform (ref. 84 has details about this transformation). The relative phase that occurred for a given trial was distributed across six 30° bins (i.e., 0°–30°, 30°–60°…150°–180°). For these distributions, in-phase and antiphase coordination was indicated by a concentration of relative-phase angles near 0° and 180°, respectively (45). Trials were classified as in phase (0–30°) or antiphase (150–180°) if their respective bins reached a threshold of 17.933%; this cutoff criterion corresponded to P = 0.05 or the 950th largest value from 1,000 randomly generated relative-phase distributions (85). After this, the number of trials that were significantly classified as in phase and/or antiphase was counted and compared across conditions. The stability of overall coordination was also assessed by taking the mean resultant vector of the relative-phase distribution for a given trial, where a value of one indicates absolute coordination or a perfectly stable relative-phase relationship and zero indicates the complete absence of coordination (i.e., no stable relative-phase relationship).

The following performance measures were used to determine differences between conditions in both experiments: completion time—the time (minutes) elapsed to complete the experiment; containment time—the amount of time (seconds) that all sheep were contained within the containment region (experiment 1) or within the invisible 19.2-cm circle centered on the herd’s COM (experiment 2); sheep distance—the mean sheep distance from the center of the target containment region (experiment 1) or the herd’s COM (experiment 2); herd spread—the average herd spread (centimeters squared) measured by computing the convex hull formed by all of the sheep (the convex hull is defined by the smallest convex polygon that can encompass an entire set of objects, like a rubber band placed over a set of pegs); and herd travel—defined as the cumulative distance (centimeters) that the herd’s COM moved during the trial.

All data have been made publicly available via the Open Science Framework and can be accessed at https://osf.io/ke5mv/ (86).