Autogenous and efficient acceleration of energetic ions upstream of Earth’s bow shock

Abstract

Earth and its magnetosphere are immersed in the supersonic flow of the solar-wind plasma that fills interplanetary space. As the solar wind slows and deflects to flow around Earth, or any other obstacle, a ‘bow shock’ forms within the flow. Under almost all solar-wind conditions, planetary bow shocks such as Earth’s are collisionless, supercritical shocks, meaning that they reflect and accelerate a fraction of the incident solar-wind ions as an energy dissipation mechanism^1,2, which results in the formation of a region called the ion foreshock³. In the foreshock, large-scale, transient phenomena can develop, such as ‘hot flow anomalies’^4–9, which are concentrations of shock-reflected, suprathermal ions that are channelled and accumulated along certain structures in the upstream magnetic field. Hot flow anomalies evolve explosively, often resulting in the formation of new shocks along their upstream edges^5,10, and potentially contribute to particle acceleration^11–13, but there have hitherto been no observations to constrain this acceleration or to confirm the underlying mechanism. Here we report observations of a hot flow anomaly accelerating solar-wind ions from roughly 1–10 kiloelectronvolts up to almost 1,000 kiloelectronvolts. The acceleration mechanism depends on the mass and charge state of the ions and is consistent with first-order Fermi acceleration^14,15. The acceleration that we observe results from only the interaction of Earth’s bow shock with the solar wind, but produces a much, much larger number of energetic particles compared to what would typically be produced in the foreshock from acceleration at the bow shock. Such autogenous and efficient acceleration at quasi-parallel bow shocks (the normal direction of which are within about 45 degrees of the interplanetary magnetic field direction) provides a potential solution to Fermi’s ‘injection problem’, which requires an as-yet-unexplained seed population of energetic particles, and implies that foreshock transients may be important in the generation of cosmic rays at astrophysical shocks throughout the cosmos.

Since the start of its first science phase in September 2015, NASA’s Magnetospheric Multiscale mission (MMS)¹⁶ has provided an unprecedented set of observatories with which transient foreshock phenomena can be studied. MMS involves four identically instrumented spacecraft (MMS-1–4) that are held in a tight, tetrahedron formation with inter-satellite separations ranging throughout the mission from less than 10 km to around 100 km. The four-point configuration enables multipoint analysis and the disambiguation of spatiotemporal features in observables that include plasma, fields and waves, energetic particles and ion composition at resolutions not previously available for in situ space plasma experiments. Here, we report on MMS observations of a hot flow anomaly (HFA) from 28 December 2015 that was associated with an unusual observation of energetic ions up to several hundred kiloelectronvolts in the solar wind and magnetosheath (the region of shocked solar-wind plasma flowing around Earth’s magnetosphere downstream of the bow shock). Using the multipoint nature of the mission and its comprehensive suite of instrumentation, we are able to examine this event in detail to determine whether and how the accelerated ions are related to the HFA and its interaction with the bow shock.

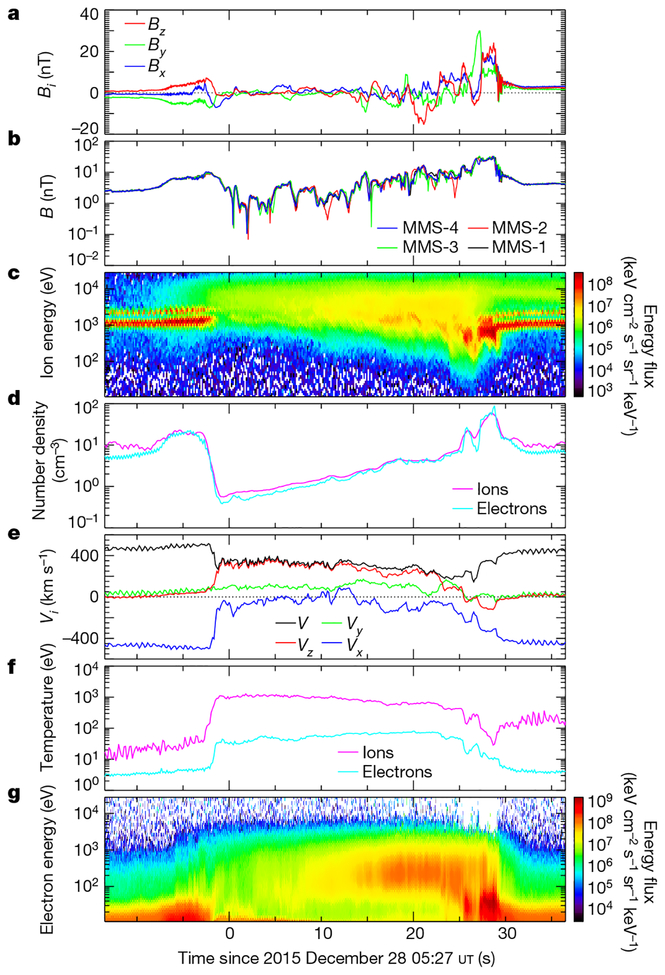
HFAs are characterized by superheated, tenuous, low-field-strength core regions that exhibit strong deflections of the plasma velocity¹⁷. As the structure responsible for their formation convects away from the Sun with the solar wind through the foreshock, HFA cores intensify and, in an attempt to maintain pressure balance, expand into the surrounding solar-wind plasma, forming compression regions on either side and often resulting in the formation of fast magnetosonic shocks at their upstream edges. In Fig. 1 we show 50 s of MMS burst magnetic field and ion and electron plasma data encompassing a transit of the spacecraft through a well-developed HFA. MMS first encountered the downstream edge of the HFA (with respect to the flow of the solar wind away from the Sun) around 05:26:53 ut, where the enhanced density and magnetic-field strength indicated a region of compressed solar-wind plasma. The spacecraft passed into the core of the HFA from about 05:26:58 ut to 05:27:25 ut, observing plasma that was highly tenuous (density of less than 1 cm⁻³), had a low field strength (|B| < 2 nT) and was strongly deflected (V_z > 300 km s⁻¹ and V_x > −200 km s⁻¹; the velocity V was towards the Sun for several seconds). MMS next encountered shocked plasma and strong magnetic-field variations just before the spacecraft passed through a fast magnetosonic shock at the upstream edge of the HFA at around 05:27:29 ut.

Fig. 1 |. Overview of the MMS burst data during the HFA.

a–g, Quantities shown (all from MMS-1 unless otherwise specified) are the components of the magnetic-field vector B = (B_x, B_y, B_z) (a) and the magnetic-field strength B = |B| from the flux-gate magnetometers on each of the four spacecraft (b); the omni-directional, averaged energy distributions of the ions from the fast plasma investigation dual ion spectrometer (FPI/DIS) (c); the ion and electron densities (d); the components of the velocity vector of the ions (V_x, V_y, V_z) and its magnitude V = |V| (e); the ion and electron temperatures (f); and the omni-directional, averaged energy distributions of the electrons from the FPI dual electron spectrometer (FPI/DES) (g). With the geometry and multipoint observations of the HFA, its size, expansion rate and motion along the bow shock can be calculated. Using the rotation of the IMF before and after the HFA, we estimate the normal direction of the IMF discontinuity that is responsible for the formation of the HFA to be n = (0.70, −0.44, −0.57) in the geocentric solar ecliptic coordinate system. We calculated the normal direction of the upstream shock of the HFA using co-planarity and multi-spacecraft analysis (Methods), yielding n_sh = (0.85, −0.16, −0.53) and n_sh = (0.84, −0.44, −0.31), respectively, which are generally consistent. In the solar-wind frame, the HFA shock was expanding upstream (towards the Sun) at about 360 km s⁻¹. When MMS observed the HFA, it was expanding at a rate of 108 km s⁻¹ along the IMF discontinuity normal and was approximately 16,000 km (2.5 Earth radii) in size from edge to edge along the track taken by MMS through the HFA. The geometry of the HFA and the values that we have calculated are critical for enabling comparisons between observed particle acceleration signatures and theory.

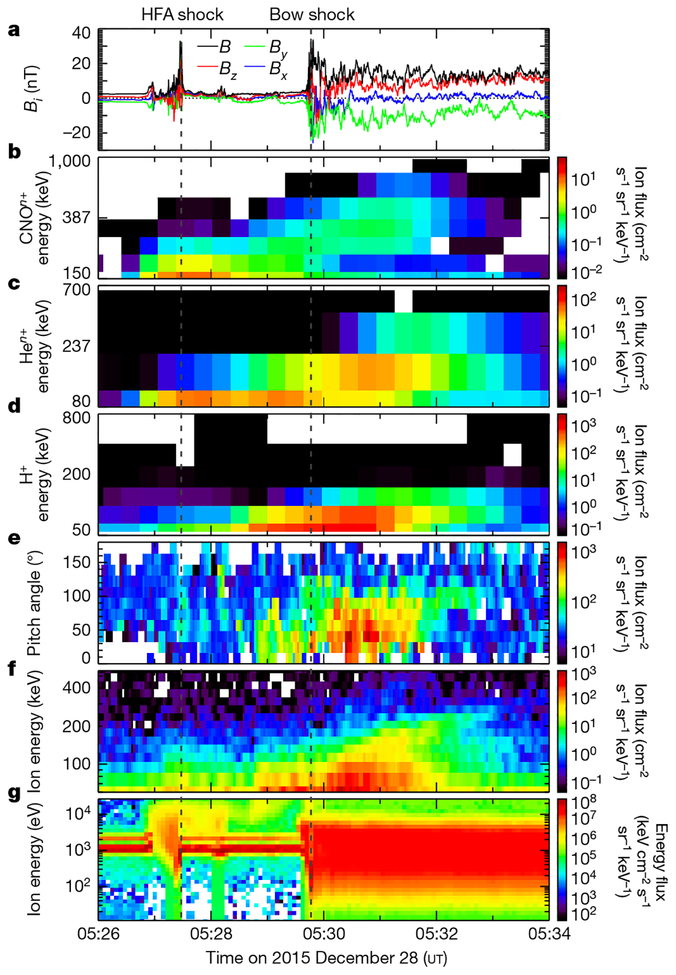
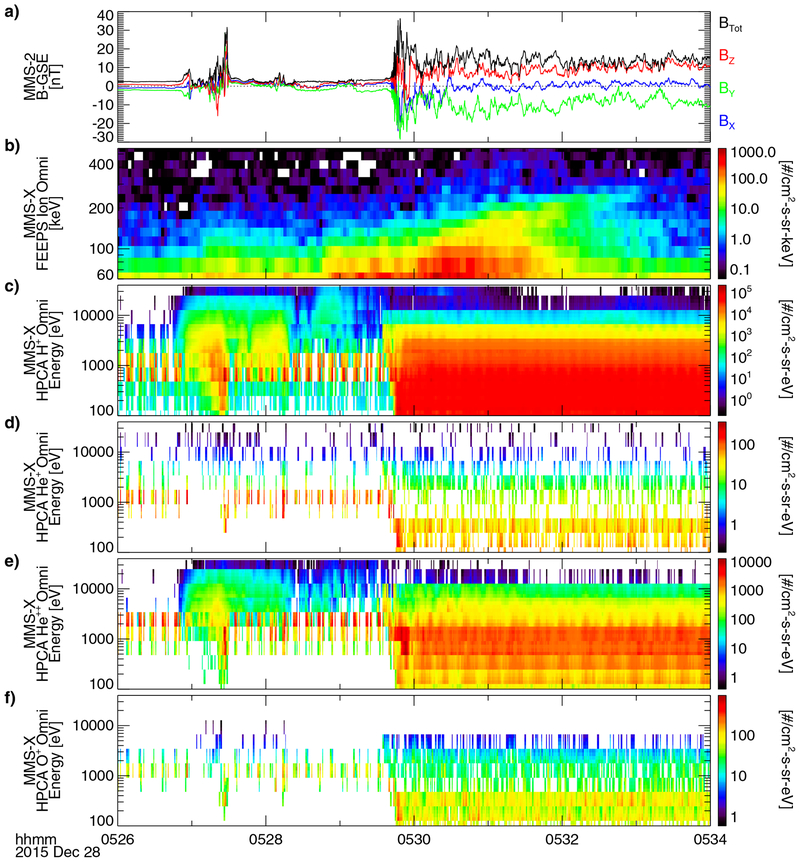
Unusually high intensities of energetic ions were observed by the Energetic Ion Spectrometer (EIS) and Fly’s Eye Energetic Particle Spectrometer (FEEPS) instruments on MMS during and for several minutes following the encounter with the HFA. Figure 2 reveals an enhancement in the number of protons and of helium and heavier (carbon–nitrogen–oxygen, CNO) ions with energies of more than 50 keV starting at around 05:27 ut, which coincides with the initial encounter with the HFA, and persisting until about 05:33 ut, after MMS exited the HFA and transited the bow shock into the magnetosheath. The peak intensities and the upper energy thresholds in the energy distributions of these ions increased exponentially over time, and the rate of increase and the upper energy limits were mass and/or charge dependent: the heaviest ions observed (CNOⁿ⁺) exhibited a faster rate of energy increase and a higher upper energy limit (up to about 800 keV) than did the helium ions (Heⁿ⁺, energy limit up to about 400 keV) and protons (H⁺, energy limit less than 200 keV). From the highest energy channels (roughly 10–40 keV) of the Hot Plasma Composition Analyzers (HPCAs) on MMS, which can distinguish the charge state of helium and heavier ions (see Extended Data Fig. 1), we determined that the helium ions observed were clearly α particles (He²⁺). In addition, there were no observable levels of O⁺, which indicates that the heaviest energetic ions observed were also at a high charge state (such as O⁶⁺ or C⁶⁺, the predominant heavy ions and charge states in the CNO branch in the solar wind). Both of those observations are consistent with these accelerated ions being of solar-wind origin.

Fig. 2 |. MMS observations of energetic ions and context data during and after the encounter with the HFA.

b–d, Heavy-ion (CNOⁿ⁺; b), helium (Heⁿ⁺; c) and proton (H⁺; d) data from the energetic particle detector EIS (EPD/EIS). The colour scales show the differential fluxes and the energies shown (on the y axes) are the total energy per incident ion. e, Pitch angle distributions for 70–105-keV ions from the EPD/FEEPS instruments. For b–e, the data were compiled from counts on the EIS or FEEPS instruments on all four spacecraft. f, g, Total ion energy distributions from all four FEEPS instruments (f) and the DIS instrument on MMS-3 (g). a, Magnetic-field vector components and strength from MMS-3, for context. The grey, dashed, vertical lines mark the HFA shock and the bow shock, as labelled. The energetic ions were first observed within the HFA around 05:27 ut and then continuously after the HFA through the ion foreshock and into the magnetosheath until around 05:33 ut.

From the pitch-angle distributions from FEEPS, we determined that the energetic ions were observed streaming along magnetic field lines between about 05:29 ut and 05:32 ut, when the interplanetary magnetic field (IMF) was generally steady, with an average of (1.1, −2.6, 1.6) ± (0.4, 0.4, 0.5) nT in the solar wind and (−1.1, −11.1, 7.7) ± (2.7, 3.6, 2.6) nT in the magnetosheath. HPCA also observed perpendicularly heated, field-aligned beams of He²⁺ and H⁺ ions with energies of more than 10 keV that are consistent with the energetic ion distributions observed by EIS and FEEPS. The pitch-angle distributions and field orientations are consistent with ions streaming along field lines away from the location of the HFA, as illustrated in Fig. 3. In addition, the magnetic-field orientation in the magnetosheath was nearly perpendicular to the magnetopause-boundary normal on the side of the system adjacent to MMS, providing additional evidence that the accelerated ions (H⁺, He²⁺ and CNOⁿ⁺) were not of magnetospheric origin. Furthermore, magnetospheric escape is inconsistent with the continuous, high intensities that originated in and continued after the HFA and the limited extent of these ions within the magnetosheath.

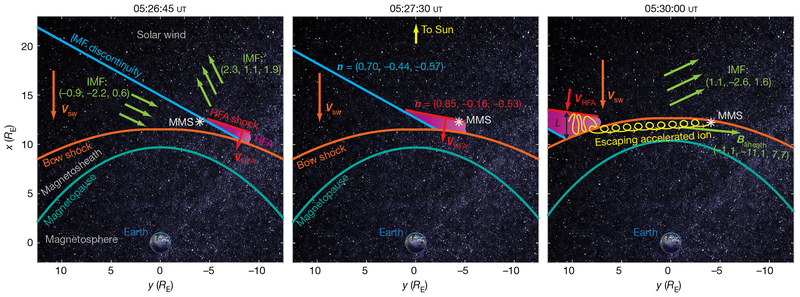
Fig. 3 |. Conceptual scenario for the HFA observed by MMS on 28 December 2015.

Earth is shown at the origin of three two-dimensional cross-sections (approximately in Earth’s equatorial plane; R_E is the radius of Earth), which capture the geometry of the system at 05:26:45 ut, 05:27:30 ut and 05:30:00 ut (left to right). The position of MMS is marked by the white asterisk. Slices of Earth’s magnetopause, Earth’s bow shock, the IMF discontinuity and the HFA shock are shown in turquoise, orange, blue and red, respectively. Velocity vectors for the solar wind (V_sw) and the HFA shock (V_HFA) are also shown. IMF geometries and vectors are shown in green, and the normal vectors of the IMF discontinuity (n = (0.70, −0.44, −0.57)) and the HFA shock (n = (0.85, −0.16, −0.53)) are also labelled. The core of the HFA is shown in magenta. As the IMF discontinuity and HFA convect with the solar wind, they sweep from right to left across the bow shock, as shown here. The HFA grows in time as it sweeps up and concentrates more and more suprathermal ions in the quasi-parallel foreshock that forms on the upstream side (towards the Sun) of the IMF discontinuity. In the solar-wind rest frame, Earth’s bow shock is moving towards the Sun at V_sw (orange velocity vector) and is perpetually converging on and overtaking the IMF discontinuity and the HFA with its shock (moving at V_HFA < V_sw and shown as the red velocity vector). This situation enabled continuous first-order Fermi acceleration to occur during the life of the HFA. In this case, we were afforded a period of fortuitous IMF orientation after MMS observed the HFA: ions that were accelerated within the Fermi acceleration trap between the HFA shock and the bow shock escaped the trap and were then observed by MMS streaming away from the HFA, allowing for direct, observationally constrained comparison between the observations and theory. The yellow spiral trace in the 05:30:00 ut snapshot shows an ion escaping the trap and streaming towards MMS, which is consistent with the observed FEEPS ion and high-energy HPCA He²⁺ and H⁺ angular distributions. L is the length scale between the HFA shock and the bow shock, and the average field in the magnetosheath observed by MMS is shown as B_sheath. Image of Earth from NASA’s From Earth to the Solar System collection (image credit: Data-AVHRR, NDVI, Seawifs, MODIS, NCEP, DMSP and Sky2000 star catalogue; AVHRR and Seawifs texture-Reto Stockli; Visualization-Marit Jentoft-Nilsen).

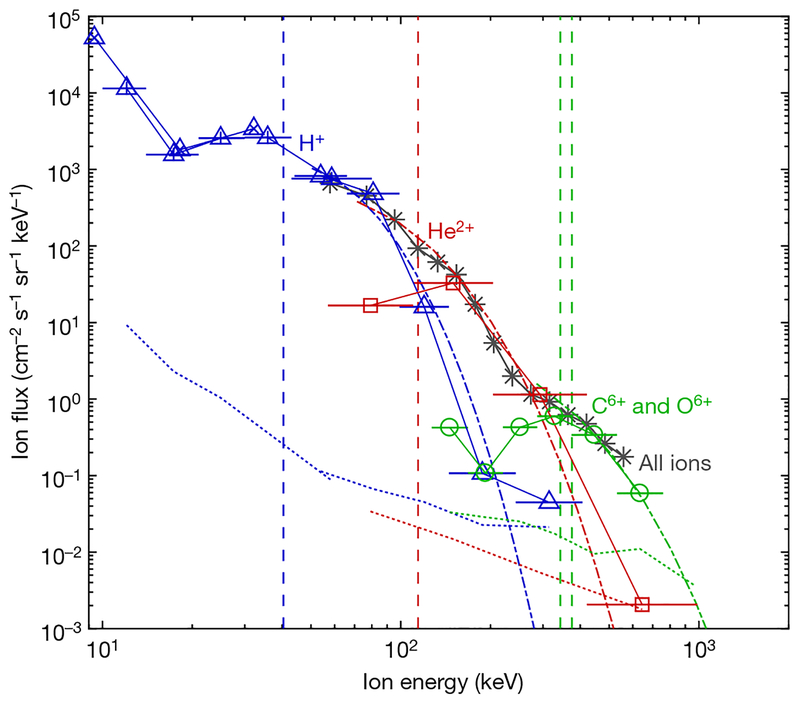
Using these observations, we test the hypothesis that these energetic ions were accelerated in—and subsequently observed after escaping from—a Fermi-type acceleration ‘trap’ between two converging magnetic mirrors, that is, the HFA shock or sheath and Earth’s bow shock or magnetosheath. Following Fermi’s work on particle acceleration in astrophysical plasmas, a relationship can be derived that relates the maximum energy, mass and charge state of an ion for any particular Fermi acceleration trap (equation (2) in Methods). The energy thresholds (Fig. 4, dashed vertical lines) derived from this theoretical relationship, calculated for protons, α particles and heavier CNO ions, agree well with the energy spacing between the observed peaks in the energetic ion spectra from MMS, to within the energy resolution of the EIS instruments.

Fig. 4 |. Comparing observations and theory.

Energy distributions of ions with energies of tens to hundreds of kiloelectronvolts determined from the HPCA, EIS and FEEPS instruments on all four MMS spacecraft for the period 05:30:00–05:31:25 ut are shown as solid lines and markers. Data for heavy (CNO branch) and helium ions are shown as green circles and red squares, respectively. Proton data from HPCA are shown as blue triangles around blue crosses; proton data from the EIS energy-by-time-of-flight (E × TOF) technique are shown as open blue triangles; and proton data from the EIS pulse-height-by-time-of-flight (PH × TOF) technique are shown as blue triangles around blue plus signs. On all EIS data points, the solid horizontal lines show the energy range of each channel. The dotted lines show one-count background levels for the EIS data. EIS PH × TOF data have been cross-calibrated to HPCA and E × TOF data where there is overlap between those instruments. FEEPS data, which do not distinguish between different ion species, are shown as grey lines and asterisks. FEEPS data have had a constant cross-calibration factor of two applied to all energy channels. The dashed vertical lines represent E_max from equation (2) in Methods (the maximum energy in a Fermi acceleration trap of size L) for protons (H⁺, blue), α particles (He²⁺, red) and heavy ions (C⁶⁺ and O⁶⁺, green) using a constant in equation (2) in Methods calculated for 40-keV protons (with mass m = 1 and charge q = 1). The dash-dotted, exponentially decaying lines show numerical solutions for the high-energy tails of the distributions of protons (blue), α particles (red) and O⁶⁺ ions (green) accelerated between the observed HFA and Earth’s bow shock, using the Fermi acceleration model derived in Methods.

We elaborate on this comparison to theory using an independent and more advanced model for ions interacting with an HFA shock or sheath of finite thickness. In this model (Methods), we consider the gyroradius, gyrophase and pitch angle of an ion as it intersects the HFA shock or sheath region, so that finite-gyroradius effects are included whereby only a fraction of ions that intersect this region are reflected and accelerated by it and remain within the acceleration trap. With this model, the energy spectrum of accelerated ions that escape the trap can be estimated for each species, because the distributions also depend on the mass and charge of the ions. Solutions to this model are shown in Fig. 4 (dash-dotted curves) and are in excellent agreement with the observed spectra of the accelerated ions considering the energy resolution and one-count levels of the EIS instruments. FEEPS data, which do not distinguish different ion species, captured the multiple ‘knees’ in the energetic ion distribution, also in excellent agreement with the theoretical spectra for the three ion species.

A third, independent, theoretical test estimates the length scale of a Fermi acceleration trap using the average rate of energy increase and momentum of the accelerated particles and the convergence speed of the trap (Methods). With the observed values of these quantities, we can estimate the length scale between the HFA shock or sheath region and Earth’s bow shock or magnetosheath. If Fermi acceleration between the two was the mechanism of acceleration, then the length scale that we calculate should be comparable to that observed by MMS within the HFA. We find a length scale of 3.2 Earth radii, which is remarkably consistent with that observed by MMS (2.5 Earth radii), especially considering any growth of the HFA over time.

On the basis of the observational evidence and excellent agreement with theory, we conclude that the energetic ions observed by MMS during and after the HFA were accelerated via a first-order Fermi acceleration process between the converging HFA shock or sheath and Earth’s bow shock or magnetosheath. Figure 3 illustrates the conceptual scenario in three cross-sectional snapshots for the observed geometry of the system. State-of-the-art global hybrid models that are capable of simulating HFAs at planetary bow shocks may not capture such acceleration owing to limitations in their system sizes or spatial and temporal resolution at sub-ion scales, particularly at shock fronts, in turbulent sheaths and within simulated HFAs. Our observations link intense bursts of energetic ions in the foreshock and magnetosheath to HFAs, which occur frequently (several per day) upstream of Earth’s bow shock, particularly for fast solar wind with radial IMF^9,18,19. Because HFAs are localized structures, it is possible that spacecraft can observe the particles accelerated by an HFA remotely, without ever observing the HFA itself. Shocks are important sites of particle acceleration^20–24, and our observational confirmation of how ions are accelerated in HFAs has important implications for particle acceleration at supercritical, collisionless shocks in other astrophysical plasmas.

Unlike the traditional understanding of diffusive shock acceleration, in which particles are scattered randomly by kinetic-scale waves propagating on either side of a single shock, the more efficient form of Fermi acceleration that we have identified here involves two large-scale shocks that converge continuously on each other throughout the life of the HFA. The supercritical bow shock interacting with the inhomogeneous solar wind (which is responsible for the formation of the bow shock) results in the formation of the HFA, and HFAs can also form independently of IMF discontinuities^25,26. Thus, the Fermi acceleration of ions—as observed here—occurs autogenously within the ion foreshock, independently of any interaction with an external system (such as an interplanetary shock²⁷). This result provides important insights into and suggests new factors to consider concerning the ‘injection problem’ of shock acceleration²⁸. Furthermore, the newly identified acceleration mechanism may be even more effective in systems with more uniformly planar shocks (such as interplanetary shocks, astrospherical shocks and supernova shocks), in which HFAs can interact with the parent shock for much longer time scales and any curvature of the parent shock is perpetually much greater than the gyroradii of the accelerated ions. The discovery that first-order Fermi acceleration between two shocks occurs autogenously upstream of a supercritical, collisionless shock implies that quasi-parallel foreshock regions (where the interplanetary magnetic field and the normal direction of the bow shock are within about 45° of each other) and the foreshock transients that form within them, such as HFAs, may be important in particle acceleration and the generation of cosmic rays at other astrophysical shocks throughout the cosmos.

METHODS

Data handling.

For this study, MMS data from the following instrument suites were used: FIELDS (electric and magnetic fields and waves)²⁹, EPD (energetic particle distributions)^30,31, FPI (electron and ion plasma distributions and moments)³² and HPCA (ion plasma composition, distributions and moments)³³. All data used for this study were from the standard level-2 data products, which are publicly available at the MMS Science Data Center (https://lasp.colorado.edu/mms/sdc/public).

Multipoint analysis.

Much of the analysis of the HFA examined here follows previous work⁷, with additional multipoint analysis techniques³⁴ and analysis techniques for shock and discontinuity normals³⁵ detailed elsewhere.

First, to determine the normal direction of the IMF discontinuity responsible for the formation of the HFA, cross-product analysis was performed using the B-field observations before and after the HFA³⁵. These vectors were B_pre = (−0.89, −2.24, 0.62) nT from 05:26:25 ut to 05:26:45 ut and B_post = (2.25, 1.14, 1.89) nT from 05:27:35 ut to 05:27:55 ut, both in geocentric solar ecliptic (GSE) coordinates, yielding a discontinuity (current sheet) normal direction of n = (0.70, −0.44, −0.57) in GSE coordinates. This current-sheet orientation satisfies the HFA formation criterion that the convection electric field is pointed back into the current sheet on at least one side.

For the normal direction of the HFA shock, we compared two methods³⁵: shock co-planarity and multi-spacecraft timing analysis. For shock co-planarity, the normal direction of a shock can be determined using the upstream and downstream magnetic-field and velocity vectors:

$${\mathit{n}}_{\text{sh}}=\pm \frac{\left[\left({\mathit{B}}_{\text{up}}-{\mathit{B}}_{\text{dn}}\right)\times \left({\mathit{V}}_{\text{up}}-{\mathit{V}}_{\text{dn}}\right)\right]\times \left({\mathit{B}}_{\text{up}}-{\mathit{B}}_{\text{dn}}\right)}{\left|\left[\left({\mathit{B}}_{\text{up}}-{\mathit{B}}_{\text{dn}}\right)\times \left({\mathit{V}}_{\text{up}}-{\mathit{V}}_{\text{dn}}\right)\right]\times \left({\mathit{B}}_{\text{up}}-{\mathit{B}}_{\text{dn}}\right)\right|}$$

with upstream conditions from 05:27:32 ut to 05:27:34 ut and downstream conditions from 05:27:28.0 ut to 05:27:28.8 ut such that B_up = (2.87, 1.74, 2.31) nT, B_dn = (15.33, 11.56, 21.85) nT, V_up = (−447.0, 19.4, 13.2) km s⁻¹ and V_dn = (−317.5, 1.0, −111.6) km s⁻¹. With these values, n_sh = (0.85, −0.02, −0.53) in GSE coordinates. Using the four-point, multi-spacecraft timing, the speed of the shock V_sh and the shock normal direction n_sh can be determined using

$$\left[\begin{array}{l}{\mathit{r}}_{12}\hfill \\ {\mathit{r}}_{13}\hfill \\ {\mathit{r}}_{14}\hfill \end{array}\right]\frac{1}{V_{\text{sh}}}\left[\begin{array}{l}{n}_{\text{sh},x}\hfill \\ n_{\text{sh},y}\hfill \\ n_{\text{sh},z}\hfill \end{array}\right]=\left[\begin{array}{c}{t}_{12}\\ t_{13}\\ t_{14}\end{array}\right]$$

where r_xy is the distance vector between spacecraft x and y and t_xy is the timing difference of the same boundary observed by both spacecraft. Using this with the four-point observations of MMS crossing the HFA shock, the shock normal direction is calculated as n_sh = (0.84, −0.44, −0.31) in GSE coordinates, which is generally consistent with the result from co-planarity analysis, the speed as V_sh = −134 km s⁻¹, which when transformed into the solar-wind frame yields a speed of about 360 km s⁻¹ upstream (towards the Sun). As a simple, independent check, these shock normal directions can also be compared to an idealized solution in which the velocity tangential to the shock is conserved, meaning that the difference in velocity from upstream to downstream is approximately along the shock normal. With V_up and V_dn as listed above, this yields a shock normal of n_sh = (0.72, −0.10, −0.69), which again is a rough approximation and is generally in the same sense as the more accurate forms above.

The size of the HFA is calculated using the normalized tracking speed of the HFA along the bow shock⁷. With this and the observed time of transit through the HFA, a size of 2.51 Earth radii is calculated. Finally, the expansion speed of the HFA is calculated using the boundary motion of the upstream and downstream boundaries of the HFA⁷, yielding an expansion speed of about 108 km s⁻¹.

Conceptual model for the Fermi acceleration trap.

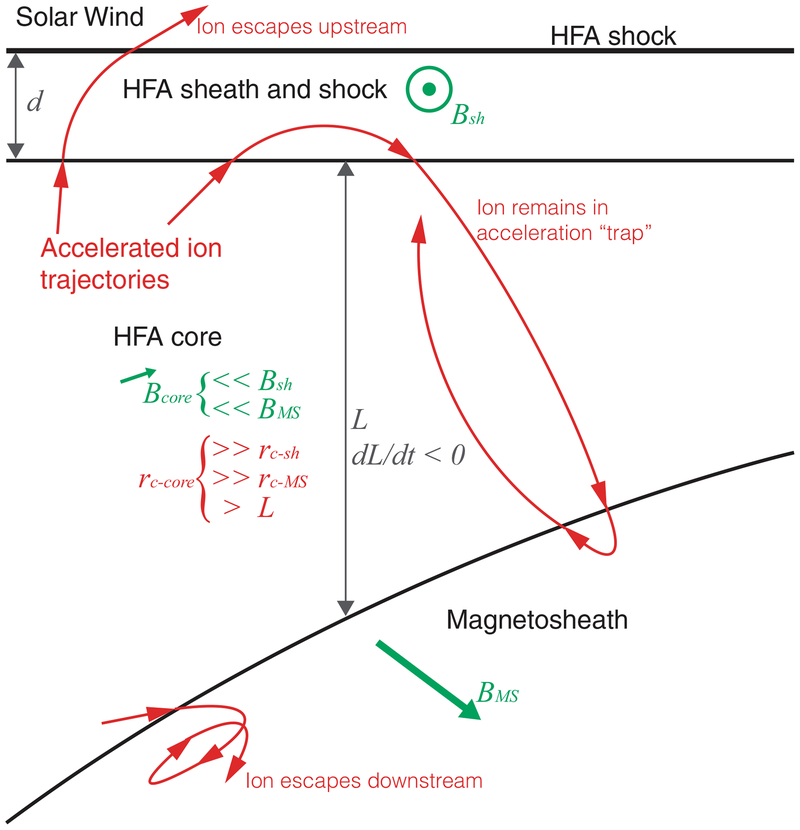
Figure 3 and Extended Data Fig. 2 illustrate the conceptual model of the Fermi acceleration trap that we worked with for this study. In essence, ions within the very low-field-strength core of the HFA can reflect back and forth between the regions of higher field strength at the HFA sheath or shock and Earth’s bow shock or magnetosheath. Although the local bow shock may be destroyed in an effective manner adjacent to the HFA, on the basis of simulations there is still a strong magnetic gradient at the transition from the core of the HFA (very low field strength) into the magnetosheath plasma. This magnetic gradient can serve as a mirror point and reflect particles in the acceleration trap. A key aspect here is that in the very low-field-strength field (at most 1 nT) in the core of the HFA, ions with energies of tens of kiloelectronvolts to more than 100 keV have gyroradii that are larger than the length scale of the trap L. Thus, the ion trajectories are essentially ballistic within the core. However, the fields on either side of the HFA core, in the HFA sheath or shock and at Earth’s bow shock or magnetosheath are much stronger, roughly 10–30 nT. Thus, on either side of the HFA core, the ions will experience a strong magnetic gradient that is capable of reflecting a subset of the incident particles (depending on their gyrophase and pitch angle, as we account for in the model that is described below). Because the HFA sheath or shock is converging continuously on Earth’s bow shock or magnetosheath (dL/dt < 0), this establishes ideal conditions for first-order Fermi acceleration to accelerate some subset of the particles within the trap. Only a small subset of the particles in our model acceleration trap will remain trapped for a long time and attain very high energies. However, because there are exponentially more particles at lower energies, even if a small fraction of these particles are efficiently accelerated up to several hundred kiloelectronvolts in the trap, the result can be quite drastic compared to the usual population at those energies (typically at unobservable or near instrument-background levels). Considering that the ions might experience additional acceleration at the HFA shock or due to reflections from waves within the system adds to the efficiency of the system’s acceleration effect.

Maximum energy in the Fermi acceleration trap.

From Fermi¹⁴, a formula was previously derived¹⁵ to calculate an accelerated ion’s energy at some time E(t), using its initial energy E₀ and the ratio of the initial length scale L₀ of the Fermi acceleration trap (the distance between converging magnetic mirror points) to the length at the same time L(t):

$$E(t)=E_0{\left[\frac{L_0}{L(t)}\right]}^{2/3}$$ (1)

This equation assumes that the speed of the ion is much greater than that of the convergence of the trap (v ≫ U), which enables higher-order terms to be excluded. Considering that we are studying ions with kinetic energies of about 100 keV to 1 MeV, their speeds of thousands of kilometres per second far exceed the converging speed of about 300 km s⁻¹, and thus the assumption is valid. We also assume that the initial seed population consists of the suprathermal ions in the quasi-parallel foreshock, with energies in the range of tens of kiloelectronvolts to about 150 keV, which also satisfy the required condition. Next, we make two further assumptions: first, that the initial energy of the accelerated ion is proportional to the kinetic energy of the solar wind, $E_0\propto m{V}_{\text{sw}}^2/2$; and second, that the minimum size of the Fermi acceleration trap that can effectively accelerate an ion is proportional to the ion’s gyroradius, L_min ∝mv_max/(qB), where m the mass of the ion, V_sw is the solar-wind speed, q is the ion’s charge state, B is the magnetic field strength and v_max is the limit of the ion’s velocity assuming it can escape the Fermi acceleration trap once its gyroradius is some substantial fraction of the trap length scale. Using the assumptions with equation (1), with $E(t)=E_{\text{max}}=m{v}_{\text{max}}^2/2$ and L(t) = L_min, we can easily derive a relationship between the expected maximum energy E_max, mass and charge state of an escaping ion for any particular Fermi acceleration trap (that is, L₀, B and V_sw are constants for all ion species in the trap):

$$\frac{E_{\text{max}}^2}{mq}=\text{constant}$$ (2)

Accelerated ion energy distribution in the Fermi acceleration trap.

Because the accelerated ion gyroradii are very large compared to the HFA boundary, during each bounce in the Fermi acceleration trap between the bow shock and HFA shock, a fraction of ions can escape the trap. To obtain the fraction of ions that escape the trap, we develop a new model. The field strength at the HFA boundary is typically much stronger than in the core, so the magnetic field (B) at the boundary is approximately along the boundary surface to maintain divergenceless B. This is illustrated in Extended Data Fig. 3.

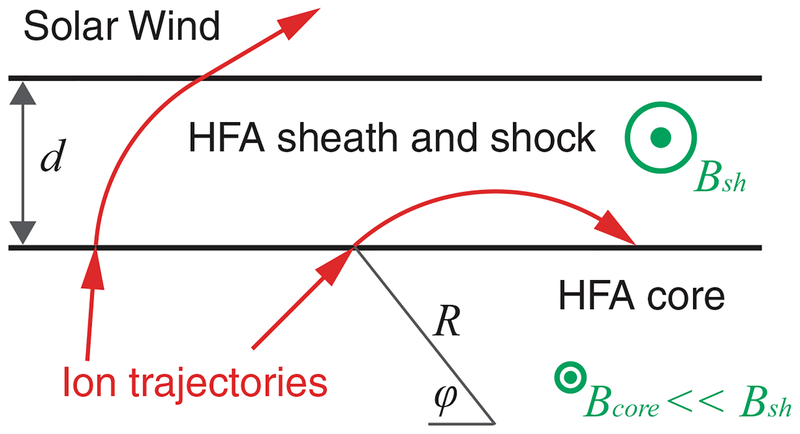
How far into a HFA sheath or shock boundary of thickness d an ion can penetrate is determined by p = R − Rsin(φ), with φ ∈ (−π/2, π/2], where R is the ion’s gyroradius and φ is the gyrophase when the ion enters the HFA boundary. When P > d, that is, sin(φ) < 1 − d/R, ions escape through the HFA boundary; but for P < d ions are reflected at the boundary and can remain within the Fermi acceleration trap. For a certain R (or certain energy and pitch angle) and assuming a gyrotropic distribution, the fraction of leaked ion flux is

$$X=\frac{1}{2}\underset{-\pi /2}{\overset{{\phi }_c}{\int }}\text{cos}(\phi )\text{d}\phi =\frac{\text{sin}\left({\phi }_{\text{c}}\right)+1}{2}=1-\frac{d}{2R}$$

where φ_c is the critical gyrophase for escape, the cosine function results from the flux of ions that move towards the boundary being proportional to v_n = v_⊥cos(φ), and the factor of 1/2 is from normalization.

Next, we can calculate the fraction of leaked ion flux as a function of pitch angle θ. For any ion speed v, ions can leak out only when the pitch angle allows for R > d, so there is a critical pitch angle: sin(θ_c) = qBd/(mv). Assuming an isotropic pitch angle distribution within the trap, the fraction of leaked ion flux as a function of pitch angle is³⁶

$$X=\frac{4}{\pi }\underset{{\theta }_c}{\overset{\pi /2}{\int }}\left[1-\frac{\text{sin}\left({\theta }_{\text{c}}\right)}{2\text{ sin}(\theta )}\right]{\text{sin}}^2(\theta )\text{d}\theta =1-\frac{2{\theta }_{\text{c}}}{\pi }$$

With this function, X linearly decreases from 1 to 0 as θ_c increases from 0 to π/2. Note that θ_c is a function of charge, mass and momentum.

This model can now be used to calculate the energy spectra of ions accelerated within the Fermi trap. Here, we make the assumption that the ions are always reflected by the bow shock without any substantial energy gain; that is, we focus on how multiple reflections at the converging HFA shock affect the ion energy spectrum when considering this model for accelerated ion escape.

After some number n of reflections within the Fermi acceleration trap, the speed of an accelerated ion is

$$v_n^2=v_{n-1}^2+4v_{n-1}U\text{cos}(\alpha )+4U^2$$

where U is the convergence speed of the HFA shock upon the bow shock and α is the angle between the injection speed and the boundary normal. Assuming an isotropic particle distribution, on average

$$v_n^2=v_{n-1}^2+\frac{8}{3}{v}_{n-1}U+4U^2$$

Next, the probability of an ion reflecting n times within the trap is

$$P_n=\prod _{i=0}^{n-1}\left(1-X_i\right)=\prod _0^{n-1}\frac{2{\theta }_{ci}}{\pi }$$

The normalized ion distribution function f can be approximated as f ≈ ∂P/∂v, and the result using this model must be calculated numerically. Guided by the MMS observations, we used d = 1,000 km and U = 220 km s⁻¹ over n = 20 bounces to obtain the distributions shown in Fig. 4.

We compared these results with those when also including escape on the downstream side (away from the Sun) of the bow shock. To do this, we used a model³⁷ to include loss of particles into the magnetosheath. In this model, the probability of escape to the sheath is P = 4U_sh/v, where U_sh is the speed of plasma in the magnetosheath (around 100 km s⁻¹) and v is the particle velocity, such that most particles cross the bow shock many times before escaping downstream. For ions with energies of more than about 100 keV, the probability of escape from the trap is much, much higher in the model developed here than for the bow-shock model. The bow-shock-escape model results in a power-law distribution of the escaping particles, and when included with the model developed here contributes a negligible amount of loss that still results in an exponential distribution for the accelerated ions escaping from the trap, like those shown in Fig. 4 for the three different ion species.

Estimating the length of the Fermi acceleration trap.

Using the observed energy gain of the accelerated ions, we can estimate the length scale between the HFA shock and bow shock assuming that the ions were accelerated within a first-order Fermi trap between those two boundaries. With the average energy gain from a particle bouncing between the two converging shocks and assuming isotropic scattering, the average energy gain of the particle is 〈ΔE〉 = 4mvU/3. Using this, along with the particle’s bounce frequency in the trap, f_b = 〈v〉/(2L) = v/(4L), where 〈v〉 is the average velocity accounting for pitch angle and L is the length scale of the trap, we can approximate the average rate of energy gain:

$$\frac{\text{d}E}{\text{d}t}=\frac{m{v}^{2}U}{3L}$$ (3)

Using α particles (which allow multiple data points over a broad energy range, unlike protons, and an exact mass, unlike the CNO ions) with an energy of about 200 keV, we can estimate the length scale using the following observed quantities: dE/dt ≈ 220 keV/(180 s) = 1.96 × 10⁻¹⁶ J s⁻¹, v ≈ 3 × 10⁶ m s⁻¹ (for a 200-keV α particle), U ≈ 200 km s⁻¹ (approximation of HFA shock expansion speed plus motion of the bow shock towards the Sun from multi-spacecraft timing during the crossing) and m = 6.6951 × 10⁻²⁷ kg. Using these values in equation (3) yields a length scale of about 20,516 km = 3.2 Earth radii, which is consistent with the HFA scale observed by MMS (about 2.5 Earth radii). Note that this is only an order-of-magnitude scale comparison: the size of the HFA observed by MMS depends on where and how the HFA passed over the spacecraft, whereas the length scale calculated from theory is the most effective or representative length within the acceleration trap between the HFA and the bow shock. We expect the two to be of the same order for scale (that is several Earth radii), which is exactly as we have calculated here.

Code availability.

All code used to analyse the MMS data in this study is based on the publicly available SPEDAS tools (http://themis.ssl.berkeley.edu/software.shtml). The code and theoretical results used for model–data comparisons will be made available on request to the corresponding author.

Data availability.

All MMS data used for this study are publicly available via the MMS Science Data Center at https://spdf.gsfc.nasa.gov/pub/data/mms.

Extended Data

Extended Data Fig. 1 |. Solar-wind ion species observed by MMS HPCA.

a, Magnetic-field vector and strength from MMS-2. b–f, FEEPS total energetic ion (b) and HPCA ion (c–f) composition flux energy spectra (omni-directional) combined from all four spacecraft (MMS-X). HPCA observed many fewer He⁺ ion than He²⁺ ions (α particles) and no O⁺ ions (all zero counts despite energy channels up to about 38 keV) at E > 10 keV during the observation of the energetic ions between the HFA and the magnetosheath. The absence of low-charge-state oxygen in HPCA data (O⁺, O²⁺) indicates that the energetic CNO ions observed by EIS were at a high charge state. This confirms that the accelerated ions were high-charge-state ions (q/m ≥ 2) and thus of solar-wind origin. Like FEEPS, HPCA also shows that the most energetic beam of α particles and protons is streaming away from the HFA.

Extended Data Fig. 2 |. Conceptual model of the Fermi acceleration trap created by an HFA evolving along Earth’s bow shock.

At the top of this schematic is the solar wind, which is the ‘upstream’ direction to which some ions within the trap might escape. The region at the bottom of the schematic is the magnetosheath plasma, which is the ‘downstream’ direction to which some ions might also escape. The HFA sheath and shock region, with some finite thickness d, lies between the two horizontal black lines. The HFA core region lies between the HFA sheath/shock and magnetosheath regions. The HFA core has a characteristic length scale L and is perpetually converging on the magnetosheath such that dL/dt < 0 at any point along the core. Critical to the model (and as observed and simulated in HFAs), the magnetic-field strength within the HFA core (less than 1 nT) is much, much weaker than that in the HFA sheath or shock and in Earth’s bow shock or magnetosheath (more than 10 nT); this geometry ensures that some subset of ions within the HFA core can remain trapped between the two regions of higher field strength, owing to differences in the ion gyroradii (r_c) in the different regions. We note that the orientations of the magnetic fields are sketched arbitrarily here. Three example ion trajectories are sketched: (i) escaping to the solar wind; (ii) escaping to the magnetosheath; and (iii) remaining trapped within the HFA core.

Extended Data Fig. 3 |. Simplified model of the HFA.

This model includes a finite thickness of the HFA sheath (that is, shocked plasma) and shock d, which is used to determine the energy spectra of ions accelerated within the trap considering losses through the boundary. In this picture, the HFA sheath and shock fall between the two horizontal black lines, with the HFA core being a larger region below this and the solar wind being the region above this. Only ions at particular energies, pitch angles and gyrophase can remain trapped in the Fermi acceleration trap between Earth’s bow shock or magnetosheath and the HFA shock. For example, the two ion trajectories shown are at the same energy but different gyrophase when they enter the HFA sheath with enhanced magnetic field strength: the rightmost ion is reflected and can continue to be accelerated, whereas the leftmost ion escapes the trap and is lost to the solar wind.